Abstract
We revisit the question of constructing public-key encryption and signature schemes with security in the presence of bounded leakage and tampering memory attacks. For signatures we obtain the first construction in the standard model; for public-key encryption we obtain the first construction free of pairing (avoiding non-interactive zero-knowledge proofs). Our constructions are based on generic building blocks, and, as we show, also admit efficient instantiations under fairly standard number-theoretic assumptions.
The model of bounded tamper resistance was recently put forward by Damgård et al. (Asiacrypt 2013) as an attractive path to achieve security against arbitrary memory tampering attacks without making hardware assumptions (such as the existence of a protected self-destruct or key-update mechanism), the only restriction being on the number of allowed tampering attempts (which is a parameter of the scheme). This allows to circumvent known impossibility results for unrestricted tampering (Gennaro et al., TCC 2010), while still being able to capture realistic tampering attacks.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Motivated by the proliferation of memory tampering attacks and fault injection [11, 13, 46], a recent line of research—starting with the seminal work of Bellare and Kohno [8] on the related-key attack (RKA) security of blockciphers—aims at designing cryptographic primitives that provably resist such attacks. Briefly, memory tampering attacks allow an adversary to modify the secret key of a targeted cryptographic scheme, and later violate its security by observing the effect of such changes at the output. In practice such attacks can be implemented by several means, both in hardware and software.
This paper is focused on designing public-key primitives—i.e., public-key encryption (PKE) and signature schemes—with provable security guarantees against memory tampering attacks. In this setting, the modified secret key might be the signing key of a certification authority or of an SSL server, or the decryption key of a user. Informally, security of a signature scheme under tampering attacks can be cast as follows. The adversary is given a target verification key \( vk \) and can observe signatures of adaptively chosen messages both under the original secret key \( sk \) and under related keys \( sk '= T( sk )\), derived from \( sk \) by applying efficient tampering functions \(T\) chosen by the adversary; the goal of the adversary is to forge a signature on a “fresh message” (i.e., a message not asked to the signing oracle) under the original verification key. Tamper resistance of PKE schemes under chosen-ciphertext attacks (CCA) can be defined similarly, the difference being that the adversary is allowed to observe decryption of adaptively chosen ciphertexts under related secret keys \( sk '\), and its goal is now to violate semantic security.
Unrestricted tampering. The best we could hope for would be, of course, to allow the adversary to make any polynomial number of arbitrary, efficiently computable, tampering queries. Unfortunately, this type of “unrestricted tampering” is easily seen to be impossible without making further assumptions, as observed for the first time by Gennaro et al. [29]. The attack of [29] is simple enough to recall it here. The first tampering attempt defines \( sk '_1\) to be equal to \( sk \) with the first bit set to zero, so that verifying a signature under \( sk '_1\) essentially allows to learn the first bit \(b_1\) of the secret key with overwhelming probability. The second tampering attempt defines \( sk '_2\) to be equal to \( sk \) with the second bit set to zero, and with the first bit equal to \(b_1\), and so on. This way each tampering attempt can be exploited to reveal one bit of the secret key, yielding a total security breach after \(s(\kappa )\) queries, where \(s(\kappa )\) is the bit-length of the secret key as a function of the security parameter.Footnote 1
A possible way out to circumvent such an attack is to rely on the so-called self-destruct feature: Find a way how to detect tampering with high probability, and completely erase the memory or “blow-up the device” whenever tampering is detected. While this is indeed a viable approach, it has some shortcomings (at it can, e.g., be exploited for carrying out denial-of-service attacks), and so finding alternatives is an important research question. One natural such alternative is to simply restrict the power of the tampering functions \(T\), in such a way that carrying out the above attack simply becomes impossible. This approach led to the design of several public-key primitives resisting an arbitrary polynomial number of restricted tampering attempts. All these schemes share the feature that the secret key belongs to some finite field, and the set of allowed modifications consist of all linear or affine functions, or all polynomials of bounded degree, applied to the key [7, 10, 54].
Bounded tampering. Unfortunately, the approach of restricting the tampering class only offers a partial solution to the problem; the main reason for this is that it is not a priori clear how the above mentioned algebraic relations capture realistic tampering attacks (where, e.g., a chip is shot with a laser). Motivated by this shortcoming, in a recent work, Damgård et al. [18] suggested the model of bounded tampering, where one assumes an upper-bound \(\tau \in \mathbb {N}\) on the total number of tampering attempts the adversary is allowed to ever make; apart from this, and from the fact that the tampering functions \(T\) should be efficiently computable, there is no further restriction on the adversarial tampering. Arguably, such form of tamper-proof security is sufficient to capture realistic attacks in which tampering might anyway destroy the device under attack or it could be detected by auxiliary hardware countermeasures; moreover, this model allows to analyze the security of cryptographic primitives already “in the wild,” without the need to modify the implementation to include, e.g., a self-destruct feature.
An important parameter in the model of bounded tampering is the so-called tampering rate \(\rho (\kappa ) := \tau (\kappa )/s(\kappa )\) defined to be the ratio between the number of allowed tampering attempts and the size \(s(\kappa )\) of the secret key in bits. The attack of Gennaro et al. [29] shows that necessarily \(\rho (\kappa ) \le 1 - 1/p(\kappa )\) for some polynomial \(p(\cdot )\). The original work of [18] shows how to obtain signature schemes and PKE schemes tolerating linear tampering rate \(\rho (\kappa ) = O(1/\kappa )\). However, the signature construction relies on the so-called Fiat–Shamir heuristic [28], whose security can only be proven in the random oracle model; the PKE construction can be instantiated in the standard model, but requires an untamperable common reference string (CRS), being based on (true simulation-extractable) non-interactive zero-knowledge (NIZK) [20].
In a follow-up work [19], the same authors show that resilience against bounded tampering can be obtained via a generic transformation yielding tampering rate \(\rho (\kappa ) = O(1/\root 3 \of {\kappa ^2})\); however, the transformation only gives a weaker form of security against non-adaptive (or semi-adaptive [19]) tampering attacks.
1.1 Our Contribution
In this work we improve the current state of the art on signature schemes and PKE schemes provably resisting bounded memory tampering. In the case of signatures, we obtain the first constructions in the standard model based on generic building blocks; as we argue, this yields concrete signature schemes tolerating tampering rate \(\rho (\kappa ) = O(1/\kappa )\) under standard complexity assumptions such as the Symmetric External Diffie-Hellman (SXDH) [12, 52] and the Decisional Linear (DLIN) [35, 53] assumptions. In the case of PKE, we obtain a direct, pairing-free, construction based on certain hash-proof systems [17], yielding concrete PKE schemes tolerating tampering rate \(\rho (\kappa ) = O(1/\kappa )\) under a particular instantiation of the Refined Subgroup Indistinguishability (RSI) assumption [45].
More precisely, we show that already existing schemes can be proved secure against bounded tampering. We do not view this as a limitation of our result, as it confirms the perspective that the model of bounded tamper resilience allows to make statements about cryptographic primitives already used “in the wild” (that might have already been implemented and adopted in applications). Additionally, our security arguments are non-trivial, requiring significant modifications to the original proofs (more on this below). In what follows we explain our contributions and techniques more in details. We refer the reader to Table 1 for a summary of our results and a comparison with previous work.
Signatures. We prove that the leakage-resilient signature scheme by Dodis et al. [20] is secure against bounded tampering attacks. The scheme of [20] satisfies the property that it remains unforgeable even given bounded leakage on the signing key. The main idea for showing security against bounded tampering, is to reduce tampering to leakage. Notice that this is non-trivial, because in the tampering setting the adversary is allowed to see polynomially many signatures corresponding to each of the tampered secret keys (which are at most \(\tau \)), and this yields a total amount of key-dependent information which is much larger than the tolerated leakage.
We now explain how to overcome this obstacle. The scheme exploits a so-called leakage-resilient hard relation \(R\); such a relation satisfies the property that, given a statement y generated together with a witness x, it is unfeasible to compute a witness \(x^*\) for \((x^*,y)\in R\); moreover the latter holds even given bounded leakage on x. The verification key of the signature scheme consists of a random y, while the secret key is equal to x, where (x, y) is a randomly generated pair belonging to the relation \(R\). In order to sign a message m, one simply outputs a non-interactive zero-knowledge proof of knowledge \(\pi \) of x, where the message m is used as a label in the proof. Verification of a signature can be done by verifying the accompanying proof.
In the security proof, by the zero-knowledge property, we can replace real proofs with simulated proofs. Moreover, by the proof of knowledge property, we can actually extract a valid witness \(x^*\) for \((x^*,y)\) from the adversarial forgery \(\pi ^*\); note that, since the forger gets to see simulated proofs, the extractability requirement must hold even after seeing proofs generated via the zero-knowledge simulator. Finally, we can transform a successful forger for the signature scheme into an adversary breaking the underlying leakage-resilient relation; the trick is that the reduction can leak the statement \(y'\) corresponding to any tampered witness \(x' = T(x)\), which allows to simulate an arbitrary polynomial number of signature queries corresponding to \(x'\) by running several independent copies of the zero-knowledge simulator upon input \(y'\). Thus bounded tamper resilience follows by bounded leakage resilience.
A subtle technicality in the above argument is that the statement \(y'\) must be efficiently computable as a function of \(x'\). We call a relation \(R\) satisfying this property a complete relation. As we define it, completeness additionally requires that any derived witness \(x' = T(x)\) is a witness for a valid statement \(y'\) (i.e., \((x',y')\in R\)); importantly this allows us to argue that simulated proofs are always for true statements, which leads to practical instantiations of the scheme. When we instantiate the signature scheme, of course, we need to make sure that the underlying relation meets our completeness requirement. Unfortunately, this is not directly the case for the constructions given in [20], but, as we show, such a difficulty can be overcome by carefully twisting the instantiation of the underlying relations.
Public-key encryption. Next, we prove that the PKE scheme by Qin and Liu [49] is secure against bounded tampering. The scheme is based on a variant of the classical Cramer-Shoup paradigm for constructing CCA-secure PKE [16, 17]. Specifically, the PKE scheme combines a universal hash-proof system (HPS) together with a one-time lossy filter (OTLF) used to authenticate the ciphertext; the output of a randomness extractor is then used in order to mask the message in a one-time pad fashion. Since the OTLF is unkeyed, the secret key simply consists of the private evaluation key of the HPS, which makes it easier to analyze the security of the PKE scheme in the presence of memory tampering. The bulk of our proof is, indeed, to show that HPS with certain parameters already satisfy bounded tamper resilience.
More in details, every HPS is associated to a set \(\mathcal {C} \) of ciphertexts and a subset \(\mathcal {V} \subset \mathcal {C} \) of so-called valid ciphertexts, together with (the description of) a keyed hash function with domain \(\mathcal {C} \). The hash function can be both evaluated privately (using a secret evaluation key) and publicly (on ciphertexts in \(\mathcal {V} \), and using a public evaluation key). The main security guarantee is that for any \(C\in \mathcal {C} \setminus \mathcal {V} \) the output of the hash function upon input C is unpredictable even given the public evaluation key. In the construction of [49] a ciphertext consists of an element \(C\in \mathcal {V} \), from which we derive an hash value K which serves for two purposes: (i) To extract a random pad via a seeded extractor, used to mask the plaintext; (ii) To authenticate the ciphertext by producing an encoding \(\varPi \) of K via the OTLF. The decryption algorithm first derives the value K using the secret evaluation key for the HPS, and then it uses this value to unmask the plaintext provided that the value \(\varPi \) can be verified correctly (otherwise decryption results in \(\bot \)).
In the reduction, the OTLF encoding will be programmed in such a way that, for all ciphertexts asked to the decryption oracle, the encoding is an injective function. This implies that, in order to create a ciphertext with a correct encoding \(\varPi \), one has to know the underlying hash value K. To prove (standard) CCA security, one argues that all decryption queries with values \(C\in \mathcal {V} \) do not reveal any additional information about the secret key, since the corresponding value K could be computed via the public evaluation procedure; as for decryption queries with values \(C\in \mathcal {C} \setminus \mathcal {V} \), the corresponding value K is unpredictable, and therefore the decryption oracle will output \(\bot \) with overwhelming probability which, again, does not reveal any additional information about the secret key.
The scenario in the case of tampering is more complicated. Consider a decryption oracle instantiated with a tampered secret key \( sk '= T( sk )\). A decryption query containing a value \(C\in \mathcal {V} \) might now reveal some information about the secret key; however, as we show, this information can be simulated by leaking the public key \( pk '\) corresponding to \( sk '\). Decryption queries containing values \(C\in \mathcal {C} \setminus \mathcal {V} \) are harder to simulate. This is because the soundness property of the HPS only holds for a uniformly chosen evaluation key, while \( sk '\), clearly, is not uniform. To overcome this obstacle we distinguish two cases:
-
In case the value \(T( sk )\) has low entropy, such a value does not reveal too much information on the secret key, and thus, at least intuitively, even if the decryption does not output \(\bot \) the resulting plaintext should not decrease the entropy of the secret key by too much;
-
In case the value \(T( sk )\) has high entropy, we argue that it is safe to use this key within the HPS, i.e. we show that the soundness of the HPS is preserved as long as the secret key hash high entropy (even if it is not uniform).
With the above in mind, the security proof is similar to the ones in [44, 49].
Trading tampering and leakage. Since our security arguments essentially reduce bounded tampering to bounded leakage (by individuating a short secret-key-dependent hint that allows to simulate polynomially many tampering queries for a given modified key), the theorems we get show a natural tradeoff between the obtained bounds for leakage and tamper resistance.
In particular, our results nicely generalizes previous work, in that we obtain the same bounds as in [20, 49] by plugging \(\tau = 0\) in our theorem statements.
1.2 Related Work
Bounded leakage. The signature scheme of Dodis et al. [20] generalizes and improves a previous construction by Katz and Vaikuntanathan [39]. Similarly, the PKE construction by Qin and Liu builds upon the seminal work of Naor and Segev [44]; the scheme was further improved in [50].
Related-key security. Related-key security was first studied in the context of symmetric encryption [2, 3, 8, 30, 43]. With time a number of cryptographic primitives with security against related-key attacks have emerged, including pseudorandom functions [1, 4, 6, 40], hash functions [31], identity-based encryption [7, 10], public-key encryption [7, 10, 42, 54], signatures [7, 9, 10], and more [15, 37, 51].
All the above works achieve security against an unbounded number of restricted tampering attacks (typically, algebraic relations). Kalai, Kanukurthi, and Sahai [38], instead, show how to achieve security against unrestricted tampering without self-destruct, by assuming a protected mechanism to update the secret key of certain public-key cryptosystems (without modifying the corresponding public key).
Non-malleable codes. An alternative approach to achieve tamper-proof security of arbitrary cryptographic primitives against memory tampering is to rely on so-called non-malleable codes. While this solution yields security against an unbounded number of tampering queries, it relies on self-destruct and moreover it requires to further assume that the tampering functions are restricted in granularity (see, e.g., [22, 25, 41]) and/or computational complexity [5, 26, 37].
Tamper-proof computation. A related line of work (starting with [27, 36]), finally, aims at constructing secure compilers protecting against tampering attacks targeting the computation carried out by a cryptographic device (typically in the form of boolean and arithmetic circuits).
2 Preliminaries
2.1 Notation
Notation. For \(a,b \in \mathbb {R}\), we let \([a,b]=\{x\in \mathbb {R}:a\le x\le b\}\); for \(a\in \mathbb N\) we let \([a] = \{1,2,\ldots ,a\}\). If x is a string, we denote its length by |x|; if \(\mathcal {X}\) is a set, \(|\mathcal {X}|\) represents the number of elements in \(\mathcal {X}\). When x is chosen randomly in \(\mathcal {X}\), we write  . When \(\mathsf {A}\) is an algorithm, we write
. When \(\mathsf {A}\) is an algorithm, we write  to denote a run of \(\mathsf {A}\) on input x and output y; if \(\mathsf {A}\) is randomized, then y is a random variable and \(\mathsf {A}(x;r)\) denotes a run of \(\mathsf {A}\) on input x and randomness r. An algorithm \(\mathsf {A}\) is probabilistic polynomial-time (PPT) if \(\mathsf {A}\) is randomized and for any input \(x,r\in \{0,1\}^*\) the computation of \(\mathsf {A}(x;r)\) terminates in at most \( poly (|x|)\) steps.
to denote a run of \(\mathsf {A}\) on input x and output y; if \(\mathsf {A}\) is randomized, then y is a random variable and \(\mathsf {A}(x;r)\) denotes a run of \(\mathsf {A}\) on input x and randomness r. An algorithm \(\mathsf {A}\) is probabilistic polynomial-time (PPT) if \(\mathsf {A}\) is randomized and for any input \(x,r\in \{0,1\}^*\) the computation of \(\mathsf {A}(x;r)\) terminates in at most \( poly (|x|)\) steps.
Throughout the paper we let \(\kappa \in \mathbb N\) denote the security parameter. We say that a function \(\nu : \mathbb N\rightarrow \mathbb {R}\) is negligible in the security parameter \(\kappa \) if \(\nu (\kappa ) = \kappa ^{-\omega (1)}\). For two ensembles \(\mathcal {X} = \{\mathbf {X}_\kappa \}_{\kappa \in \mathbb N}\) and \(\mathcal {Y}=\{\mathbf {Y}_\kappa \}_{\kappa \in \mathbb N}\), we write \(\mathcal X \equiv \mathcal Y\) if they are identically distributed, \(\mathcal X \approx _{s} \mathcal Y\) to denote that the corresponding distributions are statistically close, and \(\mathcal X \approx _c \mathcal Y\) to denote that the two ensembles are computationally indistinguishable.
Languages and relations. A decision problem related to a language \(L\subseteq \{0,1\}^*\) requires to determine if a given string y is in \(L\) or not. We can associate to any \( NP \)-language \(L\) a polynomial-time recognizable relation \(R\subseteq \{0,1\}^{*}\times \{0,1\}^{*}\) defining \(L\) itself, i.e. \(L=\{y:\exists x\text { s.t. }(x,y)\in R\}\) for \(|x|\leqslant poly(|y|)\). The string y is called theorem, and the string x is called a witness for membership of \(y\in L\).
Random variables. The min-entropy of a random variable \(\mathbf {X}\), defined over a set \(\mathcal {X}\), is \(\mathbb {H}_\infty (\mathbf {X}) := -\log \max _{x\in \mathcal {X}}{\mathbb {P}\left[ \mathbf {X} = x\right] }\), and it measures how \(\mathbf {X}\) can be predicted by the best (unbounded) predictor. The average conditional min-entropy of a random variable \(\mathbf {X}\) given a random variable \(\mathbf {Y}\) and conditioned on an event E is defined as  . We rely on the following basic facts.
. We rely on the following basic facts.
Lemma 1
([21]). Let \(\mathbf {X},\mathbf {Y}\) and \(\mathbf {Z}\) be random variables. If \(\mathbf {Y}\) has at most \(2^\ell \) possible values, then \(\widetilde{\mathbb {H}}_\infty (\mathbf {X}|\mathbf {Y},\mathbf {Z}) \geqslant \widetilde{\mathbb {H}}_\infty (\mathbf {X},\mathbf {Y}|\mathbf {Z}) - \ell \geqslant \widetilde{\mathbb {H}}_\infty (\mathbf {X}|\mathbf {Z}) - \ell \).
Lemma 2
Let \(\mathbf {X},\mathbf {Y}, \mathbf {Z}\) be random variables such that \(\mathbf {Y}=f(\mathbf {X},\mathbf {Z})\) for an efficiently computable function f. Then \(\widetilde{\mathbb {H}}_\infty (\mathbf {X}|\mathbf {Y},\mathbf {Z},E) \geqslant \widetilde{\mathbb {H}}_\infty (\mathbf {X}|\mathbf {Z}, E) - \beta \), where the event E is defined as \(\{\forall z:~\mathbb {H}_\infty (\mathbf {Y}|\mathbf {Z} = z) \leqslant \beta \}\).
Proof
Let \(\mathsf {A}\) be the best predictor for \(\mathbf {X}\), given \(\mathbf {Y}\) and \(\mathbf {Z}\) and conditioned on the event E. Consider the predictor \(\mathsf {A}'\) that upon input \(\mathbf {Z}\) first samples an independent copy \(\mathbf {X}'\) of the random variable \(\mathbf {X}\) and then runs \(\mathsf {A}\) upon input \(f(\mathbf {X}',\mathbf {Z})\). Note that the event E holds for the inputs given to \(\mathsf {A}'\), therefore the probability that \(f(\mathbf {X}',\mathbf {Z})= f(\mathbf {X},\mathbf {Z})\) is bounded above by \(2^{-\beta }\). This implies the lemma. \(\square \)
2.2 Public-Key Encryption
A public-key encryption (PKE) scheme is a tuple of algorithms \(\mathcal {PKE}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) defined as follows. (1) Algorithm \(\mathsf {Setup}\) takes as input the security parameter and outputs public parameters \( pub \in \{0,1\}^*\); all algorithms are implicitly given \( pub \) as input. (2) Algorithm \(\mathsf {Gen}\) takes as input the security parameter and outputs a public/secret key pair \(( pk , sk )\); the set of all secret keys is denoted by \(\mathcal {SK}\) and the set of all public keys by \(\mathcal {PK}\). (3) The randomized algorithm \(\mathsf {Enc}\) takes as input the public key \( pk \), a message \(m\in \mathcal {M}\), and randomness \(r\in \mathcal {R}\), and outputs a ciphertext \(c = \mathsf {Enc}( pk ,m;r)\); the set of all ciphertexts is denoted by \(\mathcal {C}\). (4) The deterministic algorithm \(\mathsf {Dec}\) takes as input the secret key \( sk \) and a ciphertext \(c\in \mathcal {C}\), and outputs \(m = \mathsf {Dec}( sk ,c)\) which is either equal to some message \(m\in \mathcal {M}\) or to an error symbol \(\bot \).
Correctness. We say that \(\mathcal {PKE}\) satisfies correctness if for all  and
and  we have that \(\mathbb {P}[\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m))= m]=1\) (where the randomness is taken over the internal coin tosses of algorithm \(\mathsf {Enc}\)).
we have that \(\mathbb {P}[\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m))= m]=1\) (where the randomness is taken over the internal coin tosses of algorithm \(\mathsf {Enc}\)).
BLT Security. We now turn to defining indistinguishability under chosen-ciphertext attacks (IND-CCA) in the bounded leakage and tampering (BLT) setting.
Definition 1
For \(\kappa \in \mathbb {N}\), let \(\ell = \ell (\kappa )\) and \(\tau = \tau (\kappa )\) be parameters. We say that \(\mathcal {PKE}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) is \((\tau ,\ell )\)-BLT-IND-CCA if for all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu :\mathbb {N}\rightarrow [0,1]\) such that
where the experiment \(\mathbf {Exp}^{\mathrm {blt\text {-}cca}}_{\mathcal {PKE},\mathsf {A}}(\kappa ,\ell ,\tau )\) is defined in Fig. 1.
A few remarks on the definition are in order. In the specification of the BLT-IND-CCA security experiment, oracle \(\mathcal {O}^\ell _{ sk }\) takes as input (arbitrary polynomial-time computable) functions \(L:\mathcal {SK}\rightarrow \{0,1\}^*\), and returns \(L( sk )\) for a total of at most \(\ell \) bits. In a similar fashion, oracle \(\mathcal {O}^\tau _{ sk }\) takes as input (arbitrary polynomial-time computable) functions \(T:\mathcal {SK}\rightarrow \mathcal {SK}\), and defines the i-th tampered secret key as \( sk '_i = T( sk )\); the oracle accepts at most \(\tau \) queries. Oracle \({\mathsf {Dec}}^*\) can be used to decrypt arbitrary ciphertexts c under the i-th tampered secret key (or under the original secret key), provided that c is different from the challenge ciphertext.
Notice that \(\mathsf {A}\) is not allowed to tamper with or leak from the secret key after seeing the challenge ciphertext. As shown in [18] this restriction is necessary already for the case \((\tau ,\ell ) = (1,0)\). Finally, we observe that in case \((\tau ,\ell ) = (0,0)\) we get, as a special case, the standard notion of IND-CCA security. Similarly, for \(\tau = 0\) and \(\ell > 0\), we obtain as a special case the notion of “semantic security against a-posteriori chosen-ciphertext \(\ell \)-key-leakage attacks” from [44].
2.3 Signatures
A signature scheme is a tuple of algorithms \(\mathcal {SIG}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Sign},{\mathsf {Vrfy}})\) specified as follows. (1) Algorithm \(\mathsf {Setup}\) takes as input the security parameter and outputs public parameters \( pub \in \{0,1\}^*\); all algorithms are implicitly given \( pub \) as input. (2) Algorithm \(\mathsf {Gen}\) takes as input the security parameter and outputs a public/secret key pair \(( vk , sk )\); the set of all signing keys is denoted by \(\mathcal {SK}\). (3) The randomized algorithm \(\mathsf {Sign} \) takes as input the signing key \( sk \), a message \(m\in \mathcal {M}\), and randomness \(r\in \mathcal {R}\), and outputs a signature \(\sigma := \mathsf {Sign} ( sk ,m;r)\) on m. (4) The deterministic algorithm \({\mathsf {Vrfy}}\) takes as input the verification key \( vk \) and a pair \((m,\sigma )\), and outputs a decision bit (indicating whether \((m,\sigma )\) is a valid signature with respect to \( vk \)).
Correctness. We say that \(\mathcal {SIG}\) satisfies correctness if for all messages \(m\in \mathcal {M}\) and for all  and \(( vk , sk )\leftarrow \mathsf {Gen}(1^\kappa )\), algorithm \({\mathsf {Vrfy}}( vk ,m,\mathsf {Sign} ( sk ,m))\) outputs 1 with all but negligible probability (over the coin tosses of the signing algorithm).
and \(( vk , sk )\leftarrow \mathsf {Gen}(1^\kappa )\), algorithm \({\mathsf {Vrfy}}( vk ,m,\mathsf {Sign} ( sk ,m))\) outputs 1 with all but negligible probability (over the coin tosses of the signing algorithm).
BLT Security. We now define what it means for a signature scheme to be existentially unforgeable against chosen-message attacks (EUF-CMA) in the bounded leakage and tampering (BLT) setting.
Definition 2
For \(\kappa \in \mathbb {N}\), let \(\ell = \ell (\kappa )\) and \(\tau = \tau (\kappa )\) be parameters. We say that \(\mathcal {SIG}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Sign},{\mathsf {Vrfy}})\) is \((\tau ,\ell )\)-BLT-EUF-CMA if for all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu :\mathbb {N}\rightarrow [0,1]\) such that
where the experiment \(\mathbf {Exp}^{\mathrm {blt\text {-}cma}}_{\mathcal {SIG},\mathsf {A}}(\kappa ,\ell ,\tau )\) is defined in Fig. 2.
The syntax of oracles \(\mathcal {O}^\ell _{ sk }\) and \(\mathcal {O}^\tau _{ sk }\) is the same as before. Oracle \(\mathsf {Sign} ^*\) can be used to sign arbitrary messages m under the i-th tampered signing key \( sk '_i = T( sk )\), or under the original signing key \( sk \); the goal of the adversary is to forge a signature on a “fresh” message, i.e. a message that was never queried to oracle \(\mathsf {Sign} ^*\). Note that for \((\tau ,\ell ) = (0,0)\) we obtain the standard notion of existential unforgeability under chosen-message attacks. Similarly, for \(\tau = 0\) and \(\ell > 0\), we obtain the definition of leakage-resilient signatures [39].
3 Signatures
In this section we give a generic construction of signature schemes with BLT-EUF-CMA in the standard model. In particular, we show that the construction by Dodis et al. [20] is already resilient to bounded leakage and tampering attacks.
3.1 The Scheme of Dodis, Haralambiev, Lòpez-Alt, and Wichs
The signature scheme is based on the following ingredients.
Hard relations. A leakage-resilient hard relation [20].
Definition 3
A relation \(R\) is an \(\ell \)-leakage-resilient hard relation, with witness space \(\mathcal {X}\) and theorem space \(\mathcal {Y}\), if the following requirements are met.
-
Samplability: There exists a PPT algorithm \(\mathsf {SamR}\) such that for all pairs
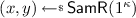 we have \((x,y) \in R\), with \(x\in \mathcal {X}\) and \(y\in \mathcal {Y}\).
we have \((x,y) \in R\), with \(x\in \mathcal {X}\) and \(y\in \mathcal {Y}\). -
Verifiability: There exists a PPT algorithm that decides if a given pair (x, y) satisfies \((x,y)\in R\).
-
Completeness: There exists an efficient deterministic function \(\xi \) that given as input any \(x\in \mathcal {X}\) returns \(y = \xi (x)\in \mathcal {Y}\) such that \((x,y)\in R\).
-
Hardness: For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu :\mathbb {N}\rightarrow [0,1]\) such that

where the probability is taken over the random coin tosses of \(\mathsf {SamR}\) and \(\mathsf {A}\), and where oracle \(\mathcal {O}^\ell _x(\cdot )\) takes as input efficiently computable functions \(L:\mathcal {X}\rightarrow \{0,1\}^*\) and returns \(L(x)\) for a total of at most \(\ell \) bits.
NIZK. A true-simulation extractable non-interactive zero-knowledge (tSE NIZK) argument system \(\mathcal {NIZK}= (\mathsf {I},\mathsf {P},\mathsf {V})\) for the relation \(R\), supporting labels [20]. Recall that a NIZK argument system supporting labels has the following syntax: (i) Algorithm \(\mathsf {I}\) takes as input the security parameter \(\kappa \in \mathbb {N}\) and generates a common reference string (CRS)  . (ii) Algorithm \(\mathsf {P}\) takes as input the CRS, a label \(\lambda \in \{0,1\}^*\), and some pair \((x,y)\in R\), and returns a proof
. (ii) Algorithm \(\mathsf {P}\) takes as input the CRS, a label \(\lambda \in \{0,1\}^*\), and some pair \((x,y)\in R\), and returns a proof  . (iii) Algorithm \(\mathsf {V}\) takes as input the CRS, a label \(\lambda \in \{0,1\}^*\), and some pair \((x,\pi )\), and returns a decision bit \(\mathsf {V}^\lambda ( crs ,y,\pi )\). Moreover:
. (iii) Algorithm \(\mathsf {V}\) takes as input the CRS, a label \(\lambda \in \{0,1\}^*\), and some pair \((x,\pi )\), and returns a decision bit \(\mathsf {V}^\lambda ( crs ,y,\pi )\). Moreover:
Definition 4
We say that \(\mathcal {NIZK}= (\mathsf {I},\mathsf {P},\mathsf {V})\) is a tSE NIZK for the relation \(R\), supporting labels, if the following requirements are met.
-
Correctness: For all pairs \((x,y)\in R\) and for all labels \(\lambda \in \{0,1\}^*\) we have that \(\mathsf {V}^\lambda ( crs ,y,\mathsf {P}^\lambda ( crs ,x,y)) = 1\) with overwhelming probability over the coin tosses of \(\mathsf {P}\), \(\mathsf {V}\), and over the choice of
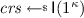 .
. -
Unbounded zero-knowledge: There exists a PPT simulator \(\mathsf {S}:= (\mathsf {S}_1,\mathsf {S}_2)\) such that for all PPT adversaries \(\mathsf {A}\) the following quantity is negligible:Footnote 2
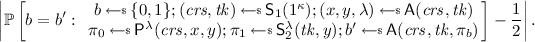
-
True-simulation extractability: There exists a PPT extractor \(\mathsf {K} \) such that for all PPT adversaries \(\mathsf {A}\) the following quantity is negligible:

where oracle \(\mathcal {O}_{\mathsf {S}_2,\tau }\) takes as input tuples \((x_i,y_i,\lambda _i)\) and returns the same as \(\mathsf {S}_2^{\lambda _i}( tk ,y_i)\) as long as \((x_i,y_i)\in R\) (and \(\bot \) otherwise), and \(\mathcal {Q}\) is the set of all labels \(\lambda _i\) asked to oracle \(\mathcal {O}_{\mathsf {S}_2,\tau }\).
The signature scheme. Consider now the following signature scheme \(\mathcal {SIG}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Sign},{\mathsf {Vrfy}})\), based on a relation \(R\), and on a non-interactive argument system \(\mathcal {NIZK}= (\mathsf {I},\mathsf {P},\mathsf {V})\) for \(R\), supporting labels.
-
\(\underline{\mathsf {Setup}(1^\kappa )\!:}\) Sample
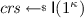 and return \( pub := ( crs ,R)\). (Recall that all algorithms implicitly take \( pub \) as input.)
and return \( pub := ( crs ,R)\). (Recall that all algorithms implicitly take \( pub \) as input.) -
\(\underline{\mathsf {Gen}(1^\kappa )\!:}\) Run
 and define \( vk := y\) and \( sk := x\).
and define \( vk := y\) and \( sk := x\). -
\(\underline{\mathsf {Sign} ( sk ,m)\!:}\) Compute
 and return \(\sigma := \pi \); note that the message m is used as a label in the argument system, and that the value \(y = \xi (x)\) can be efficiently computed as a function of x.
and return \(\sigma := \pi \); note that the message m is used as a label in the argument system, and that the value \(y = \xi (x)\) can be efficiently computed as a function of x. -
\(\underline{{\mathsf {Vrfy}}( vk ,m,\sigma )\!:}\) Parse \(( vk ,\sigma )\) as \( vk := y\) and \(\sigma := \pi \), and output the same as \(\mathsf {V}^m( crs ,y,\pi )\).
Theorem 1
For \(\kappa \in \mathbb {N}\), let \(\ell := \ell (\kappa )\), \(\ell ' := \ell '(\kappa )\), \(\tau := \tau (\kappa )\), and \(n := n(\kappa )\) be parameters. Assume that \(R\) is an \(\ell '\)-leakage-resilient hard relation with theorem space \(\mathcal {Y}:= \{0,1\}^n\), and that \(\mathcal {NIZK}\) is a tSE NIZK for \(R\). Then the signature scheme \(\mathcal {SIG}\) described above is \((\ell ,\tau )\)-BLT-EUF-CMA with \(\ell + (\tau +1)\cdot n \le \ell '\).
3.2 Security Proof
We consider a sequence of mental experiments, starting with the initial game \(\mathbf {Exp}^{\mathrm {blt\text {-}cma}}_{\mathcal {SIG},\mathsf {A}}(\kappa ,\ell ,\tau )\) which for simplicity we denote by \(\mathbf {G}_0\).
-
Game \(\mathbf {G}_0\) . This is exactly the game of Definition 2, where the signature scheme \(\mathcal {SIG}\) is the scheme described in the previous section. In particular, upon input the i-th tampering query \(T_i\) the modified secret key \(x_i' = T_i(x)\) is computed. Hence, the answer to a query (i, m) to oracle \(\mathsf {Sign} ^*\) is computed by parsing \( pub = ( crs ,R)\), computing the statement \(y_i' = \xi (x_i')\) corresponding to \(x_i'\), and outputting \(\sigma := \pi \) where
 .
. -
Game \(\mathbf {G}_1\) . We change the way algorithm \(\mathsf {Setup}\) generates the CRS. Namely, instead of sampling
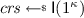 we now run
we now run  and additionally we replace the proofs output by oracle \(\mathsf {Sign} ^*\) by simulated proofs, i.e.,
and additionally we replace the proofs output by oracle \(\mathsf {Sign} ^*\) by simulated proofs, i.e.,  where \(y_i' = \xi (x_i')\).
where \(y_i' = \xi (x_i')\). -
Game \(\mathbf {G}_2\) . We change the winning condition of the previous game. Namely, the game now outputs one if and only if \(\pi ^*\) is valid w.r.t. y (as before) and additionally \((x^*,y)\in R\) where the value \(x^*\) is computed from the proof \(\pi ^*\) running the extractor \(\mathsf {K} \) of the underlying argument system.
We now establish a series of lemmas, showing that the above games are computationally indistinguishable. The first lemma states that \(\mathbf {G}_0\) and \(\mathbf {G}_1\) are indistinguishable, down to the unbounded zero-knowledge property of the argument system.
Lemma 3
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{0,1}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_0(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_1(\kappa ) = 1\right] }\right|\le \nu _{0,1}(\kappa )\).
Proof
We prove a stronger statement, namely that \(\mathbf {G}_0(\kappa ) \approx _c \mathbf {G}_1(\kappa )\). By contradiction, assume that there exists a PPT distinguisher \(\mathsf {D}_{0,1}\) and a polynomial \(p_{0,1}(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), we have that \(\mathsf {D}_{0,1}\) distinguishes between game \(\mathbf {G}_0\) and game \(\mathbf {G}_1\) with probability at least \(1/p_{0,1}(\kappa )\). Let \(q\in poly (\kappa )\) be the number of signature queries asked by \(\mathsf {D}_{0,1}\). For an index \(j\in [q+1]\) consider the hybrid game \(\mathbf {H}_j\) that answers the first \(j-1\) queries as in game \(\mathbf {G}_0\) and all subsequent queries as in game \(\mathbf {G}_1\). Note that \(\mathbf {H}_1 \equiv \mathbf {G}_1\) and \(\mathbf {H}_{q+1} \equiv \mathbf {G}_0\).
By a standard hybrid argument, we have that there exists an index \(j^*\in [q]\) such that \(\mathsf {D}_{0,1}\) tells apart \(\mathbf {H}_{j^*}\) and \(\mathbf {H}_{j^*+1}\) with non-negligible probability \(1/q\cdot 1/p_{0,1}(\kappa )\). We build a PPT adversary \(\mathsf {A}_{0,1}\) that (using distinguisher \(\mathsf {D}_{0,1}\) and knowledge of \(j^*\in [q]\)) breaks the non-interactive zero-knowledge property of the argument system. A formal description of \(\mathsf {A}_{0,1}\) follows.
\(\underline{\mathrm{Adversary}\,\mathsf {A}_{0,1}\!:}\)
Receive \(( crs , tk )\) from the challenger, where
.
Run
, set \( pub := ( crs ,R)\), \( vk := y\), \(x_0' \leftarrow x\), \(x_i' \leftarrow \bot \) for all \(i\in [\tau ]\), and send \(( pub , vk )\) to \(\mathsf {D}_{0,1}\).
Upon input a leakage query \(L\) return \(L(x)\) to \(\mathsf {D}_{0,1}\); upon input a tampering query \(T\), set \(x_i' = T(x)\).
Upon input the j-th signature query of type (i, m), if \(i\not \in [0,\tau ]\) or \(x_i' = \bot \), answer with \(\bot \). Otherwise, proceed as follows:
If \(j \le j^*-1\), return
to \(\mathsf {D}_{0,1}\).
Else, if \(j = j^*\), forward \((x_i',\xi (x_i'),m)\) to the challenger, receiving back a proof \(\pi _b\); return \(\sigma := \pi _b\) to \(\mathsf {D}_{0,1}\).
Else, if \(j \ge j^*+1\), forward
to \(\mathsf {D}_{0,1}\).
Output whatever \(\mathsf {D}\) outputs.
For the analysis, note that the only difference between game \(\mathbf {H}_{j^*}\) and game \(\mathbf {H}_{j^*+1}\) is on how the \(j^*\)-th signature query is answered. In particular, in case the hidden bit b in the definition of non-interactive zero-knowledge equals zero, \(\mathsf {A}_{0,1}\)’s simulation produces exactly the same distribution as in \(\mathbf {H}_{j^*}\), and otherwise \(\mathsf {A}_{0,1}\)’s simulation produces exactly the same distribution as in \(\mathbf {H}_{j^*+1}\). Hence, \(\mathsf {A}_{0,1}\) breaks the NIZK property with non-negligible advantage \(1/q\cdot 1/p_{0,1}(\kappa )\), a contradiction. This concludes the proof. \(\square \)
The second lemma states that \(\mathbf {G}_1\) and \(\mathbf {G}_2\) are indistinguishable, down to the true-simulation extractability property of the argument system.
Lemma 4
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{1,2}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_1(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_2(\kappa ) = 1\right] }\right|\le \nu _{1,2}(\kappa )\).
Proof
We prove a stronger statement, namely that \(\mathbf {G}_1(\kappa ) \approx _c \mathbf {G}_2(\kappa )\). Define the following “bad event” \( Bad \), in the probability space of game \(\mathbf {G}_{1}\): The event becomes true if the adversarial forgery \((m^*,\sigma ^* := \pi ^*)\) is valid (i.e., the proof \(\pi ^*\) is valid w.r.t. statement y and label \(m^*\)), but running the extractor \(\mathsf {K} ( tk ,\cdot ,\cdot )\) on \((y,\pi ^*)\) yields a value \(x^*\) such that \((x^*,y)\not \in R\).
Notice that \(\mathbf {G}_1(\kappa )\) and \(\mathbf {G}_2(\kappa )\) are identically distributed conditioning on \( Bad \) not happening. Hence, by a standard argument, it suffices to bound the probability of provoking event \( Bad \) by all PPT adversaries \(\mathsf {A}\). By contradiction, assume that there exists a PPT adversary \(\mathsf {A}_{1,2}\) and a polynomial \(p_{1,2}(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), we have that \(\mathsf {A}_{1,2}\) provokes event \( Bad \) with probability at least \(1/p_{1,2}(\kappa )\). We build an adversary \(\mathsf {A}'\) that (using \(\mathsf {A}_{1,2}\)) breaks true-simulation extractability of the argument system. A formal description of \(\mathsf {A}'\) follows.
\(\underline{\mathrm{Adversary}\,\mathsf {A}'\!:}\)
Receive \( crs \) from the challenger, where
.
Sample
, set \( pub := ( crs ,R)\), \( vk := y\), \(x_0'\leftarrow x\), \(x_i'\leftarrow \bot \) (for all \(i\in [\tau ]\)), and forward \(( pub , vk )\) to \(\mathsf {A}_{1,2}\).
Upon input a leakage query \(L\) return \(L(x)\) to \(\mathsf {A}_{1,2}\); upon input a tampering query \(T\), set \(x_i' = T(x)\).
Upon input the j-th signature query of type (i, m), if \(i\not \in [0,\tau ]\) or \(x_i' = \bot \), answer with \(\bot \). Otherwise, forward \((x_i',\xi (x_i'),m)\) to the challenger obtaining a proof \(\pi \) as a response, and return \(\sigma := \pi \) to \(\mathsf {A}_{1,2}\).
Whenever \(\mathsf {A}_{1,2}\) returns a pair \((m^*,\sigma ^*)\), define \(\pi ^* := \sigma ^*\) and output \((y,\pi ^*,m^*)\).
For the analysis, we note that \(\mathsf {A}'\) perfectly simulates signature queries. In fact, by completeness of the underlying relation, the pair \((x_i',\xi (x_i'))\) is always in the relation \(R\), and thus the proof \(\pi \) obtained by the reduction is always for a true statement and has exactly the same distribution as in game \(\mathbf {G}_1\). As a consequence, \(\mathsf {A}_{1,2}\) will provoke event \( Bad \) with probability \(1/p_{1,2}(\kappa )\), and thus the pair \((y,\pi ^*)\) output by the reduction violates the tSE property of the non-interactive argument with non-negligible probability \(1/p_{1,2}(\kappa )\). This finishes the proof. \(\square \)
Finally, we show that the advantage of any PPT adversary in game \(\mathbf {G}_2\) must be negligible, otherwise one could violate the hardness of the underlying leakage-resilient relation.
Lemma 5
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _2:\mathbb {N}\rightarrow [0,1]\) such that \({\mathbb {P}\left[ \mathbf {G}_2 = 1\right] } \le \nu _{2}(\kappa )\).
Proof
By contradiction, assume there exists a PPT adversary \(\mathsf {A}_2\) and a polynomial \(p_2(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), adversary \(\mathsf {A}_2\) makes game \(\mathbf {G}_2\) output 1 with probability at least \(1/p_2(\kappa )\). We construct a PPT adversary \(\mathsf {A}''\) (using \(\mathsf {A}_2\)) breaking hardness of the leakage-resilient relation \(R\). A description of \(\mathsf {A}''\) follows.
\(\underline{\mathrm{Adversary}\,\mathsf {A}''\!:}\)
Receive y from the challenger, where
.
Sample
, set \( pub := ( crs ,R)\), \(y_i'\leftarrow \bot \) (for all \(i\in [\tau ]\)), \( vk := y\), and forward \(( pub , vk )\) to \(\mathsf {A}_{2}\).
Define the leakage function \(L_{\xi }(x) := \xi (x)\) and forward \(L_{\xi }\) to the target leakage oracle \(\mathcal {O}^\ell _x\), obtaining a value \(y_0'\).
Upon input a leakage query \(L\), forward \(L\) to the target leakage oracle \(\mathcal {O}^\ell _x\) and return to \(\mathsf {A}_{2}\) the answer received from the oracle.
Upon input the i-th tampering query \(T\), define the function \(L_{T,\xi }(x) := \xi (T(x))\), and forward \(L_{T,\xi }\) to the target leakage oracle \(\mathcal {O}^\ell _x\); set the value \(y_i'\) equal to the answer obtained from the oracle.
Upon input the j-th signature query of type (i, m), if \(i\not \in [0,\tau ]\) or \(y_i' = \bot \), answer with \(\bot \). Otherwise, run
and return \(\sigma := \pi \) to \(\mathsf {A}_{2}\).
Whenever \(\mathsf {A}_{1,2}\) returns a forgery \((m^*,\sigma ^*)\), define \(\pi ^* := \sigma ^*\) and output \(x^*\) such that
.
For the analysis, note that \(\mathsf {A}''\) perfectly simulates signature queries. In fact, for each tampering query \(T\) the reduction obtains the statement \(y_i'\) corresponding to \(x_i' := T(x)\) via a leakage query; given this value a signature for key \(x_i'\) is computed by running the zero-knowledge simulator (as defined in \(\mathbf {G}_2\)). Moreover, the total leakage asked by \(\mathsf {A}''\) equals \(\ell \) (as \(\mathsf {A}_2\) leaks at most \(\ell \) bits from the secret key) plus \(n\cdot \tau \) (as for each tampering function \(T\) the reduction leaks n bits, and \(\mathsf {A}_2\) makes at most \(\tau \) such queries), plus n bits (as the value \(y_0' = \xi (x)\) is needed for simulating signature queries w.r.t. the original secret key), and by assumption \(\ell + (\tau +1)\cdot n \le \ell '\). Hence, \(\mathsf {A}''\) breaks the hardness of the leakage-resilient relation with non-negligible probability \(1/p_2(\kappa )\). This concludes the proof. \(\square \)
The proof of the theorem follows by combining the above lemmas.
3.3 Concrete Instantiations
We now explain how to instantiate the signature scheme from the previous section using standard complexity assumptions. We need two ingredients: (i) A leakage-resilient hard relation \(R\); (ii) A tSE NIZK for the same relation \(R\), supporting labels. For the latter component, we rely on the construction due to Dodis et al. [20] that allows to obtain a tSE NIZK for arbitrary relations, based on a standard (non-extractable) NIZK for a related relation (see below) and an IND-CCA-secure PKE scheme supporting labels.
Let \(\mathcal {PKE}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},{\mathsf {Dec}})\) be an IND-CCA-secure PKE scheme supporting labels, with message space \(\mathcal {X}\). Plugging in the construction from [20] a signature has the form \(\sigma := (c,\pi )\), where  and \(\pi \) is a standard NIZK argument for the following derived relation:
and \(\pi \) is a standard NIZK argument for the following derived relation:
Diffie-Hellman Assumptions. In what follows, let \(\mathbb {G}\) be a group with prime order q and with generator g. Also, let \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) be groups of prime order q and \(\mathsf {e}:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\) be a non-degenerate, efficiently computable, bilinear map.
Discrete Logarithm. Let  and
and  . The Discrete Logarithm (DL) assumption holds in \(\mathbb {G}\) if it is computationally hard to find \(x\in \mathbb {Z}_q\) given \(y = g^x\in \mathbb {G}\).
. The Discrete Logarithm (DL) assumption holds in \(\mathbb {G}\) if it is computationally hard to find \(x\in \mathbb {Z}_q\) given \(y = g^x\in \mathbb {G}\).
Decisional Diffie-Hellman. Let  and
and  . The Decisional Diffie-Hellman (DDH) assumption holds in \(\mathbb {G}\) if the following distributions are computationally indistinguishable: \((\mathbb {G},g_1,g_2,g_1^{x_1},g_2^{x_2})\) and \((\mathbb {G},g_1,g_2,g_1^{x},g_2^x)\).
. The Decisional Diffie-Hellman (DDH) assumption holds in \(\mathbb {G}\) if the following distributions are computationally indistinguishable: \((\mathbb {G},g_1,g_2,g_1^{x_1},g_2^{x_2})\) and \((\mathbb {G},g_1,g_2,g_1^{x},g_2^x)\).
Symmetric External Diffie-Hellman. The Symmetric External Diffie-Hellman (SXDH) assumption states that the DDH assumption holds in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\). Such an assumption is not satisfied in case \(\mathbb {G}_1 = \mathbb {G}_2\), but it is believed to hold in case there is no efficiently computable mapping between \(\mathbb {G}_1\) and \(\mathbb {G}_2\) [12, 52].
D
-Linear [35, 53]. Let \(D \ge 1\) be a constant, and let  and
and  . We say that the D-linear assumption holds in \(\mathbb {G}\) if the following distributions are computationally indistinguishable: \((\mathbb {G},g_1^{x_1},\ldots ,g_D^{x_D},g_{D+1}^{x_{D+1}})\) and \((\mathbb {G},g_1^{x_1},\ldots ,g_D^{x_D},g_{D+1}^{\sum _{i=1}^{D}x_i})\). Note that for \(D = 1\) we obtain the DDH assumption, and for \(D = 2\) we obtain the so-called Linear assumption [53].
. We say that the D-linear assumption holds in \(\mathbb {G}\) if the following distributions are computationally indistinguishable: \((\mathbb {G},g_1^{x_1},\ldots ,g_D^{x_D},g_{D+1}^{x_{D+1}})\) and \((\mathbb {G},g_1^{x_1},\ldots ,g_D^{x_D},g_{D+1}^{\sum _{i=1}^{D}x_i})\). Note that for \(D = 1\) we obtain the DDH assumption, and for \(D = 2\) we obtain the so-called Linear assumption [53].
Construction Based on SXDH. The first instantiation is based on the SXDH assumption, working with asymmetric pairing based groups \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\). The construction below is similar to the one given in [20, Sect. 1.2.2], except that we had to modify the underlying hard relation, in that the one used by Dodis et al. does not meet our completeness requirement.Footnote 3
-
Hard relation: Let \(N \ge 2\), and
 be generators. The sampling algorithm chooses a random
be generators. The sampling algorithm chooses a random 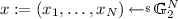 and defines \(y := \prod _{i=1}^{N}\mathsf {e}(g_i,x_i)\in \mathbb {G}_T\). Notice that the relation satisfies completeness, with mapping function \(\xi (\cdot )\) defined by \(\xi (x) := \prod _{i=1}^{N}\mathsf {e}(g_i,x_i)\). In the full version [24], we argue that this relation is leakage-resilient under the SXDH assumption.
and defines \(y := \prod _{i=1}^{N}\mathsf {e}(g_i,x_i)\in \mathbb {G}_T\). Notice that the relation satisfies completeness, with mapping function \(\xi (\cdot )\) defined by \(\xi (x) := \prod _{i=1}^{N}\mathsf {e}(g_i,x_i)\). In the full version [24], we argue that this relation is leakage-resilient under the SXDH assumption.
Lemma 6
Under the SXDH assumption in \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\), the above defined relation is an \(\ell \)-leakage-resilient hard relation for \(\ell \le (N-1)\log q\).
-
PKE: We use the Cramer-Shoup PKE scheme in \(\mathbb {G}_2\) [16], optimized as described in [20]. The public key consists of random generators \((h_1,h_2,h_{3,1},\ldots ,h_{3,N},h_4,h_5)\) of \(\mathbb {G}_2\), and in order to encrypt \(x = (x_1,\ldots ,x_N)\in \mathbb {G}_2^N\) under label \(m\in \{0,1\}^*\) we return a ciphertext:
$$ c := (c_1,\ldots ,c_{N+3}) = (h_1^r,h_2^r,h_{3,1}^r\cdot x_1,\ldots ,h_{3,N}^r\cdot x_N,(h_4\cdot h_5^t)^r) $$with
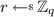 , and where \(t := H(c_1||\cdots ||c_{N+2}||m)\) is computed using a standard collision-resistant hash function.
, and where \(t := H(c_1||\cdots ||c_{N+2}||m)\) is computed using a standard collision-resistant hash function. -
NIZK: We use the Groth-Sahai proof system [32]. In order to prove that a given pair \(x^* := (x,r)\) and \(y^* := (y,c, pk ,m)\) belongs to the relation of Eq. (1), we first prove that \((x,y)\in R\). This requires to show satisfiability of a one-sided pairing product equation, which can be done with a proof consisting of \(2N + 16\) elements in \(\mathbb {G}_1\) and 2 elements in \(\mathbb {Z}_q\) (under the SXDH assumption). Next, we prove validity of a ciphertext which requires to show satisfiability of a system of \(N+3\) one-sided multi-exponentiation equations; the latter can be done with a proof consisting of \((N+3) + 2N = 3N + 3\) group elements (under the SXDH assumption).
Corollary 1
Let \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\) be asymmetric pairing based groups with prime order q. Under the SXDH assumption there exists a signature scheme satisfying BLT-EUFCMA with tampering rate \(\rho (\kappa ) = O(1/\kappa )\). For \(N \ge 2\), the public key consists of a single group element, the secret key consists of N group elements, and a signature consists of \(6N + 22\) group elements and 2 elements in \(\mathbb {Z}_q\).
Construction Based on DLIN. The second instantiation is based on the DLIN assumption, working with symmetric pairing based groups \((\mathbb {G},\mathbb {G}_T)\). The construction below is similar to one of the instantiations given in [20, Sect. 1.2.3], except that we had to modify the underlying hard relation, in that the one used by Dodis et al. does not meet our completeness requirement.
-
Hard relation: Let \(N \ge 3\), and
 be generators. The sampling algorithm chooses a random
be generators. The sampling algorithm chooses a random 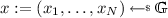 and defines \(y_1 := \prod _{i=1}^{N}\mathsf {e}(g_i,x_i)\in \mathbb {G}_T\) and \(y_2 := \prod _{i=1}^{N}\mathsf {e}(g_i',x_i)\). Notice that the relation satisfies completeness, with mapping function \(\xi (\cdot )\) defined by \(\xi (x) := (\prod _{i=1}^{N}\mathsf {e}(g_i,x_i),\prod _{i=1}^{N}\mathsf {e}(g_i',x_i))\). In the full version [24], we argue that this relation is leakage-resilient under the DLIN assumption.
and defines \(y_1 := \prod _{i=1}^{N}\mathsf {e}(g_i,x_i)\in \mathbb {G}_T\) and \(y_2 := \prod _{i=1}^{N}\mathsf {e}(g_i',x_i)\). Notice that the relation satisfies completeness, with mapping function \(\xi (\cdot )\) defined by \(\xi (x) := (\prod _{i=1}^{N}\mathsf {e}(g_i,x_i),\prod _{i=1}^{N}\mathsf {e}(g_i',x_i))\). In the full version [24], we argue that this relation is leakage-resilient under the DLIN assumption.
Lemma 7
Under the DLIN assumption in \((\mathbb {G},\mathbb {G}_T)\), the above defined relation is an \(\ell \)-leakage-resilient hard relation for \(\ell \le (N-2)\log q\).
-
PKE: We use the Linear Cramer-Shoup PKE scheme in \(\mathbb {G}\) [53], optimized as described in [20]. The public key consists of random generators \((h_0,h_1,h_2,h_{3,1},\ldots ,h_{3,N},h_{4,1},\ldots ,h_{4,N},h_{5,1},h_{5,2},h_{6,1},h_{6,2})\) of \(\mathbb {G}\), and in order to encrypt \(x = (x_1,\ldots ,x_N)\in \mathbb {G}^N\) under label \(m\in \{0,1\}^*\) we return a ciphertext:
$$\begin{aligned} c := (c_1,\ldots ,c_{N+4})&= (h_0^{r_1+r_2},h_1^{r_1},h_2^{r_2},h_{3,1}^{r_1}\cdot h_{4,1}^{r_2}\cdot x_1, \ldots ,h_{3,N}^{r_1}\\&\qquad \cdot h_{4,N}^{r_2}\cdot x_N,(h_{4,1}\cdot h_{5,1}^t)^{r_1} \cdot (h_{4,2}\cdot h_{5,2}^t)^{r_2}) \end{aligned}$$with
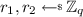 , and where \(t := H(c_1||\cdots ||c_{N+3}||m)\) is computed using a standard collision-resistant hash function.
, and where \(t := H(c_1||\cdots ||c_{N+3}||m)\) is computed using a standard collision-resistant hash function. -
NIZK: We use again the Groth-Sahai proof system. In order to prove that a given pair \(x^* := (x,r)\) and \(y^* := ((y_1,y_2),c, pk ,m)\) belongs to the relation of Eq. (1), we first prove that \((x,(y_1,y_2))\in R\). This requires to show satisfiability of two one-sided pairing product equations, which can be done with a proof consisting of \(3N + 42\) elements in \(\mathbb {G}\) and 6 elements in \(\mathbb {Z}_q\) (under the DLIN assumption). Next, we prove validity of a ciphertext which requires to show satisfiability of a system of \(N+4\) one-sided multi-exponentiation equations; the latter can be done with a proof consisting of \(2(N+4) + 3N = 5N + 8\) group elements (under the DLIN assumption).
Corollary 2
Let \((\mathbb {G},\mathbb {G}_T)\) be symmetric pairing based groups with prime order q. Under the DLIN assumption there exists a signature scheme satisfying BLT-EUFCMA with tampering rate \(\rho (\kappa ) = O(1/\kappa )\). For \(N \ge 3\), the public key consists of two group elements, the secret key consists of N group elements, and a signature consists of \(9N + 54\) group elements and 6 elements in \(\mathbb {Z}_q\).
4 Public-Key Encryption
We give a construction of an efficient PKE scheme satisfying BLT-IND-CCA security in the standard model. In particular, we prove that the PKE scheme of Qin and Liu [49] is already resilient to bounded leakage and tampering attacks.
4.1 The Scheme of Qin and Liu
The encryption scheme is a twist of the well-known Cramer-Shoup paradigm for CCA security [17], and is based on the following ingredients.
Hash-proof systems. An \(\epsilon \)-universal hash-proof system (HPS) \(\mathcal {HPS} = (\mathsf {Gen}_\mathrm{hps},\mathsf {Pub},\mathsf {Priv})\). Recall that a HPS has the following syntax: (i) Algorithm \(\mathsf {Gen}_\mathrm{hps}\) takes as input the security parameter, and outputs public parameters \( pub :=( aux ,\mathcal {C},\mathcal {V},\mathcal {K},\mathcal {SK},\mathcal {PK},\varLambda _{(\cdot )}:\mathcal {C} \rightarrow \mathcal {K},\mu :\mathcal {SK}\rightarrow \mathcal {PK})\) where \( aux \) might contain additional structural parameters, and where \(\varLambda _{ sk }\) is a hash function and, for any \( sk \in \mathcal {SK}\), the function \(\mu ( sk )\) defines the action of \(\varLambda _{ sk }\) over the subset \(\mathcal {V} \) of valid ciphertexts (i.e., \(\varLambda _{ sk }\) is projective). Moreover the function \(\varLambda _{ sk }\) is \(\epsilon \)-almost universal:
Definition 5
A projective hash function \(\varLambda _{(\cdot )}\) is \(\epsilon \) -almost universal, if for all \( pk \), \(C\in \mathcal {C} \setminus \mathcal {V} \), and all \(K\in \mathcal {K} \), it holds that \({\mathbb {P}\left[ \varLambda _{\mathbf {SK}}(C)=K|\mathbf {PK}= pk ,C\right] }\leqslant \epsilon \), where \(\mathbf {SK}\) is uniform over \(\mathcal {SK}\) conditioned on \(\mathbf {PK}=\mu (\mathbf {SK})\).
(ii) Algorithm \(\mathsf {Pub}\) takes as input a public key \( pk = \mu ( sk )\), a valid ciphertext \(C\in \mathcal {V} \), and a witness w for \(C\in \mathcal {V} \), and outputs the value \(\varLambda _{ sk }(C)\). (iii) Algorithm \(\mathsf {Priv}\) take as input the secret key \( sk \) and a ciphertext \(C\in \mathcal {C} \), and outputs the value \(\varLambda _{ sk }(C)\).
Definition 6
A hash-proof system \(\mathcal {HPS} \) is \(\epsilon \)-almost universal if the following holds:
-
1.
For all sufficiently large \(\kappa \in \mathbb N\), and for all possible outcomes of \(\mathsf {Gen}_\mathrm{hps}(1^\kappa )\), the underlying projective hash function is \(\epsilon (\kappa )\)-almost universal.
-
2.
The underlying set membership problem is hard. Specifically, for any \(\text {PPT}\) adversary \(\mathsf {A}\) the following quantity is negligible:
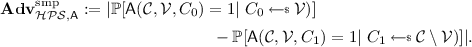
The lemma below directly follows from the definition of hash-proof system and the notion of min-entropy.
Lemma 8
Let \(\varLambda _{(\cdot )}\) be \(\epsilon \)-almost universal. Then for all \( pk \) and \(C\in \mathcal {C} \setminus \mathcal {V} \) it holds that \(\mathbb {H}_\infty (\varLambda _{\mathbf {SK}}(C)|\mathbf {PK}= pk ,C)\geqslant -\log \epsilon \) where \(\mathbf {SK}\) is uniform over \(\mathcal {SK}\) conditioned on \(\mathbf {PK} = \mu (\mathbf {SK})\).
One-time lossy filters [49]. A One-Time Lossy Filter (OTLF) \(\mathcal {LF}= (\mathsf {Gen}_\mathrm{lf},\mathsf {Eval},\mathsf {LTag})\) is a family of functions \(\mathsf {LF}_{\phi ,t}(X)\) indexed by a public key \(\phi \) and a tag t. Recall that a OTLF has the following syntax: (i) Algorithm \(\mathsf {Gen}_\mathrm{lf}\) takes as input the security parameter, and outputs a public key \(\phi \) and a trapdoor key \(\psi \). The public key \(\phi \) defines a tag space \(\mathcal {T}:= \{0,1\}^*\times \mathcal {T} _c\) that contains two disjoint subsets \(\mathcal {T} _\mathrm{inj}\) and \(\mathcal {T} _\mathrm{loss}\) and a domain space \(\mathcal {D} \). (ii) Algorithm \(\mathsf {Eval}\) takes as input \(\phi \), a tag \(t=(t_a,t_c)\in \mathcal {T} \) (where we call \(t_a\) the auxiliary tag and \(t_c\) the core tag), and \(X\in \mathcal {D} \), and outputs \(\mathsf {LF}_{\phi ,t}(X)\). (iii) Algorithm \(\mathsf {LTag}\) takes as input \(\psi \) and an auxiliary tag \(t_a\in \{0,1\}^*\), and outputs a core tag \(t_c\) such that \(t=(t_a,t_c)\in \mathcal {T} _\mathrm{loss}\).
Definition 7
We say that \(\mathcal {LF}= (\mathsf {Gen}_\mathrm{lf},\mathsf {Eval},\mathsf {LTag})\) is an \(\ell _\mathrm{lf}\)-OTLF with domain \(\mathcal {D} \) if the following proprieties hold:
-
Lossiness: In case the tag t is injective (i.e., \(t\in \mathcal {T} _\mathrm{inj}\)), so is the function \(\mathsf {LF}_{\phi ,t}(\cdot ):=\mathsf {Eval}(\phi ,t,\cdot )\). In case t is lossy (i.e., \(t\in \mathcal {T} _\mathrm{loss}\)), then \(\mathsf {LF}_{\phi ,t}(\cdot )\) has image size at most \(2^{\ell _\mathrm{lf}}\).
-
Indistinguishability: No \(\text {PPT}\) adversary \(\mathsf {A}\) is able to distinguish lossy tags from random tags, i.e. the following quantity is negligible:
$$ \mathbf {Adv}_{\mathcal {LF},\mathsf {A}}^{\mathrm {ind}}:=\left| {\mathbb {P}\left[ \mathsf {A}(\phi ,(t_a,t_c^0)) = 1\right] } - {\mathbb {P}\left[ \mathsf {A}(\phi ,(t_a,t_c^1)) = 1\right] }\right| $$where
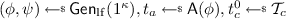 and
and  .
. -
Evasiveness: No \(\text {PPT}\) adversary \(\mathsf {A}\) is able to generate a non-injective tag even given a lossy tag, i.e. the following quantity is negligible:
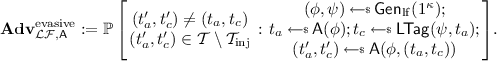
Randomness extractors. An average-case strong randomness extractor.
Definition 8
An efficient function \(\mathsf {Ext}:\mathcal {X}\times \mathcal {S} \rightarrow \mathcal {Y} \) is an average-case \((\delta ,\epsilon )\)-strong extractor if for all pair of random variables \((\mathbf {X},\mathbf {Z})\), where \(\mathbf {X}\) is defined over a set \(\mathcal {X}\) and \(\widetilde{\mathbb {H}}_\infty (\mathbf {X}|\mathbf {Z})\geqslant \delta \), we have
with \(\mathbf {S}\) uniform over \(\mathcal {S} \) and \(\mathbf {U}\) uniform over \(\mathcal {Y} \).
The encryption scheme. Consider now the following PKE scheme \(\mathcal {PKE}= (\mathsf {Setup},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) with message space \(\mathcal {M}:= \{0,1\}^m\), based on a HPS \(\mathcal {HPS} = (\mathsf {Gen}_\mathrm{hps},\mathsf {Pub},\mathsf {Priv})\), on a OTLF \(\mathcal {LF}= (\mathsf {Gen}_\mathrm{lf},\mathsf {Eval},\mathsf {LTag})\) with domain \(\mathcal {K} \), and on an average-case strong extractor \(\mathsf {Ext}:\mathcal {K} \times \{0,1\}^d\rightarrow \{0,1\}^m\).
-
\(\underline{\mathsf {Setup}(1^\kappa )\!:}\) Sample
 and compute
and compute  . Return \( pub := ( pub _\mathrm{hps},\phi )\). (Recall that all algorithms implicitly take \( pub \) as input.)
. Return \( pub := ( pub _\mathrm{hps},\phi )\). (Recall that all algorithms implicitly take \( pub \) as input.) -
\(\underline{\mathsf {Gen}(1^\kappa )\!:}\) Choose a random
 , define \( pk =\mu ( sk )\), and return \(( pk , sk )\).
, define \( pk =\mu ( sk )\), and return \(( pk , sk )\). -
\(\underline{\mathsf {Enc}( pk ,M)\!:}\) Sample
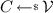 (with witness w),
(with witness w),  , and a core tag
, and a core tag  . Compute \(K:=\mathsf {Pub}( pk ,C,w)\), \(\varPhi := \mathsf {Ext}(K,S) \oplus M\), and \(\varPi := \mathsf {Eval}(\phi ,(t_a,t_c),K)\) where \(t_a:=(C,S,\varPhi )\). Output \(\hat{C} := (C,S,\varPhi ,\varPi ,t_c)\).
. Compute \(K:=\mathsf {Pub}( pk ,C,w)\), \(\varPhi := \mathsf {Ext}(K,S) \oplus M\), and \(\varPi := \mathsf {Eval}(\phi ,(t_a,t_c),K)\) where \(t_a:=(C,S,\varPhi )\). Output \(\hat{C} := (C,S,\varPhi ,\varPi ,t_c)\). -
\(\underline{\mathsf {Dec}( sk ,\hat{C})\!:}\) Parse \(\hat{C} := (C,S,\varPhi ,\varPi ,t_c)\). Compute \(\hat{K}:=\mathsf {Priv}( sk ,C)\) and check if \(\mathsf {Eval}(\phi ,t,\hat{K}) = \varPi \) where \(t:=((C,S,\varPhi ),t_c)\). If the check fails, reject and output \(\bot \); else output \(M := \varPhi \oplus \mathsf {Ext}(\hat{K},S)\).
Theorem 2
Let \(\kappa \in \mathbb {N}\) be the security parameter. Assume that \(\mathcal {HPS} \) is \(\epsilon \)-almost universal, \(\mathcal {LF}\) is an \(\ell _\mathrm{lf}\)-OTLF with domain \(\mathcal {K} \), and \(\mathsf {Ext}\) is an average-case \((\delta ,\epsilon ')\)-strong extractor for a negligible function \(\epsilon '\). Let \(s = s(\kappa )\) and \(p = p(\kappa )\) be parameters such that \(s \leqslant \log |\mathcal {SK}|\) and \(p \geqslant \log |\mathcal {PK}|\) for any \(\mathcal {SK},\mathcal {PK}\) generated by \(\mathsf {Gen}_\mathrm{hps}(1^\kappa )\), and define \(\alpha = -\log \epsilon \) and \(\beta = s -\alpha \).
For any \(\delta \leqslant \alpha - \tau (p + \beta + \kappa )-\ell _\mathrm{lf}-\ell \) the PKE scheme \(\mathcal {PKE}\) described above is \((\tau ,\ell )\)-BLT-IND-CCA with \(\ell + \tau (p+\beta +\kappa ) \leqslant \alpha - \ell _\mathrm{lf}\).
4.2 Security Proof
We consider a sequence of mental experiments, starting with the initial game \(\mathbf {Exp}^{\mathrm {blt\text {-}cca}}_{\mathcal {PKE},\mathsf {A}}(\kappa ,\ell ,\tau )\) which for simplicity we denote by \(\mathbf {G}_0\).
-
Game \(\mathbf {G}_0\) . This is exactly the game of Definition 1, where \(\mathcal {PKE}\) is the PKE scheme described above. In particular, upon input the i-th tampering query \(T_i\) the modified secret key \( sk '_i = T_i( sk )\) is computed (where \( sk \) is the original secret key). Hence, the answer to a query \((i,\hat{C})\) to oracle \({\mathsf {Dec}}^*\) is computed by parsing \(\hat{C} := (C,S,\varPhi ,\varPi ,t_c)\), computing \(\hat{K} :=\mathsf {Priv}( sk '_i,C)\), and checking \(\varPi = \mathsf {Eval}(\phi ,((C,S,\varPhi ),t_c), \hat{K})\); if the check fails the answer is \(\bot \) and otherwise the answer is \(M := \varPhi \oplus \mathsf {Ext}(\hat{K},S)\).
-
Game \(\mathbf {G}_1\) . We change the way the tag \(t^*_c\) corresponding to the challenge ciphertext is computed, namely we now let \(t^*_c\leftarrow \mathsf {LTag}(\psi ,t^*_a)\) (i.e., the tag \(t^*=(t^*_a,t^*_c)\in \mathcal {T} _\mathrm{loss}\) is now lossy).
-
Game \(\mathbf {G}_2\) . We add an extra check to the decryption oracle. Namely, upon input a decryption query \((i,(C,S,\varPhi ,\varPi ,t_c))\) we check whether \(t_a:=(C,S,\varPhi )\) and \(t_c\) satisfy \((t_a,t_c) = (t^*_a,t^*_c)\) (where \(t_a^*\) and \(t_c^*\) are the auxiliary and core tag corresponding to the challenge ciphertext). If the check succeeds, the oracle returns \(\bot \). Notice that \(t_a^*\) and \(t_c^*\) are initially set to \(\bot \), and remain equal to \(\bot \) until the challenge ciphertext is generated.
-
Game \(\mathbf {G}_3\) . We change the way the challenge ciphertext is computed. Namely, we now compute the value \(K^*\) as \(K^*:=\mathsf {Priv}(sk,C^*)\).
-
Game \(\mathbf {G}_4\) . We change the way the challenge ciphertext is computed. Namely, we now sample \(C^*\) as
 .
. -
Game \(\mathbf {G}_5\) . We add an extra check to the decryption oracle; the check is performed only for decryption queries corresponding to tampered secret keys (i.e., \(i \ge 1\)). At setup, the experiment initializes an additional set \(\mathcal {Q} '\leftarrow \emptyset \). Denote by \(\mathbf {V}\) the random variable containing all the answers from the decryption and leakage oracles, and define the quantity
$$ \gamma _i(\kappa ) := \mathbb {H}_\infty (\mathbf {SK}_i'|\mathbf {V} = v,\{\mathbf {SK}_j' = sk '_j\}_{j\in \mathcal {Q} '},\{\mathbf {PK}_j' = pk _j'\}_{j\in [\tau ]\cup \{0\}}) $$where we write \(\mathbf {SK}_i'\) for the random variable of the i-th tampered secret key and \(\mathbf {PK}_i'\) for the random variable of the corresponding public key (by default \( pk '_i = \bot \) if \( sk '_i\) is undefined and \( pk '_0 = pk \)).
Upon input a decryption query \((i,(C,S,\varPhi ,\varPi ,t_c))\) such that \(i\ge 1\) we proceed exactly as in \(\mathbf {G}_4\) but, for all ciphertexts such that \(C\in \mathcal {C} \setminus \mathcal {V} \), in case the decryption oracle did not already return \(\bot \), we additionally check whether \(\gamma _i(\kappa ) \le \beta (\kappa ) + \log ^2\kappa \); if that happens, we add the index i to the set \(\mathcal {Q} '\) and otherwise we do not modify \(\mathcal {Q} '\) and we additionally answer the decryption query with \(\bot \).
-
Game \(\mathbf {G}_6\) . We change the way decryption queries corresponding to the original secret key are answered. Namely, upon input a decryption query \((0,(C,S,\varPhi ,\varPi ,t_c))\) we proceed as in \(\mathbf {G}_5\) but, in case \(C\in \mathcal {C} \setminus \mathcal {V} \), we answer the query with \(\bot \).
-
Game \(\mathbf {G}_7\) . We change the way the challenge ciphertext is computed. Namely, we now sample
 . Notice that the challenge ciphertext is now independent of the message being encrypted.
. Notice that the challenge ciphertext is now independent of the message being encrypted.
Next, we turn to showing that the above defined games are indistinguishable. In what follows, given a ciphertext \(\hat{C} = (C,S,\varPhi ,\varPi ,t_c)\), we say that \(\hat{C}\) is valid if \(C\in \mathcal {V} \) (i.e., if C is a valid ciphertext for the underlying HPS).
Lemma 9
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{0,1}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_0(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_1(\kappa ) = 1\right] }\right|\le \nu _{0,1}(\kappa )\).
Proof
We prove a stronger statement, namely that \(\mathbf {G}_0(\kappa ) \approx _c \mathbf {G}_1(\kappa )\). By contradiction, assume there exists a PPT distinguisher \(\mathsf {D}_{0,1}\) and a polynomial \(p_{0,1}(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), we have that \(\mathsf {D}_{0,1}\) distinguishes between \(\mathbf {G}_0\) and \(\mathbf {G}_1\) with probability at least \(\ge 1/p_{0,1}(\kappa )\). We construct an adversary \(\mathsf {A}_{0,1}\) breaking the indistinguishability property of the underlying OTLF \(\mathcal {LF}\). At the beginning, adversary \(\mathsf {A}_{0,1}\) receives the evaluation key \(\phi \) from its own challenger, and simulates the entire experiment \(\mathbf {G}_0\) with \(\mathsf {D}_{0,1}\) by sampling all other parameters by itself; notice that this can be done because \(\mathbf {G}_0\) does not depend on the secret trapdoor \(\psi \). Whenever \(\mathsf {D}_{0,1}\) outputs \((M_0,M_1)\), adversary \(\mathsf {A}_{0,1}\) samples \(t_a^*\) as defined in \(\mathbf {G}_0\) and returns \(t_a^*\) to its own challenger. Upon receiving a value \(t_c^*\) from the challenger, \(\mathsf {A}_{0,1}\) embeds \(t_c^*\) in the challenge ciphertext, and keeps simulating all queries done by \(\mathsf {D}_{0,1}\) as before. Finally, \(\mathsf {A}_{0,1}\) outputs the same as \(\mathsf {D}_{0,1}\).
We observe that \(\mathsf {A}_{0,1}\) perfectly simulates the decryption oracle (which is identical in both \(\mathbf {G}_0\) and \(\mathbf {G}_1\)). Moreover, depending on the challenge tag \(t_c^*\) being random or lossy, the distribution of the challenge ciphertext produced by \(\mathsf {A}_{0,1}\) is identical to that of either \(\mathbf {G}_0\) or \(\mathbf {G}_1\). Thus, \(\mathsf {A}_{0,1}\) retains the same advantage as that of \(\mathsf {D}_{0,1}\). This concludes the proof. \(\square \)
Lemma 10
\(\mathbf {G}_1 \equiv \mathbf {G}_2\).
Proof
Notice that \(\mathbf {G}_1\) and \(\mathbf {G}_2\) only differ in how decryption queries such that \((t_a,t_c) = (t_a^*,t_c^*)\) are answered. Clearly, such queries are answered identically in the two games for all decryption queries before the generation of the challenge ciphertext. As for decryption queries after the challenge ciphertext has been computed, we distinguish two cases: (i) \(\varPi = \varPi ^*\), and (ii) \(\varPi \ne \varPi ^*\). In case (i) we get that \(\hat{C} = \hat{C}^*\), and thus both games return \(\bot \). In case (ii), note that \(\mathbf {G}_1\) checks whether \(\varPi = \mathsf {Eval}(\phi ,(t^*_a,t^*_c),\mathsf {Priv}( sk '_i,C^*))\) and thus it returns \(\bot \) whenever \(\varPi \ne \varPi ^*\). Hence, the two games are identically distributed. \(\square \)
Lemma 11
\(\mathbf {G}_2 \equiv \mathbf {G}_3\).
Proof
The difference between \(\mathbf {G}_2\) and \(\mathbf {G}_3\) is only syntactical, as \(\mathsf {Priv}( sk ,C^*) = K^* = \mathsf {Pub}( pk ,C^*,w)\) by correctness of the underlying HPS. \(\square \)
Lemma 12
For all PPT adversaries \(\mathsf {A}\), there exists a negligible function \(\nu _{3,4}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_3(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1\right] }\right|\le \nu _{3,4}(\kappa )\).
Proof
We prove a stronger statement, namely that \(\mathbf {G}_3(\kappa ) \approx _c \mathbf {G}_4(\kappa )\). By contradiction, assume there exists a PPT distinguisher \(\mathsf {D}_{3,4}\) and a polynomial \(p_{3,4}(\cdot )\) such that, for infinitely many values of \(\kappa \in \mathbb {N}\), we have that \(\mathsf {D}_{3,4}\) distinguishes between \(\mathbf {G}_3\) and \(\mathbf {G}_4\) with probability at least \(\ge 1/p_{3,4}(\kappa )\). We construct a PPT adversary \(\mathsf {A}_{3,4}\) solving the set membership problem of the underlying HPS. \(\mathsf {A}_{3,4}\) receives as input \( pub _\mathrm{hps}\) and a challenge \(C^*\) such that either  or
or  . Hence, \(\mathsf {A}_{3,4}\) perfectly simulates the challenger for \(\mathsf {D}_{3,4}\), by sampling all required parameters by itself, and embeds the value \(C^*\) in the challenge ciphertext. In case
. Hence, \(\mathsf {A}_{3,4}\) perfectly simulates the challenger for \(\mathsf {D}_{3,4}\), by sampling all required parameters by itself, and embeds the value \(C^*\) in the challenge ciphertext. In case  we get exactly the same distribution as in \(\mathbf {G}_3\), and in case
we get exactly the same distribution as in \(\mathbf {G}_3\), and in case  we get exactly the same distribution as in \(\mathbf {G}_4\). Hence, \(\mathsf {A}_{3,4}\) retains the same advantage as that of \(\mathsf {D}_{3,4}\). This finishes the proof. \(\square \)
we get exactly the same distribution as in \(\mathbf {G}_4\). Hence, \(\mathsf {A}_{3,4}\) retains the same advantage as that of \(\mathsf {D}_{3,4}\). This finishes the proof. \(\square \)
For the j-th query \((i,\hat{C})\) to the decryption oracle, such that \(\hat{C} = (C,S,\varPhi ,\varPi ,t_c)\), we let \( Inj _j\) be the event that the corresponding core tag \(t_c\) is injective. We also define \( Inj := \bigwedge _{j\in [q]} Inj _j\) where \(q \in poly (\kappa )\) is the total number of decryption queries asked by the adversary.
Lemma 13
For all PPT adversaries \(\mathsf {A}\) there exists a negligible function \(\nu _{4}:\mathbb {N}\rightarrow [0,1]\) such that: \(\left|{\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1| Inj \right] }\right|\le \nu _{4}(\kappa )\).
Proof
The lemma follows by a simple reduction to the evasiveness property of the OTLF \(\mathcal {LF}\). By contradiction, assume there exists a PPT adversary \(\mathsf {A}_4\) and a polynomial \(p_4(\cdot )\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1\right] } - {\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1| Inj \right] }\right|\ge 1/p_4(\kappa )\) for infinitely many values of \(\kappa \in \mathbb {N}\). This implies:
We build a PPT adversary \(\mathsf {B}_4\) with non-negligible advantage in the evasiveness game. The adversary \(\mathsf {B}_4\) receives as input a public key \(\phi \) for the OTLF and perfectly simulates a run of game \(\mathbf {G}_4\) for \(\mathsf {A}_4\) by sampling all parameters by itself. After \(\mathsf {A}_4\) returns \((M_0,M_1)\), adversary \(\mathsf {B}_4\) samples \(t_a^*\) as defined in \(\mathbf {G}_4\), and forwards \(t_a^*\) to its own challenger. Upon receiving \(t^*_c\) from the challenger, \(\mathsf {B}_4\) embeds \(t_c^*\) in the challenge ciphertext for \(\mathsf {A}_4\).
Let \(\mathcal {Q} \) be the list of decryption queries made by \(\mathsf {A}_4\). At the end of the simulation, adversary \(\mathcal {B} _4\) picks uniformly at random a ciphertext \(\hat{C} = (C,S,\varPhi ,t_c)\) from the list \(\mathcal {Q} \) and outputs the tuple \((t_a:=(C,S,\varPhi ),t_c)\). Clearly, the advantage of \(\mathsf {B}_4\) in the evasiveness game is equal to the probability of event \( Inj \) happening times the probability of guessing one of the ciphertexts containing a non-injective tag. Let \(q(\kappa ) \in poly (\kappa )\) be the total number of decryption queries made by \(\mathsf {A}_4\). We have obtained,
which is a non-negligible quantity. This concludes the proof. \(\square \)
From now on, all of our arguments will be solely information-theoretic, and hence we do not mind if the remaining experiments will no longer be efficient.
Lemma 14
For all (possibly unbounded) adversaries \(\mathsf {A}\) making polynomially many decryption queries, there exists a negligible function \(\nu _{4,5}:\mathbb {N}\rightarrow [0,1]\) such that \(|{\mathbb {P}\left[ \mathbf {G}_4(\kappa ) = 1| Inj \right] } - {\mathbb {P}\left[ \mathbf {G}_5(\kappa ) = 1| Inj \right] }| \le \nu _{4,5}(\kappa )\).
Proof
Recall that \(\mathbf {G}_4\) and \(\mathbf {G}_5\) differ only in the way decryption queries are handled. In particular, upon input a query \((i,(C,S,\varPhi ,\varPi ,t_c))\) such that \(i \ge 1\) and \(C\in \mathcal {C} \setminus \mathcal {V} \), the decryption oracle in \(\mathbf {G}_5\) checks whether \(\gamma _i(\kappa ) \leqslant \beta (\kappa ) + \log ^2\kappa \). In case that happens, \(\mathbf {G}_5\) proceeds identically to \(\mathbf {G}_4\) and additionally updates the set \(\mathcal {Q} '\) by including the index i; otherwise \(\mathbf {G}_5\) answers the query with \(\bot \). Intuitively, the set \(\mathcal {Q} '\) keeps track of the tampered secret keys that did not return \(\bot \) upon input an invalid ciphertext; the variable \(\gamma _i(\kappa )\), instead, measures the conditional min-entropy of the i-th tampered secret key conditioned on all values returned by the decryption and leakage oracles, all tampered secret keys within the set \(\mathcal {Q} '\), and all public keys corresponding to the tampered secret keys generated so far.
It follows that the distribution of the two games differ only in case the adversary makes a decryption query \((i,(C,S,\varPhi ,\varPi ,t_c))\) such that: (i) \(\gamma _i(\kappa ) > \beta (\kappa ) + \log ^2\kappa \); (ii) \(C\in \mathcal {C} \setminus \mathcal {V} \); (iii) \(\varPi =\mathsf {Eval}(\phi ,(t_a,t_c),\mathsf {Priv}( sk '_i,C))\). Let \( Bad \) be the event that any (possibly unbounded) adversary makes a decryption query as above. Clearly,
For all \(j\in [q]\), let \( Bad _j\) be the event that \( Bad \) happens for the j-th decryption query, which as usual we denote by \((i,(C,S,\varPhi ,\varPi ,t_c))\). Since we are conditioning on \( Inj \), we have that there exists a unique value K that is the pre-image of \(\varPi \) under function \(\mathsf {Eval}(\phi ,(t_a,t_c),\cdot )\). Thus, by averaging over all the possible views for the adversary, we obtain:
Define the set \(\mathcal {SK}^*_{K,C} := \{ sk :~\mathsf {Priv}( sk ,C) = K\ \wedge \ pk =\mu ( sk )\}\). We can write:
where in the last line we used the \(\epsilon \)-almost universality of the underlying HPS, together with the fact that \(\gamma _i(\kappa ) > \beta (\kappa ) + \log ^2\kappa \). Finally, by a union bound over all decryption queries, we obtain that there exists a negligible function \(\nu _{4,5}:\mathbb {N}\rightarrow [0,1]\) such that \({\mathbb {P}\left[ Bad | Inj \right] } \leqslant q\cdot 2^{-\log ^2\kappa } \le \nu _{4,5}(\kappa )\), which concludes the proof of the lemma. \(\square \)
Lemma 15
For all (possibly unbounded) adversaries \(\mathsf {A}\), there exists a negligible function \(\nu _{5,6}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_5(\kappa ) = 1| Inj \right] } - {\mathbb {P}\left[ \mathbf {G}_6(\kappa ) = 1| Inj \right] }\right|\le \nu _{5,6}(\kappa )\).
Proof
Let \( Bad \) be the event that the adversary submits a decryption query \((0,(C,S,\varPhi ,\varPi ,t_c))\) such that: (i) \(C\in \mathcal {C} \setminus \mathcal {V} \); (ii) \(\varPi =\mathsf {Eval}(\phi ,(t_a,t_c),\mathsf {Priv}( sk ,C))\). Similarly to the proof of the previous lemma, it suffices to bound the probability of the event \( Bad \) conditioned on \( Inj \). Denote by \((0,(C,S,\varPhi ,\varPi ,t_c))\) the first decryption query (w.r.t. the original secret key) that triggers event \( Bad \). Recall that the view of adversary \(\mathsf {A}\) in a run of game \(\mathbf {G}_5\) consists of its own coin tosses, the public key \( pk \), the answers to all queries to the decryption and leakage oracles, and the challenge ciphertext \(\hat{C}^*\). In what follows, we write \(\mathbf {L}\) for the random variable corresponding to the leakage queries; furthermore, for an index \(i\in [\tau ]\), we denote with \(\mathbf {D}_i\) the random variable corresponding to all decryption queries relative to the i-th tampered secret key. Note that we can partition \(\mathbf {D}_i\) in two parts: \(\mathbf {D}^{-}_i\) for all decryption queries (w.r.t. the i-th tampered secret key) with an invalid ciphertext, and \(\mathbf {D}^{+}_i\) for all decryption queries (w.r.t. the i-th tampered secret key) with a valid ciphertext. We also write \(\mathbf {W}\) for the random variable corresponding to the overall view in game \(\mathbf {G}_5\).
As in the previous lemma, since we are conditioning on event \( Inj \), it suffices to analyze the conditional average min-entropy of \(\mathsf {Priv}(\mathbf {SK},C)\) conditioned on the adversarial view.
Here, Eq. (2) uses the fact that the coin tosses of the adversary are independent of \(\mathbf {SK}\), Eq. (3) follows by the chain rule for conditional average min-entropy (cf. Lemma 1), Eq. (4) uses the fact that, by definition of \(\mathbf {G}_5\), all decryption queries for keys outside \(\mathcal {Q} '\) and with an invalid ciphertext are answered with \(\bot \), and Eq. (5) follows by the fact that \(\mathbf {D}^{-}_i\) is a deterministic function of \(\mathbf {SK}_i'\).
Let \(\mathcal {Q} ' = \{i_1,\dots ,i_{q'}\}\), as defined in game \(\mathbf {G}_5\). Since the fact that \( sk _{i_{q'}}\in \mathcal {Q} '\) implies that \(\mathbb {H}_\infty (\mathbf {SK}'_{i_{q'}}|\mathbf {W}) \leqslant \beta (\kappa ) + \log ^2\kappa \), we can first apply Lemma 2 and then Lemma 1 to obtain
where \(\mathcal {Q} '' := \mathcal {Q} '\setminus \{i_{q'}\}\). Notice to apply Lemma 2 we need to condition on \( sk _{i_{q'}}\in \mathcal {Q} '\), however, such condition holds with probability 1 and by conditioning on a sure event the min-entropy does not change. By iterating the above argument for each key in \(\mathcal {Q} '\):
and relying on the fact that the answer to decryption queries for a valid ciphertext and w.r.t. index \(j\in [\tau ]\) can be computed using the “tampered” projection key \( pk _i' = \mu ( sk '_i)\), we obtain
where Eq. (7) follows by Lemmas 1 and 8. Combining together Eqs. (5), (6) and (7), yields:
It follows that the decryption oracle in game \(\mathbf {G}_5\) does not reject the first invalid ciphertext with probability at most \(\epsilon \cdot 2^{\tau (p + \beta + \log ^2\kappa + \log \tau ) + \ell _\mathrm{lf}+ \ell }\). A generalization of this argument implies that, for all \(j\in [q]\), the probability that the decryption oracle does not reject the j-th decryption query of type \((0,\cdot )\) containing an invalid ciphertext is at most \(2^{\tau (p + \beta + \log ^2\kappa + \log \tau ) + \ell _\mathrm{lf}+ \ell }/(1/\epsilon - q(\kappa ))\). Finally, by a union bound over the total number of decryption queries, there exists a negligible function \(\nu _{5,6}:\mathbb {N}\rightarrow [0,1]\) such that:
where the last inequality follows by the fact that \(\alpha \geqslant \ell + \ell _\mathrm{lf}+ \tau (p+\beta + \kappa )\) and additionally \(\kappa - \log ^2\kappa - \log \tau - \log q/\tau - q\epsilon /\tau \in \omega (\log \kappa )\). \(\square \)
Lemma 16
For all (possibly unbounded) adversaries \(\mathsf {A}\), there exists a negligible function \(\nu _{6,7}:\mathbb {N}\rightarrow [0,1]\) such that \(\left|{\mathbb {P}\left[ \mathbf {G}_6(\kappa ) = 1| Inj \right] } - {\mathbb {P}\left[ \mathbf {G}_7(\kappa ) = 1| Inj \right] }\right|\le \nu _{6,7}(\kappa )\).
Proof
We analyze the conditional average min-entropy of \(\mathsf {Priv}(\mathbf {SK},C^*)\) conditioned on the view of the adversary. By a previous argument, we can write:
and thus the statement follows by our choice of parameters for the strong average-case extractor. \(\square \)
The statement of the theorem now follows by combining the above lemmas together with the fact that in \(\mathbf {G}_7\) the challenge ciphertext is independent of the hidden bit b, and thus \({\mathbb {P}\left[ \mathbf {G}_7(\kappa )| Inj \right] } = 1/2\) for all (even unbounded) adversaries. This finishes the proof.
4.3 Concrete Instantiations
The ratio \(\tfrac{\alpha - \ell - \ell _\mathrm{lf}}{p+\beta }\) plays an important role in evaluating the tampering rate of a given instantiation. Ideally, we would like to have an HPS where \(\alpha \) is as big as possible while p and \(\beta = \alpha -s\) are as small as possible. Below, we give an instantiation based on the Refined Subgroup Indistinguishability (RSI) assumption.
Instantiation based on RSI. Let \(\xi \in \mathbb {N}\) be a parameter. For security parameter \(\kappa \in \mathbb {N}\), let p and q be primes of size respectively \(\kappa \) bits and \(\xi \cdot \kappa \) bits and define \({\bar{p}}= 2pq+1\). For this choice of parameters, we have that \(\mathbb {Z} ^*_{\bar{p}}\) has a unique subgroup of order \(N = pq\). Denote by \(\mathbb {QR}_{\bar{p}}\) the set of quadratic residues modulo \({\bar{p}}\); the group \(\mathbb {QR}_{\bar{p}}\) can be decomposed as a direct product of \(\mathbb {G}_p\times \mathbb {G}_q\) where \(\mathbb {G}_p\) and \(\mathbb {G}_q\) are cyclic groups of prime order p and q (respectively).
For random  , one can show that, with overwhelming probability, \(g= x^{q} \bmod {\bar{p}}\) and \(h=y^{p} \bmod {\bar{p}}\) are generators of \(\mathbb {G}_p\) and \(\mathbb {G}_q\) (respectively). Let \( pub _\mathrm{rsi} := (\mathbb {QR}_{\bar{p}},{\bar{p}},g,h)\). The RSI assumption over \(\mathbb {QR}_{\bar{p}}\) states that for all \(\text {PPT} \) adversary \(\mathsf {A}\) the following quantity is negligible in the security parameter:
, one can show that, with overwhelming probability, \(g= x^{q} \bmod {\bar{p}}\) and \(h=y^{p} \bmod {\bar{p}}\) are generators of \(\mathbb {G}_p\) and \(\mathbb {G}_q\) (respectively). Let \( pub _\mathrm{rsi} := (\mathbb {QR}_{\bar{p}},{\bar{p}},g,h)\). The RSI assumption over \(\mathbb {QR}_{\bar{p}}\) states that for all \(\text {PPT} \) adversary \(\mathsf {A}\) the following quantity is negligible in the security parameter:

The RSI assumption over \(\mathbb {QR}_{\bar{p}}\) is conjectured to hold if factoring \(N=pq\) is hard [45]. We can derive a HPS as follow. We set \(\mathcal {C}:= \mathbb {QR}_{\bar{p}}\), \(\mathcal {V}:= \mathbb {G}_p\), \(\mathcal {SK}:= \mathbb {Z} _{\bar{p}}\), and \(\mathcal {PK}:= \mathbb {G}_p\). Given a random secret key  , the corresponding public key \( pk \) is computed as \(\mu ( sk ) := g^{ sk } \bmod {\bar{p}}\). Algorithm \(\mathsf {Pub}\), upon input \(C := g^{w}\) (where w is the witness for \(C\in \mathcal {V} \)) and \( pk \) outputs \( pk ^w \bmod {\bar{p}}\). Algorithm \(\mathsf {Priv}\), upon input C and \( sk \), outputs \(\varLambda _ sk (C) := C^ sk \bmod {\bar{p}}\). It was shown in [50] that the above construction defines a 1 / q-almost universal HPS based on the RSI assumption. The work of [50] additionally presents a construction of a OTLF achieving \(\ell _\mathrm{lf}:= \log p\) based on the RSI assumption.
, the corresponding public key \( pk \) is computed as \(\mu ( sk ) := g^{ sk } \bmod {\bar{p}}\). Algorithm \(\mathsf {Pub}\), upon input \(C := g^{w}\) (where w is the witness for \(C\in \mathcal {V} \)) and \( pk \) outputs \( pk ^w \bmod {\bar{p}}\). Algorithm \(\mathsf {Priv}\), upon input C and \( sk \), outputs \(\varLambda _ sk (C) := C^ sk \bmod {\bar{p}}\). It was shown in [50] that the above construction defines a 1 / q-almost universal HPS based on the RSI assumption. The work of [50] additionally presents a construction of a OTLF achieving \(\ell _\mathrm{lf}:= \log p\) based on the RSI assumption.
Finally, by instantiating the average-case strong extractor using universal hash functions as required by the left-over hash lemma [34] we note that the PKE scheme allows to encrypt messages with bit-length \(m = O(\xi \kappa - \tau \kappa - \ell - \kappa )\). We obtain the following result:
Corollary 3
Let \({\bar{p}}\) be as above. Under the RSI assumption over \(\mathbb {QR}_{\bar{p}}\), for any \(\xi (\kappa )=\omega (1)\), there exists a PKE scheme satisfying \((\tau ,\ell )\)-BTL-IND-CCA with tampering rate \(\rho (\kappa ) = O(1/\kappa - \tfrac{\ell }{\xi ^2\kappa })\). The size of the secret key is \(\varOmega (\xi \kappa )\), and the PKE scheme allows to encrypt messages with bit-length \(m=O(\xi \kappa - \tau \kappa - \ell - \kappa )\).
5 Conclusions and Open Problems
We have shown new constructions of public-key cryptosystems with provable security guarantees against bounded leakage and tampering attacks. The proposed schemes are in the standard model, and can be instantiated efficiently under standard complexity assumptions.
There are several interesting problems left open by our work. First, our constructions only achieve sub-optimal tampering rate \(\rho (\kappa ) = O(1/\kappa )\), so it would be interesting to find alternative constructions achieving optimal rate in the standard model. Second, it would be interesting to combine related-key attacks with related-randomness attacks [47, 48], where the adversary might force a cryptographic scheme to re-use (functions of) its own random coins; a promising idea in this direction is to combine our leakage-to-tamper reduction to so called fully leakage-resilient signatures [14, 23], where the adversary can additionally leak on the random coins of the signature algorithm. Third, it remains open how to obtain CCA security for PKE against “after-the-fact” tampering and leakage, where both tampering and leakage can still occur after the challenge ciphertext is generated (in the spirit of [33]). Finally, one could try to come-up with new hash-proof systems meeting the requirements needed for our PKE instantiation under alternative hardness assumptions.
Notes
- 1.
A similar attack works for PKE schemes, and more generally for a large class of cryptographic primitives that can be tested for malfunctioning [29]; one can also make the above attack completely stateless.
- 2.
Strictly speaking we should quantify the definition over all adversaries returning pairs \((x,y)\in R\); alternatively, we can slightly abuse notation and assume that both \(\mathsf {P}\) and \(\mathsf {S}_2\) return \(\bot \) if that is not the case.
- 3.
In particular, a pair \((x,y)\in R\) is computed by sampling random exponents
 and outputting \(x_i := g^{r_i}\) and \(y := \prod _{i=1}^{N}g_i^{r_i}\), where g is a generator of \(\mathbb {G}_2\) and \(g_1,\ldots ,g_N\) are generators of \(\mathbb {G}_1\); thus, by the SXDH assumption, it is hard to compute y given only \(x_1,\ldots ,x_N\), without knowledge of the randomness \(r_1,\ldots ,r_N\).
and outputting \(x_i := g^{r_i}\) and \(y := \prod _{i=1}^{N}g_i^{r_i}\), where g is a generator of \(\mathbb {G}_2\) and \(g_1,\ldots ,g_N\) are generators of \(\mathbb {G}_1\); thus, by the SXDH assumption, it is hard to compute y given only \(x_1,\ldots ,x_N\), without knowledge of the randomness \(r_1,\ldots ,r_N\).
References
Abdalla, M., Benhamouda, F., Passelègue, A.: An algebraic framework for pseudorandom functions and applications to related-key security. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 388–409. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_19
Applebaum, B.: Garbling XOR gates “for free” in the standard model. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 162–181. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36594-2_10
Applebaum, B., Harnik, D., Ishai, Y.: Semantic security under related-key attacks and applications. In: Innovations in Computer Science, pp. 45–60 (2011)
Applebaum, B., Widder, E.: Related-key secure pseudorandom functions: the case of additive attacks. IACR Cryptology ePrint Archive 2014, 478 (2014). http://eprint.iacr.org/2014/478
Ball, M., Dachman-Soled, D., Kulkarni, M., Malkin, T.: Non-malleable codes for bounded depth, bounded fan-in circuits. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 881–908. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_31
Bellare, M., Cash, D.: Pseudorandom functions and permutations provably secure against related-key attacks. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 666–684. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_36
Bellare, M., Cash, D., Miller, R.: Cryptography secure against related-key attacks and tampering. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 486–503. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_26
Bellare, M., Kohno, T.: A theoretical treatment of related-key attacks: RKA-PRPs, RKA-PRFs, and applications. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 491–506. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_31
Bellare, M., Meiklejohn, S., Thomson, S.: Key-versatile signatures and applications: RKA, KDM and joint Enc/Sig. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 496–513. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_28
Bellare, M., Paterson, K.G., Thomson, S.: RKA security beyond the linear barrier: IBE, encryption and signatures. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 331–348. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34961-4_21
Biham, E., Shamir, A.: Differential fault analysis of secret key cryptosystems. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 513–525. Springer, Heidelberg (1997). doi:10.1007/BFb0052259
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_3
Boneh, D., DeMillo, R.A., Lipton, R.J.: On the importance of checking cryptographic protocols for faults. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 37–51. Springer, Heidelberg (1997). doi:10.1007/3-540-69053-0_4
Boyle, E., Segev, G., Wichs, D.: Fully leakage-resilient signatures. J. Cryptology 26(3), 513–558 (2013)
Chen, Y., Qin, B., Zhang, J., Deng, Y., Chow, S.S.M.: Non-malleable functions and their applications. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 386–416. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49387-8_15
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998). doi:10.1007/BFb0055717
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). doi:10.1007/3-540-46035-7_4
Damgård, I., Faust, S., Mukherjee, P., Venturi, D.: Bounded tamper resilience: how to go beyond the algebraic barrier. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 140–160. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_8
Damgård, I., Faust, S., Mukherjee, P., Venturi, D.: The chaining lemma and its application. In: Lehmann, A., Wolf, S. (eds.) ICITS 2015. LNCS, vol. 9063, pp. 181–196. Springer, Heidelberg (2015). doi:10.1007/978-3-319-17470-9_11
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Efficient public-key cryptography in the presence of key leakage. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 613–631. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17373-8_35
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Dziembowski, S., Pietrzak, K., Wichs, D.: Non-malleable codes. In: Innovations in Computer Science, pp. 434–452 (2010)
Faonio, A., Nielsen, J.B., Venturi, D.: Mind your coins: fully leakage-resilient signatures with graceful degradation. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9134, pp. 456–468. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47672-7_37
Faonio, A., Venturi, D.: Efficient public-key cryptography with bounded leakage and tamper resilience. Cryptology ePrint Archive, Report 2016/529 (2016). http://eprint.iacr.org/2016/529
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: Continuous non-malleable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 465–488. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_20
Faust, S., Mukherjee, P., Venturi, D., Wichs, D.: Efficient non-malleable codes and key-derivation for poly-size tampering circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 111–128. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_7
Faust, S., Pietrzak, K., Venturi, D.: Tamper-proof circuits: how to trade leakage for tamper-resilience. In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011. LNCS, vol. 6755, pp. 391–402. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22006-7_33
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). doi:10.1007/3-540-47721-7_12
Gennaro, R., Lysyanskaya, A., Malkin, T., Micali, S., Rabin, T.: Algorithmic tamper-proof (ATP) security: theoretical foundations for security against hardware tampering. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 258–277. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24638-1_15
Goldenberg, D., Liskov, M.: On related-secret pseudorandomness. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 255–272. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11799-2_16
Goyal, V., O’Neill, A., Rao, V.: Correlated-input secure hash functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 182–200. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_12
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_24
Halevi, S., Lin, H.: After-the-fact leakage in public-key encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 107–124. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_8
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Hofheinz, D., Kiltz, E.: Secure hybrid encryption from weakened key encapsulation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 553–571. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74143-5_31
Ishai, Y., Prabhakaran, M., Sahai, A., Wagner, D.: Private circuits II: keeping secrets in tamperable circuits. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 308–327. Springer, Heidelberg (2006). doi:10.1007/11761679_19
Jafargholi, Z., Wichs, D.: Tamper detection and continuous non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 451–480. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_19
Katz, J., Vaikuntanathan, V.: Signature schemes with bounded leakage resilience. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 703–720. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_41
Katz, J., Vaikuntanathan, V.: Signature schemes with bounded leakage resilience. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 703–720. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_41
Lewi, K., Montgomery, H., Raghunathan, A.: Improved constructions of PRFs secure against related-key attacks. In: Boureanu, I., Owesarski, P., Vaudenay, S. (eds.) ACNS 2014. LNCS, vol. 8479, pp. 44–61. Springer, Heidelberg (2014). doi:10.1007/978-3-319-07536-5_4
Liu, F.-H., Lysyanskaya, A.: Tamper and leakage resilience in the split-state model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 517–532. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_30
Lu, X., Li, B., Jia, D.: Related-key security for hybrid encryption. In: Chow, S.S.M., Camenisch, J., Hui, L.C.K., Yiu, S.M. (eds.) ISC 2014. LNCS, vol. 8783, pp. 19–32. Springer, Heidelberg (2014). doi:10.1007/978-3-319-13257-0_2
Lucks, S.: Ciphers secure against related-key attacks. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 359–370. Springer, Heidelberg (2004). doi:10.1007/978-3-540-25937-4_23
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 18–35. Springer, Heidelberg (2009)
Nieto, J.M.G., Boyd, C., Dawson, E.: A public key cryptosystem based on a subgroup membership problem. Des. Codes Crypt. 36(3), 301–316 (2005)
Otto, M.: Fault Attacks and Countermeasures. Ph.D. thesis, University of Paderborn, Germany (2006)
Paterson, K.G., Schuldt, J.C.N., Sibborn, D.L.: Related randomness attacks for public key encryption. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 465–482. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_27
Paterson, K.G., Schuldt, J.C.N., Sibborn, D.L., Wee, H.: Security against related randomness attacks via reconstructive extractors. In: Groth, J. (ed.) IMACC 2015. LNCS, vol. 9496, pp. 23–40. Springer, Heidelberg (2015). doi:10.1007/978-3-319-27239-9_2
Qin, B., Liu, S.: Leakage-resilient chosen-ciphertext secure public-key encryption from hash proof system and one-time lossy filter. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 381–400. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_20
Qin, B., Liu, S.: Leakage-flexible CCA-secure public-key encryption: simple construction and free of pairing. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 19–36. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_2
Qin, B., Liu, S., Yuen, T.H., Deng, R.H., Chen, K.: Continuous non-malleable key derivation and its application to related-key security. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 557–578. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_25
Scott, M.: Authenticated ID-based key exchange and remote log-in with simple token and PIN number. IACR Cryptology ePrint Archive 2002, 164 (2002). http://eprint.iacr.org/2002/164
Shacham, H.: A Cramer-Shoup encryption scheme from the linear assumption and from progressively weaker linear variants. IACR Cryptology ePrint Archive 2007, 74 (2007). http://eprint.iacr.org/2007/074
Wee, H.: Public key encryption against related key attacks. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 262–279. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_16
Acknowledgments
The authors would like to thank Jesper Buus Nielsen for an interesting conversation regarding the result in Sect. 4. Antonio Faonio was supported by European Research Council Starting Grant 279447.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Faonio, A., Venturi, D. (2016). Efficient Public-Key Cryptography with Bounded Leakage and Tamper Resilience. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10031. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53887-6_32
Download citation
DOI: https://doi.org/10.1007/978-3-662-53887-6_32
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53886-9
Online ISBN: 978-3-662-53887-6
eBook Packages: Computer ScienceComputer Science (R0)







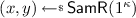 we have
we have 
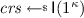 .
.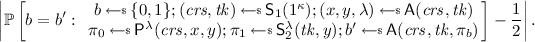

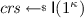 and return
and return  and define
and define  and return
and return  .
.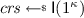 we now run
we now run  and additionally we replace the proofs output by oracle
and additionally we replace the proofs output by oracle  where
where  .
. , set
, set  to
to  to
to  .
. , set
, set  .
. , set
, set  and return
and return  .
. be generators. The sampling algorithm chooses a random
be generators. The sampling algorithm chooses a random 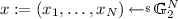 and defines
and defines 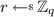 , and where
, and where  be generators. The sampling algorithm chooses a random
be generators. The sampling algorithm chooses a random 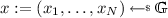 and defines
and defines 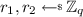 , and where
, and where 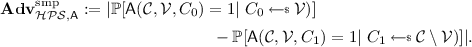
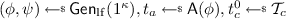 and
and  .
.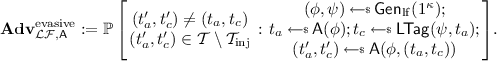
 and compute
and compute  . Return
. Return  , define
, define  (with witness w),
(with witness w),  , and a core tag
, and a core tag  . Compute
. Compute  .
. . Notice that the challenge ciphertext is now independent of the message being encrypted.
. Notice that the challenge ciphertext is now independent of the message being encrypted. and outputting
and outputting