When Are Fuzzy Extractors Possible?

Abstract

Fuzzy extractors (Dodis et al., Eurocrypt 2004) convert repeated noisy readings of a high-entropy secret into the same uniformly distributed key. A minimum condition for the security of the key is the hardness of guessing a value that is similar to the secret, because the fuzzy extractor converts such a guess to the key.

We define fuzzy min-entropy to quantify this property of a noisy source of secrets. Fuzzy min-entropy measures the success of the adversary when provided with only the functionality of the fuzzy extractor, that is, the ideal security possible from a noisy distribution. High fuzzy min-entropy is necessary for the existence of a fuzzy extractor.

We ask: is high fuzzy min-entropy a sufficient condition for key extraction from noisy sources? If only computational security is required, recent progress on program obfuscation gives evidence that fuzzy min-entropy is indeed sufficient. In contrast, information-theoretic fuzzy extractors are not known for many practically relevant sources of high fuzzy min-entropy.

In this paper, we show that fuzzy min-entropy is sufficient for information theoretically secure fuzzy extraction. For every source distribution W for which security is possible we give a secure fuzzy extractor.

Our construction relies on the fuzzy extractor knowing the precise distribution of the source W. A more ambitious goal is to design a single extractor that works for all possible sources. Our second main result is that this more ambitious goal is impossible: we give a family of sources with high fuzzy min-entropy for which no single fuzzy extractor is secure. We show three flavors of this impossibility result: for standard fuzzy extractors, for fuzzy extractors that are allowed to sometimes be wrong, and for secure sketches, which are the main ingredient of most fuzzy extractor constructions.

1 Introduction

Sources of reproducible secret random bits are necessary for many cryptographic applications. In many situations these bits are not explicitly stored for future use, but are obtained by repeating the same process (such as reading a biometric or a physically unclonable function) that generated them the first time. However, bits obtained this way present a problem: noise [4, 8, 12, 14, 19, 30, 31, 33, 37, 39, 43]. That is, when a secret is read multiple times, readings are close (according to some metric) but not identical. To utilize such sources, it is often necessary to remove noise, in order to derive the same value in subsequent readings.

The same problem occurs in the interactive setting, in which the secret channel used for transmitting the bits between two users is noisy and/or leaky [42]. Bennett, Brassard, and Robert [4] identify two fundamental tasks. The first, called information reconciliation, removes the noise without leaking significant information. The second, known as privacy amplification, converts the high entropy secret to a uniform random value. In this work, we consider the noninteractive version of these problems, in which these tasks are performed together with a single message.

The noninteractive setting is modeled by a primitive called a fuzzy extractor [13], which consists of two algorithms. The generate algorithm (${\mathsf {Gen}}$) takes an initial reading w and produces an output ${\mathsf {key}}$ along with a nonsecret helper value p. The reproduce (${\mathsf {Rep}}$) algorithm takes the subsequent reading $w'$ along with the helper value p to reproduce ${\mathsf {key}}$. The correctness guarantee is that the key is reproduced precisely when the distance between w and $w'$ is at most t.

The security requirement for fuzzy extractors is that ${\mathsf {key}}$ is uniform even to a (computationally unbounded) adversary who has observed p. This requirement is harder to satisfy as the allowed error tolerance t increases, because it becomes easier for the adversary to guess ${\mathsf {key}}$ by guessing a $w'$ within distance t of w and running ${\mathsf {Rep}} (w',p)$.

Fuzzy Min-Entropy. We introduce a new entropy notion that precisely measures how hard it is for the adversary to guess a value within distance t of the original reading w. Suppose w is sampled from a distribution W. To have the maximum chance that $w'$ is within distance t of w, the adversary would want to maximize the total probability mass of W within the ball $B_t(w')$ of radius t around $w'$. We therefore define fuzzy min-entropy

$$\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) \mathop {=}\limits ^\mathrm{def}-\log \max _{w'} \Pr [W\in B_t(w')].$$

The security of the resulting key cannot exceed the fuzzy min-entropy (Proposition 1).

However, existing constructions do not measure their security in terms of fuzzy min-entropy; instead, their security is shown to be the min-entropy of W, denoted $\mathrm {H}_\infty (W)$, minus some loss, for error-tolerance, that is at least $\log |B_t|$.¹ Since (trivially) $\mathrm {H}_\infty (W)-\log |B_t| \le \mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$, it is natural to ask whether this loss is necessary. This question is particularly relevant when the gap between the two sides of the inequality is high.² As an example, iris scans appear to have significant $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ (because iris scans for different people appear to be well-spread in the metric space [11]) but negative $\mathrm {H}_\infty (W) -\log |B_t|$ [6, Sect. 5]. We therefore ask: is fuzzy min-entropy sufficient for fuzzy extraction? There is evidence that it may be sufficient when the security requirement is computational rather than information-theoretic—see Sect. 1.2. We provide an answer for the case of information-theoretic security in two settings.

Contribution 1: Sufficiency of $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ for a Precisely Known W . It should be easier to construct a fuzzy extractor when the designer has precise knowledge of the probability distribution function of W. In this setting, we show that it is possible to construct a fuzzy extractor that extracts a ${\mathsf {key}}$ almost as long as $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ (Theorem 1). Our construction crucially utilizes the probability distribution function of W and, in particular, cannot necessarily be realized in polynomial time (this is similar, for example, to the interactive information-reconciliation feasibility result of [34]). This result shows that $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ is a necessary and sufficient condition for building a fuzzy extractor for a given distribution W.

A number of previous works in the precise knowledge setting have provided efficient algorithms and tight bounds for specific distributions—generally the uniform distribution or i.i.d. sequences (for example, [20, 26–28, 38, 41]). Our characterization unifies previous work, and justifies using $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ as the measure of the quality of a noisy distribution, rather than cruder measures such as $\mathrm {H}_\infty (W)-\log |B_t|$. Our construction can be viewed as a reference to evaluate the quality of efficient constructions in the precise knowledge setting by seeing how close they get to extracting all of $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$.

Contribution 2: The Cost of Distributional Uncertainty. Assuming precise knowledge of a distribution W is often unrealistic for high-entropy distributions; they can never be fully observed directly and must therefore be modeled. It is imprudent to assume that the designer’s model of a distribution is completely accurate—the adversary, with greater resources, would likely be able to build a better model. (In particular, the adversary has more time to build the model after a particular construction is deployed.) Because of this, existing designs work for a family of sources (for example, all sources of min-entropy at least m with at most t errors). The fuzzy extractor is designed given only knowledge of the family. The attacker may know more about the distribution than the designer. We call this the distributional uncertainty setting.

Our second contribution is a set of negative results for this more realistic setting. We provide two impossibility results for fuzzy extractors. Both demonstrate families $\mathcal {W}$ of distributions over $\{0,1\}^n$ such that each distribution in the family has $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$ linear in n, but no fuzzy extractor can be secure for most distributions in $\mathcal {W}$. Thus, a fuzzy extractor designer who knows only that the distribution comes from $\mathcal {W}$ is faced with an impossible task, even though our positive result, Theorem 1, shows that fuzzy extractors can be designed for each distribution in the family individually.

The first impossibility result (Theorem 2) assumes that ${\mathsf {Rep}}$ is perfectly correct and rules our fuzzy extractors for entropy rates as high as $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)\approx 0.18n$. The second impossibility result (Theorem 3), relying on the work of Holenstein and Renner [25], also rules out fuzzy extractors in which ${\mathsf {Rep}}$ is allowed to make a mistake, but applies only to distributions with entropy rates up to $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)\approx 0.07n$.

We also provide a third impossibility result (Theorem 4), this time for an important building block called “secure sketch,” which is used in most fuzzy extractor constructions (in order to allow ${\mathsf {Rep}}$ to recover the original w from the input $w'$). The result rules out secure sketches for a family of distributions with entropy rate up to 0.5n, even if the secure sketches are allowed to make mistakes. Because secure sketches are used in most fuzzy extractors constructions, the result suggests that building a fuzzy extractor for this family will be very difficult. We define secure sketches formally in Sect. 7.

These impossibility results motivate further research into computationally, rather information-theoretically, secure fuzzy extractors (Sect. 1.2).

1.1 Our Techniques

Techniques for Positive Results for a Precisely Known Distribution. We now explain how to construct a fuzzy extractor for a precisely known distribution W with fuzzy min-entropy. We begin with distributions in which all points in the support have the same probability (so-called “flat” distributions). ${\mathsf {Gen}}$ simply extracts a key from the input w using a randomness extractor. Consider some subsequent reading $w'$. To achieve correctness, the string p must permit ${\mathsf {Rep}}$ to disambiguate which point $w\in W$ within distance t of $w'$ was given to ${\mathsf {Gen}}$. Disambiguating multiple points can be accomplished by universal hashing, as long as the size of hash output space is slightly greater than the number of possible points. Thus, ${\mathsf {Rep}}$ includes into the public value p a “sketch” of w computed via a universal hash of w. To determine the length of that sketch, consider the heaviest (according to W) ball $B^*$ of radius t. Because the distribution is flat, $B^*$ is also the ball with the most points of nonzero probability. Thus, the length of the sketch needs to be slightly greater than the logarithm of the number of non-zero probability points in $B^*$. Since $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ is determined by the weight of $B^*$, the number of points cannot be too high and there will be entropy left after the sketch is published. This remaining entropy suffices to extract a key.

For an arbitrary distribution, we cannot afford to disambiguate points in the ball with the greatest number of points, because there could be too many low-probability points in a single ball despite a high $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$. We solve this problem by splitting the arbitrary distribution into a number of nearly flat distributions we call “levels.” We then write down, as part of the sketch, the level of the original reading w and apply the above construction considering only points in that level. We call this construction leveled hashing (Construction 1).

Techniques for Negative Results for Distributional Uncertainty. We construct a family of distributions $\mathcal {W}$ and prove impossibility for a uniformly random $W \leftarrow \mathcal {W}$. We start by observing the following asymmetry: ${\mathsf {Gen}}$ sees only the sample w (obtained via $W\leftarrow \mathcal {W}$ and $w\leftarrow W$), while the adversary knows W.

To exploit the asymmetry, in our first impossibility result (Theorem 2), we construct $\mathcal {W}$ so that conditioning on the knowledge of W reduces the distribution to a small subspace (namely, all points on which a given hash function produces a given output), but conditioning on only w leaves the rest of the distribution uniform on a large fraction of the entire space. An adversary can exploit the knowledge of the hash value to reduce the uncertainty about ${\mathsf {key}}$, as follows.

The nonsecret value p partitions the metric space into regions that produce a consistent value under ${\mathsf {Rep}}$ (preimages of each ${\mathsf {key}}$ under ${\mathsf {Rep}} (\cdot , p)$). For each of these regions, the adversary knows that possible w lie at distance at least t from the boundary of the region (else, the fuzzy extractor would have a nonzero probability of error). However, in the Hamming space, the vast majority of points lie near the boundary (this result follows by combining the isoperimetric inequality [21], which shows that the ball has the smallest boundary, with bounds on the volume of the interior of a ball, which show that this boundary is large). This allows the adversary to rule out so many possible w that, combined with the adversarial knowledge of the hash value, many regions become empty, leaving ${\mathsf {key}}$ far from uniform.

For the second impossibility result (Theorem 3, which rules out even fuzzy extractors that are allowed a possibility of error), we let the adversary know some fraction of the bits of w. Holenstein and Renner [25] showed that if the adversary knows each bit of w with sufficient probability, and bits of $w'$ differ from bits of w with sufficient probability, then so-called “information-theoretic key agreement” is impossible. Converting the impossibility of information-theoretic key agreement to impossibility of fuzzy extractors takes a bit of technical work.

1.2 Related Settings

Other Settings with Close Readings: $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$ is Sufficient. The security definition of fuzzy extractors can be weakened to protect only against computationally bounded adversaries [17]. In this computational setting, for most distance metrics a single fuzzy extractor can simultaneously secure all possible distributions by using virtual grey-box obfuscation for all circuits in $\mathtt {NC}^1$ [5]. This construction is secure when the adversary can rarely learn ${\mathsf {key}}$ with oracle access to the program functionality. The set of distributions with fuzzy min-entropy are exactly those where an adversary learns ${\mathsf {key}}$ with oracle access to the functionality with negligible probability. Thus, extending our negative result to the computational setting would have negative implications on the existence of obfuscation.

Furthermore, the functional definition of fuzzy extractors can be weakened to permit interaction between the party having w and the party having $w'$. Such a weakening is useful for secure remote authentication [7]. When both interaction and computational assumptions are allowed, secure two-party computation can produce a key that will be secure whenever the distribution W has fuzzy min-entropy. The two-party computation protocol needs to be secure without assuming authenticated channels; it can be built under the assumptions that collision-resistant hash functions and enhanced trapdoor permutations exist [3].

Correlated Rather than Close Readings. A different model for the problem of key derivation from noisy sources does not explicitly consider the distance between w and $w'$, but rather views w and $w'$ as samples of drawn from a correlated pair of random variables. This model is considered in multiple works, including [1, 10, 29, 42]; recent characterizations of when key derivation is possible in this model include [35, 40]. In particular, Hayashi et al. [22] independently developed an interactive technique similar to our non-interactive leveled hashing, which they called “spectrum slicing.” To the best of our knowledge, prior results on correlated random variables are in the precise knowledge setting; we are unaware of works that consider the cost of distributional uncertainty.

2 Preliminaries

Random Variables. We generally use uppercase letters for random variables and corresponding lowercase letters for their samples. A repeated occurrence of the same random variable in a given expression signifies the same value of the random variable: for example $(W, {\mathsf {SS}} (W))$ is a pair of random variables obtained by sampling w according to W and applying the algorithm ${\mathsf {SS}}$ to w.

The statistical distance between random variables A and B with the same domain is $\mathbf {SD}(A,B) = \frac{1}{2} \sum _a |\Pr [A=a] - \Pr [B=b]| = \max _S \Pr [A\in S]-\Pr [B\in ~S]$.

Entropy. Unless otherwise noted logarithms are base 2. Let (X, Y) be a pair of random variables. Define min-entropy of X as $\mathrm {H}_\infty (X) = -\log (\max _x \Pr [X=x])$, and the average (conditional) min-entropy of X given Y as $\tilde{\mathrm {H}}_\infty (X|Y) =~-\log ({{\mathrm{\mathbb {E}}}}_{y\in Y} \max _{x} \Pr [X=x|Y=y])$ [13, Sect. 2.4]. Define Hartley entropy $H_0(X)$ to be the logarithm of the size of the support of X, that is $H_0(X) = \log |\{x | \Pr [X=x]>0\}|$. Define average-case Hartley entropy by averaging the support size: $\tilde{H}_0(X |Y) = \log ({{\mathrm{\mathbb {E}}}}_{y\in Y} |\{y | \Pr [X=x |Y=y]>0\}|)$. For $0<a<1$, define the binary entropy $h_2(p) = -p \log p - (1-p)\log (1-p)$ as the Shannon entropy of any random variable that is 0 with probability p and 1 with probability $1-p$.

Randomness Extractors. We use randomness extractors [32], as defined for the average case in [13, Sect. 2.5].

Definition 1

Let $\mathcal {M}$, $\chi$ be finite sets. A function $\mathtt {ext}: \mathcal {M}\times \{0,1\}^d \rightarrow \{0,1\}^\kappa$ a $(\tilde{m}, \epsilon )$ -average case extractor if for all pairs of random variables X, Y over $\mathcal {M}, \chi$ such that $\tilde{H}_\infty (X|Y) \ge \tilde{m}$, we have

$$\mathbf {SD}((\mathtt {ext}(X, U_d), U_d, Y), U_\kappa \times U_d \times Y) \le \epsilon .$$

Metric Spaces and Balls. For a metric space $(\mathcal {M}, \mathsf {dis})$, the (closed) ball of radius t around w is the set of all points within radius t, that is, $B_t(w) = \{w'| \mathsf {dis}(w, w')\le t\}$. If the size of a ball in a metric space does not depend on w, we denote by $|B_t|$ the size of a ball of radius t. We consider the Hamming metric over vectors in $\mathcal {Z}^n$ for some finite alphabet $\mathcal {Z}$, defined via $\mathsf {dis}(w,w') = |\{i | w_i \ne w'_i\}|$. $U_\kappa$ denotes the uniformly distributed random variable on $\{0,1\}^\kappa$.

We will use the following bounds on $|B_t|$ in $\{0,1\}^n$, see [2, Lemma 4.7.2, Eq. 4.7.5, p. 115] for proofs.

Lemma 1

Let $\tau =t/n$. The volume $|B_t|$ of the ball of radius in t in the Hamming space $\{0,1\}^n$ satisfies

$$ \frac{1}{\sqrt{8n\tau (1-\tau )}} \cdot 2^{nh_2(\tau )}\le |B_t|\le 2^{nh_2(\tau )}. $$

2.1 Fuzzy Extractors

In this section, we define fuzzy extractors, slightly modified from the work of Dodis et al. [13, Sect. 3.2]. First, we allow for error as discussed in [13, Sect. 8]. Second, in the distributional uncertainty setting we consider a general family $\mathcal {W}$ of distributions instead of families containing all distributions of a given min-entropy. Let $\mathcal {M}$ be a metric space with distance function $\mathsf {dis}$.

Definition 2

An $(\mathcal {M}, \mathcal {W}, \kappa , t, \epsilon )$-fuzzy extractor with error $\delta$ is a pair of randomized procedures, “generate” $({\mathsf {Gen}})$ and “reproduce” $({\mathsf {Rep}})$. ${\mathsf {Gen}}$ on input $w\in \mathcal {M}$ outputs an extracted string ${\mathsf {key}} \in \{0,1\}^\kappa$ and a helper string $p\in \{0,1\}^*$. ${\mathsf {Rep}}$ takes $w'\in \mathcal {M}$ and $p\in \{0,1\}^*$ as inputs. $({\mathsf {Gen}}, {\mathsf {Rep}})$ have the following properties:

• 1. Correctness: if $\mathsf {dis}(w, w')\le t$ and $({\mathsf {key}}, p)\leftarrow {\mathsf {Gen}} (w)$, then $\Pr [{\mathsf {Rep}} (w', p) = {\mathsf {key}} ] \ge 1-\delta .$

• 2. Security: for any distribution $W\in \mathcal {W}$, if $({\mathsf {Key}},P)\leftarrow {\mathsf {Gen}} (W)$, then $\mathbf {SD}(({\mathsf {Key}},P),(U_\kappa ,P))\le \epsilon .$

In the above definition, the errors must be chosen before p is known in order for the correctness guarantee to hold.

The Case of a Precisely Known Distribution. If in the above definition we take $\mathcal {W}$ to be a one-element set containing a single distribution W, then the fuzzy extractor is said to be for a precisely known distribution. In this case, we need to require correctness only for w that have nonzero probability. Note that we have no requirement that the algorithms are compact or efficient, and so the distribution can be fully known to them.

3 New Notion: Fuzzy Min-Entropy

The fuzzy extractor helper string p allows everyone, including the adversary, to find the output of ${\mathsf {Rep}} (\cdot , p)$ on any input $w'$. Ideally, p should not provide any useful information beyond this ability, and the outputs of ${\mathsf {Rep}}$ on inputs that are too distant from w should provide no useful information, either. In this ideal scenario, the adversary is limited to trying to guess a $w'$ that is t-close to w. Letting $w'$ be the center of the maximum-weight ball in W is optimal, we measure the quality of a source by (the negative logarithm of) this weight.

Definition 3

The t-fuzzy min-entropy of a distribution W in a metric space $(\mathcal {M}, \mathsf {dis})$ is:

$$ \mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) = -\log \left( \max _{w'} \sum _{w\in \mathcal {M}| \mathsf {dis}(w, w')\le t} \Pr [W=w] \right) $$

Fuzzy min-entropy measures the functionality provided to the adversary by ${\mathsf {Rep}}$ (since p is public), and thus is a necessary condition for security. We formalize this statement in the following proposition.

Proposition 1

Let W be a distribution over $(\mathcal {M}, \mathsf {dis})$ with $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) =m$. Let $({\mathsf {Gen}}, {\mathsf {Rep}})$ be a $(\mathcal {M}, \{W\}, \kappa , t, \epsilon )$-fuzzy extractor with error $\delta$. Then

$$ 2^{-\kappa }\ge 2^{-m}-\delta -\epsilon . $$

If $\delta =\epsilon =2^{-\kappa }$, then $\kappa$ cannot exceed $m+2$. Additionally, if fuzzy min-entropy of the source is only logarithmic in a security parameter while the $\delta$ and $\epsilon$ parameters are negligible, then extracted key must be of at most logarithmic length.

Proof

Let W be a distribution where $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) = m$. This means that there exists a point $w' \in \mathcal {M}$ such that $\Pr _{w\in W}[\mathsf {dis}(w, w')\le t] = 2^{-m}$. Consider the following distinguisher D: on input $({\mathsf {key}}, p)$, if ${\mathsf {Rep}} (w', p) = {\mathsf {key}}$, then output 1, else output 0.

$\Pr [D({\mathsf {Key}}, P) = 1]\ge 2^{-m} - \delta$, while $\Pr [D(U_\kappa , P)=1 ]= 1/2^{-\kappa }$. Thus,

$$ \mathbf {SD}(({\mathsf {Key}}, P), (U_\kappa , P)) \ge \delta ^D(({\mathsf {Key}}, P), (U_\kappa , P))\ge 2^{-m} -\delta -2^{-\kappa }. $$

   $\square$

Proposition 1 extends to the settings of computational security and interactive protocols. Fuzzy min-entropy represents an upper bound on the security from a noisy source. However, there are many distributions with fuzzy min-entropy with no known information-theoretically secure fuzzy extractor (or corresponding impossibility result).

We explore other properties of fuzzy min-entropy, not necessary for the proofs presented here, in the full version [18, Appendix E].

4 $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ is Sufficient in the Precise Knowledge Setting

In this section, we build fuzzy extractors that extract almost all of $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ for any distribution W. We reiterate that these constructions assume precise knowledge of W and are not necessarily polynomial-time. They should thus be viewed as feasibility results. We begin with flat distributions and then turn to arbitrary distributions.

4.1 Warm-Up for Intuition: Fuzzy Extractor for Flat Distributions

Let ${\text {supp}}(W)=\{w|\Pr [W=w]>0\}$ denote the support of a distribution W. A distribution W is flat if all elements of ${\text {supp}}(W)$ have the same probability. Our construction for this case is quite simple: to produce p, ${\mathsf {Gen}}$ outputs a hash of its input point w and an extractor seed; to produce ${\mathsf {key}}$, ${\mathsf {Gen}}$ applies the extractor to w. Given $w'$, ${\mathsf {Rep}}$ looks for $w\in {\text {supp}}(W)$ that is near $w'$ and has the correct hash value, and applies the extractor to this w to get ${\mathsf {key}}$.

The specific hash function we use is universal. (We note that universal hashing has a long history of use for information reconciliation, for example [4, 34, 36]. This construction is not novel; rather, we present it as a stepping stone for the case of general distributions).

Definition 4

([9]). Let $F : \mathcal {K} \times \mathcal {M}\rightarrow R$ be a function. We say that F is universal if for all distinct $x_1, x_2 \in \mathcal {M}$:

$$ \mathop {\Pr }\limits _{K \leftarrow \mathcal {K}}[F(K, x_1) = F(K, x_2)] = \frac{1}{|R|} \;. $$

In our case, the hash output length needs to be sufficient to disambiguate elements of ${\text {supp}}(W) \cap B_t(w')$ with high probability. Observe that there are at most $2^{\mathrm {H}_\infty (W)-\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)}$ such elements when W is flat, so output length slightly greater (by $\log 1/\delta$) than $\mathrm {H}_\infty (W)-\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ will suffice. Thus, the output ${\mathsf {key}}$ length will be $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)-\log 1/\delta - 2\log 1/\epsilon +2$ (by using average-case leftover hash lemma, per [13, Lemmas 2.2b and 2.4]). As this construction is only a warm-up, so we do not state it formally and proceed to general distributions.

4.2 Fuzzy Extractor for Arbitrary Distributions

The hashing approach used in the previous subsection does not work for arbitrary sources. Consider a distribution W consisting of the following balls: $B^1_t$ is a ball with $2^{\mathrm {H}_\infty (W)}$ points with total probability $\Pr [W\in B^1_t] =2^{-\mathrm {H}_\infty (W)}$, $B^2_t,..., B^{2^{-\mathrm {H}_\infty (W)}}_t$ are balls with one point each with probability $\Pr [W\in B^i_t] = 2^{-\mathrm {H}_\infty (W)}$. The above hashing algorithm writes down $\mathrm {H}_\infty (W)$ bits to achieve correctness on $B^1_t$. However, with probability $1-2^{-\mathrm {H}_\infty (W)}$ the initial reading is outside of $B^1_t$, and the hash completely reveals the point.

Instead, we use a layered approach: we separate the input distribution W into nearly-flat layers, write down the layer from which the input w came (i.e., the approximate probability of w) as part of p, and rely on the construction from the previous part for each layer. In other words, the hash function output is now variable-length, longer if probability of w is lower. Thus, p now reveals a bit more about w. To limit this information and the resulting security loss, we limit number of layers. As a result, we lose only $1+\log H_0(W)$ more bits of security compared to the previous section. We emphasize that this additional loss is quite small: if W is over $\{0,1\}^n$, it is only $1+\log n$ bits (so, for example, only 11 bits if W is 1000 bits long, and no more than 50 bits for any remotely realistic W). We thus obtain the following theorem.

Theorem 1

For any metric space $\mathcal {M}$, distribution W over $\mathcal {M}$, distance t, error $\delta >0$, and security $\epsilon >0$, there exists a $(\mathcal {M}, \{W\}, \kappa , t, \epsilon )$-known distribution fuzzy extractor with error $\delta$ for $\kappa = \mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) - \log H_0(W) - \log 1/\delta - 2\log 1/\epsilon + 1$. (Note that the value $\log H_0(W)$ is doubly logarithmic in the size of the support of W and is smaller than $\log 1/\delta$ and $\log 1/\epsilon$ for typical setting of parameters.)

We provide the construction and the proof in Appendix A. The main idea is that providing the level information makes the distribution look nearly flat (the probability of points differs by at most a factor of two, which increases the entropy loss as compared to the flat case by only one bit). And the level information itself increases the entropy loss by $\log H_0(W)$ bits, because there are only $H_0(W)$ levels that contain enough weight to matter.

5 Impossibility of Fuzzy Extractors for Family with $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$

In the previous section, we showed the sufficiency of $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ for building fuzzy extractors when the distribution W is precisely known. However, it may be infeasible to completely characterize a high-entropy distribution W. Traditionally, algorithms deal with this distributional uncertainty by providing security for a family of distributions $\mathcal {W}$. In this section, we show that distributional uncertainty comes at a real cost.

We demonstrate an example over the binary Hamming metric in which every $W\in \mathcal {W}$ has linear $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)$ (which is in fact equal to $\mathrm {H}_\infty (W)$), and yet there is some $W\in \mathcal {W}$ where even for 3-bit output keys and high constant $\epsilon =\frac{1}{4}$. In fact, we show that the adversary need not work hard: even a uniformly random choice of distribution W from $\mathcal {W}$ will thwart the security of any $({\mathsf {Gen}}, {\mathsf {Rep}})$. The one caveat is that, for this result, we require ${\mathsf {Rep}}$ to be always correct (i.e., $\delta =0$). As mentioned in the introduction, this perfect correctness requirement is removed in Sects. 6 and 7 at a cost of lower entropy rate and stronger primitive, respectively.

As basic intuition, the result is based on the following reasoning: ${\mathsf {Gen}}$ sees only a random sample w from a random $W\in \mathcal {W}$, but not W. The adversary sees W but not w. Because ${\mathsf {Gen}}$ does not know which W the input w came from, ${\mathsf {Gen}}$ must produce p that works for many distributions W that contain w in their support. Such p must necessarily reveal a lot of information. The adversary can combine information gleaned from p with information about W to narrow down the possible choices for w and thus distinguish ${\mathsf {key}}$ from uniform.

Theorem 2

Let $\mathcal {M}$ denote the Hamming space $\{0, 1\}^n$. There exists a family of distributions $\mathcal {W}$ over $\mathcal {M}$ such that for each element $W \in \mathcal {W}$, $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)=\mathrm {H}_\infty (W) \ge m$, and yet any $(\mathcal {M}, \mathcal {W}, \kappa , t, \epsilon )$-fuzzy extractor with error $\delta = 0$ has $\epsilon > 1/4$.

This holds as long as $\kappa \ge 3$ and under the following conditions on the entropy rate $\mu =m/n$, noise rate $\tau =t/n$, and n:

• any $0\le \tau < \frac{1}{2}$ and $\mu >0$ such that $\mu< 1-h_2(\tau ) \text{ and } \mu < 1- h_2\left( \frac{1}{2}-\tau \right)$

• any $n\ge \max \left( \frac{2}{1-h_2(\tau )-\mu },\frac{5}{1- h_2\left( \frac{1}{2}-\tau \right) -\mu }\right)$.

Fig. 1.

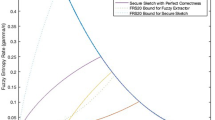
The region of $\tau$ (x-axis) and $\mu$ (y-axis) pairs for which Theorem 2 applies is the region below both curves.

Note that the conditions on $\mu$ and $\tau$ imply the result applies to any entropy rate $\mu \le .18$ as long as $\tau$ is set appropriately and n is sufficiently large (for example, the result applies to $n\ge 1275$ and $\tau = .6\sqrt{\mu }$ when $0.08\le \mu \le .18$; similarly, it applies to $n\ge 263$ and $\tau = \sqrt{\mu }$ when $0.01\le \mu \le 0.08$). The $\tau$ vs. $\mu$ tradeoff is depicted in Fig. 1.

Proof (Sketch)

Here we describe the family $\mathcal {W}$ and provide a brief overview of the main proof ideas. We provide a full proof in Appendix B. We will show the theorem holds for an average member of $\mathcal {W}$. Let Z denote a uniform choice of W from $\mathcal {W}$ and denote by $W_z$ the choice specified by a particular value of z.

Let $\{\mathsf {Hash}_\mathsf {k}\}_{\mathsf {k}\in {\mathcal {K}}}$ be a family of hash function with domain $\mathcal {M}$ and the following properties:

• $2^{-{a}}$-universality: for all $v_1\ne v_2 \in \mathcal {M}$, $\Pr _{\mathsf {k}\leftarrow {\mathcal {K}}} [\mathsf {Hash}_\mathsf {k}(v_1)=\mathsf {Hash}_\mathsf {k}(v_2)]\le 2^{-{a}}$, where ${a}= n\cdot h_2\left( \frac{1}{2}-\tau \right) +3$.

• $2^m$-regularity: for each $\mathsf {k}\in {\mathcal {K}}$ and $\mathsf {h}$ in the range of $\mathsf {Hash}_\mathsf {k}$, $|\mathsf {Hash}_\mathsf {k}^{-1}(\mathsf {h})|=2^m$, where $m\ge \mu n$.

• preimage sets have minimum distance $t+1$: for all $\mathsf {k}\in {\mathcal {K}}$, if $v_1\ne v_2$ but $\mathsf {Hash}_\mathsf {k}(v_1)=\mathsf {Hash}_\mathsf {k}(v_2)$, then $\mathsf {dis}(v_1, v_2)> t$.

We show such a hash family exists in Appendix B. Let Z be the random variable consisting of pairs $(\mathsf {k}, \mathsf {h})$, where $\mathsf {k}$ is uniform in ${\mathcal {K}}$ and $\mathsf {h}$ is uniform in the range of $\mathsf {Hash}_\mathsf {k}$. Let $W_z$ for $z=(\mathsf {k}, \mathsf {h})$ be the uniform distribution on $\mathsf {Hash}_\mathsf {k}^{-1}(\mathsf {h})$. By the $2^m$-regularity and minimum distance properties of $\mathsf {Hash}$, $\mathrm {H}_\infty (W_z)=\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W_z)=m$. Let $\mathcal {W}=\{W_z\}$.

The intuition is as follows. We now want to show that for a random $z\leftarrow Z$, if $({\mathsf {key}}, p)$ is the output of ${\mathsf {Gen}} (W_z)$, then ${\mathsf {key}}$ can be easily distinguished from uniform in the presence of p and z.

In the absence of information about z, the value w is uniform on $\mathcal {M}$ (by regularity of $\mathsf {Hash}$). Knowledge of p reduces the set of possible w from $2^n$ to $2^{n\cdot h_2\left( \frac{1}{2}-\tau \right) }$, because, by correctness of ${\mathsf {Rep}}$, every candidate input w to ${\mathsf {Gen}}$ must be such that all of its neighbors $w'$ of distance at most t produce the same output of ${\mathsf {Rep}} (w', p)$. And knowledge of z reduces the set of possible w by another factor of $2^{{a}}$, because a hash value with a random hash function key likely gives fresh information about w.

6 Impossibility in the Case of Imperfect Correctness

The impossibility result in the previous section applies only to fuzzy extractors with perfect correctness. In this section, we build on the work of Holenstein and Renner [25] to show the impossibility of fuzzy extractors even when they are allowed to make mistakes a constant fraction $\delta$ (as much as $4\,\%$) of the time. However, the drawback of this result, as compared to the previous section, is that we can show impossibility only for a relatively low entropy rate of at most $7\,\%$. In Sect. 7, we rule out stronger primitives called secure sketches with nonzero error (which are used in most fuzzy extractor constructions), even for entropy rate as high as $50\,\%$.

Theorem 3

Let $\mathcal {M}$ denote the Hamming space $\{0, 1\}^n$. There exists a family of distributions $\mathcal {W}$ over $\mathcal {M}$ such that for each element $W \in \mathcal {W}$, $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)=\mathrm {H}_\infty (W) \ge m$, and yet any $(\mathcal {M}, \mathcal {W}, \kappa , t, \epsilon )$-fuzzy extractor with error $\delta \le \frac{1}{25}$ has $\epsilon > \frac{1}{25}$.

This holds for any $\kappa >0$ under the following conditions on the entropy rate $\mu =m/n$, noise rate $\tau =t/n$, and n:

• any $0\le \tau \le \frac{1}{2}$ and $\mu$ such that $\mu < 4\tau (1-\tau ) \left( 1-h_2\left( \frac{1}{4-4\tau }\right) \right)$

• any sufficiently large n (as a function of $\tau$ and $\mu$)

Note that the conditions on $\mu$ and $\tau$ imply that the result applies to any entropy rate $\mu \le \frac{1}{15}$ as long as $\tau$ is set appropriately and n is sufficiently large. The $\tau$ vs. $\mu$ tradeoff is depicted in Fig. 2.

Fig. 2.

The region of $\tau$ (x-axis) and $\mu$ (y-axis) pairs for which Theorem 3 applies is the region below this curve.

Proof (Proof Sketch)

We now describe the family $\mathcal {W}$ and provide an overview of the main ideas. The full proof is in Appendix C.

Similarly to the proof of Theorem 2, we will prove that any fuzzy extractor fails for an element $W_z$ of $\mathcal {W}$ chosen according to the distribution Z. In this case, Z will not be uniform but rather binomial (with tails cut off). Essentially, Z will contain each bit of w with (appropriately chosen) probability $\beta$; given $Z=z$, the remaining bits of w will be uniform and independent.

For a string $z\in \{0,1,\perp \}^n$, denote by $info (z)$ the number of entries in z that are not $\perp$: $info (z)=|\{i \text{ s.t } z_i\ne \perp \}|$. Let $W_z$ be the uniform distribution over all strings in $\{0,1\}^n$ that agree with z in positions that are not $\perp$ in z (i.e., all strings $w\in \{0,1\}^n$ such that for $1\le i\le n$, either $z_i=\perp$ or $w_i=z_i$).

We will use $\mathcal {W}$ to prove the theorem statement. First, we show that every distribution $W_z\in \mathcal {W}$ has sufficient $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$. Indeed, z constrains $info (z)$ coordinates out of n and leaves the rest uniform. Thus, $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W_z)$ is the same as $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$ of the uniform distribution on the space $\{0,1\}^{n- info (z)}$. Second, we now want to show that $\mathbf {SD}(({\mathsf {Key}},P, Z), (U_\kappa , P, Z))>\frac{1}{25}$. To show this, we use a result of Holenstein and Renner [25, Theorem 4]. Their result shows impossibility of interactive key agreement for a noisy channel where the adversary observes each bit with some probability. Several technical results are necessary to apply the result in our setting (presented in Appendix C).

7 Stronger Impossibility Result for Secure Sketches

Most fuzzy extractor constructions share the following feature with our construction in Sect. 4: p includes information that is needed to recover w from $w'$; both ${\mathsf {Gen}}$ and ${\mathsf {Rep}}$ simply apply an extractor to w. The recovery of w from $w'$, known as information-reconciliation, forms the core of many fuzzy extractor constructions. The primitive that performs this information reconciliation is called secure sketch. In this section we show stronger impossibility results for secure sketches. First, we recall their definition from [13, Sect. 3.1] (modified slightly, in the same way as Definition 2).

Definition 5

An $(\mathcal {M},\mathcal {W}, \tilde{m}, t)$-secure sketch with error $\delta$ is a pair of randomized procedures, “sketch” $({\mathsf {SS}})$ and “recover” $({\mathsf {Rec}})$. ${\mathsf {SS}}$ on input $w\in \mathcal {M}$ returns a bit string $ss\in \{0,1\}^*$. ${\mathsf {Rec}}$ takes an element $w'\in \mathcal {M}$ and $ss\in \{0,1\}^*$. $({\mathsf {SS}}, {\mathsf {Rec}})$ have the following properties:

• 1. Correctness: $\forall w, w'\in \mathcal {M}$ if $\mathsf {dis}(w,w')\le t$ then $\Pr [{\mathsf {Rec}} (w',{\mathsf {SS}} (w))=w]\ge 1-\delta .$

• 2. Security: for any distribution $W\in \mathcal {W}$, $\tilde{\mathrm {H}}_\infty (W|{\mathsf {SS}} (W))\ge \tilde{m}$.

Secure sketches are more demanding than fuzzy extractors (secure sketches can be converted to fuzzy extractors by using a randomness extractors like in our Construction 1 [13, Lemma 4.1]). We prove a stronger impossibility result for them. Specifically, in the case of secure sketches, we can extend the results of Theorems 2 and 3 to cover imperfect correctness (that is, $\delta >0$) and entropy rate $\mu$ up to $\frac{1}{2}$. Since most fuzzy extractor constructions rely on secure sketches, this result gives evidence that fuzzy extractors even with imperfect correctness and for high entropy rates are difficult to construct in the case of distributional uncertainty.

Fig. 3.

The region of $\tau$ (x-axis) and $\mu$ (y-axis) pairs for which Theorem 4 applies is the region below both curves.

Theorem 4

Let $\mathcal {M}$ denote the Hamming space $\{0, 1\}^n$. There exists a family of distributions $\mathcal {W}$ over $\mathcal {M}$ such that for each element $W \in \mathcal {W}$, $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)=\mathrm {H}_\infty (W) \ge m$, and yet any $(\mathcal {M}, \mathcal {W}, \tilde{m}, t)$-secure sketch with error $\delta$ has $\tilde{m} \le 2$.

This holds under the following conditions on $\delta$, the entropy rate $\mu =m/n$, noise rate $\tau =t/n$, and n:

• any $0\le \tau < \frac{1}{2}$ and $\mu >0$ such that $\mu< h_2(\tau ) \text{ and } \mu < 1-h_2(\tau )$

• any $n\ge \max \left( \frac{.5\log n +4\delta n + 4}{h_2(\tau )-\mu }, \frac{2}{1-h_2(\tau )-\mu }\right)$

Note that the result holds for any $\mu <0.5$ as long as $\delta < (h_2(\tau )-\mu )/4$ and n is sufficiently large. The $\tau$ vs. $\mu$ tradeoff is depicted in Fig. 3.

We provide the proof, which uses similar ideas to the proof of Theorem 2, in Appendix D.

Appendices

A Proof of Theorem 1

We first provide a full description of the layered hashing construction.

Construction 1

Let W be a distribution over a metric space $\mathcal {M}$ with $\mathrm {H}_\infty (W)= m$.

• Let $\delta \le \frac{1}{2}$ be the error parameter.

• Let $\ell = m+H_0(W)-1$; round $\ell$ down so that $\ell -m$ is an integer (i.e., set $\ell = m+\lfloor (\ell -m)\rfloor$).

• For each $i = m, m+1, \dots , \ell -1$, let $L_i = (2^{-(i+1)}, 2^{-i}]$ and let $F_i :\mathcal {K}_i\times \mathcal {M}\rightarrow R_i$ be a family of universal hash functions with $\log |R_i|=i+1-\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)+\log 1/\delta$. Let $L_{\ell } = (0, 2^{-\ell }]$.

• Let $\mathtt {ext}$ be an $(\tilde{m}, \epsilon )$-average-case extractor for $\tilde{m} = \mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) - \log H_0(W) - \log 1/\delta - 1$ with output length $\kappa$.

Define ${\mathsf {Gen}} _W, {\mathsf {Rep}} _W$ as:

We instantiate this construction with the extractor parameters given by [13, Lemma 2.4] (namely, $\kappa = \tilde{m}-2\log 1/\epsilon +2$) in order to prove Theorem 1.

Proof

(Proof of Theorem 1 ). We first argue correctness. Fix some $w, w'$ within distance t. When $\Pr [W=w]\in L_\ell$, then ${\mathsf {Rep}}$ is always correct, so let’s consider only the case when $\Pr [W=w]\not \in L_\ell$. The algorithm ${\mathsf {Rep}}$ will never output $\perp$ since at least the correct w will match the hash. Thus, an error happens when another element $w^*\in W^*$ has the same hash value $F(K_i, w^*)$ as $F(K_i, w)$. Observe that the total probability mass of $W^*$ is less than $|W^*|\cdot 2^{-(i+1)}$ but greater than or equal to the maximum probability mass in a ball of radius t, $2^{-\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)}$. Therefore, $|W^*| \le 2^{i+1-\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)}$. Each element of $W^*$ has the same hash as F(K, w) with probability at most $1/|R_i|$, and thus correctness with error $|W^*|/|R|\le \delta$ follows by the union bound.

Security: We now argue security of the construction. Let $W_i=\{w|\Pr [W=w]\in L_i\}$. For ease of notation, let us make the special case of $i=\ell$ as part of the general case, as follows: define $\mathcal {K}_{\ell }=\{0\}$, $F_{\ell }(0, w)=w$, and $R_{\ell } =W_\ell$. Also, denote by ${\mathsf {SS}}$ the randomized function that maps w to ss. First, we set up the analysis by levels:

$$\begin{aligned} 2&^{-\tilde{\mathrm {H}}_\infty (W | {\mathsf {SS}} (W))} = {\mathop {{{\mathrm{\mathbb {E}}}}}\limits _{ss}} \max _w \Pr [W=w\, |\, {\mathsf {SS}} (W)=ss] \\&= \mathop {\sum }\limits _{ss} \max _w \Pr [W=w \wedge {\mathsf {SS}} (W)=ss] \\&= \sum _{i=m}^\ell \sum _{K\in \mathcal {K}_i} \sum _{y\in R_i} \max _w \Pr [W=w \wedge {\mathsf {SS}} (W)=(i, y, K)]\\&\le \sum _{i=m}^\ell \sum _{K\in \mathcal {K}_i} \sum _{y\in R_i}\max _{w\in W_i} \Pr [W=w \wedge F_i(K, w)=y \wedge K \text{ output } \text{ by } {\mathsf {Gen}} ]. \end{aligned}$$

We now pay the penalty of $|R_i|$ for the presence of y (observe that removing the condition that $F_i(K,w)=y$ from the conjunction cannot reduce the probability):

$$\begin{aligned} 2^{-\tilde{\mathrm {H}}_\infty (W | {\mathsf {SS}} (W))}&\le \sum _{i=m}^\ell \sum _{K\in \mathcal {K}_i} \sum _{y\in R_i}\max _{w\in W_i} \Pr [W=w \wedge K \text{ is } \text{ chosen } \text{ by } {\mathsf {SS}} ]\\&= \sum _{i=m}^\ell \sum _{K\in \mathcal {K}_i} |R_i|\cdot \max _{w\in W_i} \Pr [W=w \wedge K \text{ is } \text{ chosen } \text{ by } {\mathsf {SS}} ]. \end{aligned}$$

We now get rid of the key, because it is independent:

$$\begin{aligned} 2^{-\tilde{\mathrm {H}}_\infty (W | {\mathsf {SS}} (W))}&\le \sum _{i=m}^\ell \sum _{K\in \mathcal {K}_i} |R_i|\cdot \max _{w\in W_i} \Pr [W=w]\cdot \frac{1}{|\mathcal {K}_i|} \\&= \sum _{i=m}^\ell |R_i| \cdot \max _{w\in W_i} \Pr [W=w] \\&\le |R_{\ell }| \cdot 2^{-\ell }+ \sum _{i=m}^{\ell -1} |R_i|\cdot 2^{-i}. \end{aligned}$$

Finally, we add everything up, recalling that $|R_i|$ for $i<\ell$ is $2^{i+1-\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W)+\log 1/\delta }$.

Taking the negative logarithm of both sides, we obtain $\tilde{m}\mathop {=}\limits ^\mathrm{def}\tilde{\mathrm {H}}_\infty (W|{\mathsf {SS}} (W))= \mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W) - \log H_0(W) - \log 1/\delta - 1$. Applying the $(\tilde{m}, \epsilon )$ randomness extractor gives us the desired result.    $\square$

B Proof of Theorem 2

Proof

As a reminder, we show the impossibility for an average member of $\mathcal {W}$. For completeness, we reiterate the family $\mathcal {W}$ introduced in the proof sketch.

Let $\{\mathsf {Hash}_\mathsf {k}\}_{\mathsf {k}\in {\mathcal {K}}}$ be a family of hash function with domain $\mathcal {M}$ and the following properties:

• $2^{-{a}}$-universality: for all $v_1\ne v_2 \in \mathcal {M}$, $\Pr _{\mathsf {k}\leftarrow {\mathcal {K}}} [\mathsf {Hash}_\mathsf {k}(v_1)=\mathsf {Hash}_\mathsf {k}(v_2)]\le 2^{-{a}}$, where ${a}= n\cdot h_2\left( \frac{1}{2}-\tau \right) +3$.

• $2^m$-regularity: for each $\mathsf {k}\in {\mathcal {K}}$ and $\mathsf {h}$ in the range of $\mathsf {Hash}_\mathsf {k}$, $|\mathsf {Hash}_\mathsf {k}^{-1}(\mathsf {h})|=2^m$, where $m\ge \mu n$.

• preimage sets have minimum distance $t+1$: for all $\mathsf {k}\in {\mathcal {K}}$, if $v_1\ne v_2$ but $\mathsf {Hash}_\mathsf {k}(v_1)=\mathsf {Hash}_\mathsf {k}(v_2)$, then $\mathsf {dis}(v_1, v_2)> t$.

We demonstrate the existence of such a hash family in Lemma 4. Let Z be the random variable consisting of pairs $(\mathsf {k}, \mathsf {h})$, where $\mathsf {k}$ is uniform in ${\mathcal {K}}$ and $\mathsf {h}$ is uniform in the range of $\mathsf {Hash}_\mathsf {k}$. Let $W_z$ for $z=(\mathsf {k}, \mathsf {h})$ be the uniform distribution on $\mathsf {Hash}_\mathsf {k}^{-1}(\mathsf {h})$. By the $2^m$-regularity and minimum distance properties of $\mathsf {Hash}$, $\mathrm {H}_\infty (W_z)=\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W_z)=m$. Let $\mathcal {W}=\{W_z\}$.

We now want to show that for a random $z\leftarrow Z$, if $({\mathsf {key}}, p)$ is the output of ${\mathsf {Gen}} (W_z)$, then ${\mathsf {key}}$ can be easily distinguished from uniform in the presence of p and z. The intuition is as follows: in the absence of information about z, the value w is uniform on $\mathcal {M}$ (by regularity of $\mathsf {Hash}$). Knowledge of p reduces the set of possible w from $2^n$ to $2^{n\cdot h_2\left( \frac{1}{2}-\tau \right) }$, because, by correctness of ${\mathsf {Rep}}$, every candidate input w to ${\mathsf {Gen}}$ must be such that all of its neighbors $w'$ of distance at most t produce the same output of ${\mathsf {Rep}} (w', p)$ (see Lemma 2). And knowledge of z reduces the set of possible w by another factor of $2^{{a}}$, because a hash value with a random hash function key likely gives fresh information about w (see Lemma 3).

To formalize the intuition of the previous two sentences, view the sequence of events that we are trying to analyze as a game. The adversary chooses a uniform $\mathsf {k}\in {\mathcal {K}}$ and uniform $\mathsf {h}$ in the range of $\mathsf {Hash}_\mathsf {k}$. A uniform w from $\mathcal {M}$ s.t. $\mathsf {Hash}_\mathsf {k}(w)=\mathsf {h}$ then gets chosen, $({\mathsf {key}},p)={\mathsf {Gen}} (w)$ gets computed, and the adversary receives p. The output of this game is $(\mathsf {k}, \mathsf {h}, w, p, {\mathsf {key}})$. Note that, by regularity of $\mathsf {Hash}_\mathsf {k}$, w is uniform in $\mathcal {M}$.

Consider now an alternative game. A uniform w gets chosen from $\mathcal {\mathcal {M}}$ and uniform key $\mathsf {k}$ gets chosen from ${\mathcal {K}}$. $({\mathsf {key}},p) ={\mathsf {Gen}} (w)$ gets computed. The adversary receives $(\mathsf {k}, \mathsf {h}=\mathsf {Hash}_\mathsf {k}(w), p)$. The output of the game is $(\mathsf {k}, \mathsf {h}, w, p,{\mathsf {key}})$.

The distributions of the adversary’s views and the outputs in the two games are identical: indeed, in both games, three random variable are uniform and independent (i.e., w is uniform in $\mathcal {M}$, $\mathsf {k}$ is uniform in ${\mathcal {K}}$, and the random coins of ${\mathsf {Gen}}$ are uniform in their domain), and the rest are determined fully by these three. However, the second game is easier to analyze, which is what we now do.

The following lemma shows that the knowledge of p and ${\mathsf {key}}$ reduces the entropy of w.

Lemma 2

Suppose $\mathcal {M}$ is $\{0,1\}^n$ with the Hamming metric, $\kappa \ge 2$, $0\le t\le n/2$, and $\epsilon \ge 0$. Suppose $({\mathsf {Gen}}, {\mathsf {Rep}})$ is a $(\mathcal {M}, \mathcal {W}, \kappa , t, \epsilon )$-fuzzy extractor with error $\delta = 0$, for some distribution family $\mathcal {W}$ over $\mathcal {M}$. Let $\tau = t/n$. For any fixed p, there is a set $\mathsf {GoodKey_p}\subseteq \{0,1\}^\kappa$ of size at least $2^{\kappa -1}$ such that for every ${\mathsf {key}} \in \mathsf {GoodKey_p}$,

$$ \log |\{v\in \mathcal {M}|({\mathsf {key}},p)\in {\text {supp}}({\mathsf {Gen}} (v))\}| \le n \cdot h_2\left( \frac{1}{2}-\tau \right) \le n\cdot \left( 1-\frac{2}{\ln 2}\cdot \tau ^2\right) , $$

and, therefore, for any distribution $D_\mathcal {M}$ on $\mathcal {M}$,

$$ H_0(D_\mathcal {M}|{\mathsf {Gen}} (D_\mathcal {M}) = ({\mathsf {key}}, p)) \le n \cdot h_2\left( \frac{1}{2}-\tau \right) \le n\cdot \left( 1-\frac{2}{\ln 2}\cdot \tau ^2\right) . $$

Proof

The set $\mathsf {GoodKey_p}$ consists of all keys for which $H_0(\mathcal {M}|{\mathsf {Rep}} (\mathcal {M},p)={\mathsf {key}}) \le 2^{n-\kappa +1}$.

The intuition is as follows. By perfect correctness of ${\mathsf {Rep}}$, the input w to ${\mathsf {Gen}}$ has the following property: for all $w'$ within distance t of w, ${\mathsf {Rep}} (w', p)={\mathsf {Rep}} (w,p)$. Thus, if we partition $\mathcal {M}$ according to the output of ${\mathsf {Rep}}$, the true w is t away from the interior of a part. Interior sets are small, which means the set of possible of w values is small. (We note that by perfect correctness, ${\mathsf {Rep}}$ has a deterministic output even if the algorithm is randomized, so this partition is well-defined.)

To formalize this intuition, fix p and partition $\mathcal {M}$ according to the output of ${\mathsf {Rep}} (\cdot , p)$ as follows: let $Q_{p,{\mathsf {key}}} = \{w'\in \mathcal {M}| {\mathsf {Rep}} (w', p) = {\mathsf {key}} \}$. Note that there are $2^\kappa$ keys and thus $2^\kappa$ parts $Q_{p,{\mathsf {key}}}$. Let $\mathsf {GoodKey_p}$ by the set of keys for which these parts are not too large: ${\mathsf {key}} \in \mathsf {GoodKey_p}\Leftrightarrow |Q_{p, {\mathsf {key}}}|\le 2\cdot \mathcal {M}/2^{\kappa } = 2^{n-\kappa +1}$. Observe that $\mathsf {GoodKey_p}$ contains at least half the keys: $|\mathsf {GoodKey_p}|\ge 2^{\kappa -1}$ (if not, then $\cup _{{\mathsf {key}}} |Q_{p, {\mathsf {key}}}| > |\mathcal {M}|$). For the remainder of the proof we focus on elements in $\mathsf {GoodKey_p}$.

As explained above, if w is the input to ${\mathsf {Gen}}$, then every point $w'$ within distance t of w must be in the same part $Q_{p,{\mathsf {key}}}$ as w, by correctness of ${\mathsf {Rep}}$. Thus, w must come from the interior of some $Q_{p, {\mathsf {key}}}$, where interior is defined as

$$\begin{aligned} {\mathsf {Inter}} (Q_{p, {\mathsf {key}}}) = \{w\in Q_{p, {\mathsf {key}}} | \forall w' \text{ s.t. } \mathsf {dis}(w, w') \le t, w'\in Q_{p, {\mathsf {key}}}\}. \end{aligned}$$

We now use the isoperimetric inequality to bound the size of ${\mathsf {Inter}} (Q_{p, {\mathsf {key}}})$. Define a near-ball ³ centered at x to be any set S that is contained in a ball of some radius $\eta$ and contains the ball of radius $\eta -1$ around x. The inequality of [16, Theorem 1] (the original result is due to Harper [21]) says that for any sets $A, B \subset \{0,1\}^n$, there are near-balls X and Y centered at $0^n$ and $1^n$, respectively, such that $|A|=|X|$, $|B|=|Y|$, and $\min _{a\in A, b\in B} \mathsf {dis}(a, b) \le \min _{x\in X, y\in Y} \mathsf {dis}(x, y)$.

Letting A be the ${\mathsf {Inter}} (Q_{p, {\mathsf {key}}})$ and B be the complement of $Q_{p, {\mathsf {key}}}$ and applying this inequality, we get a near-ball $S_{p, {\mathsf {key}}}$ centered at $0^n$ and a near-ball D centered at $1^n$, such that $|S_{p, {\mathsf {key}}}| = |{\mathsf {Inter}} (Q_{p, {\mathsf {key}}})|$, $|D| = 2^n- |Q_{p, {\mathsf {key}}}|$, and $\forall s\in S_{p, {\mathsf {key}}}, d\in D$, $\mathsf {dis}(s, d) > t$. Note that since ${\mathsf {key}} \in \mathsf {GoodKey_p}$ and $\kappa \ge 2$, we have $|Q_{p, {\mathsf {key}}} | \le 2^{n-\kappa +1}$, and therefore $|D| \ge 2^{n-1}$.

Thus, D includes all the strings of Hamming weight $\lceil n/2 \rceil$ (because it is centered at $1^n$ and takes up at least half the space), which means that the maximum Hamming weight of an element of $S_{p, {\mathsf {key}}}$ is $\lceil n/2 \rceil - t-1 \le n/2-t$ (because each element of $S_{p, {\mathsf {key}}}$ is at distance more than t from D). We can now use binary entropy to bound the size of $S_{p,{\mathsf {key}}}$ by Lemma 1:

$$\begin{aligned} |{\mathsf {Inter}} (Q_{p, {\mathsf {key}}})| = |S_{p, {\mathsf {key}}}|&\le |\{ x | \mathsf {dis}(x, 0)\le n/2-t\}| \le 2^{n\cdot h_2\left( \frac{1}{2}-\frac{t}{n}\right) }. \end{aligned}$$

The theorem statement follows by taking the logarithm of both sides and by observing (using Taylor series expansion at $\tau = 0$ and noting that the third derivative is negative) that $h_2\left( \frac{1}{2}-\tau \right) \le 1-\frac{2}{\ln 2}\cdot \tau ^2$.    $\square$

We now analyze how the entropy drops further when the adversary learns $\mathsf {Hash}_\mathsf {k}(w)$. Let $\mathsf {K}$ denote the uniform distribution on ${\mathcal {K}}$. We defer the proof to the full version of this work [18, Lemma B.2].

Lemma 3

Let L be a distribution. Let $\{\mathsf {Hash}_\mathsf {k}\}_{\mathsf {k}\in {\mathcal {K}}}$ be a family of $2^{-{a}}$-universal hash functions on the support of L. Assume $\mathsf {k}$ is uniform in ${\mathcal {K}}$ and independent of L. Then

$$ \tilde{H}_0(L | \mathsf {K}, \mathsf {Hash}_\mathsf {K}(L)) < \log (1+|{\text {supp}}(L)|\cdot 2^{-{a}}) \le \max (1, 1+H_0(L)-{a}). $$

Let $\mathsf {M}$ denote the uniform distribution on $\mathcal {M}$. By Lemma 2, for any p, $H_0(\mathsf {M}|{\mathsf {Gen}} (\mathsf {M}) = ({\mathsf {key}}, p) \text{ s.t. } {\mathsf {key}} \in \mathsf {GoodKey_p}) \le n \cdot h_2\left( \frac{1}{2}-\frac{t}{n}\right) +\kappa$ (because there are most $2^\kappa$ keys in $\mathsf {GoodKey_p}$). Applying Lemma 3 (and recalling that $\kappa \ge 3$), we get that for any p,

$$\begin{aligned}&\tilde{H}_0 (\mathsf {M} | {\mathsf {Gen}} (\mathsf {M}) = ({\mathsf {key}}, p) \text{ s.t. } {\mathsf {key}} \in \mathsf {GoodKey_p}, \mathsf {K}, \mathsf {Hash}_\mathsf {K}(\mathsf {M})) \\&< \max \left( 1, 1 + n\cdot h_2\left( \frac{1}{2}-\frac{t}{n}\right) +\kappa -{a}\right) \le \kappa -2. \end{aligned}$$

(Note carefully the somewhat confusing conditioning notation above, because we are conditioning on both events and variables. The event is ${\mathsf {key}} \in \mathsf {GoodKey_p}$ and the variables are $\mathsf {k}$ and $\mathsf {Hash}_\mathsf {k}(\mathsf {M})$.)

By correctness, for a fixed p, ${\mathsf {Rep}} (w, p)$ can produce only one ${\mathsf {key}}$—the same one that was produces during ${\mathsf {Gen}} (w)$. Since applying a deterministic function (in this case, ${\mathsf {Rep}}$) cannot increase $H_0$, we get that for each p,

$$\begin{aligned} \tilde{H}_0 ({\mathsf {key}} | {\mathsf {Gen}} (\mathsf {M}) = ({\mathsf {key}}, p) \text{ s.t. } {\mathsf {key}} \in \mathsf {GoodKey_p}, \mathsf {K}, \mathsf {Hash}_\mathsf {K}(\mathsf {M}))< \kappa -2. \end{aligned}$$

Thus, on average over $z=(\mathsf {k}, \mathsf {h})$, over half the keys in $\mathsf {GoodKey_p}$ (i.e., over a quarter of all possible $2^\kappa$ keys) cannot be produced. Let $\mathsf {Implausible}$ be the set of triples $({\mathsf {key}},p,z=(\mathsf {k}, \mathsf {h}))$ such that $\Pr [{\mathsf {Gen}} (W_z)=({\mathsf {key}},p)]=0$. Triples drawn by sampling w from $W_z$ and computing $(p, {\mathsf {key}}) = {\mathsf {Gen}} (w)$ never come from this set. On other hand, random triples come $\mathsf {Implausible}$ at over quarter of the time. Thus, by definition of statistical distance, $\epsilon >\frac{1}{4}$.

It remains to show that the hash family with the desired properties exists.

Lemma 4

For any $0\le \tau < \frac{1}{2}$, $\mu >0$, $\alpha$, and n such that $\mu \le 1-h_2(\tau )-\frac{2}{n}$ and $\mu \le 1-\alpha -\frac{2}{n}$, there exists a family of hash functions $\{\mathsf {Hash}_\mathsf {k}\}_{\mathsf {k}\in {\mathcal {K}}}$ on $\{0, 1\}^n$ that is $2^{-{a}}$-universal for ${a}=\alpha n$, $2^m$ regular for $m\ge \mu n$, and whose preimage sets have minimum distance $t+1$ for $t=\tau n$.

Proof

Let $\mathcal {C}$ be the set of all binary linear codes of rate $\mu$ (to be precise, dimension $m=\lceil \mu n\rceil$), length n, and minimum distance $t+1$:

$$ \mathcal {C} = \{C| C \text{ is } \text{ a } \text{ linear } \text{ subspace } \text{ of } \{0, 1\}^n, \dim (C) = m, \min _{c\in C-\{0^n\}} \mathsf {dis}(c,0^n) > t\}. $$

For each $C\in \mathcal {C}$, fix $H_C$, an $(n-m)\times n$ parity check matrix for C, such that $C=\ker H_C$. For $v\in \{0, 1\}^n$, let the syndrome $\mathsf {syn}_C(v) = H_C\cdot v$. Let $\{\mathsf {Hash}_\mathsf {k}\}_{\mathsf {k}\in {\mathcal {K}}} = \{\mathsf {syn}_C\}_{C\in \mathcal {C}}$.

$2^m$ regularity follows from the fact that for each $h\in \{0, 1\}^{n-\mu n}$, $\mathsf {Hash}_\mathsf {k}^{-1}(h)$ is a coset of C, which has size $2^m$. The minimum distance property is also easy: if $v_1\ne v_2$ but $\mathsf {syn}_C(v_1)=\mathsf {syn}_C(v_2)$, then $H_C(v_1-v_2) = 0^n$, hence $v_1-v_2 \in C-\{0^n\}$ and hence $\mathsf {dis}(v_1, v_2) = \mathsf {dis}(v_1-v_2, 0)>t$.

We show $2^{-{a}}$-universality by first considering a slightly larger hash family. Let ${\mathcal {K}}'$ be the set of all m-dimensional subspaces of $\{0, 1\}^n$; for each $C'\in {\mathcal {K}}'$, choose a parity check matrix $H_{C'}$ such that $C'=\ker H_{C'}$, and let $\mathsf {syn}_{C'}(v) = H_{C'}\cdot v$. Let $\{\mathsf {Hash}'_{\mathsf {k}'}\}_{\mathsf {k}'\in {\mathcal {K}}'} = \{\mathsf {syn}_{C'}\}_{C'\in {\mathcal {K}}'}$. This family is $2^{m-n}$-universal: for $v_1\ne v_2$, $\Pr _{C' \in {\mathcal {K}}'} [H_{C'}\cdot v_1 = H_{C'}\cdot v_2] = \Pr _{C' \in {\mathcal {K}}'} [v_1-v_2 \in \ker H_{C'}=C'] = \frac{2^m}{2^n}$, because $C'$ is a random m-dimensional subspace. Note that this family is not much bigger than our family $\{\mathsf {Hash}_\mathsf {k}\}_{\mathsf {k}\in {\mathcal {K}}}$, because, as long as $\mu <1-h_2(\tau )$, almost every subspace of $\{0, 1\}^n$ of dimension m has minimum distance $t+1$ for a sufficiently large n. Formally,

(the penultimate inequality follows by Lemma 1 and the last one from $m\le \mu n+1$ and $\mu \le 1-h_2(\tau )-\frac{2}{n}$).

Since this larger family is universal and at most factor of two bigger than our family, our family is also universal:

$$\begin{aligned} \Pr _{C \in \mathcal {C}} [\mathsf {syn}_C(v_1) = \mathsf {syn}_C(v_2)] = \frac{|\{C\in \mathcal {C}| \mathsf {syn}_C(v_1)=\mathsf {syn}_C(v_2)\}|}{|\mathcal {C}|}\\ \le \frac{|\{C\in {\mathcal {K}}' | \mathsf {syn}_C(v_1)=\mathsf {syn}_C(v_2)\}|}{|{\mathcal {K}}'|}\cdot \frac{|{\mathcal {K}}'|}{|\mathcal {C}|} \le 2^{m-n+1} \end{aligned}$$

Thus, we obtain the desired result as long as $m-n+1\le -{a}$, which is implied by the condition $\mu \le 1-\alpha -\frac{2}{n}$ and the fact that $m\le \mu n+1$.    $\square$

Applying Lemma 4 with $\alpha = h_2\left( \frac{1}{2}-\tau \right) +\frac{3}{n}$, we see that the largest possible $\mu$ is $\max _\tau \min \left( 1-h_2(\tau ), 1-h_2\left( \frac{1}{2}-\tau \right) \right) \approx 0.1887$. Using the quadratic approximation to $h_2\left( \frac{1}{2}-\tau \right)$ (see Lemma 2), we can let $\mu$ be a free variable and set $\tau = .6 \sqrt{\mu }$, in which case both constraints will be satisfied for all $0<\mu \le .18$ and sufficiently large n, as in the theorem statement. This concludes the proof of Theorem 2.    $\square$

C Proof of Theorem 3

Proof

Similarly to the proof of Theorem 2, we will prove that any fuzzy extractor fails for an average element of $\mathcal {W}$: letting Z denote a choice of W from $\mathcal {W}$, we will show that $\mathbf {SD}(({\mathsf {Key}},P, Z), (U_\kappa , P, Z))> \frac{1}{25}$.

For completeness, we reiterate the family of distributions introduced in the proof sketch. In this case, Z will not be uniform but rather binomial (with tails cut off). Essentially, Z will contain each bit of w with (appropriately chosen) probability $\beta$; given $Z=z$, the remaining bits of w will be uniform and independent.

For a string $z\in \{0,1,\perp \}^n$, denote by $info (z)$ the number of entries in z that are not $\perp$: $info (z)=|\{i \text{ s.t } z_i\ne \perp \}|$. Let $W_z$ be the uniform distribution over all strings in $\{0,1\}^n$ that agree with z in positions that are not $\perp$ in z (i.e., all strings $w\in \{0,1\}^n$ such that for $1\le i\le n$, either $z_i=\perp$ or $w_i=z_i$).

Let $0\le \beta ' \le 1$ be a parameter (we will set it at the end of the proof). Let $Z'$ denote the distribution on strings in $\{0,1, \perp \}^n$ in which each symbol is, independently of other symbols, $\perp$ with probability $1-\beta '$, 0 with probability $\beta '/2$, and 1 with probability $\beta '/2$. Let $\beta = \beta ' +\frac{1.4}{\sqrt{n}}$. Consider two distribution families: $\mathcal {W'}=\{W_z\}_{z\leftarrow Z'}$ and a smaller family $\mathcal {W}=\{W_z\}_{z\leftarrow Z}$, where $Z= Z'| info (Z')\le \beta n$ (the second family is smaller because, although on average $info (Z') = \beta 'n$, there is a small chance that $info (Z')$ is higher than even $\beta n$).

We will use $\mathcal {W}$ to prove the theorem statement. First, we will show that every distribution $W_z\in \mathcal {W}$ has sufficient $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$. Indeed, z constrains $info (z)$ coordinates out of n and leaves the rest uniform. Thus, $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W_z)$ is the same as $\mathrm {H}^{\mathtt {fuzz}}_{t,\infty }$ of the uniform distribution on the space $\{0,1\}^{n- info (z)}$. Let $a=n- info (z)$. By Lemma 1

$$\begin{aligned} \mathrm {H}^{\mathtt {fuzz}}_{t,\infty }(W_z)&\ge a\left( 1-h_2\left( \frac{t}{a} \right) \right) \ge n(1-\beta ) \left( 1-h_2\left( \frac{t}{n(1-\beta )}\right) \right) \\&=n(1-\beta ) \left( 1-h_2\left( \frac{\tau }{1-\beta }\right) \right) . \end{aligned}$$

and therefore

$$\begin{aligned} \mu = (1-\beta ) \left( 1-h_2\left( \frac{\tau }{1-\beta }\right) \right) . \end{aligned}$$

(1)

Note that smaller $\beta$ gives a higher fuzzy entropy rate.

Second, we now want to show, similarly to the proof of Theorem 2, that $\mathbf {SD}(({\mathsf {Key}},P, Z), (U_\kappa , P, Z))>\frac{1}{25}$. We will do so by considering the family $\mathcal {W}$. Observe that by triangle inequality

$$\begin{aligned} \mathbf {SD}(({\mathsf {Key}},P, Z), (U_\kappa , P, Z))&\ge \mathbf {SD}(({\mathsf {Key}},P, Z'), (U_\kappa , P, Z')) \\ {}&- {\,\,}\mathbf {SD}(({\mathsf {Key}},P, Z'), ({\mathsf {Key}},P, Z))\\ {}&- {\,\,} \mathbf {SD}( (U_\kappa , P, Z), (U_\kappa , P, Z'))\\&\ge \mathbf {SD}(({\mathsf {Key}},P, Z'), (U_\kappa , P, Z')) - 2\cdot \mathbf {SD}(Z', Z)\\&\ge \mathbf {SD}(({\mathsf {Key}},P, Z'), (U_\kappa , P, Z')) -\frac{1}{25}. \end{aligned}$$

The last line follows by Hoeffding’s inequality [23],

$$ \mathbf {SD}(Z', Z) = \Pr [ info (Z')>\beta n] \le \exp \left( -2n \left( \frac{1.4}{\sqrt{n}}\right) ^2\right) < \frac{1}{50}. $$

Denote $\mathbf {SD}(({\mathsf {Key}},P, Z'), (U_\kappa , P, Z'))$ by $\epsilon '$. To bound $\epsilon '$, we recall a result of Holenstein and Renner [25, Theorem 4] (we will use the version presented in [24, Lemma 4.4]). For a random variable W with a values in $\{0,1\}^n$, let $W^{ noisy }$ denote a noisy copy of W: namely, the random variable obtained by passing W through a binary symmetric channel with error rate $\frac{1-\alpha }{2}$ (that is, ${W_i^{ noisy }} = W_i$ with probability $\frac{1+\alpha }{2}$ and ${W_i^{ noisy }} = 1- W_i$ with probability $\frac{1-\alpha }{2}$, independently for each position i). Holenstein and Renner show that if $\alpha ^2 \le \beta$, then Shannon entropy of ${\mathsf {Key}}$ conditioned on P and $W^{ noisy }$ is greater than Shannon entropy of ${\mathsf {Key}}$ conditioned on Z and $W^{ noisy }$. Intuitively, this means that the ${\mathsf {Rep}}$, when given P and $W^{ noisy }$, knows less about ${\mathsf {Key}}$ than the adversary (who knows P and Z).

Recall the definitions of Shannon entropy $H_1(X)\mathop {=}\limits ^\mathrm{def}{{\mathrm{\mathbb {E}}}}_{x\leftarrow X} -\log \Pr [X=x]$ and conditional Shannon entropy $H_1(X|Y) \mathop {=}\limits ^\mathrm{def}{{\mathrm{\mathbb {E}}}}_{y\leftarrow Y} H_1(X|Y=y)$.

Theorem 5

([25, Theorem 4]; [24, Lemma 4.4]). Suppose that $(P,{\mathsf {Key}})$ is a pair of random variables derived from W. If $\alpha ^2 \le \beta '$, then

$$H_1({\mathsf {Key}} | P,Z') \le H_1({\mathsf {Key}} | P, W^{ noisy })\,$$

where $H_1$ denotes Shannon entropy, $W^{ noisy }$ is W passed through a binary symmetric channel with error rate $\frac{1-\alpha }{2}$, and $Z'$ is W passed through a binary erasure channel with erasure rate $1-\beta '$.

(For a reader interested in how our statement of Lemma 5 follows from [24, Lemma 4.4], note that what we call ${\mathsf {Key}}, P, W^{ noisy }$, and $Z'$ are called U, V, Y, and Z, respectively, in [24]. Note also that we use only the part of the lemma that says that secret key rate $S_{\rightarrow }=0$ when $\alpha ^2 \le \beta$, and the definition [24, Definition 3.1] of the notion $S_{\rightarrow }$ in terms of Shannon entropy.)

We now need to translate this bound on Shannon entropy to the language of statistical distance $\epsilon$ of the key from uniform, reliability $\delta$ of the procedure ${\mathsf {Rep}}$, and key length $\kappa$, as used in the definition of fuzzy extractors. First, we will do this translation for the case of noisy rather than worst-case input to ${\mathsf {Rep}}$.

Corollary 1

Let $(W, W^{ noisy }, Z')$ be a triple of correlated random variables such that

• W and $W^{ noisy }$ are uniform over $\{0,1\}^n$,

• $W^{ noisy }$ is W passed through a binary symmetric channel with error rate $\frac{1-\alpha }{2}$ (that is, each bit position of W agrees with corresponding bit position of $W^{ noisy }$ with probability $\frac{1+\alpha }{2}$), and

• $Z'$ is W passed through a binary erasure channel with erasure rate $1-\beta '$ (that is, each bit position of $Z'$ agrees with the corresponding bit position of W with probability $\beta '$ and is equal to $\perp$ otherwise).

Suppose ${\mathsf {Gen}} (W)$ produces $({\mathsf {Key}}, P)$ with ${\mathsf {Key}}$ of length $\kappa$. Suppose $\Pr [{\mathsf {Rep}} ({W^{ noisy }},$ $P) ={\mathsf {Key}} ] = 1-\delta ']$. Suppose further that $\mathbf {SD}(({\mathsf {Key}},P, Z'), (U_\kappa , P, Z')) = \epsilon '$. If $\alpha ^2 \le \beta '$, then

$$\kappa \le \frac{h_2(\epsilon ') + h_2(\delta ')}{1-\epsilon '-\delta '}.$$

In other words, if $\alpha ^2\le \beta '$, $\epsilon '\le \frac{1}{12}$, and $\delta ' \le \frac{1}{12}$, then even a 1-bit ${\mathsf {Key}}$ is impossible to obtain.

(We note that a similar result follows from [24, Theorem 3.17] if we set the variables $S_{\rightarrow }$, $\gamma$, and m in that theorem to $0, \delta$, and $\kappa$, respectively. However, we could not verify the correctness of that theorem due to its informal treatment of what “$\epsilon$-close to uniform” means; it seems that the small correction term $-h_2(\epsilon )$, just like in our result, is needed on the right-hand side to make that theorem correct.)

Proof

Reliability allows us to bound the entropy of the key. By Fano’s inequality [15, Sect. 6.2, p. 187], $H_1({\mathsf {Key}} | P, {W^{ noisy }}) \le \kappa \delta ' + h_2(\delta ')$. Hence, by Theorem 5 (and the assumption that $\alpha ^2> \beta '$), we have

$$\begin{aligned} H_1({\mathsf {Key}} | P,Z') \le \kappa \delta ' + h_2(\delta '). \end{aligned}$$

(2)

We now need the following lemma, which shows that near-uniformity implies high entropy.

Lemma 5

For a pair of random variables (A, B) such that the statistical distance between (A, B) and $U_\kappa \times B$ is $\epsilon$, then $H_1(A|B) \ge (1-\epsilon ) \kappa - h_2(\epsilon ).$

Proof

Let E denote a binary random variable correlated with (A, B) as follows: when $A=a$ and $B=b$, then $E=0$ with probability

$$ \max (\Pr [(A, B)=(a,b)]-\Pr [U_\kappa \times B=(a, b)], 0). $$

Similarly, let F denote a binary random variable correlated with $U_\kappa \times B$ as follows: when $U_\kappa =a$ and $B=b$, then $F=0$ with probability

$$ \max (\Pr [U_\kappa \times B=(a,b)]-\Pr [(A, B)=(a, b)], 0). $$

Note that $\Pr [E=0] = \Pr [F=0] = \epsilon$, by definition of statistical distance. Note also that $(A, B | E=1)$ is the same distribution as $(U_\kappa \times B | F=1)$. Since conditioning cannot increase Shannon entropy (by a simple argument — see, e.g., [2, Theorem 1.4.4]), we get

$$\begin{aligned} H_1(A|B)&\ge H_1(A|B,E) \\ {}&= \Pr [E=1]H_1(A | B, E=1) + \Pr [E=0] H_1(A | B,E=0) \\ {}&\ge (1-\epsilon )H_1(A | B,E=1) = (1-\epsilon )H_1(U_\kappa | B, F=1). \end{aligned}$$

To bound this latter quantity, note that (the first line follows from the chain rule $H_1(X)\le H_1(X, Y)=H_1(X|Y)+H_1(Y)$ [2, Theorem 1.4.4])

$$\begin{aligned} \kappa = H_1(U_\kappa |B)\le & {} H_1(U_\kappa |B,F) + H_1(F) \\= & {} (1-\epsilon ) H_1(U_\kappa | B,F=1) + \epsilon \cdot H_1(U_\kappa | B,F=0) + h_2(\epsilon ) \\\le & {} (1-\epsilon ) H_1(U_\kappa | B,F=1) + \epsilon \cdot \kappa + h_2(\epsilon ) \end{aligned}$$

Rearranging terms, we get $H_1(U_\kappa |B,F=1) \ge \kappa - h_2(\epsilon )/(1-\epsilon )$, and thus

$$\begin{aligned} H_1(A|B) \ge (1-\epsilon ) \kappa - h_2(\epsilon ). \end{aligned}$$

This concludes the proof of Lemma 5.   $\square$

Combining (2) and Lemma 5 (applied to $A={\mathsf {Key}}$, $B=(P, Z')$, and $\epsilon =\epsilon '$), we get the claimed bound. This concludes the proof of Corollary 1.    $\square$

Next, we translate this result from the noisy-input-case to the worst-case input case. Set $\alpha = \sqrt{\beta '}$. Suppose $t\ge n\left( \frac{1-\sqrt{\beta '}}{2}+\frac{1.4}{\sqrt{n}}\right)$. By Hoeffding’s inequality [23],

$$ \Pr [\mathsf {dis}(W, {W^{ noisy }})>t] \le \exp \left( -2n \left( \frac{1.4}{\sqrt{n}}\right) ^2\right) < \frac{1}{50}. $$

Thus, a fuzzy extractor that corrects t errors with reliability $\delta$ implies that $\Pr [{\mathsf {Rep}} ({W^{ noisy }}, P)={\mathsf {Key}} ] \ge 1-\delta ']$ for $\delta ' = \delta +\frac{1}{50}$. Since $\delta \le 1/25$, we have $\delta ' < 1/12$ and Corollary 1 applies to gives us $\epsilon '> 1/12$ and $\epsilon> 1/12-1/25> 1/25$ as long as $\kappa >0$.

Finally, we work out the relationship between $\mu$ and $\tau$ and eliminate $\beta$, as follows. Recall that $\beta =\beta '+ \frac{1.4}{\sqrt{n}}$; therefore $\sqrt{\beta } \le \sqrt{\beta '}+\frac{1.2}{n^{1/4}}$, and it suffices to take $\tau \ge \frac{1-\sqrt{\beta }}{2}+\frac{2}{\root 4 \of {n}}$. Thus, we can set any $\tau > \frac{1-\sqrt{\beta }}{2}$ as long as n is sufficiently large. Solving for $\beta$ (that is, taking any $\beta >(1-2\tau )^2$) and substituting into Eq. 1, we can get any $\mu < 4\tau (1-\tau ) \left( 1-h_2\left( \frac{1}{4-4\tau }\right) \right)$ for a sufficiently large n.    $\square$

D Proof of Theorem 4

Proof

Similarly to the proof of Theorem 2, we will prove that any secure sketch algorithm fails for an average element of $\mathcal {W}$: letting Z denote a uniform choice of W from $\mathcal {W}$, we will show that $\tilde{\mathrm {H}}_\infty (W_Z|{\mathsf {SS}} (W_Z), Z) \le 2$. The overall proof strategy is the same as for Theorem 2. We highlight only the changes here. Recall that $|B_t|$ denotes the volume of the ball of radius t in the space $\{0,1\}^n$. The parameters of the hash family are the same, except for universality: we require $2^{-{a}}$-universality for ${a}= (n-\log |B_t| + h_2(2\delta ))/(1-2\delta ).$

We postpone the question of the existence of such a hash family until the end of the proof.

We can now state and the analogue of Lemma 2. This result is an extension of lower bounds from [13, Appendix C], which handles only the case of perfect correctness. It shows that the value of the sketch reduces the entropy of a uniform point by approximately $\log |B_t|$.

Lemma 6

Let $\mathcal {M}$ denote the Hamming space $\{0,1\}^n$ and $|B_t|$ denote the volume of a Hamming ball of radius t in $\{0,1\}^n$. Suppose $({\mathsf {SS}}, {\mathsf {Rec}})$ is a $(\mathcal {M}, \mathcal {W}, \tilde{m}, t)$ secure sketch with error $\delta$, for some distribution family $\mathcal {W}$ over $\mathcal {M}$. Then for every $v\in \mathcal {M}$ there exists a set $\mathsf {GoodSketch}_v$ such that $\Pr [{\mathsf {SS}} (v)\in \mathsf {GoodSketch}_v]\ge 1/2$ and for any fixed ss,

$$ \log |\{v\in \mathcal {M}|ss\in \mathsf {GoodSketch}_v\}| \le \frac{n-\log |B_t| + h_2(2\delta )}{1-2\delta }, $$

and, therefore, for any distribution $D_\mathcal {M}$ over $\mathcal {M}$,

$$ H_0(D_\mathcal {M}| ss\in \mathsf {GoodSketch}_{D_\mathcal {M}} ) \le \frac{n-\log |B_t| + h_2(2\delta )}{1-2\delta }. $$

Proof

For any $v\in M$, define ${\mathsf {Neigh}} _t(v)$ be the uniform distribution on the ball of radius t around v and let

$$ \mathsf {GoodSketch}_v = \{ss | \mathop {\Pr }\limits _{v'\leftarrow {\mathsf {Neigh}} _t(v)} [{\mathsf {Rec}} (v', ss)\ne v] \le 2\delta ]\}. $$

We prove the lemma by showing two propositions.

Proposition 2

For all $v\in \mathcal {M}$, $\Pr [{\mathsf {SS}} (v) \in \mathsf {GoodSketch}_v] \ge 1/2$.

Proof

Let the indicator variable $1_{v',ss}$ be 1 if ${\mathsf {Rec}} (v', ss) =v$ and 0 otherwise. Let $q_{ss}$ be the quality of the sketch on the ball $B_t(v)$:

$$ q_{ss} = \mathop {\Pr }\limits _{v'\leftarrow {\mathsf {Neigh}} _t(v)} [{\mathsf {Rec}} (v', ss)= v] = \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{v' \in {\mathsf {Neigh}} _t(v)} 1_{v',ss}. $$

By the definition of correctness for $({\mathsf {SS}}, {\mathsf {Rec}})$, for all $v' \in B_t(v)$,

$$\mathop {\Pr }\limits _{ss\leftarrow {\mathsf {SS}} (v)} [{\mathsf {Rec}} (v', ss) = v] \ge 1- \delta .$$

Hence, ${{\mathrm{\mathbb {E}}}}_{ss \leftarrow {\mathsf {Gen}} (v)} 1_{v', ss} \ge 1-\delta$. Therefore,

$$ \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{ss \leftarrow {\mathsf {Gen}} (v)} q_{ss} = \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{ss} \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{v'} 1_{v', ss} = \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{v'} \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{ss} 1_{v', ss} \ge \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{v'} (1-\delta ) = 1-\delta . $$

Therefore, applying Markov’s inequality to $1-q_{ss}$, we get $\Pr [q_{ss} \ge 1-2\delta ] = \Pr [1-q_{ss} \le 2\delta ] \le 1/2$.

   $\square$

To finish the proof of Lemma 6, we will show that the set $\{v\in \mathcal {M}|ss\in \mathsf {GoodSketch}_v\}$ forms a kind of error-correcting code, and then bound the size of the code.

Definition 6

We say that a set C is an $(t,\delta )$-Shannon code if there exists a (possibly randomized) function $\mathsf {Decode}$ such that for all $c\in C$,

$$\begin{aligned} \mathop {\Pr }\limits _{c'\leftarrow {\mathsf {Neigh}} _t(c)} [\mathsf {Decode}(c') \ne c]\le \delta . \end{aligned}$$

The set $\{v\in \mathcal {M}|ss\in \mathsf {GoodSketch}_v\}$ forms $(t, 2\delta )$ Shannon code if we set $\mathsf {Decode}(y)={\mathsf {Rec}} (y, ss)$. We now bound the size of such a code.

Proposition 3

If $C\subseteq \{0,1\}^n$ is a $(t, \delta )$-Shannon code, then

$$ \log |C| \le \frac{n-\log |B_t| + h_2(\delta )}{1-\delta }. $$

Proof

Let the pair of random variables (X, Y) be obtained as follows: let X be a uniformly chosen element of C and Y be a uniformly chosen element of the ball of radius t around Y. By the existence of $\mathsf {Decode}$ and Fano’s inequality [15, Sect. 6.2, p. 187], $H_1(X|Y) \le h_2(\delta )+\delta \log |C|$. At the same time, $H_1(X|Y)= H_1(X)-H_1(Y)+H_1(Y|X)$ (because $H_1(X, Y)=H_1(X)+H_1(Y|X)=H_1(Y)+H_1(X|Y)$), and therefore $H_1(X|Y)\ge \log |C|-n+\log |B_t|$ (because $H_1(Y)\le n$). Therefore, $\log |C|-n+\log |B_t| \le h_2(\delta )+\delta \log |C|$, and the lemma follows by rearranging terms.

   $\square$

Lemma 6 follows from Proposition 3.    $\square$

We now show that entropy drops further when the adversary learns $\mathsf {Hash}_\mathsf {k}(w)$. Let $\mathsf {M}$ denote the uniform distribution on $\mathcal {M}$ and $\mathsf {K}$ denote the uniform distribution on ${\mathcal {K}}$. Applying Lemma 3 to Lemma 6, we get that for any ss,

$$\begin{aligned} \tilde{H}_0 (&\mathsf {M} | ss \in \mathsf {GoodSketch}_{\mathsf {M}}, \mathsf {K}, \mathsf {Hash}_\mathsf {K}(\mathsf {M})) \nonumber \\ {}&< \max \left( 1, 1 + \frac{n -\log |B_t| + h_2(2\delta )}{1-2\delta }-{a}\right) . \end{aligned}$$

(3)

To complete the proof, we will use this bound on $\tilde{H}_0$ as a bound on $\tilde{\mathrm {H}}_\infty$, as justified by the following lemma (proof in the full version of this work [18, Lemma D.7]).

Lemma 7

For any random variables X and Y, $\tilde{\mathrm {H}}_\infty (X|Y)\le \tilde{H}_0(X|Y)$.

We need just one more lemma before we can complete the result, an analogue of [13, Lemma 2.2b] for conditioning on a single value $Z=z$ rather than with Z on average (we view conditioning on a single value as equivalent to conditioning on an event). The proof of this lemma is natural and is shown in the full version of this work [18, Lemma D.8].

Lemma 8

For any pair of random variables (X, Y) and event $\eta$ that is a (possibly randomized) function of (X, Y), $\tilde{\mathrm {H}}_\infty (X|\eta , Y) \ge \tilde{\mathrm {H}}_\infty (X|Y) - \log 1/\Pr [\eta ]$.

Combining Lemmas 8 and 7 with Eq. 3, we get

$$\begin{aligned} \tilde{\mathrm {H}}_\infty&(W_Z|Z, {\mathsf {SS}} (W_Z)) = \tilde{\mathrm {H}}_\infty (\mathsf {M} | {\mathsf {SS}} (\mathsf {M}), \mathsf {K}, \mathsf {Hash}_\mathsf {K}(\mathsf {M})) \\ \le&\log \frac{1}{\Pr [{\mathsf {SS}} (\mathsf {M})\in \mathsf {GoodSketch}_{\mathsf {M}}]} + \\ {}&\tilde{\mathrm {H}}_\infty (\mathsf {M} | ss \text{ s.t. } ss={\mathsf {SS}} (\mathsf {M}) \text{ and } ss\in \mathsf {GoodSketch}_{\mathsf {M}}, \mathsf {K}, \mathsf {Hash}_\mathsf {K}(\mathsf {M})) \\ \le&\log \frac{1}{\Pr [{\mathsf {SS}} (\mathsf {M})\in \mathsf {GoodSketch}_{\mathsf {M}}]}+ \\ {}&\tilde{H}_0 (\mathsf {M} | ss \text{ s.t. } ss={\mathsf {SS}} (\mathsf {M}) \text{ and } ss\in \mathsf {GoodSketch}_{\mathsf {M}}, \mathsf {K}, \mathsf {Hash}_\mathsf {K}(\mathsf {M})) \\ <&\log \frac{1}{\Pr [{\mathsf {SS}} (\mathsf {M})\in \mathsf {GoodSketch}_{\mathsf {M}}]}+ \max \left( 1, 1 + \frac{n-\log |B_t| + h_2(2\delta )}{1-2\delta }-{a}\right) . \end{aligned}$$

We can have shown that $\tilde{\mathrm {H}}_\infty (W_Z|Z, {\mathsf {SS}} (W_Z))\le 2$, because the first term of the above sum is at most 1 by Proposition 2 and the second term is 1 by our choice of ${a}$ as ${a}= \frac{n-\log |B_t| + h_2(2\delta )}{1-2\delta }.$

It remains to show that the desired hash family exists. Note in that (because $\delta <.25$) setting any $\alpha \ge 1-h_2(\tau )+ \frac{.5 \log n + 4\delta n + 2}{n}$ and choosing an $\alpha n$-universal hash function will be sufficient, because, by Lemma 1, $\log |B_t| \ge nh_2(\tau )-\frac{1}{2} \log n -1$, and so

$$\begin{aligned} {a}=\frac{n-\log |B_t| + h_2(2\delta )}{1-2\delta } \le&n\cdot \frac{1-h_2(\tau ) + (.5 \log n + 1 + h_2(2\delta ))/n}{1-2\delta } \\ <&n\cdot (1-h_2(\tau ) + \frac{.5 \log n + 1 + h_2(2\delta )}{n}+4\delta ) \\ \le&n\cdot \left( 1-h_2(\tau ) + \frac{.5 \log n + 4\delta n + 2}{n}\right) \\ \le&n \cdot \alpha \end{aligned}$$

(the second inequality is true because for any $x<1$ and $0<y<.5$, $x/(1-y) < x+2y$, because $x<(x+2y)(1-y)$, because $0<y(2-x-2y)$; the third inequality follows from $h_2(2\delta )<1$).

Such a hash family exists by Lemma 4 as long as $\mu \le 1-\alpha -2/n \le h_2(\tau )-(.5\log n +4\delta n + 4 )/n$ and $\mu \le 1-h_2(\tau )-2/n$).    $\square$