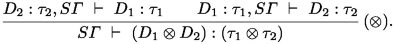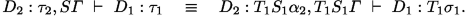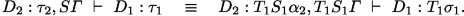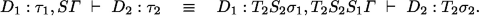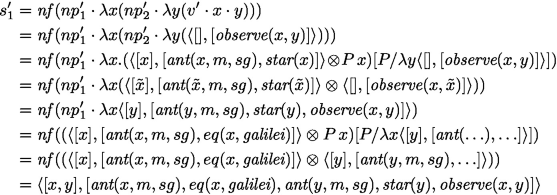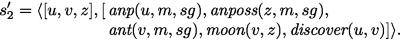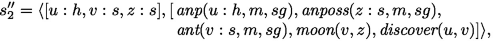Type Reconstruction for $\lambda$-DRT Applied to Pronoun Resolution

Abstract

$\lambda$-DRT is a typed theory combining simply typed $\lambda$-calculus with discourse representation theory, used for modelling the semantics of natural language. With the aim of type-checking natural language texts in the same vein as is familiar from type-checking programs, we propose untyped $\lambda$-DRT with automatic type reconstruction. We show a principal types theorem for $\lambda$-DRT and how type reconstruction can be used to make pronoun resolution type-correct, i.e. the inferred types of a pronoun occurrence and its antecedent noun phrase have to be compatible, thereby reducing the number of possible antecedents.

1 Introduction

In order to give a compositional semantics for discourse, [2] have extended the non-compositional and first-order approach of Discourse Representation Theory (DRT, [10]) by adding $\lambda$-abstraction and functional application. As is familiar from Montague-semantics, the meaning of an expression can then be defined bottom-up, by abstracting from the meaning contribution of the context; function application is then used to combine this meaning with those of expressions from the context.

While DRT uses discourse representation structures, i.e. pairs of variables and quantifier-free formulas, and avoids higher-order logic on its way to translate natural language to first-order logic, Montague-grammar and $\lambda$-DRT make heavy use of higher order types and are commonly expressed in a simply typed language.

Our first goal is to have a type-free notation of $\lambda$-DRS-terms, such that meanings can be written without types, but checked for typeability by “reconstructing” suitable types from types of built-in constants (polymorphic function words and monomorphic content words in the lexicon) and the context of occurrence. For this, we will show that most general types exist and can be inferred automatically. The second goal is to integrate the type reconstruction into a program for pronoun resolution. We want to be able to type-check when a pronoun resolution (i.e. the unification of the discourse variable of a pronoun with the discourse referent of an antecedent) is type-correct, and moreover, we want to use the type reconstruction for unresolved pronouns to filter possible antecedents by their types and the type of the unresolved pronoun.

2 $\lambda$-DRT

Where [18] uses meanings like $a \mapsto \lambda P\lambda Q\exists x(P\, x\wedge Q\, x)$, $\textit{man}\mapsto \lambda x.\textit{man}(x)$ and $\textit{walks}\mapsto \lambda x.{\textit{w}alk}(x)$ and combines these by application to $\textit{a man walks}\mapsto \exists x({\textit{m}an}(x)\wedge {\textit{w}alk}(x))$, in $\lambda$-DRT of [2], one uses somewhat different lexical entries

and an operation $\otimes$ of merging discourse representation structures as in

In general, two discourse structures are merged by appending their (disjoint) lists of discourse referents (variables) and formulas, respectively:

Since a variable in the referent list is seen as a binding, a binder of each merge-factor can bind free variable occurrences in the formulas of both merge-factors. In a discourse A man walks. He talks., the meanings of the sentences have to be combined. The pronoun he in the second sentence introduces a new discourse referent y with the appropriate property. The combination of the meanings of the sentences is the merging

of their discourse structures, followed by pronoun resolution: the referent y of the anaphoric pronoun is resolved against some previously introduced discourse referent, here x. This can be implemented by adding an equational constraint $x=y$ to the merged DRS, or by unifying the variables.

If one assumes some co-indexing of pronouns and antecedent noun phrases as a result of syntactic analysis, one can use the referent of the antecedent noun phrase as referent of the anaphoric pronoun. Then, the binding is dynamic, i.e. the scope extends beyond sentence boundaries as the discourse goes on:

With type reconstruction for $\lambda$-DRT, one could just check the type-soundness of pronoun resolution, i.e. that the semantic type of the pronoun occurrence fits the semantic type of the referent of its antecedent. However, we want to use type reconstruction to help pronoun resolution. To do so, we mark discourse referents as anaphors or possible antecedents, use type reconstruction for $\lambda$-DRT to infer types for the discourse referents, and then do pronoun resolution with typed referents. Our typing rules for DRSs and DRT’s accessibility relation are closely related.

2.1 Untyped $\lambda$-DRS-Terms

We use four kinds of raw expressions: terms, formulas, discourse representation structures, and discourses:

All terms are atomic. Formulas are built from atomic formulas by conjunction of formulas and (non-conjunctive) Boolean combinations of $\lambda$-DRSs.

A box or value-DRS D is a pair $\langle [x_{1},\ldots ,x_{n}],\varphi \rangle$ of a list $[x_{1},\ldots ,x_{n}]$ of variables and a formula $\varphi$, recursively defined by

Two DRSs $D_1$ and $D_2$ may be merged to a DRS $(D_1\otimes D_2)$. So far, the merge-operator $\otimes$ is just a constructor. We will later add reduction rules which provide the intended meaning of the merge of two value-DRSs (with disjoint variable lists) as

Finally, we want to have abstraction and application of $\lambda$-DRSs. Note: We use the pair notation $\langle s,t\rangle$ not for arbitrary terms s, t. Likewise for the types $\sigma \times \tau$: the intention is that $\sigma$ is an individual type, $\tau$ a DRS-type.

The toplevel referents and the free variables of D are defined by

For formulas built from DRSs, we put

This is motivated by considering free variables of $D_2$ (representing pronouns) as bound by toplevel referents of $D_1$ (their antecedents). However, these notions are not stable under $\beta$-reduction $\rightarrow$: for example, for $D_1=\lambda y\langle [x],\varphi \rangle \cdot y$ and $D_1'=\langle [x],\varphi \rangle$ we have $D_1\rightarrow D_1'$, but $\textit{top}(D_1)=\emptyset \not = \textit{top}(D_1')$, and so $(D_1\Rightarrow D_2)$ may bind less variables of $D_2$ than $(D_1'\Rightarrow D_2)$. Hence these definitions make sense for expressions in $\beta$-normal form only.¹

In Sect. 5 we define the meaning of application $\cdot$ by $\beta$-reduction, i.e. by reducing an application $(t\cdot s)$ to the substitution t[x / s] of free occurrences of x in t by s. Some care is needed to avoid variable capture.

We treat toplevel referents of a merge-factor as binders with scope over all factors. Hence, when substituting a free occurrence of x in $(D_1\otimes D_2)$ by s, we have to $\alpha$-rename the top-level referents of $D_1$ and $D_2$ to avoid capturing free variables of s. But we also have to rename toplevel referents of s when applying [x / s] to $(D_1\otimes D_2)$, since s might become a merge-factor, as for $D_1=x$, and then its toplevel referents would capture free variables of $D_2$. Since $D_1,D_2,s$ might have toplevel referents after some reductions, we define t[x / s] in such a way that all bound variables and referents of t and s are renamed to fresh ones before the free occurrences of x are replaced.²

An essential clause in the definition of D[x / s] is:

$$\begin{aligned} (D_1\otimes D_2)[x/s]= & {} (D_1'[x/s']\otimes D_2'[x/s'']), \end{aligned}$$

where $D_i'$ is $D_i$ with $\textit{top}(D_1\otimes D_2)\cap \textit{free}(s)$ renamed, and $s',s''$ are s with $\textit{bound}(s)$ renamed. Similar clauses are needed to treat $(D_1\Rightarrow D_2)[x/s]$ and $(D_1\vee D_2)[x/s]$. For example, if P is not in $\varphi$, then in

$D'$ is D with toplevel referents renamed and hence does not bind free variables of $\varphi$.

3 Typing Rules

Montague-semantics and $\lambda$-DRT usually come with base types e for entities and t for truth values. As boxes are pairs $\langle {\varvec{x}},\varphi \rangle$ of a list of individual variables and a formula, it seems natural to give them the pair type $e^*\times \mathbf{t}$, where $e^*$ is the type of lists of entities. Instead, all boxes have another base type in [2], and the type $s\rightarrow (s\rightarrow t)$ of binary relations between situations s (resp. assignments of entities to discourse referents) in [19]).

For the kind of semantic checking of texts we want to do, a more fine-grained typing of DRSs is needed. One should distinguish between entities of different kinds, i.e. replace the base type e by a family $\langle {e_i}\rangle _{i\in I}$ of base types or sorts. The type of a box $\langle {\varvec{x}},\varphi \rangle$ then becomes a pair ${\varvec{e}}\times \mathbf{t}$, so that, essentially, a typed DRS $\langle {\varvec{x}},\varphi \rangle :{\varvec{e}}\times \mathbf{t}$ is a pair of a type environment ${\varvec{x}}:{\varvec{e}}$ and a formula $\varphi :\mathbf{t}$.

The type ${\varvec{e}}\times \mathbf{t}$ of a merge-DRS $D_1\otimes D_2$ then ought to be related to the types ${\varvec{e}}_1\times \mathbf{t}$ and ${\varvec{e}}_2\times \mathbf{t}$ of the constituents $D_1$ and $D_2$ in that ${\varvec{e}}$ is obtained by appending ${\varvec{e}}_1$ and ${\varvec{e}}_2$, so ${\varvec{e}} = \textit{append}({\varvec{e}}_1,{\varvec{e}}_2)$. However, since $\otimes$ is just a DRS-constructor, we will likewise introduce a type constructor $\otimes$ and use a constraint ${\varvec{e}} = {\varvec{e}}_1\otimes {\varvec{e}}_2$ in the type reconstruction process. Since the length of referent- and type-lists have to match –even if we had only a single sort of entities–, we cannot use the list type constructor ${}^*$, but build type lists by consing a type $e_i$ to a list ${\varvec{e}}$ of types, $e_i\times {\varvec{e}}$, beginning with the type ${1\!\!1}$ for the empty list paired with a truth value.

Types:

We call a type a drs-type, if it is of the forms $\alpha$, ${1\!\!1}$, $e_i\times \tau$, or $\sigma \otimes \tau$ with drs-types $\sigma$ and $\tau$. We write $\sigma \times \tau \times {1\!\!1}$ for $(\sigma \times (\tau \times {1\!\!1}))$ and $[\sigma _1,\ldots ,\sigma _n]$ for $\sigma _1\times \ldots \times \sigma _n\times {1\!\!1}$.

Typing rules:

An assumption $D:\sigma$ can only be used when D is a variable, a value-DRS, or a merged DRS. The rules $(var_3)$ and $(var_4)$ amount to a typing rule

which says that a typed DRS as assumption is used as a list of typing assumptions of its top-level discourse referents. By $(var_5)$, assuming a typed merged DRS amounts to assuming suitably typed merge-factors. By $(var_6)$ and $(var_7)$, assumptions for typed applications and abstractions can be ignored.

We need typed DRSs as assumptions to type merge-DRSs, disjunctions, implications and discourses (rules $(\otimes ),(\textit{impl}),(\textit{disj}),(\,;)$), where part of the DRS to be typed contains top-level referents whose types have to be assumed to type the rest of the DRS.

Notice that in $(drs^+_2$) a variable is removed from the context and built into a DRS. Hence, $\langle x,D\rangle$ corresponds to a binding operator, written $\delta x.D$ in Kohlhase e.a. [13] But in $(\otimes )$ a typed DRS is used like a type context to type another DRS, whereby the scope of $\langle x,D\rangle :\sigma$ is extended to terms outside of D. This is what Kohlhase e.a. [13] call “dynamic” binding of variables in $D_2$ by binding operators of $D_1$.

Discourses are sequences of sentences; to type the sequence of their DRSs, each DRS is typed in the context extended by the previous DRSs. (Thereby we can resolve pronouns anaphoric ally, to referents in the left textual context.)

In typing a term, a typed assumption $D:\sigma$ can only be used by decomposing it to the typed top-level discourse referents of D, using $(var_3)$ to $(var_5)$. This cannot be done if D is a variable, application, or abstraction. We ignore assumed typed abstractions by $(var_7)$, which is harmless since they cannot evaluate to boxes, but $(var_6)$, ignoring assumed typed applications, is not: they may reduce to a box containing x as a top-level discourse referent and thus block an assumption $x:\tau$ in $\varGamma$. We need to restrict $(var_6)$ to have a form of subject-reduction, see Sect. 5.

By induction on the structure of terms, formulas and $\lambda$-DRSs t, we obtain:

Lemma 1

Suppose for all $x\in \textit{free}(t)$ and all types $\sigma$, ${\varGamma }\ \vdash \ {x}:{\sigma }$ iff ${\varDelta }\ \vdash \ {x}:{\sigma }$. Then ${\varGamma }\ \vdash \ {t}:{\tau }$ iff ${\varDelta }\ \vdash \ {t}:{\tau }$.

Corollary 1

• 1. If ${\varGamma ,\langle [],\varphi \rangle :{1\!\!1},\varDelta }\ \vdash \ {s}:{\sigma }$, then ${\varGamma ,\varDelta }\ \vdash \ {s}:{\sigma }$.

• 2. If ${x:\rho ,E:\tau ,\varGamma }\ \vdash \ {s}:{\sigma }$ and x is not a top-level referent of E, then ${E:\tau ,x:\rho ,\varGamma }\ \vdash \ {s}:{\sigma }$.

4 Type Reconstruction

We want to extend Hindley’s well-known “principal types”-theorem from (simply typed) $\lambda$-calculus to $\lambda$-DRT. The theorem says that the set of typings $\varGamma \vdash t:\tau$ of a term t is the set of instances $S\varGamma _0 \vdash t:S\tau _0$ of a single typing $\varGamma _0\vdash t:\tau _0$, where $S:\textit{TyVar}\rightarrow \textit{Ty}$ are the assignments of types to type variables. Then $\varGamma _0 \vdash t:\tau _0$ is a most general or principal typing of t. A (principal) typing of t modulo $\varGamma$ is a (principal) typing ${S\varGamma }\ \vdash \ {t}:{\sigma }$ for some type substitution S and type $\sigma$.

It is not hard to see that instances of a DRS-typing are also typings of the DRS.

Lemma 2

If ${\varGamma }\ \vdash \ {D}:{\sigma }$ and $S:\textit{TyVar}\rightarrow \textit{Ty}$, then ${S\varGamma }\ \vdash \ {D}:{S\sigma }$.

More work is needed to show the existence of principal typings.

Theorem 1

There is an algorithm W that, given a type context $\varGamma$ and a term t, either returns a pair $(U,\tau )$ of a type substitution $U:\textit{TyVar}\rightarrow \textit{Ty}$ and a type $\tau$ such that ${U\varGamma }\ \vdash \ {t}:{\tau }$ is a most general typing of t modulo $\varGamma$, or returns ‘${\textit{f}ail}$’, if there is no $(U,\tau )$ such that ${U\varGamma }\ \vdash \ {t}:{\tau }$.

The algorithm W has an easy modification which, on input $(\varGamma ,e)$ where e has a type in some instance of $\varGamma$, not only delivers $(U,\tau )$ such that ${U\varGamma }\ \vdash \ {e}:{\tau }$, but also a variant $e'$ of e where variable bindings are annotated with types.

Proof

The proof is an extension of the proof of [6, 9]. We only consider the cases of variables and terms that are new in $\lambda$-DRT over the $\lambda$-calculus. Define W as follows:

By induction on t, we want to show that for all $\varGamma ,S,\tau$:

• (i) $W(\varGamma ,t)$ terminates.

• (ii) If $W(\varGamma ,t) = {\textit{f}ail}$, then there is no typing of t modulo $\varGamma$.

• (iii) If $W(\varGamma ,t)=(S,\tau )$, then ${S\varGamma }\ \vdash \ {t}:{\tau }$ is a principal typing of t modulo $\varGamma$.

Case $t = x$: (i) $W(\varGamma ,x)$ searches the type context from left to right, unpacking boxes and merge-DRSs to lists of typed referents, and applies $(var_1)$ to the first assumption $x:\tau$ found. Clearly, this terminates. (ii) If $W(\varGamma ,x)= \textit{fail}$, then no assumption $x:\tau$ is found in the (unpacked) context, so x is untypeable, since $(var_1)$ cannot be applied to x. (iii) If $W(\varGamma ,x)=(S,\tau )$, then $S=Id$ and $\varGamma =x:\tau ,\varGamma '$ for some $\varGamma '$. Suppose ${R\varGamma }\ \vdash \ {x}:{\rho }$ is a typing of x modulo $\varGamma$. Then $R\varGamma = x:R\tau , R\varGamma '$, and hence $\rho = R\tau$ by $(var_1)$. So ${R\varGamma }\ \vdash \ {x}:{\rho }$ is obtained from ${S\varGamma }\ \vdash \ {x}:{\tau }$ by instantiating with R.

Case $t = (D_1\otimes D_2)$:

• (i) $W(\varGamma ,(D_1\otimes D_2))$ terminates, since by induction, $W((D_2:\alpha ,\varGamma ),D_1)$ terminates, for each $(S_1,\tau _1)$, $W((D_1:\tau _1, S_1\varGamma ),D_2)$ terminates, and for each $(S_2,\tau _2)$, $mgu(\tau _2,S_2S_1\alpha )$ terminates.

• (ii) Suppose there is a typing of $(D_1\otimes D_2)$ modulo $\varGamma$. For some $S,\tau _1,\tau _2$, the typing derivation ends in

  

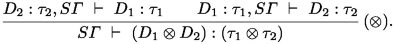
  Thus there is a typing of $D_1$ modulo $D_2:\alpha _2,\varGamma$, whence, by induction, $W((D_2:\alpha _2,\varGamma ),D_1)\not ={\textit{f}ail}$, and there is a most general typing ${D_2:S_1\alpha _2,S_1\varGamma }\ \vdash \ {D_1}:{\sigma _1}$ of $D_1$ modulo $(D_2:\alpha _2,\varGamma )$. Since it is most general, there is a type substitution $T_1$ such that

  

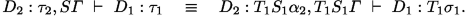
  There is also a typing of $D_2$ modulo

  $$ (D_1:\tau _1,S\varGamma ) \equiv (D_1:T_1\sigma _1,T_1S_1\varGamma ), $$

  hence a typing of $D_2$ modulo $(D_1:\sigma _1,S_1\varGamma )$. Therefore, by induction, $W((D_1:\sigma _1,S_1\varGamma ),D_2)\not ={\textit{f}ail}$, and there is a most general typing ${D_1:S_2\sigma _1,S_2S_1\varGamma }\ \vdash \ {D_2}:{\sigma _2}$ of $D_2$ modulo $(D_1:\sigma _1,S_1\varGamma )$. Since it is most general, there is a type substitution $T_2$ such that

  

  So we have $T_2\sigma _2=\tau _2=T_1S_1\alpha _2$, and on the type variables of $S_1\varGamma$ and $\sigma _1$, $T_1=T_2S_2$. On type variables $\beta$ of $S_1\alpha _2$ which are not in $S_1\varGamma$ or $\sigma _1$, we have $S_2\beta =\beta$ as $S_2$ is idempotent. We can assume that $\beta$ is not in the support of $T_2$ and put $T_2\beta := T_1\beta$, obtaining $T_1\beta = T_2S_2\beta$. Then from $T_2\sigma _2 =\tau _2= T_1S_1\alpha _2=T_2S_2S_1\alpha _2$, we know that $\sigma _2$ and $S_2S_1\alpha _2$ unify, so $mgu(\sigma _2,S_2S_1\alpha _2) \not ={\textit{f}ail}$. By the definition of W, it then follows that $W(\varGamma ,(D_1\otimes D_2))\not ={\textit{f}ail}$.

• (iii) Suppose $W(\varGamma ,(D_1\otimes D_2))=(US_2S_1,(US_2\sigma _1\otimes U\sigma _2))$ with $U,S_1,S_2,\sigma _1,\sigma _2$ as in the definition of W. Then with fresh $\alpha _2$, $W((D_2:\alpha _2,\varGamma ),D_1) = (S_1,\sigma _1)$, $W((D_1:\sigma _1,S_1\varGamma ),D_2) = (S_2,\sigma _2)$, and $U=mgu(\sigma _2,S_2S_1\alpha _2)\not ={\textit{f}ail}$. By induction, we know that

  • (a) ${D_2:S_1\alpha _2,S_1\varGamma }\ \vdash \ {D_1}:{\sigma _1}$   is a principal typing of $D_1$ modulo $(D_2:\alpha _2,\varGamma )$,

  • (b) ${D_1:S_2\sigma _1,S_2S_1\varGamma }\ \vdash \ {D_2}:{\sigma _2}$    is a principal typing of $D_2$ modulo $(D_1:\sigma _1,S_1\varGamma )$.

  By specializing the typing in (a) with $US_2$ and the one in (b) with U, one obtains

  

  Since $US_2S_1\alpha _2= U\sigma _2$, we can apply the rule $(\otimes )$ and obtain a typing

  

  of $(D_1\otimes D_2)$ modulo $\varGamma$. It remains to be shown that this is a most general typing.

  So suppose $(D_1\otimes D_2)$ has a typing modulo $\varGamma$. The last step in the typing derivation is

  

  For the left subderivation of ${D_2:\tau _2,S\varGamma }\ \vdash \ {D_1}:{\tau _1}$ we may assume $\tau _2=S\alpha _2$ for some fresh type variable $\alpha _2$. So $D_1$ has a typing $(S,\tau _1)$ modulo $D_2:\alpha _2,\varGamma$. By a) there is a type substitution $T_1$ such that $(S,\tau _1) = (T_1S_1,T_1\sigma _1)$, whence

  

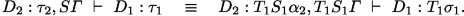
  Now the right subderivation ${D_1:\tau _1,S\varGamma }\ \vdash \ {D_2}:{\tau _2}$ is a derivation of

  

  which is a typing of $D_2$ modulo $(D_1:\sigma _1,S_1\varGamma )$. By b), there is a type substitution $T_2$ with

  

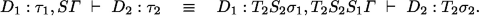
  It follows that

  

  To show that this is an instance of the typing

  

  we need a type substitution R such that $T_2=RU$ on the type variables of $S_2S_1\varGamma$, $S_2\sigma _1$ and $\sigma _2$. We have $T_2\sigma _2=T_1S_1\alpha _2$. As in (ii), $T_1=T_2S_2$ on the type variables of $S_1\alpha _2$, so $T_2\tau _2=T_2S_2S_1\alpha$, and since $U=mgu(\tau _2,S_2S_1\alpha _2)$, $T_2=RU$ on the type variables of $\tau _2$ and $S_2S_1\alpha _2$. On other type variables $\beta$, we have $U\beta =\beta =R\beta$ and can redefine $R\beta := T_2\beta$, to obtain $T_2=RU$ on all type variables of $S_2S_1\varGamma$, $S_2\sigma _1$ and $\sigma _2$.

The remaining cases of t can be treated similarly.

Example 1

The lexicon entry for the indefinite article a in $\lambda$-DRT of [13] is

$$ \lambda P\lambda Q(\delta x_i\top \otimes P(\hat{\ } x_i)\otimes Q(\hat{\ } x_i)) : (d,t),((d,t),t) $$

where d is the type of individual concepts and t the type of DRSs. Simplifying this to the extensional case and using the DRS-notation from above, type reconstruction yields the principal typing

Instead of the basic type t for DRSs in [13], we have infinitely many types $[\sigma _1,\ldots ,\sigma _n]$. Moreover, we have the principal typing

The unreduced meaning term for a man therefore is

and has the principal type $(e\rightarrow \delta )\rightarrow [e]\otimes {1\!\!1}\otimes \delta$.

For the kind of semantic checking of natural language text that we are interested in, we need to distinguish between different sorts of individuals. Lexical entries should assign different base types to the arguments of content words, in particular verbs and nouns. It is then useful, if not imperative, to have a lexicon with polymorphic types for the functional words like the indefinite article above, rather than be forced to put into the lexicon all the instance types needed for a specific application.

The type-checking in texts is slightly different from the one in programs: in programs, we need to check that in applications $f(a_1,\ldots ,a_n)$, the type of the arguments equal (or are subtypes of) the argument types of the function, while in texts, in predications $v(np_1,\ldots ,np_k)$ the types of the (generally quantified) argument noun phrases have to be related by type-raising to the argument types of the verb.

But in principle, we want to have the same phase distinction between type checking and evaluation: we want to build meaning terms according to the syntactic structure, then check if the meaning is typable, and only then perform semantic evaluation. Thus, evaluation only needs to be defined on typed expressions, and type checking would be pointless if evaluation would not preserve the type of expressions.

5 Reduction

We assume the familiar $\beta$-reduction and congruence rules of $\lambda$-calculus,

The intended meaning of the merge $(D_1\otimes D_2)$ of two value-DRSs with disjoint referent lists, $D_1 = \langle [x_{1},\ldots ,x_{n}],\varphi \rangle$ and $D_2= \langle [y_{1},\ldots ,y_{m}],\psi \rangle$, is the value-DRS

We therefore define the reduction (resp. evaluation) of DRS-expressions by the following $\delta$-reduction rules:

From these, the intended meaning for the merge of value-DRSs follows:

In order to use $(\delta _1)$ - ($\delta _3)$, by reductions we must achieve that arguments of $\otimes$ are value-DRSs. Hence we also need congruence rules for $\delta =\langle \cdot ,\cdot \rangle$ and $\otimes$:

so that reductions can be performed in subterms of $\langle x,D\rangle$, $(D\otimes E)$ as well as $\lambda x D$ and $(D_1\cdot D_2)$. Then the following reduction rules are derivable:

Normalization

It is obvious that applications of the $\delta$-reduction rules do not lead to new occurrences of $\beta$-redexes. Therefore, expressions can be reduced by first performing $\beta$-reductions as long as possible, and only then apply $\delta$-reduction rules. If we start with a typed expression, then from the strong normalization property for simply typed $\lambda$-calculus the first will terminate. It is also clear that the $\delta$-reduction rules cannot lead to infinite reduction sequences.

Notice that on value-DRSs with disjoint top-level referents, $\otimes$ is associative, if we consider formula conjunction to be associative, i.e. use list $[\varphi _1,\ldots ,\varphi _n]$ of formulas, as we do in Sect. 6.2.

We would like to show that in a derivable typing statement ${\varGamma }\ \vdash \ {s}:{\sigma }$, where the “predicate” $\sigma$ applies to the “subject” s, we may reduce the subject and still the predicate $\sigma$ applies. However, this is not quite true: when we reduce a merge-DRS, the type constructor $\times$ is interpreted as a cons of a referent and a referent list, and $\otimes$ is interpreted as an append of referent lists, and since the type of a DRS mirrors its construction, we need to cons resp. append the lists of types of the referents.

We use the following type reductions, which amount to a recursive definition of append ($\otimes$) in terms of the empty list (${1\!\!1}$) and cons ($\times$):

Moreover, type reduction may operate on embedded type expressions:

Example 1

(continued) Reducing the above term

by $\beta$-reductions gives $\lambda Q(\langle [x],\top \rangle \otimes \langle [],man'\,x\rangle \otimes Qx)$ and reducing further by $\delta$-reductions leads to

Its principal type $(e\rightarrow \delta ) \rightarrow [e]\otimes \delta$ is obtained from the one of the unreduced term by applications of ($\otimes '$), $(\delta _3')$, and $(\delta _1')$ that simplify $[e]\otimes {1\!\!1}\otimes \delta$ to $[e]\otimes \delta$.

Since our types of DRSs closely reflect the construction of their top-level referent lists, in order to have a subject reduction property we need to consider types equivalent when they get equal by interpreting $\otimes$ as append, $\times$ as cons, and ${1\!\!1}$ as the empty list.

A more serious obstacle to subject-reduction is the typing rule $(var_6)$ which permits us to ignore assumptions $(D_1\cdot D_2):\sigma$. In fact, the subject-reduction property does not hold in general.

Example 2

Consider the application of

Suppose $(D_1\otimes D_2)\rightarrow (D_1'\otimes D_2)$ via $D_1\rightarrow D_1'$. As we have seen above, we may have $x \in \textit{top}(D_1')\setminus \textit{top}(D_1)$. In the left subderivation ${D_1:\tau _1,\varGamma }\ \vdash \ {D_2}:{\tau _2}$, a free occurrence of x in $D_2$ gets its type from $\varGamma$, while in the context $D_1':\tau _1,\varGamma$, it gets its type from $D_1':\tau _1$. Hence, it may be impossible to obtain ${D_1':\tau _1,\varGamma }\ \vdash \ {D_2}:{\tau _2}$. (For example, take $D_1:\tau _1=\lambda y\langle x,E\rangle \cdot a:(\sigma \times \tau )$, $D_2:\tau _2=\langle [],Px\rangle :{1\!\!1}$.) Thus, ${\varGamma }\ \vdash \ {(D_1\otimes D_2)}:{(\tau _1\otimes \tau _2)}$ does not imply ${\varGamma }\ \vdash \ {(D_1'\otimes D_2)}:{(\tau _1\otimes \tau _2)}$.

The problem similarly arises for $(D_1\Rightarrow D_2)$, $(D_1\vee D_2)$, or $(D_1\,;\,D_2)$, where $D_1$ may $\beta$-reduce to a DRS with a new top-level referent occurring free in $D_2$. This is a defect of $\lambda$-DRT terms which admit the binding part $D_1$ of such expressions to arise from a $\beta$-redex like $(\lambda zz\cdot D_1)$.

We will sidestep this problem for the application to pronoun resolution below by assuming

• 1. all $\lambda$-DRS-expressions used as meanings of lexical entries are closed and in normal form,

• 2. in substitution t[x / s], bound variables (including referents) in t are renamed to make them distinct from free variables of s,

• 3. in t[x / s], s is in normal form, and referents of s are renamed at each occurrence of x in t (in merge-factors, so that their scope does not extend).³

• 4. all bound variables are pairwise distinct; in particular, no referent is used twice as a binding variable.

In particular, we will use a call-by-value strategy when computing the meaning of phrases: if the meaning of a phrase is an application $\lambda xt\cdot s$, we will have $\lambda xt$ and s in normal form, and deliver a normal form ${\textit{nf}}(t[x/s])$ of t[x / s] as value, see the computation rules in Sect. 6.2. We think that the following weak form of the subject reduction property holds under the above assumptions:

Conjecture 1

If t and s are in normal form, and ${\varGamma }\ \vdash \ {(\lambda xt\cdot s)}:{\tau }$, then there is $\tau '$ with $\tau \rightharpoonup ^*\tau '$ and ${\varGamma }\ \vdash \ {{\textit{nf}}(t[x/s])}:{\tau '}$.

However, we do not make use of that in the following; termination of reduction suffices.

6 Application to Pronoun Resolution

There are two possible ways to combine type reconstruction and pronoun resolution. Either one applies a pronoun resolution algorithm and then uses type reconstruction to check if the resolution is type-correct, or one first applies type reconstruction and then does pronoun resolution by exploiting the type information.

6.1 Type Informed Pronoun Resolution

The second way has been implemented [22]. It roughly proceeds as follows:

• Step 1: for each pronoun occurrence, introduce a fresh discourse referent x and extend the DRS by an anaphor-declaration like $\textit{anp}(x,\textit{fem},\textit{sg})$. For the discourse referent y of each noun phrase that is not a pronoun, add an antecedent-declaration like $\textit{ant}(y,\textit{masc},\textit{sg})$ to the DRS.

• Step 2: apply type reconstruction to get a most general typing for the discourse, including individual types $e_i$ for discourse referents x as inferred from the occurrence context of the pronoun.

• Step 3: “resolve” an anaphoric (or cataphoric) pronoun by unifying its typed discourse referent $x:\alpha$ with some discourse referent $y:\beta$ of a possible antecedent of the same type, observing the grammatical properties of gender and number in the corresponding declarations $\textit{anp}(x,g_x,n_x)$ and $\textit{ant}(y,g_y,n_y)$.

A more detailed description is best obtained by explaining the relevant parts of the Prolog-program of [22].

A parse tree is represented as a list [Root|Subtrees] where the root is the syntactic category of the parsed expression. A discourse is either empty, with tree [d], or the extension of a discourse by a sentence, and then has tree [d,S,D] where S is the parse tree of the final sentence and D the parse tree of the initial discourse.⁴ For each parse tree, sem(+Tree,-DRS) computes a number of meanings. If the tree is a discourse, each meaning is a typed $\lambda$-DRS, otherwise an untyped $\lambda$-DRS in normal form.

Having computed a typed meaning SemD for the initial discourse and an untyped meaning SemS for the final sentence, we try to resolve anaphors of SemS, using SemD as accessible DRS for possible antecedents.

First, type reconstruction type/4 is applied to SemS; as pronouns get fresh discourse referents in SemS, we can use the empty type context to find a principal type TypS for the DRS SemS. Actually, we use a modification of the type reconstruction algorithm that also returns a typed version SemSTy of SemS, which has type annotations at variable bindings (including referents in referent lists). This typed DRS SemSTy is resolved with SemD as accessible DRS, using resolve_drs/2; the modifications DrsS and DrsD are finally merged by appending the referents and formulas of DrsS to those of DrsD.

To resolve a DRS drs(Refs,Fmls) with respect to a stack Ds1 of partially resolved accessible DRSs, we go through the formulas, which may contain unresolved DRSs, resolve these, and construct a resolved form of drs(Refs,Fmls) on top of the stack:

If a formula is built from DRSs, like $(D_1\Rightarrow D_2)$, $(D_1 \vee D_2)$, or $\lnot D$, the component DRSs are resolved in term, respecting the accessibility conditions of DRT, and the formula built form the resolved component DRSs is added to the result-DRS under construction, before the remaining formulas are processed:

If the formula is an anaphor anp(Ref,Gen,Num) with typed(!) referent Ref and gender and number information, one tries to find a suitable antecedent in the result-DRS under construction (i.e. in the pronoun’s left textual context in the current sentence) or the accessible DRSs, or in the remaining formulas of the DRS currently under process:

Possessive pronouns are handled by looking for antecedents in their left context only.

To find a suitable antecedent, simply choose some of the accessible DRSs and some antecedent among its formulas that can be unified with the referent:

By using the same variables Ref, Gen, Num, Prolog unifies a typed anaphor R:Ty with a typed antecedent R$^\prime$:Ty$^\prime$ of the same number and gender features.

Atomic formulas can just be transferred to the result-DRS under construction, and when all formulas of the DRS are processed, the sequence of resolved formulas is reversed to its expected order:

The stack of resolved DRSs with a resolved form of the DRS drs(Refs,Fmls) on top is returned.

6.2 Example

We assume that nouns N and relational nouns RN are classified according to gender $g\in \{m,f,n\}$ (masculine, feminine, neuter), and implicitly inflect for number $n\in \{sg,pl\}$ and case c. (We use gender m as in the corresponding German nouns and pronouns to get more possible antecedents below.)

• 1. Content words are assigned a meaning and a type in the lexicon, for example:

  

  Pronouns inflect for number, gender, and case, if we consider person fixed to 3rd person. Like determiners, pronouns have polymorphic type; i.e. from their untyped $\lambda$-DRS-meaning we reconstruct their most general (schematic) type.

  

  Each use of a personal, relative, or possessive pronoun uses a new referent x. Moreover, eq, anp, anposs, ant have polymorphic lexical (not reconstructed) type.

• 2. Compound expressions are built according to grammar rules; each grammar rule is accompanied by one or several meaning computation rules. Some examples are:

  

  An additional computation rule $(C\ 5')$ for sentences np$_1$ v np$_2$ : S might give $np_2$ wide scope. In (C 7), $d''$ and $s''$ are obtained by pronoun-resolution from most general typings of $d'$ and $s'$ in the empty type context, i.e. $\textit{resolve}(s',d',d''\otimes s'')$ by the resolution algorithm explained above.

• 3. Let us consider the sample discourse Galilei observed a star. He discovered his moon. The first sentence is constructed with (S 1), (S 3), and (S 5). We compute the meaning of the subject as

  $$\begin{aligned} np_1' = \lambda P({\langle {[x]},[\textit{ant}(x,m,sg), eq(x,\textit{galilei})]\rangle }\otimes P\cdot x), \end{aligned}$$

  the meaning of the object as

  

  and from those obtain the sentence meaning by the computation rule for (S 5) as

  

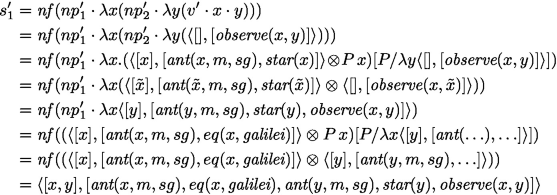
  From the type assumptions for nouns and verbs (and eq), type reconstruction can annotate the bound variables of $s_1'$ as

  $$ {\langle {[x:h,y:s]},[\textit{ant}(x:h,m,sg), eq(x,\textit{galilei}), \textit{ant}(y:s,m,sg), \ldots ]\rangle } $$

  and return a most general type $\langle [h,s],t\rangle$. In the second sentence, the subject he has meaning

  $$\begin{aligned} np_1' = \lambda P({\langle {[x]},[\textit{anp}(x,m,sg)]\rangle }\otimes P\,x), \end{aligned}$$

  which receives the following annotation and principal type:

  $$ \lambda P:(\alpha \rightarrow \beta )({\langle {[x:\alpha ]},[\textit{anp}(x:\alpha ,m,sg)]\rangle }\otimes P\,x) : (\alpha \rightarrow \beta )\rightarrow [\alpha ]\otimes \beta . $$

  The object his moon gets the meaning⁵

  $$\begin{aligned} np_2'= & {} {\textit{nf}}(\lambda R\lambda P({\langle {[x,y]},[\textit{anposs}(y,m,sg)]\rangle } \otimes (R\,x\,y \otimes P\,x)) \\&\qquad \cdot \lambda x\lambda y{\langle {[]},[\textit{ant}(x,m,sg), \textit{moon}(x,y)]\rangle }) \\= & {} \lambda P({\langle {[x,y]},[\textit{anposs}(y,m,sg),\textit{ant}(x,m,sg), \textit{moon}(x,y)]\rangle } \otimes P\,x), \end{aligned}$$

  which type reconstruction annotates to

  $$ \lambda P:(s\rightarrow \alpha )({\langle {[x:s,y:s]},[\begin{array}[t]{l}\textit{anposs}(y:s,m,sg), \\ \textit{ant}(x:s,m,sg), \textit{moon}(x,y)]\rangle {\, \otimes P\,x)}\end{array}} $$

  and to which it assigns a most general type $(s\rightarrow \alpha )\rightarrow [s,s]\otimes \alpha$. By the computation rule for (S 5), the meaning of the second sentence is

  

  If several computation rules can be applied, a sentence can get several untyped meanings this way. As normalisation has to return fresh bound variables, we write

  

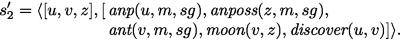
• 4. Pronoun resolution for the discourse $\epsilon \,;\,s_1\,;\,s_2$ proceeds as follows.

  • (a) The most general typing of the meaning ${\langle {[]},[]\rangle }$ of $\epsilon$ in the empty context is ${}\ \vdash \ {{\langle {[]},[]\rangle }}:{{1\!\!1}}$.

  • (b) Type reconstruction is applied to the first sentence, followed by pronoun resolution with ${\langle {[]},[]\rangle }:{1\!\!1}$. As no pronoun occurred in $s_1$, the type-annotated version of $s_1'$ is returned:

    

  • (c) Type reconstruction is applied to (each of) the meaning(s) of the next sentence, followed by pronoun resolution with $s_1''$. Here type reconstructions just returns

    

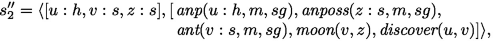
    where the types of u, v, z are derived from the argument types of nouns and verbs whose argument positions they occupy. The anaphor u : h has no antecedent in the current sentence, as v : s has different type. Assuming that possessives have to be resolved in their left context, the possessive anaphor z : s also cannot be resolved against v : s.

  • (d) Pronouns of $s_2$ may also be resolved against antecedents in the type-annotated left context, $s_1''$. For each typed anaphor, we search for a suitably typed antecedent, unify the referents and remove the anaphor referent in the DRS of the current sentence, $s_2''$. For the anaphor $\textit{anp}(u:h,m,sg)$, the only type-compatible antecedent in $s_1''$ is $\textit{ant}(x:h,m,sg)$, so we unify u with x (i.e. rename u by x in $s_2''$), remove x : h from its referent list and $\textit{anp}(x:h,m,sg)$ from its formulas, getting a partially resolved DRS

    $$ {\langle {[v:s,z:s]},[\begin{array}[t]{l}\textit{anposs}(z:s,m,sg),\textit{ant}(v:s,m,sg), \\ \textit{moon}(v,z),\textit{discover}(x,v)]\rangle {.}\end{array}} $$

    The next formula is a possessive anaphor $\textit{anposs}(z:s,m,sg)$. As we want these to be resolved in their left context only, z : s cannot be resolved against v : s. But it can be resolved against $\textit{ant}(y:s,m,sg)$ in $s_1''$, which leads to

    $$\begin{aligned} r(s_2'') = {\langle {[v:s]},[\textit{ant}(v:s,m,sg), \textit{moon}(v,y),\textit{discover}(x,v)]\rangle } \end{aligned}$$

    as the resolved"‘result"’-DRS of $s_2''$.

  • (e) Finally, the resolved version of $s_2''$ is merged with $s_1''$, yielding

    

    as the typed meaning of the discourse $d = \epsilon \,;\,s_1\,;\,s_2$.

6.3 Type Reconstruction for Bach-Peters-Sentences

One of the motivations for the symmetric merge-operator $\otimes$ was hinted at, but not elaborated in [13, p. 480]: the potential to treat Bach-Peters-sentences “in which two phrases are connected by both an anaphor and a cataphor”, like [The boy who deserved it$_y$]$_x$ got [the prize he$_x$ wanted]$_y$. We use variants of (S 2), (S 5) and (C 2), (C 5) as syntax and computation rules for relative clauses

Omitting the grammatical features and the uniqueness conditions for the definite article, the untyped meaning of a boy who deserves it gets the prize he wanted is obtained via

From suitable type assumptions for nouns and verbs in the lexicon, with a type h of humans and e of objects, type reconstruction would infer types $x:h,y:e,x':h,y':e$, and hence type-respecting pronoun resolution could only resolve $x'$ against x and y against $y'$, as expected.

The typing rule for $\otimes$-DRSs was designed for merge-DRSs whose factors are linked through resolving cataphors and anaphors by type-independent “coindexing” or referent unification. Type-checking a DRS $\langle [x],\varphi (x,y)\rangle \otimes \langle [y],\psi (x,y)\rangle$ of this kind leads to a typing problem of the form

The type variables $\alpha ,\beta$ get instantiated when the two typing problems in the premise are solved. As we perform merging of value-DRSs during normalization, we need the typing rule $(\otimes )$ only when a merge-factor is not a value-DRS, not for Bach-Peters-sentences.

6.4 Supporting Pronoun Translation

To translate between natural languages, we need to resolve pronouns in order to translate them correctly: the gender of the translated pronoun is generally not the gender of the source language pronoun, but the gender of the antecedent noun phrase in the target language, which in turn depends on the antecedent of the pronoun in the source sentence. For example, Google translates the English text The child opened the box. It contained a pen. into the German Das Kind öffnete die Schachtel. Es enthielt einen Stift., where neuter es should be feminine sie. A type difference between humans h and things e and the verb type $\textit{contain}/\textit{enthalten} : e\rightarrow e\rightarrow t$ shows that it at position of type e cannot refer to $\textit{the child}:(h\rightarrow t)\rightarrow t$ at position of type h. But only if it is resolved to $\textit{the box}:(e\rightarrow t)\rightarrow t$, the gender for the German pronoun er/sie/es can be inferred to be the gender of the translation die Schachtel of the box, i.e. feminine.

6.5 Related Work

On the practical side, discourse representation structures are used as intermediate representation of meaning when translating texts from natural language to first-order logic. This is done for large-scale processing of newspaper texts by the ${C \& C/Boxer}$ program⁶ [5] and for mathematical texts by the Naproche system [4].

The Groningen Meaning Bank [3] (GMB) is a large collection of English texts for which $C \& C$ computes syntactic analyses in categorial grammar and Boxer turns them into DRSs and first-order formulas. By using referents for individuals, events and times and predicates for thematic roles, Boxer covers far more of discourse representation theory than we do. In the examples of the GMB, nouns are classified according to animacy (human, non-concrete, etc.), which can be seen as type assignments. But, apparently, these classifications are not related to the meaning of verbs and hence not used in the pronoun resolution process. For example, in Ein Mann füttert einen Hund; wenn er ihn beißt, schlägt er ihn., our system correctly resolves the four pronouns in the only type-compatible way (the first er to Hund, the second to Mann etc.), if we provide types h for humans, a for animals and typings for nouns $\textit{Mann} : h \rightarrow t$, $\textit{Hund} : a\rightarrow t$ and verbs and . The ${C \& C/Boxer}$ program, when we use masculine pronouns in the English input A man feeds a dog. If he bites him, he beats him., resolves both subject pronouns he to the man and both object pronouns to the dog (as one can infer from the logical formula). Thus, if the argument slots of verbs of the GMB were annotated with animacy, too, its pronoun resolution and meaning translation could be improved by using our type-respecting resolution procedure. As type distinctions are easier to make in mathematics than for natural language, a similar improvement can be expected for the anaphora resolution in systems using DRS-like proof representations like [4, 8].

On the theoretical side, there is a growing amount of work (cf. [1, 14, 17, 20]) that uses constructive type theory to develop semantic representations for natural language. In this setting, the notion of type is extended (from simple types, i.e. intuitionistic propositional formulas) to first-order formulas, and proofs of the formulas are the objects of these types. In particular, proofs of existential statements $\exists x \varphi$ consist of pairs (t, p) where t is a term denoting an individual and p a proof of $\varphi [x/t]$. Such terms t may then be used to resolve anaphoric expressions. For example, Mineshima [17] uses constructive type theory enriched by $\epsilon$-terms to treat definite descriptions; the use of an $\epsilon$-term has to be justified by an existential sentence, whose proof object then contains a referent for the description. Instead of $\epsilon$-terms, Bekki [1] has terms $(@: \gamma \rightarrow e)(c)$ of unknown choice functions @ applied to contexts c to select suitable referents of type e; by instantiating $\gamma$ and constructing an object of type $\gamma \rightarrow e$ from proof objects in the typing environment $\varGamma$, this amounts to “anaphora resolution by proof search and type checking”. Clearly, the contexts $\varGamma$ used in constructive type theory provide a more general domain to search for referents than the typed DRS of the textual left context in our system; for example, one can have background assumptions that do not arise from translation of the textual left context, which is useful to handle bridging anaphora [14]. However, the formulation of background knowledge may often be unfeasible, and proof search in constructive type theory seems more complex that type reconstruction by unification from simple type annotations in the lexicon.

7 Open Problems

Extension to generalized quantifiers and plural pronouns. In [16], we have shown that type reconstruction for Montague grammar with plural noun phrases can be used to resolve some plural ambiguities. The idea is that plural noun phrases in general have several types, for distributive, reciprocal and collective readings, but argument types of predicates only unify with one of those. The type reconstruction program of [16] has been changed in [22] to type reconstruction for $\lambda$-DRT and extended to type-respecting pronoun resolution for singular pronouns. So far, type reconstruction for plurals is not adapted to $\lambda$-DRT yet. To interpret She introduced the guests to each other, for example, we would need discourse referents X for sets of individuals and apply the symmetric predicate distributively to any 2-element subset of X. As our system admits second-order discourse referents X, it seems possible to add type-respecting pronoun resolution for plural pronouns. For this, one should consider if the treatment of plurals and generalised quantifiers via “duplex conditions” [10] can be given a formulation that allows for principal types and type reconstruction.

First-order $\varvec{\lambda }$-DRT. In contrast to typed versions of $\lambda$-DRT, our untyped version is a kind of “higher-order” DRT: there is no demand that discourse referents have individual type. So we can type some expressions which, from a traditional point of view, should be untypable. For example,

$$ {P:\sigma \rightarrow t}\ \vdash \ {([Arrayht]\begin{array}{|l|}\hline x \\ \hline Px \\ \hline \end{array}\otimes x)}:{[\sigma ]\otimes \sigma } $$

is a most general typing, using $\sigma$ both as a referent-type and as a drs-type. To avoid such defects, we could introduce different kinds of types, notice when a type variable must be instantiated by an individual resp. by a drs-type, and forbid to equate types of different kinds. But in realistic cases, conditions of a DRS express properties of referents using predicates with individual argument type, which makes a formal restriction to first-order referents unnecessary.

Principal typings for pronoun resolved discourses. Does type-respecting pronoun resolution as suggested above “preserve principal types”? More precisely, in a merge-DRS $D_1\otimes D_2$ of two typed DRSs with disjoint toplevel referent lists and principal types, we unify referents $x:\sigma$ of $D_1$ and $x':\sigma '$ of $D_2$ by substituting x for y in $D_2$ and removing $x':\sigma '$ from its referent list. Applying the most general unifier U of $x:\sigma$ and $x':\sigma '$ gives a typed DRS $UD_1\otimes UD_2$. Can one prove that $UD_1\otimes UD_2'$ corresponds to the principal typing of $\tilde{D}_1\otimes \tilde{D}_2'$, where $D_2'$ is the modification of $D_2$ by the pronoun resolution, and $\tilde{D}_1$ resp. $\tilde{D}_2'$ are the untyped versions of $D_1$ and $D_2'$?

Semantics. A semantics for typed $\lambda$-DRT is given in [13, 15], with a compositional meaning for the symmetric $\otimes$. The relational interpretation of [19] for the unsymmetric merge (; ) is not sufficient for our purposes. The Dynamic lambda calculus DLC of [11, 12] claims to give a typed semantics for a system subsuming typed $\lambda$-DRT, but we found their types involving individual variables fairly incomprehensible. In order to show that the typing and reduction rules given here are correct, we ought to interprete typings ${\varGamma }\ \vdash \ {t}:{\tau }$ in a suitable domain-model of the untyped $\lambda$-calculus, like the one in [21], and handle free type variables as universally quantified. We have not yet tried to do so.

8 Conclusion

Our aim was to use semantic type information from the lexicon to reduce the number of possible antecedents of an anaphor to type-compatible ones. For this, a single type e of entities is too crude. Many verbs and nouns in natural language can only be applied to facts/propositions, inanimate physical objects, animals, or humans, respectively. Candidates for pronoun resolution can be reduced with these types quite reasonably in many situations. Of course, in a discourse about humans only, the reduction in candidates may be minimal.

The basic idea is simple: a pronoun gets a type from its occurrence as an argument of a verb, and a noun phrase gets a type from its head noun and the verb argument type of its occurrence; hence, one can filter the set of possible antecedents of a pronoun by comparing their types. To do this efficiently, we prefer a system of simple types with schematic types for function words like determiners, in which complex expressions have principal types that can easily be reconstructed from type assumptions for content words. (A complex expression can have a principal type for each choice of types of its words.)

Using DRSs provides us with DRTs [10] notion of possible “accessible” antecedent noun phrases. Our typing rules for $\lambda$-DRT expressions closely reflect the accessibility conditions of DRT; this is to be expected, as the antecedent noun phrase provides a type assumption for its discourse referent, which in turn corresponds to the pronoun occurrences referring to the antecedent. However, the peculiarities of $\lambda$-DRT concerning the subject-reduction property might be a good reason to consider a mathematically “cleaner” language for expressing the dynamics of discourse, such as simply typed $\lambda$-calculus with continuation semantics [7]. But in contrast to [7], we are not assuming pronoun resolution via some oracles, but rather integrate a type reconstruction algorithm into a pronoun resolution algorithm – in a particularly simple way.