Abstract
Separating public key encryption from one way functions is one of the fundamental goals of complexity-based cryptography. Beginning with the seminal work of Impagliazzo and Rudich (STOC, 1989), a sequence of works have ruled out certain classes of reductions from public key encryption (PKE)—or even key agreement—to one way function. Unfortunately, known results—so called black-box separations—do not apply to settings where the construction and/or reduction are allowed to directly access the code, or circuit, of the one way function. In this work, we present a meaningful, non-black-box separation between public key encryption (PKE) and one way function.
Specifically, we introduce the notion of \(\mathsf {BBN}^-\) reductions (similar to the \(\mathsf {BBN}\)p reductions of Baecher et al. (ASIACRYPT, 2013)), in which the construction E accesses the underlying primitive in a black-box way, but wherein the universal reduction \({{\mathbb R}}\) receives the efficient code/circuit of the underlying primitive as input and is allowed oracle access to the adversary \(\mathsf {Adv}\). We additionally require that the functions describing the number of oracle queries made to \(\mathsf {Adv}\), and the success probability of \({{\mathbb R}}\) are independent of the run-time/circuit size of the underlying primitive. We prove that there is no non-adaptive, \(\mathsf {BBN}^-\) reduction from PKE to one way function, under the assumption that certain types of strong one way functions exist. Specifically, we assume that there exists a regular one way function f such that there is no Arthur-Merlin protocol proving that \(z \notin \mathsf {Range}(f)\), where soundness holds with high probability over “no instances,” \(y \sim f(U_n)\), and Arthur may receive polynomial-sized, non-uniform advice. This assumption is related to the average-case analogue of the widely believed assumption \(\mathsf {coNP}\not \subseteq \mathbf {NP}/{\mathrm{poly}}\).
This work is supported in part by an NSF CAREER Award #CNS-1453045 and by a Ralph E. Powe Junior Faculty Enhancement Award. This work was done in part while the author was visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #CNS-1523467.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Complexity-based cryptography seeks to formalize generic assumptions, such as the existence of one way functions or trapdoor functions, and then determine which cryptographic primitives can be constructed from these assumptions. For example, it has been shown that the existence of one way functions implies the existence of pseudorandom generators [24], pseudorandom functions [20], digital signatures [26, 31] and symmetric key encryption. For other primitives, such as public key encryption, it is believed that stronger assumptions are necessary. Indeed, a gap between symmetric key and public key encryption schemes also emerges in practice: Practical symmetric key encryption schemes, such as AES, are far more efficient and have proven to be less susceptible to attack, than practical public key encryption schemes, such as RSA. Understanding whether this gap in security and efficiency is inherent seems tied to determining whether public key encryption requires stronger complexity assumptions than one way functions. Unfortunately, even formalizing this question is difficult: We cannot hope to prove that one way function does not imply public key encryption in the logical sense, i.e. \(\mathsf {OWF}\not \rightarrow \mathsf {PKE}\), since if public key encryption exists then the logical statement \(\mathsf {OWF}\rightarrow \mathsf {PKE}\) is always true. Therefore, one approach has been to ask whether there exists a black-box reduction of public key encryption to one way function, wherein the construction and security proof (reduction) only access the one way function in an input/output manner, but cannot make use of its code. The answer turns out to be negative as shown by the seminal work of Impagliazzo and Rudich [25] (who proved that even key agreement cannot be black-box reduced to one way function) and, in fact, their oracle separation technique was subsequently used to rule out black-box reductions between various primitives such as collision resistant hash functions to one way functions [34], oblivious transfer to public key encryption [18] and many more. But what about non-black-box reductions between these primitives, where the construction/reduction may use the code of the underlying primitive?
Pass et al. [29] initiated a systematic study of this question, ruling out a type of non-black-box reduction called a Turing-reductions—where the code of the underlying primitive is used in an arbitrary manner, but the adversary is used in a black-box manner only—under the assumption that one way functions with very strong properties exist. Briefly, languages coupled with an efficiently samplable distribution over the no instances are considered to be in \(\mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}\) if there exists an \(\mathsf {A}\mathsf {M}\) (constant-round) protocol that accepts the language, with the relaxation that soundness only needs to hold with high probability over the no instances. For efficiently computable f, Pass et al. [29] consider the distributional language \(\overline{\mathsf {Range}(f)} = \{z : \forall x \in \{0,1\}^*, f(x) \ne z\}\) along with the distribution \(f(U_n)\) over the “No” instances. Their assumption is that there exists an efficiently computable function f such that \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}\). Pass et al. [29] justify their assumption by arguing that it is a natural average-case analogue of the widely believed assumption \(\mathsf {coNP}\not \subseteq \mathsf {A}\mathsf {M}\). Based on this assumption, [29] rule out various Turing reductions including, reductions from one-way permutations to one-way functions. Additionally, based on other newly introduced complexity assumptions, Pass et al. [29] prove separations among various other primitives. However, none of their results address the case of constructing key agreement (or even public key encryption) from one way function. Separating key agreement from one way function is especially significant, since it implies a separation of public key cryptography from private key cryptography. Indeed, resolving this question is one of the fundamental goals of complexity-based cryptography.
In order to make progress towards this goal, we seek to formalize a meaningful, non-black-box separation between one way function and public key encryption (PKE). To the best of our knowledge, the only known separations to date between one way function and public key encryption (PKE) are oracle separations. Such separations instantiate the one way function with a random oracle and so do not apply to settings where the construction and/or reduction are allowed to access the code of the one way function. We first define Turing reductions and discuss why it seems hard to rule out all Turing reductions from PKE to one-way function based on the assumption that there exist (classes of) one-way functions f for which \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}\). We then introduce and motivate a new, more restricted type of non-black-box reduction, \(\mathsf {BBN}^-\) reductions, which are related to the \(\mathsf {BBN}\)p reductions considered in the taxonomy of Baecher et al. [3]. Looking ahead, our main theorem will rule out non-adaptive, \(\mathsf {BBN}^-\) reductions from public key encryption to one-way functions based on the assumption that there exists a regular one-way-function f such that \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}^{\mathrm{poly}}\), where \(\mathsf {A}\mathsf {M}^{\mathrm{poly}}\) is the non-uniform analogue of \(\mathsf {A}\mathsf {M}\) (i.e. \(\mathsf {A}\) is allowed to receive polynomial-sized, non-uniform advice).
1.1 Turing Reductions and the Difficulty of Ruling Them Out
We begin by recalling the definition of a type of non-black-box reduction known in the literature as a Turing reduction. The formal definition below will be useful when we define our new class of non-black-box reductions (\(\mathsf {BBN}^-\) reductions) and compare to the notion of a Turing reduction.
Turing reductions. A Turing reduction from a primitive \(\mathcal {Q}\) to a primitive \(\mathcal {P}\) is a pair of oracle PPT Turing machines \((E, {{\mathbb R}})\) such that the following two properties hold:
- Construction. :
-
For every efficient implementation f of primitive \(\mathcal {P}\), E(f) implements \(\mathcal {Q}\).
- Reduction. :
-
For every efficient implementation f of \(\mathcal {P}\), and every (inefficient) adversary \(\mathsf {Adv}\) who breaks E(f) with probability \(\varepsilon =\varepsilon (n)\), on security parameter n, we have that \({{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{\varepsilon }, f)\) breaks f with probability \(1/t(\max (n,1/\varepsilon (n)))\) and \({{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{1/\varepsilon }, f)\) makes at most \(v(\max (n,1/\varepsilon (n)))\) oracle queries to \(\mathsf {Adv}\), for polynomials t, v.
Difficulty of ruling out Turing reductions. To rule out Turing reductions from PKE to one-way function based on the assumption that there exist efficiently computable f for which \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}\), one must construct an \(\mathsf {A}\mathsf {M}\) protocol proving \(z \notin \mathsf {Range}(f)\) (i.e. that z is “invalid”) for any efficiently computable f, assuming there exists a Turing reduction from PKE to one-way function. The following is the natural way to do this: Let \({{\mathbb R}}\) be the assumed Turing reduction from PKE to one-way function. The protocol does the following: \(\mathsf {A}\) emulates the reduction \({{\mathbb R}}^{\mathsf {Adv}}(f, z)\), using the all-powerful \(\mathsf {M}\) to respond to queries made to the adversary \(\mathsf {Adv}\). Queries made to \(\mathsf {Adv}\) will be of the form  where
where  is a public key and \(\mathsf {e}\) is a ciphertext and in return, \(\mathsf {M}\) should return the message m encrypted in \(\mathsf {e}\), along with a proof (e.g. the coins for \(\mathsf {Gen}\) and \(\mathsf {Enc}\) showing that this is a correct decryption). If the emulation of \({{\mathbb R}}^\mathsf {Adv}\) outputs a value x such that \(f(x) = z\), then \(\mathsf {A}\) rejects; otherwise, \(\mathsf {A}\) accepts. Intuitively, the reason this should work, is that if \({{\mathbb R}}\) is a “good” reduction, then \({{\mathbb R}}\) should invert w.h.p. for most \(z \sim f(U_n)\), whereas if \(z \notin \mathsf {Range}(f)\), no matter what \({{\mathbb R}}\) does, it cannot invert.
is a public key and \(\mathsf {e}\) is a ciphertext and in return, \(\mathsf {M}\) should return the message m encrypted in \(\mathsf {e}\), along with a proof (e.g. the coins for \(\mathsf {Gen}\) and \(\mathsf {Enc}\) showing that this is a correct decryption). If the emulation of \({{\mathbb R}}^\mathsf {Adv}\) outputs a value x such that \(f(x) = z\), then \(\mathsf {A}\) rejects; otherwise, \(\mathsf {A}\) accepts. Intuitively, the reason this should work, is that if \({{\mathbb R}}\) is a “good” reduction, then \({{\mathbb R}}\) should invert w.h.p. for most \(z \sim f(U_n)\), whereas if \(z \notin \mathsf {Range}(f)\), no matter what \({{\mathbb R}}\) does, it cannot invert.
Of course, there is a huge hole in the above argument: The reduction \({{\mathbb R}}\) may send queries to \(\mathsf {Adv}\), that “look like” valid transcripts  , but actually do not correspond to the output of \(\mathsf {Gen}\), \(\mathsf {Enc}\) on any valid input and randomness. So, we must allow \(\mathsf {M}\) to claim to \(\mathsf {A}\) that
, but actually do not correspond to the output of \(\mathsf {Gen}\), \(\mathsf {Enc}\) on any valid input and randomness. So, we must allow \(\mathsf {M}\) to claim to \(\mathsf {A}\) that  is invalid, but to prevent \(\mathsf {M}^*\) from cheating, we must also demand a proof of invalidity. But note that whatever protocol we use to prove that
is invalid, but to prevent \(\mathsf {M}^*\) from cheating, we must also demand a proof of invalidity. But note that whatever protocol we use to prove that  is invalid should not work for proving \(z \notin \mathsf {Range}(f)\) for general one way functions f, since this would contradict our assumption. On the other hand, since the \(\mathsf {A}\mathsf {M}\) protocol must work for every construction of PKE from one-way function, it is not clear how to restrict the class of functions.
is invalid should not work for proving \(z \notin \mathsf {Range}(f)\) for general one way functions f, since this would contradict our assumption. On the other hand, since the \(\mathsf {A}\mathsf {M}\) protocol must work for every construction of PKE from one-way function, it is not clear how to restrict the class of functions.
Nevertheless, there is a difference between the two settings: When proving \(z \notin \mathsf {Range}(f)\), \(\mathsf {M}^*\) knows the “statement,” i.e., the value of z. On the other hand, during the proof of the statement \(z \notin \mathsf {Range}(f)\), \(\mathsf {A}\) samples  by running the randomized reduction \({{\mathbb R}}(f,z)\) and outputting its queries to \(\mathsf {Adv}\). Moreover, if \(\mathsf {M}^*\) cannot distinguish transcripts
by running the randomized reduction \({{\mathbb R}}(f,z)\) and outputting its queries to \(\mathsf {Adv}\). Moreover, if \(\mathsf {M}^*\) cannot distinguish transcripts  sampled using the reduction \({{\mathbb R}}\), from
sampled using the reduction \({{\mathbb R}}\), from  sampled honestly using \(\mathsf {Gen}\) and \(\mathsf {Enc}\), then \(\mathsf {M}^*\) cannot “cheat.” At first glance, it seems that, indeed, the two distributions must be close, since if \({{\mathbb R}}\)’s output is far from the output of \(\mathsf {Gen}\) and \(\mathsf {Enc}\), then \(\mathsf {Adv}\) can always reject (and thus is useless for inverting f). However, there is a subtle issue here: For \(\mathsf {Adv}\) to be useful for breaking f, we only need that the output queries of \({{\mathbb R}}(f, f(U_n))\) (over random variable \(f(U_n)\)) is close to the output of \(\mathsf {Gen}\) and \(\mathsf {Enc}\); whereas in order to force \(\mathsf {M}^*\) to behave honestly, we need that the output queries of \({{\mathbb R}}(f, z)\), with fixed input z, are close to the output of \(\mathsf {Gen}\) and \(\mathsf {Enc}\). Thus, in order to force honest behavior from \(\mathsf {M}^*\), we would need to show that with high probability over choice of \(z \sim f(U_n)\), the queries output by \({{\mathbb R}}(f, f(U_n))\) are distributed closely to the queries outputted by \({{\mathbb R}}(f, z)\). In other words, the queries made by \({{\mathbb R}}(f, z)\) should be (close to) independent of z. But this seems highly implausible since in order for \({{\mathbb R}}\) to invert z, given oracle access to \(\mathsf {Adv}\), a successful \({{\mathbb R}}\) should embed z in the transcripts
sampled honestly using \(\mathsf {Gen}\) and \(\mathsf {Enc}\), then \(\mathsf {M}^*\) cannot “cheat.” At first glance, it seems that, indeed, the two distributions must be close, since if \({{\mathbb R}}\)’s output is far from the output of \(\mathsf {Gen}\) and \(\mathsf {Enc}\), then \(\mathsf {Adv}\) can always reject (and thus is useless for inverting f). However, there is a subtle issue here: For \(\mathsf {Adv}\) to be useful for breaking f, we only need that the output queries of \({{\mathbb R}}(f, f(U_n))\) (over random variable \(f(U_n)\)) is close to the output of \(\mathsf {Gen}\) and \(\mathsf {Enc}\); whereas in order to force \(\mathsf {M}^*\) to behave honestly, we need that the output queries of \({{\mathbb R}}(f, z)\), with fixed input z, are close to the output of \(\mathsf {Gen}\) and \(\mathsf {Enc}\). Thus, in order to force honest behavior from \(\mathsf {M}^*\), we would need to show that with high probability over choice of \(z \sim f(U_n)\), the queries output by \({{\mathbb R}}(f, f(U_n))\) are distributed closely to the queries outputted by \({{\mathbb R}}(f, z)\). In other words, the queries made by \({{\mathbb R}}(f, z)\) should be (close to) independent of z. But this seems highly implausible since in order for \({{\mathbb R}}\) to invert z, given oracle access to \(\mathsf {Adv}\), a successful \({{\mathbb R}}\) should embed z in the transcripts  it submits to \(\mathsf {Adv}\), and so the queries to \(\mathsf {Adv}\) will clearly depend on z!
it submits to \(\mathsf {Adv}\), and so the queries to \(\mathsf {Adv}\) will clearly depend on z!
Unfortunately, we do not know how to get around this problem for the case of general Turing reductions. However, for the restricted class of non-adaptive, \(\mathsf {BBN}^-\) reductions, which we introduce next, we will show how to overcome this apparent contradiction.
\(\mathsf {BBN}^-\) reductions. A \(\mathsf {BBN}^-\) reduction from a primitive \(\mathcal {Q}\) to a primitive \(\mathcal {P}\) is a pair of oracle PPT Turing machines \((E, {{\mathbb R}})\) such that the following two properties holdFootnote 1:
- Construction. :
-
For every implementation f of primitive \(\mathcal {P}\), \(E^f\) implements \(\mathcal {Q}\).
- Reduction. :
-
There exist polynomials \(t(\cdot ), v(\cdot )\) such that: For every efficient implementation f of \(\mathcal {P}\), and every (inefficient) adversary \(\mathsf {Adv}\) who breaks \(E^{f}\) with probability \(\varepsilon = \varepsilon (n)\), on security parameter n, we have that \({{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{\varepsilon }, f)\) breaks f with probability \(1/t(\max (n,\varepsilon (n)))\) and \({{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{1/\varepsilon }, f)\) makes at most \(v(\max (n,\varepsilon (n)))\) oracle queries to \(\mathsf {Adv}\).
We remark that an implementation of a primitive is any specific scheme that meets the requirements of that primitive (e.g., an implementation of a publickey encryption scheme provides samplability of key pairs, encryption with the public-key, and decryption with the private key).
In the above definition, the construction E makes only black-box calls to f, but the reduction \({{\mathbb R}}^{\mathsf {Adv}}(f)\) receives the description of f as input and so is non-black-box. Allowing only \({{\mathbb R}}\) access to the code of f already thwarts known techniques (e.g., oracle separations) for proving impossibility results. We also require that the functions describing the number of oracle queries made to \(\mathsf {Adv}\), and the success probability of \({{\mathbb R}}\) are independent of the run-time/circuit size of f.
1.2 Necessity of the Restrictions
The notion of \(\mathsf {BBN}^-\) reductions is supposed to capture the setting where the construction is “black-box” in the underlying primitive, but the proof is “non-black-box” in the underlying primitive but “black-box” in the adversary. This is a natural subclass of Turing reductions, in which the construction/reduction may both be “non-black-box” in the underlying primitive, but the reduction is “black-box” in the adversary.
However, a careful reader will notice that we placed additional restrictions when defining \(\mathsf {BBN}^-\) reductions (this was why we called our notion “\(\mathsf {BBN}\) minus” in that the polynomials \(t(\cdot ), v(\cdot )\) are independent of the particular function f and so specifically, the polynomials \(t(\cdot ), v(\cdot )\) must be independent of the run-time (i.e. circuit size) of f. Specifically, consider the following alternative definition, which we call \(\mathsf {BBN}\)’:
An Alternative Definition \(\mathsf {BBN}\)’:
- Construction. :
-
For every implementation f of primitive \(\mathcal {P}\), \(E^f\) implements \(\mathcal {Q}\).
- Reduction. :
-
For every efficient implementation f of \(\mathcal {P}\), and every (inefficient) adversary \(\mathsf {Adv}\) who breaks \(E^f\) with probability \(\varepsilon = \varepsilon (n)\), on security parameter n, we have that \({{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{\varepsilon }, f)\) breaks f with probability \(1/t(\max (n,\varepsilon (n)))\) and \({{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{1/\varepsilon }, f)\) makes at most \(v(\max (n,1/\varepsilon (n)))\) oracle queries to \(\mathsf {Adv}\), for polynomials t, v.
In the following, we argue that the more restrictive notion of \(\mathsf {BBN}^-\) is necessary in the following sense: If there exists a Turing reduction from PKE to OWF, then there also exists a \(\mathsf {BBN}\)’ reduction from PKE to OWF. Therefore, ruling out \(\mathsf {BBN}\)’ reductions from PKE to OWF also implies ruling out Turing reductions from PKE to OWF. Since our goal is to relax the notion of Turing reduction in a meaningful way, in order to make progress on this fundamental question, it is necessary to restrict \(t(\cdot ), v(\cdot )\) as in the definition of \(\mathsf {BBN}^-\).
Theorem 1
(Informal). If there exists a Turing reduction from PKE to (uniform) OWF, then there also exists a \(\mathsf {BBN}\)’ reduction from PKE to OWF.
We sketch the proof of the above theorem.
Proof of Theorem 1 (Sketch): Assume there exists a Turing reduction \((E, {{\mathbb R}})\) from PKE to one way function, then (using the reduction from one way function to weak one-way function), there also exists a Turing reduction \((E, {{\mathbb R}})\) from PKE to weak-one-way-function, where an efficient adversary can invert the one way function with probability at most \(1-1/\mathrm{poly}(n)\), where n is security parameter (i.e. input/output length). We will use this to build a \(\mathsf {BBN}\)’ reduction \((E', {{\mathbb R}}')\) from PKE to one way function.Footnote 2 We first define \(E'\): We completely ignore oracle f and set \(E' := E(f_{univ})\), where \(f_{univ}\) is the “weak” universal one-way function described in [19]. Namely, on input Turing machine \(f'\) and string x, \(f_{univ}(f', x)\) outputs \(f' || {f'}^{|x|^2}(x)\), where \({f'}^{|x|^2}(x)\) denotes the output of \(f'\) after running on input x for \(|x|^2\) number of steps. Now, we define the reduction \({{\mathbb R}}'\): On input (f, y), where f has (polynomial) running time \(n^c\) on inputs of length n, and oracle access to adversary \(\mathsf {Adv}\) breaking \({E'}^f\), \({{{\mathbb R}}'}^\mathsf {Adv}(f,y)\) does the following: Define the new one-way-function \(f'\) that runs in time \(\widetilde{n}^2\) on inputs of length \(\widetilde{n}\) in the following way: \(f'\) parses its input as x||a, where x has length \(\widetilde{n}^{1/c}\) and outputs \(f(x) = y\) in time \(\widetilde{n}^2\). \({{\mathbb R}}'\) then runs \({{\mathbb R}}^\mathsf {Adv}\) on inputs \((f_{univ}, (f', y || a))\), where a is a dummy string of length \(n^c - n\). Note that the input/output length \({{\mathbb R}}^\mathsf {Adv}\) gets run on is now \(n^c\). Since \({{\mathbb R}}\) is a good Turing reduction, \({{\mathbb R}}\) inverts \(f_{univ}\) with \(1-1/\mathrm{poly}(n)\) probability, which means that \({{\mathbb R}}\) will return an element in \(f^{-1}_{univ}((f',y))\) with non-negligible probability. Using this information \({{\mathbb R}}'\) can then recover an element in \(f^{-1}(y)\) with non-negligible probability. However, note that the functions describing the number of times \({{\mathbb R}}\) runs the adversary \(\mathsf {Adv}\) and the success probability of \({{\mathbb R}}\) depend on the input/output length of \((f_{univ}, (f', y || a))\), which is \(n^c\) and thus depends on the run time of f. This means that the functions describing the number of times \({{\mathbb R}}'\) runs \(\mathsf {Adv}\) and the success probability of \({{\mathbb R}}'\) depends on the runtime of f.
1.3 Our Main Result
We are now ready to state our main theorem:
Theorem 2
(Informal). Under the assumption that there exists a regular one-way function f such that the distributional language \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}^{\mathrm{poly}}\), there is no non-adaptive, \(\mathsf {BBN}^-\) reduction from PKE to one way function.
In the above, \(\mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}^{\mathrm{poly}}\) is the same as the class \(\mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}\), except that \(\mathsf {A}\) is allowed to receive polynomial-sized, non-uniform advice. Note that our result is restricted to non-adaptive reductions \({{\mathbb R}}\) which make \(v(\max (n, 1/\varepsilon (n)))\) parallel oracle queries to the adversary \(\mathsf {Adv}\).
We conjecture that using techniques of Akavia et al. [2], Theorem 2 can be proven under the assumption that there exists a regular one-way function f such that the distributional language \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}\) (i.e. without requiring the non-uniform advice). The requirement for regularity of f in the assumption comes from our use of the randomized iterate (see [21]) whose hardness amplification properties only hold for (nearly) regular functions f. Recently, the analysis of the randomized iterate was extended to a more general class of functions called “weakly-regular” functions [37]. We conjecture that our results hold for this broader class of functions as well. Extending our results to general one-way functions seems tied to the development of security-preserving hardness amplification techniques for general one-way functions. We leave these as opens problem for future work.
1.4 Our Techniques
A key insight of our work is the relationship between our newly introduced notion of \(\mathsf {BBN}^-\) reductions and the problem of instance compression. Instance compression [7, 11, 14, 23] is the fundamental complexity-theoretic problem of taking an instance of a hard problem and compressing it into a smaller, equivalent instance, of the same or different problem.Footnote 3 The relationship between \(\mathsf {BBN}^-\) reductions and instance compression is the following: The reduction \({{\mathbb R}}\) takes as input an instance (y, c), where y is a random image of c, and submits queries to \(\mathsf {Adv}\), which take the form of transcripts  where
where  is the public key and \(\mathsf {e}\) is a ciphertext. Since the public key encryption scheme uses the underlying one-way function in a black-box manner, the size of the transcript
is the public key and \(\mathsf {e}\) is a ciphertext. Since the public key encryption scheme uses the underlying one-way function in a black-box manner, the size of the transcript  must be a fixed polynomial in the security parameter n (i.e. the input-output size of the one-way function). Thus, as long as \({{\mathbb R}}\) (on input security parameter n) does not query \(\mathsf {Adv}\) with security parameter \(\widetilde{n}\) that is too large and depends on the circuit size (i.e. runtime) of c, then it must be the case that the total length of the messages sent from \({{\mathbb R}}\) to \(\mathsf {Adv}\) is independent of the size of the circuit c. In order to force \({{\mathbb R}}\) to have this behavior, we instantiate \(\mathsf {Adv}\) in such a way that queries submitted by \({{\mathbb R}}\) with security parameter which is too large are “useless” due to the restrictions of the \(\mathsf {BBN}^-\) reduction. Now, in the \(\mathsf {A}\mathsf {M}\) protocol proving statement \(z \notin \mathsf {Range}(f)\), instead of using (z, f) itself as the input to \({{\mathbb R}}\), we construct a new one-way function instance (c, y) (with the same input-output length) using \(k = k(n)\) instances \((x_1, y_1), \ldots , (x_{k}, y_{k})\). I.e., \((c,y) \leftarrow \varPhi (x_1, y_1), \ldots , (x_{k}, y_{k})\), where \(\varPhi \) is some randomized function, each \((x_i, y_i)\) is an input-output pair of f, and one of the \(y_i\)’s is set to the common input z. The requirement on \((c,y) \leftarrow \varPhi (x_1, y_1), \ldots , (x_{k}, y_{k})\) is that inverting c (i.e. finding x such that \(c(x) = y\)) implies inverting \(y_i\) (i.e. finding \(x_i\) such that \(f(x_i) = y_i\)) with probability \(1/\mathrm{poly}(k)\). By choosing \(k = k(n)\) to be a sufficiently large polynomial, it is possible to ensure that there is not enough room for all individual instances \(y_1, \ldots , y_k\) to be embedded in the interaction with \(\mathsf {Adv}\). Thus, the reduction \({{\mathbb R}}\) itself which takes as input (c, y) and produces queries to \(\mathsf {Adv}\) can be viewed as an instance compression algorithm. Using techniques of Drucker [11] (similar to techniques that appeared previously in [30, 33]), we will now be able to circumvent the problem with the naive attempt to rule out Turing reductions discussed above, which was that with high probability over \(z \sim f(U_n)\), the distribution over \({{\mathbb R}}(f, f(U_n))\) will be far from the distribution over \({{\mathbb R}}(f, z)\). We elaborate further below on the necessary steps of our proof and in the discussion below, we point out where each restriction we place on the class of reductions is being used:
must be a fixed polynomial in the security parameter n (i.e. the input-output size of the one-way function). Thus, as long as \({{\mathbb R}}\) (on input security parameter n) does not query \(\mathsf {Adv}\) with security parameter \(\widetilde{n}\) that is too large and depends on the circuit size (i.e. runtime) of c, then it must be the case that the total length of the messages sent from \({{\mathbb R}}\) to \(\mathsf {Adv}\) is independent of the size of the circuit c. In order to force \({{\mathbb R}}\) to have this behavior, we instantiate \(\mathsf {Adv}\) in such a way that queries submitted by \({{\mathbb R}}\) with security parameter which is too large are “useless” due to the restrictions of the \(\mathsf {BBN}^-\) reduction. Now, in the \(\mathsf {A}\mathsf {M}\) protocol proving statement \(z \notin \mathsf {Range}(f)\), instead of using (z, f) itself as the input to \({{\mathbb R}}\), we construct a new one-way function instance (c, y) (with the same input-output length) using \(k = k(n)\) instances \((x_1, y_1), \ldots , (x_{k}, y_{k})\). I.e., \((c,y) \leftarrow \varPhi (x_1, y_1), \ldots , (x_{k}, y_{k})\), where \(\varPhi \) is some randomized function, each \((x_i, y_i)\) is an input-output pair of f, and one of the \(y_i\)’s is set to the common input z. The requirement on \((c,y) \leftarrow \varPhi (x_1, y_1), \ldots , (x_{k}, y_{k})\) is that inverting c (i.e. finding x such that \(c(x) = y\)) implies inverting \(y_i\) (i.e. finding \(x_i\) such that \(f(x_i) = y_i\)) with probability \(1/\mathrm{poly}(k)\). By choosing \(k = k(n)\) to be a sufficiently large polynomial, it is possible to ensure that there is not enough room for all individual instances \(y_1, \ldots , y_k\) to be embedded in the interaction with \(\mathsf {Adv}\). Thus, the reduction \({{\mathbb R}}\) itself which takes as input (c, y) and produces queries to \(\mathsf {Adv}\) can be viewed as an instance compression algorithm. Using techniques of Drucker [11] (similar to techniques that appeared previously in [30, 33]), we will now be able to circumvent the problem with the naive attempt to rule out Turing reductions discussed above, which was that with high probability over \(z \sim f(U_n)\), the distribution over \({{\mathbb R}}(f, f(U_n))\) will be far from the distribution over \({{\mathbb R}}(f, z)\). We elaborate further below on the necessary steps of our proof and in the discussion below, we point out where each restriction we place on the class of reductions is being used:
Eliminating security parameter blow-up. We construct an adversary \(\mathsf {Adv}\) that has the following property: When the one-way function has input/output length \(\widetilde{n}\), \(\mathsf {Adv}\) flips a coin and returns \(\bot \) with probability \(1-1/\widetilde{n}\). Note that this means that we can replace any reduction \({{\mathbb R}}\) that on security parameter n makes queries to \(\mathsf {Adv}\) with extremely large security parameter (i.e. input/output length) greater than \(\widetilde{n} := 2 \cdot t(\max (n, 1/\varepsilon (n))) \cdot v(\max (n, 1/\varepsilon (n)))\), with another reduction \({{\mathbb R}}'\) that simulates all answers of \(\mathsf {Adv}\) to queries with security parameter greater than \(\widetilde{n}\) with \(\bot \) without actually making the query. The probability that the view of \({{\mathbb R}}\) and \({{\mathbb R}}'\) differs is at most \(v(\max (n, 1/\varepsilon (n))) \cdot 1/(2 \cdot t(\max (n, 1/\varepsilon (n))) \cdot v(\max (n, 1/\varepsilon (n))))\) and thus \({{\mathbb R}}'\) should still succeed with probability at least \(1/2t(\varepsilon (n))\). This means that the length of the total output of \({{\mathbb R}}'\) to \(\mathsf {Adv}\) depends only on n, but not on the size (runtime) of c and so \({{\mathbb R}}'\) is indeed a compression function, when we choose appropriate circuit c. Here we use the restriction that \(t(), v(), \varepsilon ()\) are all independent of the runtime of c.
Designing a circuit-oblivious adversary. The adversary \(\mathsf {Adv}= (\mathsf {Adv}_1\), \(\mathsf {Adv}_2\), \(\mathsf {Adv}_3)\) will have the property that \(\mathsf {Adv}_1, \mathsf {Adv}_3\) are efficient algorithms, whereas \(\mathsf {Adv}_2\) is inefficient but does not require access to the one-way function c. Looking ahead, \(\mathsf {M}\) will be used to implement \(\mathsf {Adv}_2\) only. The fact that \(\mathsf {Adv}_2\) does not require access to c is crucial, since otherwise, the size of the interaction would be at least |c| and there would be no compression. The techniques of [5, 25, 35] are crucial for constructing such \(\mathsf {Adv}\). Allowing the construction only black-box access to the underlying one-way function is necessary for this step in the proof, since \(\mathsf {Adv}_2\) will essentially emulate the adversary from the black-box separation of OWF and PKE of [5, 25, 35]. See Sect. 3.
Applying instance compression techniques. For a fixed f, denote by \(\varPhi ((x^1, y^1)\), \(\ldots ,\) \((x^{k}, y^{k}))\) the randomized mapping that derives (c, y) from \((x^1, y^1), \ldots , (x^{k}, y^{k})\), where \(y^i = f(x^i)\) and view \({{\mathbb R}}\circ \varPhi \) as a compression algorithm. For \(z \sim f(U_n)\), we would like to embed \((x^i, y^i) = (x,z)\), where \(f(x) = z\), for a random position \(i \in [k]\). Call this randomized mapping \(\varPhi _z\). Using techniques of Drucker [11], we will choose \(\varPhi \) so that with high probability over \(z \sim f(U_n)\), the distribution over the output of \({{\mathbb R}}\circ \varPhi _z\), denoted \(\mathcal {T}(z)\), where a fixed z is embedded in a random position and the remaining inputs are random, is statistically close to the distribution over the output of \({{\mathbb R}}\circ \varPhi \), denoted \(\mathcal {T}\) when all \((x^i, y^i)\) are sampled at random. Here also it is crucial to allow the construction only black-box access to the underlying one-way function since otherwise the length of the transcript could depend on the size of c, instead of just the input-output length. We also use here the fact that \({{\mathbb R}}\)’s success probability is independent of the size/run-time of c. This is because the closeness in distributions that we are able to show using techniques of [11], will be significantly larger than 1 / |c|. If \({{\mathbb R}}\) only achieved success probability smaller than 1 / |c| to begin with, then switching the distributions as discussed above would lead to a “useless” \({{\mathbb R}}\), which might never succeed in inverting the one-way function.
Designing an \(\mathsf {A}\mathsf {M}\) verifier—first stage. Unfortunately, even in the “no case,” when \(z \sim f(U_n)\), \(\mathsf {A}\) will not be able to sample directly from \(\mathcal {T}(z)\) since it will not know a preimage x such that \(z = f(x)\). Instead, \(\mathsf {A}\) will sample from a simulated distribution, denoted by \(\widetilde{\mathcal {T}}(z)\). We use techniques of Haitner et al. [21] to show that \(\widetilde{\mathcal {T}}(z)\) and \(\mathcal {T}(z)\) are somewhat close.
Designing an \(\mathsf {A}\mathsf {M}\) prover. On input an instance z, where z is not in the image of f, we must provide an \(\mathsf {A}\mathsf {M}\) prover who uses \({{\mathbb R}}\) to prove that z is not in the image. This will yield a contradiction to the existence of \({{\mathbb R}}\). To construct the \(\mathsf {A}\mathsf {M}\) proof, we use the fact that \(\widetilde{\mathcal {T}}(z)\) and \(\mathcal {T}\) are somewhat close to allow \(\mathsf {A}\) to run a rejection sampling protocol with the help of \(\mathsf {M}\). This allows \(\mathsf {A}\) to essentially output transcripts to \(\mathsf {M}\) that are sampled as in the “honest” distribution \(\mathcal {T}\). Using techniques of Bogdanov and Trevisan [8] and Akavia et al. [2], we can then provide \(\mathsf {A}\) with non-uniform advice in the form of statistics on the distribution \(\mathcal {T}\), which allows him to force \(\mathsf {M}^*\) to respond to queries honestly.
Designing an \(\mathsf {A}\mathsf {M}\) verifier—second stage. The above steps guarantee that on input (c, y), the reduction \({{\mathbb R}}^\mathsf {Adv}\) (with \(\mathsf {M}\) assisting \(\mathsf {A}\) in the simulation of \(\mathsf {Adv}\)) succeeds in recovering x such that \(c(x) = y\) with noticeable probability. However, we must now show that given x, \(\mathsf {A}\) can also recover \(x^*\) such that \(f(x^*) = z\) with noticeable probability. Since the circuit c output by \(\varPhi \) is a slight modification of the k-th randomized iterate, defined by Haitner et al. [21], we can now leverage hardness amplification properties of the k-th randomized iterate to show that \(\mathsf {A}\) recovers \(x^*\) with \(1/\mathrm{poly}\) probability for most \(z \sim f(U_n)\) We must also be careful since the argument above guarantees that x can be recovered when the adversary is stateless. It is possible that a stateful \(\mathsf {M}^*\) can respond in such a way that \(\mathsf {A}\) recovers x such that \(c(x) = y\), but cannot recover \(x^*\) such that \(f(x^*) = z\). The key to ruling out such a case is that, because of the nature of public key encryption wherein ciphertexts encrypt either a 0 or a 1, for almost all transcripts output to \(\mathsf {M}^*\), there is actually a single “correct” response and we force \(\mathsf {M}^*\) to respond with this “correct” response with very high probability over the transcripts outputted by the reduction.
1.5 Related Work
In their seminal work, Impagliazzo and Rudich [25] ruled out black-box reductions from key agreement to one-way function. Their oracle separation technique was subsequently used to rule out black-box reductions between various primitives such as collision resistant hash functions to one way functions [34], oblivious transfer to public key encryption [18] and many more. The oracle separation technique cannot be used to rule out non-black-box reductions, since the underlying primitive is modeled as an oracle with an exponentially large description size.
The meta-reduction technique (cf. [1, 6, 10, 13, 15–17, 27, 28, 32]) has been useful for ruling out Turing reductions—reductions where the construction is arbitrary, but the reduction must use the adversary in a black-box manner. Often these techniques are used to give evidence that a construction of primitive P along with a security proof of the above form is impossible under “standard assumptions” (e.g. falsifiable assumptions or non-interactive assumptions). This differs from our setting of separating one-way function from public key encryption, since in this case we can construct public key encryption from most well-studied, concrete assumptions for which we can construct one-way functions (such as factoring, Diffie-Hellman assumptions, and lattice assumptions).
The power of non-black-box usage of the adversary in security reductions has been well-studied since the seminal work of Barak [4]. In this case it is well-known that non-black-box techniques are more powerful than black-box techniques. However, in our work, we are interested in non-black-box use of the underlying primitive, as opposed to non-black-box use of the adversary. Several recent works have dealt with the systematic study of the power of non-black-box reductions in such settings. These include the aforementioned work of Pass et al. [29] as well as a work of Brakerski et al. [9], which, among other results, addresses the question of whether zero knowledge proofs can help to construct key agreement from one-way function. However, the results of Brakerski et al. hold only in an oracle setting, where an oracle is added to simulate the power of a zero-knowledge proof. Baecher et al. [3] gave a taxonomy of black-box and non-black-box reductions. Indeed, the term \(\mathsf {BBN}\) that we use is borrowed from Baecher et al. [3], who used \(\mathsf {BBN}\) to indicate reductions wherein the construction uses the primitive in a Black-box manner, the reduction uses the adversary in a Black-box manner, but the reduction uses the primitive in a Non-black-box manner. Our notion of \(\mathsf {BBN}^-\) differs from the notion of Baecher et al. [3] in that we require the reduction \({{\mathbb R}}\) to be universal, but allow \({{\mathbb R}}\) to receive the description of the code/circuit of f as input. Moreover, we allow the query complexity and success probability of \({{\mathbb R}}\) to depend on the success probability of the adversary \(\mathsf {Adv}\), but require it to be independent of the run-time/circuit size of f.
2 Preliminaries and Background
Notation. We use capital letters for random variables, standard letters for variables and calligraphic letters for sets. We adopt the convention that when the same random variable appears multiple times in an expression, all occurrences refer to the same instantiation. Given a distribution X and an event E, we denote by \(X \mid E\) the conditional distribution over X, conditioned on the event E occurring. Let X be a random variable taking values in a finite set \(\mathcal {U}\). If \(\mathcal {S}\) is a subset of \(\mathcal {U}\), then \(x \sim \mathcal {S}\) means that x is selected according to the uniform distribution on \(\mathcal {S}\). We write \(U_n\) to denote the random variable distributed uniformly over \(\{0,1\}^n\) and \(U_{[0,1]}\) to denote the continuous random variable distributed uniformly over [0, 1]. In general, for a finite set S, we denote by \(U_S\) the uniform distribution over S.
Two distributions X and Y over \(\mathcal {U}\) are \(\varepsilon \) close, denoted \(\varDelta (X,Y) \le \varepsilon \), if \(\frac{1}{2}\sum _{x \in \mathcal {U}} \left| \Pr _X[x] - \Pr _Y[x] \right| \le \varepsilon \). For a set \(\mathcal {S} \subseteq \mathcal {U}\), we denote by \(\Pr _X[S] := \sum _{x \in \mathcal {S}} \Pr _X[x]\), i.e. the weight placed on \(\mathcal {S}\) by the distribution X.
For functions \(f: \{0,1\}^n \rightarrow \{0,1\}^n\) and \(y \in \{0,1\}^{n}\), we denote by \(f(U_n)\) the distribution induced by f operating on \(U_n\) and we denote by \(f^{-1}(y)\) the set \(f^{-1}(y) := \{x \in \{0,1\}^n: f(x) = y\}\). For a distribution X with (implicit) sampling algorithm \(\mathsf {Samp}\), that takes n coins, we denote by X(r) for \(r \in \{0,1\}^n\), the output x of \(\mathsf {Samp}(r)\). For an element x in the support of X, we denote by \(X^{-1}(x)\) the set of random coins \(r \in \{0,1\}^n\) such that \(X(r) = x\).
Let \(\mathcal {C}=\{\mathcal {C}_{k,n}\}\) be a parametrized collection of uniformly generated polynomially-sized circuits, indexed by \(n \in \mathbb {N}\) and \(k = k(n) = \mathrm{poly}(n)\). For a fixed (n, k) pair, let \(C_{k,n}\) denote the random variable representing the choice of circuit \(c_{k,n} \sim \mathcal {C}_{k,n}\), where \(\mathcal {C}_{k,n}\) is a family of one-way functions. We require that with probability 1, \(C_{k,n}\) implements a one-way function.
Definition 1
( \(\mathsf {BBN}^-\) reduction from PKE to OWF). A \(\mathsf {BBN}^-\) reduction from public key encryption (PKE) to one-way function (OWF) is a pair of oracle PPT Turing machines \((E, {{\mathbb R}})\) with the following properties:
- Construction. :
-
With all but negligible probability over \(C_{k,n}\), \(E^{C_{k,n}}(1^n)\) implements a PKE scheme.
- Reduction. :
-
There exist polynomials \(t(\cdot ), v(\cdot )\) such that: For every (inefficient) adversary \(\mathsf {Adv}\) who, with probability \(\varepsilon _1 = \varepsilon _1(n) = 1/\mathrm{poly}(n)\) over \(c_{k,n} \sim C_{k,n}\), breaks \(E^{c_{k,n}}(1^n)\) with probability \(\varepsilon _2 = \varepsilon _2(n) = 1/\mathrm{poly}(n)\), we have:
$$ \Pr _{c_{k,n}\sim C_{k,n}} \left[ \Pr \left[ {{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{\frac{1}{\varepsilon _2}}, c_{k,n}, c_{k,n}(U_n)) \in c^{-1}_{k,n}(c_{k,n}(U_n)) \right] \ge \frac{1}{t(\max (n, \frac{1}{\varepsilon _2(n)}))} \right] \ge \varepsilon _1, $$and \({{\mathbb R}}^\mathsf {Adv}(1^n, 1^{1/\varepsilon }, c_{k,n},y)\) makes at most \(v(\max (n,1/\varepsilon _2(n)))\) oracle queries to the adversary \(\mathsf {Adv}\).
Definition 2
( \(\mathsf {BBN}^-\) reduction from PKE to \((1-\delta /2)\) -weak one way function). A \(\mathsf {BBN}^-\) reduction from public key encryption (PKE) to \((1-\delta )\)-weak one-way function (for \(q = \mathrm{poly}(n)\)) is a pair of oracle PPT Turing machines \((E, {{\mathbb R}})\) with the following properties:
- Construction. :
-
With all but negligible probability over \(C_{k,n}\), \(E^{C_{k,n}}(1^n)\) implements a PKE scheme.
- Reduction. :
-
There exists a polynomial \(v(\cdot )\) such that: For every (inefficient) adversary \(\mathsf {Adv}\) who, with probability \(\varepsilon _1 = \varepsilon _1(n) = 1/\mathrm{poly}(n)\) over \(c_{k,n} \sim C_{k,n}\), breaks \(E^{c_{k,n}}(1^n)\) with probability \(\varepsilon _2 = \varepsilon _2(n) = 1/\mathrm{poly}(n)\), we have:
$$ \Pr _{c_{k,n}\sim C_{k,n}} \left[ \Pr \left[ {{\mathbb R}}^{\mathsf {Adv}}(1^n, 1^{1/\varepsilon _2}, c_{k,n}, c_{k,n}(U_n)) \in c^{-1}_{k,n}(c_{k,n}(U_n)) \right] \ge 1-\delta /2 \right] \ge \varepsilon _1, $$and \({{\mathbb R}}^\mathsf {Adv}(1^n, 1^{1/\varepsilon _2}, c_{k,n},y)\) makes at most \(v(\max (n,1/\varepsilon _2(n)))\) oracle queries to the adversary \(\mathsf {Adv}\).
Definition 3
(Non-adaptive Reductions \({{\mathbb R}}\) ). The reduction \({{\mathbb R}}= ({{\mathbb R}}_1, {{\mathbb R}}_2)\) is non-adaptive if it interacts with the adversary \(\mathsf {Adv}\) in the following way:
-
On input \((1^n, 1^{1/\varepsilon _2}, c_{k,n}, y)\) and random coins, \({{\mathbb R}}_1\) produces a transcript \(\mathsf {tr}\) consisting of \(v(\max (n,1/\varepsilon _2(n)))\) parallel queries to \(\mathsf {Adv}\), as well as the intermediate state \(\mathsf {st}\).
-
On input \(\mathsf {tr}\), \(\mathsf {Adv}\) returns responses \(d_1, \ldots , d_{v(\max (n,1/\varepsilon _2(n)))}\). \({{\mathbb R}}_2(\mathsf {st},\) \(d_1,\) \(\ldots ,\) \(d_{v(\max (n,1/\varepsilon _2(n)))})\) returns either x such that \(c_{k,n}(x) = y\) or returns \(\bot \).
For fixed \((\mathsf {tr}, \mathsf {st})\) pair, we also denote the output of \({{\mathbb R}}_2\) with respect to an oracle \(\mathsf {Adv}\) and a fixed \((\mathsf {tr}, \mathsf {st})\) output by \({{\mathbb R}}_1\), by \({{\mathbb R}}^{\mathsf {Adv}}(c,y,\mathsf {tr},\mathsf {st}; r)\) or \({{\mathbb R}}^{\mathsf {Adv}}(c,y,\mathsf {tr},\mathsf {st})\) (depending on whether the coins of \({{\mathbb R}}_2\) are explicit or implicit). Note that in the above, r denotes the coins used by \({{\mathbb R}}_2\) only (and not the coins of \({{\mathbb R}}_1\) or \(\mathsf {Adv}\)).
Constant-round interactive protocols with advice. An interactive protocol with advice consists of a pair of interactive machines \(\langle P, V \rangle \), where P is a computationally unbounded prover and V is a PPT verifier which receive a common input x and advice string a. Feigenbaum and Fortnow [12] define the class \(\mathsf {A}\mathsf {M}^{\mathrm{poly}}\) as the class of languages L for which there exists a constant c, a polynomial p and an interactive protocol \(\langle P, V \rangle \) with advice such that for every n, there exists an advice string a of length p(n) such that for every x of length n, on input x and advice a, \(\langle P, V \rangle \) produces an output after c rounds of interaction and, for small constant \(\varepsilon '\):
-
If \(x \in L\), then \(\Pr [\langle P, V \rangle \text{ accepts } x \text{ with } \text{ advice } a] \ge 1-\varepsilon '\).
-
If \(x \notin L\), then for every prover \(P^*\), \(\Pr [\langle P^*, V \rangle \text{ accepts } x \text{ with } \text{ advice } a] \le \varepsilon '\).
It was shown by [12] that \(\mathsf {A}\mathsf {M}^{\mathrm{poly}}\) is equal to \(\mathbf {NP}/{\mathrm{poly}}\). Thus, \(\mathsf {coNP}\subseteq \mathsf {A}\mathsf {M}^{\mathrm{poly}}\) implies \(\mathsf {coNP}\subseteq \mathbf {NP}/{\mathrm{poly}}\), which gives \(\varSigma _3 = \varPi _3\) [36]. We use the terms \(\mathsf {M}\), “prover” and P (resp. \(\mathsf {A}\), “verifier” and V) interchangeably.
Definition 4
A distributional language (L, D) is in \(\mathsf {Heur}_{1/\mathrm{poly}}\mathsf {A}\mathsf {M}^{\mathrm{poly}}\) if for every inverse polynomial q, there exists an \(\mathsf {A}\mathsf {M}\) (i.e., constant-round public-coin) protocol (P, V) where \(\mathsf {A}\) receives advice of length polynomial in the input length such that, for small constant \(\varepsilon '\):
-
Completeness: If \(x \in L\), \(\Pr [\langle P,V \rangle (x) = 1] \ge 1-\varepsilon '\).
-
Soundness: For every \(n \in \mathbb {N}\) and every machine \(P^*\), with probability \(1-q(n)\), and \(x \in \{0,1\}^n\) sampled from \(D_n\) conditioned on \(x \notin L\) satisfies \(\Pr [\langle P^*, V \rangle (x) = 1] \le \varepsilon '\).
Our protocols will use the \(\mathsf {A}\mathsf {M}\) protocol \(\mathsf {RandSamp}^m\) (the multi-query variant of \(\mathsf {RandSamp}\)) with the following properties as a subroutine. \(\mathsf {RandSamp}\) has been used extensively in the literature; the formalization below is due to [22].
Lemma 3
Let \(w = g(r)\) for a \(\mathrm{poly}(n)\)-time computable, randomized function g and random coins r. Assume w has bit length \(\widehat{n}\). Then there exists an \(\mathsf {A}\mathsf {M}\) protocol \(\mathsf {RandSamp}^m\) with an efficient verifier V that gets as input a security parameter \(1^n\), \(\delta ' = 1/\mathrm{poly}(n)\) (as the approximation and soundness parameter), \(s_1, \ldots , s_m\) (as size of \(f^{-1}(w_1), \ldots , f^{-1}(w_m)\)) such that for all \(i \in [m]\), \(s_i \in (1 \pm \lambda )|f^{-1}(w_i)|\) (for \(\lambda = \mathrm{poly}(1/m, 1/(\widehat{n} \cdot m), \delta ')\) and returns \((r_1, \ldots , r_m)\) such that:
-
Completeness: There is a prover strategy (the honest prover) s.t. V aborts with probability at most \(\delta \).
-
Soundness: For any prover \(P^*\) either
-
\(\langle P^*, V \rangle \) aborts with probability \(1-\delta '\) OR
-
\(\varDelta ((U_{f^{-1}(w_1)}, \ldots , U_{f^{-1}(w_m)}), (r_1, \ldots , r_m))) \le \delta ' + \Pr [\langle P^*, V \rangle \text{ aborts }]\).
-
The following fact will be useful when protocol \(\mathsf {RandSamp}^m\) is employed:
Fact 4
Let X, Y be random variables distributed over the set \(\mathcal {S} \cup \{\bot \}\) such that \(\Pr [Y = \bot ] = 0\) and \(\varDelta (X,Y) \le \Pr [X = \bot ] + \delta '\). Then for any event \(T \subset \mathcal {S}\) it holds that:
and so
Definition 5
(Enhanced Randomized Iterate). Let \(f: \{0,1\}^n \rightarrow \{0,1\}^n\), let \(\mathcal {H}\) be a family of pairwise-independent length-preserving hash functions over strings of length n and let \(\widehat{\mathcal {H}}\) be a family of \(p' \cdot p_q(\widetilde{n}) + p(\widetilde{n})\)-wise independent length-preserving hash functions (where \(p', p_q(\widetilde{n}), p(\widetilde{n})\) are polynomials in n that will be defined later) over strings of length n. Define the k-th enhanced randomized iterate \(F:\{0,1\}^n \times \mathcal {H}^{k-1} \times \widehat{\mathcal {H}}^2 \rightarrow \{0,1\}^n\) as
We denote by \(H_j\) (resp. \(\hat{H}_b\), \(b \in \{1,2\}\)) random variables uniformly distributed over \(\mathcal {H}\) (resp. \(\hat{\mathcal {H}}\)).
Let \(c_{k,n} = c_{k,n}(\cdot , \overline{h} = h_1, \ldots , h_{k-1}, \widehat{h}_1, \widehat{h}_2)\) denote the circuit which has \(\overline{h}, \widehat{h}_1, \widehat{h}_2\) hardwired and on input x computes \(y = F(x, \overline{h}, \widehat{h}_1, \widehat{h}_2)\). Let \(\mathcal {C}_{k,n}\) denote the set of circuits \(c_{k,n}\) obtained when taking \(h_1, \ldots , h_{k-1} \in \mathcal {H}, \widehat{h}_1, \widehat{h}_2 \in \hat{\mathcal {H}}\). Let \(C_{k,n}\) be the random variable defined as \(C_{k,n} = c_{k,n}(\cdot , H_1, \ldots , H_{k-1}, \hat{H}_b, \hat{H}_b)\).
Lemma 5
[21]. For \(i \in [k]\), let \(c^i_{k,n} = c^i_{k,n}(\cdot , \overline{h} = h_1, \ldots , h_{i-1}, \widehat{h}_1)\) denote the circuit which has \(\overline{h}, \widehat{h}_1\) hardwired and on input x computes \(y^i = \mathbb {Y}^i(c_{k,n}, x) = F^i(x, \overline{h}, \widehat{h}_1)\). Let the random variable \(C^i_{k,n}\) denote the distribution over circuits \(c^i := c^i_{k,n}\) as above.
Then for any set \(\mathcal {L} \subseteq \{0,1\}^n \times \mathcal {C}^i_{k,n}\) with
it holds that
We now describe a transformation (folklore, formalized by Haitner et al. [21]), of an arbitrary one-way function into a length-preserving one-way function.
Lemma 6
Let \(f: \{0,1\}^n \rightarrow \{0,1\}^{\ell (n)}\) be a \((T = T(n), \varepsilon = \varepsilon (n))\)-OWF and let \(\mathcal {H}\) be an efficient family of \(2^{-2n}\)-almost pairwise-independent hash functions from \(\{0,1\}^{\ell (n)}\) to \(\{0,1\}^{2n}\). We define \(\overline{f}\) as
where \(x_a, x_b \in \{0,1\}^n\) and \(h \in \mathcal {H}\). Then \(\overline{f}\) is a length-preserving \((T-n^{O(1)}, \varepsilon + 2^{-n+1})\)-one-way function.
If the original function f is regular, then the output function \(\overline{f}\) is nearly regular: There is some fixed s such that with all but negligible probability over \(y \sim \overline{f}(U_{2n}, H)\), the number of pre-images of y is exactly s. It turns out that nearly regular functions are sufficient for all of our results.
3 The Circuit-Oblivious Adversary \(\mathsf {Adv}\)
Let \(E^f = (\mathsf {Gen}^f, \mathsf {Enc}^f, \mathsf {Dec}^f)\) be a public key encryption scheme making oracle calls to one-way function f. Assume polynomial \(p_q(n)\) is an upperbound on the total number of queries made by \(\mathsf {Gen}^f\), \(\mathsf {Enc}^f\), \(\mathsf {Dec}^f\) on input security parameter n and message of length n. We consider the following two distributions corresponding to sampling the function f from two different distributions.
In the following, \(\mathcal {F}_n\) denotes the set of all functions from \(\{0,1\}^n \rightarrow \{0,1\}^n\). Note that when \(c \sim \mathcal {C}_{k,n}\) is fixed, we write \(\mathcal {E}^c\) to denote the distribution \(\mathcal {E}^C\), with a fixed oracle c (whereas C denotes a random variable).
We next describe a modification (folklore and formally proved in [35]) of the well-known \(\mathsf {Eve}\) algorithm, which is tailored for breaking public key encryption  in the random oracle model. The advantage of this \(\mathsf {Eve}= (\mathsf {Eve}_1, \mathsf {Eve}_2, \mathsf {Eve}_3)\) algorithm is that \(\mathsf {Eve}_1, \mathsf {Eve}_3\) are polynomial-time and \(\mathsf {Eve}_2\) is inefficient but does not require oracle access to \(\mathcal {O}\).
in the random oracle model. The advantage of this \(\mathsf {Eve}= (\mathsf {Eve}_1, \mathsf {Eve}_2, \mathsf {Eve}_3)\) algorithm is that \(\mathsf {Eve}_1, \mathsf {Eve}_3\) are polynomial-time and \(\mathsf {Eve}_2\) is inefficient but does not require oracle access to \(\mathcal {O}\).
\(\mathsf {Eve}\) runs on transcripts of the form  , where
, where  is the public key and \(\mathsf {e}\) is the ciphertext. \(\mathsf {Eve}\)’s goal is to correctly decrypt \(\mathsf {e}\). Sotakova [35] proves the existence of an \(\mathsf {Eve}\) with the following properties:
is the public key and \(\mathsf {e}\) is the ciphertext. \(\mathsf {Eve}\)’s goal is to correctly decrypt \(\mathsf {e}\). Sotakova [35] proves the existence of an \(\mathsf {Eve}\) with the following properties:
\(\mathsf {Eve}_1\) is an efficient oracle algorithm which takes input  and outputs \(\mathcal {Q}_\mathsf {Eve}\):
and outputs \(\mathcal {Q}_\mathsf {Eve}\):
-
Initialize \(\mathcal {Q}_\mathsf {Eve}:= \emptyset \). Choose \(\hat{p}\) random strings \(r^1, \ldots , r^{\hat{p}}\) and messages \(m^1, \ldots , m^{\hat{p}}\).
-
For \(1 \le i \le \hat{p}\), run
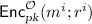 . Add all queries and responses to \(\mathcal {Q}_\mathsf {Eve}\). Let \(p(n) = \mathrm{poly}(n)\) be the total number of queries made. \(p(\cdot )\) depends only on \(p_q(n)\) and the desired success probability \(1-\delta /8\).
. Add all queries and responses to \(\mathcal {Q}_\mathsf {Eve}\). Let \(p(n) = \mathrm{poly}(n)\) be the total number of queries made. \(p(\cdot )\) depends only on \(p_q(n)\) and the desired success probability \(1-\delta /8\).
\(\mathsf {Eve}_2\) takes  as input and outputs \([(\mathcal {I}_i, r_i)]_{i \in [p'(n)]}\) (note that \(\mathsf {Eve}_2\) does not have oracle access):
as input and outputs \([(\mathcal {I}_i, r_i)]_{i \in [p'(n)]}\) (note that \(\mathsf {Eve}_2\) does not have oracle access):
-
Return \(p'\) number of elements \(\{(\mathcal {I}_1, r_1), \ldots , (\mathcal {I}_{p'}, r_{p'})\}\) chosen uniformly at random from the set
 .Footnote 4
.Footnote 4
\(\mathsf {Eve}_3\) is an efficient oracle algorithm which takes \([(\mathcal {I}_i, r_i, \mathsf {e})]_{i \in [p']}\) as input and outputs a bit d.
-
For \(i \in [p']\), run \(\mathsf {Gen}^{\mathcal {I}_i}(r_i)\) to generate a
 -pair and compute
-pair and compute  . By this notation we mean that whenever \(\mathsf {Dec}\) queries the oracle, if the query is in \(\mathcal {I}\), respond according to \(\mathcal {I}\). Otherwise, respond according to \(\mathcal {O}\).
. By this notation we mean that whenever \(\mathsf {Dec}\) queries the oracle, if the query is in \(\mathcal {I}\), respond according to \(\mathcal {I}\). Otherwise, respond according to \(\mathcal {O}\). -
Given the resulting set of decryptions \(\{\widetilde{d}_1, \ldots , \widetilde{d}_{p'} \}\), let \(\mathsf {num}_0\) denote the number of decryptions equaling 0 and \(\mathsf {num}_1\) denote the number of decryptions equaling 1. Let \(b = 0\) if \(\mathsf {num}_0 > \mathsf {num}_1\) and \(b = 1\) otherwise.
-
If \(V := \mathsf {num}_{0}/p' \in [3/8 + (\ell -1)/4p'', 3/8 + (\ell +1)/4p'']\), return \(d := 0\). Otherwise, return \(d:= b\).
We define parameters \(p', p'', \ell \) in the full version. The exact setting will depend on properties of the given \(\mathsf {BBN}^-\) reduction \({{\mathbb R}}\).
We next turn to proving success of the adversary.
Lemma 7
([35], restated). For  outputs m with probability at least \(1-\delta /8\).
outputs m with probability at least \(1-\delta /8\).
The basic intuition is the following: Given the first message  sent from receiver to the sender, w.h.p, the set \(\mathcal {Q}_\mathsf {Eve}\) will contain all queries made by the sender when computing the second message (the ciphertext \(\mathsf {e}\)) with probability greater than some threshold \(1/p_{th}(n)\). Now, we sample a view for the receiver consistent with
sent from receiver to the sender, w.h.p, the set \(\mathcal {Q}_\mathsf {Eve}\) will contain all queries made by the sender when computing the second message (the ciphertext \(\mathsf {e}\)) with probability greater than some threshold \(1/p_{th}(n)\). Now, we sample a view for the receiver consistent with  , which will contain a secret key
, which will contain a secret key  and use this secret key
and use this secret key  to decrypt the real ciphertext \(\mathsf {e}\) sent by the real sender. Loosely speaking,
to decrypt the real ciphertext \(\mathsf {e}\) sent by the real sender. Loosely speaking,  should only decrypt \(\mathsf {e}\) “incorrectly” if there is a query q to the random oracle that is answered inconsistently in the sampled receiver’s view and the real sender’s view. However, note that any individual query q that is made in the sampled receiver’s view but is not contained in \(\mathcal {Q}_\mathsf {Eve}\), is made by the real sender with probability less than \(1/p_{th}(n)\). Now, since we choose \(p_{th}\) far larger than the number of queries contained in the receiver’s view, it is unlikely that there are any queries in the sampled receiver’s view that were also made by the sender, but do not appear in \(\mathcal {Q}_\mathsf {Eve}\). Thus, w.h.p, there are no queries q answered inconsistently in the sampled receiver’s view and real sender’s view and thus with high probability, the sampled
should only decrypt \(\mathsf {e}\) “incorrectly” if there is a query q to the random oracle that is answered inconsistently in the sampled receiver’s view and the real sender’s view. However, note that any individual query q that is made in the sampled receiver’s view but is not contained in \(\mathcal {Q}_\mathsf {Eve}\), is made by the real sender with probability less than \(1/p_{th}(n)\). Now, since we choose \(p_{th}\) far larger than the number of queries contained in the receiver’s view, it is unlikely that there are any queries in the sampled receiver’s view that were also made by the sender, but do not appear in \(\mathcal {Q}_\mathsf {Eve}\). Thus, w.h.p, there are no queries q answered inconsistently in the sampled receiver’s view and real sender’s view and thus with high probability, the sampled  decrypts \(\mathsf {e}\) correctly.
decrypts \(\mathsf {e}\) correctly.
We now describe the actual adversary \(\mathsf {Adv}= (\mathsf {Adv}_1, \mathsf {Adv}_2, \mathsf {Adv}_3)\):
-
\(\mathsf {Adv}_1\): On input
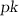 , and oracle access to c, \(\mathsf {Adv}_1\) computes
, and oracle access to c, \(\mathsf {Adv}_1\) computes 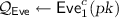 , where \(\mathsf {Eve}\)’s queries are answered according to c (instead of the random oracle \(\mathcal {O}\)). \(\mathsf {Adv}_1\) outputs \(\mathcal {Q}_\mathsf {Eve}\).
, where \(\mathsf {Eve}\)’s queries are answered according to c (instead of the random oracle \(\mathcal {O}\)). \(\mathsf {Adv}_1\) outputs \(\mathcal {Q}_\mathsf {Eve}\). -
\(\mathsf {Adv}_2\): On input
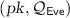 ,
,  and outputs \([(\mathcal {I}_i, r_i)]_{i \in [p'(n)]}\).
and outputs \([(\mathcal {I}_i, r_i)]_{i \in [p'(n)]}\). -
\(\mathsf {Adv}_3\): On input \([(\mathcal {I}_i, r_i, \mathsf {e})]_{i \in [p'(n)]}\), \(\mathsf {Adv}_3\) runs \(\mathsf {Eve}^c_3([(\mathcal {I}_i, r_i, \mathsf {e})]_{i \in [p'(n)]})\) where \(\mathsf {Eve}\)’s queries are answered according to c (instead of the random oracle \(\mathcal {O}\)). \(\mathsf {Adv}_3\) flips a coin and outputs \(\bot \) with probability \(1-1/n\). With probability 1 / n, \(\mathsf {Adv}\) outputs the same bit d that is outputted by \(\mathsf {Eve}^c_3\).
We purposely “weaken” the adversary, by defining \(\mathsf {Adv}\) such that it outputs \(\bot \) with probability \(1-1/n\)—where n is the input/output length of the one-way function—in order to argue that queries made by the reduction, \({{\mathbb R}}\), to \(\mathsf {Adv}\) with security parameter n set too large are “useless.” See Sect. 1.4 for further discussion. We next turn to proving success of the adversary:
Lemma 8
For  , d computed by
, d computed by  is equal to m with probability at least \(1-\delta /4\).
is equal to m with probability at least \(1-\delta /4\).
Intuitively, Lemma 8 holds since \(\mathsf {Adv}^c\) makes at most \(p(n) + p' \cdot p_q(n)\) queries and so since \(\hat{h}_1\), \(\hat{h}_2\) are \(p(n) + p' \cdot p_q(n)\)-wise independent, the view of the adversary is nearly the same when interacting with a random oracle \(\mathcal {O}\) or with the randomly sampled circuit C. For the full proof, see the full version.
Now, using Markov’s inequality and the fact that \(\mathsf {Adv}_3\) tosses a coin independently of all its other coins to decide whether to output \(\bot \) at the final stage with probability \(1-1/n\), we have that:
Corollary 9
With probability \(\varepsilon _1 := 1-\delta /2\) over choice of \(c \sim C\), we have that for  , the output of
, the output of  is equal to m with probability is at least \(\varepsilon _2 := \delta /4n\).
is equal to m with probability is at least \(\varepsilon _2 := \delta /4n\).
4 The Mapping \(\varPhi \)
Instead of sampling \(c \sim C_{k,n}\), \(x \sim U_n\), and outputting \((c,x,y:=c(x))\), we can alternatively sample \((x^{1}, y^{1}), \ldots , (x^k, y^k) \sim (U_n, f(U_n))\) and \(r \sim \{0,1\}^*\), set \((x,c,y) := \varPhi ((x^{1}, y^{1}), \ldots , (x^k, y^k); r)\), for \(\varPhi \) defined below:  It is straightforward to see that the two sampling methods described above induce the same distribution. We additionally introduce the notation \(\varPhi _2\) to denote the second and third coordinates of the output of \(\varPhi \) (i.e. (c, y)).
It is straightforward to see that the two sampling methods described above induce the same distribution. We additionally introduce the notation \(\varPhi _2\) to denote the second and third coordinates of the output of \(\varPhi \) (i.e. (c, y)).
5 Useful Distributions
For public key encryption scheme \(E^\mathcal {O} = (\mathsf {Gen}^\mathcal {O}, \mathsf {Enc}^{\mathcal {O}}, \mathsf {Dec}^{\mathcal {O}})\), relative to random oracle \(\mathcal {O}\), the following distribution (Fig. 1) corresponds to sampling a partial random oracle and running \(\mathsf {Gen}\).
We assume that security parameter n can be determined given the generated  . We slightly abuse notation and for a fixed
. We slightly abuse notation and for a fixed  , we denote by
, we denote by  the set of pairs \((\mathcal {I}, r)\) that yield output
the set of pairs \((\mathcal {I}, r)\) that yield output  when sampling from \(\mathcal {PK}_n\), for appropriate n.
when sampling from \(\mathcal {PK}_n\), for appropriate n.
For each of the following distributions \(\chi \), we refer by \(\chi _2\) to the marginal distribution over the final coordinate, the transcript \(\widetilde{\mathsf {tr}}\). For marginal distributions (e.g. the marginal distribution over the second, third and sixth coordinates) we use full-length tuples with \(*\) symbols in the “don’t care” positions (e.g. \((*,c,y,*,*,i,*,*) \sim \mathcal {T}\) or \(\Pr _{\mathcal {T}}[(*,c,y,*,*,i,*,*)]\)). To denote the distribution \(\chi \), conditioned on one of the tuple coordinates fixed to some value v, we write \(\chi \mid v\), where it is understood from context which coordinate is fixed (e.g. \(\mathcal {T} \mid c\) means that the second coordinate is fixed to constant c). Note that if \(\chi \) is a distribution over tuples with t number of coordinates, then \(\chi \mid v\) is a distribution over tuples with \(t-1\) number of coordinates.
Henceforth, we fix a particular \(\mathsf {BBN}^-\) reduction \({{\mathbb R}}\) with parameters \((v(\cdot ), t(\cdot ))\) and use the particular adversary \(\mathsf {Adv}\) with success probability \((\varepsilon _1 = 1-\delta /4, \varepsilon _2 = \delta )\) defined in Sect. 3. We denote by \(v'(\cdot ), t'(\cdot )\) the following polynomials: \(v'(n) := v(\max (n, 1/\varepsilon _2(n))\) and \(t'(n) := t(\max (n, 1/\varepsilon _2(n)))\).
We next define the distributions \(\mathcal {T}\) and \(\widetilde{\mathcal {T}}\) in Figs. 2 and 3.
Let \(\mathsf {num}_{\mathcal {T}}\) be the number of random coins to sample from \(\mathcal {T}\). Let \(\mathsf {N}_{\mathcal {T}} := 2^{\mathsf {num}_{\mathcal {T}}}\).
We additionally define the distribution \(\mathcal {T}^{i^*}\) (resp. \(\widetilde{\mathcal {T}}^{i^*}\)) for \(i^* \in [k]\) as the distribution \(\mathcal {T}\) (resp. \(\widetilde{\mathcal {T}}\)), conditioned on \(i := i^*\), and the distribution \(\mathcal {T}(z)\) (resp. \(\widetilde{\mathcal {T}}(z)\)) for \(z \in \mathsf {Range}(f)\) as the distribution \(\mathcal {T}\) (resp. \(\widetilde{\mathcal {T}}\)), conditioned on \(y^i := z\). Even when \(z \notin \mathsf {Range}(f)\), we still use the notation \(\widetilde{\mathcal {T}}(z)\). This refers to a distribution which is sampled with the same sampling algorithm as the one used for \(\widetilde{\mathcal {T}}\), except \(y^i := z\) is always fixed to a constant value (not necessarily in the range of f). Let \(\mathsf {num}_{\widetilde{\mathcal {T}}}\) be the number of random coins to sample from \(\mathcal {T}(z)\). Let \(\mathsf {N}_{\widetilde{\mathcal {T}}} := 2^{\mathsf {num}_{\widetilde{\mathcal {T}}}}\).
6 The AM Protocol
We begin with a high-level overview of the protocol: Recall that we fix a particular \(\mathsf {BBN}^-\) reduction \({{\mathbb R}}\) with parameters \((v(\cdot ), t(\cdot ))\) and use the particular adversary \(\mathsf {Adv}\) with success probability \((\varepsilon _1 = 1-\delta /4, \varepsilon _2 = \delta )\) defined in Sect. 3. Additionally, recall that we denote by \(v'(\cdot ), t'(\cdot )\) the following polynomials: \(v'(n) := v(\max (n, 1/\varepsilon _2(n))\) and \(t'(n) := t(\max (n, 1/\varepsilon _2(n)))\) and that we assume WLOG (see discussion in Sect. 1.4) that \({{\mathbb R}}\) never makes calls to \(\mathsf {Adv}\) with security parameter \(\widetilde{n} > 2 \cdot t'(n) \cdot v'(n)\). On input z, \(\mathsf {A}\) constructs many (c, y) pairs and runs many copies of the \(\mathsf {BBN}^-\) reduction \({{\mathbb R}}^\mathsf {Adv}(c,y)\), using Merlin to help simulate the adversary \(\mathsf {Adv}\).
Our \(\mathsf {A}\mathsf {M}\) protocol uses the \(\mathsf {HidProt}\) and \(\mathsf {CBC}\) protocols of Akavia et al. [2] (see also the full version for more details.) and the \(\mathsf {RandSamp}\) protocol (See Lemma 3) as subroutines. Parameters \(\widetilde{\delta } := (\varepsilon ')^2/2, \lambda := 1/k^{1/11}\) are both of order \(1/\mathrm{poly}(n)\). For \(\widetilde{\mathsf {tr}}\) sampled from \(\widetilde{\mathcal {T}}(z)_2\), \(\mathsf {HidProt}\) will be used to determine the size of the sets \(\widetilde{\mathcal {T}}(z)_2^{-1}(\widetilde{\mathsf {tr}})\) and \(\mathcal {T}_2^{-1}(\widetilde{\mathsf {tr}})\). For  , \(\mathsf {CBC}\) (along with the non-uniform advice provided to \(\mathsf {A}\)) will be used to determine the size \(\alpha \) of the set
, \(\mathsf {CBC}\) (along with the non-uniform advice provided to \(\mathsf {A}\)) will be used to determine the size \(\alpha \) of the set  . Given \(\alpha \), \(\mathsf {RandSamp}\) will be used to sample preimages from the set
. Given \(\alpha \), \(\mathsf {RandSamp}\) will be used to sample preimages from the set  , thus simulating the adversary’s (\(\mathsf {Adv}_2\)’s) response. Note that soundness of \(\mathsf {HidProt}\) and \(\mathsf {CBC}\) only hold under specific conditions (see the full version for more details.). Indeed, a key technical part of the proof is showing that the necessary conditions hold. The purpose of the testing for goodness subroutine is the following: We show in the analysis that w.h.p when \(z \sim f(U_n)\), the distribution \(\widetilde{\mathcal {T}}(z)\) is “good,” i.e. somewhat close to the distribution \(\mathcal {T}\), so the rejection sampling procedure can be employed. On the other hand, if \(\widetilde{\mathcal {T}}(z)\) is not “good” (i.e. very far from \(\mathcal {T}\)), then \(\mathsf {A}\) can safely output \(\mathsf {ACCEPT}\). Our \(\mathsf {A}\mathsf {M}\) protocol is presented in Fig. 4. We next state our main technical result.
, thus simulating the adversary’s (\(\mathsf {Adv}_2\)’s) response. Note that soundness of \(\mathsf {HidProt}\) and \(\mathsf {CBC}\) only hold under specific conditions (see the full version for more details.). Indeed, a key technical part of the proof is showing that the necessary conditions hold. The purpose of the testing for goodness subroutine is the following: We show in the analysis that w.h.p when \(z \sim f(U_n)\), the distribution \(\widetilde{\mathcal {T}}(z)\) is “good,” i.e. somewhat close to the distribution \(\mathcal {T}\), so the rejection sampling procedure can be employed. On the other hand, if \(\widetilde{\mathcal {T}}(z)\) is not “good” (i.e. very far from \(\mathcal {T}\)), then \(\mathsf {A}\) can safely output \(\mathsf {ACCEPT}\). Our \(\mathsf {A}\mathsf {M}\) protocol is presented in Fig. 4. We next state our main technical result.
Theorem 10
Assume that there exists a non-adaptive, \(\mathsf {BBN}^-\) reduction \((E, {{\mathbb R}})\) from PKE to \((1-\delta /2)\)-weak one way function. Then for any efficiently computable, length-preserving, (nearly) regular function f, the above non-uniform AM protocol \(\varPi _f\) has completeness \(1-\varepsilon '\) and soundness \(1-\varepsilon '\) (for small constant \(\varepsilon '\)), for the distributional language \(\overline{\mathsf {Range}(f)}\), where soundness holds with probability \(1-7\delta \) over \(z \sim f(U_n)\).
We note that if f is not length-preserving, it can be made length-preserving, while (nearly) preserving regularity, via the transformation described in Lemma 6.
To rule out non-adaptive, \(\mathsf {BBN}^-\) reductions from PKE to one way function, recall that there is a non-adaptive, black-box reduction from OWF to \((1-\delta /2)\)-weak OWF, where the parameters of the reduction depend only on the input-output size and on \(\delta \). but not on the description size of the function. Therefore, if there exists a non-adaptive \(\mathsf {BBN}^-\) reduction \((E, {{\mathbb R}})\) from PKE to OWF, then for every polynomial q there also exists a non-adaptive, \(\mathsf {BBN}^-\) reduction \((E, {{\mathbb R}})\) from PKE to \((1-\delta /2)\)-weak OWF, where \(\delta = 1/7q\). By Theorem 10 (and the extension to non-length-preserving f discussed above) this means that that for every efficiently computable, regular function f and every polynomial q, there exists a non-uniform AM protocol for proving \(z \notin \mathsf {Range}(f)\), where soundness holds with probability \(1-7\delta = 1-1/q\) over \(z \in f(U_n)\). This contradicts our assumption that there exists an efficiently computable, (nearly) regular function f such that \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}^{\mathrm{poly}}\).
Theorem 11
Under the assumption that there exists an efficiently computable, regular function f such that \(\overline{\mathsf {Range}(f)} \notin \mathsf {Heur}_{1/\mathrm{poly}} \mathsf {A}\mathsf {M}^{\mathrm{poly}}\), there is no non-adaptive, \(\mathsf {BBN}^-\) reduction from PKE to one way function.
It remains to prove Theorem 10, which we defer to the full version.
Notes
- 1.
We may also consider families of primitives—e.g. families of one-way functions \(\mathcal {F}\) with uniform generation algorithms. Here, the generation algorithm is represented as a Turing Machine and each function \(f \in \mathcal {F}\) is represented as a circuit.
- 2.
Note that the argument also holds in the case that the Turing reduction works for a family \(\mathcal {F}\) of one way functions f with a uniform generation algorithm. Specifically, if \(\mathsf {Gen}\) is a uniform, public-coin, generation algorithm that samples a circuit \(f \in \mathcal {F}\), then we can construct a single one way function \(\widetilde{f}\) that on input randomness r and input x, first runs \(\mathsf {Gen}(r)\) to select f, then evaluates \(y = f(x)\) and then outputs (r, y).
- 3.
[23] showed that strong instance compression algorithms imply a non-black-box construction of public key encryption from one-way function. It was later shown that, under standard complexity assumptions, instance compression for certain NP-hard problems is impossible [11, 14], indicating that the approach of [23] is unlikely to succeed.
- 4.
\(\mathcal {I}\) is an ordered set of \(p_q(n) + p(n)\) length n strings. Whenever \(\mathsf {Gen}\) or \(\mathsf {Eve}_1\) make a query, if the query has not been made before, the next string is used to respond to the query. If the query has previously been made, the same string is returned.
References
Abe, M., Groth, J., Ohkubo, M.: Separating short structure-preserving signatures from non-interactive assumptions. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 628–646. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_34
Akavia, A., Goldreich, O., Goldwasser, S., Moshkovitz, D.: On basing one-way functions on NP-hardness. In: Kleinberg, J.M. (ed.) 38th Annual ACM Symposium on Theory of Computing, pp. 701–710. ACM Press, May 2006
Baecher, P., Brzuska, C., Fischlin, M.: Notions of black-box reductions, revisited. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 296–315. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42033-7_16
Barak, B.: How to go beyond the black-box simulation barrier. In: 42nd Annual Symposium on Foundations of Computer Science, pp. 106–115. IEEE Computer Society Press, October 2001
Barak, B., Mahmoody-Ghidary, M.: Merkle puzzles are optimal — an O(n 2)-query attack on any key exchange from a random Oracle. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 374–390. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_22
Bitansky, N., Dachman-Soled, D., Garg, S., Jain, A., Kalai, Y.T., López-Alt, A., Wichs, D.: Why “Fiat-Shamir for Proofs” lacks a proof. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 182–201. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36594-2_11
Bodlaender, H.L., Downey, R.G., Fellows, M.R., Hermelin, D.: On problems without polynomial kernels. J. Comput. Syst. Sci. 75(8), 423–434 (2009)
Bogdanov, A., Trevisan, L.: On worst-case to average-case reductions for NP problems. In: 44th Annual Symposium on Foundations of Computer Science, pp. 308–317. IEEE Computer Society Press, October 2003
Brakerski, Z., Katz, J., Segev, G., Yerukhimovich, A.: Limits on the power of zero-knowledge proofs in cryptographic constructions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 559–578. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_34
Coron, J.-S.: Optimal security proofs for PSS and other signature schemes. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 272–287. Springer, Heidelberg (2002). doi:10.1007/3-540-46035-7_18
Drucker, A.: New limits to classical and quantum instance compression. In: 53rd Annual Symposium on Foundations of Computer Science, pp. 609–618. IEEE Computer Society Press, October 2012
Feigenbaum, J., Fortnow, L.: Random-self-reducibility of complete sets. SIAM J. Comput. 22(5), 994–1005 (1993)
Fischlin, M., Schröder, D.: On the impossibility of three-move blind signature schemes. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 197–215. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_10
Fortnow, L., Santhanam, R.: Infeasibility of instance compression and succinct PCPs for NP. In: Ladner, R.E., Dwork, C. (eds.) 40th Annual ACM Symposium on Theory of Computing, pp. 133–142. ACM Press, May 2008
Fuchsbauer, G., Konstantinov, M., Pietrzak, K., Rao, V.: Adaptive security of constrained PRFs. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 82–101. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45608-8_5
Garg, S., Bhaskar, R., Lokam, S.V.: Improved bounds on security reductions for discrete log based signatures. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 93–107. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_6
Gentry, C., Wichs, C.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd Annual ACM Symposium on Theory of Computing, pp. 99–108. ACM Press, June 2011
Gertner, Y., Kannan, S., Malkin, T., Reingold, O., Viswanathan, M.: The relationship between public key encryption and oblivious transfer. In: 41st Annual Symposium on Foundations of Computer Science, pp. 325–335. IEEE Computer Society Press, November 2000
Goldreich, O.: Foundations of Cryptography: Basic Tools, vol. 1. Cambridge University Press, Cambridge (2001)
Goldreich, O., Goldwasser, S., Micali, S.: On the cryptographic applications of random functions. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 276–288. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_22
Haitner, I., Harnik, D., Reingold, O.: On the power of the randomized iterate. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 22–40. Springer, Heidelberg (2006). doi:10.1007/11818175_2
Haitner, I., Mahmoody, M., Xiao, D.: A new sampling protocol and applications to basing cryptographic primitives on the hardness of NP. In: Proceedings of the 25th Annual IEEE Conference on Computational Complexity, CCC 2010, 9–12 June 2010, Cambridge, Massachusetts, pp. 76–87 (2010)
Harnik, D., Naor, M.: On the compressibility of NP instances and cryptographic applications. In: 47th Annual Symposium on Foundations of Computer Science, pp. 719–728. IEEE Computer Society Press, October 2006
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: 21st Annual ACM Symposium on Theory of Computing, pp. 44–61. ACM Press, May 1989
Lamport, L.: Constructing digital signatures from a one-way function. Technical report SRI-CSL-98, SRI International Computer Science Laboratory, October 1979
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). doi:10.1007/11593447_1
Pass, R.: Limits of provable security from standard assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd Annual ACM Symposium on Theory of Computing, pp. 109–118. ACM Press, June 2011
Pass, R., Tseng, W.-L.D., Venkitasubramaniam, M.: Towards non-black-box lower bounds in cryptography. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 579–596. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_35
Raz, R.: A parallel repetition theorem. SIAM J. Comput. 27(3), 763–803 (1998)
Rompel, J.: One-way functions are necessary and sufficient for secure signatures. In: 22nd Annual ACM Symposium on Theory of Computing, pp. 387–394. ACM Press, May 1990
Seurin, Y.: On the exact security of Schnorr-Type signatures in the random Oracle model. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 554–571. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_33
Shaltiel, R.: Derandomized parallel repetition theorems for free games. In: Proceedings of the 25th Annual IEEE Conference on Computational Complexity, CCC 2010, 9–12 June 2010, Cambridge, Massachusetts, pp. 28–37 (2010)
Simon, D.R.: Finding collisions on a one-way street: can secure hash functions be based on general assumptions? In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 334–345. Springer, Heidelberg (1998). doi:10.1007/BFb0054137
Sotakova, M.: Breaking one-round key-agreement protocols in the random Oracle model. Cryptology ePrint Archive, Report 2008/053 (2008). http://eprint.iacr.org/2008/053
Yap, C.-K.: Some consequences of non-uniform conditions on uniform classes. Theoret. Comput. Sci. 26, 287–300 (1983)
Yu, Y., Gu, D., Li, X., Weng, J.: The randomized iterate, revisited - almost linear seed length PRGs from a broader class of one-way functions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 7–35. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_2
Acknowledgements
We thank Tal Malkin for insightful discussions on the notion of \(\mathsf {BBN}^-\) reductions and the anonymous reviewers for TCC B-2016 for their many helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Dachman-Soled, D. (2016). Towards Non-Black-Box Separations of Public Key Encryption and One Way Function. In: Hirt, M., Smith, A. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9986. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53644-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-662-53644-5_7
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53643-8
Online ISBN: 978-3-662-53644-5
eBook Packages: Computer ScienceComputer Science (R0)





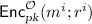 . Add all queries and responses to
. Add all queries and responses to  .
. -pair and compute
-pair and compute  . By this notation we mean that whenever
. By this notation we mean that whenever 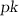 , and oracle access to c,
, and oracle access to c, 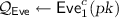 , where
, where 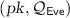 ,
,  and outputs
and outputs 



