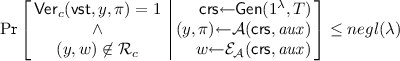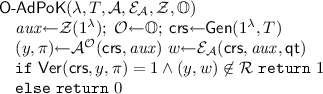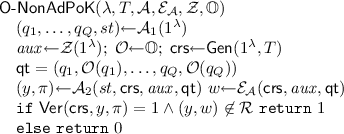On the (In)Security of SNARKs in the Presence of Oracles

Abstract

In this work we study the feasibility of knowledge extraction for succinct non-interactive arguments of knowledge (SNARKs) in a scenario that, to the best of our knowledge, has not been analyzed before. While prior work focuses on the case of adversarial provers that may receive (statically generated) auxiliary information, here we consider the scenario where adversarial provers are given access to an oracle. For this setting we study if and under what assumptions such provers can admit an extractor. Our contribution is mainly threefold.

First, we formalize the question of extraction in the presence of oracles by proposing a suitable proof of knowledge definition for this setting. We call SNARKs satisfying this definition O-SNARKs. Second, we show how to use O-SNARKs to obtain formal and intuitive security proofs for three applications (homomorphic signatures, succinct functional signatures, and SNARKs on authenticated data) where we recognize an issue while doing the proof under the standard proof of knowledge definition of SNARKs. Third, we study whether O-SNARKs exist, providing both negative and positive results. On the negative side, we show that, assuming one way functions, there do not exist O-SNARKs in the standard model for every signing oracle family (and thus for general oracle families as well). On the positive side, we show that when considering signature schemes with appropriate restrictions on the message length O-SNARKs for the corresponding signing oracles exist, based on classical SNARKs and assuming extraction with respect to specific distributions of auxiliary input.

1 Introduction

Succinct Arguments. Proof systems [GMR89] are fundamental in theoretical computer science and cryptography. Extensively studied aspects of proof systems are the expressivity of provable statements and the efficiency. Related to efficiency, it has been shown that statistically-sound proof systems are unlikely to allow for significant improvements in communication [BHZ87, GH98, GVW02, Wee05]. When considering proof systems for $\mathsf{NP}$ this means that, unless some complexity-theoretic collapses occur, in a statistically sound proof system any prover has to communicate, roughly, as much information as the size of the $\mathsf{NP}$ witness. The search of ways to beat this bound motivated the study of computationally-sound proof systems, also called argument systems [BCC88]. Assuming existence of collision-resistant hash functions, Kilian [Kil92] showed a four-message interactive argument for $\mathsf{NP}$. In this protocol, membership of an instance x in an $\mathsf{NP}$ language with $\mathsf{NP}$ machine M can be proven with communication and verifier’s running time bounded by $p(\lambda , |M|, |x|, \log t)$, where $\lambda$ is a security parameter, t is the $\mathsf{NP}$ verification time of machine M for the instance x, and p is a universal polynomial. Argument systems of this kind are called succinct.

Succinct Non-interactive Arguments. Starting from Kilian’s protocol, Micali [Mic94] constructed a one-message succinct argument for $\mathsf{NP}$ whose soundness is set in the random oracle model. The fact that one-message succinct arguments are unlikely to exist for hard-enough languages in the plain model motivated the consideration of two-message non-interactive arguments, in which the verifier generates its message (a common reference string, if this can be made publicly available) ahead of time and independently of the statement to be proved. Such systems are called succinct non-interactive arguments (SNARGs) [GW11]. Several SNARGs constructions have been proposed [CL08, Mie08, Gro10, BCCT12, Lip12, BCC+14, GGPR13, BCI+13, PHGR13, BSCG+13, BCTV14] and the area of SNARGs has become popular in the last years with the proposal of constructions which gained significant improvements in efficiency. Noteworthy is that all such constructions are based on non-falsifiable assumptions [Nao03], a class of assumptions that is likely to be inherent in proving the security of SNARGs (without random oracles), as shown by Gentry and Wichs [GW11].

Almost all SNARGs are also arguments of knowledge—so called SNARKs [BCCT12, BCC+14]. Intuitively speaking, this property (which replaces soundness) says that every prover producing a convincing proof must “know” a witness. On the one hand, proof of knowledge turns out to be useful in many applications, such as delegation of computation where the untrusted worker contributes its own input to the computation, or recursive proof composition [Val08, BCCT13]. On the other hand, the formalization of proof of knowledge in SNARKs is a delicate point. Typically, the concept that the prover “must know” a witness is expressed by assuming that such knowledge can be efficiently extracted from the prover by means of a so-called knowledge extractor. In SNARKs, extractors are inherently non-black-box and proof of knowledge requires that for every adversarial prover $\mathcal{A}$ generating an accepting proof $\pi$ there must be an extractor $\mathcal{E}_{\mathcal{A}}$ that, given the same input of $\mathcal{A}$, outputs a valid witness.

Extraction with Auxiliary Input. Unfortunately, stated as above, proof of knowledge is insufficient for being used in many applications. The problem is that, when using SNARKs in larger cryptographic protocols, adversarial provers may get additional information which can contribute to the generation of adversarial proofs. To address this problem, a stronger, and more useful, definition of proof of knowledge requires that for any adversary $\mathcal{A}$ there is an extractor $\mathcal{E}_{\mathcal{A}}$ such that, for any honestly generated $\mathsf{crs}$ and any polynomial-size auxiliary input $aux$, whenever $\mathcal{A}(\mathsf{crs}, aux )$ returns an accepting proof, $\mathcal{E}_{\mathcal{A}}(\mathsf{crs}, aux )$ outputs a valid witness. This type of definition is certainly more adequate when using SNARKs in larger cryptographic protocols, but it also introduces other subtleties. As first discussed in [HT98], extraction in the presence of arbitrary auxiliary input can be problematic, if not implausible. Formal evidence of this issue has been recently given in [BCPR14, BP15]. Bitansky et al. [BCPR14] show that, assuming indistinguishability obfuscation, there do not exist extractable one-way functions (and thus SNARKs) with respect to arbitrary auxiliary input of unbounded polynomial length. Boyle and Pass [BP15] generalize this result showing that assuming collision-resistant hash functions and differing-input obfuscation, there is a fixed auxiliary input distribution for which extractable one-way functions do not exist.

1.1 Extraction in the Presence of Oracles

In this work we continue the study on the feasibility of extraction by looking at a scenario that, to the best of our knowledge, has not been explicitly analyzed before. We consider the case in which adversarial provers run in interactive security experiments where they are given access to an oracle. For this setting we study if and under what assumptions such provers can admit an extractor.

Before giving more detail on our results, let us discuss a motivation for analyzing this scenario. To keep the presentation simple, here we give a motivation via a hypotetical example; more concrete applications are discussed later.

A case study application. Consider an application where Alice gets a collection of signatures generated by Bob, and she has to prove to a third party that she owns a valid signature of Bob on some message m such that $P(m)=1$. Let us say that this application is secure if Alice, after asking for signatures on several messages, cannot cheat letting the third party accept for a false statement (i.e., $P(m) =0$, or $P(m)=1$ but Alice did not receive a signature on m). If messages are large and one wants to optimize bandwidth, SNARKs can be a perfect candidate solution for doing such proofs,¹ i.e., Alice can generate a proof of knowledge of $(m, \sigma )$ such that “$(m, \sigma )$ verifies with Bob’s public key and $P(m)=1$”.

An attempt of security proof. Intuitively, the security of this protocol should follow easily from the proof of knowledge of the SNARK and the unforgeability of the signature scheme. However, somewhat surprisingly, the proof becomes quite subtle. Let us consider a cheating Alice that always outputs a proof for a statement in the language.² If Alice is still cheating, then it must be that she is using a signature on a message that she did not query – in other words a forgery. Then one would like to reduce such a cheating Alice to a forger for the signature scheme. To do this, one would proceed as follows. For any Alice one defines a forger that, on input the verification key $\mathsf{vk}$, generates the SNARK $\mathsf{crs}$, gives $(\mathsf{crs},\mathsf{vk})$ to Alice, and simulate’s Alice’s queries using its own signing oracle. When Alice comes with the cheating proof, the forger would need an extractor for Alice in order to obtain the forgery from her. However, even if we see Alice as a SNARK prover with auxiliary input $\mathsf{vk}$, Alice does not quite fit the proof of knowledge definition in which adversaries have no oracles. To handle similar cases, one typically shows that for every, interactive, Alice there is a non-interactive algorithm $\mathcal{B}$ that runs Alice simulating her oracles (i.e., $\mathcal{B}$ samples the signing key) and returns the same output. The good news is that for such $\mathcal{B}$ one can claim the existence of an extractor $\mathcal{E}_{\mathcal{B}}$ as it fits the proof of knowledge definition. The issue is though that $\mathcal{E}_{\mathcal{B}}$ expects the same input of $\mathcal{B}$, which includes the secret signing key. This means that our candidate forger mentioned above (which does not have the secret key) cannot run $\mathcal{E}_{\mathcal{B}}$.

Applications that need extraction with oracles. Besides the above example, this issue can show up essentially in every application of SNARKs in which adversaries have access to oracles with a secret state, and one needs to run an extractor during an experiment (e.g., a reduction) where the secret state of the oracle is not available. For instance, we recognize this issue while trying to formally prove the security of a “folklore” construction of homomorphic signatures based on SNARKs and digital signatures that is mentioned in several papers (e.g., [BF11, GW13, CF13, GVW15]). The same issue appears in a generic construction of SNARKs on authenticated data in [BBFR15] (also informally discussed in [BCCT12]), where the security proof uses the existence of an extractor for the oracle-aided prover, but without giving particular justification. A similar issue also appears in the construction of succinct functional signatures of [BGI14]. To be precise, in [BGI14] the authors provide a (valid) proof but under a stronger definition of SNARKs in which the adversarial prover and the extractor are independent PPT machines without common auxiliary input: a notion for which we are not aware of standard model constructions. In contrast, if one attempts to prove the succinct functional signatures of [BGI14] using the standard definition of SNARKs, one incurs the same issues illustrated above, i.e., the proof would not go through.

In this work we address this problem by providing both negative and positive results to the feasibility of extraction in the presence of oracles. On one hand, our negative results provide an explanation of why the above proofs do not go through so easily. On the other hand, our positive results eventually provide some guidelines to formally state and prove the security of the cryptographic constructions mentioned above (albeit with various restrictions).

1.2 An Overview of Our Results

Defining SNARKs in the Presence of Oracles. As a first step, we formalize the definition of non-black-box extraction in the presence of oracles by proposing a notion of SNARKs in the presence of oracles (O-SNARKs, for short). In a nutshell, an O-SNARK is like a SNARK except that adaptive proof of knowledge must hold with respect to adversaries that have access to an oracle $\mathcal{O}$ sampled from some oracle family $\mathbb O$.³ Slightly more in detail, we require that for any adversary $\mathcal{A}^{\mathcal{O}}$ with access to $\mathcal{O}$ there is an extractor $\mathcal{E}_\mathcal{A}$ such that, whenever $\mathcal{A}^{\mathcal{O}}$ outputs a valid proof, $\mathcal{E}_{\mathcal{A}}$ outputs a valid witness, by running on the same input of $\mathcal{A}$, plus the transcript of oracle queries-answers of $\mathcal{A}$.

Existence of O-SNARKs. Once having defined their notion, we study whether O-SNARKs exist and under what assumptions. Below we summarize our results.

O-SNARKs in the random oracle model. As a first positive result, we show that the construction of Computationally Sounds (CS) proofs of Micali [Mic00] yields an O-SNARK for every oracle family, in the random oracle model. This result follows from the work of Valiant [Val08] which shows that Micali’s construction already allows for extraction. More precisely, using the power of the random oracle model, Valiant shows a black-box extractor. This powerful extractor can then be used to build an O-SNARK extractor that works for any oracle family.

Insecurity of O-SNARKs for every oracle family. Although the above result gives a candidate O-SNARK, it only works in the random oracle model, and it is tailored to one construction [Mic00]. It is therefore interesting to understand whether extraction with oracles is feasible in the standard model. And it would also be interesting to see if this is possible based on the classical SNARK notion. Besides its theoretical interest, the latter question has also a practical motivation since there are several efficient SNARK constructions proposed in the last years that one might like to use in place of CS proofs. Our first result in this direction is that assuming existence of one way functions (OWFs) there do not exist O-SNARKs for $\mathsf{NP}$ with respect to every oracle family. More precisely, we show the following:

Theorem 1 (Informal)

Assume OWFs exist. Then for any polynomial $p(\cdot )$ there is an unforgeable signature scheme $\varSigma _p$ such that any candidate O-SNARK, that is correct and succinct with proofs of length bounded by $p(\cdot )$, cannot satisfy adaptive proof of knowledge with respect to signing oracles corresponding to $\varSigma _p$.

The above result shows the existence of an oracle family for which O-SNARKs do not exist. A basic intuition behind it is that oracles provide additional auxiliary input to adversaries and, as formerly shown in [BCPR14, BP15], this can create issues for extraction. In fact, to obtain our result we might also have designed an oracle that simply outputs a binary string following a distribution with respect to which extraction is impossible due to [BCPR14, BP15]. However, in this case the result should additionally assume the existence of indistinguishability (or differing-input) obfuscation. In contrast, our result shows that such impossibility holds by only assuming existence of OWFs, which is a much weaker assumption.

In addition to ruling out existence of O-SNARKs for general oracles, our theorem also rules out their existence for a more specific class of oracle families – signing oracles – that is motivated by the three applications mentioned earlier.⁴ Its main message is thus that one cannot assume existence of O-SNARKs that work with any signature scheme. This explains why the security proofs of the primitives considered earlier do not go through, if one wants to base it on an arbitrary signature scheme.

Existence of O-SNARKs for specific families of signing oracles. We study ways to circumvent our impossibility result for signing oracles of Theorem 1. Indeed, the above result can be interpreted as saying that there exist (perhaps degenerate) signature schemes such that there are no O-SNARKs with respect to the corresponding signing oracle family. This is not ruling out that O-SNARKs may exist for specific signature schemes, or – even better – for specific classes of signature schemes. We provide the following results:

• 1. Hash-and-sign signatures, where the hash is a random oracle, yield “safe oracles”, i.e., oracles for which any SNARK is an O-SNARK for that oracle, in the ROM.

• 2. Turning to the standard model setting, we show that any classical SNARK is an O-SNARK for signing oracles if the message space of the signature scheme is properly bounded, and O-SNARK adversaries query “almost” the entire message space. This positive result is useful in applications that use SNARKs with signing oracles, under the condition that adversaries make signing queries on almost all messages.

Non-adaptive O-SNARKs. Finally, we consider a relaxed notion of O-SNARKs in which adversaries are required to declare in advance (i.e., before seeing the common reference string) all the oracle queries. For this weaker notion we show that, in the standard model, every SNARK (for arbitrary auxiliary inputs) is a non-adaptive O-SNARK.

Applications of O-SNARKs. A nice feature of the O-SNARK notion is that it lends itself to easy and intuitive security proofs in all those applications where one needs to execute extractors in interactive security games with oracles. We show that by replacing SNARKs with O-SNARKs (for appropriate oracle families) we can formally prove the security of the constructions of homomorphic signatures, succinct functional signatures and SNARKs on authenticated data that we mentioned in the previous section. By combining these O-SNARK-based constructions with our existence results mentioned earlier we eventually reach conclusions about the possible secure instantiations of these constructions. The first option is to instantiate them by using Micali’s CS proofs as an O-SNARK: this solution essentially yields secure instantiations in the random oracle model that work with a specific proof system [Mic00] (perhaps not the most efficient one in practice). The second option is to instantiate them using hash-and-sign signatures, apply our result on hash-and-sign signatures mentioned above, and then conjecture that replacing the random oracle with a suitable hash function preserves the overall security.⁵ Third, one can instantiate the constructions using a classical SNARK scheme $\varPi$ and signature scheme $\varSigma$, and then conjecture that $\varPi$ is also an O-SNARK with respect to the family of signing oracles corresponding to $\varSigma$. Compared to the first solution, the last two ones have the advantage that one could use some of the recently proposed efficient SNARKs (e.g., [PHGR13, BSCG+13]); on the other hand, these solutions have the drawback that security is based only on a heuristic argument. Finally, as a fourth option we provide security proofs of these primitives under a weak, non-adaptive, notion where adversaries declare all their queries in advance. Security in this weaker model can be proven assuming non-adaptive O-SNARKs, and thus classical SNARKs. The advantage of this fourth option is that one obtains a security proof for these instantiations based on clear – not newly crafted – assumptions, although under a much weaker security notion. Finally, worth noting is that we cannot apply the positive result on O-SNARK for signing oracles to the O-SNARK-based constructions of homomorphic signatures, functional signatures and SNARKs on authenticated data that we provide, and thus conclude their security under classical SNARKs. The inapplicability is due to the aforementioned restriction of our result, for which adversaries have to query almost the entire message space.⁶

Interpretation of Our Results. In line with recent work [BCPR14, BP15] on the feasibility of extraction in the presence of auxiliary input, our results indicate that additional care must be taken when considering extraction in the presence of oracles. While for auxiliary input impossibility of extraction is known under obfuscation-related assumptions, in the case of oracles we show that extraction becomes impossible even by only assuming one-way functions. Our counterexamples are of artificial nature and do not rule out the feasibility of extraction in the presence of “natural, benign” oracles. Nevertheless, our impossibility results provide formal evidence of why certain security proofs do not go through, and bring out important subtle aspects of security proofs. Given the importance of provable security and considered the increasing popularity of SNARKs in more practical scenarios, we believe these results give a message that is useful to protocol designers and of interest to the community at large.

1.3 Organization

The paper is organized as follows. In Sect. 2 we recall notation and definitions used in the rest of our work. Section 3 introduces the notion of O-SNARKs, Sect. 4 includes positive and negative results about the existence of O-SNARKs, and in Sect. 5 we give three applications where our new notion turns out to be useful. For lack of space, additional definitions and detailed proofs are deferred to the full version [FN16].

2 Preliminaries

Notation. We denote with $\lambda \in \mathbb N$ the security parameter. We say that a function $\epsilon (\lambda )$ is negligible if it vanishes faster than the inverse of any polynomial in $\lambda$. If not explicitly specified otherwise, negligible functions are negligible with respect to $\lambda$. If S is a set, $x \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}S$ denotes the process of selecting x uniformly at random in S. If $\mathcal{A}$ is a probabilistic algorithm, $x \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{A}(\cdot )$ denotes the process of running $\mathcal{A}$ on some appropriate input and assigning its output to x. For binary strings x and y, we denote by x|y their concatenation and by $x_i$ the i-th bit of x. For a positive integer n, we denote by [n] the set $\{1,\ldots , n\}$. For a random-access machine M we denote by $\#M(x, w)$ the number of execution steps needed by M to accept on input (x, w).

The Universal Relation and NP Relations. We recall the notion of universal relation from [BG08], here adapted to the case of non-deterministic computations.

Definition 1

The universal relation is the set $\mathcal{R}_{\mathcal{U}}$ of instance-witness pairs $(y, w) = ((M, x, t), w)$, where $|y|, |w| \le t$ and M is a random-access machine such that M(x, w) accepts after running at most t steps. The universal language $\mathcal{L}_{\mathcal{U}}$ is the language corresponding to $\mathcal{R}_{\mathcal{U}}$.

For any constant $c \in \mathbb N$, $\mathcal{R}_{c}$ denotes the subset of $\mathcal{R}_{\mathcal{U}}$ of pairs $(y, w) = ((M, x, t), w)$ such that $t \le |x|^{c}$. $\mathcal{R}_{c}$ is a “generalized” $\mathsf{NP}$ relation that is decidable in some fixed time polynomial in the size of the instance.

2.1 Succinct Non-interactive Arguments

In this section we provide formal definitions for the notion of succinct non-interactive arguments of knowledge (SNARKs).

Definition 2 (SNARGs)

A succinct non-interactive argument (SNARG) for a relation $\mathcal{R}\subseteq \mathcal{R}_{\mathcal{U}}$ is a triple of algorithms $\varPi =(\mathsf{Gen}, \mathsf{Prove}, \mathsf{Ver})$ working as follows  

$\mathsf{Gen}(1^{\lambda }, T) \rightarrow \mathsf{crs}$ : :

On input a security parameter $\lambda \in \mathbb N$ and a time bound $T \in \mathbb N$, the generation algorithm outputs a common reference string $\mathsf{crs}= (\mathsf{prs}, \mathsf{vst})$ consisting of a public prover reference string $\mathsf{prs}$ and a verification state $\mathsf{vst}$.

$\mathsf{Prove}(\mathsf{prs}, y, w) \rightarrow \pi$ : :

Given a prover reference string $\mathsf{prs}$, an instance $y=(M, x, t)$ with $t \le T$ and a witness w s.t. $(y, w) \in \mathcal{R}$, this algorithm produces a proof $\pi$.

$\mathsf{Ver}(\mathsf{vst}, y, \pi ) \rightarrow b$ : :

On input a verification state $\mathsf{vst}$, an instance y, and a proof $\pi$, the verifier algorithm outputs $b=0$ (reject) or $b=1$ (accept).

  and satisfying completeness, succinctness, and (adaptive) soundness:

• Completeness. For every time bound $T \in \mathbb N$, every valid $(y, w) \in \mathcal{R}$ with $y=(M, x, t)$ and $t \le T$, there exists a negligible function $\mathsf{negl}$ such that

  

• Succinctness. There exists a fixed polynomial $p(\cdot )$ independent of $\mathcal{R}$ such that for every large enough security parameter $\lambda \in \mathbb N$, every time bound $T \in \mathbb N$, and every instance $y = (M, x, t)$ such that $t \le T$, we have

  • $\mathsf{Gen}$ runs in time ${\left\{ \begin{array}{ll} p(\lambda + \log T) &{} \text { for a fully-succinct SNARG} \\ p(\lambda + T) &{} \text { for a pre-processing SNARG} \end{array}\right. }$

  • $\mathsf{Prove}$ runs in time

    $${\left\{ \begin{array}{ll} p(\lambda + |M| + |x| + t + \log T) &{} \text { for fully-succinct SNARG} \\ p(\lambda + |M| + |x| + T) &{} \text { for pre-processing SNARG} \end{array}\right. }$$

  • $\mathsf{Ver}$ runs in time $p(\lambda + |M| + |x| + \log T)$

  • a honestly generated proof has size $|\pi |=p(\lambda + \log T)$.

• Adaptive Soundness. For every non-uniform $\mathcal{A}$ of size $s(\lambda ) = \mathsf{poly}(\lambda )$ there is a negligible function $\epsilon (\lambda )$ such that for every time bound $T \in \mathbb N$,

  

The notion of SNARG can be extended to be an argument of knowledge (a SNARK) by replacing soundness by an appropriate proof of knowledge property.

Definition 3

(SNARKs [BCC+14]). A succinct non-interactive argument of knowledge (SNARK) for a relation $\mathcal{R}\subseteq \mathcal{R}_{\mathcal{U}}$ is a triple of algorithms $\varPi =(\mathsf{Gen}, \mathsf{Prove}, \mathsf{Ver})$ that constitutes a SNARG (as per Definition 2) except that soundness is replaced by the following property:

• Adaptive Proof of Knowledge. For every non-uniform prover $\mathcal{A}$ of size $s(\lambda ) = \mathsf{poly}(\lambda )$ there exists a non-uniform extractor $\mathcal{E}_{\mathcal{A}}$ of size $t(\lambda )=\mathsf{poly}(\lambda )$ and a negligible function $\epsilon (\lambda )$ such that for every auxiliary input $aux \in \{0,1\}^{poly(\lambda )}$, and every time bound $T \in \mathbb N$,

  

  Furthermore, we say that $\varPi$ satisfies $(s, t, \epsilon )$-adaptive proof of knowledge if the above condition holds for concrete values $(s, t, \epsilon )$.

Remark 1 (Publicly verifiable vs. designated verifier)

If security (adaptive PoK) holds against adversaries that have also access to the verification state $\mathsf{vst}$ (i.e., $\mathcal{A}$ receives the whole $\mathsf{crs}$) then the SNARK is called publicly verifiable, otherwise it is designated verifier. For simplicity, in the remainder of this work all definitions are given for the publicly verifiable setting; the corresponding designated-verifier variants are easily obtained by giving to the adversary only the prover state $\mathsf{prs}$.

Remark 2 (About extraction and auxiliary input)

First, we stress that in the PoK property the extractor $\mathcal{E}_{\mathcal{A}}$ takes exactly the same input of $\mathcal{A}$, including its random tape. Second, the PoK definition can also be relaxed to hold with respect to auxiliary inputs from specific distributions (instead of arbitrary ones). Namely, let $\mathcal{Z}$ be a probabilistic algorithm (called the auxiliary input generator) that outputs a string $aux$, and let compactly denote this process as $aux {\leftarrow }\mathcal{Z}$. Then we say that adaptive proof of knowledge holds for $\mathcal{Z}$ if the above definition holds for auxiliary inputs sampled according to $\mathcal{Z}$ – $aux {\leftarrow }\mathcal{Z}$ – where $\mathcal{Z}$ is also a non-uniform polynomial-size algorithm. More formally, we have the following definition.

Definition 4

( $\mathcal{Z}$ -auxiliary input SNARKs). $\varPi$ is called a $\mathcal{Z}$-auxiliary input SNARK if $\varPi$ is a SNARK as in Definition 3 except that adaptive proof of knowledge holds for auxiliary input $aux {\leftarrow }\mathcal{Z}$.

For ease of exposition, in our proofs we compactly denote by $\mathsf{AdPoK}(\lambda , T, \mathcal{A}, \mathcal{E}_{\mathcal{A}}, \mathcal{Z})$ the adaptive proof of knowledge experiment executed with adversary $\mathcal{A}$, extractor $\mathcal{E}_{\mathcal{A}}$ and auxiliary input generator $\mathcal{Z}$. See below its description:

We say that $\varPi$ satisfies adaptive proof of knowledge for $\mathcal{Z}$-auxiliary input if for every non-uniform $\mathcal{A}$ of size $s(\lambda )=\mathsf{poly}(\lambda )$ there is a non-uniform extractor of size $t(\lambda )=\mathsf{poly}(\lambda )$ and a negligible function $\epsilon (\lambda )$ such that for every time bound T we have $\Pr [\mathsf{AdPoK}(\lambda , T, \mathcal{A}, \mathcal{E}_{\mathcal{A}}, \mathcal{Z}) \,{\Rightarrow }\,1] \le \epsilon .$ Furthermore, $\varPi$ has $(s, t, \epsilon )$-adaptive proof of knowledge for $\mathcal{Z}$-auxiliary input if the above condition holds for concrete $(s, t, \epsilon )$.

SNARKs for $\mathsf{NP}$. A SNARK for the universal relation $\mathcal{R}_{\mathcal{U}}$ is called a universal SNARK. SNARKs for $\mathsf{NP}$ are instead SNARKs in which the verification algorithm $\mathsf{Ver}$ takes as additional input a constant $c > 0$, and adaptive proof of knowledge is restricted to hold only for relations $\mathcal{R}_{c} \subset \mathcal{R}_{\mathcal{U}}$. More formally,

Definition 5

(SNARKs for $\mathsf{NP}$ ). A SNARK for $\mathsf{NP}$ is a tuple of algorithms $\varPi = (\mathsf{Gen}, \mathsf{Prove}, \mathsf{Ver})$ satisfying Definition 3 except that the adaptive proof of knowledge property is replaced by the following one:

• Adaptive Proof of Knowledge for $\mathsf{NP}$ . For every non-uniform polynomial-size prover $\mathcal{A}$ there exists a non-uniform polynomial-size extractor $\mathcal{E}_{\mathcal{A}}$ such that for every large enough $\lambda \in \mathbb N$, every auxiliary input $aux \in \{0,1\}^{poly(\lambda )}$, and every time bound $T \in \mathbb N$, and every constant $c > 0$,

  

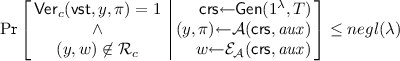
In the case of fully-succinct SNARKs for $\mathsf{NP}$, it is not necessary to provide a time bound as one can set $T = \lambda ^{\log \lambda }$. In this case we can write $\mathsf{Gen}(1^{\lambda })$ as a shorthand for $\mathsf{Gen}(1^{\lambda }, \lambda ^{\log \lambda })$.

3 SNARKs in the Presence of Oracles

In this section we formalize the notion of extraction in the presence of oracles for SNARKs. We do this by proposing a suitable adaptive proof of knowledge definition, and we call a SNARK satisfying this definition a SNARK in the presence of oracles (O-SNARK, for short). As we shall see, the advantage of O-SNARKs is that this notion lends itself to easy and intuitive security proofs in all those applications where one needs to execute extractors in interactive security games with oracles (with a secret state). Below we provide the definition while the existence of O-SNARKs is discussed in Sect. 4.

3.1 O-SNARKs: SNARKs in the Presence of Oracles

Let $\mathbb O= \{\mathcal{O}\}$ be a family of oracles. We denote by $\mathcal{O}{\leftarrow }\mathbb O$ the process of sampling an oracle $\mathcal{O}$ from the family $\mathbb O$ according to some (possibly probabilistic) process. For example, $\mathbb O$ can be a random oracle family, i.e., $\mathbb O=\{\mathcal{O}: \{0,1\}^{\ell } \rightarrow \{0,1\}^{L}\}$ for all possible functions from $\ell$-bits strings to L-bits strings, in which case $\mathcal{O}{\leftarrow }\mathbb O$ consists of choosing a function $\mathcal{O}$ uniformly at random in $\mathbb O$. As another example, $\mathbb O$ might be the signing oracle corresponding to a signature scheme, in which case the process $\mathcal{O}{\leftarrow }\mathbb O$ consists of sampling a secret key of the signature scheme according to the key generation algorithm (and possibly a random tape for signature generation in case the signing algorithm is randomized).

For any oracle family $\mathbb O$, we define an O-SNARK $\varPi$ for $\mathbb O$ as follows.

Definition 6

( $\mathcal{Z}$ -auxiliary input O-SNARKs for $\mathbb O$ ). We say that $\varPi$ is a $\mathcal{Z}$-auxiliary input O-SNARK for the oracle family $\mathbb O$, if $\varPi$ satisfies the properties of completeness and succinctness as in Definition 3, and the following property of adaptive proof of knowledge for $\mathbb O$:

• Adaptive Proof of Knowledge for $\mathbb O$. Consider the following experiment for security parameter $\lambda \in \mathbb N$, time bound $T \in \mathbb N$, adversary $\mathcal{A}$, extractor $\mathcal{E}_{\mathcal{A}}$, auxiliary input generator $\mathcal{Z}$ and oracle family $\mathbb O$:

  

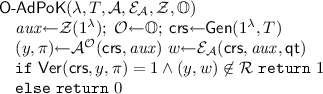
  where $\mathsf{qt}= \{q_i, \mathcal{O}(q_i)\}$ is the transcript of all oracle queries and answers made and received by $\mathcal{A}$ during its execution.

  $\varPi$ satisfies adaptive proof of knowledge with respect to oracle family $\mathbb O$ and auxiliary input from $\mathcal{Z}$ if for every non-uniform oracle prover $\mathcal{A}^{\mathcal{O}}$ of size $s(\lambda ) = \mathsf{poly}(\lambda )$ making at most $Q(\lambda ) = \mathsf{poly}(\lambda )$ queries there exists a non-uniform extractor $\mathcal{E}_{\mathcal{A}}$ of size $t(\lambda ) = \mathsf{poly}(\lambda )$ and a negligible function $\epsilon (\lambda )$ such that for every time bound T, $\Pr [\mathsf{O\text{- }AdPoK}(\lambda , T, \mathcal{A}, \mathcal{E}_{\mathcal{A}}, \mathcal{Z}, \mathbb O) \,{\Rightarrow }\,1] \le \epsilon (\lambda )$. Furthermore, we say that $\varPi$ satisfies $(s, t, Q, \epsilon )$-adaptive proof of knowledge with respect to oracle family $\mathbb O$ and auxiliary input from $\mathcal{Z}$ if the above condition holds for concrete values $(s, t, Q, \epsilon )$.

3.2 Non-adaptive O-SNARKs

In this section we define a relaxation of O-SNARKs in which the adversary is non-adaptive in making its queries to the oracle. Namely, we consider adversaries that first declare all their oracle queries $q_1, \ldots , q_{Q}$ and then run on input the common reference string as well as the queries’ outputs $\mathcal{O}(q_1), \ldots , \mathcal{O}(q_Q)$. More formally,

Definition 7

( $\mathcal{Z}$ -auxiliary input non-adaptive O-SNARKs for $\mathbb O$ ). We say that $\varPi$ is a $\mathcal{Z}$-auxiliary input non-adaptive O-SNARK for the oracle family $\mathbb O$, if $\varPi$ satisfies the properties of completeness and succinctness as in Definition 3, and the following property of non-adaptive queries proof of knowledge for $\mathbb O$:

• Non-adaptive Proof of Knowledge for $\mathbb O$. Consider the following experiment for security parameter $\lambda \in \mathbb N$, time bound $T \in \mathbb N$, adversary $\mathcal{A}= (\mathcal{A}_1, \mathcal{A}_2)$, extractor $\mathcal{E}_{\mathcal{A}}$, auxiliary input generator $\mathcal{Z}$ and oracle family $\mathbb O$:

  

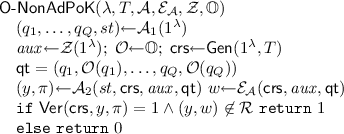
  where st is simply a state information shared between $\mathcal{A}_1$ and $\mathcal{A}_2$.

  $\varPi$ satisfies non-adaptive proof of knowledge with respect to oracle family $\mathbb O$ and auxiliary input from $\mathcal{Z}$ if for every non-uniform prover $\mathcal{A}= (\mathcal{A}_1, \mathcal{A}_2)$ of size $s(\lambda ) = \mathsf{poly}(\lambda )$ making at most $Q(\lambda ) = \mathsf{poly}(\lambda )$ non-adaptive queries there exists a non-uniform extractor $\mathcal{E}_{\mathcal{A}}$ of size $t(\lambda ) = \mathsf{poly}(\lambda )$ and a negligible function $\epsilon (\lambda )$ such that for every time bound T, $\Pr [\mathsf{O\text{- }NonAdPoK}(\lambda , T, \mathcal{A}, \mathcal{E}_{\mathcal{A}}, \mathcal{Z}, \mathbb O) \,{\Rightarrow }\,1] \le \epsilon (\lambda )$. Furthermore, we say that $\varPi$ satisfies $(s, t, Q, \epsilon )$-non-adaptive proof of knowledge with respect to oracle family $\mathbb O$ and auxiliary input from $\mathcal{Z}$ if the above condition holds for concrete values $(s, t, Q, \epsilon )$.

It is also possible to define a stronger variant of the above definition in which $\mathcal{A}_1$ is given (adaptive) oracle access to $\mathcal{O}$, whereas $\mathcal{A}_2$ has no access to $\mathcal{O}$, except for the query transcript obtained by $\mathcal{A}_1$. It is not hard to see that the result given in the following paragraph works under this intermediate definition as well.

Existence of Non-adaptive O-SNARKs from SNARKs. Below we prove a simple result showing that non-adaptive O-SNARKs follow directly from classical SNARKs for which the proof of knowledge property holds for arbitrary auxiliary input distributions.

Theorem 2

Let $\mathbb O$ be any oracle family. If $\varPi$ is a SNARK satisfying $(s, t, \epsilon )$-adaptive PoK (for arbitrary auxiliary input), then $\varPi$ is a non-adaptive O-SNARK for $\mathbb O$ satisfying $(s, t, Q, \epsilon )$-non-adaptive PoK.

For lack of space we only provide an intuition of the proof, which is given in detail in the full version. The idea is that the second stage adversary $\mathcal{A}_2$ of non-adaptive O-SNARKs is very much like a classical SNARK adversary that makes no queries and receives a certain auxiliary input which contains the set of oracle queries chosen by $\mathcal{A}_1$ with corresponding answers. The fact that the auxiliary input includes the set of queries chosen by $\mathcal{A}_1$, which is an arbitrary adversary, implies that the SNARK must support arbitrary, not necessarily benign, auxiliary inputs (i.e., it is not sufficient to fix an auxiliary input distribution that depends only on the oracle family $\mathbb O$).

4 On the Existence of O-SNARKs

In this section we study whether O-SNARKs exist and under what assumptions. In the following sections we give both positive and negative answers to this question. For lack of space, a positive existence result about O-SNARKs for (pseudo)random oracles is given in the full version [FN16].

4.1 O-SNARKs in the ROM from Micali’s CS Proofs

In this section we briefly discuss how the construction of CS proofs of Micali [Mic00] can be seen as an O-SNARK for any oracle family, albeit in the random oracle model. To see this, we rely on the result of Valiant [Val08] who shows that Micali’s construction is a “CS proof of knowledge” in the random oracle model. The main observation is in fact that Valiant’s proof works by showing a black-box extractor working for any prover.

Proposition 1

Let $\mathbb O$ be any oracle family and $\mathsf{RO}$ be a family of random oracles. Let $\varPi _{\mathsf{Mic}}$ be the CS proof construction from [Mic00]. Then $\varPi _{\mathsf{Mic}}$ is an O-SNARK for $(\mathsf{RO}, \mathbb O)$, in the random oracle model.

Proof (Sketch)

Let $\mathcal{E}^{\mathsf{RO}}$ be Valiant’s black-box extractor⁷ which takes as input the code of the prover and outputs a witness w. For any adversary $\mathcal{A}^{\mathsf{RO},\mathcal{O}}$ we can define its extractor $\mathcal{E}_{\mathcal{A}}$ as the one that, on input the query transcript $\mathsf{qt}$ of $\mathcal{A}$, executes $w \leftarrow \mathcal{E}^{\mathsf{RO}}(\mathcal{A})$ by simulating all the random oracle queries of $\mathcal{E}^\mathsf{RO}$ using $\mathsf{qt}$, and finally outputs the same w. The reason why $\mathsf{qt}$ suffices to $\mathcal{E}_{\mathcal{A}}$ for simulating random oracle queries to $\mathcal{E}^{\mathsf{RO}}$ is that Valiant’s extractor $\mathcal{E}^{\mathsf{RO}}$ makes exactly the same queries of the prover.

4.2 Impossibility of O-SNARKs for Every Family of Oracles

In this section we show that, in the standard model, there do not exist O-SNARKs with respect to every family of oracles. We show this under the assumption that universal one-way hash functions (and thus one-way functions [Rom90]) exist. To show the impossibility, we describe an oracle family in the presence of which any candidate O-SNARK that is correct and succinct cannot satisfy adaptive proof of knowledge with respect to that oracle family. Our impossibility result is shown for designated-verifier O-SNARKs, and thus implies impossibility for publicly verifiable ones as well (since every publicly verifiable O-SNARK is also designated-verifier secure). More specifically, we show the impossibility by means of a signing oracle family. Namely, we show a secure signature scheme $\varSigma _p$ such that every correct and succinct O-SNARK $\varPi$ cannot satisfy adaptive proof of knowledge in the presence of the signing oracle corresponding to $\varSigma _p$. Interestingly, such a result not only shows that extraction cannot work for general families of oracles, but also for families of signing oracles, a class which is relevant to several applications.

For every signature scheme $\varSigma = (\mathsf{kg}, \mathsf{sign}, \mathsf{vfy})$ we let $\mathbb O_{\varSigma }$ be the family of oracles $\mathcal{O}(m) = \mathsf{sign}(\mathsf{sk}, m)$, where every family member $\mathcal{O}$ is described by a secret key $\mathsf{sk}$ of the signature scheme, i.e., the process $\mathcal{O}\leftarrow \mathbb O_{\varSigma }$ corresponds to obtaining $\mathsf{sk}$ through a run of $(\mathsf{sk}, \mathsf{vk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{kg}(1^{\lambda })$. For the sake of simplicity, we also assume that the oracle allows for a special query, say $\mathcal{O}(`vk\text {'})$,⁸ whose answer is the verification key $\mathsf{vk}$.

Theorem 3

Assume that one-way functions exist. Then for every polynomial $p(\cdot )$ there exists a $\mathsf{UF\text{- }CMA}$-secure signature scheme $\varSigma _p$ such that every candidate designated-verifier O-SNARK $\varPi$ for $\mathsf{NP}$, that is correct and succinct with proofs of length bounded by $p(\cdot )$, does not satisfy adaptive proof of knowledge with respect to $\mathbb O_{\varSigma _p}$.

An intuition of the result. Before delving into the details of the proof, we provide the main intuition of this result. This intuition does not use signature schemes but includes the main ideas that will be used in the signature counterexample. Given a UOWHF function family $\mathcal{H}$, consider the $\mathsf{NP}$ binary relation $\tilde{R}_{\mathcal{H}} = \{((h, x), w): h \in \mathcal{H}, h(w)=x\}$, let $\varPi$ be a SNARK for $\mathsf{NP}$ and consider $p(\cdot )$ the polynomial for which $\varPi$ is succinct. The idea is to show an oracle family and an adversary $\bar{\mathcal{A}}$ for which there is no extractor unless $\mathcal{H}$ is not a universal one-way family. For every polynomial $p(\cdot )$, the oracle family contains oracles $\mathcal{O}_p$ that given a query q, interpret q as the description of a program $\mathcal{P}(\cdot , \cdot )$, samples a random member of the hash family $h \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{H}$, a random w, computes $x=h(w)$, and outputs (h, x) along with $\pi \leftarrow \mathcal{P}((h,x), w)$. If $\mathcal{P}(\cdot , \cdot )=\mathsf{Prove}(\mathsf{prs},\cdot , \cdot )$, then the oracle is simply returning an hash image with a proof of knowledge of its (random) preimage. The adversary $\bar{\mathcal{A}}^{\mathcal{O}_p}$ is the one that on input $\mathsf{prs}$, simply asks one query $q=\mathcal{P}(\cdot , \cdot )=\mathsf{Prove}(\mathsf{prs},\cdot , \cdot )$, gets $((h,x), \pi ) {\leftarrow }\mathcal{O}_p(q)$ and outputs $((h,x), \pi )$. Now, the crucial point that entails the non-existence of an extractor is that, provided that the input w is sufficiently longer than $\pi$, every valid extractor for such $\bar{\mathcal{A}}$ that outputs a valid $w'$ immediately implies a collision $(w, w')$ for h.⁹ Finally, to prevent adversarially chosen $\mathcal{P}$ from revealing too much information, we require the oracle to check the length of $\pi$, and the latter is returned only if $|\pi |\le p(\lambda )$.

Proof

(Proof of Theorem 3 ). The proof consists of two main steps. First, we describe the construction of the signature scheme $\varSigma _p$ based on any other $\mathsf{UF\text{- }CMA}$-secure signature scheme $\widehat{\varSigma }$ with message space $\mathcal{M}= \{0,1\}^*$ (that exists assuming OWFs [Lam79, Rom90]), and show that $\varSigma _p$ is $\mathsf{UF\text{- }CMA}$-secure. $\varSigma _p$ uses also an UOWHF family $\mathcal{H}$. Second, we show that, when considering the oracle family $\mathbb O_{\varSigma _p}$ corresponding to the signature scheme $\varSigma _p$, a correct $\varPi$ with succinctness $p(\cdot )$ cannot be an O-SNARK for $\mathbb O_{\varSigma _p}$, i.e., we show an efficient O-SNARK adversary $\mathcal{A}_p^{\mathcal{O}}$ (with access to a $\varSigma _p$ signing oracle $\mathcal{O}(\cdot ) = \mathsf{sign}(\mathsf{sk}, \cdot )$), for which there is no extractor unless $\mathcal{H}$ is not one-way.

The Counterexample Signature Scheme $\varSigma _p$ . Let $\widehat{\varSigma }$ be any $\mathsf{UF\text{- }CMA}$-secure scheme with message space $\mathcal{M}=\{0,1\}^*$. Let $\mathbb {H}=\{\mathcal{H}\}_{\lambda }$ be a collection of function families $\mathcal{H}= \{ h: \{0,1\}^{L(\lambda )} \rightarrow \{0,1\}^{\ell (\lambda )}\}$ where each $\mathcal{H}$ is an universal one-way hash family with $L(\lambda ) \ge p(\lambda ) + \ell (\lambda ) + \lambda$. Let $M_{\mathcal{H}}((h,x), w)$ be the machine that on input ((h, x), w) accepts iff $h(w)=x$, and $\mathcal{R}_{\mathcal{H}}$ be the $\mathsf{NP}$ relation consisting of all pairs (y, w) such that, for $y=(M_{\mathcal{H}}, (h,x), t)$, $M_{\mathcal{H}}((h,x),w)$ accepts in at most t steps.

The scheme $\varSigma _p$ has message space $\mathcal{M}=\{0,1\}^*$; its algorithms work as follows:

• $\mathsf{kg}(1^{\lambda })$: Run $(\widehat{\mathsf{vk}}, \widehat{\mathsf{sk}}) \leftarrow \widehat{\varSigma }.\mathsf{kg}(1^{\lambda })$, set $\mathsf{vk}= \widehat{\mathsf{vk}}$, $\mathsf{sk}= \widehat{\mathsf{sk}}$.

• $\mathsf{sign}(\mathsf{sk}, m)$: Signing works as follows

  • – generate $\hat{\sigma }{\leftarrow }\widehat{\varSigma }.\mathsf{sign}(\widehat{\mathsf{sk}}, m)$;

  • – sample $h \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{H}$ and $w \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}^{L(\lambda )}$;

  • – compute $x=h(w)$, $t = \#M_{\mathcal{H}}((h,x),w)$, and set $y = (M_{\mathcal{H}}, (h,x), t)$;

  • – interpret m as the description of program $\mathcal{P}(\cdot , \cdot )$ and thus run $\pi {\leftarrow }\mathcal{P}( y, w)$;

  • – if $|\pi | \le p(\lambda )$, set $\pi ' = \pi$, else set $\pi ' = 0$;

  • – output $\sigma = (\hat{\sigma }, h,x, \pi ')$.

• $\mathsf{vfy}(\mathsf{vk}, m, \sigma )$: Parse $\sigma = (\hat{\sigma }, h, x, \pi ')$ and return the output of $\widehat{\varSigma }.\mathsf{vfy}(\widehat{\mathsf{vk}}, m, \hat{\sigma })$.

It is trivial to check that, as long as $\widehat{\varSigma }$ is a $\mathsf{UF\text{- }CMA}$-secure scheme, $\varSigma _p$ is also $\mathsf{UF\text{- }CMA}$-secure. Moreover, remark that the scheme $\varSigma _p$ does not depend on the specific O-SNARK construction $\varPi$ but only on the universal polynomial $p(\cdot )$ bounding its succinctness.

Impossibility of O-SNARKs for $\mathbb O_{\varSigma _p}$ . To show that $\varPi$ is not an O-SNARK for $\mathbb O_{\varSigma _p}$ (under the assumption that $\mathcal{H}$ is universally one-way), we prove that there is an adversary $\mathcal{A}_p^{\mathcal{O}}$ such that every candidate extractor $\mathcal{E}$ fails in the adaptive proof of knowledge game.

Lemma 1

If $\mathcal{H}$ is universally one way then every $\varPi$ for $\mathsf{NP}$ that is correct and succinct with proofs of length $p(\cdot )$ is not a designated-verifier O-SNARK for $\mathbb O_{\varSigma _p}$.

Proof

Let $\mathcal{A}_p^{\mathcal{O}}$ be the following adversary: on input $\mathsf{prs}$, encode the $\mathsf{Prove}$ algorithm of $\varPi$ with hardcoded $\mathsf{prs}$ as a program $\mathcal{P}(\cdot ,\cdot ) := \mathsf{Prove}(\mathsf{prs},\cdot ,\cdot )$; let q be $\mathcal{P}$’s description, and make a single query $\sigma = (\hat{\sigma }, h, x , \pi ') \leftarrow \mathcal{O}(q)$; return $(y, \pi ')$ where $y = (M_{\mathcal{H}},(h,x), t)$ is appropriately reconstructed. We show that for every polynomial-size extractor $\mathcal{E}$ it holds

$$ \Pr [\mathsf{O\text{- }AdPoK}(\lambda , \mathcal{A}_p, \mathcal{E}, \mathbb O_{\varSigma _p}) \,{\Rightarrow }\,0] \le \nu _{\mathcal{H}}(\lambda ) + 2^{-\lambda } $$

where $\nu _{\mathcal{H}}(\lambda ) = \mathbf {Adv}_{\mathcal{B},\mathcal{H}}^{UOWHF}(\lambda )$ is the advantage of any adversary $\mathcal{B}$ against $\mathcal{H}$’s universal one-wayness. This means that there is no extractor unless $\mathcal{H}$ is not an universal one-way family.

We proceed by contradiction assuming the existence of a polynomial-size extractor $\mathcal{E}$ such that the above probability is greater than some non-negligible $\epsilon$. We show how to build an adversary $\mathcal{B}$ that breaks universal one-wayness of $\mathcal{H}$ with non-negligible probability.

$\mathcal{B}$ first chooses an hash input $w \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}^{L(\lambda )}$, and then receives an instance h of $\mathcal{H}$. Next, $\mathcal{B}$ generates $(\mathsf{prs}, \mathsf{vst}) {\leftarrow }\mathsf{Gen}(1^{\lambda })$ and $(\widehat{\mathsf{vk}}, \widehat{\mathsf{sk}}) \leftarrow \widehat{\varSigma }.\mathsf{kg}(1^{\lambda })$, and runs $\mathcal{A}_p^{\mathcal{O}}(\mathsf{prs})$ simulating the oracle $\mathcal{O}$ on the single query $q:=\mathcal{P}(\cdot , \cdot ) = \mathsf{Prove}(\mathsf{crs},\cdot , \cdot )$ asked by $\mathcal{A}_p$. In particular, to answer the query $\mathcal{B}$ uses the secret key $\widehat{\mathsf{sk}}$ to generate $\hat{\sigma }$, and computes $x=h(w)$ using the function h received from its challenger, and the input w chosen earlier. Notice that such a simulation can be done perfectly in a straightforward way, and that $\mathcal{A}_p$’s output is the pair $(y, \pi )$ created by $\mathcal{B}$. Next, $\mathcal{B}$ runs the extractor $w' {\leftarrow }\mathcal{E}(\mathsf{prs}, \mathsf{qt}=(\mathcal{P}(\cdot , \cdot ), (\hat{\sigma }, h, x, \pi ))$, and outputs $w'$.

By correctness of $\varPi$ it holds that the pair $(y, \pi )$ returned by $\mathcal{A}_p$ satisfies $\mathsf{Ver}(\mathsf{vst}, y, \pi )=1$. Thus, by our contradiction assumption, with probability $\ge \epsilon (\lambda )$, $\mathcal{E}$ outputs $w'$ such that $(y, w') \in \mathcal{R}_{\mathcal{H}}$. Namely, $h(w')=x=h(w)$. To show that this is a collision, we argue that, information-theoretically, $w'\ne w$ with probability $\ge 1 - 1/2^{\lambda }$. This follows from the fact that w is randomly chosen of length $L(\lambda ) \ge p(\lambda ) + \ell (\lambda ) + \lambda$ and the only information about w which is leaked to $\mathcal{E}$ is through $\pi$ and $x=h(w)$, an information of length at most $p(\lambda ) + \ell (\lambda )$. Therefore there are at least $\lambda$ bits of entropy in w, from which $\Pr [w'=w] \le 2^{-\lambda }$ over the random choice of w. Hence, $\mathcal{B}$ can break the universal one-wayness of $\mathcal{H}$ with probability $\ge \epsilon (\lambda ) - 2^{-\lambda }$.    $\square$

4.3 O-SNARKs for Signing Oracles from SNARKs in the Random Oracle Model

In this section we show that it is possible to “immunize” any signature scheme in such a way that any classical SNARK is also an O-SNARK for the signing oracle corresponding to the transformed scheme. The idea is very simple and consists into applying the hash-then-sign approach using a hash function that will be modeled as a random oracle. A limitation of this result is that, since the verification algorithm uses a random oracle, in all those applications where the SNARK is used to prove knowledge of valid signatures, one would need a SNARK for $\mathsf{NP}^{\mathcal{O}}$. Hence, the best one can do is to conjecture that this still works when replacing the random oracle with a suitable hash function.

Let us now state formally our result. To this end, for any signature scheme $\varSigma$ and polynomial $Q(\cdot )$ we define $\mathcal{Z}_{Q, \varSigma }$ as the distribution on tuples $\langle \mathsf{vk}, m_1, \sigma _1, \ldots , m_{Q}, \sigma _{Q} \rangle$ obtained by running the following probabilistic algorithm:

where $\mathsf{MsgSample}(\mathcal{M}, Q)$ is an algorithm that returns Q distinct messages, each randomly chosen from $\mathcal{M}$. The proof of the following theorem appears in the full version.

Theorem 4

Let $\varSigma$ be a $\mathsf{UF\text{- }CMA}$-secure signature scheme, and $\mathcal{H}$ be a family of hash functions modeled as a random oracle. Let $\mathcal{U}_n$ be the uniform distribution over strings of length n, and $\mathcal{Z}_{Q,\varSigma }$ be the distribution defined above, where Q is any polynomial in the security parameter. Then there exists a signature scheme $\varSigma _{\mathcal{H}}$ such that every $(\mathcal{Z}, \mathcal{U}, \mathcal{Z}_{\varSigma ,Q})$-auxiliary input SNARK $\varPi$ is a $\mathcal{Z}$-auxiliary input O-SNARK for $(\mathbb O_{\mathcal{H}}, \mathbb O_{\varSigma _\mathcal{H}})$ where $\mathbb O_{\mathcal{H}}$ is a random oracle.

4.4 O-SNARKs for Signing Oracles from SNARKs

In this section we give a positive result showing that any SNARK $\varPi$ is an O-SNARK for the signing oracle of signature scheme $\varSigma$ if: (i) the message space of $\varSigma$ is appropriately bounded (to be polynomially or at most superpolynomially large); (ii) $\varPi$ tolerates auxiliary input consisting of the public key of $\varSigma$ plus a collection of signatures on randomly chosen messages; (iii) one considers O-SNARK adversaries that query the signing oracle on almost the entire message space. Furthermore, in case of superpolynomially large message spaces, one needs to assume sub-exponential hardness for $\varPi$.

The intuition behind this result is to simulate the O-SNARK adversary by using a (non-interactive) SNARK adversary that receives the public key and a set of signatures on (suitably chosen) messages as its auxiliary input. If these messages exactly match¹⁰ those queried by the O-SNARK adversary, the simulation is perfect. However, since the probability of matching exactly all the $Q = \mathsf{poly}(\lambda )$ queries may decrease exponentially in Q (making the simulation meaningless), we show how to put proper bounds so that the simulation can succeed with probability depending only on the message space size.

More formally, our result is stated as follows. Let $\varSigma$ be a signature scheme with message space $\mathcal{M}$, and let $Q := Q(\cdot )$ be a function of the security parameter. Let $\mathcal{Z}_{Q, \varSigma }$ be the following auxiliary input distribution

where $\mathsf{MsgSample}(\mathcal{M}, Q)$ is a probabilistic algorithm that returns a subset $\tilde{\mathcal{M}}\subseteq \mathcal{M}$ of cardinality Q chosen according to some strategy that we discuss later. At this point we only assume a generic strategy such that $\delta (|\mathcal{M}|, Q) = \Pr [\mathsf{MsgSample}(\mathcal{M}, Q) = \mathcal{M}^{*}]$ for any $\mathcal{M}^{*} \subseteq \mathcal{M}$ of cardinality Q. The proof is in the full version.

Theorem 5

Let $\varSigma$ be a signature scheme with message space $\mathcal{M}$, let $\mathbb O_{\varSigma }$ be the associated family of signing oracles, and let $\mathcal{Z}_{Q, \varSigma }$ be as defined above. If $\varPi$ is a $\mathcal{Z}_{Q, \varSigma }$-auxiliary input SNARK satisfying $(s, t, \epsilon )$-adaptive PoK, then $\varPi$ is an O-SNARK for $\mathbb O_{\varSigma }$ satisfying $(s', t', Q, \epsilon ')$-adaptive PoK, where $\epsilon ' = \epsilon / \delta (|\mathcal{M}|, Q)$, $s' = s - O(Q \cdot \log |\mathcal{M}|)$, and $t' = t$.

Implications of Theorem 5 . The statement of Theorem 5 is parametrized by values $|\mathcal{M}|, Q$ and the function $\delta (|\mathcal{M}|, Q)$, which in turn depends on the query guessing strategy. As for the $\mathsf{MsgSample}(\mathcal{M}, Q)$ algorithm, let us consider the one that samples a random subset $\tilde{\mathcal{M}}\subseteq \mathcal{M}$ of cardinality Q. For this algorithm we have $\delta (|\mathcal{M}|, Q) = \frac{1}{{|\mathcal{M}| \atopwithdelims ()Q}}$. Notice that $\delta (|\mathcal{M}|, Q)$ is governing the success probability of our reduction, and thus we would like this function not to become negligible. However, since $Q = \mathsf{poly}(\lambda )$ is a parameter under the choice of the adversary, it might indeed be the case that $\delta (|\mathcal{M}|, Q) \approx 2^{-Q} \approx 2^{-\lambda }$, which would make our reduction meaningless. To avoid this bad case, we restrict our attention to adversaries for which $Q = |\mathcal{M}| - c$ for some constant $c \ge 1$, i.e., adversaries that ask for signatures on the entire message but a constant number of messages. For this choice of Q we indeed have that $\delta (|\mathcal{M}|, Q) = \frac{1}{|\mathcal{M}|^{c}}$ depends only on the cardinality of $|\mathcal{M}|$. This gives us

Corollary 1

Let $\varSigma$ be a signature scheme with message space $\mathcal{M}$ where $|\mathcal{M}| = \mathsf{poly}(\lambda )$ (resp. $|\mathcal{M}| = \lambda ^{\omega (1)}$), and let $Q = |\mathcal{M}| - c$ for constant $c \in \mathbb N$. If $\varPi$ is a polynomially (resp. sub-exponentially) secure $\mathcal{Z}_{Q, \varSigma }$-auxiliary input SNARK, then $\varPi$ is an O-SNARK for $\mathbb O_{\varSigma }$ (for adversaries making Q queries).

5 Applications of O-SNARKs

In this section we show three applications of O-SNARKs for building homomorphic signatures [BF11], succinct functional signatures [BGI14], and SNARKs on authenticated data [BBFR15].

Generally speaking, our results show constructions of these primitives based on a signature scheme $\varSigma$ and a succinct non-interactive argument $\varPi$, and show their security by assuming that $\varPi$ is an O-SNARK for signing oracles corresponding to $\varSigma$. Once these results are established, we can essentially reach the following conclusions about the possible secure instantiations of these constructions. First, one can instantiate them by using Micali’s CS proofs as O-SNARK (cf. Sect. 4.1): this solution essentially yields secure instantiations in the random oracle model that work with a specific proof system (perhaps not the most efficient one in practice). Second, one can instantiate them with a classical SNARK and a hash-and-sign signature scheme (cf. Sect. 4.3), and conjecture that replacing the random oracle with a suitable hash function preserves the overall security. Third, one can instantiate the constructions using a classical SNARK construction $\varPi$ and signature scheme $\varSigma$, and then conjecture that $\varPi$ is an O-SNARK with respect to the family of signing oracles corresponding to $\varSigma$. Compared to the first solution, the last two ones have the advantage that one could use some of the recently proposed efficient SNARK schemes (e.g., [PHGR13, BSCG+13]); on the other hand these solutions have the drawback that the security of the instantiations would be heavily based on a heuristic argument. Finally, a fourth option that we provide are security proofs of these primitives which consider only non-adaptive adversaries (i.e., adversaries that declare all their queries in advance). In this case we can prove security based on non-adaptive O-SNARKs, and thus based on classical SNARKs (applying our Theorem 2). The advantage of this fourth option is that one obtains a security proof for these instantiations based on classical, not new, assumptions, although the proof holds only for a much weaker security notion.

5.1 Homomorphic Signatures

As first application of O-SNARKs we revisit a “folklore” construction of homomorphic signatures from SNARKs. This construction has been mentioned several times in the literature (e.g., [BF11, GW13, CF13, CFW14, GVW15]) and is considered as the ‘straightforward’ approach for constructing this primitive. In this section we formalize this construction, and notice that its security proof is quite subtle as one actually incurs the extraction issues that we mentioned in the introduction. Namely, one needs to run an extractor in an interactive security game in the presence of a signing oracle. Here we solve this issue by giving a simple proof based on our notion of O-SNARKs (for families of signing oracles).

Definition of Homomorphic Signatures. We begin by recalling the definition of homomorphic signatures. The definition below can be seen as the public key version of the notion of homomorphic message authenticators for labeled programs of Gennaro and Wichs [GW13].

Labeled Programs [GW13]. A labeled program consists of a tuple $\mathcal{P}=(F, \tau _1, \dots \tau _n)$ such that $F : \mathcal{M}^n \rightarrow \mathcal{M}$ is a function on n variables (e.g., a circuit), and ${\tau }_i \in \{0,1\}^{\ell }$ is the label of the i-th variable input of F. Let $F_{id}:\mathcal{M}\rightarrow \mathcal{M}$ be the canonical identity function and ${\tau }\in \{0,1\}^\ell$ be a label. We consider $\mathcal{I}_{{\tau }} = (F_{id}, {\tau })$ as the identity program for input label ${\tau }$. Given t labeled programs $\mathcal{P}_1, \dots \mathcal{P}_t$ and a function $G : \mathcal{M}^t \rightarrow \mathcal{M}$, the composed program $\mathcal{P}^*$ is the one obtained by evaluating G on the outputs of $\mathcal{P}_1, \dots \mathcal{P}_t$, and is compactly denoted as $\mathcal{P}^* = G(\mathcal{P}_1, \dots \mathcal{P}_t)$. The labeled inputs of $\mathcal{P}^*$ are all distinct labeled inputs of $\mathcal{P}_1, \dots \mathcal{P}_t$, i.e., all inputs with the same label are grouped together in a single input of the new program.

Definition 8 (Homomorphic Signatures for Labeled Programs)

A homomorphic signature scheme $\mathsf{HomSig}$ is a tuple of probabilistic, polynomial-time algorithms $(\mathsf{HomKG}, \mathsf{HomSign}, \mathsf{HomVer}, \mathsf{HomEval})$ that work as follows  

$\mathsf{HomKG}(1^\lambda )$ :

takes a security parameter $\lambda$ and outputs a public key $\mathsf{VK}$ and a secret key $\mathsf{SK}$. The public key $\mathsf{VK}$ defines implicitly a message space $\mathcal{M}$, the label space $\mathcal{L}$, and a set $\mathcal{F}$ of admissible functions.

$\mathsf{HomSign}(\mathsf{SK}, \tau , m)$ :

takes a secret key $\mathsf{SK}$, a (unique) label $\tau \in \mathcal{L}$ and a message $m \in \mathcal{M}$, and it outputs a signature $\sigma$.

$\mathsf{HomEval}(\mathsf{VK}, F, (\sigma _1, \dots \sigma _n))$ :

takes a public key $\mathsf{VK}$, a function $F \in \mathcal{F}$ and a tuple of signatures $(\sigma _1, \dots \sigma _n)$. It outputs a new signature $\sigma$.

$\mathsf{HomVer}(\mathsf{VK}, \mathcal{P}, m, \sigma )$ :

takes a public key $\mathsf{VK}$, a labeled program $\mathcal{P}= (F, (\tau _1 \dots \tau _n))$ with $F \in \mathcal{F}$, a message $m \in \mathcal{M}$, and a signature $\sigma$. It outputs either 0 (reject) or 1 (accept).

  and satisfy authentication correctness, evaluation correctness, succinctness, and security, as described below.

• Authentication Correctness. Informally, we require that signatures generated by $\mathsf{HomSign}(\mathsf{SK}, \tau , m)$ verify correctly for m as the output of the identity program $\mathcal{I}=(F_{id}, \tau )$.

• Evaluation Correctness. Intuitively, we require that running the evaluation algorithm on signatures $(\sigma _1, \dots \sigma _n)$, where $\sigma _i$ is a signature for $m_i$ on label $\tau _i$, produces a signature $\sigma$ which verifies for $F(m_1, \dots m_n)$.

• Succinctness. For every large enough security parameter $\lambda \in \mathbb N$, there is a polynomial $p(\cdot )$ such that for every $(\mathsf{SK}, \mathsf{VK}) {\leftarrow }\mathsf{HomKG}(1^\lambda )$ the output size of $\mathsf{HomSign}$ and $\mathsf{HomEval}$ is bounded by $p(\lambda )$ for any choice of their inputs.

• Security. A homomorphic signature scheme $\mathsf{HomSig}$ is secure if for every PPT adversary $\mathcal{A}$ there is a negligible function $\epsilon$ such that $\Pr [\mathbf {Exp}^\mathsf{HomSig\text{- }UF}_{\mathcal{A}, \mathsf{HomSig}}(\lambda ) = 1] \le \epsilon (\lambda )$ where the experiment $\mathbf {Exp}^\mathsf{HomSig\text{- }UF}_{\mathcal{A}, \mathsf{HomSig}}(\lambda )$ is described in the following:

  • Key generation: Run $(\mathsf{VK},\mathsf{SK}) {\leftarrow }\mathsf{HomKG}(1^\lambda )$ and give $\mathsf{VK}$ to $\mathcal{A}$.

  • Signing queries: $\mathcal{A}$ can adaptively submit queries of the form $(\tau , m)$, where $\tau \in \mathcal{L}$ and $m \in \mathcal{M}$. The challenger initializes an empty list T and proceeds as follows:

    • * If $(\tau , m)$ is the first query with label $\tau$, then the challenger computes $\sigma {\leftarrow }\mathsf{HomSign}(\mathsf{SK}, \tau ,m)$, returns $\sigma$ to $\mathcal{A}$ and updates the list of queries $T {\leftarrow }T \;\cup \;\lbrace (\tau ,m)\rbrace$.

    • * If $(\tau , m) \in T$ (i.e., the adversary had already queried the tuple $(\tau , m)$), then the challenger replies with the same signature generated before.

    • * If T contains a tuple $(\tau , m_0)$ for some different message $m_0 \ne m$, then the challenger ignores the query.

    Note that each label $\tau$ can be queried only once.

  • Forgery: After the adversary is done with the queries of the previous stage, it outputs a tuple $(\mathcal{P}^*, m^*, \sigma ^*)$. Finally, the experiment outputs 1 iff the tuple returned by the adversary is a forgery (as defined below). Forgeries are tuples $(\mathcal{P}^*=(F^*, (\tau ^*_1, \dots \tau ^*_n)), m^*, \sigma ^*)$ such that $\mathsf{HomVer}( \mathsf{VK}, \mathcal{P}^*, m^*, \sigma ^*)=1$ and they satisfy one the following conditions:

    • * Type 1 Forgery: There is $i \in [n]$ such that $(\tau _i^*, \cdot ) \notin T$ (i.e., no message m has ever been signed w.r.t. label $\tau _i^*$ during the experiment).

    • * Type 2 Forgery: All labels $\tau _i^*$ have been queried—$\forall i \in [n], (\tau _i^*, m_i) \in T$—but $m^* \ne F^*(m_1, \dots m_n)$ (i.e., $m^*$ is not the correct output of the labeled program $\mathcal{P}^*$ when executed on the previously signed messages.

A homomorphic signature scheme can also be required to be context-hiding [BF11]. Intuitively this property says that signatures on outputs of functions do not reveal information about the inputs. The formal definition is recalled in the full version.

Homomorphic Signatures from O-SNARKs. To build the homomorphic signature we use a regular signature scheme $\varSigma$ and a fully-succinct O-SNARK $\varPi$ for NP. The resulting scheme is homomorphic for all functions F whose running time is upper bounded by some fixed polynomial $t_{\mathcal{F}}(\cdot )$, and the scheme is 1-hop, i.e., it is not possible to apply $\mathsf{HomEval}$ on signatures obtained from other executions of $\mathsf{HomEval}$.¹¹

Defining the machine $M_{\varSigma ,F}$. Let $\varSigma$ be a signature scheme, and F be the description of a function $F: \mathcal{X}^{n} \rightarrow \mathcal{X}$ where $\mathcal{X}$ is some appropriate domain (e.g., $\mathcal{X}=\{0,1\}^{\mu }$). Then $M_{\varSigma ,F}(x, w)$ is the random-access machine that works as follows. It takes inputs (x, w) where values x are of the form $x = (\mathsf{vk}, m, {\tau }_1, \ldots , {\tau }_n)$ where $\mathsf{vk}$ is a public key of the scheme $\varSigma$, $m \in \mathcal{X}$ is a message and ${\tau }_i \in \{0,1\}^{\ell }$ are labels, for $1 \le i \le n$. The values w are instead tuples $w = (m_1, \sigma _1, \ldots , m_n, \sigma _n)$ where for every $i \in [n]$, $m_i \in \mathcal{X}$ is a message and $\sigma _i$ is a signature of the scheme $\varSigma$. On input such a pair (x, w), $M_{\varSigma ,F}(x,w)$ accepts iff

$$m = F(m_1, \ldots , m_n) \; \wedge \; \mathsf{vfy}(\mathsf{vk}, {\tau }_i | m_i, \sigma _i) = 1, \forall i = 1, \ldots , n$$

Associated to such machine there is also a polynomial time bound $t_{\varSigma ,\mathcal{F}}(k) = k^{e_{\varSigma ,\mathcal{F}}}$, such that $M_{\varSigma ,F}$ rejects if it does more than $t_{\varSigma ,F}(|x|)$ steps. Finally, we note that given a polynomial bound $t_{\mathcal{F}}(k) = k^{e_{\mathcal{F}}}$ on the running time of every F supported by the scheme, a polynomial bound $t_{\varSigma }(k)=k^{e_{\varSigma }}$ on the running time of $\varSigma$’s verification algorithm, and values $n, \mu , \ell$, one can efficiently deduce the constant exponent $e_{\varSigma ,\mathcal{F}}$ for the time bound $t_{\varSigma ,\mathcal{F}}(|x|) = |x|^{e_{\varSigma ,\mathcal{F}}}$.

We call $\mathcal{R}_{\varSigma }$ the $\mathsf{NP}$ binary relation consisting of all pairs (y, w) such that, parsing $y = (M_{\varSigma ,F}, x, t)$, $M_{\varSigma ,F}(x, w)$ accepts in at most t steps and $t \le t_{\varSigma ,\mathcal{F}}(|x|)$.

The construction. Let $\varSigma = (\mathsf{kg}, \mathsf{sign}, \mathsf{vfy})$ be a signature scheme and $\varPi =(\mathsf{Gen}, \mathsf{Prove}, \mathsf{Ver})$ be a fully-succinct O-SNARK for $\mathsf{NP}$. The homomorphic signature scheme $\mathsf{HomSig} [\varSigma , \varPi ]$ is defined as follows.

 

$\mathsf{HomKG}(1^{\lambda }){:}$ :

Run $(\mathsf{sk}, \mathsf{vk}) {\leftarrow }\mathsf{kg}(1^{\lambda })$ and $\mathsf{crs}{\leftarrow }\mathsf{Gen}(1^{\lambda })$. Define $\mathsf{SK}= \mathsf{sk}$ and $\mathsf{VK}=(\mathsf{vk}, \mathsf{crs})$. Let the message be $\mathcal{M}= \{0,1\}^{\mu }$ and the label space be $\mathcal{L}= \{0,1\}^{\ell }$. Output $(\mathsf{SK},\mathsf{VK})$.

$\mathsf{HomSign}(\mathsf{SK}, \tau , m){:}$ :

Run $\sigma {\leftarrow }\mathsf{sign}(\mathsf{sk}, {\tau }|m)$. Output $\bar{\sigma }=(signature, ({\tau }, m, \sigma ))$.

$\mathsf{HomEval}(\mathsf{VK}, m, F, (\bar{\sigma }_1, \ldots , \bar{\sigma }_n)) {:}$ :

Parse every $\bar{\sigma }_i=(signature, ({\tau }_i, m_i, \sigma _i))$, compute $m = F(m_1, \ldots , m_n)$, reconstruct an instance $y=(M_{\varSigma ,F}, x, t)$ where $x=(\mathsf{vk}, m, {\tau }_1, \ldots , {\tau }_n)$ and $t = |x|^{e_{\varSigma ,\mathcal{F}}}$, and the witness $w=(m_1, \sigma _1, \ldots , m_n, \sigma _n)$. Finally, run $\pi {\leftarrow }\mathsf{Prove}(\mathsf{crs}, y, w)$ and output $\bar{\sigma }=(proof, \pi )$.

$\mathsf{HomVer}(\mathsf{VK}, \mathcal{P}=(F, (\tau _1, \dots \tau _n)), m, \bar{\sigma }){:}$ :

Parse the signature $\bar{\sigma }=(flag, \cdot )$ and output the bit b computed as follows:

If $\bar{\sigma }=(signature, ({\tau }, m, \sigma ))$ and $\mathcal{P}=\mathcal{I}=(F_{id}, {\tau })$ run $\mathsf{vfy}(\mathsf{vk},{\tau }| m, \sigma ) \rightarrow b$.

If $\bar{\sigma }=(proof, \pi )$ run $\mathsf{Ver}_{e_{\varSigma ,\mathcal{F}}}(\mathsf{crs}, y, \pi ) \rightarrow b$ where $y=(M_{\varSigma ,F}, x =(\mathsf{vk}, m, {\tau }_1, \ldots , {\tau }_n), |x|^{e_{\varSigma ,\mathcal{F}}})$.

Recall that in a SNARK for $\mathsf{NP}$, $\mathsf{Ver}_{c}$ is given a constant $c>0$ and only works for relation $\mathcal{R}_{c}$.

  In what follows we show that the scheme above is a homomorphic signature. Correctness follows from the correctness of $\varSigma$ and $\varPi$, while succinctness is implied by that of $\varPi$. More precise arguments are given in the full version.

Security. As in Sect. 4.2, for every signature scheme $\varSigma = (\mathsf{kg}, \mathsf{sign}, \mathsf{vfy})$ we denote by $\mathbb O_{\varSigma }$ the family of oracles $\mathcal{O}(m) = \mathsf{sign}(\mathsf{sk}, m)$ (where the verification key is returned as output of a special query $\mathcal{O}(`vk')$). We show the security of the scheme $\mathsf{HomSig} [\varSigma , \varPi ]$ via the following theorem. The proof is in the full version.

Theorem 6

Let $\varSigma$ be a signature scheme. If $\varPi$ is an O-SNARK for $\mathbb O_{\varSigma }$, and $\varSigma$ is $\mathsf{UF\text{- }CMA}$-secure, then $\mathsf{HomSig} [\varSigma , \varPi ]$ is a secure homomorphic signature scheme.

Non-adaptive Security. Alternatively, one can modify the previous proof to show that the scheme has security against homomorphic signature adversaries that make non-adaptive signing queries, assuming the weaker assumption that $\varPi$ is a non-adaptive O-SNARK (see Definition 7). In particular, combining this change with the result of Theorem 2 one obtains the following:

Theorem 7

If $\varPi$ is a SNARK, and $\varSigma$ is a $\mathsf{UF\text{- }CMA}$-secure signature scheme, then $\mathsf{HomSig} [\varSigma , \varPi ]$ is secure against adversaries that make non-adaptive signing queries.

Remark 3

(On the applicability of Corollary 1 ). We note that we cannot combine the positive result of Corollary 1 with Theorem 6 to conclude that the security of the homomorphic signature scheme holds under classical SNARKs. The inapplicability of Corollary 1 is due to its restriction for which adversaries have to query almost the entire message space. By looking at the $\mathsf{HomSig}$ construction (and the definition of homomorphic signatures too) one can note that an adversary who queries almost the entire message space of the underlying signature scheme can trivially break the security (for example he could obtain signatures on two distinct messages under the same label).

Insecurity of $\mathsf{HomSig}$ . In the full version we show that the generic homomorphic signature construction $\mathsf{HomSig}$ is not (adaptive) secure for an arbitrary choice of the signature scheme $\varSigma$. This insecurity result does not contradict our Theorem 6, but is closely related with (and confirms) our impossibility of O-SNARKs for any signing oracles (Theorem 3).

5.2 Succinct Functional Signatures

As second application of O-SNARKs we revisit the construction of succinct functional signatures of Boyle, Goldwasser, and Ivan [BGI14]. In [BGI14] this construction is proven secure using a notion of SNARKs which significantly differs from the standard one [BCC+14]. To the best of our knowledge, there are no known instantiations of SNARKs under this definition, in the standard model (and is not clear whether it is possible to find some). On the other hand, if one wants to prove the security of this construction using the classical SNARK definition, the security proof incurs the same subtleties related to running an extractor in the presence of a signing oracle.

In this section, we revisit the construction of [BGI14], and we prove its security using O-SNARKs. Interestingly, this proof differs a little from the one of homomorphic signature as here we have to consider O-SNARKs for multiple signing oracles.

Definition 9

(Functional Signatures [BGI14]). A functional signature scheme $\mathsf{FS}$ for a message space $\mathcal{M}$ and function family $\mathcal{F}=\lbrace f:\mathcal{D}_f \rightarrow \mathcal{M}\rbrace$ is a tuple of probabilistic, polynomial-time algorithms $(\mathsf{FS.Setup}, \mathsf{FS.KeyGen}, \mathsf{FS.Sign}, \mathsf{FS.Ver})$ that work as follows

 

$\mathsf{FS.Setup}(1^\lambda )$ :

takes a security parameter $\lambda$ and outputs a master verification key $\mathsf{mvk}$ and a master secret key $\mathsf{msk}$.

$\mathsf{FS.KeyGen}(\mathsf{msk}, f)$ :

takes the master secret key $\mathsf{msk}$ and a function $f \in \mathcal{F}$ (represented as a circuit) and it outputs a signing key $\mathsf{sk}_f$ for f.

$\mathsf{FS.Sign}(\mathsf{mvk}, f, \mathsf{sk}_f, m)$ :

takes as input a function $f \in \mathcal{F}$, a signing key $\mathsf{sk}_f$, and a message $m \in \mathcal{D}_f$, and it outputs $(f(m), \sigma )$.

$\mathsf{FS.Ver}(\mathsf{mvk}, m^*, \sigma )$ :

takes as input the master verification key $\mathsf{mvk}$, a message $m^* \in \mathcal{M}$ and a signature $\sigma$, and outputs either 1 (accept) or 0 (reject).

  and satisfy correctness, unforgeability, and function privacy as described below.

• Correctness. A functional signature scheme is correct if the following holds with probability 1:

  $$\forall f \in \mathcal{F}, \ \forall m \in \mathcal{D}_f, \ (\mathsf{msk}, \mathsf{mvk}) \leftarrow \mathsf{FS.Setup}(1^\lambda ), \ \mathsf{sk}_f \leftarrow \mathsf{FS.KeyGen}(\mathsf{msk}, f), $$
  $$ (m^*,\sigma ) \leftarrow \mathsf{FS.Sign}(\mathsf{mvk}, f, \mathsf{sk}_f, m), \mathsf{FS.Ver}(\mathsf{mvk}, m^*, \sigma ) = 1 $$

• Unforgeablity. A functional signature scheme is unforgeable if for every PPT adversary $\mathcal{A}$ there is a negligible function $\epsilon$ such that $\Pr [\mathbf {Exp}^\mathsf{FS\text{- }UF}_{\mathcal{A}, \mathsf{FS}}(\lambda ) = 1] \le \epsilon (\lambda )$ where the experiment $\mathbf {Exp}^\mathsf{FS\text{- }UF}_{\mathcal{A}, \mathsf{FS}}(\lambda )$ is described in the following:

  • Key generation: Generate $(\mathsf{msk}, \mathsf{mvk}) \leftarrow \mathsf{FS.Setup}(1^\lambda )$, and gives $\mathsf{mvk}$ to $\mathcal{A}$.

  • Queries: The adversary is allowed to adaptively query a key generation oracle $\mathcal O_{\mathsf {key}}$ and a signing oracle $\mathcal O_{\mathsf {sign}}$, that share a dictionary D indexed by tuples $(f, i) \in \mathcal{F}\times \mathbb {N}$, whose entries are signing keys. For answering these queries, the challenger proceeds as follows:

    • $\bullet$ $\mathcal O_{\mathsf {key}}$ (f, i):

      • * If $(f, i) \in D$ (i.e., the adversary had already queried the tuple (f, i)), then the challenger replies with the same key $\mathsf{sk}_f^i$ generated before.

      • * Otherwise, generate a new $\mathsf{sk}_f^i \leftarrow \mathsf{FS.KeyGen}(\mathsf{msk},f)$, add the entry $(f,i) \rightarrow \mathsf{sk}_f^i$ in D, and return $\mathsf{sk}_f^i$.

    • $\bullet$ $\mathcal O_{\mathsf {sign}}$ (f, i, m):

      • * If there is an entry for the key (f, i) in D, then the challenger generates a signature on f(m) using this key, i.e., $\sigma \leftarrow \mathsf{FS.Sign}(\mathsf{mvk}, f, \mathsf{sk}_f^i, m)$.

      • * Otherwise, generate a new key $\mathsf{sk}_f^i \leftarrow \mathsf{FS.KeyGen}(\mathsf{msk},f)$, add an entry $(f,i) \rightarrow \mathsf{sk}_f^i$ to D, and generate a signature on f(m) using this key, i.e., $\sigma \leftarrow \mathsf{FS.Sign}(\mathsf{mvk}, f, \mathsf{sk}_f^i, m)$.

  • Forgery: After the adversary is done with its queries, it outputs a pair $(m^*, \sigma )$, and the experiment outputs 1 iff the following conditions hold

    • * $\mathsf{FS.Ver}(\mathsf{mvk}, m^*, \sigma )=1$.

    • * there does not exist m such that $m^* = f(m)$ for any f which was sent as a query to the $\mathcal O_{\mathsf {key}}$ oracle.

    • * there does not exist a pair (f, m) such that (f, m) was a query to the $\mathcal O_{\mathsf {sign}}$ oracle and $m^*= f(m)$.

• Function privacy. Intuitively, function privacy requires that the distribution of signatures on a message m that are generated via different keys $\mathsf{sk}_f$ should be computationally indistinguishable, even given the secret keys and master signing key. See [BGI14] or the full version for a more formal definition.

Definition 10 (Succinct Functional Signatures)

A functional signature scheme is called succinct if there exists a polynomial $s(\cdot )$ such that, for every security parameter $\lambda \in \mathbb N$, $f \in \mathcal{F}$, $m \in \mathcal{D}_{f}$, it holds with probability 1 over $(\mathsf{mvk}, \mathsf{msk}) \leftarrow \mathsf{FS.Setup}(1^\lambda )$, $\mathsf{sk}_{f} \leftarrow \mathsf{FS.KeyGen}(\mathsf{msk}, f)$, $(f(m), \sigma ) \leftarrow \mathsf{FS.Sign}(\mathsf{sk}_{f}, m)$ that $|\sigma | \le s(\lambda , |f(m)|)$. In particular, the size of $\sigma$ is independent of the function’s size, |f|, and the function’s input size, |m|.

Succinct Functional Signatures from O-SNARKs. In the following we show a construction for message space $\mathcal{M}$ and family of functions $\mathcal{F}= \{f: \mathcal{D}_f \rightarrow \mathcal{M}\}$ whose running time is bounded by some fixed polynomial $t_{\mathcal{F}}(|m|)$. To build the scheme, we use two $\mathsf{UF\text{- }CMA}$-secure signature schemes, $\varSigma _0=(\mathsf{kg}_0, \mathsf{sign}_0, \mathsf{vfy}_0)$ for message space $\mathcal{M}_0$ and $\varSigma '=(\mathsf{kg}', \mathsf{sign}', \mathsf{vfy}')$ for message space $\mathcal{D}$, together with a fully succinct zero-knowledge O-SNARK $\varPi =(\mathsf{Gen}, \mathsf{Prove}, \mathsf{Ver})$ for the $\mathsf{NP}$ language L defined below. While in [BGI14] a single signature scheme is used, we prefer to use two different ones as this allows for a more precise statement since we will need to apply different restrictions to $\mathcal{M}_0$ and $\mathcal{D}$ to obtain a precise proof.

Defining the relation $\mathcal{R}_{L}$. Let $M_{L}$ be a random-access machine as defined below, and $t_{L}(k) = k^{e_{L}}$ be a polynomial. $\mathcal{R}_{L}$ is the binary relation consisting of all pairs (y, w) such that, parsing $y = (M_{L}, x, t)$, $M_{L}(x, w)$ accepts in at most t steps and $t \le t_{L}(|x|)$. The values x are of the form $x = (m^{*}, \mathsf{mvk}_0)$ where $\mathsf{mvk}_0$ is a public key of the scheme $\varSigma _0$, and $m^{*} \in \mathcal{M}$ is a message. The values w are instead tuples $w = (m, f, \mathsf{vk}', \sigma _{\mathsf{vk}'}, \sigma _m)$ such that $m \in \mathcal{D}_f$ with $\mathcal{D}_f \subset \mathcal{D}$, and $\sigma _{\mathsf{vk}'}$, $\sigma _m$ are signatures for the schemes $\varSigma _0$ and $\varSigma '$ respectively. On input such a pair (x, w), $M_{L}(x,w)$ is the random-access machine that accepts iff the following conditions (1), (2) and (3) hold:

• (1) $m^* = f(m)$

• (2) $\mathsf{vfy}'(\mathsf{vk}', m, \sigma _m) = 1$

• (3) $\mathsf{vfy}_0(\mathsf{mvk}_0, f|\mathsf{vk}', \sigma _{\mathsf{vk}'}) = 1$

Given polynomial bounds on the running times of verification algorithms $\mathsf{vfy}'$ and $\mathsf{vfy}_0$, and a (fixed) bound $t_{\mathcal{F}}(\cdot )$ on the size and running time of every $f \in \mathcal{F}$, one can deduce a polynomial time bound $t_{L}(|x|) = |x|^{e_{L}}$ for the machine $M_L$.

The construction. Using the signature schemes $\varSigma _0,\varSigma '$ and a fully-succinct zero-knowledge O-SNARK $\varPi$ for $\mathsf{NP}$, we construct the functional signature scheme $\mathsf{FS} [\varSigma _0, \varSigma ', \varPi ]= (\mathsf{FS.Setup}, \mathsf{FS.KeyGen}, \mathsf{FS.Sign}, \mathsf{FS.Ver})$ as follows:  

$\mathsf{FS.Setup}(1^\lambda ){:}$ :

This probabilistic algorithm takes a security parameter $\lambda$ and outputs a master verification key $\mathsf{mvk}$ and a master secret key $\mathsf{msk}$:

Generate $(\mathsf{msk}_0, \mathsf{mvk}_0) \leftarrow \mathsf{kg}_0(1^{\lambda })$, $\mathsf{crs}\leftarrow \mathsf{Gen}(1^{\lambda })$. Set the master secret key $\mathsf{msk}= \mathsf{msk}_0$, and the master verification key $\mathsf{mvk}= (\mathsf{mvk}_0, \mathsf{crs})$.

$\mathsf{FS.KeyGen}(\mathsf{msk}, f){:}$ :

This algorithm takes the master secret key $\mathsf{msk}$ and a function $f \in \mathcal{F}$ (represented as a circuit) and it outputs a signing key $\mathsf{sk}_f$ for f.

Generate a new key pair $(\mathsf{sk}', \mathsf{vk}') \leftarrow \mathsf{kg}'(1^{\lambda })$ for the scheme $\varSigma '$, compute $\sigma _{\mathsf{vk}'} \leftarrow \mathsf{sign}_0(\mathsf{msk}_0, f|\mathsf{vk}')$, and let the certificate c be $c = (f, \mathsf{vk}', \sigma _{\mathsf{vk}'})$. Finally output $\mathsf{sk}_f = (\mathsf{sk}', c)$.

$\mathsf{FS.Sign}(\mathsf{mvk}, f, \mathsf{sk}_f, m){:}$ :

The algorithm takes as input a function $f \in \mathcal{F}$, a signing key $\mathsf{sk}_f$, and a message $m \in \mathcal{D}_f$, and it outputs $(f(m), \pi )$ where $\pi$ represents a signature on f(m).

Parse $\mathsf{sk}_f$ as $(\mathsf{sk}', c = (f, \mathsf{vk}', \sigma _{\mathsf{vk}'}))$, generate $\sigma _m \leftarrow \mathsf{sign}'(\mathsf{sk}',m)$, set $y=(M_{L}, x, t)$ with $x=(\mathsf{mvk}_0, f(m))$, $t = |x|^{e_{L}})$, and $w=(m, f, \mathsf{vk}', \sigma _{\mathsf{vk}'}, \sigma _m)$. Run $\pi {\leftarrow }\mathsf{Prove}(\mathsf{crs}, y, w)$ and output $(m^*=f(m), \pi )$.

$\mathsf{FS.Ver}(\mathsf{mvk}, m^*, \pi ){:}$ :

This algorithms takes as input the master verification key $\mathsf{mvk}$, a message $m^* \in \mathcal{M}$ and a signature $\pi$, and outputs either 1 (accept) or 0 (reject):

Parse $\mathsf{mvk}= (\mathsf{mvk}_0, \mathsf{crs})$ and set $y=(M_{L}, x, t)$ with $x=(\mathsf{mvk}_0, m^*)$ and $t = |x|^{e_{L}}$. Then output the same bit returned by $\mathsf{Ver}_{e_{L}}(\mathsf{crs}, y ,\pi )$.

 

Correctness. It is not hard to see that as long as $\varSigma _0, \varSigma '$ and $\varPi$ are correct, then $\mathsf{FS}$ is also correct.

Succinctness. Intuitively, a functional signature is succinct if the size of any signature depends only on the size of functions’ outputs (and the security parameter). In the above construction this property immediately follows from the succinctness of $\varPi$.

Unforgeability. We prove the security of $\mathsf{FS}$ under the unforgeability of schemes $\varSigma _0$ and $\varSigma '$ and using the notion of O-SNARKs for a specific family of oracles $\mathbb O_{\mathsf{m\varSigma },Q}$ that we define below.

$\mathbb O_{\mathsf{m\varSigma },Q}$ is parametrized by the algorithms of the signature schemes $\varSigma _0$, $\varSigma '$ and by a polynomial $Q = Q(\lambda )$. Every member $\mathcal{O}$ of $\mathbb O_{\mathsf{m\varSigma },Q}$ is described by a set of secret keys $\mathsf{msk}_0, \mathsf{sk}'_1, \ldots , \mathsf{sk}'_{Q}$ (i.e., the process of sampling $\mathcal{O}\leftarrow \mathbb O$ consists of running $(\mathsf{mvk}_0, \mathsf{msk}_0) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{kg}_0(1^{\lambda })$ and $(\mathsf{vk}'_i, \mathsf{sk}'_i) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{kg}'_1(1^{\lambda }), \forall i \in [Q]$). The oracle $\mathcal{O}$ works as follows:

$$ \mathcal{O}(i,`vk') = {\left\{ \begin{array}{ll} \mathsf{mvk}_0&{} \text {If } i=0, \\ \mathsf{vk}'_i &{} \text {otherwise}. \end{array}\right. } \quad \mathcal{O}(i,`sk') = {\left\{ \begin{array}{ll} \bot &{} \text {If } i=0, \\ \mathsf{sk}'_i &{} \text {otherwise}. \end{array}\right. } $$

$$ \mathcal{O}(i,m) = {\left\{ \begin{array}{ll} (\mathsf{Cnt}, \mathsf{sign}_0(\mathsf{msk}_0,m | \mathsf{vk}'_\mathsf{Cnt})), \mathsf{Cnt}{\leftarrow }\mathsf{Cnt}+1 &{} \text {If } i=0 \text { and } \mathsf{Cnt}\le Q, \\ \bot &{} \text {If } i=0 \text { and } \mathsf{Cnt}> Q, \\ \mathsf{sign}'(\mathsf{sk}'_i,m) &{} \text {otherwise}. \end{array}\right. } \quad $$

For the sake of simplicity we compactly denote $\mathcal{O}_0(\cdot ) = \mathcal{O}(0, \cdot )$ and $\mathcal{O}'_i(\cdot ) = \mathcal{O}(i, \cdot )$ for all $i>0$. From the above description, note that oracle $\mathcal{O}_0$ is stateful and we assume it starts with $\mathsf{Cnt}=1$.

Finally, we point out that for some technical reasons that we mention in Remark 5 at the end of this section, it is not possible to use the notion of O-SNARK for a single signing oracle to prove the security of the functional signature scheme. This is the reason why we explicitly considered O-SNARKs for this more complex family of multiple signing oracles.

Theorem 8

If $\varPi$ is an O-SNARK for $\mathbb O_{\mathsf{m\varSigma },Q}$ for every $Q = \mathsf{poly}(\lambda )$, and $\varSigma _0, \varSigma '$ are $\mathsf{UF\text{- }CMA}$-secure, then $\mathsf{FS} [\varSigma _0,\varSigma ',\varPi ]$ is an unforgeable functional signature.

Our proof consists of the following two steps:

• 1. We show that for every successful $\mathcal{A}_{\mathsf {FS}}$ against the unforgeability of $\mathsf{FS}$ there exists an O-SNARK adversary $\tilde{\mathcal{A}}$ for an oracle from $\mathbb O_{\mathsf{m\varSigma },Q}$ such that $\tilde{\mathcal{A}}$ outputs a valid proof with the same (non-negligible) probability of success of $\mathcal{A}_{\mathsf {FS}}$. By the adaptive proof of knowledge for $\mathbb O_{\mathsf{m\varSigma },Q}$ we then obtain that for such $\tilde{\mathcal{A}}$ there exists a suitable extractor $\mathcal{E}_{\tilde{\mathcal{A}}}$ that outputs a valid witness with all but negligible probability.

• 2. From the previous point, considering adversary $\tilde{\mathcal{A}}$ and the corresponding extractor, we can partition adversary-extractor pairs in two types: (1) those that yield a witness w containing a pair $(f, \mathsf{vk}')$ that was never signed before, and (2) those that yield w containing $(f, \mathsf{vk}')$ that was signed before. We show that adversaries of type (1) can be used to break the security of the signature scheme $\varSigma _0$, whereas adversaries of type (2) can be used to break the security of $\varSigma '$.

For lack of space the complete proof appears in the full version, where we also show that the scheme has function privacy.

Non-adaptive Unforgeability. Similarly to the homomorphic signature case, it is possible to show that the functional signature scheme achieves security against (functional signature) adversaries that make non-adaptive signing queries (i.e., all queries are declared at the beginning of the game). This weaker security can be proven assuming that $\varPi$ is a non-adaptive O-SNARK (see Definition 7). Combining this change with the result of Theorem 2 we obtain the following:

Theorem 9

If $\varPi$ is a SNARK and $\varSigma _0, \varSigma '$ are $\mathsf{UF\text{- }CMA}$-secure signature schemes, then $\mathsf{FS} [\varSigma _0,\varSigma ',\varPi ]$ is a functional signature where unforgeability holds against adversaries that make non-adaptive signing queries.

Remark 4

(On the applicability of Corollary 1 ). For the same reasons discussed in Remark 3, it is not possible to apply the result of Corollary 1 to conclude the that the (adaptive) security of the functional signature scheme holds under classical SNARKs.

Remark 5 (On the use of multiple signing oracles)

In order to prove the security of the functional signature scheme, one might be tempted to use the notion of O-SNARK with a single signing oracle. Precisely, one might use O-SNARKs for $\mathbb O_{\varSigma _0}$ when making a reduction to $\varSigma _0$ and O-SNARKs for $\mathbb O_{\varSigma '}$ when making a reduction to $\varSigma '$. Unfortunately, this approach does not work for an intricate technical reason that we explain here. Intuitively, assume that one wants to build an O-SNARK adversary $\tilde{\mathcal{A}}$ that has access to a single signing oracle, say from $\mathbb O_{\varSigma _0}$. Then the secret keys needed to simulate all the other oracles have to be given to $\tilde{\mathcal{A}}$ as part of its auxiliary input ($\tilde{\mathcal{A}}$ needs them to simulate $\mathcal{A}_{\mathsf {FS}}$). At this point the issue is that such secret keys in fact give an efficient way to compute a witness for several y in the relation $\mathcal{R}_L$. Therefore, if the extractor gets these secret keys as auxiliary information, we then have no guarantee that, while doing a reduction to the unforgeability of the signature scheme, the extractor will output a witness of the form we expect.

5.3 SNARKs on Authenticated Data

As another application of O-SNARKs we consider the generic construction of SNARKs on authenticated data that is given in [BBFR15]. Since this construction is very similar to the homomorphic signature scheme that we present in Sect. 5.1, we only provide an informal discussion of this application. In [BBFR15] Backes et al. introduce the notion of SNARKs on authenticated data to capture in an explicit way the possibility of performing (zero-knowledge) proofs about statements that are authenticated by third parties, i.e., to prove that $(x, w) \in \mathcal{R}$ for some x for which there is a valid signature. While the main focus of that work is on a concrete construction based on quadratic arithmetic programs, the authors also show a generic construction based on SNARKs and digital signatures. Roughly speaking, this construction consists in letting the prover use a SNARK to prove a statement of the form “$\exists x, w, \sigma : (x,w) \in \mathcal{R}\wedge \mathsf{vfy}(\mathsf{vk}, {\tau }|x, \sigma )=1$”, for some public label ${\tau }$ of the statement. The formalization of their model is rather similar to that of homomorphic signatures in this paper (e.g., they also use labels). Noticeable differences are that their construction uses pre-processing SNARKs for arithmetic circuit satisfiability, and that to handle several functions they use different SNARK instantiations (one per function).

In [BBFR15] the security proof of this generic construction is only sketched, and in particular they use the existence of an extractor for an adversary that interacts with a signing oracle without providing a particular justification on its existence. With a more careful look, it is possible to see that this security proof incurs the same issue of extraction in the presence of oracles. Using the same techniques that we developed in this paper for the homomorphic signature scheme,¹² it is possible to prove the security of that generic construction using O-SNARKs for signing oracles (or non-adaptive security based on classical SNARKs). In conclusion, for this construction one can either conjecture that a specific SNARK scheme (e.g., [PHGR13]) is secure in the presence of oracles, or, more conservatively, argue only the non-adaptive security of the primitive under the existence of classical SNARKs.