Abstract
A central problem in differential privacy is to accurately answer a large family Q of statistical queries over a data universe X. A statistical query on a dataset \(D \in X^n\) asks “what fraction of the elements of D satisfy a given predicate p on X?” Ignoring computational constraints, it is possible to accurately answer exponentially many queries on an exponential size universe while satisfying differential privacy (Blum et al., STOC’08). Dwork et al. (STOC’09) and Boneh and Zhandry (CRYPTO’14) showed that if both Q and X are of polynomial size, then there is an efficient differentially private algorithm that accurately answers all the queries. They also proved that if Q and X are both exponentially large, then under a plausible assumption, no efficient algorithm exists.
We show that, under the same assumption, if either the number of queries or the data universe is of exponential size, then there is no differentially private algorithm that answers all the queries. Specifically, we prove that if one-way functions and indistinguishability obfuscation exist, then:
-
1.
For every n, there is a family Q of \({\tilde{O}}(n^7)\) queries on a data universe X of size \(2^d\) such that no \(\mathrm {poly}(n,d)\) time differentially private algorithm takes a dataset \(D \in X^n\) and outputs accurate answers to every query in Q.
-
2.
For every n, there is a family Q of \(2^d\) queries on a data universe X of size \({\tilde{O}}(n^7)\) such that no \(\mathrm {poly}(n,d)\) time differentially private algorithm takes a dataset \(D \in X^n\) and outputs accurate answers to every query in Q.
In both cases, the result is nearly quantitatively tight, since there is an efficient differentially private algorithm that answers \({\tilde{{\varOmega }}}(n^2)\) queries on an exponential size data universe, and one that answers exponentially many queries on a data universe of size \({\tilde{{\varOmega }}}(n^2)\).
Our proofs build on the connection between hardness of differential privacy and traitor-tracing schemes (Dwork et al., STOC’09; Ullman, STOC’13). We prove our hardness result for a polynomial size query set (resp., data universe) by showing that they follow from the existence of a special type of traitor-tracing scheme with very short ciphertexts (resp., secret keys), but very weak security guarantees, and then constructing such a scheme.
The full version of this work appears on the IACR Crypto ePrint [26].
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The goal of privacy-preserving data analysis is to release rich statistical information about a sensitive dataset while respecting the privacy of the individuals represented in that dataset. The past decade has seen tremendous progress towards understanding when and how these two competing goals can be reconciled, including surprisingly powerful differentially private algorithms as well as computational and information-theoretic limitations. In this work, we further this agenda by showing a strong new computational bottleneck in differential privacy.
Consider a dataset \(D \in X^n\) where each of the n elements is one individual’s data, and each individual’s data comes from some data universe X. We would like to be able to answer sets of statistical queries on D, which are queries of the form “What fraction of the individuals in D satisfy some property p?” However, differential privacy [14] requires that we do so in such a way that no individual’s data has significant influence on the answers.
If we are content answering a relatively small set of queries Q, then it suffices to perturb the answer to each query with independent noise from an appropriate distribution. This algorithm is simple, very efficient, differentially private, and ensures good accuracy—say, within \(\pm .01\) of the true answer—as long as \(|Q| \lesssim n^2\) queries [5, 13, 14, 16].
Remarkably, the work of Blum et al. [6] showed that it is possible to output a summary that allows accurate answers to an exponential number of queries—nearly \(2^n\)—while ensuring differential privacy. However, neither their algorithm nor the subsequent improvements [15, 17, 22, 23, 29, 30, 35] are computationally efficient. Specifically, they all require time at least \(\mathrm {poly}(n, |X|, |Q|)\) to privately and accurately answer a family of statistical queries Q on a dataset \(D \in X^{n}\). Note that the size of the input is \(n \log |X|\) bits, so a computationally efficient algorithm runs in time \(\mathrm {poly}(n,\log |X|)\).Footnote 1 For example, in the common setting where each individual’s data consists of d binary attributes, so \(X = \{0,1\}^{d}\), the size of the input is nd but \(|X| = 2^d\). As a result, all known private algorithms for answering arbitrary sets of statistical queries are inefficient if either the number of queries or the size of the data universe is superpolynomial.
This accuracy vs. computation tradeoff has been the subject of extensive study. Dwork et al. [15] showed that the existence of cryptographic traitor-tracing schemes [11] yields a family of statistical queries that cannot be answered accurately and efficiently with differential privacy. Applying recent traitor-tracing schemes [8], we conclude that, under plausible cryptographic assumptions (discussed below), if both the number of queries and the data universe can be superpolynomial, then there is no efficient differentially private algorithm. [34] used variants of traitor-tracing schemes to show that in the interactive setting, where the queries are not fixed but are instead given as input to the algorithm, assuming one-way functions exist, there is no private and efficient algorithm that accurately answers more than \({\tilde{O}}(n^2)\) statistical queries. All of the algorithms mentioned above work in this interactive setting, but for many applications we only need to answer a fixed family of statistical queries.
Despite the substantial progress, there is still a basic gap in our understanding. The hardness results for Dwork et al. apply if both the number of queries and the universe are large. But the known algorithms require exponential time if either of these sets is large. Is this necessary? Are there algorithms that run in time \(\mathrm {poly}(n, \log |X|, |Q|)\) or \(\mathrm {poly}(n, |X|, \log |Q|)\)?
Our main result shows that under the same plausible cryptographic assumptions, the answer is no—if either the data universe or the set of queries can be superpolynomially large, then there is some family of statistical queries that cannot be accurately and efficiently answered while ensuring differential privacy.
1.1 Our Results
Our first result shows that if the data universe can be of superpolynomial size then there is some fixed family of polynomially many queries that cannot be efficiently answered under differential privacy. This result shows that the efficient algorithm for answering an arbitrary family of \(|Q| \lesssim n^2\) queries by adding independent noise is optimal up to the specific constant in the exponent.
Theorem 1
(Hardness for small query sets). Assume the existence of indistinguishability obfuscation and one-way functions. Let \(\lambda \in {\mathbb {N}}\) be a computation parameter. For any polynomial \(n = n(\lambda )\), there is a sequence of pairs \(\{ (X_\lambda , Q_\lambda ) \}\) with \(|X_\lambda | = 2^\lambda \) and \(|Q_\lambda | = {\tilde{O}}(n^{7})\) such that there is no polynomial time differentially private algorithm that takes a dataset \(D \in X_{\lambda }^n\) and outputs an accurate answer to every query in \(Q_\lambda \) up to an additive error of \(\pm 1/3\).
Our second result shows that, even if the data universe is required to be of polynomial size, there is a fixed set of superpolynomially many queries that cannot be answered efficiently under differential privacy. When we say that an algorithm efficiently answers a set of superpolynomially many queries, we mean that it efficiently outputs a summary such that there is an efficient algorithm for obtaining an accurate answer to any query in the set. For comparison, if \(|X| \lesssim n^{2}\), then there is a simple \(\mathrm {poly}(n, |X|)\) time differentially private algorithm that accurately answers superpolynomially many queries. Our result shows that this efficient algorithm is optimal up to the specific constant in the exponent.
Theorem 2
(Hardness for small query sets). Assume the existence of indistinguishability obfuscation and one-way functions. Let \(\lambda \in {\mathbb {N}}\) be a computation parameter. For any polynomial \(n = n(\lambda )\), there is a sequence of pairs \(\{ (X_\lambda , Q_\lambda ) \}\) with \(|X_\lambda | = {\tilde{O}}(n^{7})\) and \(|Q_\lambda | = 2^\lambda \) such that there is no polynomial time differentially private algorithm that takes a dataset \(D \in X_{\lambda }^n\) and outputs an accurate answer to every query in \(Q_\lambda \) up to an additive error of \(\pm 1/3\).
Before we proceed to describe our techniques, we make a few remarks about these results. In both of these results, the constant 1 / 3 in our result is arbitrary, and can be replaced with any constant smaller than 1 / 2. We also remark that, when we informally say that an algorithm is differentially private, we mean that it satisfies \((\varepsilon , \delta )\)-differential privacy for some \(\varepsilon = O(1)\) and \(\delta = o(1/n)\). These are effectively the largest parameters for which differential privacy is a meaningful notion of privacy. That our hardness results apply to these parameters only makes our results stronger. Finally, we remark that it is possible to show that our results also rule out the weaker notion of computational differential privacy [28].
On Indistinguishability Obfuscation. Indistinguishability obfuscation (iO) has recently become a central cryptographic primitive. The first candidate construction, proposed just a couple years ago [19], was followed by a flurry of results demonstrating the extreme power and wide applicability of iO (cf., [4, 8, 19, 24, 31]). However, the assumption that iO exists is currently poorly understood, and the debate over the plausibility of iO is far from settled. While some specific proposed iO schemes have been attacked [12, 27], other schemes seem to resist all currently known attacks [1, 20]. We also do not know how to base iO on a solid, simple, natural computational assumption (some attempts based on multilinear maps have been made [21], but they were broken with respect to all current multilinear map constructions).
Nevertheless, our results are meaningful whether or not iO exists. If iO exists, our results show that certain tasks in differential privacy are intractable. Interestingly, unlike many previous results relying on iO, these conclusions were not previously known to follow from even the much stronger (and in fact, false) assumption of virtual black-box obfuscation. If, on the other hand, iO does not exist, then our results still demonstrate a barrier to progress in differential privacy—such progress would need to prove that iO does not exist. Alternatively, our results highlight a possible path toward proving that iO does not exist. We note that other “incompatibility” results are known for iO; for example, iO and certain types of hash functions cannot simultaneously exist [3, 9].
1.2 Techniques
(Weak) PLBE Schemes and the Hardness of Privacy. We prove our results by building on the connection between differentially private algorithms for answering statistical queries and traitor-tracing schemes discovered by Dwork et al. [15]. Traitor-tracing schemes were introduced by Chor et al. [11] for the purpose of identifying pirates who violate copyright restrictions.
Although previous results are described in the language of traitor-tracing, our results are simpler to describe in the language of private linear broadcast encryption (PLBE), which is a simpler primitive that implies traitor-tracing in a very direct way (e.g. [7]). We will thus refer to PLBE rather than traitor-tracing in all technical discussions going forward. A PLBE scheme allows a sender to generate keys for n users so that (1) the sender can broadcast an encrypted message that can be decrypted by any subset of users [1, i] for \(0 \le i \le n\),Footnote 2 so that any user outside of [1, i] will decrypt 0, and (2) the index i describing the set of users is hidden in the sense that any coalition of users that excludes user i cannot distinguish messages sent to the set [1, i] from messages sent to the set \([1,i-1]\).
Dwork et al. show that the existence of traitor-tracing schemes implies hardness results for differential privacy. In the language of PLBE, the reduction is as follows: Suppose a coalition of users takes their keys and builds a dataset \(D \in X^n\) where each element of the dataset contains one of their user keys. The family Q will contain a query \(q_c\) for each possible ciphertext c. The query \(q_c\) asks “What fraction of the elements (user keys) in D would decrypt the ciphertext c to the message 1?”
Suppose there were an efficient algorithm that accurately answers every query \(q_c\) in Q. Then the coalition could run it on the dataset D to produce a summary that can efficiently decrypt the ciphertexts. That means if c encrypts the message 1 to all users [1, n], the summary outputs an answer close to 1, and if c encrypts a message 1 to the empty set of users, the summary outputs an answer close to 0. Thus, there exists a user i such that the summary is distinguishing encryptions to the group [1, i] from encryptions to \([1,i-1]\). Differential privacy requires that the summary’s behavior is essentially the same even if run it on the dataset \(D'\) that excludes the secret key of user i. However, that means there is an efficient algorithm that takes the keys of all users excluding i and distinguishes encryptions to the group [1, i] from encryptions to the group \([1,i-1]\), which violates the second property of the PLBE scheme.
To instantiate this result, we need a PLBE. Observe that the data universe contains one element for every possible user key, and the set of queries contains one query for every ciphertext, and we want to minimize the size of these sets. Boneh and Zhandry constructed a traitor-tracing scheme where both the keys and the ciphertexts have length equal to the security parameter \(\lambda \), which under the Dwork et al. reduction yields hardness for a data universe and query set each of size \(2^{\lambda }\). The main contribution of this work is to show that we can reduce either the number of possible ciphertexts or the number of possible keys to \(\mathrm {poly}(n)\) while the other remains of size \(2^{\lambda }\).
But how is it possible to have a secure PLBE scheme with \(\mathrm {poly}(n)\) ciphertexts (resp., keys)? Even a semantically secure private key encryption scheme requires superpolynomially many ciphertexts (resp., keys)! Here we rely on observations from [34] showing that in order to show hardness for differential privacy, it suffices to have a PLBE scheme with very weak functionality and security. First, in the reduction, we only encrypt the message 1, so only the group [1, i] is actually hidden. Second, in the reduction, the differentially private algorithm only has access to the user’s keys, and there does not need to be a public encryption key or access to an encryption oracle. Thus, the adversary does not have the ability to generate encryptions to arbitrary groups [1, i]. Finally, the quantitative version of the reduction only requires that the coalition has advantage o(1 / n) in distinguishing encryptions to different groups, rather than negligible. All three of these relaxations are necessary for making the number of ciphertexts (resp., keys) \(\mathrm {poly}(n)\), and, as we show, are sufficient as well.
Weak PLBE Schemes from Obfuscation. In order to provide intuition for how we can achieve PLBE with a ciphertext or key space of size \(\mathrm {poly}(n)\), we will assume the existence of virtual black-box obfuscation (VBB). While our actual results use iO, we emphasize that a PLBE scheme with the right properties to establish our results was previously not even known to follow from VBB.
Polynomially Many Ciphertexts. Consider the following simple scheme: Let the set of ciphertexts be [m] for an appropriate \(m = \mathrm {poly}(n)\). Choose a pseudorandom function \(f: [m] \rightarrow \left\{ 0,1,\dots ,n\right\} \) and associate each ciphertext \(c \in [m]\) with the group of users [1, f(c)]. Pseudorandomness is only used to keep the description of f short, and for intuition it’s fine to think of f as truly random. To encrypt to a set [1, i], choose a random ciphertext \(c \in f^{-1}(i)\) and send it. Each user i will get a secret key containing an obfuscation of the program \(P_i(c)\) that computes \(j = f(c)\) and, if outputs 1 if \(j \ge i\) and otherwise outputs 0.
Consider a coalition with keys for every user except some user i. Since there are only \(\mathrm {poly}(n)\) ciphertexts, we may as well assume that these users evaluate each of their obfuscated programs on every ciphertext c, and VBB security of the obfuscation ensures that they “cannot learn anything else” from their keys. By evaluating their programs on every ciphertext, they can determine the value of f(c) exactly on every ciphertext c such that \(f(c) < i-1\) or \(f(c) > i\). Since f is pseudorandom, for ciphertexts such that \(f(c) \in \{i-1, i\}\), they have at most a negligible advantage in guessing whether \(f(c) = i\) or \(f(c) = i-1\), for any ciphertext c. Thus, if the coalition guesses the value of f(c) on all ciphertexts \(c \in f^{-1}(\left\{ i-1, i\right\} )\), a simple Chernoff bound shows that they will guess at most \(1/2 + O(\sqrt{\log (n)/T})\) of them correctly, where T is the size of \(f^{-1}(\left\{ i-1, i\right\} )\). For a PRF, the size of this set will be at least m / 2n with overwhelming probability. Thus, in order to ensure that his overall advantage is o(1 / n), it suffices to choose \(m = {\tilde{O}}(n^3)\).
In this straw-man scheme, the length of the ciphertext will clearly be \(O(\log (n))\). The user keys contain an obfuscation of a \(\mathrm {poly}(\lambda + \log (n))\) time program, so the user keys are \(\mathrm {poly}(\lambda + \log (n))\), so this scheme satisfies our efficiency requirements.
While the scheme is very simple to describe using VBB, replacing VBB with iO introduces some additional technicalities, and requires a new notion of puncturable PRF (Sect. 5.2). These technicalities are also the reason we use \(m = {\tilde{O}}(n^7)\) ciphertexts.
Polynomially Many Keys. Our scheme with polynomially many keys is roughly “dual” to the scheme with polynomially many ciphertexts. Let the set of user keys be \([n] \times [m]\) for an appropriate choice of \(m = \mathrm {poly}(n)\). Each user \(i = 1,\dots ,n\) will receive a secret key \((i, sk _i)\) for a random  . To encrypt a message to a group [1, i] produce a VBB obfuscation \({\mathcal {O}}\) of the following program: The input is a pair \((j,s) \in [n] \times [m]\). If \(s = sk _j\), then output 1 if \(j \in [1,i]\) and otherwise output 0. Otherwise, output the value r(j, s) for a pseudorandom function r. Again, pseudorandomness is only used to keep the description of the r short, and for intuition it’s fine to think of r as an independent random value for each input (j, s).
. To encrypt a message to a group [1, i] produce a VBB obfuscation \({\mathcal {O}}\) of the following program: The input is a pair \((j,s) \in [n] \times [m]\). If \(s = sk _j\), then output 1 if \(j \in [1,i]\) and otherwise output 0. Otherwise, output the value r(j, s) for a pseudorandom function r. Again, pseudorandomness is only used to keep the description of the r short, and for intuition it’s fine to think of r as an independent random value for each input (j, s).
Suppose the coalition has the keys for every user except i and a ciphertext encrypted to the group \([1, i-b]\) for \(b \in \left\{ 0,1\right\} \). We want to claim that the coalition has advantage at most o(1 / n) in trying to determine b. Since there are only polynomially many pairs (j, s), the coalition might as well evaluated the obfuscated program on every one of the inputs, and VBB security of the obfuscation ensures that they “cannot learn anything else” from their keys and the ciphertext. Observe that by evaluating the ciphertext on all inputs (j, s), they will actually evaluate the ciphertext on the input \((i, sk _i)\) belonging to user i, but they do not actually know which input of the form (i, s) was the correct one.
By (pseudo)randomness of r, the only values that contain any information about the bit b are \(o = ({\mathcal {O}}(i, s))_{s \in [m]}\). In the case that \(b = 0\), meaning the ciphertext was for group \([1,i-1]\), o is distributed as a (pseudo)random vector in \(\{0,1\}^m\) except that one random entry corresponding to the pair \((i, sk _i)\) is set to 1. Similarly, if \(b = 1\), then o is distributed as a (pseudo)random vector in \(\{0,1\}^m\) with one random entry set to 0. A simple argument based on Renyi-divergence shows that these two distributions are \(O(1/\sqrt{m})\)-close in statistical distance, so the coalition’s advantage in determining b is at most \(O(1/\sqrt{m})\). Thus, it suffices to take \(m = {\tilde{O}}(n^2)\) to obtain the level of security we need, corresponding to \(nm = {\tilde{O}}(n^3)\) keys.
As before, moving from VBB to iO introduces additional technicalities, leading to \({\tilde{O}}(n^7)\) keys. We remark that for both the short-ciphertext and short-key schemes, obtaining the optimal \({\tilde{O}}(n^2)\) ciphertexts or keys seems to require both coming up with a more efficient VBB scheme and avoiding the loss in efficiency from moving to iO, or using another approach entirely.
1.3 Related Work
Theorem 1 should be contrasted with the line of work showing that differentially private algorithms can efficiently answer many more than \(n^2\) simple queries. These results include algorithms for highly structured queries like point queries, threshold queries, and conjunctions (see e.g. [2, 33] and the references therein).
Ullman and Vadhan [36] (building on Dwork et al. [15]) show that, assuming one-way functions, no differentially private and computationally efficient algorithm that outputs a synthetic dataset can accurately answer even the very simple family of 2-way marginals. This result is incomparable to ours, since it applies to a very small and simple family of statistical queries, but necessarily only applies to algorithms that output synthetic data.
There is also a line of work using fingerprinting codes to prove information-theoretic lower bounds on differentially private mechanisms [10, 18, 32]. Namely, that if the data universe is of size \(\exp (n^2)\), then there is no differentially private algorithm, even a computationally unbounded one, that can answer more than \(n^2\) statistical queries. Fingerprinting codes are essentially the information-theoretic analogue of traitor-tracing schemes, and thus these results are technically related, although the models are incomparable.
1.4 Paper Outline
In Sect. 2 we will give the necessary background on differential privacy. In Sect. 3 we will give our definition of weak PLBE schemes, and in Sect. 4 we will connect them to differential privacy. In Sect. 5 we will define some cryptographic tools that we use to construct PLBE schemes. In Sect. 6 we will construct the short-ciphertext scheme we use to prove Theorem 1 and in Sect. 7 we will construct the short-key scheme we use to prove Theorem 2.
2 Differential Privacy Preliminaries
2.1 Differentially Private Algorithms
A dataset \(D \in X^{n}\) is an ordered set of n rows, where each row corresponds to an individual, and each row is an element of some the data universe \(X\). We write \(D = (D_1,\dots ,D_n)\) where \(D_i\) is the i-th row of D. We will refer to n as the size of the dataset. We say that two datasets \(D, D' \in X^*\) are adjacent if \(D'\) can be obtained from D by the addition, removal, or substitution of a single row, and we denote this relation by \(D \sim D'\). In particular, if we remove the i-th row of D then we obtain a new dataset \(D_{-i} \sim D\). Informally, an algorithm A is differentially private if it is randomized and for any two adjacent datasets \(D \sim D'\), the distributions of A(D) and \(A(D')\) are similar.
Definition 3
(Differential Privacy [14]). Let \(A :X^n \rightarrow S\) be a randomized algorithm. We say that A is \((\varepsilon , \delta )\) -differentially private if for every two adjacent datasets \(D \sim D'\) and every subset \(T \subseteq S\), \(\underset{}{{\mathbb {P}}}\left[ A(D) \in T \right] \le e^{\varepsilon } \cdot \underset{}{{\mathbb {P}}}\left[ A(D') \in T \right] + \delta .\) In this definition, \(\varepsilon , \delta \) may be a function of n.
2.2 Algorithms for Answering Statistical Queries
In this work we study algorithms that answer statistical queries (which are also sometimes called counting queries, predicate queries, or linear queries in the literature). For a data universe \(X\), a statistical query on \(X\) is defined by a predicate \(q :X\rightarrow \{0,1\}\). Abusing notation, we define the evaluation of a query q on a dataset \(D = (D_1,\dots ,D_n) \in X^n\) to be \(\frac{1}{n} \sum _{i=1}^{n} q(D_i)\).
A single statistical query does not provide much useful information about the dataset. However, a sufficiently large and rich set of statistical queries is sufficient to implement many natural machine learning and data mining algorithms [25], thus we are interesting in differentially private algorithms to answer such sets. To this end, let \(Q = \left\{ q :X\rightarrow \{0,1\}\right\} \) be a set of statistical queries on a data universe \(X\).
Informally, we say that a mechanism is accurate for a set Q of statistical queries if it answers every query in the family to within error \(\pm \alpha \) for some suitable choice of \(\alpha > 0\). Note that \(0 \le q(D) \le 1\), so this definition of accuracy is meaningful when \(\alpha < 1/2\).
Before we define accuracy, we note that the mechanism may represent its answer in any form. That is, the mechanism outputs may output a summary \(S \in {\mathcal {S}}\) that somehow represents the answers to every query in Q. We then require that there is an evaluator \( Eval :{\mathcal {S}}\times {\mathcal {Q}}\rightarrow [0,1]\) that takes the summary and a query and outputs an approximate answer to that query. That is, we think of \( Eval (S,q)\) as the mechanism’s answer to the query q. We will abuse notation and simply write q(S) to mean \( Eval (S,q)\).Footnote 3
Definition 4
(Accuracy). For a family Q of statistical queries on \(X\), a dataset \(D \in X^n\) and a summary \(s \in S\), we say that s is \(\alpha \) -accurate for Q on D if \(\forall q \in Q ~~~~ \left| q(D) - q(s) \right| \le \alpha .\) For a family of statistical queries Q on \(X\), we say that an algorithm \(A :X^n \rightarrow S\) is \((\alpha , \beta )\) -accurate for Q given a dataset of size n if for every \(D \in X^n\), \(\underset{}{{\mathbb {P}}}\left[ A(D)~is~\alpha \hbox {-}accurate~for~Q~on~X \right] \ge 1-\beta \).
In this work we are typically interested in mechanisms that satisfy the very weak notion of (1 / 3, o(1 / n))-accuracy, where the constant 1 / 3 could be replaced with any constant \(<1/2\). Most differentially private mechanisms satisfy quantitatively much stronger accuracy guarantees. Since we are proving hardness results, this choice of parameters makes our results stronger.
2.3 Computational Efficiency
Since we are interested in asymptotic efficiency, we introduce a computation parameter \(\lambda \in {\mathbb {N}}\). We then consider a sequence of pairs \(\{ (X_{\lambda }, Q_{\lambda }) \}_{\lambda \in {\mathbb {N}}}\) where \(Q_{\lambda }\) is a set of statistical queries on \(X_{\lambda }\). We consider databases of size n where \(n = n(\lambda )\) is a polynomial. We then consider algorithms A that take as input a dataset \(X_{\lambda }^n\) and output a summary in \(S_{\lambda }\) where \(\{ S_{\lambda } \}_{\lambda \in {\mathbb {N}}}\) is a sequence of output ranges. There is an associated evaluator \( Eval \) that takes a query \(q \in Q_{\lambda }\) and a summary \(s \in S_{\lambda }\) and outputs a real-valued answer. The definitions of differential privacy and accuracy extend straightforwardly to such sequences.
We say that such an algorithm is computationally efficient if the running time of the algorithm and the associated evaluator run in time polynomial in the computation parameter \(\lambda \). We remark that in principle, it could require at many as |X| bits even to specify a statistical query, in which case we cannot hope to answer the query efficiently, even ignoring privacy constraints. In this work we restrict attention exclusively to statistical queries that are specified by a circuit of size \(\mathrm {poly}(\log |X|)\), and thus can be evaluated in time \(\mathrm {poly}(\log |X|)\), and so are not the bottleneck in computation. To remind the reader of this fact, we will often say that \({\mathcal {Q}}\) is a family of efficiently computable statistical queries.
3 Weakly Secure Private Linear Broadcast Schemes
We now describe a very relaxed notion of private linear broadcast schemes whose existence will imply the hardness of differentially private data release.
3.1 Syntax and Correctness
For a function \(n :{\mathbb {N}}\rightarrow {\mathbb {N}}\) and a sequence \(\{ K_\lambda , C_\lambda \}_{\lambda \in {\mathbb {N}}}\), a \((n, \{K_\lambda , C_\lambda \})\) -private linear broadcast scheme is a tuple of efficient algorithms \({\varPi } = (\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\) with the following syntax.
-
\(\mathsf {Setup}\) takes as input a security parameter \(\lambda \), runs in time \(\mathrm {poly}(\lambda )\), and outputs \(n = n(\lambda )\) secret user keys \( sk _1,\dots , sk _n \in K_\lambda \) and a secret master key \( mk \). We will write \({\varvec{k}}= ( sk _1,\dots , sk _n, mk )\) to denote the set of keys.
-
\(\mathsf {Enc}\) takes as input a master key \( mk \) and an index \(i \in \left\{ 0,1,\dots ,n\right\} \), and outputs a ciphertext \(c \in C_\lambda \). If
 then we say that c is encrypted to index j.
then we say that c is encrypted to index j.
-
\(\mathsf {Dec}\) takes as input a ciphertext c and a user key \( sk _i\) and outputs a single bit \(b \in \{0,1\}\). We assume for simplicity that \(\mathsf {Dec}\) is deterministic.
Correctness of the scheme asserts that if \({\varvec{k}}\) are generated by \(\mathsf {Setup}\), then for any pair i, j, \(\mathsf {Dec}( sk _i, \mathsf {Enc}( mk , j)) = {\mathbb {I}}\{i \le j\}\). For simplicity, we require that this property holds with probability 1 over the coins of \(\mathsf {Setup}\) and \(\mathsf {Enc}\), although it would not affect our results substantively if we required only correctness with high probability.
Definition 5
(Perfect Correctness). An \((n, \{K_\lambda , C_\lambda \})\)-private linear broadcast scheme is perfectly correct if for every \(\lambda \in {\mathbb {N}}\), and every \(i,j \in \left\{ 0,1,\dots ,n\right\} \)
3.2 Weak Index-Hiding Security
Intuitively, the security property we want is that any computationally efficient adversary who is missing one of the user keys \( sk _{i^*}\) cannot distinguish ciphertexts encrypted with index \(i^*\) from index \(i^*-1\), even if that adversary holds all \(n-1\) other keys \( sk _{-i^*}\). In other words, an efficient adversary cannot infer anything about the encrypted index beyond what is implied by the correctness of decryption and the set of keys he holds.
More precisely, consider the following two-phase experiment. First the adversary is given every key except for \( sk _{i^*}\), and outputs a decryption program S. Then, a challenge ciphertext is encrypted to either \(i^*\) or to \(i^*-1\). We say that the private linear broadcast scheme is secure if for every polynomial time adversary, with high probability over the setup and the decryption program chosen by the adversary, the decryption program has small advantage in distinguishing the two possible indices.
Definition 6
(Weak Index Hiding). A private linear broadcast scheme \({\varPi }\) satisfies weak index-hiding security if for every sufficiently large \(\lambda \in {\mathbb {N}}\), every \(i^* \in [n(\lambda )],\) and every adversary A with running time \(\mathrm {poly}(\lambda )\),
In the above, the inner probabilities are taken over the coins of \(\mathsf {Enc}\) and S.
Note that in the above definition we have fixed the success probability of the adversary for simplicity. Moreover, we have fixed these probabilities to relatively large ones. Requiring only a polynomially small advantage is crucial to achieving the key and ciphertext lengths we need to obtain our results, while still being sufficient to establish the hardness of differential privacy.
The Index-Hiding and Two-Index-Hiding Games. While Definition 6 is the most natural, in this section we consider some related ways of defining security that will be easier to work with when we construct and analyze our schemes. Consider the following \(\mathbf {IndexHiding}\) game (Fig. 1).
Let \(\mathbf {IndexHiding}[i^*, {\varvec{k}}, S]\) be the game \(\mathbf {IndexHiding}[i^*]\) where we fix the choices of \({\varvec{k}}\) and S. Also, define
so that
Then the following is equivalent to (1) in Definition 6 as
In order to prove that our schemes satisfy weak index-hiding security, we will go through an intermediate notion that we call two-index-hiding security. To see why this is useful, In our constructions it will be fairly easy to prove that \(\mathrm {Adv}[i^*]\) is small, but because \(\mathrm {Adv}[i^*, {\varvec{k}}, S]\) can be positive or negative, that alone is not enough to establish (2). Thus, in order to establish (2) we will analyze the following variant of the index-hiding game (Fig. 2).
Analogous to what we did with \(\mathbf {IndexHiding}\), we can define the quantity \(\mathbf {TwoIndexHiding}[i^*, {\varvec{k}}, S]\) to be the game \(\mathbf {TwoIndexHiding}[i^*]\) where we fix the choices of \({\varvec{k}}\) and S, and define
so that
The crucial feature is that if we can bound the expectation of \(\mathrm {TwoAdv}\) then we get a bound on the expectation of \(\mathrm {Adv}^2\). Since \(\mathrm {Adv}^2\) is always positive, we can apply Markov’s inequality to establish (2). Formally, we have the following claim.
Claim 1
Suppose that for every efficient adversary A, \(\lambda \in {\mathbb {N}}\), and index \(i^* \in [n(\lambda )],\) \(\mathrm {TwoAdv}[i^*] \le \varepsilon \). Then for every efficient adversary A, \(\lambda \in {\mathbb {N}}\), and index \(i^* \in [n(\lambda )],\)
Proof
Given any adversary A in the \(\mathbf {IndexHiding}\) game, consider the following adversary \(A_2\) in the \(\mathbf {TwoIndexHiding}\) game, which, when given a set of keys, runs A with the same keys to get program \(S_A\), then creates and outputs the program \(S_{A_2}\), which on input \(c_0, c_1\), runs S on \(c_0\) to get output \(b'_0\), runs S on \(c_1\) to get output \(b'_1\), then outputs \(b' = b'_0 \oplus b'_1\). Then, for this \(A_2\),

So if every efficient adversary \(A'\), \(\lambda \in {\mathbb {N}}\), and index \(i^* \in [n(\lambda )]\) satisfies \(\mathrm {TwoAdv}[i^*] \le \varepsilon \), then this condition also holds for \(A_2\)’s \(\mathrm {TwoAdv}[i^*] = \underset{{\varvec{k}}= \mathsf {Setup}(\lambda ), \atop S_{A} \leftarrow A( sk _{-i^*})}{{\mathbb {E}}}\left[ 2 \cdot \mathrm {Adv}[i^*, {\varvec{k}}, S_{A}]^{2} \right] \), which implies \(\underset{{\varvec{k}}= \mathsf {Setup}(\lambda ), \atop S_{A} \leftarrow A( sk _{-i^*})}{{\mathbb {E}}}\left[ \mathrm {Adv}[i^*, {\varvec{k}}, S_{A}]^{2} \right] \le \frac{\varepsilon }{2}\).
Using this claim we can prove the following lemma.
Lemma 7
Let \({\varPi }\) be a private linear broadcast scheme such that for every efficient adversary A, \(\lambda \in {\mathbb {N}}\), and index \(i^* \in [n(\lambda )],\) \(\mathrm {TwoAdv}[i^*] \le \frac{1}{200 n^3}\). Then \({\varPi }\) satisfies weak index-hiding security.
Proof
By applying Claim 1 to the assumption of the lemma, we have that for every efficient adversary A,
Now we have
To complete the proof, observe that this final condition is equivalent to the definition of weak index-hiding security (Definition 6).
In light of this lemma, we will focus on proving that the schemes we construct in the following sections satisfying the condition \( \mathrm {TwoAdv}[i^*] \le \frac{1}{200 n^3}, \) which will be easier than directly establishing Definition 6.
4 Hardness of Differential Privacy from PLBE
In this section we prove that a private linear broadcast scheme satisfying perfect correctness and index-hiding security yields a family of statistical queries that cannot be answered accurately by an efficient differentially private algorithm. The proof is a fairly straightforward adaptation of the proofs in Dwork et al. [15] and Ullman [34] that various sorts of traitor-tracing schemes imply hardness results for differential privacy. We include the result for completeness, and to verify that our very weak definition of private linear broadcast is sufficient to prove hardness of differential privacy.
Theorem 8
Suppose there is an \((n, \{K_\lambda , C_\lambda \})\)-private linear broadcast scheme that satisfies perfect correctness (Definition 5) and weak index-hiding security (Definition 6). Then there is a sequence of of pairs \(\{X_\lambda , Q_\lambda \}_{\lambda \in {\mathbb {N}}}\) where \(Q_\lambda \) is a set of statistical queries on \(X_\lambda \), \(|Q_\lambda | = |C_\lambda |\), and \(|X_\lambda | = |K_\lambda |\) such that there is no algorithm A that is simultaneously,
-
1.
(1, 1 / 2n)-differentially private,
-
2.
(1 / 3, 1 / 2n)-accurate for \(Q_\lambda \) on datasets \(D \in X_{\lambda }^{n(\lambda )}\), and
-
3.
computationally efficient.
Theorems 1 and 2 in the introduction follow by combining Theorem 8 above with the constructions of private linear broadcast schemes in Sect. 6. The proof of Theorem 8 closely follows the proofs in Dwork et al. [15] and Ullman [34]. We give the proof both for completeness and to verify that our definition of private linear broadcast suffices to establish the hardness of differential privacy.
Proof
Let \({\varPi } = (\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\) be the promised \((n, \{K_\lambda , C_\lambda \})\) private linear broadcast scheme. For every \(\lambda \in {\mathbb {N}}\), we can define a distribution on datasets \(D \in X_{\lambda }^{n(\lambda )}\) as follows. Run \(\mathsf {Setup}(\lambda )\) to obtain \(n = n(\lambda )\) secret user keys \( sk _1,\dots , sk _n \in K_\lambda \) and a master secret key \( mk \). Let the dataset be \(D = ( sk _1,\dots , sk _n) \in X_{\lambda }^{n}\) where we define the data universe \(X_{\lambda } = K_{\lambda }\). Abusing notation, we’ll write  .
.
Now we define the family of queries \(Q_\lambda \) on \(X_\lambda \) as follows. For every ciphertext \(c \in C_\lambda \), we define the predicate \(q_{c} \in Q_{\lambda }\) to take as input a user key \( sk _i \in K_{\lambda }\) and output \(\mathsf {Dec}( sk _i, c)\). That is, \( Q_{\lambda } = \left\{ q_{c}( sk ) = \mathsf {Dec}( sk , c) \; \mid \; c \in C_\lambda \right\} . \) Recall that, by the definition of a statistical query, for a dataset \(D = ( sk _1,\dots , sk _n)\), we have
Suppose there is an algorithm A that is computationally efficient and is (1 / 3, 1 / 2n)-accurate for \(Q_{\lambda }\) given a dataset \(D \in X_{\lambda }^{n}\). We will show that A cannot satisfy (1, 1 / 2n)-differential privacy. By accuracy, for every \(\lambda \in {\mathbb {N}}\) and every fixed dataset \(D \in X_{\lambda }^{n}\), with probability at least \(1-1/2n\), A(D) outputs a summary \(S \in {\mathcal {S}}_{\lambda }\) that is 1 / 3-accurate for \(Q_{\lambda }\) on D. That is, for every \(D \in X_{\lambda }^{n}\), with probability at least \(1-1/2n\),
Suppose that S is indeed 1 / 3-accurate. By perfect correctness of the private linear broadcast scheme (Definition 5), and the definition of Q, we have that since \((D, mk ) = \mathsf {Setup}(\lambda )\),
Combining Eqs. (4) and (5), we have that if \((D, mk ) = \mathsf {Setup}(\lambda )\),  , and S is 1 / 3-accurate, then we have both
, and S is 1 / 3-accurate, then we have both  and
and  Thus, for every \((D, mk )\) and S that is 1 / 3-accurate, there exists an index \(i \in \left\{ 1,\dots ,n\right\} \) such that
Thus, for every \((D, mk )\) and S that is 1 / 3-accurate, there exists an index \(i \in \left\{ 1,\dots ,n\right\} \) such that

By averaging, using the fact that S is 1 / 3-accurate with probability at least \(1-1/2n\), there must exist an index \(i^* \in \left\{ 1,\dots ,n\right\} \) such that

Assume, for the sake of contradiction that A is (1, 1 / 2n)-differentially private. For a given \(i, mk \), let \({\mathcal {S}}_{i, mk } \subseteq {\mathcal {S}}_{\lambda }\) be the set of summaries S such that (6) holds. Then, by (7), we have  By differential privacy of A, we have
By differential privacy of A, we have

Thus, by our definition of \({\mathcal {S}}_{i^*, mk }\), and by averaging over  , we have
, we have
But this violates the weak index hiding property of the private linear broadcast scheme. Specifically, if we consider an adversary for the private linear broadcast scheme that runs A on the keys \( sk _{-i^*}\) to obtain a summary S, then decrypts a ciphertext c by computing \(q_{c}(S)\) and rounding the answer to \(\{0,1\}\), then by (8) this adversary violates weak index-hiding security (Definition 6).
Thus we have obtained a contradiction showing that A is not (1, 1 / 2n)-differentially private. This completes the proof.
5 Cryptographic Primitives
We will make use of several cryptographic tools and information-theoretic primitives. Due to space, we will omit a formal definition of standard concepts like almost-pairwise-independent hash functions, pseudorandom generators, and pseudorandom functions and defer these to the full version.
5.1 Puncturable Pseudorandom Functions
A pseudorandom function family \({\mathcal {F}}_{\lambda } = \left\{ \mathsf {PRF}:[m] \rightarrow [n]\right\} \) is puncturable if there is a deterministic procedure \(\mathsf {Puncture}\) that takes as input \(\mathsf {PRF}\in {\mathcal {F}}_{\lambda }\) and \(x^* \in [m]\) and outputs a new function \(\mathsf {PRF}^{\{x^*\}}: [m] \rightarrow [n]\) such that \(\mathsf {PRF}^{\{x^*\}}(x) = \mathsf {PRF}(x)\) if \(x \ne x^*\) and \(\mathsf {PRF}^{\{x^*\}}(x) = \bot \) if \(x = x^*\).
The definition of security for a punctured pseudorandom function states that for any \(x^*\), given the punctured function \(\mathsf {PRF}^{\{x^*\}}\), the missing value \(\mathsf {PRF}(x^*)\) is computationally unpredictable. Specifically, we define the game \(\mathbf {Puncture}\) to capture the desired security property (Fig. 3).
Definition 9
(Puncturing Secure PRF). A pseudorandom function family \({\mathcal {F}}_{\lambda } = \left\{ \mathsf {PRF}:[m] \rightarrow [n]\right\} \) is \(\varepsilon \) -puncturing secure if for every \(x^* \in [m]\),
5.2 Twice Puncturable PRFs
A twice puncturable PRF is a pair of algorithms \(( PRFSetup , \mathsf {Puncture})\).
-
\( PRFSetup \) is a randomized algorithm that takes a security parameter \(\lambda \) and outputs a function \(\mathsf {PRF}: [m] \rightarrow [n]\) where \(m = m(\lambda )\) and \(n = n(\lambda )\) are parameters of the construction. Technically, the function is parameterized by a seed of length \(\lambda \), however for notational simplicity we will ignore the seed and simply use \(\mathsf {PRF}\) to denote this function. Formally
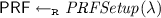 .
. -
\(\mathsf {Puncture}\) is a deterministic algorithm that takes a \(\mathsf {PRF}\) and a pair of inputs \(x_0, x_1 \in [m]\) and outputs a new function \(\mathsf {PRF}^{\{x_0, x_1\}}: [m] \rightarrow [n]\) such that
$$\begin{aligned}\mathsf {PRF}^{\{x_0,x_1\}}= {\left\{ \begin{array}{ll} \mathsf {PRF}(x)&{}\text {if }x\notin \{x_0,x_1\}\\ \bot &{}\text {if }x\in \{x_0,x_1\} \end{array}\right. } \end{aligned}$$Formally, \(\mathsf {PRF}^{\{x_0, x_1\}} = \mathsf {Puncture}(\mathsf {PRF}, x_0, x_1)\).
In what follows we will always assume that m and n are polynomial in the security parameter and that \(m = \omega (n \log (n))\).
In addition to requiring that this family of functions satisfies the standard notion of cryptographic pseudorandomness, we will now define a new security property for twice puncturable PRFs, called input matching indistinguishability. For any two distinct outputs \(y_0,y_1\in [n],y_0 \ne y_1\), consider the following game (Fig. 4).
Notice that in this game, we have assured that every \(y \in [n]\) has a preimage under \(\mathsf {PRF}\). We need this condition to make the next step of sampling random preimages well defined. Technically, it would suffice to have a preimage only for \(y_{b_0}\) and \(y_{b_1}\), but for simplicity we will assume that every possible output has a preimage. When \(f : [m] \rightarrow [n]\) is a random function, the probability that some output has no preimage is at most \(n \cdot \exp (-{\varOmega }(m/n))\) which is negligible when \(m = \omega (n \log (n))\). Since m, n are assumed to be a polynomial in the security parameter, we can efficiently check if every output has a preimage, thus if \(\mathsf {PRF}\) is pseudorandom it must also be the case that every output has a preimage with high probability. Since we can efficiently check whether or not every output has a preimage under \(\mathsf {PRF}\), and this event occurs with all but negligible probability, we can efficiently sample the pseudorandom function in the first step of \(\mathsf{InputMatching}[y_0, y_1]\).
Definition 10
(Input-Matching Secure PRF). A function family \(\left\{ \mathsf {PRF}:[m] \rightarrow [n]\right\} \) is \(\varepsilon \) -input-matching secure if the function family is a secure pseudorandom function and additionally for every \(y_0, y_1 \in [n]\) with \(y_0 \ne y_1\),
In the full version of this work we show that input-matching secure twice puncturable pseudorandom functions with suitable parameters exist.
Theorem 11
Assuming the existence of one-way functions, if m, n are polynomials such that \(m = \omega (n \log (n))\), then there exists a pseudorandom function family \({\mathcal {F}}_{\lambda } = \left\{ \mathsf {PRF}:[m(\lambda )] \rightarrow [n(\lambda )]\right\} \) that is twice puncturable and is \({\tilde{O}}(\sqrt{n/m})\)-input-matching secure.
5.3 Indistinguishability Obfuscation
We use the following formulation of Garg et al. [19] for indistinguishability obfuscation:
Definition 12
(Indistinguishability Obfuscation). A indistinguishability obfuscator \({\mathsf {O}}\) for a circuit class \(\{{\mathcal {C}}_{\lambda }\}\) is a probabilistic polynomial-time uniform algorithm satisfying the following conditions:
-
1.
\({\mathsf {O}}(\lambda , C)\) preserves the functionality of C. That is, for any \(C \in {\mathcal {C}}_{\lambda }\), if we compute \(C' = {\mathsf {O}}(\lambda , C)\), then \(C'(x) = C(x)\) for all inputs x.
-
2.
For any \(\lambda \) and any two circuits \(C_0, C_1\) with the same functionality, the circuits \({\mathsf {O}}(\lambda , C_0)\) and \({\mathsf {O}}(\lambda , C_1)\) are indistinguishable. More precisely, for all pairs of probabilistic polynomial-time adversaries \((\text {Samp}, D)\), if
$$\begin{aligned} \mathop {\Pr }\limits _{(C_0, C_1, \sigma ) \leftarrow \text {Samp}(\lambda )}[(\forall x), \; C_0(x) = C_1(x)] > 1 - \mathrm {negl}(\lambda ) \end{aligned}$$then
$$\begin{aligned} | \Pr [D(\sigma , {\mathsf {O}}(\lambda , C_0)) = 1 ] - \Pr [D(\sigma , {\mathsf {O}}(\lambda , C_1)) = 1 ] | < \mathrm {negl}(\lambda ) \end{aligned}$$
The circuit classes we are interested in are polynomial-size circuits - that is, when \({\mathcal {C}}_\lambda \) is the collection of all circuits of size at most \(\lambda \). When clear from context, we will often drop \(\lambda \) as an input to \({\mathsf {O}}\) and as a subscript for \({\mathcal {C}}\).
6 A PLBE Scheme with Very Short Ciphertexts
In this section we construct a private linear broadcast scheme for n users where the key length is polynomial in the security parameter \(\lambda \) and the ciphertext length is only \(O(\log (n))\). This scheme will be used to establish our hardness result for differential privacy when the data universe can be exponentially large but the family of queries has only polynomial size. The construction of a weak private linear broadcast scheme with user keys of length \(O(\log (n))\) is in Sect. 7.
6.1 Construction
Let \(n = \mathrm {poly}(\lambda )\) denote the number of users for the scheme. Let \(m = {\tilde{O}}(n^{7})\) be a parameter. Our construction will rely on the following primitives:
-
A pseudorandom generator \(\mathsf {PRG}:\{0,1\}^{\lambda /2} \rightarrow \{0,1\}^{\lambda }\).
-
A puncturable PRF family \({\mathcal {F}}_{\lambda , sk } = \left\{ \mathsf {PRF}_{ sk } :[n] \rightarrow \{0,1\}^{\lambda }\right\} \).
-
A twice-puncturable PRF family \({\mathcal {F}}_{\lambda , \mathsf {Enc}} = \left\{ \mathsf {PRF}_{\mathsf {Enc}} :[m] \rightarrow [n]\right\} \).
-
An iO scheme \(\mathsf {Obfuscate}\).
Theorem 13
Assuming the existence of one-way functions and indistinguishability obfuscation. For every polynomial n, the scheme \({\varPi }_{\mathrm {short-ctext}}\) (Fig. 5) is an \((n, d, \ell )\)-private linear broadcast scheme for \(d = \mathrm {poly}(\lambda )\) and \(2^{\ell } = {\tilde{O}}(n^{7})\) and satisfies: \( \mathrm {TwoAdv}[i^*] \le \frac{1}{200 n^3}. \)
Combining this theorem with Lemma 7 and Theorem 8 establishes Theorem 1 in the introduction.
Parameters. First we verify that \({\varPi }_\mathrm {short-ctext}\) is an \((n,d,\ell )\)-private linear broadcast scheme for the desired parameters. Observe that the length of the secret keys is \(\log (n) + \lambda + |{\mathsf {O}}|\). By the efficiency of the pseudorandom functions and the specification of \({\mathsf {P}}\), the running time of \({\mathsf {P}}\) is \(\mathrm {poly}(\lambda + \log (n))\). Thus, by the efficiency of \(\mathsf {Obfuscate}\), \(|{\mathsf {O}}| = \mathrm {poly}(\lambda + \log (n))\). Therefore the total key length is \(\mathrm {poly}(\lambda + \log (n))\). Since n is assumed to be a polynomial in \(\lambda \), we have that the secret keys have length \(d = \mathrm {poly}(\lambda )\) as desired. By construction, the ciphertext is an element of [m]. Thus, since \(m = {\tilde{O}}(n^7)\) the ciphertexts length \(\ell \) satisfies \(2^{\ell } = {\tilde{O}}(n^{7})\) as desired.
6.2 Proof of Weak Index-Hiding Security
In light of Lemma 7, in order to prove that the scheme satisfies weak index-hiding security, it suffices to show that for every sufficiently large \(\lambda \in {\mathbb {N}}\), and every \(i^* \in [n(\lambda )]\), \( \underset{\mathbf {TwoIndexHiding}[i^*]}{{\mathbb {P}}}\left[ b' = b_0 \oplus b_1 \right] - \frac{1}{2} ={} o(1/n^3). \) We will demonstrate this using a series of hybrids to reduce security of the scheme in the \(\mathbf {TwoIndexHiding}\) game to input-matching security of the pseudorandom function family \(\mathsf {PRF}_{\lambda , \mathsf {Enc}}\).
Before we proceed with the argument, we remark a bit on how we will present the hybrids. Note that the view of the adversary consists of the keys \( sk _{-i^*}\). Each of these keys is of the form \((i, s_i, {\mathsf {O}})\) where \({\mathsf {O}}\) is an obfuscation of the same program \({\mathsf {P}}\). Thus, for brevity, we will discuss only how we modify the construction of the program \({\mathsf {P}}\) and it will be understood that each user’s key will consist of an obfuscation of this modified program. We will also rely crucially on the fact that, because the challenge ciphertexts depend only on the master key \( mk \), we can generate the challenge ciphertexts \(c_0\) and \(c_1\) can be generated before the users’ secret keys \( sk _1,\dots , sk _n\). Thus, we will be justified when we modify \({\mathsf {P}}\) in a manner that depends on the challenge ciphertexts and include an obfuscation of this program in the users’ secret keys. We also remark that we highlight the changes in the hybrids in green.
Breaking the Decryption Program for Challenge Index. We use a series of hybrids to ensure that the obfuscated program reveals no information about the secret \(s_{i^*}\) for the specified user \(i^*\). First, we modify the program by hardcoding the secret \(s_{i^*}\) into the program. The obfuscated versions of \({\mathsf {P}}\) and \({\mathsf {P}}^1\) (Fig. 6) are indistinguishable because the input-output behavior of the programs are identical, thus the indistinguishability obfuscation guarantees that the obfuscations of these programs are computationally indistinguishable.
Next we modify the setup procedure to give a uniformly random value for \(s_{i^*}\). The new setup procedure is indistinguishable from the original setup procedure by the pseudorandomness of \(s_{i^*} = \mathsf {PRF}_{ sk }(i^*)\). Finally, we modify the decryption program to use a truly random value \(x^*\) instead of \(x^* = \mathsf {PRG}(\mathsf {PRF}_{ sk }(i^*))\). The new decryption program is indistinguishable from the original by pseudorandomness of \(\mathsf {PRG}\) and \(\mathsf {PRF}_{ sk }\).
After making these modifications, with probability at least \(1 - 2^{-\lambda /2}\), the random value \(x^*\) is not in the image of \(\mathsf {PRG}\). Thus, with probability at least \(1 - 2^{-\lambda /2}\), the condition \(\mathsf {PRG}( sk ) = x^*\) will be unsatisfiable. Therefore, we can simply remove this test without changing the program on any inputs. Thus, the obfuscation of \({\mathsf {P}}^1\) will be indistinguishable from the obfuscation of the following program \({\mathsf {P}}^2\) (Fig. 7).
Breaking the Decryption Program for the Challenge Ciphertexts. First we modify the program so that the behavior on the challenge ciphertexts is hardcoded and \(\mathsf {PRF}_{\mathsf {Enc}}\) is punctured on the challenge ciphertexts. The new decryption program is as follows. Note that the final line of the program is never reached when the input satisfies \(c = c_0\) or \(c = c_1\), so puncturing \(\mathsf {PRF}_{\mathsf {Enc}}\) at these points does not affect the output of the program on any input. Thus, \({\mathsf {P}}^3\) (Fig. 8) is indistinguishable from \({\mathsf {P}}^2\) by the security of indistinguishability obfuscation.
Next, since, \(b_0, b_1 \in \{0,1\}\), and the decryption program halts immediately if \(i = i^*\), the values of \(b_0, b_1\) do not affect the output of the program. Thus, we can simply drop them from the description of the program without changing the program on any input. So, by security of the indistinguishability obfuscation, \({\mathsf {P}}^3\) is indistinguishable from the following program \({\mathsf {P}}^4\) (Fig. 9).
Reducing to Input-Matching Security. Finally, we claim that if the adversary is able to win at \(\mathbf {TwoIndexHiding}\) then he can also win the game \(\mathbf {InputMatching}[i^*-1, i^*]\), which violates input-matching security of \({\mathcal {F}}_{\lambda , \mathsf {Enc}}\).
Recall that the challenge in the game \(\mathbf {InputMatching}[i^*-1,i^*]\) consists of a tuple \((c_0, c_1, \mathsf {PRF}^{\{c_0, c_1\}})\) where \(\mathsf {PRF}_{\mathsf {Enc}}\) is sampled subject to 1) \(\mathsf {PRF}_{\mathsf {Enc}}(c_0) = i^* - b_0\) for a random \(b_0 \in \{0,1\}\), 2) \(\mathsf {PRF}_{\mathsf {Enc}}(c_1) = i^* - b_1\) for a random \(b_1 \in \{0,1\}\), and 3) \(\mathsf {PRF}_{\mathsf {Enc}}^{-1}(i) \ne \emptyset \) for every \(i \in [n]\). Given this input, we can precisely simulate the view of the adversary in \(\mathbf {TwoIndexHiding}[i^*]\). To do so, we can choose \(\mathsf {PRF}_{ sk }\) and give the keys \( sk _{-i^*}\) and obfuscations of \({\mathsf {P}}^4_{\mathsf {PRF}^{\{i^*\}}_{ sk }, \mathsf {PRF}^{\{c_0, c_1\}}_{\mathsf {Enc}}, i^*, c_0, c_1}\) to the adversary. Then we can user \(c_0, c_1\) as the challenge ciphertexts and obtain a bit \(b'\) from the adversary. By input-matching security, we have that \( \underset{}{{\mathbb {P}}}\left[ b' = b_0 \oplus b_1 \right] - \frac{1}{2} ={} o(1/n^3). \) Since, as we argued above, the view of the adversary in this game is indistinguishable from the view of the adversary in \(\mathbf {TwoIndexHiding}[i^*]\), we conclude that \( \underset{\mathbf {TwoIndexHiding}[i^*]}{{\mathbb {P}}}\left[ b' = b_0 \oplus b_1 \right] - \frac{1}{2} ={} o(1/n^3), \) as desired. This completes the proof.
7 A Private Linear Broadcast Scheme with Very Short Keys
In this section we construct a different private linear broadcast scheme for n users where the parameters are essentially reversed—the length of the secret user keys is \(O(\log (n))\) and the length of the ciphertexts is \(\mathrm {poly}(\lambda )\). This scheme will be used to establish our hardness result for differential privacy when the number of queries is exponentially large but the data universe has only polynomial size.
7.1 Construction
Let \(n = \mathrm {poly}(\lambda )\) denote the number of users for the scheme. Let \(m = {\tilde{O}}(n^{6})\) be a parameter. Our construction will rely on the following primitives:
-
A puncturable PRF family \({\mathcal {F}}_{\lambda , sk } = \left\{ \mathsf {PRF}_ sk :[n] \rightarrow [m]\right\} \).
-
A puncturable PRF family \({\mathcal {F}}_{\lambda , \mathsf {Enc}} = \left\{ \mathsf {PRF}_\mathsf {Enc}:[n] \times [m] \rightarrow \{0,1\}\right\} \).
-
An iO scheme \(\mathsf {Obfuscate}\).
Theorem 14
Assuming the existence of one-way functions and indistinguishability obfuscation, for every polynomial n, the scheme \({\varPi }_{\mathrm {short-key}}\) (Fig. 10) is an \((n, d, \ell )\)-private linear broadcast scheme for \(2^{d} = {\tilde{O}}(n^{7})\) and \(\ell = \mathrm {poly}(\lambda )\), and is weakly index-hiding secure.
Combining this theorem with Lemma 7 and Theorem 8 establishes Theorem 2 in the introduction.
Parameters. First we verify that \({\varPi }_\mathrm {short-key}\) is an \((n,d,\ell )\)-private linear broadcast scheme for the desired parameters. Observe that the length of the secret keys is d such that \(2^d = n m\). By construction, since \(m = {\tilde{O}}(n^{6})\), \(2^d = {\tilde{O}}(n^{7})\). The length of the ciphertext is \(|{\mathsf {O}}|\), which is \(\mathrm {poly}(|{\mathsf {P}}|)\) by the efficiency of the obfuscation scheme. By the efficiency of the pseudorandom function family and the pairwise independent hash family, the running time of \({\mathsf {P}}\) is at most \(\mathrm {poly}(\lambda + \log (n))\). Since n is assumed to be a polynomial in \(\lambda \), the ciphertexts have length \(\mathrm {poly}(\lambda )\).
7.2 Proof of Weak Index-Hiding Security
Just as in Sect. 6, we will rely on Lemma 7 so that we only need to show that for every \(\lambda \in {\mathbb {N}}\), and every \(i^* \in [n(\lambda )]\),
We will demonstrate this using a series of hybrids to reduce security of the scheme in the \(\mathbf {TwoIndexHiding}\) game to the security of the pseudorandom function families.
In our argument, recall that the adversary’s view consists of the keys \( sk _{-i^*}\) and the challenge ciphertexts \(c_0, c_1\). In our proof, we will not modify how the keys are generated, so we will present the hybrids only by how the challenge ciphertexts are generated. Also, for simplicity, we will focus only on how \(c_0\) is generated as a function of \(i^*, b_0\) and \( mk \). The ciphertext \(c_1\) will be generated in exactly the same way but as a function of \(i^*, b_1\) and \( mk \). We also remark that we highlight the changes in the hybrids in green.
Hiding the Missing User Key. First we modify the encryption procedure to one where \(\mathsf {PRF}_{ sk }\) is punctured on \(i^*\) and the value \(s^* = \mathsf {PRF}_{ sk }(i^*)\) is hardcoded into the program (Fig. 11).
We claim that, by the security of the iO scheme, the distribution of \(c_0, c_1\) under \(\mathsf {Enc}^1\) is computationally indistinguishable from the distribution of \(c_0, c_1\) under \(\mathsf {Enc}\). The reason is that the obfuscation \({\mathsf {P}}\) and \({\mathsf {P}}^1\) compute the same function. Consider two cases, depending on whether \(i = i^*\) or \(i \ne i^*\). If \(i \ne i^*\), since \(b_0 \in \{0,1\}\), and \(i \ne i^*\), replacing \({\mathbb {I}}\{i \le i^* - b_0\}\) with \({\mathbb {I}}\{i \le i^* - 1\}\) does not change the output. Moreover, since we only reach the branch involving \(\mathsf {PRF}_{ sk }^{\{i^*\}}\) when \(i \ne i^*\), the puncturing does not affect the output of the program. If \(i = i^*\), then the program either outputs \(\mathsf {PRF}_\mathsf {Enc}(i^*, s)\) as it did before when \(s \ne s^*\) or it outputs \(1 - b_0\): equivalent to \({\mathbb {I}}\{i \le i^* - b_0\}\). Thus, by iO, the obfuscated programs are indistinguishable.
Next, we argue that, since \(\mathsf {PRF}_{ sk }^{\{i^*\}}\) is sampled from a puncturable pseudorandom function family, and the adversary’s view consists of \(s_{-i^*} = \{\mathsf {PRF}_{ sk }(i)\}_{i \ne i^*}\) but not \(\mathsf {PRF}_{ sk }(i^*)\), the value of \(\mathsf {PRF}_{ sk }(i^*)\) is computationally indistinguishable to the adversary from a random value. Thus, we can move to another hybrid \((\mathsf {Enc}^2, {\mathsf {P}}^2)\) where the value \(s^*\) is replaced with a uniformly random value \({\tilde{s}}\) (Fig. 12).
Hiding the Challenge Index. Now we want to remove any explicit use of \(b_0\) from \({\mathsf {P}}^2\). The natural way to try to do this is to remove the line where the program outputs \(1 - b_0\) when the input is \((i^*, {\tilde{s}})\), and instead have the program output \(\mathsf {PRF}_\mathsf {Enc}(i^*, {\tilde{s}})\). However, this would involve changing the program’s output on one input, and indistinguishability obfuscation does not guarantee any security in this case. We get around this problem in two steps. First, we note that the value of \(\mathsf {PRF}_\mathsf {Enc}\) on the point \((i^*,{\tilde{s}})\) is never needed in \({\mathsf {P}}^2\), so we can move to a new procedure \({\mathsf {P}}^3\) where we puncture at that point without changing the program functionality. Indistinguishability obfuscation guarantees that \({\mathsf {P}}^2\) and \({\mathsf {P}}^3\) are computationally indistinguishable (Fig. 13).
Next, we define another hybrid \({\mathsf {P}}^4\) where change how we sample \(\mathsf {PRF}_\mathsf {Enc}\) and sample it so that \(\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})=1-b_0\). Observe that the hybrid only depends on \(\mathsf {PRF}_\mathsf {Enc}^{\{(i^*,{\tilde{s}})\}}\). We claim the distributions of \(\mathsf {PRF}_\mathsf {Enc}^{\{(i^*,{\tilde{s}})\}}\) when \(\mathsf {PRF}_\mathsf {Enc}\) is sampled correctly versus sampled conditioned on \(\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})=1-b_0\) are computationally indistinguishable. This follows readily from punctured PRF security. Suppose to the contrary that the two distributions were distinguishable with non-negligible advantage \(\delta \) by adversary A. Then consider a punctured PRF adversary B that is given \(\mathsf {PRF}_\mathsf {Enc}^{\{(i^*,{\tilde{s}})\}},b\) where b is chosen at random, or \(b=\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})\). B distinguishes the two cases as follows. If \(b\ne 1-b_0\), then B outputs a random bit and stops. Otherwise, it runs A on \(\mathsf {PRF}_\mathsf {Enc}^{\{(i^*,{\tilde{s}})\}}\), and outputs whatever A outputs. If b is truly random and independent of \(\mathsf {PRF}_\mathsf {Enc}\), then conditioned on \(b=1-b_0\), \(\mathsf {PRF}_\mathsf {Enc}\) is sampled randomly. However, if \(b=\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})\), then conditioned on \(b=1-b_0\), \(\mathsf {PRF}_\mathsf {Enc}\) is sampled such that \(\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})=1-b_0\). These are exactly the two cases that A distinguishes. Hence, conditioned on \(b=1-b_0\), B guesses correctly with probability \(\frac{1}{2}+\delta \). Moreover, by PRF security, \(b=1-b_0\) with probability \(\ge \frac{1}{2} - \varepsilon \) for some negligible quantity \(\varepsilon \), and in the case \(b\ne 1-b_0\), B guess correctly with probability \(\frac{1}{2}\). Hence, overall B guesses correctly with probability \(\ge \frac{1}{2} (\frac{1}{2} + \varepsilon ) +(\frac{1}{2}+\delta )(\frac{1}{2} - \varepsilon ) = \frac{1}{2} + \frac{\delta }{2} - \varepsilon \delta \). Hence, B has non-negligible advantage \( \frac{\delta }{2} - \varepsilon \delta \). Thus, changing how \(\mathsf {PRF}_\mathsf {Enc}\) is sampled is computationally undetectable, and \({\mathsf {P}}\) is otherwise unchanged. Therefore \({\mathsf {P}}^3\) and \({\mathsf {P}}^4\) are computationally indistinguishable (Fig. 14).
Next, since \(\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})=1-b_0\), we can move to another hybrid \({\mathsf {P}}^5\) where we delete the line “If \(s= {\tilde{s}}\), output \(1-b_0\)” without changing the functionality. Thus, by indistinguishability obfuscation, \({\mathsf {P}}^4\) and \({\mathsf {P}}^5\) are computationally indistinguishable (Fig. 15).
Now notice that \({\mathsf {P}}^5\) is independent of \(b_0\). However, \(\mathsf {Enc}^5\) still depends on \(b_0\). We now move to the final hybrid \({\mathsf {P}}^6\) where we remove the condition that \(\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})=1-b_0\), which will completely remove the dependence on \(b_0\) (Fig. 16).
To prove that \(\mathsf {Enc}^6\) is indistinguishable from \(\mathsf {Enc}^5\), notice that they are independent of \({\tilde{s}}\), except through the sampling of \(\mathsf {PRF}_\mathsf {Enc}\). Using this, and the following lemma, we argue that we can remove the condition that \(\mathsf {PRF}_\mathsf {Enc}(i^*,{\tilde{s}})=1-b_0\).
Lemma 15
Let \({\mathcal {H}}= \left\{ h:[T] \rightarrow [K]\right\} \) be a \(\delta \)-almost pairwise independent hash family. Let \(y \in [K]\) and \(M \subseteq [T]\) of size m be arbitrary. Define the following two distributions.
-
\(D_1\): Choose
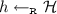 .
. -
\(D_2\): Choose a random \(x \in M\), and then choose
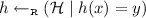 .
.
Then \(D_1\) and \(D_2\) are \((\frac{1}{2}\sqrt{K/m+7K^2 \delta })\)-close in statistical distance.
We defer the proof to the full version. The natural way to try to show that \((\mathsf {Enc}^6, {\mathsf {P}}^6)\) is \(o(1/n^3)\) statistically close to \((\mathsf {Enc}^5, {\mathsf {P}}^5)\) is to apply this lemma to the hash family \({\mathcal {H}}={\mathcal {F}}_{\lambda ,\mathsf {Enc}}\). Recall that a pseudorandom function family is also \(\mathrm {negl}(\lambda )\)-pairwise independent. Here, the parameters would be \([T] = [n] \times [m]\), \(M = \left\{ (i^*, s) \mid s \in [m]\right\} \) and \(b = 1-b_0\), and the random choice \(x \in M\) is the pair \((i^*, {\tilde{s}})\).
However, recall that the adversary not only sees \(c_0 = \mathsf {Enc}^5(i^*,b_0, mk )\), but also sees \(c_1 = \mathsf {Enc}^5(i^*,b_1, mk )\), and these share the same \({\tilde{s}}\). Hence, we cannot directly invoke Lemma 15 on the \(\mathsf {PRF}_{\mathsf {Enc},0}\) sampled in \(c_0\), since \({\tilde{s}}\) is also used to sample \(\mathsf {PRF}_{\mathsf {Enc},1}\) when sampling \(c_1\), and is therefore not guaranteed to be random given \(c_1\).
Instead, we actually consider the function family \({\mathcal {H}}={\mathcal {F}}_{\lambda ,\mathsf {Enc}}^2\), where we define
In \(\mathsf {Enc}^5\), h is drawn at random conditioned on \(h(i^*,{\tilde{s}})=(1-b_0,1-b_1)\), whereas in \(\mathsf {Enc}^6\), it is drawn at random.
\({\mathcal {H}}\) is still a pseudorandom function family, so it must be \(\mathrm {negl}(\lambda )\)-almost pairwise independent with \(\delta \) negligible. In particular, \(\delta =o(1/m)\). Hence, the conditions of Lemma 15 are satisfied with \(K=4\). Since the description of \({\mathsf {P}}^5, {\mathsf {P}}^6\) is the tuple \((i^*, {\tilde{s}}, \mathsf {PRF}_{ sk }^{\{i^*\}}, \mathsf {PRF}_{\mathsf {Enc},0},\mathsf {PRF}_{\mathsf {Enc},1})\), and by Lemma 15 the distribution on these tuples differs by at most \(O(\sqrt{1/m})\) in statistical distance, we also have that the distribution on obfuscations of \({\mathsf {P}}^5, {\mathsf {P}}^6\) differs by at most \(O(\sqrt{1/m})\). Finally, we can choose a value of \(m = {\tilde{O}}(n^{6})\) so that \(O(\sqrt{1/m}) = o(1/n^3)\).
Observe that when we generate user keys \( sk _{-i^*}\) and the challenge ciphertexts according to \((\mathsf {Enc}^6, {\mathsf {P}}^6)\), the distribution of the adversary’s view is completely independent of the random values \(b_0, b_1\). Thus no adversary can output \(b' = b_0 \oplus b_1\) with probability greater than 1 / 2. Since the distribution of these challenge ciphertexts is \(o(1/n^3)\)-computationally indistinguishable from the original distribution on challenge ciphertexts, we have that for every efficient adversary,
as desired. This completes the proof.
Notes
- 1.
It may require exponential time just to describe and evaluate an arbitrary counting query, which would rule out efficiency for reasons that have nothing to do with privacy. In this work, we restrict attention to queries that are efficiently computable in time \(\mathrm {poly}(n,\log |X|)\), so they are not the bottleneck in the computation.
- 2.
We use [1, i] to denote the discrete interval \(\left\{ 1,2,\dots ,i\right\} \), with the convention that \([1,0] = \emptyset \).
- 3.
If we do not restrict the running time of the algorithm, then it is without loss of generality for the algorithm to simply output a list of real-valued answers to each queries by computing \( Eval (S,q)\) for every \(q \in Q\). However, this transformation makes the running time of the algorithm at least |Q|. The additional generality of this framework allows the algorithm to run in time sublinear in |Q|. Using this framework is crucial, since some of our results concern settings where the number of queries is exponential in the size of the dataset.
References
Badrinarayanan, S., Miles, E., Sahai, A., Zhandry, M.: Post-zeroizing obfuscation: new mathematical tools, and the case of evasive circuits. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 764–791. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_27
Beimel, A., Nissim, K., Stemmer, U.: Private learning and sanitization: pure vs. approximate differential privacy. In: Raghavendra, P., Raskhodnikova, S., Jansen, K., Rolim, J.D.P. (eds.) APPROX/RANDOM -2013. LNCS, vol. 8096, pp. 363–378. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40328-6_26
Bellare, M., Stepanovs, I., Tessaro, S.: Contention in cryptoland: obfuscation, leakage and UCE. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 542–564. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_20
Bitansky, N., Paneth, O., Wichs, D.: Perfect structure on the edge of chaos. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 474–502. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_20
Blum, A., Dwork, C., McSherry, F., Nissim, K.: Practical privacy: the SuLQ framework. In: PODS (2005)
Blum, A., Ligett, K., Roth, A.: A learning theory approach to noninteractive database privacy. J. ACM 60(2), 12 (2013)
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). doi:10.1007/11761679_34
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_27
Brzuska, C., Farshim, P., Mittelbach, A.: Indistinguishability obfuscation and UCEs: the case of computationally unpredictable sources. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 188–205. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_11
Bun, M., Ullman, J., Vadhan, S.P.: Fingerprinting codes and the price of approximate differential privacy. In: STOC (2014)
Chor, B., Fiat, A., Naor, M.: Tracing traitors. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 257–270. Springer, Heidelberg (1994). doi:10.1007/3-540-48658-5_25
Coron, J.-S., Gentry, C., Halevi, S., Lepoint, T., Maji, H.K., Miles, E., Raykova, M., Sahai, A., Tibouchi, M.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_12
Dinur, I., Nissim, K.: Revealing information while preserving privacy. In: PODS (2003)
Dwork, C., McSherry, F., Nissim, K., Smith, A.: Calibrating noise to sensitivity in private data analysis. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 265–284. Springer, Heidelberg (2006). doi:10.1007/11681878_14
Dwork, C., Naor, M., Reingold, O., Rothblum, G.N., Vadhan, S.P.: On the complexity of differentially private data release: efficient algorithms and hardness results. In: STOC (2009)
Dwork, C., Nissim, K.: Privacy-preserving datamining on vertically partitioned databases. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 528–544. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_32
Dwork, C., Rothblum, G.N., Vadhan, S.P.: Boosting and differential privacy. In: FOCS. IEEE (2010)
Dwork, C., Smith, A.D., Steinke, T., Ullman, J., Vadhan, S.P.: Robust traceability from trace amounts. In: FOCS (2015)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS, pp. 40–49 (2013)
Garg, S., Mukherjee, P., Srinivasan, A.: Obfuscation without the vulnerabilities of multilinear maps. Cryptology ePrint Archive, Report 2016/390 (2016). http://eprint.iacr.org/
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: FOCS (2015)
Gupta, A., Roth, A., Ullman, J.: Iterative constructions and private data release. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 339–356. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28914-9_19
Hardt, M., Rothblum, G.N.: A multiplicative weights mechanism for privacy-preserving data analysis. In: FOCS (2010)
Hohenberger, S., Sahai, A., Waters, B.: Replacing a random oracle: full domain hash from indistinguishability obfuscation. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 201–220. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_12
Kearns, M.J.: Efficient noise-tolerant learning from statistical queries. J. ACM 45(6), 983–1006 (1998)
Kowalczyk, L., Malkin, T., Ullman, J., Zhandry, M.: Strong hardness of privacy from weak traitor tracing. IACR Cryptology ePrint Archive 2016/721 (2016)
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_22
Mironov, Ilya, Pandey, Omkant, Reingold, Omer, Vadhan, Salil: Computational Differential Privacy. In: Halevi, Shai (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 126–142. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_8
Nikolov, A., Talwar, K., Zhang, L.: The geometry of differential privacy: the sparse and approximate cases. In: STOC (2013)
Roth, A., Roughgarden, T.: Interactive privacy via the median mechanism. In: STOC, pp. 765–774. ACM, 5–8 June 2010
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: STOC (2014)
Steinke, T., Ullman, J.: Between pure and approximate differential privacy. CoRR abs/1501.06095 (2015). http://arxiv.org/abs/org/abs/1501.06095
Thaler, J., Ullman, J., Vadhan, S.: Faster algorithms for privately releasing marginals. In: Czumaj, A., Mehlhorn, K., Pitts, A., Wattenhofer, R. (eds.) ICALP 2012. LNCS, vol. 7391, pp. 810–821. Springer, Heidelberg (2012). doi:10.1007/978-3-642-31594-7_68
Ullman, J.: Answering \(n^{2+o(1)}\) counting queries with differential privacy is hard. In: STOC (2013)
Ullman, J.: Private multiplicative weights beyond linear queries. In: PODS (2015)
Ullman, J., Vadhan, S.: PCPs and the hardness of generating private synthetic data. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 400–416. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_24
Acknowledgments
We thank Dan Boneh for helpful discussions in the early stages of this work. The first author is supported by an NSF Graduate Research Fellowship #DGE-11-44155. The first and second authors are supported in part by the Defense Advanced Research Project Agency (DARPA) and Army Research Office (ARO) under Contract #W911NF-15-C-0236, and NSF grants #CNS-1445424 and #CCF-1423306. Part of this work was done while the third author was a postdoctoral fellow in the Columbia University Department of Computer Science, supported by a junior fellowship from the Simons Society of Fellows. Any opinions, findings and conclusions or recommendations expressed are those of the authors and do not necessarily reflect the views of the the Defense Advanced Research Projects Agency, Army Research Office, the National Science Foundation, or the U.S. Government.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Kowalczyk, L., Malkin, T., Ullman, J., Zhandry, M. (2016). Strong Hardness of Privacy from Weak Traitor Tracing. In: Hirt, M., Smith, A. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9985. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53641-4_25
Download citation
DOI: https://doi.org/10.1007/978-3-662-53641-4_25
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53640-7
Online ISBN: 978-3-662-53641-4
eBook Packages: Computer ScienceComputer Science (R0)


 then we say that c is encrypted to index j.
then we say that c is encrypted to index j.



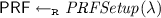 .
.












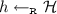 .
.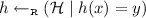 .
.