Abstract
This work exploits internal differentials within a cipher in the context of Differential Fault Analysis (DFA). This in turn overcomes the nonce barrier which acts as a natural counter-measure against DFA. We introduce the concept of internal differential fault analysis which requires only one faulty ciphertext. In particular, the analysis is applicable to parallelizable ciphers that use the counter-mode. As a proof of concept we develop an internal differential fault attack called  on PAEQ which is an AES based parallelizable authenticated cipher presently in the second round of on-going CAESAR competition. The attack is able to uniquely retrieve the key of three versions of full-round PAEQ of key-sizes 64, 80 and 128 bits with complexities of about \(2^{16}\), \(2^{16}\) and \(2^{50}\) respectively. Finally, this work addresses in detail the instance of fault analysis with varying amounts of partial state information and also presents the first analysis of PAEQ.
on PAEQ which is an AES based parallelizable authenticated cipher presently in the second round of on-going CAESAR competition. The attack is able to uniquely retrieve the key of three versions of full-round PAEQ of key-sizes 64, 80 and 128 bits with complexities of about \(2^{16}\), \(2^{16}\) and \(2^{50}\) respectively. Finally, this work addresses in detail the instance of fault analysis with varying amounts of partial state information and also presents the first analysis of PAEQ.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The popularity of cryptanalyzing a cipher by observing its behavior under the influence of faults is mainly attributed to the ease of such fault induction and overhead in incorporating a counter-measure. Among different types of fault based cryptanalysis, Differential Fault Analysis (DFA) [1–7] has garnered particular attention of the side-channel research community since it has been one of the most effective side-channel attacks on symmetric-key constructions. DFA puts in the hand of an attacker an interesting ability: The possibility of performing a differential analysis starting from an intermediate state of the cipher. This ability could be fatal in case of iterated symmetric-key designs since it is equivalent to cryptanalyzing a round-reduced version of the cipher. However, classical DFA has a specific requirement known as the replaying criterion which states that the attacker must be able to induce faults while replaying a previous fault-free run of the algorithm. In this scenario, the introduction of a nonce constraint comes in as a direct contradiction to the ability to replay.
The notion of nonce-based encryption was formalized by Rogaway in [8] where the security proofs relied on the pre-condition of the uniqueness of the nonce in every instantiation of the cipher. Thus, it can be easily inferred why nonces provide an in-built protection against DFA. Usage of nonces to counter fault attacks are already available in Public-Key literature. The famous Bellcore attack [9, 10] on RSA-CRT signatures can be prevented if the message is padded with a random nonce which is recoverable only when verifying a correct signature. It was shown by Coron et al. [11] that in some limited setting these nonces can be tackled. However, the techniques used rely on theoretical constructs which may not be applicable to their private-key counterparts. Though there have also been attempts to mount DFA attacks on symmetric-key designs in the presence of a nonce, the solutions are very specific to the underlying cipher. Such an instance can be found in [12], where the authors studied the impact of the nonce constraint on the fault-attack vulnerability of authenticated cipher APE [13] and demonstrated the idea of faulty collisions to overcome it.
This work tries to address the nonce barrier in a more general setting by totally bypassing the replaying criterion which amplifies the scope of the ideas presented here. This is made possible by a DFA strategy that no longer requires a fault-free run of the cipher. Instead the strategy needs only one multi-block plaintext and faulty ciphertext pair to mount an attack. The nonce constraint is no longer a threat to DFA if the analysis relies on a single faulty ciphertext. The idea of using single faulty ciphertext stems from the prospect of using internal differentials within the cipher. This type of analysis is well-studied and has been successfully used in cryptanalysis of symmetric-key designs [14, 15]. We explore the possibility of deploying this in the context of DFA. In particular, we look at parallelizable authenticated encryption (AE) schemes that use the counter mode of operation to separate the branches. The parallel branches of these schemes provide a good platform for injecting faults and studying the fault propagation in the internal difference of the branches. The main idea is to nullify very low hamming distance between the inputs of the parallel branches using a primary fault and subsequently employ internal differential fault analysis using a secondary fault. To undertake a case-study we select PAEQ which is among the 30 Round-2 candidates in the on-going CAESAR [16] competition on authenticated ciphers. PAEQ meets the basic criteria for analysis since it is parallelizable and uses the counter mode. Moreover, the underlying permutation follows AES [17] very closely which provides an edge in terms of fault analysis. In this work, we present the first analysis of PAEQ in form of an internal difference based fault attack called  on full-round paeq-64, paeq-80 and paeq-128 using a 4-round distinguishing property. Two byte faults are required to be injected in one of the parallel branches during the encryption phase of PAEQ.
on full-round paeq-64, paeq-80 and paeq-128 using a 4-round distinguishing property. Two byte faults are required to be injected in one of the parallel branches during the encryption phase of PAEQ.  uses only one 255-block known plaintext and corresponding faulty ciphertext to significantly reduce the average key-search space of the three versions of PAEQ. Finally, one might be tempted to believe that classical differential fault analysis results on AES would suffice to analyze an AE scheme like PAEQ which is inherently AES based. However, there is a fundamental difference given the fact that the output here is truncated giving an attacker access to only partial information of the state. Thus the current work provides an instance of a fault based analysis of partially specified states.
uses only one 255-block known plaintext and corresponding faulty ciphertext to significantly reduce the average key-search space of the three versions of PAEQ. Finally, one might be tempted to believe that classical differential fault analysis results on AES would suffice to analyze an AE scheme like PAEQ which is inherently AES based. However, there is a fundamental difference given the fact that the output here is truncated giving an attacker access to only partial information of the state. Thus the current work provides an instance of a fault based analysis of partially specified states.
Our Results
-
Introduce the concept of internal differential fault analysis (IDFA) in the context of parallelizable ciphers in the counter mode
-
Showcase that IDFA requires only one run of the algorithm thereby overcoming the nonce barrier of DFA.
-
Present a 4-round internal differential distinguisher for PAEQ.
-
Use the distinguisher to develop the
 attack on full-round PAEQ using only two faults in the same instance of PAEQ
attack on full-round PAEQ using only two faults in the same instance of PAEQ
-
Reduces average key-space of primary PAEQ variants to practical limits viz., paeq-64: \(2^{64}\) to \(2^{16}\), paeq-80: \(2^{80}\) to \(2^{16}\), paeq-128: \(2^{128}\) to \(2^{50}\).
-
Present instances of fault analysis of an AES based design with various types of partially specified internal states.
The rest of the paper is organized as follows. Section 2 provides a brief description of PAEQ. The notations used is the work are given in Sect. 3. The concept of internal differential fault analysis is introduced in Sect. 4. A 4-round distinguisher of PAEQ is showcased in Sect. 5. Section 6 introduces the notion of fault quartets. The  attack on PAEQ is devised in Sect. 7 and its complexity analysis is furnished in Subsect. 7.5. The experimental results are presented in Sect. 8 while the concluding remarks are given in Sect. 9.
attack on PAEQ is devised in Sect. 7 and its complexity analysis is furnished in Subsect. 7.5. The experimental results are presented in Sect. 8 while the concluding remarks are given in Sect. 9.
2 The Design of PAEQ
PAEQ which stands for Parallelizable Authenticated Encryption based on Quadrupled AES was introduced by Biryukov and Khovratovich in ISC 2014 [18] along with a new generic mode of operation PPAE (Parallelizable Permutation-based Authenticated Encryption). It was also submitted to the on-going CAESAR competition for authenticated cipher and is presently one of the 30 round 2 candidates. The design of PAEQ was mainly driven by simplicity and to achieve a security level equal to the key-length. Hence the authors argued in favor of a permutation based design. It is fully parallelizable and on-line and offers a security level up to 128 bits and higher (up to w / 3, \(w \leftarrow \) width of internal permutation) and equal to the key length. An interesting aspect of the PPAE mode of operation (denoted  ) is that the inputs to the internal permutation
) is that the inputs to the internal permutation  are only linked by counters. This property makes PAEQ a prime candidate to apply the concept of fault based internal differentials proposed in this work. Next we touch upon
are only linked by counters. This property makes PAEQ a prime candidate to apply the concept of fault based internal differentials proposed in this work. Next we touch upon  and the internal permutation of PAEQ called AESQ.
and the internal permutation of PAEQ called AESQ.
2.1 PPAE Mode of Operation
 (illustrated in Algorithm 1) can be instantiated with an n-bit permutation
(illustrated in Algorithm 1) can be instantiated with an n-bit permutation  . The inputs to the permutation are formatted as (\(D_i||counter||N||K\)) for each plaintext block and (\(D_i||counter||AD\text{- }block||K\)) for processing associated data (AD) where \(D_i \leftarrow \) domain separator, \(N \leftarrow \) nonce and \(K \leftarrow \) key. The plaintext and AD are divided into blocks of size \(n- k-16\) and \(n- 2k-16\), respectively, where k is the key-size. Incomplete last blocks are padded using the byte-length of the block and domain separators are changed accordingly. Plaintext processing and authentication calls
. The inputs to the permutation are formatted as (\(D_i||counter||N||K\)) for each plaintext block and (\(D_i||counter||AD\text{- }block||K\)) for processing associated data (AD) where \(D_i \leftarrow \) domain separator, \(N \leftarrow \) nonce and \(K \leftarrow \) key. The plaintext and AD are divided into blocks of size \(n- k-16\) and \(n- 2k-16\), respectively, where k is the key-size. Incomplete last blocks are padded using the byte-length of the block and domain separators are changed accordingly. Plaintext processing and authentication calls  twice while AD data is authenticated using a single call. Partial authentication data from all branches are passed to a final call to
twice while AD data is authenticated using a single call. Partial authentication data from all branches are passed to a final call to  , the output of which is optionally truncated to get the tag. The entire operation is depicted in Fig. 1. An interested reader can refer to [18, 19] for details.
, the output of which is optionally truncated to get the tag. The entire operation is depicted in Fig. 1. An interested reader can refer to [18, 19] for details.

2.2 The Internal Permutation: \(\texttt {AESQ} \)
AESQ operates on a 512-bit internal state which can be subdivided into 128-bit substates. Before going into details we introduce some definitions.
Definition 1
(Word). Let \(\mathbb {T} = \mathbb {F}[x]/(x^8 + x^4 + x^3 + x + 1)\) be the field \(\mathbb {F}_{2^8}\) used in the AES MixColumns operation. Then a word is defined as an element of \(\mathbb {T}\).
A word is just a byte redefined to account for the field arithmetic. In this work, we will come across partially specified states/substates where certain words might have unknown values. To capture this scenario, we use the symbol ‘X’ to represent unknown words. Thus, to be precise a word is an element of  .
.
Definition 2
(Substate, State). The internal state of the \(\texttt {AESQ} \) permutation is defined as a 4-tuple of substates where each substate is a \((4 \times 4)\)-word matrix.
A state is denoted by s, while each substate is represented by \(s^m = [s^m_{i,j}]\) where \(s^m_{i,j}\) are the elements of \(s^m\) and m denotes the substate index. We denote a column of \([s^m_{i,j}]\) as \(s^m_{*,j}\) while a row is referred to as \(s^m_{i,*}\).

\(\texttt {AESQ} \) is a composition of 20 round functions with a Shuffle operation (denoted by \({\mathscr {S}}\), Refer Table 1) after every 2 rounds. Each round-function is denoted by \(\mathcal {R}_r\) where the index r denotes the \(r^{th}\) round of AESQ. Every round applies on the internal state a composition of four bijective functions which are basically the standard AES round operations SubBytes, ShiftRows, MixColumns, AddRoundConstants applied individually on each substate. In the context, of a state we denote these functions as \(\beta _r, \rho _r, \mu _r\) and \(\alpha _r\) respectively. The reference to a substate is addressed by including the substate index in notation. For example, to refer to the MixColumns on the second substate in \(\mathcal {R}_{17}\) we use \(\mu ^2_{17}\). Similarly, when considering a substate in \(\mathcal {R}_r\) we refer to the round function applied individually to the substate as \(\mathcal {R}^m_r\) by including the substate index in the notation. This implies that for an internal state s the output of the \(r^{th}\) round of AESQ is  .
.

Round-reduced AESQ permutation is denoted by \(\texttt {AESQ} ^n\) where \(n=2k, 1\le k \le 9\). Thus \(\texttt {AESQ} ^n = \mathscr {S}\circ \mathcal {R}_{n} \circ \mathcal {R}_{n-1} \circ \cdots \circ \mathscr {S} \circ \mathcal {R}_2\circ \mathcal {R}_{1}\). Since n is even, it implies that we consider reductions in steps of two-rounds and \(\texttt {AESQ} ^n\) always ends in the \({\mathscr {S}}\) operation. Finally, the round constant for substate m in round r of AESQ is given by: \(rc^m_r = ((r-1)*4+m)\). In \(\alpha ^m_r\), \(rc^m_r\) is added to all words of row \(s^m_{1,*}\).
2.3 Handling Partially Specified States/Substates
As mentioned earlier in this work we have to handle states or substates that may have multiple unknown values. We now define how the operations \(\beta ^m_r, \rho ^m_r, \mu ^m_r\) and \(\alpha ^m_r\) behave in case of a partially specified substate \(s^m = [s^m_{i,j}]\). Here SBOX denotes the AES Substitution box and \(M_{\mu }\) denotes the MixColumns matrix. \(\rho ^m_r\) does not rely on values of \(s^m\) and just shifts the positions of unknown values.

3 Notations
Definition 3
(Diagonal). A diagonal of a substate \((s^m = [s^m_{i,j}])\) is the set of words which map to the same column under the Shift-Row operation.
Definition 4
(Differential State). A differential state is defined as the element-wise XOR between an internal state \(s = (s^1,s^2,s^3,s^4)\) and the corresponding state \(s' = (s'^1,s'^2,s'^3,s'^4)\) belonging to a different branch of PAEQ.
Definition 5
(Column Vector). A Column Vector, is a set of columns where each element is a candidate for one particular column of a substate.
Definition 6
(State/Substate Vector). A Substate Vector, identified by \([s^m]^v\), is a set of substates where each element is a prospective candidate for substate \(s^m\). A State Vector of state s is the cross-product of its substate vectors.
4 Internal Differential Fault Analysis
In this work, for the first time, we explore the idea of using internal differentials to mount fault based attacks. Though the concept of internal differentials is well-known in cryptanalysis [14, 15], the idea has never been applied in fault based Side Channel Analysis. Our research reveals that the best crypto-primitives to mount such a type of attack are the ones that employ a parallel mode of operation. In principle, internal differentials exploit self-symmetric structures present within a construction. In the parallel mode of operation all parallel branches are structurally similar exhibiting nice instances of such self-symmetry. We look at inputs of such branches. Parallelizable ciphers using the counter mode are generally characterized by the common property that the inputs to the parallel branches only differ in the counter value. Thus, the hamming distance of the inputs are quite low. More interestingly, we can find branches in which the bit positions where the inputs differ are very localized. Footnote 1 This localization can be fatal from the perspective of fault analysis since a fault injection in the counter could possibly lead to a collision in the counter values. So the faulty counter could become equal to a fault-free counter and since the inputs differ only in the counter value this would give us two branches with the same input. This forms a pre-condition for deploying internal differentials analysis since under this scenario, we could inject a second fault in the internal state of any of these two identical branches and study how the fault diffuses in internal difference of the corresponding states. The problem now reduces to classical DFA and hence we may apply standard techniques pertaining to differential fault analysis. Figure 2 depicts the concept visually in a very generic sense.
An interesting aspect of this strategy is that it requires only one multi-block ciphertext with a single faulty block thereby making the analysis independent of the effect of a nonce which prohibits usage of standard DFA. One could argue regarding the viability of the first fault in terms of achieving the counter collision. However, in this work we introduce the concept of Fault Quartets (Refer Sect. 6) which can use a round-reduced distinguisher of the underlying cipher to locate the fault-free branch corresponding to a faulty branch due to the first fault under reasonable assumptions. Building upon these ideas a practical IDFA attack is mounted on PAEQ. Though the specifics rely on the underlying construction, the overall notion of IDFA can be adapted to other ciphers which meet the properties discussed earlier. In the next section we develop a four-round distinguisher of PAEQ based on internal differentials arising from counter values.
5 An Internal Differential Distinguisher for 4-Round \(\texttt {PAEQ} \)
In this section we showcase a 4-round internal differential distinguisher which surfaces due to low Hamming-distance between inputs to various parallel branches of the first call to the \(\texttt {AESQ} \) permutation during the encryption phase. Here we deal with \(\texttt {AESQ} \) reduced to 4-rounds. We start devising the distinguisher by making the following observation which is due to the PPAE mode of operation.
Observation 1
Two parallel branches of \(\texttt {PAEQ} \) with the same domain separator differ only in the counter value.
Based on Observation 1, we first choose any branch of \(\texttt {PAEQ} \) in the encryption phase with counter value i. We next find a branch with counter value j such that their corresponding c-bitFootnote 2 binary representations differ in exactly oneFootnote 3 byte. The main idea is to restrict the internal-difference to a byte and later study its diffusion from \(\mathcal {R}_1\) to \(\mathcal {R}_4\). The differential propagation in an AES round is quite well-known. However, the presence of quadruple \(\texttt {AES} \) instantiations in \(\texttt {AESQ} \) and the inclusion of \({\mathscr {S}}\) operation that mixes the substates make the analysis interesting. Here, we are particularly interested in studying how the bytes belonging to the same column become interrelated as the difference diffuses.
Four Round Differential Propagation in AESQ :
-
\(\mathcal {R}_1\): Difference spreads to entire column, and the bytes are related by factors governed by the MixColumns matrix.
-
\(\mathcal {R}_2\): Entire substate affected; columns of the substate are related by factors.
-
\({\mathscr {S}}\): One column of each substate affected; factor relations unaffected.
-
\(\mathcal {R}_3\): All substates affected. All columns exhibit byte inter-relations due \(\mu _3\).
-
\(\mathcal {R}_4\): All substates still affected with all relations destroyed due to \(\beta _4\)
-
\({\mathscr {S}}\): Columns permute.
This process is illustrated in Fig. 3a. After every round the corresponding byte inter-relations are given. Recall that here we are dealing with a differential state (Definition 4). Here, the numbers in a particular column indicate the factor by which the byte-wise differences in that column are related. In the first substate \(\{2,1,1,3\}\) imply that differences are of the form \(\{2\times f,1 \times f, 1 \times f, 3 \times f\}\) where \( f \in \mathbb {T} \setminus \{0\}\). The byte inter-relations after \(\mathcal {R}_3\) translates into the following observation:
Observation 2
The byte inter-relations after \(\mathcal {R}_r\) due to a difference in \(\mathcal {R}_{r-2}\) input is invariant based on which substate the initial difference was located.Footnote 4
The implication of Observation 2 is that there is a bijective relation between byte inter-relations after \(\mathcal {R}_3\) and substate where we had the initial internal difference in \(\mathcal {R}_1\) input. As there are four substates so we have four unique byte inter-relations (Fig. 6) after \(\mathcal {R}_3\). We can now present the proposed distinguisher in Algorithm 2 which passes with probability 1 for PAEQ if \(n = 4\).

Remark 1
 will fail for any \(n > 4\) because Observation 2 only holds for three rounds while the last round is handled by inversion to get a meet-in-the-middle scenario to verify the byte inter-relations (Fig. 3). Moreover, it might also fail if i and j differ in more than one byte since in that case the internal difference in \(\mathcal {R}_1\) input might span multiple substates. Finally, Distinguisher constitutes a general 3-round differential characteristic which will hold for any 3 consecutive rounds of \(\texttt {AESQ} \) as long as the starting states have an internal difference of one byte. This is what is exploited to develop an internal differential fault attack on \(\texttt {PAEQ} \).
will fail for any \(n > 4\) because Observation 2 only holds for three rounds while the last round is handled by inversion to get a meet-in-the-middle scenario to verify the byte inter-relations (Fig. 3). Moreover, it might also fail if i and j differ in more than one byte since in that case the internal difference in \(\mathcal {R}_1\) input might span multiple substates. Finally, Distinguisher constitutes a general 3-round differential characteristic which will hold for any 3 consecutive rounds of \(\texttt {AESQ} \) as long as the starting states have an internal difference of one byte. This is what is exploited to develop an internal differential fault attack on \(\texttt {PAEQ} \).
From the above remark we get the impression that if somehow we could get a one-byte internal difference in \(\mathcal {R}_{17}\) then the 4-round distinguishing property could be verified from \(\mathcal {R}_{20}\) i.e. the full \(\texttt {AESQ} \) permutation. In order to achieve this scenario we introduce the concept of Fault Quartets in the next section.
6 The Fault Quartet
Definition 7
A fault quartet (\(\mathcal {Q}_{i,j}\)) is a configuration of four internal states of the \(\texttt {AESQ} \) belonging to two different branches i and j of an instance of \(\texttt {PAEQ} \) in the encryption phase. It is uniquely identified by the ordered pair of the branch indexes (i,j). \(\mathcal {Q}_{i,j}\) is of the following form and has the following constraints:
where \({\left\{ \begin{array}{ll} s,t \rightarrow \text{ branch } \text{ input } \text{ states, }\; s^\# = \texttt {AESQ} ^{16}(s), \;t^\# = \texttt {AESQ} ^{16}(t)\\ \text{ Constraint } \text{1 }: s \oplus t = \mathbf {0} \\ \text{ Constraint } \text{2 }: s^\# \text{ and } t^\# \text{ have } \text{ an } \text{ internal } \text{ difference } \text{ of } \text{ one } \text{ byte }. \end{array}\right. }\)
To generate a fault quartet, we take a plaintext of 255 blocksFootnote 5 and induce two random byte faults during the encryption phase of \(\texttt {PAEQ} \). The first fault, called the equalizer is injected in the last byte of the counter of any branch i. The second fault called the differentiator is injected anywhere in the input of \(\mathcal {R}_{17}\) of \(\texttt {AESQ} \) in the same branch. The equalizer achieves the first constraint of \(\mathcal {Q}_{i,j}\) which states that the input states must have no internal difference while the differentiator induces a one-byte internal difference between the outputs of \(\mathcal {R}_{16}\) which constitutes the second constraint. Figure 4 demonstrates the fault injection. The following observation accounts for the choice of a 255-block message above.
Observation 3
The number of the plaintext blocks required to guaranteeFootnote 6 the existence of a fault quartet with the \( \texttt {equalizer} \) fault injected in the last byte of the counter of any branch is 255 with a complete last block.
The complete block at the end ensures that all inputs to AESQ have the same domain separator. The choice of 255 implies that all of these differ only in the last byte of the counter. Due to equalizer fault the counter value of branch i changes to j which is equal to the counter value of anyFootnote 7 one of the remaining 254 fault-free branches. Thus, this outlines the condition to guarantee that a fault quartet is generated. But how would one find such a quartet since neither the input states nor the output of of \(\texttt {AESQ} ^{16}\) is visible to an adversary. This is addressed next where we give an algorithm to find such a quartet.
Finding \(\mathcal {Q}_{i,j}\): Finding a fault-quartet translates into finding the branch-index ordered pair (i, j) where i corresponds to the branch of \(\texttt {PAEQ} \) where the faults have been introduced and the j corresponds to the fault-free branch. This is done by Algorithm 3 using the distinguisher developed earlier as a sub-routine. One can recall that due to the \(\texttt {differentiator} \) there will be a one-byte internal difference between branch i and j in the input of \(\mathcal {R}_{17}\). Thus distinguishing property can be verified from \(\mathcal {R}_{20}\) i.e., the full \(\texttt {AESQ} \) permutation.

\(\mathcal {Q}_{i,j}\) gives us the opportunity to exploit the distinguishing property of \(\texttt {PAEQ} \) in the last four rounds of \(\texttt {AESQ} \). With these concepts we are in a position to finally introduce the  attack which exploits the property further to recover the entire internal state of \(\texttt {AESQ} \) thereby revealing the key.
attack which exploits the property further to recover the entire internal state of \(\texttt {AESQ} \) thereby revealing the key.
7 EnCounter: Fault Analysis of \(\texttt {PAEQ} \) using Internal Differentials
The  attack proceeds in two phases:
attack proceeds in two phases:  and
and  . The
. The  phase is common to all \(\texttt {PAEQ} \) variants while the
phase is common to all \(\texttt {PAEQ} \) variants while the  phase varies. In this work we focus on paeq-64, paeq-80 and paeq-128 which constitute the primary set of \(\texttt {PAEQ} \) family as specified by the designers. We first provide a high-level description of the attack and then delve into the details.
phase varies. In this work we focus on paeq-64, paeq-80 and paeq-128 which constitute the primary set of \(\texttt {PAEQ} \) family as specified by the designers. We first provide a high-level description of the attack and then delve into the details.
High-level Description of

- \(\rightarrow \) :
-
Fault-Injection: Run PAEQ on a plaintext with 255 complete blocks. Inject the equalizer and differentiator faults in any branch i.
- \(\rightarrow \) :
-
Find Fault-Quartet: Use
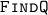 to get index of the fault-free branch.
to get index of the fault-free branch. - \(\rightarrow \) :
-
 Invert states from output of AESQ for both branches and reconstruct internal differential state after \(\mathcal {R}_{19}\). Guess diagonal of differentiator fault to get a set of four column vectors for the state after \(\beta _{19}\).
Invert states from output of AESQ for both branches and reconstruct internal differential state after \(\mathcal {R}_{19}\). Guess diagonal of differentiator fault to get a set of four column vectors for the state after \(\beta _{19}\). - \(\rightarrow \) :
-
 Recovers candidates for all substates at the end of \(\mathcal {R}_{20}\) for the fault-free branch using the column vectors from
Recovers candidates for all substates at the end of \(\mathcal {R}_{20}\) for the fault-free branch using the column vectors from  phase. Return them is the form of substate vectors.
phase. Return them is the form of substate vectors. - \(\rightarrow \) :
-
Complete Attack: Repeat
 phase for every guess of the diagonal and consequently
phase for every guess of the diagonal and consequently  too. Accumulate substate vectors from every guess. Their cross-product gives the reduced state-space for the state after \(\mathcal {R}_{20}\). Inverting every candidate state and verifying the known part of the input reveals the correct key.
too. Accumulate substate vectors from every guess. Their cross-product gives the reduced state-space for the state after \(\mathcal {R}_{20}\). Inverting every candidate state and verifying the known part of the input reveals the correct key.
7.1 The Fault Model
Firstly, as  is an IDFA attack it needs only a single run of PAEQ. Secondly, it is based on a random byte fault model requiring 2 faults: equalizer and differentiator, induced in any branch of AESQ while encrypting the plaintext. equalizer targets the last byte of the counter while differentiator targets any byte at the input of \(\mathcal {R}_{17}\) (Fig. 4). While classical DFA generally deals with single block messages, IDFA uses a single multi-block message as it targets parallelizable ciphers. In the context of
is an IDFA attack it needs only a single run of PAEQ. Secondly, it is based on a random byte fault model requiring 2 faults: equalizer and differentiator, induced in any branch of AESQ while encrypting the plaintext. equalizer targets the last byte of the counter while differentiator targets any byte at the input of \(\mathcal {R}_{17}\) (Fig. 4). While classical DFA generally deals with single block messages, IDFA uses a single multi-block message as it targets parallelizable ciphers. In the context of  the plaintext itself is a 255-block message. After fault injection the attacker uses faulty and fault-free blocks of the same ciphertext and corresponding plaintext blocks to mount the attack. Assuming the faulty branch to be i, faulty ciphertext block
the plaintext itself is a 255-block message. After fault injection the attacker uses faulty and fault-free blocks of the same ciphertext and corresponding plaintext blocks to mount the attack. Assuming the faulty branch to be i, faulty ciphertext block  is identified below.
is identified below.

7.2 The  Phase
Phase
As the name suggests the  phase tries to invert the the faulty and fault-free branches using the observable part of the output. A pictorial abstraction of the process is provided in Fig. 5 for early reference. After identifying the fault-free branch using
phase tries to invert the the faulty and fault-free branches using the observable part of the output. A pictorial abstraction of the process is provided in Fig. 5 for early reference. After identifying the fault-free branch using  , the attacker separately inverts the partially known outputFootnote 8 of AESQ for both branches up to the input of \(\mathcal {R}_{20}\). He then computes the internal difference of the states which gives him a partially specified differential state. This state, by virtue of fault diffusion, has a special property that the differences in individual columns are related. These relations are given in Fig. 6 and help to recover the complete differential state. Further, by Obervation 2 the verified byte inter-relations will also reveal the substate where the differentiator fault got injected.
, the attacker separately inverts the partially known outputFootnote 8 of AESQ for both branches up to the input of \(\mathcal {R}_{20}\). He then computes the internal difference of the states which gives him a partially specified differential state. This state, by virtue of fault diffusion, has a special property that the differences in individual columns are related. These relations are given in Fig. 6 and help to recover the complete differential state. Further, by Obervation 2 the verified byte inter-relations will also reveal the substate where the differentiator fault got injected.
The attacker inverts the reconstructed state up to input of \(\rho _{19}\). Again, due to fault diffusion every substate of this state has exactly one column with non-zero related differences (Refer Fig. 3a). However, the relations differ based on the location of differentiator fault. By virtue of the Diagonal Principle Footnote 9 [7] which is a well-known result of DFA on AES, we know that for a particular substate there can be four kinds of relations based on the diagonal where the differentiator was injected. Figure 7 shows all these possible byte inter-relations based on the source of the byte-fault at the input of \(\mathcal {R}_{17}\).
The attacker already knows which quadrant to look at in Fig. 7 since he knows the substate location of differentiator. However, he has no idea about the source diagonal and has to resort to guessing. So like classical DFA using the input and output difference of \(\beta _{19}\), the attacker solves differential equations to generate candidates for the four columns which are stored in column vectors. At the end of  phase the attacker has a set of four column vectors for the particular guess of the fault diagonal.
phase the attacker has a set of four column vectors for the particular guess of the fault diagonal.
7.3 The  Phase
Phase
Unlike the  phase, the
phase, the  phase works only on the fault-free branch of AESQ specifically on the partial state at the end of \(\mathcal {R}_{20}\). Additionally, the column vectors generated above are also used. Let us look at the nature of the substate in the state determined by \({\mathscr {S}}^{-1}(P_j \oplus C_j)\). This is captured by Fig. 8 for \(\texttt {PAEQ} \) variants analyzed in this work.
phase works only on the fault-free branch of AESQ specifically on the partial state at the end of \(\mathcal {R}_{20}\). Additionally, the column vectors generated above are also used. Let us look at the nature of the substate in the state determined by \({\mathscr {S}}^{-1}(P_j \oplus C_j)\). This is captured by Fig. 8 for \(\texttt {PAEQ} \) variants analyzed in this work.
There are four types of substates with varying number of unknown bytes. The primary aim of this phase is to reduce the search space for these substates. A Type-1 substate is left unaltered since it has no unknown byte. Type-2 and Type-3 are equivalent in the sense that both have three completely known columns while Type-4 can be converted to the same form by guessing 2 bytes of the first column. Thus for the rest of the analysis we assume that we are dealing with a substate with only one unknown column. We now describe how the attacker produces candidates for such a substate. Again Fig. 9 visually illustrates this process for easy reference. Let us consider the \(m^{th}\) substate.
-
1.
The substate is inverted up to output of \(\mu ^m_{19}\). At this point the substate bears a property that every column has exactly one unknown byte.
-
2.
Any column from the corresponding column vectorFootnote 10 is used to form a partial substate which is propagated forward up to the input of \(\mu ^m_{19}\). At this point the substate has exactly one known byte in every column.
-
3.
The attacker exploits linear relations between the partial input and partial output of \(\mu ^m_{19}\) to uniquely retrieve the substate. The recovered substate is propagated forward up to the end of \(\mathcal {R}_{20}\).
-
4.
The process repeated for all columns in the column vector and all computed substates are stored in the corresponding substate vectors.
At the end of the  phase we have a set of substate vectors for all substates of the state after \(\mathcal {R}_{20}\).
phase we have a set of substate vectors for all substates of the state after \(\mathcal {R}_{20}\).
Remark 2
Unlike a Type-3 substate, a Type-2 substate has two extra known bytes in the fourth column which can be exploited. Thus, substate vector is reduced by comparing candidates with respect to these two bytes and eliminated if unmatched. This should lead to large scale reduction of candidates. As regards a Type-4 substate 2 bytes need to be guessed to make it like a Type-3. Thus we have to repeat the process of candidate generation \(2^{16}\) times.
7.4 The Complete Attack
At the outset  repeats the
repeats the  phase four times for different diagonals positions of differentiator. Every iteration returns four column vectors one for each substate of the state after \(\beta _{19}\). The
phase four times for different diagonals positions of differentiator. Every iteration returns four column vectors one for each substate of the state after \(\beta _{19}\). The  phase then follows, iterating over different types of substates \(\in {\mathscr {S}}^{-1}(P_j \oplus C_j)\) from the fault-free branch j returning corresponding substate candidates in substate vectors. The cross-product of the substate vectors forms the state vector which constitutes the reduced state-space for \({\mathscr {S}}^{-1}(P_j \oplus C_j)\). The last step is to invert every candidate state to get the input of branch j. Here, we can exploit the knowledge of the domain separator \(D_0\), the counter value j and the nonce N. This helps to eliminate all wrong candidates and reveals the master key \(\mathcal {K}\). It must be noted that for a particular diagonal guess in
phase then follows, iterating over different types of substates \(\in {\mathscr {S}}^{-1}(P_j \oplus C_j)\) from the fault-free branch j returning corresponding substate candidates in substate vectors. The cross-product of the substate vectors forms the state vector which constitutes the reduced state-space for \({\mathscr {S}}^{-1}(P_j \oplus C_j)\). The last step is to invert every candidate state to get the input of branch j. Here, we can exploit the knowledge of the domain separator \(D_0\), the counter value j and the nonce N. This helps to eliminate all wrong candidates and reveals the master key \(\mathcal {K}\). It must be noted that for a particular diagonal guess in  phase if the size of any substate vector returned by
phase if the size of any substate vector returned by  is empty, all substate vectors generated for that guess are discarded. Algorithm 4 presents
is empty, all substate vectors generated for that guess are discarded. Algorithm 4 presents  at an abstract level. In the next subsection, we perform a complexity analysis.
at an abstract level. In the next subsection, we perform a complexity analysis.
Remark 3
Retrieving diagonal for paeq-64 : In case of paeq-64 since second substate after \(\mathcal {R}_{20}\) (Refer Fig. 8) is completely known (\(\texttt {Type-1} \)), it can be inverted two rounds to reach input of \(\mathcal {R}^2_{19}\) for both branches i, j. The byte inter-relations in the internal-difference of these inputs is verified against the ones given in Fig. 7. This reveals the fault diagonal of differentiator. Thus as a special case, for paeq-64 the diagonal guess can be avoided.

7.5 Complexity Analysis
Here we are mainly interested in getting the size of set \(\mathcal {S}\) since from Algorithm 4 it is evident that \(\texttt {AESQ} ^{-1}\) constitutes the most expensive operation of  and the number of calls is bounded by \(|\mathcal {S}|\). Equation 3 gives the upper bound on the size of \(\mathcal {S}\) assuming that \(s \leftarrow {\mathscr {S}}^{-1}(P_j \oplus C_j)\).
and the number of calls is bounded by \(|\mathcal {S}|\). Equation 3 gives the upper bound on the size of \(\mathcal {S}\) assuming that \(s \leftarrow {\mathscr {S}}^{-1}(P_j \oplus C_j)\).

It implies that it suffices to study the sizes of substate vectors. It was seen in  phase that Type-2 and Type-4 substates are related to Type-3. Accordingly, the sizes of the corresponding substate vectors can be expressed in terms of a Type-3 substate vector. This is furnished in Table 2 where q denotes the size of a Type-3 substate vector while p and r denote sizes of Type-2 and Type-4 substate vectors respectively. Table 3 enumerates the theoretical upper bounds of the complexities individually identifying sizes of the substate vectors.
phase that Type-2 and Type-4 substates are related to Type-3. Accordingly, the sizes of the corresponding substate vectors can be expressed in terms of a Type-3 substate vector. This is furnished in Table 2 where q denotes the size of a Type-3 substate vector while p and r denote sizes of Type-2 and Type-4 substate vectors respectively. Table 3 enumerates the theoretical upper bounds of the complexities individually identifying sizes of the substate vectors.
8 Experimental Results
Computer simulations of  were performed over 1000 randomly chosen nonces, keys. The results for paeq-64/80 are shown in the form of bar diagrams in Figs. 10 and 11 respectively. The bars segregate the substate vectors in terms of their sizes (the value at the base) with the frequency of occurrence given at the top. The figures mainly show that in the average case q is concentrated around \(2^8\). It was mentioned in Remark 2 that in the presence of additional information p could be further reduced such that \(p \ll q\). This is confirmed by the results which show that \(p = 1\) with a few exceptions when \(p = 2\). Table 3 summaries the results while the details are given below:
were performed over 1000 randomly chosen nonces, keys. The results for paeq-64/80 are shown in the form of bar diagrams in Figs. 10 and 11 respectively. The bars segregate the substate vectors in terms of their sizes (the value at the base) with the frequency of occurrence given at the top. The figures mainly show that in the average case q is concentrated around \(2^8\). It was mentioned in Remark 2 that in the presence of additional information p could be further reduced such that \(p \ll q\). This is confirmed by the results which show that \(p = 1\) with a few exceptions when \(p = 2\). Table 3 summaries the results while the details are given below:
-
paeq-64: By Remark 3 we know that the diagonal for differentiator can be recovered thereby avoiding the guessing step in Algorithm 4 and reducing the complexity by a factor of four. So the final experimentally verified size of \(\mathcal {S}\) for paeq-64 stands at \(72292 \approx 2^{16.14}\).
-
paeq-80: During simulation it was found that for Type-2 substates
 phase returned empty substate vectors for a wrong guess of faulty diagonal. This made Step 6 of Algorithm 4 to be TRUE reducing \(|\mathcal {S}|\) by four times. So the final verified size \(72578 \approx 2^{16.14}\) is very close to paeq-64.
phase returned empty substate vectors for a wrong guess of faulty diagonal. This made Step 6 of Algorithm 4 to be TRUE reducing \(|\mathcal {S}|\) by four times. So the final verified size \(72578 \approx 2^{16.14}\) is very close to paeq-64. -
paeq-128: It has three Type-3 substates contributing around \(2^{24}\) while a Type-4 substate is supposed to contribute over \(2^{16}\times 2^8\). Finally, the complexity is increased four times due to diagonal guess. Thus the estimated value of \(|\mathcal {S}|\) is around \(2^{50}\).
 Complexities
Complexities9 Conclusion
This work introduces the notion of fault analysis using internal differentials. Parallelizable ciphers using the counter mode are found to be good targets for such kind of analysis though the real attack relies on the underlying construction. A 4-round distinguisher for authenticated cipher PAEQ is demonstrated. Using this the idea of fault quartets is proposed which can locate the fault-free branch corresponding to a faulty branch. Finally, an internal differential fault attack  is devised against PAEQ using just two random byte faults with only a single faulty ciphertext and the corresponding plaintext. The attack reduces the key-space of paeq-64, paeq-80 and paeq-128 to around \(2^{16}\), \(2^{16}\) and \(2^{50}\) respectively. The ability to mount an attack using a single faulty run of the cipher makes IDFA independent of the effect of nonce thereby breaking the nonce barrier of DFA. Moreover, the fault analysis presented here is of particular interest since it deals with internal states that are partially specified which deviates it from classical DFA. Finally, this work constitutes the first analysis of CAESAR candidate PAEQ.
is devised against PAEQ using just two random byte faults with only a single faulty ciphertext and the corresponding plaintext. The attack reduces the key-space of paeq-64, paeq-80 and paeq-128 to around \(2^{16}\), \(2^{16}\) and \(2^{50}\) respectively. The ability to mount an attack using a single faulty run of the cipher makes IDFA independent of the effect of nonce thereby breaking the nonce barrier of DFA. Moreover, the fault analysis presented here is of particular interest since it deals with internal states that are partially specified which deviates it from classical DFA. Finally, this work constitutes the first analysis of CAESAR candidate PAEQ.
Notes
- 1.
For instance, the differing bits could be localized within a byte.
- 2.
Recall, the counter is of size \(c = n - k - 16\) bits.
- 3.
For instance, \(i = 5\) and \(j = 8\) differ only in the least significant byte.
- 4.
It is understood that \(r>2\) and \(2|(r-1)\).
- 5.
Last block is a complete block (i.e., block-size \(= n-k-16\)) due to Observation 1.
- 6.
With a probability of
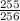 .
. - 7.
Except for the case when \(j=0\) when it matches none of the remaining branches.
- 8.
Computed using the XOR of plaintext and ciphertext blocks.
- 9.
Faults injected in the same diagonal of an AES state in round r input lead to the same byte interrelations at the end of round \((r+1)\).
- 10.
Recall that the column vector corresponds to the state after \(\beta _{19}\).
References
Biham, E., Shamir, A.: Differential fault analysis of secret key cryptosystems. In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 513–525. Springer, Heidelberg (1997)
Giraud, C.: DFA on AES. In: Dobbertin, H., Rijmen, V., Sowa, A. (eds.) AES 2005. LNCS, vol. 3373, pp. 27–41. Springer, Heidelberg (2005)
Dusart, P., Letourneux, G., Vivolo, O.: Differential fault analysis on A.E.S. IACR Cryptology ePrint Archive, 2003:10 (2003). http://eprint.iacr.org/2003/010
Piret, G., Quisquater, J.-J.: A differential fault attack technique against SPN structures, with application to the AES and KHAZAD. In: Walter, C.D., Koç, Ç.K., Paar, C. (eds.) CHES 2003. LNCS, vol. 2779, pp. 77–88. Springer, Heidelberg (2003)
Moradi, A., Shalmani, M.T.M., Salmasizadeh, M.: A generalized method of differential fault attack against AES cryptosystem. In: Goubin, L., Matsui, M. (eds.) CHES 2006. LNCS, vol. 4249, pp. 91–100. Springer, Heidelberg (2006)
Mukhopadhyay, D.: An improved fault based attack of the advanced encryption standard. In: Preneel, B. (ed.) AFRICACRYPT 2009. LNCS, vol. 5580, pp. 421–434. Springer, Heidelberg (2009)
Saha, D., Mukhopadhyay, D., Chowdhury, D.R.: A diagonal fault attack on the advanced encryption standard. IACR Cryptology ePrint Archive, 2009:581 (2009). http://eprint.iacr.org/2009/581
Rogaway, P.: Nonce-based symmetric encryption. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 348–359. Springer, Heidelberg (2004)
Boneh, D., DeMillo, R.A., Lipton, R.J.: On the importance of eliminating errors in cryptographic computations. J. Cryptol. 14(2), 101–119 (2001)
Joye, M., Lenstra, A.K., Quisquater, J.-J.: Chinese remaindering based cryptosystems in the presence of faults. J. Cryptol. 12(4), 241–245 (1999)
Coron, J.-S., Joux, A., Kizhvatov, I., Naccache, D., Paillier, P.: Fault attacks on RSA signatures with partially unknown messages. In: Clavier, C., Gaj, K. (eds.) CHES 2009. LNCS, vol. 5747, pp. 444–456. Springer, Heidelberg (2009)
Saha, D., Kuila, S., Chowdhury, D.R.: EscApe: diagonal fault analysis of APE. In: Progress in Cryptology - INDOCRYPT 2014 - 15th International Conference on Cryptology in India, New Delhi, India, December 14–17, 2014, pp. 197–216 (2014)
Andreeva, E., Bilgin, B., Bogdanov, A., Luykx, A., Mennink, B., Mouha, N., Wang, Q., Yasuda, K.: PRIMATEs v1.02. Submission to the CAESAR Competition (2014). http://competitions.cr.yp.to/round2/primatesv102.pdf
Peyrin, T.: Improved differential attacks for ECHO and Grøstl. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 370–392. Springer, Heidelberg (2010)
Dinur, I., Dunkelman, O., Shamir, A.: Collision attacks on up to 5 rounds of SHA-3 using generalized internal differentials. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 219–240. Springer, Heidelberg (2014)
CAESAR: Competition for Authenticated Encryption: Security, Applicability, and Robustness. http://competitions.cr.yp.to/caesar.html
Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard. Information Security and Cryptography. Springer, Heidelberg (2002)
Biryukov, A., Khovratovich, D.: PAEQ: parallelizable permutation-based authenticated encryption. In: Chow, S.S.M., Camenisch, J., Hui, L.C.K., Yiu, S.M. (eds.) ISC 2014. LNCS, vol. 8783, pp. 72–89. Springer, Heidelberg (2014)
Khovratovich, D., Biryukov, A.: PAEQ v1. Submission to the CAESAR Competition (2014). http://competitions.cr.yp.to/round1/paeqv1.pdf
Acknowledgement
We would like to thank the anonymous reviewers for their invaluable comments and Orr Dunkelman for helping us in preparing the final version of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Saha, D., Chowdhury, D.R. (2016). EnCounter: On Breaking the Nonce Barrier in Differential Fault Analysis with a Case-Study on PAEQ . In: Gierlichs, B., Poschmann, A. (eds) Cryptographic Hardware and Embedded Systems – CHES 2016. CHES 2016. Lecture Notes in Computer Science(), vol 9813. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53140-2_28
Download citation
DOI: https://doi.org/10.1007/978-3-662-53140-2_28
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53139-6
Online ISBN: 978-3-662-53140-2
eBook Packages: Computer ScienceComputer Science (R0)





 attack on full-round
attack on full-round 



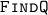 to get index of the fault-free branch.
to get index of the fault-free branch. Invert states from output of
Invert states from output of  Recovers candidates for all substates at the end of
Recovers candidates for all substates at the end of  phase. Return them is the form of substate vectors.
phase. Return them is the form of substate vectors. phase for every guess of the diagonal and consequently
phase for every guess of the diagonal and consequently  too. Accumulate substate vectors from every guess. Their cross-product gives the reduced state-space for the state after
too. Accumulate substate vectors from every guess. Their cross-product gives the reduced state-space for the state after  Phase
Phase
 phase. Returns candidates for columns after
phase. Returns candidates for columns after 

 Phase
Phase

 phase. Returns candidates for substates after
phase. Returns candidates for substates after  phase returned empty substate vectors for a wrong guess of faulty diagonal. This made Step 6 of Algorithm 4 to be
phase returned empty substate vectors for a wrong guess of faulty diagonal. This made Step 6 of Algorithm 4 to be 

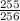 .
.