Efficient Fuzzy Extraction of PUF-Induced Secrets: Theory and Applications

Abstract

The device-unique response of a physically unclonable function (PUF) can serve as the root of trust in an embedded cryptographic system. Fuzzy extractors transform this noisy non-uniformly distributed secret into a stable high-entropy key. The overall efficiency thereof, typically depending on error-correction with a binary [n, k, d] block code, is determined by the universal and well-known $(n-k)$ bound on the min-entropy loss. We derive new considerably tighter bounds for PUF-induced distributions that suffer from, e.g., bias or spatial correlations. The bounds are easy-to-evaluate and apply to large non-trivial codes, e.g., BCH, Hamming and Reed-Muller codes. Apart from an inherent reduction in implementation footprint, the newly developed theory also facilitates the analysis of state-of-the-art error-correction methods for PUFs. As such, we debunk the reusability claim of the reverse fuzzy extractor. Moreover, we provide proper quantitative motivation for debiasing schemes, as this was missing in the original proposals.

1 Introduction

Cryptography relies on reproducible uniformly distributed secret keys. Obtaining affordable physically secure key-storage in embedded non-volatile memory is hard though. Harvesting entropy from physically unclonable functions (PUFs) comprehends an alternative that lowers the vulnerability during the power-off state. Unfortunately, PUF responses are corrupted by noise and non-uniformities are bound to occur. A fuzzy extractor [11] provides an information-theoretically secure mechanism to convert PUF responses into high-quality keys. The essential building block for handling noisiness is the secure sketch, providing error-correction with most frequently a binary [n, k, d] block code. Associated public helper data reveals information about the PUF response though; the system provider should hence quantify how much min-entropy remains. So far, the conservative $(n-k)$ upper bound on the min-entropy loss has been applied. Unfortunately, the residual min-entropy is underestimated, implying that more PUF response bits than necessary have to be used. Expensive die area is hence blocked by PUF circuits that are not strictly required to obtain the desired security level, i.e., symmetric key length.

1.1 Contribution

The novelty of our work is twofold:

• First, we derive new bounds on the secure sketch min-entropy loss for PUF-induced distributions with practical relevance. Our bounds are considerably tighter than the well-known $(n-k)$ formula, hereby improving the implementation efficiency of PUF-based key generators. The discrepancy is showcased for two predominant PUF imperfections, i.e., biased and spatially correlated response bits. It is important to note that a variety of commonly used codes is covered, e.g., BCH and Reed-Muller codes, regardless of their algebraic complexity. Furthermore, a large variety of distributions could be supported. Therefore, our scope reaches considerably further than related work in [8, 22], focussing on simple repetition codes and biased distributions only. As in the latter works, our bounds are easy-to-evaluate and able to support large codes.

• Second, the newly developed theory is applied to state-of-the-art error-correction methods for PUFs. As such, we reveal a fundamental flaw in the reverse fuzzy extractor, proposed by Van Herrewege et al. [28] at Financial Crypto 2012. The latter lightweight primitive is gaining momentum and has also been adopted in the CHES 2015 protocol of Aysu et al. [1]. We debunk the main security claim that repeated helper data exposure does not result in additional min-entropy loss. Furthermore, we contribute to the motivation of debiasing schemes such as the index-based syndrome (IBS) proposal of Yu et al. [30], and the CHES 2015 proposal of Maes et al. [22]. The latter proposals assume that a stand-alone sketch cannot handle biased distributions. We eliminate the need for an educated guess that originates from the extrapolation of repetition code insights and/or the application of the overly conservative $(n-k)$ bound.

1.2 Organization

The remainder of this manuscript is organized as follows. Section 2 introduces notation and preliminaries. Section 3 derives new tight bounds on the secure sketch min-entropy loss. Section 4 elaborates applications of the newly developed theory. Section 5 concludes the work.

2 Preliminaries

2.1 Notation

Binary vectors are denoted with a bold lowercase character, e.g., $\varvec{x}$. All vectors are row vectors. All-zeros and all-ones vectors are denoted with $\varvec{0}$ and $\varvec{1}$ respectively. Binary matrices are denoted with a bold uppercase character, e.g., $\varvec{H}$. A random variable and its corresponding set of outcomes are denoted with an uppercase italic and calligraphic character respectively, e.g., $X$ and $\mathcal {X}$. Variable assignment is denoted with an arrow, e.g., $\varvec{x} \leftarrow X$. Custom-defined procedure names are printed in a sans-serif font, e.g., Hamming weight $\mathsf {HW}(\varvec{x})$ and Hamming distance $\mathsf {HD}(\varvec{x},\widetilde{\varvec{x}})$. The probability of an event A is denoted as $\mathbb {P}(A)$. The expected value of a function $g(X)$ of random variable $X$ is denoted as $\mathbb {E}_{x \leftarrow X}[g(X)]$. The probability density function and cumulative distribution function of a standard normal distribution N(0, 1) are denoted as $\mathsf {f}_\mathsf {norm}(\cdot )$ and $\mathsf {F}_\mathsf {norm}(\cdot )$ respectively. For a binomial distribution with n trials and success probability p, we use $\mathsf {f}_\mathsf {bino}(\cdot ;n,p)$ and $\mathsf {F}_\mathsf {bino}(\cdot ;n,p)$ respectively.

2.2 Min-Entropy Definitions

The min-entropy of a random variable $X$ is as defined in (1). Consider now a pair of possibly correlated random variables: $X$ and $P$. The conditional min-entropy [11] of $X$ given $P$ is as defined in (2). Terms with $\mathbb {P}(P = p) = 0$ are evaluated as 0. Both definitions quantify the probability that an attacker guesses $x \leftarrow X$ first time right, on a logarithmic scale. We emphasize that min-entropy is a more conservative notion than Shannon entropy and therefore often preferred within cryptology.

$$\begin{aligned} \mathbb {H}_{\infty }(X) = - \log _2 \bigl ( \max _{x \in \mathcal {X}} \mathbb {P}(X = x) \bigr ). \end{aligned}$$

(1)

$$\begin{aligned} \widetilde{\mathbb {H}}_{\infty }(X|P) = -\log _2 \Bigl (\mathbb {E}_{p \leftarrow P}\bigl [\max _{x \in \mathcal {X}} \mathbb {P}((X = x)|(P = p))\bigr ]\Bigr ). \end{aligned}$$

(2)

2.3 Physically Unclonable Functions

A prominent category of PUFs, suitable for key generation in particular, consists of an array of identically designed cells. Each cell produces a single bit, or occasionally a few bits. This includes memory-based designs, such as the SRAM PUF [16], as well as the coating PUF [25] and a subset of the large number of ring oscillator-based designs, e.g., [29]. The most prominent entropy-degrading effects for such PUFs are bias and spatial correlations. Bias comprehends an imbalance between the number of zeros and ones. Spatial correlations implicate that neighboring cells might influence each other.

We describe a parameterized probability distribution for the error rate of individual PUF response bits $\widetilde{\varvec{x}}(i)$, with $i \in [1,n]$. Experimental validation on various PUF circuits, e.g., in [10, 20], labelled the model as accurate. Two hidden random variables are incorporated: the normalized manufacturing variability $V_i \sim N(0,1)$, drawn only once for each response bit, and additive noise $N_{ij} \sim N(0,\sigma _N)$, drawn for each evaluation j of a given response bit. A response bit $\widetilde{\varvec{x}}(i)$ evaluates to 1 if $(v_i + n_{ij}) > t$ and 0 otherwise, with threshold t a fixed parameter. Bias corresponds to a nonzero t. Spatial correlations can be incorporated via a multivariate normal distribution $\begin{pmatrix}V_1&\ldots&V_n \end{pmatrix}\sim N(\varvec{0},\varvec{\varSigma })$, with $\varvec{\varSigma }$ the symmetric $n \times n$ covariance matrix.

For ease of analysis, we consider the response bits $\varvec{x}(i)$ obtained by thresholding $v_i > t$ as a reference. In practice, these nominal values can be approximated via a majority vote among noisy replicas $\widetilde{\varvec{x}}(i)$, possibly accelerated via circuit techniques [4, 30]. Bias parameter b, defined as the probability $\mathbb {P}(\varvec{x}(i) = 1)$, then equals $\mathsf {F}_\mathsf {norm}(-t)$. Zero bias corresponds to $b = 0.5$. The error rate $p_E$ of a response bit $\widetilde{\varvec{x}}(i)$ with respect to its reference, i.e., the probability $\mathbb {P}(\varvec{x}(i) \ne \widetilde{\varvec{x}}(i))$, then equals $\mathsf {F}_\mathsf {norm}(-|v_i-t|/\sigma _N)$.

2.4 Secure Sketch and Fuzzy Extractor Definitions

Secure sketches operate on a metric space $\mathcal {X}$ with distance function $\mathsf {dist}$. For PUFs, we can restrict our attention to binary vectors $\varvec{x} \in \{0,1\}^{1 \times n}$ and the Hamming distance $\mathsf {HD}$ therebetween. An attacker knows the probability distribution of $\varvec{x} \leftarrow X$. Consider a noisy version $\widetilde{\varvec{x}}$ of sample $\varvec{x}$. A secure sketch [11] is a pair of efficient and possibly randomized procedures: the sketching procedure $\varvec{p} \leftarrow \mathsf {SSGen}(\varvec{x})$, with helper data $\varvec{p} \in \mathcal {P}$, and the recovery procedure $\widehat{\varvec{x}} \leftarrow \mathsf {SSRep}(\widetilde{\varvec{x}},\varvec{p})$. There are two defining properties:

• Correctness. If $\mathsf {HD}(\varvec{x},\widetilde{\varvec{x}}) \le t$, correctness of reconstruction is guaranteed, i.e., $\widehat{\varvec{x}} = \varvec{x}$. If $\mathsf {HD}(\varvec{x},\widetilde{\varvec{x}}) > t$, there is no guarantee whatsoever.

• Security. Given a certain lower bound $h_{\mathsf {in}}$ on the ingoing min-entropy, i.e., $\mathbb {H}_{\infty }(X)$ $\ge h_{\mathsf {in}}$, a corresponding lower bound $h_{\mathsf {out}}$ on the residual min-entropy, i.e., $\widetilde{\mathbb {H}}_{\infty }(X|P)$ $\ge h_{\mathsf {out}}$, can be imposed. Often, but not necessarily, this condition can be satisfied regardless of $h_{\mathsf {in}}$. Or stated otherwise, there is a certain upper bound on the min-entropy loss $\varDelta \mathbb {H}_{\infty }= \mathbb {H}_{\infty }(X) - \widetilde{\mathbb {H}}_{\infty }(X|P)$.

A slightly modified notion brings us to the fuzzy extractor [11]. Output $\varvec{k} \in \mathcal {K}$ is then required to be nearly-uniform, given observation $\varvec{p} \leftarrow P$, and is therefore suitable as a secret key. There is a proven standard method to craft a fuzzy extractor from a secure sketch. In particular, a randomness extractor could derive a key from the secure sketch output, i.e., $\varvec{k} \leftarrow \mathsf {Ext}(\varvec{x})$. Universal hash functions [7] are good randomness extractors, according to the (generalized) leftover hash lemma [2, 13]. Unfortunately, their min-entropy loss is quite substantial. In practice, key generators therefore often rely on a cryptographic hash function that is assumed to behave as a random oracle. The latter idealized heuristic results in zero min-entropy loss.

2.5 Coding Theory

A binary code $\mathcal {C}$ is a bijection from a message space $\mathcal {M}$ to a codeword space $\mathcal {W} \subseteq \{0,1\}^{1 \times n}$. The minimum distance d is the minimum number of bits in which any two distinct codewords differ. A procedure $\varvec{w} \leftarrow \mathsf {Encode}(\varvec{m})$ maps a message $\varvec{m} \in \mathcal {M}$ to a codeword $\varvec{w} \in \mathcal {W}$. A procedure $\widehat{\varvec{w}} \leftarrow \mathsf {Correct}(\widetilde{\varvec{w}})$ corrects up to $t = \lfloor \frac{d-1}{2} \rfloor$ errors for any noise-corrupted codeword $\widetilde{\varvec{w}} = \varvec{w} \oplus \varvec{e}$, with $\mathsf {HW}(\varvec{e}) \le t$. Equation (3) expresses the Hamming bound [18]. The equality holds for perfect codes only, implicating that any vector in $\{0,1\}^{1 \times n}$ is within distance t of a codeword. All other codes are subject to the inequality.

$$\begin{aligned} \sum _{i = 0}^t \left( {\begin{array}{c}n\\ i\end{array}}\right) |\mathcal {M}| \le 2^{n}. \end{aligned}$$

(3)

A binary [n, k, d] block code $\mathcal {C}$ restricts the message length $k = \log _2(|\mathcal {M}|)$ to an integer. For a linear block code, any linear combination of codewords is again a codeword. A $k \times n$ generator matrix $\varvec{G}$, having full rank, can then implement the encoding procedure, i.e., $\varvec{w} = \varvec{m} \cdot \varvec{G}$. For any translation $\varvec{\tau } \in {\{0,1\}}^{1 \times n}$ and linear code $\mathcal {C}$, the set $\{\varvec{\tau } \oplus \varvec{w} : \varvec{w} \in \mathcal {W}\}$ is referred to as a coset. Two cosets are either disjoint or coincide. Therefore, the vector space $\{0,1\}^{1 \times n}$ is fully covered by $2^{n-k}$ cosets, referred to as the standard array. The minimum weight vector $\varvec{\epsilon }$ in a coset is called the coset leader. In case of conflict, i.e., a common minimum $\mathsf {HW}(\varvec{\epsilon }) > t$, an arbitrary leader can be selected. The minimum distance d of a linear code equals the minimum Hamming weight of its nonzero codewords. A linear code $\mathcal {C}$ is cyclic if every circular shift of a codeword is again a codeword belonging to $\mathcal {C}$.

2.6 The Code-Offset Secure Sketch

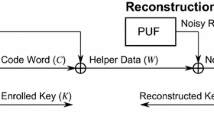
Several secure sketch constructions rely on a binary code $\mathcal {C}$. For ease of understanding, we focus on the code-offset method of Dodis et al. [11] exclusively. Nevertheless, equivalencies in the extended version of this manuscript (Cryptology ePrint Archive, Report 2015/854) prove that all results apply to six other constructions equally well. The code $\mathcal {C}$ that instantiates the code-offset method in Fig. 1 is not necessarily linear. Even more, it is not required be a block code either. Linear codes (BCH, Hamming, repetition, etc.) remain the most frequently used though due to their efficient decoding algorithms [18]. Correctness of reconstruction is guaranteed if $\mathsf {HD}(\varvec{x},\widetilde{\varvec{x}}) \le t$, with t the error-correcting capability of the code.

Fig. 1.

The code-offset secure sketch, having an n-bit reference input $\varvec{x}$.

Min-entropy loss can be understood as a one-time pad imperfection. Sketch input $\varvec{x}$ is masked with a random codeword $\varvec{w}$, i.e., an inherent entropy deficiency: $\mathbb {H}_{\infty }(W) = \log _2(|\mathcal {M}|) < n$. For linear codes in particular, we highlight a convenient interpretation using cosets. Helper data $\varvec{p}$ then reveals in which coset reference $\varvec{x}$ resides. It can be seen easily that $\varvec{p}$ is equal to a random vector in the same coset as $\varvec{x}$. The residual min-entropy in (2) hence reduces to (4) for linear codes, with $\varvec{\epsilon }$ a coset leader. We emphasize that the min-entropy loss $\varDelta \mathbb {H}_{\infty }$ does not depend on the decoding method, simply because the helper data is not affected. For [n, k, d] block codes in particular, the well-known upper bound $\varDelta \mathbb {H}_{\infty }\le (n-k)$ holds, as proven in [11]. More generally, this extends to $\varDelta \mathbb {H}_{\infty }\le n - \log _2(|\mathcal {M}|)$.

(4)

3 Tight Bounds on the Min-Entropy Loss

Currently, secure sketch implementations rely on the $(n-k)$ upper bound on the min-entropy loss, e.g., [23]. Unfortunately, this leads to an overly conservative design when instantiating security parameters accordingly. We develop a graphical framework that produces tight bounds on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ for typical PUF-induced distributions. The critical first-order effects of bias and spatial correlations are captured. Both lower and upper bounds are supported. The lower bounds are of primary interest for a conservative system provider, entertaining the worst-case scenario. We considerably improve upon the $(n-k)$ bound, i.e., the leftmost inequality in (5). We also improve upon the rather trivial upper bounds [11] that comprehend the rightmost inequality in (5).

$$\begin{aligned} \underbrace{\max (\mathbb {H}_{\infty }(X)-(n-\log _2(|\mathcal {M}|)),0)}_\text {worst-case} \le \widetilde{\mathbb {H}}_{\infty }(X|P) \le \underbrace{\min (\log _2(|\mathcal {M}|),\mathbb {H}_{\infty }(X))}_\text {best-case}. \end{aligned}$$

(5)

Our lower and upper bounds combined define a relatively narrow interval in which the exact value of $\widetilde{\mathbb {H}}_{\infty }(X|P)$ is enclosed. We considerably extend related work in [8, 22] as follows. First, we cover a variety of codes, regardless of their algebraic complexity. Prior work focussed on repetition codes only. Although frequently used as the inner code of a concatenated code [5], full-fledged key generators [23] typically rely on non-trivial codes, e.g., BCH codes [18]. Second, our techniques may be applied to a variety of distributions, while prior work covered biased distributions only. Our bounds remain easy-to-evaluate and are able to handle large codes. Although derived for the code-offset sketch of Dodis et al. [11] in particular, the extended version of this manuscript establishes the equivalence with six other constructions.

3.1 Distributions

Our work is generic in the sense that a large variety of distributions $X$ could be covered. We only require that $\mathcal {X} = \{0,1\}^{1 \times n}$ can be partitioned in a limited number of subsets $\varphi _j$, with $j \in [1,J]$, so that all elements of $\varphi _j$ have the same probability of occurrence $q_j$. Formally, $\mathbb {P}(X = \varvec{x})= q_j$ if and only if $\varvec{x} \in \varphi _j$. These probabilities are strictly monotonically decreasing, i.e., $q_1> q_2> \ldots > q_J$. Occasionally, $q_J = 0$. The ingoing min-entropy is easily computed as $\mathbb {H}_{\infty }(X) = -\log _2(q_1)$.

We determine bounds on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. The runtime of the corresponding algorithms is roughly proportional to J. The crucial observation is that even a very small J might suffice to capture realistic PUF models. Below, we describe a parameterized distribution X for both biased and spatially correlated PUFs. Both distributions are to be considered as proof-of-concept models, used in showcasing the feasibility of a new research direction. In case a given PUF is not approximated accurately enough, one can opt for an alternative and possibly more complicated second-order distribution. As long as J is limited, bounds can be evaluated in milliseconds-minutes on a standard desktop computer.

• Biased distribution. We assume response bits to be independent and identically distributed (i.i.d.) so that $\mathbb {P}(X(i) = 1) = b$, with $i \in [1,n]$ and a real-valued $b \in [0,1]$. For $b = \frac{1}{2}$, this corresponds to a uniform distribution. The latter bias model comprehends a very popular abstraction in PUF literature. The min-entropy loss of various other helper data methods has been analyzed as such, e.g., soft-decision decoding [8, 21] as well as IBS [15, 30] and von Neumann [22, 27] debiasing. Therefore, our results enable adequate comparison with related methods, all using a common baseline distribution.

• Correlated distribution. We assume response bits to be distributed so that $\mathbb {P}(X(i) = X(i+1)) = c$, with $i \in [1,n-1]$ and a real-valued $c \in [0,1]$. This extends to (6) for larger neighborhoods. There is no bias, i.e., $\mathbb {P}(X(i) = 1) = \frac{1}{2}$. For $c = \frac{1}{2}$, the latter model corresponds to a uniform distribution. Although spatial correlations are frequently encountered in experimental work, e.g., byte-level dependencies for the SRAM PUFs in [1, 14], these are often neglected in information theoretic work due to their complexity. We hope that our results may help turn the tide on this.

  $$\begin{aligned} \mathbb {P}(X(i) = X(j)) = \sum _{u=0}^{\lfloor |i-j|/2\rfloor } \mathsf {f}_\mathsf {bino}(2u;|i-j|,1-c), \quad \text {with}\ i,j \in [1,n]. \end{aligned}$$

  (6)

Figure 2 specifies the subsets $\varphi _j$ for both distributions. For the biased distribution, we partition according to $\mathsf {HW}(\varvec{x})$. This corresponds to a binomial distribution with $j-1$ successes for n Bernoulli trials, each having success probability $b_{\star } = \min (b,1-b)$. For the correlated distribution, we partition according to $\mathsf {HD}(\varvec{x}(1:n-1), \varvec{x}(2:n))$, i.e., the number of transitions in $\varvec{x}$. Inputs in subset $\varphi _j$ exhibit $j-1$ transitions and obey either one out of two forms, i.e., $\varvec{x} = (\varvec{0} \Vert \varvec{1} \Vert \varvec{0} \Vert \ldots )$ and $\varvec{x} = (\varvec{1} \Vert \varvec{0} \Vert \varvec{1} \Vert \ldots )$. A related observation is that if $\varvec{x} \in \varphi _{j}$, then so is its ones’ complement, i.e., $\overline{\varvec{x}} \in \varphi _{j}$. This explains the factors 2 and $\frac{1}{2}$ everywhere. Set size $|\varphi _j|$ is further determined with stars and bars combinatorics [12]. In particular, we separate n indistinguishable stars into j distinguishable bins by adding $j-1$ out of $n-1$ bars.

Fig. 2.

Subsets $\varphi _j$ for a biased and correlated distribution $X$, left and right respectively. We define $b_\star = \min (b,1-b)$ and $c_\star = \min (c,1-c)$.

We treat the degenerate case $b = c = \frac{1}{2}$, i.e., a uniform distribution, separately. There is only one set then. Formally, $J = 1$, $|\varphi _1| = 2^{n}$ and $q_1 = 1/2^n$. As proven by Reyzin [24], the min-entropy loss of a secure sketch is maximal for a uniformly distributed input, making this a case of special interest.

3.2 Generic Bounds

Equation (7) holds for the code-offset construction of Dodis et al. [11], given that a codeword is selected fully at random during enrollment.

$$\begin{aligned} \mathbb {P}((P = \varvec{p})|(X = \varvec{x})) = {\left\{ \begin{array}{ll} 1/|\mathcal {M}|, &{} \text {if}\ \exists \varvec{w}: \varvec{p} = \varvec{x} \oplus \varvec{w} \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(7)

Equation (8) applies Bayes’ rule to the definition of conditional min-entropy in (2) and fills in (7). The 0 case is resolved by switching variables for the $\max$ operator. A direct exhaustive evaluation of the resulting formula requires up to $2^{n}|\mathcal {M}|$ operations.

(8)

For linear codes, the workload can be reduced substantially. With a similar derivation as before, we rewrite (4) as shown in (9). Up to $2^{n}$ operations suffice. Nevertheless, direct evaluation is only feasible for small codes. We emphasize that our bounds are able to handle large codes, as is typically the case for a practical key generator.

$$\begin{aligned} \widetilde{\mathbb {H}}_{\infty }(X|P) = -\log _2 \Bigl (\sum _{\varvec{\epsilon } \in \mathcal {E}} \max _{\varvec{w} \in \mathcal {W}} \mathbb {P}(X = \varvec{\epsilon } \oplus \varvec{w}) \Bigr ). \end{aligned}$$

(9)

Equation (8) iterates over all $\varvec{p}$’s and selects each time the most likely $\varvec{x}$ that is within range, via the addition of a codeword $\varvec{w} \in \mathcal {W}$. We now reverse the roles, as shown in Fig. 3. We iterate over all $\varvec{x}$’s, from most likely to least likely, i.e., from $\varphi _1$ to $\varphi _J$. Within a certain $\varphi _j$, the order of the $\varvec{x}$’s may be chosen arbitrarily. Subsequently, we assign $\varvec{p}$’s to each $\varvec{x}$, as represented by the black squares, until the set $\mathcal {P}$ of size $2^n$ is depleted. For each assigned $\varvec{p}$, we assume that the corresponding $\varvec{x}$ is the most likely vector, according to (8). Let $s_{j}^{\varvec{p}}$ denote the number of black squares assigned to set $\varphi _j$. The residual min-entropy is then easily computed as in (10).

$$\begin{aligned} \widetilde{\mathbb {H}}_{\infty }(X|P) = -\log _2 \biggl (\frac{1}{|\mathcal {M}|} \sum _{j = 1}^J s_{j}^{\varvec{p}} q_j \biggr ). \end{aligned}$$

(10)

Fig. 3.

Reversal of the roles in (8). (a) A lower bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. (b) An upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. Black squares represent terms that contribute to $\widetilde{\mathbb {H}}_{\infty }(X|P)$, one for each $\varvec{p} \in \mathcal {P}$. White squares represent non-contributing terms, overruled by the $\max$ operator. In general, there are few black squares but many white squares, $2^n$ versus $(|\mathcal {M}|-1)2^n$ to be precise. For block codes, i.e., $|\mathcal {M}| = 2^k$, the last column of black squares is completely filled.

Both linear and non-linear codes are supported by former graphical representation. Nevertheless, we elaborate linear codes as a special case due to their practical relevance. Figure 4 swaps the order of iteration in (9). Only one row suffices, i.e., each column of helper data vectors $\varvec{p}$ in Fig. 3 is condensed to a single square. Black and white squares are now assigned to cosets, as represented by their coset leaders $\varvec{\epsilon }$. Let $s_{j}^{\varvec{\epsilon }}$ denote the number of black squares assigned to set $\varphi _j$. The residual min-entropy is then easily computed as in (11), hereby dropping denominator $|\mathcal {M}|$ compared to (10), given that $s_{j}^{\varvec{p}} = 2^k \cdot s_{j}^{\varvec{\epsilon }}$.

$$\begin{aligned} \widetilde{\mathbb {H}}_{\infty }(X|P) = -\log _2 \biggl (\sum _{j = 1}^J s_{j}^{\varvec{\epsilon }} q_j \biggr ). \end{aligned}$$

(11)

Fig. 4.

Reversal of the roles in (9), as applied to linear codes. (a) A lower bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. (b) An upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. Black squares represent terms that contribute to $\widetilde{\mathbb {H}}_{\infty }(X|P)$, one for each $\varvec{\epsilon } \in \mathcal {E}$. White squares represent non-contributing terms, overruled by the $\max$ operator.

In the worst-case scenario, the most likely $\varvec{x}$’s all map to unique $\varvec{p}$’s, without overlap, resulting in a lower bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. For a linear code, this would be the case if the first $2^{n-k}$ $\varvec{x}$’s all belong to different cosets. In the best-case scenario, our sequence of $\varvec{x}$’s exhibits maximum overlap in terms of $\varvec{p}$, resulting in an upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. For a linear code, this would be the case if the first $2^k$ $\varvec{x}$’s all map to the same coset, and this repeated for all $2^{n-k}$ cosets. Algorithms 1 and 2 comprehend a literal transcript of Fig. 3 and compute the lower bound and upper bound respectively. Auxiliary variables $s^{\varvec{p}}$ and $s^{\varvec{x}}$ accumulate black and gray squares respectively. To maintain generality, we abstain from special case algorithms for linear codes, although it would result in a few simplifications.

Algorithms 1 and 2 may now be applied to a variety of distributions. For a uniform distribution, the lower and upper bound both evaluate to $\widetilde{\mathbb {H}}_{\infty }(X|P) = log_2(|\mathcal {M}|)$, regardless of other code specifics. Or simply k, for block codes in particular. The min-entropy loss is hence exactly $(n-k)$, given that $\mathbb {H}_{\infty }(X) = n$. Reyzin’s proof [24] therefore implicates that the general-purpose $(n-k)$ bound cannot be tightened any further. Although results are fairly presentable already for the biased and correlated distributions, we further tighten these bounds first.

3.3 Tighter Bounds

Tighter bounds can be obtained by leveraging code properties more effectively. Algorithms 3 and 4 generalize Algorithms 1 and 2 respectively. In the former case, an additional input imposes an upper bound on the accumulated number of black squares, i.e., $\forall j, (s_1^{\varvec{p}} + s_2^{\varvec{p}} + \ldots + s_j^{\varvec{p}}) \le (u_1^{\varvec{p}} + u_2^{\varvec{p}} + \ldots + u_j^{\varvec{p}})$. In the latter case, an additional input imposes a lower bound on the accumulated number of black squares, i.e., $\forall j, (s_1^{\varvec{p}} + s_2^{\varvec{p}} + \ldots + s_j^{\varvec{p}}) \ge (l_1^{\varvec{p}} + l_2^{\varvec{p}} + \ldots + l_j^{\varvec{p}})$. We now provide several examples.

Worst-Case Bounds. We further tighten the lower bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ for the correlated distribution. The improvement applies to linear codes that have the all-ones vector $\varvec{1}$ of length n as a codeword. This includes Reed-Muller codes of any order [18]. This also includes many BCH, Hamming and repetition codes, on the condition that these are cyclic and having d odd, as easily proven hereafter. Consider an arbitrary codeword with Hamming weight d. XORing all $2^n$ circular shifts of this codeword results in the all-ones codeword, which ends the proof. As mentioned before, each set $\varphi _{j}$ of the correlated distribution can be partitioned in pairs $\{\varvec{x}, \overline{\varvec{x}}\}$, with $\overline{\varvec{x}}$ the ones’ complement of $\varvec{x}$. Paired inputs belong to the same coset, i.e., maximum overlap in terms of helper data $\varvec{p}$. Therefore, we impose the cumulative upper bound in (12).

$$\begin{aligned} u_{j}^{\varvec{p}} = |\mathcal {M}| \frac{|\varphi _{j}|}{2} = 2^{k-1} |\varphi _{j}|. \end{aligned}$$

(12)

For instance, consider linear/cyclic $[n,k=1,d=n]$ repetition codes, i.e., having generator matrix $\varvec{G} = \varvec{1}$, with n odd. Algorithms $\mathsf {BoundWorstCase2}$ and $\mathsf {BoundBestCase}$ then converge to the exact result $\widetilde{\mathbb {H}}_{\infty }(X|P) = 1$, not depending on parameter c. This is the best-case scenario, given the universal bound $\widetilde{\mathbb {H}}_{\infty }(X|P) \le k$. Figure 5 illustrates the former with squares for $n=5$. The result also holds if the repetition code is neither linear/cyclic nor odd. As long as $\varvec{w}_1 \oplus \varvec{w}_2 = \varvec{1}$, the elements of each $\varphi _{j}$ can be paired into cosets. Although the term coset is usually preserved for linear codes, translations of a non-linear repetition code are either disjunct or coincide and still partition the space $\{0,1\}^{1 \times n}$. As a side note, the result offers another [8] refutation of the repetition code pitfall of Koeberl et al. [17], a work that overlooks that $(n-k)$ is an upper bound only.

Fig. 5.

The exact residual min-entropy $\widetilde{\mathbb {H}}_{\infty }(X|P)$ for the correlated distribution and an $[n=5,k=1,d=5]$ repetition code.

Best-Case Bounds. We improve the upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ for both the biased and correlated distribution. In particular, we take minimum distance d into account. The main insight is that two slightly differing inputs $\varvec{x}_u \ne \varvec{x}_v$ do not overlap in terms of helper data $\varvec{p}$. More precisely, if $\mathsf {HD}(\varvec{x}_u,\varvec{x}_v) \in [1,d-1]$, then $\{\varvec{x}_u \oplus \varvec{w}\ |\ \varvec{w} \in \mathcal {W}\} \cap \{\varvec{x}_v \oplus \varvec{w}\ |\ \varvec{w} \in \mathcal {W}\} = \varnothing$. For the biased distribution, the following holds: $\mathsf {HD}(\varvec{x}_u,\varvec{x}_v) \in [1,d-1]$ if $\varvec{x}_u \ne \varvec{x}_v$ and $\varvec{x}_u, \varvec{x}_v \in (\varphi _1 \cup \varphi _2 \cup \ldots \cup \varphi _{t+1})$. Or stated otherwise, the elements of the first $t+1$ sets all result in unique $\varvec{p}$’s. Therefore, we can impose the constraint given in (13). Figure 6 depicts the squares.

$$\begin{aligned} l_j^{\varvec{p}} = {\left\{ \begin{array}{ll} |\varphi _{j}| |\mathcal {M}|, &{} \text {if}\ j \in [1,t+1] \\ 0, &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

(13)

Fig. 6.

A tightened upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ for the biased distribution, hereby making use of (13).

There is an interesting observation for perfect codes in particular. As clear from the Hamming bound in (3), all unique $\varvec{p}$’s are covered by the first $t+1$ sets exclusively. $\mathsf {BoundWorstCase}$ and $\mathsf {BoundBestCase2}$ hence produce the same output, implying that the residual min-entropy is evaluated exactly, as further simplified in (14). Delvaux et al. [8] derived the same formula for $[n,k=1,d=n]$ repetition codes with n odd. The scope of their result is hence extended from perfect repetition codes to perfect codes in general. As a side note, the formula was originally adopted to debunk the aforementioned repetition code pitfall [17]. Maes et al. [22] later presented a similar contribution at CHES 2015, differing in its use of Shannon entropy rather than min-entropy.

$$\begin{aligned} \widetilde{\mathbb {H}}_{\infty }(X|P) = - \log _2\biggl (\sum _{j=1}^{t+1} |\varphi _j| \cdot q_j\biggr ) = - \log _2(\mathsf {F}_\mathsf {bino}(t;n,\min (b,1-b))). \end{aligned}$$

(14)

Also for the correlated distribution, distance d might be incorporated to tighten the upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$. First of all, we assign $|\mathcal {M}|$ unique $\varvec{p}$’s to one out of two elements in $\varphi _1$. For ease of understanding, assume $\varvec{x} = \varvec{0}$, comprehending the first case in (15). For each set $\varphi _j$, with $j \in [2,n]$, we then count the number of inputs $\varvec{x} \in \varphi _j$ such that $h = \mathsf {HW}(\varvec{x}) \le t$. The latter constraint guarantees all assigned $\varvec{p}$’s to be unique. We distinguish between two forms, $\varvec{x} = (\varvec{0} \Vert \varvec{1} \Vert \varvec{0} \Vert \ldots )$ and $\varvec{x} =(\varvec{1} \Vert \varvec{0} \Vert \varvec{1} \Vert \ldots )$, resulting in two main terms. For each form, we apply stars and bars combinatorics twice. In particular, we assign h indistinguishable stars, i.e., ones, to distinguishable bins and independently also for $n-h$ zeros. Note that $l_{j}^{\varvec{p}} = 0$ for $j > 2t+1$. To ensure formula correctness, one may verify numerically that $l_{1}^{\varvec{p}} + l_{2}^{\varvec{p}} + \ldots + l_{2t+1}^{\varvec{p}}$ equals the left hand side of the Hamming bound in (3).

$$\begin{aligned} l_{j}^{\varvec{p}} = {\left\{ \begin{array}{ll} |\mathcal {M}|, &{} \text {if}\ j = 1 \\ |\mathcal {M}| \Bigl (\sum _{h = \lfloor j/2\rfloor }^{t} \left( {\begin{array}{c}h-1\\ \lfloor j/2\rfloor -1\end{array}}\right) \left( {\begin{array}{c}n-h-1\\ \lceil j/2\rceil -1\end{array}}\right) &{} \\ \quad + \sum _{h = \lceil j/2\rceil }^{t} \left( {\begin{array}{c}h-1\\ \lceil j/2\rceil -1\end{array}}\right) \left( {\begin{array}{c}n-h-1\\ \lfloor j/2\rfloor -1\end{array}}\right) \Bigr ),&\text {otherwise}. \end{array}\right. } \end{aligned}$$

(15)

3.4 Numerical Results

Figure 7 presents numerical results for various BCH codes. We focus on small codes, as these allow for an exact exhaustive evaluation of the residual min-entropy using (8) and/or (9). As such, the tightness of various bounds can be assessed adequately. Figure 7(d) nevertheless demonstrates that our algorithms support large codes equally well, in compliance with a practical key generator. Note that only half of the bias interval $b \in [0,1]$ is depicted. The reason is that all curves mirror around the vertical axis of symmetry $b = \frac{1}{2}$. The same holds for the correlated distribution with parameter c.

Fig. 7.

The secure sketch min-entropy loss for various BCH codes. Dots correspond to an exact exhaustive evaluation of (8)/(9). The legend of the curves is as follows. (I) The ingoing min-entropy $\mathbb {H}_{\infty }(X) = -\log _2(q_1)$. (II) The lower bound $\widetilde{\mathbb {H}}_{\infty }(X|P) = \max (\mathbb {H}_{\infty }(X) - (n-k),0)$. (III) The lower bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ according to $\mathsf {BoundWorstCase}$. (IV) The upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ according to $\mathsf {BoundBestCase}$. (V) The lower bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ according to $\mathsf {BoundWorstCase2}$. (VI) The upper bound on $\widetilde{\mathbb {H}}_{\infty }(X|P)$ according to $\mathsf {BoundBestCase2}$.

Especially the lower bounds perform well, which benefits a conservative system provider. The best lower bounds in Fig. 7(a), (b) and (c) visually coincide with the exact result. The gap with the $(n-k)$ bound is the most compelling around $b, c \approx 0.7$, where the corresponding curves hit the horizontal axis $\widetilde{\mathbb {H}}_{\infty }(X|P)$ = 0. Also our upper bounds are considerably tighter than their more general alternatives in (5). Nevertheless, the latter bounds remain open for further improvement, with the exception of Fig. 7(b). An $[n=7,k=4,d=3]$ code is perfect and lower and upper bounds then converge to the exact result for a biased distribution.

4 Applications

The newly developed theory of Sect. 3 facilitates the design and analysis of error-correction methods for PUFs, as exemplified in twofold manner. First, we point out a fundamental security flaw in the reverse fuzzy extractor [28]. Second, we provide a motivational framework for debiasing schemes [15, 22, 26, 27, 30].

4.1 A Fundamental Security Flaw in Reverse Fuzzy Extractors

The reverse fuzzy extractor, as proposed by Van Herrewege et al. [28] at Financial Crypto 2012, improves the lightweight perspectives of PUF-based authentication protocols. The construction was therefore also adopted in the CHES 2015 protocol of Aysu et al. [1]. Instead of a single helper data exposure only, $\varvec{p} \leftarrow \mathsf {SSGen}(\widetilde{\varvec{x}})$ is regenerated and transferred with each protocol run by a resource-constrained PUF-enabled device. A receiving resource-rich server, storing reference response $\varvec{x}$, can hence reconstruct $\widetilde{\varvec{x}} \leftarrow \mathsf {SSRec}(\varvec{x},\varvec{p})$ and establish a shared secret as such. The footprint of the device is reduced due to the absence of the heavyweight $\mathsf {SSRec}$ procedure.

We debunk the main security claim that repeated helper data exposure does not result in additional min-entropy loss. The revealed flaw is attributed to the misuse of a reusability proof of Boyen [6]. For the code-offset sketch with linear codes, the exposure of $\varvec{p}_1 \leftarrow \mathsf {SSGen}(\varvec{x})$ and $\varvec{p}_2 \leftarrow \mathsf {SSGen}(\varvec{x} \oplus \varvec{e})$, with perturbation $\varvec{e}$ known and fully determined by the attacker, is provably equivalent. The latter helper data reveals that $\varvec{x}$ belongs to an identical coset $\{\varvec{p}_1 \oplus \varvec{w} : \varvec{w} \in \mathcal {W}\} = \{\varvec{p}_2 \oplus \varvec{e} \oplus \varvec{w} : \varvec{w} \in \mathcal {W}\}$. However, perturbation $\varvec{e}$ is determined by PUF noisiness rather than by the attacker and its release hence reveals new information. Given a sequence of protocol runs, the attacker can approximate all individual bit error rates $p_E$ as well as the coset to which reference $\varvec{x}$ belongs.

Figure 8 quantifies the residual min-entropy of $X$ with the exclusion and inclusion of revealed bit error rates $p_E$ respectively. In the latter case, we rely on a Monte Carlo evaluation of (16), as enabled by choosing a small $[n=15,k=7,d=5]$ BCH code, given that an analytical approach is not so very straightforward. Exposure of $p_E$ boils down to knowledge of threshold discrepancy $|\varvec{v}(i)-t|$. For the biased distribution, the situation is identical to the flaw in the soft-decision decoding scheme of Maes et al. [21]. As pointed out by Delvaux of al. [8], there is a bit-specific bias $b_i = \mathbb {P}(\varvec{r}(i) = 1) = \mathsf {f}_\mathsf {norm}(t+|\varvec{v}(i)-t|)/(\mathsf {f}_\mathsf {norm}(t+|\varvec{v}(i)-t|) + \mathsf {f}_\mathsf {norm}(t-|\varvec{v}(i)-t|))$. For each $\varvec{x}$ in the coset corresponding to $\varvec{p}$, we then compute $\mathbb {P}(X = \varvec{x}) = \prod _{i = 1}^n (\varvec{x}(i) b_i + (1-\varvec{x}(i))(1-b_i))$. Similarly, for the spatially correlated distribution, we compute $\mathbb {P}(X = \varvec{x}) = \mathsf {f}_\mathsf {norm}(\varvec{v},\varvec{0},\varvec{\varSigma })$, with covariance matrix $\varvec{\varSigma }$ exclusively depending on correlation parameter c, as detailed in the extended version of this manuscript.

$$\begin{aligned} \widetilde{\mathbb {H}}_{\infty }(X|P) = -\log _2\Bigl (\mathbb {E}_{\varvec{v} \leftarrow V} \max _{\varvec{w} \in W} \mathbb {P}(V = t + (1-2\varvec{w})|\varvec{v}-t|\ |\ |\varvec{v}-t|\Bigr ). \end{aligned}$$

(16)

Fig. 8.

The residual min-entropy $\widetilde{\mathbb {H}}_{\infty }(X|P)$ for a BCH code. The solid lines that exclude revealed bit error rates are computed with $\mathsf {BoundWorstCase2}$; Fig. 7 confirms the visual overlap with the exact result. Dots that include revealed bit error rates correspond to Monte Carlo evaluations of size $10^6$.

The revealed flaw differs from existing attacks by Delvaux et al. [9] and Becker [3] that apply to the original protocol [28] exclusively. The latter attacks comprehend the modeling of the highly correlated arbiter PUF via repeated helper data exposure; a preemptive fix can be found in the PhD thesis of Maes [19]. The newly revealed flaw is more fundamentally linked to the reverse fuzzy extractor primitive and applies to all existing protocols so far [1, 19, 28]. Observe in Fig. 8 that the overly conservative $(n-k)$ bound would compensate for the additional unanticipated min-entropy loss. However, this somewhat defeats the purpose in light of the original lightweight intentions, and this observation might not necessarily hold for every possible distribution. Further theoretical work may determine to which extent and at which cost reverse fuzzy extractors can be repaired. A potential fix already exists for biased distributions, as illustrated later-on.

4.2 Motivation for Debiasing Schemes

Debiasing schemes transform a biased PUF-induced distribution into a uniform distribution. A considerable fraction of the response bits is discarded in order to restore the balance between 0 and 1. Indices of retained bits are stored as helper data. A subsequent secure sketch, known to have an exact min-entropy loss of $(n-k)$ bits for uniform inputs, still corrects the errors. A first debiasing proposal is the index-based syndrome (IBS) scheme of Yu et al. [30], further generalized by Hiller et al. [15]. Second, several variations of the von Neumann debiasing algorithm can be applied. This was first proposed by van der Leest et al. [26], and later also by Van Herrewege in his PhD thesis [27]. Most recently, Maes et al. [22] presented an optimization of the von Neumann algorithm that applies to repetition codes in particular.

Prior debiasing proposals conjectured that a stand-alone sketch cannot handle biased distributions well. This conclusion originates from the extrapolation of repetition code insights and/or application of the $(n-k)$ bound. The precise entropy loss behavior for larger codes, e.g., a BCH $[n = 127, k = 64, d = 21]$ code as in Fig. 7, was an educated guess so far. Our newly derived bounds clearly resolve this motivational uncertainty, in addition to making stand-alone sketches more competitive. For low-bias situations, the $(n-k)$ bound already resulted in a competitive sketch [22]; the new bounds can only improve hereupon. We emphasize that modern high-quality PUFs tend to have a low bias. Notable cases of a high bias can typically be attributed to an avoidable asymmetry in the circuit. Nevertheless, for high-bias situations, the new bounds clearly indicate the need of debiasing schemes. The benefit is amplified by choosing a sketch with a k-bit output, several of which are listed in the extended version of this manuscript. The uniform output is then directly usable as a key, hereby eliminating the $\mathsf {Hash}$ function and its additional min-entropy loss in case the leftover hash lemma is applied.

Finally, we highlight that one of the von Neumann debiasing schemes in [22] was claimed to be reusable. This claim holds, despite overlooking the misuse of Boyen’s proof and stating that a stand-alone sketch is reusable. A side effect of retaining pairs of alternating bits only, i.e., 01 and 10, is that the imbalance in error rates between 0 and 1 cannot be observed in the helper data. The scheme is considerably less efficient than other von Neumann variants though, showing that reusability comes at a price.

5 Conclusion

Secure sketches are the main workhorse of modern PUF-based key generators. The min-entropy loss of most sketches is upper-bounded by $(n-k)$ bits and designers typically instantiate system parameters accordingly. However, the latter bound tends to be overly pessimistic, resulting in an unfortunate implementation overhead. We showcased the proportions for a prominent category of PUFs, with bias and spatial correlations acting as the main non-uniformities. New considerably tighter bounds were derived, valid for a variety of popular but algebraically complex codes. These bounds are unified in the sense of being applicable to seven secure sketch constructions. Deriving tighter alternatives for the $(n-k)$ bound counts as unexplored territory and we established the first significant stepping stone. New techniques may have to be developed in order to tackle more advanced second-order distributions. Elaborating a wider range of applications would be another area of progress. We hope to have showcased the potential by debunking the main security claim of the reverse fuzzy extractor and by providing proper quantitative motivation for debiasing schemes.