On the Communication Required for Unconditionally Secure Multiplication

Abstract

Many information-theoretic secure protocols are known for general secure multi-party computation, in the honest majority setting, and in the dishonest majority setting with preprocessing. All known protocols that are efficient in the circuit size of the evaluated function follow the same “gate-by-gate” design pattern: we work through an arithmetic (boolean) circuit on secret-shared inputs, such that after we process a gate, the output of the gate is represented as a random secret sharing among the players. This approach usually allows non-interactive processing of addition gates but requires communication for every multiplication gate. Thus, while information-theoretic secure protocols are very efficient in terms of computational work, they (seem to) require more communication and more rounds than computationally secure protocols. Whether this is inherent is an open and probably very hard problem. However, in this work we show that it is indeed inherent for protocols that follow the “gate-by-gate” design pattern. We present the following results:

• In the honest majority setting, as well as for dishonest majority with preprocessing, any gate-by-gate protocol must communicate $\varOmega (n)$ bits for every multiplication gate, where n is the number of players.

• In the honest majority setting, we show that one cannot obtain a bound that also grows with the field size. Moreover, for a constant number of players, amortizing over several multiplication gates does not allow us to save on the computational work, and – in a restricted setting – we show that this also holds for communication.

All our lower bounds are met up to a constant factor by known protocols that follow the typical gate-by-gate paradigm. Our results imply that a fundamentally new approach must be found in order to improve the communication complexity of known protocols, such as BGW, GMW, SPDZ etc.

The authors of this work were supported by the Danish National Research Foundation and the National Science Foundation of China (under the grant 61061130540) for the Sino-Danish Center for the Theory of Interactive Computation, within which part of this work was performed; by the CFEM research center (supported by the Danish Strategic Research Council). Ivan Damgård was also supported by the Advanced ERC grant MPCPRO. Jesper Buus Nielsen is supported by European Research Council Starting Grant 279447. This work was done in [part] while Antigoni Polychroniadou was visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant CNS-1523467.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Secure Multi-Party Computation (MPC) allows n players to compute an agreed function on privately held inputs, such that the desired result is correctly computed and is the only new information released. This should hold, even if t out of n players have been actively or passively corrupted by an adversary.

If point-to-point secure channels between players are assumed, any function can be computed with unconditional (perfect) security, against a passive adversary if $n \ge 2t+1$ and against an active adversary if $n\ge 3t+1$ [BOGW88, CCD88]. If we assume a broadcast channel and accept a small error probability, $n\ge 2t+1$ is sufficient to get active security [RBO89].

The protocols behind these results require a number of communication rounds that is proportional to the depth of an (arithmetic) circuit computing the function. Moreover, the communication complexity is proportional to the size of the circuit. Whether we can have constant round protocols and/or communication complexity much smaller than the size of the circuit and still be efficient (polynomial-time) in the circuit size of the function is a long-standing open problem. Note that this is indeed possible if one makes computational assumptions. Note also that if we give up on being efficient in the circuit size, then there are unconditionally secure and constant round protocols for any function [IK00] (which will, however, be very inefficient in general with respect to the computation). Moreover, there are works that apply to special classes of circuits (e.g., constant-depth circuits [BI05]) or protocols that require exponential amount of computation [BFKR90, NN01] and exponential storage complexity [IKM+13].

The above issues are not only of theoretical interest: the methods we typically use in information-theoretic secure protocols tend to be computationally much more efficient than the cryptographic machinery we need for computational security. So unconditionally secure protocols are very attractive from a practical point of view, except for the fact that they seem to require a lot of interaction.

The Gate-by-gate Design Pattern. The fact that existing information-theoretic secure protocols (which are efficient in the circuit size of the function) have large round and communication complexity is a natural consequence of the fact that all such protocols follow the same ${typical }$ “gate-by-gate” design pattern: Initially all inputs are secret-shared among the players. Then, for each gate in the circuit, where both its inputs have been secret-shared, we execute a subprotocol that produces the output from the gate in a secret-shared form. The protocol maintains as an invariant that for all gates that have been processed so far, the secret-sharing of the output value is of the same form used for the inputs (so we can continue processing gates) and is appropriately randomised such that one could open this sharing while revealing only that output value. As a result, it is secure to reveal/open the final outputs from the circuit.

For all known constructions which are efficient in the circuit size of the function, it is the case that multiplication gates require communication to be processed (while addition/linear gates usually do not). The number of rounds is at least the (multiplicative) depth of the circuit, and the communication complexity is $\varOmega (ns)$ for a circuit of size s (the size being measured as the number of multiplication gates) in the worst case for $t <n/3$ and $t <n/2$ see the results of [DN07, BTH08] and [BSFO12, GIP+14, GIP15], respectively. Note that protocols that tolerate a sub-optimal number of corrupted parties (e.g., $t < 0.49n$) and are based on packed secret-sharing techniques can reduce the amortised cost of multiplications if they can be parallelised [DIK+08, IPS09, DIK10, GIP15]. These techniques do not apply to all circuits, in particular not to “tall and skinny” circuits whose multiplicative depth is comparable to their size. In addition, they can at best save an $\mathcal {O}(n)$ factor in communication and computational work.

The situation is essentially the same for recent protocols that are designed for dishonest majority in the preprocessing model [DPSZ12, NNOB12] (except that amortization based on packed secret-sharing does not apply here due to the dishonest majority setting).

1.1 Contributions

In this paper, we ask a very natural question for unconditionally secure protocols which, to the best of our knowledge, has not been studied in detail before:

Is it really inherent that the typical gate-by-gate approach to secure computation requires communication for each multiplication operation?

Our Model. To avoid misunderstandings, let us be more precise about the model we assume: we consider synchronous protocols that are semi-honest and statistically secure against static corruption of at most t of the n players. We assume that point-to-point secure channels are available, and protocols are allowed to have dynamic communication patterns (in a certain sense we make precise later), i.e., it is not fixed a priori whether a protocol sends a message in a given time slot. Moreover, there is no bound on the computational complexity of protocols, in particular arbitrary secret sharing schemes are allowed. A gate-by-gate protocol is a protocol that evaluates an arithmetic circuit and for every multiplication gate, it calls a certain type of subprotocol we call a Multiplication Gate Protocol ($\mathrm {\textsc {MGP}}$). We define $\mathrm {\textsc {MGP}}$s precisely later, but they basically take as input random shares of two values a, b from a field and output random shares of $c=ab$. Neither the $\mathrm {\textsc {MGP}}$ nor the involved secret sharing schemes have to be the same for all gates. We do not even assume that the same secret sharing scheme is used for the inputs and outputs of an MGP, we only require that the reconstruction threshold for the output sharing is at most 2t for honest majority and at most n for dishonest majority.

An ordered gate-by-gate protocol must call the $\mathrm {\textsc {MGP}}$’s in an order corresponding to the order in which one would visit the gates when evaluating the circuit, whereas this is not required in general. Thus the gate-by-gate notion is somewhat more general than what one might intuitively expect and certainly includes much more than, say the standard BGW protocol – which, of course, makes our negative results stronger.

Note that if multiplications did not require communication, it would immediately follow (for semi-honest security) that we would have an unconditionally secure two-round protocol for computing any function. But as mentioned above this is not a priori impossible: it follows, for instance, from [IK00, IKM+13], that if less than a third of the players are corrupted, there is indeed such a two-round protocol (which, however, requires super polynomial computational work in general).

Honest Majority Setting. For honest majority protocols it is relatively easy to show that multiplications do require communication: we argue in the paper that any $\mathrm {\textsc {MGP}}$ secure against t corruptions requires that at least $2t+1$ players communicate. For protocols with dynamic communication pattern this bound holds in expectation. It turns out that a protocol beating this bound would imply an unconditionally secure two-party protocol computing a multiplication, which is well known to be impossible. This implies that the communication complexity of any gate-by-gate protocol for honest majority must be proportional to $n\cdot s$ where s is the circuit size and that the round complexity of an ordered gate-by-gate protocol must be at least proportional to the multiplicative depth of the circuit. This matches the best protocols we know for general Boolean circuits up to a constant factor. For arithmetic circuits over large fields one might wonder whether the communication must grow with the field size. However, this cannot be shown via a general bound on MGPs: we give an example secret sharing scheme allowing for an MGP with communication complexity independent of the field size.

A gate-by-gate protocol is not allowed to amortise over several multiplications that can be done in parallel. This is anyway not possible in general, for instance if we evaluate a “tall and skinny” circuit forcing us to do multiplications sequentially. But for more benign circuits, amortization is indeed an option. However, we show that in a restricted setting, MGPs doing k multiplication gates in parallel must have communication that grows linearly with k. We also show (in full generality) that amortization can save at most an $\mathcal {O}(n)$ factor in the computational work, matching what we can get from known techniques based on packed secret-sharing. This proof technique for this bound is quite interesting: We base it on a lower bound by Winkler and Wullschleger [WW10] on the amount of preprocessed data one needs for (statistically) secure two-party computation of certain functions. We find it somewhat surprising that an information theoretic bound on the size of data translates to a bound on local computation.

Dishonest Majority Setting with Preproccesing. The argument used for the honest majority case breaks down if we consider protocols in the preprocessing model (where correlated randomness is considered): here it is indeed possible to compute multiplications with unconditional security, even if $t=n-1$ of the n players are corrupt. Nevertheless, we show similar results for this setting: here, any $\mathrm {\textsc {MGP}}$ secure against $t=n-1$ corruptions must have all n players communicate. This implies that, also in this setting, any gate-by-gate protocol has communication complexity $\varOmega (n\cdot s)$. Note that existing constructions [DPSZ12] meet the resulting bound for gate-by-gate protocols up to a constant factor.

To obtain the result, we exploit again the lower bound by Winkler and Wullschleger, but in a different way. In a nutshell, we show that constructions beating our bound would imply a protocol that is too good to be true according to [WW10].

The result holds exactly as stated above assuming that the target secret-sharing scheme that the protocol outputs shares in is of a certain type that includes the simple additive secret-sharing scheme (which is also used in [DPSZ12, NNOB12]). If we put no restrictions on the target scheme, the results get a bit more complicated. Essentially what we show is the following: suppose we replace the multiplication gate by a more general gate that does some computation on a fixed number of inputs, such as the inner product of two vectors. Then we show that once the computation done by the gate gets large enough (in a certain sense we define in the paper), again a protocol handling such a gate must communicate a lot. It is the target secret-sharing scheme that determines how “large” the gate needs to be, see more details within.

Comparison to Related Work. There is a lot of prior work on lower bounding communication in interactive protocols, see for instance [Kus92, FY92, CK93, FKN94, KM97, KR94, BSPV99, GR03] (see [DPP14] for an overview of these results). They typically provide lower bounds for very specific functions such as modular addition, and are not applicable to our situation. Probably the most relevant previous work is [DPP14]. Their model does not match ours, as they consider three parties where only two have input and only the third party gets output. Hence we cannot use their results directly, but it is instructive to consider their techniques as it shows why our problem is more tricky than it may seem at first. One important idea used in [DPP14] is to make a “cut”, i.e., one considers a (small) subset $\mathcal {C}$ of the parties and then argue that either the communication between $\mathcal {C}$ and the rest of the world must be large enough to determine their inputs, since otherwise other players could not compute the output; or that $\mathcal {C}$ must receive information of sufficient size to be able to compute its own outputs.

It turns out that these ideas are not sufficient for us: recall that we start from a situation where players already have shares of the input values a, b. Now, if $\mathcal {C}$ is large enough to be qualified in the input secret sharing scheme, then $\mathcal {C}$ already has information enough to determine a, b (and for some secret sharing schemes even the shares of all players). So $\mathcal {C}$ can in principle compute correct shares of $c=ab$ by itself without communicating with anyone. On the other hand, if $\mathcal {C}$ is unqualified, then the complement of $\mathcal {C}$ is typically qualified, and therefore does not need information from $\mathcal {C}$ to compute output. But one might think that $\mathcal {C}$ needs to receive information to determine its output, in particular, the output shares must be properly coordinated to form a consistent sharing of c. Remember, however, that players already have properly coordinated shares of the inputs, and they might be able to use those to form a correct output sharing while communicating less. Indeed, this is what happens for addition gates, where there is no communication, players just add their shares locally.

It follows that the idea of a cut is not enough, one must exploit in some non-trivial way that we are handling a multiplication gate, which is exactly what we do. It is possible that one could use the fact that we do multiplication together with the concept of residual information which was also used in [DPP14], to get better bounds than we achieve here, but this remains a speculation.

Note that our model does not count communication needed to construct the shares that are input, nor does it count any communication needed to reconstruct results from the output shares. This does count in the standard model and makes lower bounds easier to prove. For instance, in [DNOR15] lower bounds were recently proved on the message complexity of computing a large class of functions securely, primarily by showing that a significant number of messages must be sent before the input are uniquely determined. In fact, if we included a secret sharing phase before the multiplication protocol and a reconstruction phase after it, these would entail so much communication that the bounds obtained from existing results would leave nothing to explain why the privacy preserving multiplication step is communication intensive.

It is also easy to see that one cannot get bounds in our model based only on correctness, for instance by methods from communication complexity. If parties have shares in a and b, no communication is needed to produce some set of correct shares in ab: one can simply consider the shares in a and b together as a (redundant) sharing of ab. Indeed this satisfies all our demands to a multiplication gate protocol except privacy: the output threshold is the same and we can correctly reconstruct ab, but privacy is of course violated because reconstruction would tell us more than ab. So, our bounds arguably require privacy.

2 Preliminaries

Notation. We say that a function $\varepsilon$ is negligible if $\forall c~ \exists ~ \sigma _c\in \mathbb {N}$ such that if $\sigma \ge \sigma _c$ then $\varepsilon (\sigma )< \sigma ^{-c}$. We write [n] to denote the set $\{1, 2, . . . , n\}$. Moreover, calligraphic letters denote sets. The complement of a set $\mathcal {A}$ is denoted by $\overline{\mathcal {A}}$. The distribution of a random variable X over $\mathcal {X}$ is denoted by $P_X$. Given the distribution $P_{XY}$ over $\mathcal {X}\times \mathcal {Y}$, the marginal distribution is denoted by $P_X (x) := \sum _{y\in \mathcal {Y}} P_{XY}(x, y)$. A conditional distribution $P_{X|Y}(x, y)$ over $\mathcal {X}\times \mathcal {Y}$ defines for every $y \in \mathcal {Y}$ a distribution $P_{X|Y=y}$. The statistical distance between two distributions $P_X$ and $P_X'$ over the domain $\mathcal {X}$ is defined as the maximum, over all (inefficient) distinguishers $D : \mathcal {X}\rightarrow \{0,1\}$, of the distinguishing advantage ${\text {SD}}(P_X , P_X') =\big | Pr[D(X) = 1] - Pr[D(X') = 1] \big |$. The conditional Shannon entropy of X given Y is defined as $H(X | Y ) := -\sum _{x,y}P_{XY} (x, y) \log P_{X|Y} (x, y)$ where all logarithms are binary and the mutual information of X and Y as $I(X; Y ) = H(X) - H(X | Y )$. We also use $h(p) = -p \log p - (1 - p) \log (1 - p)$ for the binary entropy function. Furthermore, we denote by $\varPi _f$ an n-party protocol for a function f and by $\varPi _f^{A,B}$ a two-party protocol between parties A and B.

Protocols. We consider protocols involving n parties, denoted by the set $\mathcal {P}=\{\mathsf{P}_1,\ldots , \mathsf{P}_n\}$. The parties communicate over synchronous, point-to-point secure channels. We consider non-reactive secure computation tasks, defined by a deterministic or randomized functionality $f : \mathcal {X}_1 \times \ldots \times \mathcal {X}_n \rightarrow \mathcal {Z}_1 \times \ldots \times \mathcal {Z}_n$. The functionality specifies a mapping from n inputs to n outputs the parties want to compute. The functionality can be fully specified by a conditional probability distribution $P_{Z_1 \cdots Z_n \vert X_1 \cdots X_n}$, where $X_i$ is a random variable over $\mathcal {X}_i$, $Z_i$ is a random variable over $\mathcal {Z}_i$, and for all inputs $(x_1, \ldots , x_n)$ we have a probability function $P_{Z_1 \cdots Z_n \vert X_1 \cdots X_n = (x_1, \ldots , x_n)}$ and $P_{Z_1 \cdots Z_n \vert X_1 \cdots X_n = (x_1, \ldots , x_n)}(z_1, \ldots , z_n)$ is the probability that the output is $(z_1, \ldots , z_n)$ when the input is $(x_1, \ldots , x_n)$. Vice versa, we can consider any conditional probability distribution $P_{Z_1 \cdots Z_n \vert X_1 \cdots X_n}$ as a specification of a probabilistic functionality. In the following we will freely switch between the terminology of probabilistic functionalities and conditional probability distributions.

We consider stand-alone security as well as static and passive corruptions of t out of n parties for some $t\le n$. This means that a set of t parties are announced to be corrupted before the protocol is executed, and the corrupted parties still follow the protocol but might pool their views of the protocol to learn more than they should. We consider statistical correctness and statistical security. We allow simulators to be inefficient. Except that we do not consider computational security, the above model choices are the possible weakest ones, which just makes our impossibility proofs stronger.

The Security Parameter. The security is measured in a security parameter $\sigma$ and we require that the “insecurity” goes to 0 as $\sigma$ grows. We do not allow n to grow with $\sigma$, i.e., we require that the protocol can be made arbitrarily secure when run among a fixed set of parties by just increasing $\sigma$. The literature sometimes consider protocol which only become secure when run among a sufficiently large number of parties. We do not cover such protocols.

Communication Model. We assume that each pair of parties are connected by a secure communication channel, which only leaks to the adversary the length of each message sent¹. We consider protocols proceeding in synchronous rounds. Following [DPP14] we assume that in each round each pair of parties $(\mathsf{P}_i, \mathsf{P}_j)$ will specify a prefix free code $M_{i,j} \subset \{0,1\}^*$ and then $\mathsf{P}_i$ will send a message $m \in M_{i,j}$. The codes might be dynamically chosen, but we require that the parties agree on the codes. If the length of a sent message does not match the length specified by the receiver, the receiver will terminate with an error symbol $\bot$ as output, which will make it count as a violation of correctness.

Let $\epsilon$ denote the empty string and let $E = \{ \epsilon \}$. If $M_{i,j} = E$, then we say that $\mathsf{P}_i$ sends no message to $\mathsf{P}_j$ in that round, i.e., we use the empty string to denote the lack of a message. Notice that if $M_{i,j} \ne E$, then $\epsilon \not \in M_{i,j}$ as $M_{i,j}$ must be prefix free. Therefore, at the point where $\mathsf{P}_j$ specifies the code $M_{i,j}$ for a given round, $\mathsf{P}_j$ already knows whether or not $\mathsf{P}_i$ will send a message in that round. We in particular say that $\mathsf{P}_j$ anticipates a message from $\mathsf{P}_i$ when $M_{i,j} \ne E$. We will only be interested in counting the number of messages sent, not their size. When the protocol is correct, the number of messages sent is obviously equal to the number of messages anticipated.

Definition 1

(Anticipated message complexity). We say that the expected message complexity of a party is the expected number of times a non-empty message is sent or anticipated by the party. The expected message complexity of a protocol is simply the sum of the expected message complexity of the parties, divided by 2. We divide by 2 to avoid counting a transmitted message twice. The expectation is taken over the randomness of the players and maximised over all inputs.

The reason for insisting on a prefix free code for this slightly technical notion is to avoid a problem we would have if we allowed the communication pattern to vary arbitrarily: consider a setting where $\mathsf{P}_j$ wants to send a bit b to $\mathsf{P}_i$. If $b=0$ it sends no message to $\mathsf{P}_i$ or say the empty string. If $b=1$ it sends 0 to $\mathsf{P}_i$. If b is uniformly random, then in half the cases $\mathsf{P}_j$ sends a message of length 0 and in half the cases it sends a message of length 1. This means that a more liberal way of counting the communication complexity would say that the expected communication complexity is $\frac{1}{2}$. This would allow to exchange 1 bit of information with an expected $\frac{1}{2}$ bits of communication. This does not seem quite reasonable. The prefix-free model avoids this while still allowing the protocol to have a dynamic communication pattern. Note that since we want to prove impossibility it is stronger to allow protocols with dynamic rather than fixed communication patterns.

Protocols with Preprocessing. We will also consider protocols for the preprocessing model. In the preprocessing model, the specification of a protocol also includes a joint distribution $P_{R_1 \cdots R_n}$ over $\mathcal {R}_1 \times \ldots \times \mathcal {R}_n$, where the $\mathcal {R}_i$’s are finite randomness domains. This distribution is used for sampling correlated random inputs $(r_1,\ldots ,r_n)\leftarrow P_{R_1 \cdots R_n}$ received by the parties before the execution of the protocol. Therefore, the preprocessing is independent of the inputs. The actions of a party $\mathsf{P}_i$ in a given round may in this case depend on the private random input $r_i$ received by $\mathsf{P}_i$ from the distribution $P_{R_1 \cdots R_n}$ and on its input $x_i$ and the messages received in previous rounds. In addition, the action might depend on the statistical security paramenter $\sigma$ which is given as input to all parties along with $x_i$ and $r_i$. Using the standard terminology of secure computation, the preprocessing model can be thought of as a hybrid model where the parties have one-time access to an ideal randomized functionality P (with no inputs) providing them with correlated, private random inputs $r_i$.

Security Definition. A protocol securely implements an ideal functionality with an error of $\varepsilon$, if the entire view of each corrupted player can be simulated with an error of at most $\varepsilon$ in an ideal setting, where the players only have black-box access to the ideal functionality. Formally, consider Definition 2 below.

Definition 2

Let $\varPi$ be a protocol for the $P_{R_1 \cdots R_n}$-preprocessing model. Let $P_{Z_1 \cdots Z_n \vert X_1 \cdots X_n}$ be an n-party functionality. Let $\mathsf{Adv}$ be a randomized algorithm, which chooses to corrupt a set $\mathcal {A}\subseteq \{1,\ldots ,n\}$ of at most $t \in \mathbb {N}$ parties. Let ${\varvec{x}} = (x_1, \ldots , x_n) \in \mathcal {X}_1 \times \ldots \times \mathcal {X}_n$ be an input. Let $\mathsf {Pattern}^{\varPi }(\sigma ,{\varvec{x}})$ denote the communication pattern in a random run of the protocol $\varPi$, i.e., the list of the length of the messages exchanged between all pairs of parties in all rounds, on input ${\varvec{x}}$ and with security parameter $\sigma$. Define $\mathsf {View}^{\varPi }_\mathsf{Adv}(\sigma ,{\varvec{x}})$ to be the $\mathsf {Pattern}^{\varPi }(\sigma ,{\varvec{x}})$ concatenated with the view of the parties $\mathsf{P}_i$ for $i \in \mathcal {A}$ in the same random run of the protocol $\varPi$. Let $\mathsf {Output}^{\varPi }_{\overline{\mathcal {A}}}(\sigma ,{\varvec{x}})$ be just the inputs and outputs of the honest parties $\mathsf{P}_i$ for $i \not \in \mathcal {A}$ in the same random run of the protocol $\varPi$. Let

$$\mathsf {Exec}^{\varPi }_{\mathsf{Adv}}(\sigma ,{\varvec{x}}) = (\mathsf {View}^{\varPi }_{\mathsf{Adv}}(\sigma ,{\varvec{x}}), \mathsf {Output}^{\varPi }_{\overline{\mathcal {A}}}(\sigma ,{\varvec{x}})).$$

Let $\mathsf{S}$ be a randomized function called the simulator. Sample ${\varvec{z}}$ according to $P_{Z_1 \cdots Z_n \vert X_1 \cdots X_n}({\varvec{x}})$. Give input $\{ (x_i, z_i ) \}_{i \in \mathcal {A}}$ to $\mathsf{S}$. Let $\mathsf{S}(\{ (x_i, z_i ) \}_{i \in \mathcal {A}})$ denote the random variable describing the output of $\mathsf{S}$. Let

$$\mathsf {Sim}_\mathsf{S}(\sigma ,{\varvec{x}}) = \Big (\mathsf{S}(\{ (x_i, z_i ) \}_{i \in \mathcal {A}}), \{ (x_i, z_i ) \}_{i \not \in \mathcal {A}}\Big ).$$

The protocol is $\varepsilon$-semi-honest secure with threshold t if there exist $\mathsf{S}$ such that for all ${\varvec{x}}$ and all $\mathcal {A}$ with $\vert \mathcal {A}\vert \le t$ it holds that

$${\text {SD}}(\mathsf {Exec}^{\varPi }_\mathsf{Adv}(\sigma ,{\varvec{x}}), \mathsf {Sim}_\mathsf{S}(\sigma ,{\varvec{x}})) \le \varepsilon (\sigma ).$$

The protocol is statistically semi-honest secure with threshold t if it is $\varepsilon$-semi-honest secure for a negligible $\varepsilon$.

Secret-Sharing. A $(t+1)$-out-of-n secret-sharing scheme takes as input a secret s from some input domain and outputs n shares, with the property that it is possible to efficiently reconstruct s from every subset of $t+1$ shares, but every subset of at most t shares reveals nothing about the secret s. The value t is called the privacy threshold of the scheme.

A secret-sharing scheme consists of two algorithms: the first algorithm, called the sharing algorithm $\mathsf{Share }$, takes as input the secret s and the parameters t and n, and outputs n shares. The second algorithm, called the recovery algorithm $\mathsf{Recover }$, takes as input $t+1$ shares and outputs a value s. It is required that the reconstruction of shares generated from a value s produces the same value s. Formally, consider the above definition.

Definition 3

(Secret-sharing). Let $\mathbb {F}$ be a finite field and let $n,t \in \mathbb {N}$. A pair of algorithms where $\mathsf{Share }$ is randomized and $\mathsf{Recover }$ is deterministic are said to be a secret-sharing scheme if for every $n,t \in \mathbb {N}$, the following conditions hold.

• Reconstruction: For any set $\mathcal {T}\subseteq \{1,\ldots ,n\}$ such that $|\mathcal {T}| > t$ and for any $s \in \mathbb {F}$ it holds that

  

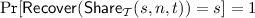
  where $\mathsf{Share }_\mathcal {T}$ is the restriction of the outputs of $\mathsf{Share }$ to the elements in $\mathcal {T}$.

• Privacy: For any set $\mathcal {T}\subseteq \{1,\ldots ,n\}$ such that $|\mathcal {T}| \le t$ and for any $s,s' \in \mathbb {F}$ it holds that

  

  where we use $\equiv$ to denote that two random variables have the same distribution.

Additive Secret-Sharing. In an additive secret-sharing scheme, n parties hold shares the sum of which yields the desired secret. By setting all but a single share to be a random field element, we ensure that any subset of $n-1$ parties cannot recover the initial secret.

Definition 4

(Additive secret-sharing). Let $\mathbb {F}$ be a finite field and let $n \in \mathbb {N}$. Consider the secret-sharing scheme $\mathrm {\mathscr {A}}^n=(\mathsf{Share },\mathsf{Recover })$ defined below.

• The algorithm $\mathsf{Share }$ on input (s, n) performs the following:

  • 1. Generate $(s_1,\ldots ,s_{n-1})$ uniformly at random from $\mathbb {F}$ and define $s_n = s - \sum _{i=1}^{n-1} s_i$.

  • 2. Output $(s_1,\ldots ,s_{n})$ where $s_i$ is the share of the i-th party.

• The recovery algorithm $\mathsf{Recover }$ on input $(s_1,\cdots ,s_{n})$, outputs $\sum _{i=1}^n s_i$.

It is easy to show that the distribution of any $n-1$ of the shares is the uniform one on $\mathbb {F}^{n-1}$ and hence independent of s.

Secret-sharing Notation. In the sequel for a value $s \in \mathbb {F}$ we denote by $[ { {s}}]^{\mathrm {\mathscr {S}}_t^n}$ a random sharing of s for the secret-sharing scheme ${\mathrm {\mathscr {S}}_t^n}$. That is, $[ { {s}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(s,n,t)$ where $[ { {s}}]^{\mathrm {\mathscr {S}}_t^n}=(s_1,\ldots ,s_n)$. Similarly, we denote by $[ { {s}}]^{\mathrm {\mathscr {A}}^n}$ a random additive sharing of s secret shared among n parties.

Primitives. In the sequel we consider the following two-party functionalities which naturally extend to the multi-party setting.

Definition 5

(Multiplication MULT functionality). Let $\mathbb {F}$ be a finite field. Consider two parties A and B. We define the two-party functionality $\mathrm {\textsc {MULT}}(a,b)$ which on input $a\in \mathbb {F}$ from party A and $b\in \mathbb {F}$ from party B outputs $\mathrm {\textsc {MULT}}(a,b)=a\cdot b$ to both parties.

Definition 6

(Inner Product $\mathbf{IP}_{\kappa }$ functionality). Let $\mathbb {F}$ be a finite field and let $\kappa \ge 1$. Consider two parties A and B. We define the two-party functionality $\mathrm {\textsc {IP}}_\kappa (a,b)$ which on input $a\in \mathbb {F}^\kappa$ from party A and $b\in \mathbb {F}^\kappa$ from party B outputs $\mathrm {\textsc {IP}}_\kappa (a,b)=\sum _{i=1}^\kappa a_ib_i$ to both parties.

3 Secure Computation in the Plain Model

We first investigate the honest majority scenario. As explained in the introduction, we will consider protocols that compute arithmetic circuits over some field securely using secret-sharing. All known protocols of this type handle multiplication gates by running a subprotocol that takes as input shares in the two inputs a and b to the gate and output shares of the product ab, such that the output shares contain only information about ab (and no side information on a nor b). Accordingly, we define below a multiplication gate protocol ($\mathrm {\textsc {MGP}}$) to be an interactive protocol for n players that does exactly this, and then show a lower bound on the communication required for such a protocol.

Definition 7

(Multiplication Gate Protocol $\varPi _\mathbf{MULT}$ ). Let $\mathbb {F}$ be a finite field and let $n \in \mathbb {N}$. Let $\mathrm {\mathscr {S}}_t^n$ and $\hat{\mathrm {\mathscr {S}}}_{t'}^n$ be two secret-sharing schemes as per Definition 3. A protocol $\varPi _\mathrm {\textsc {MULT}}$ is an n-party Multiplication Gate Protocol $(\mathrm {\textsc {MGP}})$ with thresholds $t, t'$, input sharing-scheme $\mathrm {\mathscr {S}}_t^n$ and output sharing-scheme $\hat{\mathrm {\mathscr {S}}}_{t'}^n$ if it satisfies the following properties:

• Correctness: In the interactive protocol $\varPi _\mathrm {\textsc {MULT}}$, players start from sets of shares $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(a,n,t)$ and $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(b,n,t)$. Each player outputs a share such that these together form a set of shares $[ { {ab}}]^{\hat{\mathrm {\mathscr {S}}}_{t'}^n}$. Moreover, $t' < 2t$.

• t -privacy: If the protocol is run on randomly sampled shares $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n}$ and $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n}$, then the only new information the output shares can reveal to the adversary is ab. We capture this by requiring that for any adversary corrupting a player subset $\mathcal {A}$ of size at most t, there exists a simulator $\mathsf{S}_\mathcal {A}$ which when given the input shares of the parties in $\mathcal {A}$ (denoted by $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}$, $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}$) and the product ab, will simulate the honest parties’ output shares (denoted by $[ { {ab}}]^{\hat{\mathrm {\mathscr {S}}}_{t'}^n}_{\overline{\mathcal {A}}}$) and the view of the parties in $\mathcal {A}$ with statistically indistinguishable distribution. Formally, for any adversary $\mathsf {ADV}$ corrupting a player set $\mathcal {A}$ with $\vert \mathcal {A}\vert \le t$ there exist $\mathsf{S}_\mathcal {A}$ such that for randomly sampled shares $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(a,n,t)$ and $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(b,n,t)$, it holds that

  

  (1)

  where $\sigma$ is a security parameter and where, in the underlying random experiment, probabilities are taken over the choice of input shares as well as random coins of the protocol and simulator.

Note that we do not require the input and output sharing schemes to be the same, we only require that the output threshold is not too large ($t' < 2t$). Known MPG’s actually have $t'=t$ to allow continued computation, we want to be more generous to make our lower bound stronger. Note also that we do not require the simulators to be efficient.

Recall that we use the term gate-by-gate protocol to refer to any protocol that computes an arithmetic circuit securely by invoking an $\mathrm {\textsc {MGP}}$ for each multiplication gate in the circuit such that the sets of shares that are input are randomly chosen. We leave unspecified what happens with addition gates as this is irrelevant for the bounds we show. An ordered gate-by-gate protocol invokes $\mathrm {\textsc {MGP}}$’s for multiplication gates in an order corresponding to the order in which one would visit the gates when evaluating the circuit.

In the following we show that any $\mathrm {\textsc {MGP}}$ in a gate-by-gate protocol must communicate for every multiplication gate in the honest majority setting even if only semi-honest security is required. The technique of our proof is as follows. We build an information-theoretic two-party computation protocol utilizing an n-party $\mathrm {\textsc {MGP}}$ by emulating multiple parties (in the head) and then use the impossibility result on the existence of an information-theoretic two-party computation protocol to show a contradiction.

Theorem 1

There exists no $\mathrm {\textsc {MGP}}$ $\varPi _\mathrm {\textsc {MULT}}$ as per Definition 7 with thresholds $t, t'$, and with expected anticipated message complexity $\le 2t$.

Proof

Suppose for contradiction that there exists an $\mathrm {\textsc {MGP}}$ $\varPi _\mathrm {\textsc {MULT}}$ with expected anticipated communication complexity at most 2t. We first show a proof in the simpler case where the communication pattern is fixed. This means that at most 2t parties are communicating, i.e., they send or receive messages and the set of parties that communicate is known and fixed. For simplicity of exposition, suppose that these parties are $\mathsf{P}_1, \ldots , \mathsf{P}_{2t}$. We are going to use $\varPi _\mathrm {\textsc {MULT}}$ to construct a two-party unconditionally secure protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ which securely computes the $\mathrm {\textsc {MULT}}$ function between parties A, B as per Definition 5.

In particular, given two parties A and B, with inputs $a,b\in \mathbb {F}$, respectively, involved in the $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ protocol, we are going to let A emulate the first t parties that communicate and B emulate the other t parties, say $\mathsf{P}_{t+1},\ldots ,\mathsf{P}_{2t}$. The protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ proceeds as follows:

• Protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}(\sigma , a,b)$

• Input Phase:

  • 1. Parties A, B secret share their inputs a, b using the secret-sharing scheme $\mathrm {\mathscr {S}}_t^n$. More specifically, A computes $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(a,n,t)$ and B computes $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(b,n,t)$.

  • 2. Party A sends the input shares $(a_{t+1},\ldots , a_{2t})$ to party B and Party B sends the input shares $(b_1,\ldots , b_{t})$ to party A.

  Evaluation Phase:

  • 1. Parties A, B invoke the protocol $\varPi _\mathrm {\textsc {MULT}}(\sigma , a_1,\ldots a_n,b_1,\ldots b_n)$. The emulation of $\varPi _\mathrm {\textsc {MULT}}$ yields a set of shares $[ { {c}}]^{\hat{\mathrm {\mathscr {S}}}_{t'}^n}$ and outputs $(c_1,\ldots ,c_{t})$ to party A and $(c_{t+1},\ldots , c_{2t})$ to party B.

  Output Phase:

  • 2. Party A sends the output shares $(c_1,\ldots ,c_{t})$ to party B and Party B sends the output shares $(c_{t+1},\ldots ,c_{2t})$ to party A.

  • 3. Each party given $2t > t'$ shares of c recovers the output $c=a \cdot b$

We now show that the above protocol is correct and secure. Correctness follows immediately from $t'< 2t$ - as then 2t shares are enough to reconstruct. The protocol is secure (private) due to the t-privacy property of $\varPi _\mathrm {\textsc {MULT}}$. More precisely, if party A is corrupted, we need to simulate his view of the protocol given a and the product ab. We do this as follows: Let $\mathcal {A}$ be the set of parties A emulates in the MGP. We now compute $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(a,n,t)$ and sample $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n}_{\mathcal {A}}$ which can be done by the privacy property of $\mathrm {\mathscr {S}}_t^n$. We then run the simulator $\mathsf{S}_\mathcal {A}$ guaranteed by the t-privacy property to get $\mathsf{S}_\mathcal {A}(\sigma , [ { {a}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}, [ { {b}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}, ab)$. Note that this output includes $\mathcal {A}$’s view of the MGP as well as all output shares.

The simulator now outputs $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n}$, $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n}_{\mathcal {A}}$ and $\mathsf{S}_\mathcal {A}(\sigma , [ { {a}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}, [ { {b}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}, ab)$. This is statistically indistinguishable from A’s view of $\varPi ^{A,B}_\mathrm {\textsc {MULT}}(\sigma , a,b)$ by the privacy property of $\mathrm {\mathscr {S}}_t^n$ and Eq. (1). A similar simulator for B’s view is easy to construct.

However, the above leads to a contradiction since it is well known [BGW88, CCD88] that it is impossible to realize passively secure two-party multiplication (such as the $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ protocol) in the information theoretic setting (even if inefficient simulators are allowed). Therefore, the theorem follows.

We now address the case where the communication pattern might be dynamic. We say that a party communicated if it sent a non-empty message or if it anticipated a non-empty message. So by definition, the expected number of communicating parties is $\le 2t$. Since the observed value is an integer, there is some non-zero, constant probability p such that the observed value of the number of communication parties is at most 2t. We can therefore pick a subset $\mathcal {C}$ of the parties of size 2t such that it happens with probability at least $p/{n \atopwithdelims ()2t}$ that only the parties in $\mathcal {C}$ communicate. Since we can increase the security parameter $\sigma$ independently of n, the number $p/{n \atopwithdelims ()2t}$ is a positive constant (in $\sigma$). We can then modify $\varPi ^{A,B}_\mathrm {\textsc {MULT}}(a,b)$ such that B runs t parties in $\mathcal {C}$ and A runs the other t parties. The protocol runs as $\varPi ^{A,B}_\mathrm {\textsc {MULT}}(a,b)$ except that if it A or B observe that a party in $\mathcal {C}$ anticipates a non-empty message from a party outside $\mathcal {C}$, then the execution is terminated. In case the protocol terminates, the two parties just try again. Since $p/{n \atopwithdelims ()2t}$ is a positive constant this succeeds in an expected constant number of tries. Notice that when the protocol succeeds, all parties in $\mathcal {C}$ received all the messages they would have received in a run of $\varPi ^{A,B}_\mathrm {\textsc {MULT}}(a,b)$ where all the parties were active, as parties only receive the messages they anticipate. Hence the parties in $\mathcal {C}$ have correct outputs (except with negligible probability). For the same reason the output of the parties simulated by A and B will be correct. Hence A and B can reconstruct the output from the 2t shares. We can also argue that the protocol is private: We will simulate A’s (or B)’s view by running the simulator $\mathsf{S}_{\mathcal {A}}$ (where again $\mathcal {A}$ is the set of parties emulated by A) repeatedly until a view is produced where no party in $\mathcal {C}$ anticipates a message from outside of $\mathcal C$. Note that $\mathsf{S}_\mathcal {A}$ simulates the view of an adversary corrupting $\mathcal {A}$, and this view includes the communication pattern from which it is evident who anticipates messages.    $\square$

The above theorem immediately implies:

Corollary 1

Any gate-by-gate protocol that is secure against $t = \varTheta (n)$ corruptions must communicate $\varOmega (n \cdot |C|)$ bits where |C| is the size of the circuit C to compute, and moreover, an ordered gate-by-gate protocol must have a number of rounds that is proportional to the (multiplicative) depth of C.

Jumping ahead, we note that the arguments for this conclusion break down completely when we consider secure computation in the preprocessing model with dishonest majority since in such a model it is no longer true that two-party unconditionally secure multiplication is impossible: just a single preprocessed multiplication triple will be enough to compute a multiplication. We return to this issue in the next section.

A bound that grows with the field size? It is natural to ask if we can get a lower bound on the complexity of an MPG that grows with the field size? after all, existing MGPs do need to send more bits for larger fields. However, the answer is no, as the following example shows: for $a\in \mathbb {F}$, define $z_a$ to be 0 if $a=0$ and 1 otherwise. Then we represent an element $a\in \mathbb {F}$ as a pair $(z_a, \ell _a)$ where $\ell _a$ is randomly chosen if $a=0$ and otherwise $\ell _a = \log _g(a)$, where g is a fixed generator of the multiplicative group $\mathbb {F}^*$. Let $u= |\mathbb {F}^*|$. Observe that now we have $(z_{ab}, \ell _{ab}) = (z_a\cdot z_b, (\ell _a+\ell _b) \bmod u)$.

We now construct a secret sharing scheme: given a secret $a\in \mathbb {F}$, we first compute $(z_a, \ell _a)$ and then share $z_a$ using, e.g., Shamir’s scheme and share $\ell _a$ additively modulo u. An MGP for this scheme can use a standard protocol to compute shares in $z_a\cdot z_b$ and local addition to get shares in $(\ell _a+\ell _b) \bmod u$. Clearly, the communication complexity of this MGP does not depend on $|\mathbb {F}|$.

Of course, the secret sharing scheme we defined is not efficient (at least not in all fields) because one needs to take discrete logs. This is not formally a problem since we did not make any assumptions on the efficiency of secret sharing schemes. But we can in fact get a more satisfactory solution by replacing the additive sharing of the discrete log with black-box sharing directly over the group $\mathbb {F}^*$ [CF02]. This is doable in polynomial time, will cost a factor that is logarithmic in the number of players, but since black-box secret-sharing is homomorphic over the group operation, the resulting MGP still has communication independent of $|\mathbb {F}|$.

Amortized Multiplication Gate Protocols. There is one clear possibility for circumventing the bounds we just argued for gate-by-gate protocols, namely: what if the circuit structure allows us to do, say k multiplications in parallel? Perhaps this can be done more efficiently than k separate multiplications? Of course, this will not help for a worst case circuit whose depth is comparable to its size. But in fact, for “nicer” circuits, we know that such optimizations are possible, based on so-called packed secret-sharing. The catch, however, is that apart from loosing in resilience this only works if there is a gap of size $\varTheta (k)$ between the privacy and reconstruction thresholds of the secret-sharing scheme used, so the number of players must grow with k.

One may ask if this is inherent, i.e., can we save on the communication needed for many multiplication gates in parallel, only by increasing the number of players? While we believe this is true, we were not able to show it in full generality. But we were able to do so for computational complexity, as detailed below. Furthermore, for a restricted setting we explain below and a fixed number of players, we could show that the communication must grow linearly with k.

First, we can trivially extend Definition 3 to cover schemes in which the secret is a vector ${\varvec{a}}= (a_1,\ldots ,a_k)$ of field elements instead of a single value. A further extension covers ramp schemes in which there are two thresholds: the privacy threshold t which is defined as in Definition 3 and a reconstruction threshold $r >t$, where any set of size at least r can reconstruct the secret. Such a scheme is denoted by $\mathrm {\mathscr {S}}_{t,r}^n$. Note that the shares in this case may be shorter than the secret, perhaps even a single field element per player. We can now define a simple extension of the multiplication gate protocol concept:

Definition 8

( ${{k\textsc {-}Multiplication~ Gate~ Protocol~}}$ $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ ). Let $\mathbb {F}$ be a finite field and let $n \in \mathbb {N}$. Let $\mathrm {\mathscr {S}}_{t,r}^n$ and $\hat{\mathrm {\mathscr {S}}}_{t,r}^n$ be two ramp sharing schemes defined over $\mathbb {F}$, for sharing vectors in $\mathbb {F}^k$. $\varPi _{\mathrm {\textsc {MULT}}^k}$ is said to be a ${{k\textsc {-}Multiplication~ Gate~ Protocol~}}$ $(\mathrm {{k\textsc {-}MGP}})$ with thresholds t, r, input sharing scheme $\mathrm {\mathscr {S}}_{t,r}^n$ and output sharing scheme $\hat{\mathrm {\mathscr {S}}}_{t,r}^n$ if it satisfies the following properties:

• Correctness: In the interactive protocol $\varPi _{\mathrm {\textsc {MULT}}^k}$, players start from sets of shares $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n}$ and $[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n}$. Each player outputs a share such that these together form a set of shares $[ { {{\varvec{a}}*{\varvec{b}}}}]^{\hat{\mathrm {\mathscr {S}}}_{t,r}^n}$, where ${\varvec{a}}*{\varvec{b}}$ is the coordinatewise product of ${\varvec{a}}$ and ${\varvec{b}}$.

• t-privacy: If the protocol is run on randomly sampled shares $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_t^n}$ and $[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_t^n}$, then the only new information the output shares can reveal to the adversary is ${\varvec{a}}*{\varvec{b}}$. We capture this by requiring that for any adversary corrupting player subset $\mathcal {A}$ of size at most t, there exists a simulator $\mathsf{S}_\mathcal {A}$ which when given the input shares of the parties in $\mathcal {A}$ (denoted by $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}$, $[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}$) and the product ab, will simulate the honest parties’ output shares (denoted by $[ { {{\varvec{a}}*{\varvec{b}}}}]^{\hat{\mathrm {\mathscr {S}}}_{t'}^n}_{\overline{\mathcal {A}}}$) and the view of the parties in $\mathcal {A}$ with statistically indistinguishable distribution. Formally, for any adversary $\mathsf {ADV}$ corrupting player set $\mathcal {A}$ with $\vert \mathcal {A}\vert \le t$ there exist $\mathsf{S}_\mathcal {A}$ such that for randomly sampled shares $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }({\varvec{a}},n,t)$ and $[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }({\varvec{b}},n,t)$, it holds that

  

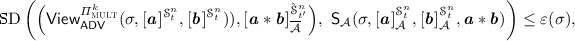  (2)

  where $\sigma$ is a security parameter and where, in the underlying random experiment, probabilities are taken over the choice of input shares as well as random coins of the protocol and simulator.

Before giving our result on k-MGPs we note that for any interactive protocol, it is always possible to represent the total computation done by the players as an arithmetic circuit over a finite field (arithmetic circuits can emulate Boolean circuit which can in turn emulate Turing machines). We can encode messages as field elements and represent sending of messages by wires between the parts of the circuit representing sender and receiver. For a protocol $\varPi$, we refer to an algorithm outputting such a circuit as an arithmetic representation of $\varPi$. Note that such a representation is not in general unique, but once we have chosen one, it makes sense to talk about, e.g., the number of multiplications done by a player in $\varPi$.

Theorem 2

Let $t< r\le n \in \mathbb {N}$. Also let $\mathcal {P}=\{\mathsf{P}_1,\ldots ,\mathsf{P}_n\}$ be a set of parties. Assume that the $\mathrm{k}$-$\mathrm{MGP}$ $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ defined over $\mathbb {F}$ has thresholds t, r. Then for any arithmetic representation of $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ (over any finite field) and for each subset $\mathcal {S}\subset \mathcal P$ of size $n-2t$, the total number of multiplications done by players in $\mathcal {S}$ is $\varOmega (k)$.

Proof

Suppose for contradiction that there exists a k-MGP $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ in which the total number of multiplications done by players in $\mathcal {S}$ is o(k). Assume for notational convenience that $\mathcal {S}= \{ \mathsf{P}_{2t+1}, \ldots , \mathsf{P}_n \}$. We are going to use it to construct a two-party unconditionally secure protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ in the preprocessing model which securely computes k multiplications as follows. We let $u\leftarrow P_U$ denote the correlated randomness we will use in $\varPi _\mathrm {\textsc {MULT}}^{A,B}$. Given two parties A and B involved in the $\varPi _\mathrm {\textsc {MULT}}^{A,B}$ protocol, the idea is to use the assumed k-MGP where A emulates t players and B emulates another t players. In addition, parties A, B together emulate the rest of the parties in $\mathcal {S}$. This can be done using the preprocessed data u: we consider the parties in $\mathcal {S}$ as a reactive functionality $f_\mathcal {S}$ which can be implemented using an existing protocol in the preprocessing model. One example of such a protocol is the SPDZ protocol [DPSZ12] denoted by $\varPi ^{SPDZ }_{f_\mathcal {S}}$ ² which uses additive-secret sharing. Therefore, protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ proceeds as follows:

• Protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}(\{a_i\}_{i\in [k]},\{b_i\}_{i\in [k]},u)$:

• Input Phase:

  • 1. $\forall i\in [k]$, parties A, B secret share their inputs $a_i,b_i$ using the ramp sharing scheme $\mathrm {\mathscr {S}}_{t,r}^n$. So A computes $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n} \leftarrow \mathsf{Share }(({\varvec{a}}),n,t)$ and B computes $[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n} \leftarrow \mathsf{Share }(({\varvec{b}}),n,t)$. For simplicity of exposition, we denote by $(\bar{a}_1,\ldots , \bar{a}_n), (\bar{b}_1,\ldots , \bar{b}_n)$ the shares of $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n}$ and $[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n}$, respectively.

  • 2. Party A sends the input shares $(\bar{a}_{1},\ldots , \bar{a}_{t})$ to party B and Party B sends the input shares $(\bar{b}_{t},\ldots , \bar{b}_{2t})$ to party A.

  • 3. Additively secret share the inputs $(\bar{a}_{2t+1},\ldots ,\bar{a}_{n}, \bar{b}_{2t+1},\ldots ,\bar{b}_{n})$ of the parties in $\mathcal {S}$ between A and B using the additive secret-sharing $\mathrm {\mathscr {A}}^2$ and obtain the shares $([ { {\bar{a}_{2t+1}}}]^{\mathrm {\mathscr {A}}^2},\ldots ,[ { {\bar{a}_{n}}}]^{\mathrm {\mathscr {A}}^2}$, $[ { {\bar{b}_{2t+1}}}]^{\mathrm {\mathscr {A}}^2} ,\ldots ,[ { {\bar{b}_{n}}}]^{\mathrm {\mathscr {A}}^2})$. For the following phase, as we mentioned above, we will think of the computation done by the parties in $\mathcal {S}$ as a reactive functionality $f_\mathcal {S}$ which is implemented using the protocol $\varPi ^{SPDZ }_{f_\mathcal {S}}$ in the preprocessing model.

  Evaluation Phase:

  • Parties A, B invoke the protocol $\varPi _{\mathrm {\textsc {MULT}}^{k}}([ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n},[ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_{t,r}^n})$ in which A, B emulate t parties each, and they together emulate the rest, $n-2t$ players, using the preprocessed data u invoking protocol $\varPi ^{SPDZ }_{f_\mathcal {S}}$. To this end, note that $\varPi ^{SPDZ }_{f_\mathcal {S}}$ represents data by additive secret-sharing. Values $(\bar{a}_{2t+1},\ldots ,\bar{a}_{n}, \bar{b}_{2t+1},\ldots ,\bar{b}_{n})$ of the parties in $\mathcal {S}$ were already additively shared, so they can be used directly as input to $\varPi ^{SPDZ }_{f_\mathcal {S}}$.

    Now, the emulation of $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ is augmented with the protocol $\varPi ^{SPDZ }_{f_\mathcal {S}}$ as follows: when a party in $\mathcal {S}$ would do a local operation, we do the same operation in $\varPi ^{SPDZ }_{f_\mathcal {S}}$. When a party outside $\mathcal {S}$ sends a message to a party in $\mathcal {S}$ an additive secret-sharing of that message is formed between A and B. When a party in $\mathcal {S}$ sends a message to a party outside $\mathcal {S}$ the corresponding additive secret-sharing is reconstructed towards A or B, depending on who emulates the receiver. In the end, we will obtain additive sharings between A and B of the outputs of parties in $\mathcal {S}$, namely $([ { {\bar{c}_{2t+1}}}]^{\mathrm {\mathscr {A}}^2},\ldots ,[ { {\bar{c}_{n}}}]^{\mathrm {\mathscr {A}}^2})$.

  Output Phase:

  • 1. A sends the output shares $(\bar{c}_{1},\ldots , \bar{c}_{t})$ to B, B sends the output shares $(\bar{c}_{t+1},\ldots , \bar{c}_{2t})$ to A computed by $\varPi _{\mathrm {\textsc {MULT}}^{k}}$, and A and B exchange their additive shares $([ { {\bar{c}_{2t+1}}}]^{\mathrm {\mathscr {A}}^2},\ldots ,[ { {\bar{c}_{n}}}]^{\mathrm {\mathscr {A}}^2})$ in order to recover $(\bar{c}_{2t+1},\ldots , \bar{c}_{n})$.

  • 2. Now both A and B have $n\ge r$ shares of the output and can recover the result ${\varvec{a}}*{\varvec{b}}$.

We now show that the above protocol is correct and secure. Correctness follows immediately from the correctness of $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ and $\varPi ^{SPDZ }_{f_\mathcal {S}}$. We argue that the protocol is secure (private) due to the security of $\varPi ^{SPDZ }_{f_\mathcal {S}}$ and the t-privacy property of the $\mathrm {\textsc {MGP}}$ $\varPi _{\mathrm {\textsc {MULT}}^k}$ (see Eq. (1)). For the case where A is corrupted, we first observe that by using the simulator for the $\varPi ^{SPDZ }_{f_\mathcal {S}}$ protocol, we can argue that the view of A in the real protocol is statistically close to the one obtained by replacing players in $\mathcal {S}$ by the ideal functionality $f_\mathcal {S}$.

We can then make a simulator for corrupt A in the $f_\mathcal {S}$-hybrid model, as follows: The shares received by A in the input phase can be simulated by the privacy property of the input sharing scheme, and the rest of the view can be simulated by invoking the simulator $\mathsf{S}_\mathcal {A}$ of the protocol $\varPi _{\mathrm {\textsc {MULT}}^{k}}$ guaranteed by Definition 7, on input $[ { {{\varvec{a}}}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}, [ { {{\varvec{b}}}}]^{\mathrm {\mathscr {S}}_t^n}_\mathcal {A}, {\varvec{a}}*{\varvec{b}}$. Note that $\mathsf{S}_A$ is in charge of simulating $f_\mathcal {S}$. It can therefore define the responses of $f_\mathcal {S}$ such that they are consistent with the view generated by $\mathsf{S}_\mathcal {A}$.³

We therefore conclude from Eq. (2) that $\mathsf{S}_A$ generates a view that is statistically indistinguishable from the real view of an adversary corrupting A. A similar argument holds for B.

Now note that the preprocessed data required by the protocol $\varPi ^{SPDZ }_{f_P}$ amount to a constant number of field elements for each multiplication done. This means that our 2-party protocol needs o(k) preprocessed field elements by assumption on $\varPi _{\mathrm {\textsc {MULT}}^{k}}$. However, this leads to a contradiction since by results in [WW10], it is impossible for two parties to compute k multiplications with statistical security using preprocessed data of size o(k) field elements.    $\square$

What this theorem shows is, for instance, that if we want each player to do only a constant number of local multiplications in a k-MGP, then n needs to be $\varOmega (k)$. Since this is precisely what protocols based on packed sharing can achieve (see, e.g., [DIK+08]), the bound in the theorem is in this sense tight. What the theorem also says is that every subset of size $n-2t$ needs to work hard, so in the case where we tolerate a maximal number of corruptions, i.e., $n=2t+1$, we see that a gate by gate protocol in this case must have computational complexity $\varOmega (n |C|)$, for any circuit of size |C|, not only for “tall and skinny” circuits as we had before.

A restricted result on communication complexity. Our final result on honest majority concerns k-MGPs that are regular by which we mean, first that the output shares they produce follow the same distribution that is also produced by the $\mathsf{Share }$ algorithm of the output secret sharing scheme. This is a rather natural condition that is satisfied by all known k-MGP’s. Second, we will assume that the input and output schemes are the same, have $r=t+1$ (thus excluding packed sharing), and is ideal, i.e., each share is a single field element. This is satisfied by Shamir’s scheme, for instance. The ideal assumption can be replaced by much weaker conditions requiring various symmetry properties, but we stick with the simpler case for brevity.

Theorem 3

A regular $\mathrm{k}$-$\mathrm{MGP}$ has (expected) $\varOmega (k)$ communication complexity.

Proof

The message pattern and -lengths in the k-MGP must not depend on the inputs $a_1,...,a_k, b_1,...,b_k$, so we are done if we show the bound for some fixed distribution of inputs. We choose the uniform distribution, and we write $A_1, A_2$ etc. for the corresponding random variables. Now consider any subset A of t players and another player P. Let U denote the joint view of players in A before we do the k-MGP and $U'$ denote the view after. $V, V'$ denote the corresponding views of P. Finally, $C_A, C_P$ denote the messages sent and received by A and P during the k-MGP. Note that $I(U;V)=0$: We have not sent any messages yet, and furthermore, even given the t shares of A in some $a_i$, since $a_i$ is uniform in $\mathbb {F}$ and the scheme is ideal, the share of P is uniform in $\mathbb {F}$ as well. Also, without loss of generality, we can set $U'= (U, C_A)$ and $V'= (V,C_P)$.

However, since the $C_i=A_iB_i$ are not uniform, we do have common information after the protocol. We see this as follows: since 0 times any value is 0, the value 0 is more likely for $c_i$ than others. So $H(C_i)\le \log q - \epsilon$ for some constant $\epsilon > 0$ that depends on $|\mathbb {F}|= q$. Furthermore, given the vector of shares ${\varvec{S}}_A$ of A in $C_i$, there is a 1-1 correspondence between possible values of $C_i$ and values of the share $S_p$ of P. This means that $H(S_p | {\varvec{S}}_A) \le \log |\mathbb {F}| - \epsilon$. On the other hand, $H(S_p) = \log q$ because the scheme is ideal, so therefore $I({\varvec{S}}_A; S_P) \ge \epsilon$. This applies to every $C_i$, so we have that $I(U';V') \ge k \epsilon$. We can now compute as follows, using a standard chain rule for mutual information:

$$\begin{aligned} \epsilon k\le & {} I((U,C_A); (V, C_P)) \\= & {} I(U; (V,C_P)) + I(C_A; (V,C_P)| U) \\\le & {} I(U; (V,C_P)) + H(C_A)\\= & {} I(U;V) + I(U; C_P | V) + H(C_A)\\\le & {} I(U;V) + H(C_P) + H(C_A)\\= & {} H(C_P) + H(C_A). \end{aligned}$$

So indeed, the expected size of the communication grows linearly with k.

4 Secure Computation in the Preprocessing Model

It is well known that all functions can be computed with unconditional security in the setting where $n-1$ of the n players may be corrupted, and where the players are given correlated randomness, also known as preprocessed data, that does not have to depend on the function to be computed, nor on the inputs. Winkler and Wullschleger [WW10] proved lower bounds on the the amount of preprocessed data needed to compute certain functions with statistical security where the bound depends on certain combinatorial properties of the target function.

All existing protocols in the preprocessing model that are efficient in the circuit size of the function, work according to the gate-by-gate approach we encountered in the previous section. We can define (ordered) gate-by-gate protocols and MGPs exactly as for the honest majority setting, with two exceptions: MGPs are allowed to consume preprocessed data, and the output threshold $t'$ must equal the input threshold t. This is because we typically have $t=n-1$ in this setting, and then it does not make sense to consider $t' > t$, then even all players cannot reconstruct the output,

As before, we want to show that multiplication gate protocols require a certain amount of communication, but as mentioned before, we can no longer base ourselves on impossibility of unconditionally secure multiplication for two parties, since this is in fact possible in the preprocessing model. Instead, the contradiction will come from the known lower bounds on the size of the preprocessed data needed to compute certain functions.

4.1 Protocols Based on Additive Secret-Sharing

We start by showing that any gate-by-gate protocol must communicate for every multiplication gate when the underlying secret sharing scheme is the additive one. We show that an $\mathrm {\textsc {MGP}}$ that does not communicate enough implied a protocol that contradicts the lower bound by Winkler and Wullschleger [WW10] on the the amount of preprocessed data needed to compute certain functions with statistical security.

Theorem 4

Consider the preprocessing model where $n-1$ of the n players may be passively corrupted. In this setting, there exists no $\mathrm {\textsc {MGP}}$ $\varPi _\mathrm {\textsc {MULT}}$ with expected anticipated communication complexity $\le n-1$ and with additive secret-sharing $\mathrm {\mathscr {A}}^n$ as output sharing scheme.

Proof

Suppose for contradiction that there exists an $\mathrm {\textsc {MGP}}$ $\varPi _\mathrm {\textsc {MULT}}$ (with preprocessed data $u\leftarrow P_U$) which contradicts the claim of the theorem. Similar to Theorem 1 we will first assume a fixed communication pattern. Assume for notational convenience that only the parties $\mathsf{P}_1, \ldots , \mathsf{P}_{n-1}$ communicate. Given two parties A and B, we are going to construct a two-party protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ which on input $a,b\in \mathbb {F}$ from A, B, respectively, securely computes ab. The idea is for A to emulate the $n-1$ players who communicate in $\varPi _\mathrm {\textsc {MULT}}$ while B emulates the last player. In particular, protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ proceeds as follows:

• Protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$

• Input Phase:

  • 1. Parties A, B secret share their inputs a, b using the input secret-sharing scheme $\mathrm {\mathscr {A}}^n$ of $\varPi _\mathrm {\textsc {MULT}}$. More specifically, A computes $[ { {a}}]^{\mathrm {\mathscr {A}}^n} \leftarrow \mathsf{Share }(a,n,n-1)$ and B computes $[ { {b}}]^{\mathrm {\mathscr {A}}^n} \leftarrow \mathsf{Share }(b,n,n-1)$.

  • 2. Party A sends the input share $a_n$ to party B and Party B sends the input shares $(b_1,.., b_{n-1})$ to party A.

  Evaluation Phase:

  • 1. Parties A, B invoke the $\mathrm {\textsc {MGP}}$ $\varPi _\mathrm {\textsc {MULT}}$ as per Definition 7 in the preprocessing model where A emulates the $n-1$ players who communicate, and we assume these are the first $n-1$ players. This means that this phase involves no communication between A and B, but it may consume some preprocessed data u. The execution of $\varPi _\mathrm {\textsc {MULT}}$ yields a sharing of $[ { {c}}]^{\mathrm {\mathscr {A}}^n}$ and outputs $(c_1,...,c_{n-1})$ to party A and $c_n$ to party B.

  Output Phase:

  • 1. A sends $\sum _{i=1}^{n-1}c_i$ to B and B sends $c_n$ to A. The parties add the received values to recover the output $c=a \cdot b$.

Correctness of this protocol follows immediately. The protocol can be argued to be secure(private). In particular, the simulator $\mathsf{S}$ for $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ proceeds as follows. The preprocessing data to be used by the corrupted party can be simulated with the correct distribution without any knowledge of the inputs. In the input phase, the corrupted party receives only an unqualified set of shares whose distribution can be simulated perfectly. There is no communication to be simulated in the evaluation phase. In the output phase, it is the case that whenever the protocol computes the correct result, then the share received from the honest party is trivial to simulate because it is determined from the corrupted party’s own share and the result ab. Hence, the only source of error is the negligible probability that the output is wrong in the real execution, so it follows that

$${\text {SD}}(\mathsf {Exec}^{\varPi ^{A,B}_\mathrm {\textsc {MULT}}}_\mathsf{Adv}(\sigma ,(a,b)), \mathsf {Sim}_{\mathsf{S}}(\sigma ,(a,b))) \le \epsilon (\sigma ).$$

However, we can say even more: Let $u\leftarrow P_U$ be the preprocessed data that is consumed during the protocol ($\varPi _\mathrm {\textsc {MULT}}$ uses preprocessed data). We now define a new protocol $\varPi ^{A,B}_{\mathrm {\textsc {MULT}}^k}$ that will compute k independent multiplications (do not confuse this protocol with the amortized and honest majority protocol in Definition 8). It does this by running k instances of $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$, using the same preprocessed data u for all instances.

Normally, it is of course not secure to reuse preprocessed data, but in this particular case it works because the communication in $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ is independent of u, and so is the simulation. More precisely, $\varPi ^{A,B}_{\mathrm {\textsc {MULT}}^k}$ is clearly correct because each instance of $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ runs with correctly distributed preprocessed data. It is also private: we can simulate by first simulating the corrupted party’s part of u and then running k instances of the rest of $\mathsf{S}$’s code. Again, the only source of error is the case where the real protocol computes an incorrect result, but the probability of this happening for any of the k instances is at most a factor k larger than for a single instance, by a union bound, and so is still negligible.

However, this leads to a contradiction with the result of [WW10]: they showed that the amount of preprocessed data needed for a secure multiplication is at least some non-zero number of bits w. It also follows from [WW10] that if we want k multiplications on independently chosen inputs this requires kw bits. So if we consider a k large enough that kw is larger than the size of u, we have a contradiction and the theorem follows.

We now generalise to dynamic communication patterns. As in the proof of Theorem 1 we can find a party $\mathsf{P}_i$ such that with some constant positive probability p the party $\mathsf{P}_i$ does not send a message and no party anticipates a message from $\mathsf{P}_i$. Assume without loss of generality that this is party $\mathsf{P}_n$. Assume first that p is negligibly close to 1. In that case the parties can apply the above protocol unmodified. Consider then the case where p is not negligibly close to 1. We also have that p is not negligibly close to 0. Hence there is a non-negligible probability that $\mathsf{P}_n$ sends a message and a non-negligible probability that $\mathsf{P}_n$ does not send a message. The decision of $\mathsf{P}_n$ to communicate or not can depend only on four values:

• Its share $a_n$ of a.

• Its share $b_n$ of b.

• Its share $u_n$ of the correlated randomness.

• Its private randomness, call it $r_n$.

This means that there exist a function $\varrho (a_n,b_n,u_n,r_n) \in \{0,1\}$ such that $\mathsf{P}_n$ communicates iff $\varrho (a_n,b_n,u_n,r_n)=1$. Observe that the decision can in fact not depend more than negligibly on $a_n$ and $b_n$. If it did, this would leak information on these shares to the parties $\mathsf{P}_1, \ldots , \mathsf{P}_{n-1}$ which already know all the other shares. This would in turn leak information on a or b to the parties $\mathsf{P}_1, \ldots , \mathsf{P}_{n-1}$, which would contradict the simulatability property of the protocol. We can therefore without loss of generality assume that there exist a function $\varrho (u_n,r_n) \in \{0,1\}$ such that $\mathsf{P}_n$ communicates iff $\varrho (u_n,r_n)=1$.

Assume that with non-negligible probability over the choice of the $u_n$ received by $\mathsf{P}_n$ it happens that the function $\varrho (u_n,r_n)$ depends non-negligibly on $r_n$, i.e., for a uniform $r_n$ it happens with non-negligible probability that $\varrho (u_n,r_n) = 0$ and it also happens with non-negligible probability that $\varrho (u_n,r_n) = 1$. Since $r_n$ is independent of the view of the parties $\mathsf{P}_1, \ldots , \mathsf{P}_{n-1}$, as it is the private randomness of $\mathsf{P}_n$, it follows that the probability that one of the other parties anticipate a message from $\mathsf{P}_n$ is independent of whether $\varrho (u_n,r_n) = 0$ or $\varrho (u_n,r_n) = 1$. Hence it either happens with non-negligible probability that $\varrho (u_n,r_n) = 0$ and yet one of the other parties anticipate a message from $\mathsf{P}_n$ or it happens with non-negligible probability that $\varrho (u_n,r_n) = 1$ and yet none of the other parties anticipate a message from $\mathsf{P}_n$. Both events contradict the correctness of the protocol. We can therefore without loss of generality assume that there exist a function $\varrho (u_n) \in \{0,1\}$ such that $\mathsf{P}_n$ communicates iff $\varrho (u_n)=1$. By assumption we have that p is non-zero, so there exist some $u_n$ such that $\varrho (u_n)=0$. We can therefore condition the execution on the event $\varrho (u_n)=0$. Let $P_U$ be the distribution from which u is sampled. Consider then the random variable $P_{U'}$ which is distributed as $P_{U}$ under the condition that $\varrho (u_n)=0$. We claim that if we run $\varPi _\mathrm {\textsc {MULT}}$ with $P_{U'}$ instead of $P_{U}$ then the protocol is still secure. Assuming that this claim is true, A and B can apply the above protocol, but simply use $(\varPi _\mathrm {\textsc {MULT}}, P_{U'})$ instead of $(\varPi _\mathrm {\textsc {MULT}}, P_{U})$.

What remains is therefore only to argue that $(\varPi _\mathrm {\textsc {MULT}}, P_{U'})$ is secure. To simulate the protocol, run the simulator $\mathsf{S}_\mathcal {A}'$ for $(\varPi _\mathrm {\textsc {MULT}}, P_{U})$ until it outputs a simulated execution where $\mathsf{P}_n$ did not communicate. Let E be the event that $\mathsf{P}_n$ does not communicate. Since it can be checked from just inspecting the view of the real execution of $(\varPi _\mathrm {\textsc {MULT}}, P_{U})$ (or the simulation) whether E occurred, it follows that E occurs with the same probability in the real execution and the simulation (or at least probabilities which are negligible close) or we could use the occurrence of E to distinguish. Since E happens with a positive constant probability it then also follows that the real execution conditioned on E and the simulation condition on E are indistinguishable, or we could apply a distinguisher for the conditioned distributions when E occurs and otherwise make a random guess to distinguish the real execution of $(\varPi _\mathrm {\textsc {MULT}}, P_{U})$ from its simulation. This shows that $\mathsf{S}_\mathcal {A}'$ simulates $(\varPi _\mathrm {\textsc {MULT}}, P_{U'})$.    $\square$

A generalisation. We note that Theorem 3 easily extends to any output secret sharing scheme with the following property: Given shares $c_1,..., c_n$ of c, there is a function $\phi$ such that one can reconstruct c from $c_1,...,c_{n-1}, \phi (c_n)$ and given c and $c_1,...,c_{n-1}$ one can simulate $\phi (c_n)$ with statistically close distribution. The proof is the same as above except that in the output phase, B sends $\phi (c_n)$ to A, who computes c and sends it to B.

Theorem 3 shows, for instance, that the SPDZ protocol [DPSZ12] has optimal communication for the class of gate-by-gate protocols using additive secret-sharing: it sends O(n) messages for each multiplication gate, and of course one needs to send $\varOmega (n)$ messages if all n players are to communicate, as mandated in the theorem. Note also that in the dishonest majority setting, the privacy threshold of the secret-sharing scheme used has to be $n-1$, so we cannot have a gap between the reconstruction and privacy thresholds, and so amortisation tricks based on packed secret-sharing cannot be applied. We therefore do not consider any lower bounds for amortised $\mathrm {\textsc {MGP}}$’s.

4.2 Protocols Based on Any Secret-Sharing Scheme

Note that if we consider an $\mathrm {\textsc {MGP}}$ whose output sharing scheme is not the additive scheme, the protocol $\varPi ^{A,B}_\mathrm {\textsc {MULT}}$ in the proof of Theorem 4 may not work. This is because it is no longer clear that given your own share of the product and the result, the other party’s share is determined. In particular, the distribution of the other share may depend on the preprocessed data we consume and so if we just send that share in the clear, it is not obvious that we can reuse the preprocessing.

The solution is to not send shares in the clear, but have the parties securely compute the output from their shares. This can be done using an existing general protocol for secure computation in the preprocessing model. This will mean that we can indeed reuse preprocessed data consumed by the $\mathrm {\textsc {MGP}}$ protocol itself. However, we now consume new preprocessed data for every instance of the reconstruction protocol since this protocol requires communication. It turns out that if we use a variant of the $\mathrm {\textsc {MGP}}$ that computes, not just one product, but an inner product of long enough vectors, we can still obtain a contradiction. This works because we can show that computing the inner product of long vectors requires lots of preprocessed data. On the other hand, the inner product itself is just one field element, therefore the cost of reconstructing such a small result is not significant.

In order to obtain the above result and give more details, we proceed by proving some auxiliary results with lower bounds on the amount of preprocessed data needed for a secure evaluation of a function f.

Lower Bounds for Secure Function Evaluation in the Preprocessing Model. In this section we will give lower bounds for secure implementations of functions $f:\mathcal {X}\times \mathcal {Y}\rightarrow \mathcal {Z}$ in the $P_{U},P_{V}$-preprocessing model, which for simplicity of exposition we refer to as $P_{U_f,V_f}$, that outputs correlated randomness for the semi-honest setting. In particular, we are in the setting where the parties A, B have access to a functionality that gives a random variable $U_f$ to A and $V_f$ to B with some guaranteed joint distribution $P_{U_f,V_f}$ of $U_f, V_f$. Given this, the parties compute securely a function $f:\mathcal {X}\times \mathcal {Y}\rightarrow \mathcal {Z}$ where A holds $x \in \mathcal {X}$, and B holds $y \in \mathcal {Y}$. This function should have no redundant inputs for party A ⁴:

$$\begin{aligned} \forall x, x' \in \mathcal {X}( x \ne x' \rightarrow \exists y\in \mathcal {Y}: f(x,y) \ne f(x',y) ) \end{aligned}$$

(3)

The authors of [WW10] obtained Theorem 5 that gives a lower bound on the conditional entropy of $P_{U_f,V_f}$. Their bound applies for input distributions X and Y which are independent and uniformly distributed. This implies worst case communication complexity. Our bound in Theorem 6 also applies to independent and uniform distributions.

Theorem 5

Let $f:\mathcal {X}\times \mathcal {Y}\rightarrow \mathcal {Z}$ be a function that satisfies property (3). Assume there exists a protocol having access to $P_{U_f,V_f}$ which is an $\varepsilon$-secure implementation of f in the semi-honest model with $t=1$ corruptions. Then

Our general result will only apply to functions where the output lives in a ring $\mathcal {Z}$. As it will become apparent, for the next theorem we require the following property for a function $f:\mathcal {X}\times \mathcal {Y}\rightarrow \mathcal {Z}$:

$$\begin{aligned} \forall x, x' \in \mathcal {X}(x \ne x' \rightarrow \exists y_1,y_2 \in \mathcal {Y}: f(x,y_1)-f(x,y_2) \ne f(x',y_1)-f(x',y_2)) \end{aligned}$$

(4)

Note that the bound in Theorem 5 still applies for functions f that satisfy properties (3) and (4).

In the following we explore the lower bounds on the amount of preprocessed data with respect to composition of functions. In Theorem 6 we prove a lower bound on the conditional entropy of $P_{U_h,V_h}$ for a function h which is a linear combination of two functions f and g. Our bound also applies to compositions of k functions where k is an arbitrary number. Basically, we show that the amount of preprocessed data you need to compute the sum of f and g is the sum of what you need to compute f and g separately, as long as f and g are applied to distinct and independent inputs. We clearly need this assumption, as otherwise the theorem is clearly false, just think of applying $f=g$ on the same inputs.

Theorem 6

Let $f:\mathcal {X}\times \mathcal {Y}\rightarrow \mathcal {Z}_f$, $g:\mathcal {Z}\times \mathcal {W}\rightarrow \mathcal {Z}_g$ be functions that satisfy properties (3) and (4). Assume that $\mathcal {Z}_f = \mathcal {Z}_g$. Let h be a linear combination of f and g, namely: $\forall x\in \mathcal {X}, y\in \mathcal {Y},z\in \mathcal {Z}, w\in \mathcal {W},$ $h(x,z,y,w):=\alpha f(x,y)+\beta g(z,w)$ for some $\alpha ,\beta \ne 0$. If there exists a protocol that securely implements the function h with access to $P_{U_h,V_h}$, then it holds that

Furthermore, the function h will have the following property:

(5)

Proof

We start by proving that the function h has this property:

(6)

By assumption we consider the following two properties on the function g:

$$\begin{aligned} \forall z \ne z' \in \mathcal {Z}~\exists w\in \mathcal {W}: g(z,w) \ne g(z',w) \end{aligned}$$

(7)

$$\begin{aligned} \forall z\ne z' \in \mathcal {Z}~\exists w_1,w_2 \in \mathcal {W}: g(z,w_1)-g(z,w_2) \ne g(z',w_1)-g(z',w_2) \end{aligned}$$

(8)

and properties (3) and (4).

In order to prove properties (6) and (5) for the function h we proceed as follows:

• Case 1. $x=x', z\ne z'$:

  Suppose that $\exists y$ such that $f(x',y)=f(x',y)$. By assumption $\exists w\in \mathcal {W}: g(z,w) \ne g(z',w)$. Therefore, it follows that $f(x',y)-f(x,y)\ne g(z,w) - g(z',w)$ and property (6) holds.

• Case 2. $x\ne x', z= z'$:

  Suppose that $\exists w$ such that $g(z',w)=g(z',w)$. By assumption $\exists y\in \mathcal {Y}: f(x,y) \ne g(x',y)$. It follows that $f(x',y)-f(x,y)\ne g(z,w) - g(z',w)$ and property (6) holds.

• Case 3. $x\ne x', z\ne z'$:

  Let $c=f(x',y)-f(x,y)$ for some $y\in \mathcal {Y}$. By assumption $\exists w_1,w_2 \in \mathcal {W}$ such that $c_1=g(z,w_1) - g(z',w_1)$ and $c_2=g(z,w_2) - g(z',w_2)$ such that $c_1\ne c_2$. Without loss of generality, assume that $c\ne c_1$ then $f(x',y)-f(x,y)\ne g(z,w_1) - g(z',w_1)$ and property (5) follows.

Since the function h satisfy property (6) it also has property (3) and hence we get from Theorem 5 that

$$H(U_h | V_h ) \ge \max _{y,w} H(X,Z | h(X,Z,y,w)).$$

We then get that:

$$\begin{aligned} H(U_h | V_h )\ge & {} {\max _{y,w}}~{H(X,Z | \alpha f(X, y)+\beta g(Z,w))} \end{aligned}$$

(9)

$$\begin{aligned}\ge & {} {\max _{y,w}}~{H(X,Z | f(X, y),g(Z,w))}\end{aligned}$$

(10)

$$\begin{aligned}\ge & {} {\max _{y}}~{H(X | f(X, y))} + {\max _{w}}~{H(Z | g(Z, w))} \end{aligned}$$

(11)

Inequality (11) follows from the independence of X, Z. This proves the theorem.    $\square$

Remark 1

The above theorem also applies to multiplicative relations ruling out the cases where $g(z,w)=0$ and $f(x,y)=0$.

Exploiting Theorem 6 we prove a lower bound for the inner product function $\mathrm {\textsc {IP}}_k$ as per Definition 6.

Lemma 1

Let $\kappa \ge 1$ and let $f:\mathcal {X}\times \mathcal {Y}\rightarrow \mathcal {Z}$ be a multiplication function as per Definition 5. If there exist a protocol $\varPi _{\mathrm {\textsc {IP}}_k}$ which securely implements the inner product function $\mathrm {\textsc {IP}}_k$ with error probability $\varepsilon$ in the semi-honest model and having access to $P_{U_{\mathrm {\textsc {IP}}_k}V_{\mathrm {\textsc {IP}}_k}}$ then

(12)

Proof

Since the function f satisfies properties (3) and (4), a straightforward application of Theorem 6 for $k=2$ yields . However it is easy to see that the proof of Theorem 6 extends to addition of k functions for any k, so the lemma follows in the same way from this more general result.   $\square$

Utilising Theorem 6 in the following we prove that any function whose “preprocessing complexity” is large enough requires lots of communication. What “large enough” means here is determined by the output secret-sharing scheme used in the protocol, in a sense we make precise below. In the following, when f is a function with two inputs and one output, we will speak about a protocol for computing shares of an f-output, denoted by $\varPi _{f-output}$. This is essentially the same as an $\mathrm {\textsc {MGP}}$ except that we replace multiplication by f. So the protocol takes as input shares of $x_1$ and $x_2$ and computes shares of $f(x_1,x_2)$ as output. Note that the inputs $x_1, x_2$ may be vectors of field elements, whereas we will by default assume that the output is a single field element.

In the sequel, for simplicity of exposition let $\mathtt {L}_f$ denote a lower bound on the amount of preprocessed data needed for a secure implementation of f in the preprocessing model and let $\mathtt {U}_f$ denote an upper bound.

Reconstruction Protocol $\varPi _{rec}$ . Let ${\mathrm {\mathscr {S}}_t^n}$ be the secret-sharing scheme as per Definition 3 and let $f'_{\mathrm {\mathscr {S}}_t^n}$ be the reconstruction function of ${\mathrm {\mathscr {S}}_t^n}$. Then, we can securely implement the function $f'_{\mathrm {\mathscr {S}}_t^n}$ in the preprocessing model via the protocol $\varPi _{SPDZ}$ yielding the protocol $\varPi _{rec}$ ⁵. It follows that $\varPi _{rec}$ demands communication and that its complexity depends only on the underlying secret-sharing scheme ${\mathrm {\mathscr {S}}_t^n}$. In this case we obtain an upper bound $\mathtt {U}_{rec}$ on the amount of preprocessed data consumed by $\varPi _{rec}$.

Theorem 7

Consider the preprocessing model where t of the n players may be passively corrupted. Let $\varPi _{rec}$ be a secure output reconstruction protocol with access to $P_{U_{rec},V_{rec}}$ for the secret-sharing scheme $\hat{\mathrm {\mathscr {S}}}^n_t$. Let f be a function with two inputs and one field element as output such that $\mathtt {U}_{rec} < \mathtt {L}_{f}$. There exists no passively secure n-player protocol $\varPi _{f-output}$ with expected anticipated communication complexity $\le t$ for computing shares of an f-output with $\hat{\mathrm {\mathscr {S}}}^n_t$ as output secret-sharing scheme.

Proof

We start by assuming a fixed communication pattern. Suppose for contradiction that there exists a protocol $\varPi _{f}$ where at most t players communicate. Assume that it is the t first parties. Given two parties A and B, we are going to construct a two-party protocol $\varPi _f^{A,B}$ which on input a, b from A, B, respectively, securely computes f(a, b). The idea is to execute the $\varPi _{f-output}$ protocol in which A emulates the t players who communicate while B emulates the rest of the parties but we are interest just for one additional party, say $\mathsf{P}_{t+1}$. In particular, protocol $\varPi ^{A,B}_f(a,b)$ proceeds as follows:

• Protocol $\varPi ^{A,B}_f(a,b)$:

• Input Phase:

  • 1. Parties A, B secret share their inputs a, b using the secret-sharing scheme $\mathrm {\mathscr {S}}_t^n$. More specifically, A computes $[ { {a}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(a,n,t)$ and B computes $[ { {b}}]^{\mathrm {\mathscr {S}}_t^n} \leftarrow \mathsf{Share }(b,n,t)$.

  • 2. Party A sends the input share $(a_{t+1},\ldots ,a_n)$ to party B and Party B sends the input shares $(b_{1},\ldots , b_{t})$ to party A.

  Evaluation Phase:

  • 1. Parties A, B invoke the protocol $\varPi _{f-output}$ where A emulates the t players who communicate, and we assume these are the first t players. This means that this phase involves no communication between A and B, but it may consume some preprocessed data. The execution of $\varPi _{f-output}$ yields a sharing of $[ { {c}}]^{\mathrm {\mathscr {S}}^n_t}$ and outputs $(c_{1},...,c_{t})$ to party A and $(c_{t+1},\ldots ,c_n)$ to party B.

  Output Phase:

  • 1. Both parties locally invoke protocol $\varPi _{Rec}$ with access to $P_{U_{rec},V_{rec}}$ which on input $[ { {c}}]^{\hat{\mathrm {\mathscr {S}}}^n_t}$ outputs the result f(a , b).

Correctness of the protocol follows immediately from the correctness of $\varPi _{f-output}$ and $\varPi _{Rec}$. The protocol can be argued to be secure(private). More specifically, the simulator $\mathsf{S}_\mathcal {A}$ of $\varPi ^{A,B}_f$ proceeds as follows. In the input phase, the parties receive only an unqualified set of shares whose distribution can be simulated perfectly. There is no communication to be simulated in the evaluation phase. In the output phase, simulation is guaranteed by the invocations of the sub-simulator of the secure protocol $\varPi _{Rec}$. Hence, it follows that

$${\text {SD}}(\mathsf {Exec}^{\varPi ^{A,B}_f}_\mathsf{Adv}(\sigma ,(a,b)), \mathsf {Sim}_{\mathsf{S}_\mathcal {A}}(\sigma ,(a,b))) \le \varepsilon (\sigma ).$$

We can claim the following: Note that the communication in $\varPi ^{A,B}_f$ is actually independent of the preprocessed data needed in order to securely compute f. Therefore, while reusing the same preprocessed data for each invocation of $\varPi _{f-output}$, we could have executed $\ell$ instances of $\varPi ^{A,B}_f$ on independent inputs without affecting correctness since the simulation is independent of the preprocessed data. However, since protocol $\varPi _{Rec}$ is interactive its preprocessed data must be refreshed for each of the $\ell$ executions of $\varPi _{Rec}$. This means that the amount of preprocessed data needed in order to compute $\ell$ instances of f is $\mathtt {U}_f + \ell \cdot \mathtt {U}_{rec}$. So if we consider an $\ell$ large enough such that $\ell \cdot \mathtt {L}_{f}>\mathtt {U}_f + \ell \cdot \mathtt {U}_{rec}$, we have a contradiction and the theorem follows.

The generalization to dynamic communication patterns follows along the lines of the proof of Theorem 4: there we split the players in a maximal unqualified set ($n-1$ players) and the rest (1 player). Here we do the same except that the maximal unqualified set has t players and $n-t$ remain. We then argue exactly as in the proof of Theorem 4 that decisions to send/receive cannot depend on private randomness or shares, and therefore we can build a new protocol that can be used in our construction of a 2-party protocol.    $\square$

Given a function f with one output and a non-zero lower bound, we can add it to itself on distinct inputs a sufficient number of times in order to satisfy the condition in the above theorem. An example of a function f is the inner product function $\mathrm {\textsc {IP}}_k$ which is the composition of k $\mathrm {\textsc {MULT}}$ functions. In Lemma 1 we obtained a lower bound $\mathtt {L}_{\mathrm {\textsc {IP}}^k}$ on the amount of preprocessed data consumed by a protocol that securely implements the function ${\mathrm {\textsc {IP}}^k}$. Now, if k is large enough to satisfy the condition $\mathtt {U}_{rec} < \mathtt {L}_{\mathrm {\textsc {IP}}_k}$, then it holds that $\ell \cdot \mathtt {U}_{rec} + \mathtt {L}_\mathrm {\textsc {MULT}}< \ell \cdot \mathtt {L}_{\mathrm {\textsc {IP}}_k}$ for large enough $\ell$ leading to a contradiction with Theorem 7.

5 Conclusions

We have shown that any information-theoretic secure protocol that follows the ${typical }$ gate-by-gate design pattern must communicate for every multiplication gate, even if only semi-honest security is required, for both honest majority and dishonest majority with preprocessing where the target secret sharing scheme is an additive one. We have also shown similar results for any target secret sharing scheme in the dishonest majority setting. This highlights a reason why, even with preprocessing, all known protocols which are efficient in the circuit size |C| of the evaluated function require $\varOmega (n|C|)$ communication and $\varOmega (d_C)$ rounds where $d_C$ is the depth of C. Our result implies that a fundamental new approach must be found in order to construct protocols with reduced communication complexity that beat the complexities of BGW, GMW, SPDZ etc. Of course, it is also possible that our bounds hold for any protocol efficient in the circuit size of the function, and this is the main problem we leave open. Another open problem is to find unrestricted bounds on MGPs for parallel multiplications.