Abstract
We revisit the question of constructing an ideal cipher from a random oracle. Coron et al. (Journal of Cryptology, 2014) proved that a 14-round Feistel network using random, independent, keyed round functions is indifferentiable from an ideal cipher, thus demonstrating the feasibility of such a transformation. Left unresolved is the number of rounds of a Feistel network that are needed in order for indifferentiability to hold. We improve upon the result of Coron et al. and show that 10 rounds suffice.
This work was performed under financial assistance award 70NANB15H328 from the U.S. Department of Commerce, National Institute of Standards and Technology.
D. Dachman-Soled—Work supported in part by NSF CAREER award #1453045. This work was done in part while the author was visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #1523467.
J. Katz and A. Thiruvengadam—Work supported in part by NSF award #1223623.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The security of practical block ciphers—i.e., pseudorandom permutations—is not currently known to reduce to well-studied, easily formulated, computational problems. Nevertheless, modern block-cipher constructions are far from ad-hoc, and a strong theory for their construction has been developed. An important area of research is to understand the provable security guarantees offered by these classical paradigms.
One of the well-known approaches for building practical block ciphers is to use a Feistel network [9], an iterated structure in which key-dependent, “random-looking” round functions on \(\{0,1\}^n\) are applied in a sequence of rounds to yield a permutation on \(\{0,1\}^{2n}\). In analyzing the security that Feistel networks provide, it is useful to consider an information-theoretic setting in which the round functions are instantiated by truly random and independent (keyed) functions. The purpose of such an analysis is to validate the structural robustness of the approach. Luby and Rackoff [12] proved that when independent, random round functions are used, a three-round Feistel network is indistinguishable from a random permutation under chosen-plaintext attacks, and a four-round Feistel network is indistinguishable from a random permutation under chosen plaintext/ciphertext attacks.
In the Luby-Rackoff result, the round functions are secretly keyed and the adversary does not have direct access to them; the security notion considered—namely, indistinguishability—is one in which the key of the overall Feistel network is also unknown to the adversary. A stronger notion of security, called indifferentiability [14], applies even when the round functions are public, and aims to show that a block cipher behaves like an ideal cipher, i.e., an oracle for which each key defines an independent, random permutation. Proving indifferentiability is more complex than proving indistinguishability: to prove indifferentiability of a block-cipher construction \(\mathbf {BC} \) (that relies on an ideal primitive \(\mathcal {O}\)) from an ideal cipher \(\mathbf {IC} \), one must exhibit a simulator \(\mathbf {S}\) such that the view of any distinguisher interacting with \((\mathbf {BC} ^{\mathcal {O}}, \mathcal {O})\) is indistinguishable from its view when interacting with \((\mathbf {IC}, \mathbf {S}^{\mathbf {IC}})\). For Feistel networks, it is known (see [1, 11]) that one can simplify the problem, and focus on indifferentiability of the Feistel network when using random and independent unkeyed round functions from a public random permutation; an ideal cipher is then obtained by keying the round functions.
In a recent result building on [2, 11, 16], Coron et al. [1] proved that when using independent, random round functions, a 14-round Feistel network is indifferentiable from a public random permutation. The main question left open by the work of Coron et al. is: precisely how many rounds of a Feistel network are needed for indifferentiability to hold? It is known from prior work [1] that 5 rounds are not sufficient, while (as we have just noted) 14 rounds are. In this work, we narrow the gap and show that 10 rounds suffice.Footnote 1
We provide an overview of our proof, and the differences from that of Coron et al., in Sect. 2.
Concurrent Work. In concurrent and independent work, Dai and Steinberger [4] have also shown indifferentiability of a 10-round Feistel network from an ideal cipher. We provide a brief comparison between our work and theirs in Sect. 2.3.
Subsequent Work. Dai and Steinberger [5] have more recently improved their analysis and shown that an 8-round Feistel network is indifferentiable from an ideal cipher. The true number of rounds needed remains open.
1.1 Other Related Work
Coron et al. [2] claimed that a 6-round Feistel network is indifferentiable from an ideal cipher. Their proof of indifferentiability introduced the partial chain detection technique that we also rely on here. Seurin [16] gave a simpler proof of indifferentiability for a 10-round Feistel network, and introduced a clever technique for bounding the simulator complexity. Holenstein et al. [11] later showed that there was a distinguishing attack against the simulator of Coron et al. [2], and a gap in the proof of the 10-round simulator by Seurin [16]; however, they prove that a 14-round Feistel network is indifferentiable from an ideal cipher by building on prior work as well as incorporating several new techniques.
Ramzan and Reyzin [15] proved that a 4-round Feistel network remains indistinguishable from a random permutation even if the adversary is given access to the middle two round functions. Gentry and Ramzan [10] showed that a 4-round Feistel network can be used to instantiate the random permutation in the Even-Mansour cipher [8], and proved that such a construction is a pseudorandom permutation even if the round functions of the Feistel network are publicly accessible. Dodis and Puniya [7] studied security of the Feistel network in a scenario where the adversary learns intermediate values when the Feistel network is evaluated, and/or when the round functions are unpredictable but not (pseudo)random.
Various relaxations of indifferentiability, such as public indifferentiability [7, 18] or honest-but-curious indifferentiability [6], have also been considered. Dodis and Puniya [6] proved that a Feistel network with super-logarithmic number of rounds is indifferentiable from an ideal cipher in the honest-but-curious setting. Mandal et al. [13] proved that the 6-round Feistel network is publicly indifferentiable from an ideal cipher.
1.2 Organization of the Paper
In Sect. 2 we provide a high-level overview of our proof, and how it differs from the proof of indifferentiability of the 14-round Feistel network [1, 11]. After some brief background in Sect. 3, we jump into the technical details, describing our simulator in Sect. 4 and giving the proof of indifferentiability in Sect. 5. Additional discussion and proofs that have been omitted here are available in the full version of this work [3].
2 Overview of Our Proof
We first describe the proof structure used for the proof of indifferentiability of the 14-round Feistel network from an ideal cipher [1, 11], and then describe how our proof differs.
2.1 Techniques for the 14-Round Simulator
Consider a naive simulator for an r-round Feistel construction, which responds to distinguisher queries to each of the round functions \(\mathbf {F} _1,\ldots ,\mathbf {F} _r\), by always returning a uniform value. Unfortunately, there is a simple distinguisher who can distinguish oracle access to \((\textsf {Feistel}_r^{\mathbf {F}}, \mathbf {F})\) from oracle access to \((\mathbf {P}, \mathbf {S}^{\mathbf {P}})\): The distinguisher queries \((x_0, x_1)\) to the first oracle, receiving \((x_r, x_{r+1})\) in return, and uses oracle access to the second oracle to evaluate the r-round Feistel and compute \((x'_r, x'_{r+1})\) on its own, creating a chain of queries \((x_1, \ldots , x'_r)\). Note that in the first case \((x_r, x_{r+1}) = (x'_r, x'_{r+1})\) with probability 1, while in the second case the probability that \((x_r, x_{r+1}) = (x'_r, x'_{r+1})\) is negligible.
An approach to addressing the above attack, which essentially gives the high-level intuition for how a successful simulator works, is as follows: If the simulator learns the value of \(\mathbf {P} (x_0, x_1) = (x_r, x_{r+1})\) before the distinguisher queries the entire chain, then the simulator assigns values for the remaining queries \(\mathbf {F} _i(x_i)\), conditioned on the restriction \(\textsf {Feistel}_r^{\mathbf {F}}(x_0, x_1) = (x_r, x_{r+1})\). More specifically, if there are two consecutive rounds \((i, i+1)\), where \(i \in \{1, \ldots , r-1\}\), which have not yet been queried, the simulator adapts its assignments to \(\mathbf {F} _i(x_i)\), \(\mathbf {F} _{i+1}(x_{i+1})\) to be consistent with \(\mathbf {P} (x_0, x_1) = (x_r, x_{r+1})\). When the simulator adapts the assignment of \(\mathbf {F} _i(x_i)\) to be consistent with a constraint \(\mathbf {P} (x_0, x_1) = (x_r, x_{r+1})\), we say that this value of \(\mathbf {F} _i(x_i)\) has been assigned via a ForceVal assignment. Further details of the 14-round simulator are discussed below.
Partial Chain Detection and Preemptive Completion. To allow the simulator to preemptively discover \(\mathbf {P} (x_0, x_1) = (x_r, x_{r+1})\), the authors fix two “detect zones” which are sets of consecutive rounds \(\{1,2,13,14\}\), \(\{7,8\}\). Each time the simulator assigns a value to \(\mathbf {F} _i(x_i)\), it also checks whether there exists a tuple of the form \((x_1,x_2,x_{13},x_{14})\) such that (1) \(\mathbf {F} _1(x_1)\), \(\mathbf {F} _2(x_2)\), \(\mathbf {F} _{13}(x_{13})\), and \(\mathbf {F} _{14}(x_{14})\) have all been assigned and (2) \(\mathbf {P} (\mathbf {F} _1(x_1) \oplus x_2, x_1) = (x_{14}, \mathbf {F} _{13}(x_{13}) \oplus x_{14})\); or whether there exists a tuple of the form \((x_7, x_8)\) such that \(\mathbf {F} _7(x_7)\) and \(\mathbf {F} _8(x_8)\) have both been assigned. A pair of consecutive round values \((x_k,x_{k+1})\) is referred to as a “partial chain,” and when a new partial chain is detected in the detect zones described above, it is “enqueued for completion” and will later be dequeued and preemptively completed. When a partial chain is detected due to a detect zone that includes both \(x_1\) and \(x_r\), we say it is a “wraparound” chain. Note that preemptive completion of a chain can cause new chains to be detected and these will then be enqueued for completion. This means that in order to prove indifferentiability, it is necessary to argue that for \(x_i\) that fall on multiple completed chains, all restrictions on the assignment of \(\mathbf {F} _i(x_i)\) can be simultaneously satisfied. In particular the “bad case” will be when some assignment \(\mathbf {F} _i(x_i)\) must be adapted via a ForceVal assignment, but an assignment to \(\mathbf {F} _i(x_i)\) has previously been made. If such a case occurs, we say the value at an adapt position has been “overwritten.” It turns out that to prove indifferentiability, it is sufficient to prove that this occurs with negligible probability.
4-Round Buffer Zone. In order to ensure that overwrites do not occur, the notion of a 4-round buffer zone is introduced in [1, 11]. Their simulator has two 4-round buffer zones, corresponding to rounds \(\{3,4,5,6\}\) or \(\{9,10,11,12\}\). Within the buffer zones, positions \(\{3,6\}\) (respectively, \(\{9,12\}\)) are known as the set uniform positions, and positions \(\{4,5\}\) (respectively, \(\{10,11\}\)) are known as the adapt positions. They prove the following property (which we call henceforth the strong set uniform property): At the moment a chain is about to be completed, the set uniform positions of the buffer zone are always unassigned. This means that the simulator will always assign uniform values to \(\mathbf {F} _{3}(x_3)\) and \(\mathbf {F} _6(x_6)\) (respectively, \(\mathbf {F} _{9}(x_9)\) and \(\mathbf {F} _{12}(x_{12})\)) immediately before assigning values to \(\mathbf {F} _{4}(x_4)\) and \(\mathbf {F} _5(x_5)\) (respectively, \(\mathbf {F} _{10}(x_{10})\) and \(\mathbf {F} _{11}(x_{11})\)) using ForceVal. This ensures that ForceVal overwrites with negligible probability, because \(x_{4} = x_2 \oplus \mathbf {F} _3(x_3)\) is only determined at the moment \(\mathbf {F} _3(x_3)\) is assigned and so the probability that \(\mathbf {F} _4(x_4)\) has already been assigned is negligible (a similar argument holds for the other adapt positions).
Rigid Structure. The rigid structure of [1, 11] helps their proof in two ways: First, since all assignments across all completed chains are uniform except in the fixed adapt positions \(\{4,5\}\) and \(\{10,11\}\), it is easier to argue about “bad events” occurring. In particular, since the 4-round buffer of one chain (\(\{3,4,5,6\}\) or \(\{9,10,11,12\}\)) cannot overlap with the detect zone of another chain (\(\{1,2,13,14\}\) or \(\{7,8\}\)), they are able to argue that if a “bad event” occurs while detecting a chain C, then either an equivalent chain was already enqueued or it must have been caused by a uniform setting of \(\mathbf {F} _i(x_i)\).
Bounding the Simulator’s Runtime. The approach of [1, 11] (originally introduced in [2]) is to bound the total number of partial chains that get completed by the simulator. In order to create a partial chain of the form \((x_1, x_2, x_{13}, x_{14})\), it must be the case that \(\mathbf {P} (\mathbf {F} _1(x_1) \oplus x_2, x_1) = (x_{14}, \mathbf {F} _{13}(x_{13}) \oplus x_{14})\) and so, intuitively, the distinguisher had to query either \(\mathbf {P} \) or \(\mathbf {P} ^{-1}\) in order to achieve this. Thus, the number of partial chains of the form \((x_1, x_2, x_{13}, x_{14})\) (i.e. wraparound chains) that get detected and completed by the simulator is at most the total number of queries made by the distinguisher. Since there is only a single middle detect zone \(\{7,8\}\), once we have a bound on the number of wraparound chains that are completed, we can also bound the number of completed partial chains of the form \((x_7, x_8)\).
2.2 Our Techniques
We next briefly discuss how our techniques differ from those of the 14-round simulator [1, 11], focusing on the four areas discussed above.
Separating Detection from Completion for Wrap-Around Chains. When the distinguisher makes a query \(\mathbf {F} _i(x_i)\) to the simulator, our simulator proceeds in two phases: In the first phase, the simulator does not make any queries, but enqueues for completion all partial chains which it predicts will require completion. In the second phase, the simulator actually completes the chains and detects and enqueues only on the middle detect zone (which in our construction corresponds to rounds \(\{5,6\}\)). This simplifies our proof since it means that after the set of chains has been detected in the first phase, the simulator can complete the chains in a manner that minimizes “bad interactions” between partial chains. In particular, in the second phase, the simulator first completes chains C with the property that one of the set uniform positions is “known” and hence could already have been assigned (in the completion of another chain D) before the chain C gets dequeued for completion. (Although this violates the strong set uniform property of [1, 11], in our proof we are able to avoid this requirement. See the discussion of the weak set uniform property below for further details). The simulator then proceeds to complete (and detect and enqueue) other chains. This allows us to reduce the complexity of our analysis.
Relaxed Properties for the 4-Round Buffer Zone. When a partial chain C is about to be completed, we allow one of the set uniform positions, say \(x_{\ell -1}\), to already be assigned, as long as the adapt position \(x_{\ell }\) adjacent to this set uniform position has not yet been assigned. Chains that exhibit the property where one of the set uniform positions is already assigned before the completion of the chain are said to exhibit the weak set uniform property. In Lemma 36, we prove that for chains exhibiting the weak set uniform property, the adapt position is not assigned till the chain is dequeued for completion.
Relaxed Structure. Requiring only the weak set uniform property allows us to consider a more relaxed structure for detect zones and 4-round buffer zones. Instead of requiring that for every chain that gets completed the 4 round buffer positions (i.e., \(\{3,4,5,6\}\) or \(\{9,10,11,12\}\) in [1, 11] are always unassigned, we allow more flexibility in the position of the 4-round buffer. For example, depending on whether the detected chain is of the form \((x_1, x_2, x_{10})\), \((x_1, x_9, x_{10})\), or \((x_5, x_6)\), our 4-round buffer will be one of: \(\{3,4,5,6\}\) or \(\{6,7,8,9\}\), \(\{2,3,4,5\}\) or \(\{5,6,7,8\}\), \(\{1,2,3,4\}\) or \(\{7,8,9,10\}\), respectively. This flexibility allows us to reduce the number of rounds. Now, however, the adapt zone of one chain may coincide with the detect zone of another chain. Since there are no dedicated roles for fixed positions, and since partial chains in the middle detect zone are detected during the completion of other chains, we define additional bad events BadlyHitFV and BadlyCollideFV and argue that they occur with low probability. Intuitively, BadlyHitFV captures the event where a \(\textsc {ForceVal} \) assignment occurs at \(x_\ell \) such that it forms a valid Feistel sub-sequence \(x_{\ell -1}\), \(x_{\ell }\) and \(x_{\ell +1}\) where \(x_{\ell -1}\) and \(x_{\ell +1}\) refer to adjacent positions to \(x_\ell \) that they have already been assigned. This is analogous to the bad event BadlyHit defined in [1, 11] with the difference being that BadlyHit refers to a uniform assignment and BadlyHitFV refers to a \(\textsc {ForceVal} \) assignment. Similarly, BadlyCollideFV captures the event where a \(\textsc {ForceVal} \) assignment occurs at \(x_\ell \) such that it causes two chains to “collide” at some position. This is analogous to the bad event BadlyCollide defined in [1, 11] with the difference being that BadlyCollide refers to a uniform assignment and BadlyCollideFV refers to a \(\textsc {ForceVal} \) assignment. Furthermore, in order to prove that a new wraparound chain does not get created during the completion of other chains we introduce and bound the probability of a new bad event BadlyCollideP. Intuitively, BadlyCollideP captures the event where a query to the random permutation returns a value \((x_0,x_1)\) such that two chains “collide” on \(x_1\) or returns a value \((x_{10},x_{11})\) such that two chains collide on \(x_{10}\).
Balancing Detection with the Simulator’s Runtime. There is a clear trade-off between the achieved security bound and the running time of the simulator. If the simulator is too “aggressive” and detects too many chains too early, then we may perhaps achieve better security at the cost of extremely high simulator complexity. In comparison to the construction of [1, 11], our construction has more detect zones and, moreover, for wraparound chains, we detect on partial chains consisting of three consecutive queries instead of four consecutive queries. Nevertheless, at a high-level, our proof that the simulator runtime is polynomial follows very similarly to the proof in [1, 11]. As there, we first bound the number of completed partial chains of the form \((x_1, x_2, x_{10})\) and \((x_1,x_9,x_{10})\) (such chains are wraparound chains since they contain both \(x_1\) and \(x_{10}\)). Once we have done this, we again have only a single non-wraparound detect zone and so we can follow the argument of [1, 11] to bound the number of completed partial chains of the form \((x_5,x_6)\). Once we have a bound on the number of completed partial chains, it is fairly straightforward to bound the simulator complexity.
2.3 Comparison with Concurrent Work
As noted previously, Dai and Steinberger [4] have independently announced the same result we claim here. The starting point of their work is the 10-round simulator proposed by Seurin [16]. They use only two adapt zones (namely, \(\{3,4\}\) and \(\{7,8\}\)) and allow the distinguisher to learn the values at both positions surrounding the adapt zones. In contrast, our simulator allows the distinguisher to learn the value at only one of the two positionsFootnote 2 surrounding the adapt zones; due to our flexible 4-round buffer zone, our adapt zones can be any pair of consecutive rounds except \(\{1,2\}\), \(\{5,6\}\), and \(\{9,10\}\). Additionally, our proof follows the same high-level structure as in [1], whereas Dai and Steinberger present a new proof inspired by changes made to Seurin’s simulator [16]. (Their subsequent improvement [5] showing indifferentiability of an 8-round Feistel network from an ideal cipher relies on the observation that detection on wrap-around chains can span only three rounds, rather than four.)
With regard to concrete security, our results are incomparable. Say q is the number of queries made by the distinguisher, and let n be the input/output length of the round functions. Dai and Steinberger [4] show indifferentiability \(\epsilon =O(q^8/2^n)\) using a simulator running in time \(T=O(q^{10})\); we show indifferentiability \(\epsilon =O(q^{12}/2^n)\) using a simulator that runs in time \(T=O(q^6)\). It is interesting to observe that both works achieve the same tradeoff for the product \(\epsilon \cdot T\).
3 Background
We use the definition of indifferentiability used by the work on 14-round Feistel network [1, 11], based on the definition of Maurer, Renner, and Holenstein [14].
Definition 1
Let \(\mathbf {C} \) be a construction that, for any n, accesses functions \(\mathbf {F} = (\mathbf {F} _1,\ldots ,\mathbf {F} _r)\) over \(\{0,1\}^n\) and implements an invertible permutation over \(\{0,1\}^{2n}\). (We stress that \(\mathbf {C} \) allows evaluation of both the forward and inverse directions of the permutation.) We say that \(\mathbf {C} \) is indifferentiable from a random permutation if there exists a simulator \(\mathbf {S} \) and a polynomial t such that for all distinguishers \(\mathbf {D} \) making at most \(q=\mathsf{poly}(n)\) queries, \(\mathbf {S} \) runs in time t(q) and
is negligible, where \(\mathbf {F} \) are random, independent functions over \(\{0,1\}^n\) and \(\mathbf {P} \) is a random permutation over \(\{0,1\}^{2n}\). (We stress that \(\mathbf {P} \) can be evaluated in both the forward and inverse directions).
The r-round Feistel construction, given access to \(\mathbf {F} = (\mathbf {F} _1,\ldots ,\mathbf {F} _r)\), is defined as follows. Let \((L_{i-1},R_{i-1})\) be the input to the i-th round, with \((L_0, R_0)\) denoting the initial input. Then, the output \((L_{i},R_{i})\) of the i-th round of the construction is given by \(L_{i} := R_{i-1}\) and \(R_i := L_{i-1} \oplus \mathbf {F} _i(R_{i-1})\). So, for a r-round Feistel, if the 2n-bit input is \((L_0,R_0)\), then the output is given by \((L_r,R_r)\).
4 Our Simulator
4.1 Informal Description of the Simulator
The queries to \(\mathbf {F} _1,\ldots ,\mathbf {F} _{10}\) are answered by the simulator through the public procedure \(\mathbf {S}.\textsc {F}(i,x)\) for \(i = 1,\ldots ,10\). When the distinguisher asks a query \(\textsc {F}(i,x)\), the simulator checks to see if the query has already been set. The queries that are already set are held in tables \(G_1,\ldots ,G_{10}\) as pairs (x, y) such that if \(\textsc {F}(i,x)\) is queried, and if \(x \in G_i\), then y is returned as the answer to query \(\textsc {F}(i,x)\). If the query has not already been set, then the simulator adds x to the set \(A_i^j\) where j indicates the jth query of the distinguisher. The simulator then checks if \(i \in \{1,2,5,6,9,10\}\) (where these positions mark the endpoints of the detect zones) and, if so, checks to see if any new partial chains of the form \((x_9,x_{10},9)\), \((x_1,x_2,1)\), or \((x_5,x_6,5)\) need to be enqueued. If no new partial chains are detected, the simulator just sets the value of \(G_i(x)\) uniformly and returns that value. If new partial chains are detected and enqueued in \({Q}_{\text {enq}}\), then the simulator evaluates these partial chains “forward” and “backward” as much as possible (without setting any new values of \(G_{m}(\cdot )\)) for all \(m \in \{1,\ldots ,10\}\). Say the evaluation stopped with \(x_{m} \notin G_{m}\). Then, the simulator adds \(x_{m}\) to \(A_{m}^j\) and checks if \(m \in \{1,2,5,6,9,10\}\) and if so, detects any additional partial chains that form with \((x_{m},m)\) and enqueues them for completion if necessary and repeats the process again until no more partial chains are detected.
The chains enqueued for completion during this process are enqueued in queues \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\) and \({Q}_{\text {all}}\). Any chain that has been enqueued in \({Q}_{\text {enq}}\) is also enqueued in \({Q}_{\text {all}}\). Chains enqueued in \(Q_{b}\) for \(b \in \{1,5,6,10\}\) are those that may exhibit the weak set uniform property. Specifically, say \(C = (x_k,x_{k+1},k,\ell ,g,b)\) is a chain that is enqueued to be adapted at position \(\ell \) i.e. the “adapt” positions for C are at \(\ell ,\ell +1\) and the “set uniform” positions are at \(\ell -1,\ell +2\) with the “set uniform” position that is adjacent to the query that caused C to be enqueued being at “good” set uniform position g and the other “set uniform” position at b. If, at the time of enqueueing, the chain C can be evaluated up to the “bad” set uniform position b and the value of chain C at b, say \(x_b\), is such that \(x_b \notin G_b\), then C is enqueued in \(Q_{b}\). (Note that there are chains that exhibit this property but are not enqueued for completion. These are the chains that belong to the set \(\mathsf{SimPChains}\). This is only to simplify the analysis for the bound of the complexity of the simulator. We will later show that ignoring these chains does not affect the simulation and in fact, these chains belong to \(\mathsf{CompChains}\) at the end of the simulator’s run while answering \(\mathbf {D} \)’s \(j^{th}\) query).
The completion of enqueued chains starts with the completion of the chains enqueued in \(Q_{b}\) for \(b \in \{1,5,6,10\}\). A chain C is dequeued from \(Q_{b}\) and if \(C \notin \mathsf{CompChains}\), the simulator “completes” the chain. This process proceeds similarly to the completion process in [1]. The simulator evaluates the chain forward/backward upto the 4-round buffer setting \(G_i(x_i)\) values uniformly for any \(x_i \notin G_i\) that comes up while evaluating forward/backward. In the 4-round buffer consisting of the “set uniform” positions and the “adapt” positions, the simulator sets the values of C at the set uniform positions uniformly (if they have not already been set) and forces the values at the adapt positions such that evaluation of the Feistel is consistent with the random permutation. (Note that this could possibly lead to a value in \(G_i(\cdot )\) getting overwritten. A major technical part of the proof is to show that this happens with negligible probability.) After this process, the simulator places C in the set \(\mathsf{CompChains}\) along with “equivalent” chains obtained by evaluating C on the detect zone positions i.e. chains of the form \((x_k,x_{k+1},k)\) for \(k = 1,5,9\).
Once the simulator completes the chains enqueued in \(Q_{b}\) for all \(b \in \{1,5,6,10\}\), the simulator completes the remaining chains enqueued in \({Q}_{\text {all}}\). The completion process for the remaining chains enqueued in \({Q}_{\text {all}}\) is the same as the completion process described above except that the simulator detects additional partial chains of the form \((x_5,x_6,5)\) during the completion and enqueues them in the queue \({Q}_{\text {mid}}\) i.e. during the completion of a chain C in \({Q}_{\text {all}}\), if an assignment occurs such that \(x_k \in G_k\) for some \(k \in \{5,6\}\) due to the assignment and \(x_k \notin G_k\) before the assignment, then the simulator enqueues the partial chain \((x_5,x_6,5)\) in \({Q}_{\text {mid}}\) for all \(x_{k'} \in G_{k'}\) such that \(k' \in \{5,6\}\) and \(k \ne k'\). (Note that the assignment could be a \(\textsc {ForceVal} \) assignment as well.) Finally, the simulator completes all the chains in \({Q}_{\text {mid}}\) that are not already in \(\mathsf{CompChains}\). The completion process again is the same as the process described for chains enqueued in \(Q_{b}\). The simulator then returns the answer \(G_i(x)\) to the query \(\textsc {F}(i,x)\).
4.2 Formal Description of the Simulator
The simulator \(\mathbf {S}\) internally uses hashtables \(G_1,\ldots ,G_{10}\) to store the function values. Additionally, it uses sets \(A^j_1,\ldots ,A^j_{10}\) for the \(j^{th}\) distinguisher query to detect partial chains that need to be completed; these sets store values that would be added to \(G_i\) in the future. A queue \({Q}_{\text {enq}}\) to detect partial chains that need to be completed and stores a copy of \({Q}_{\text {enq}}\) in a queue \({Q}_{\text {all}}\) that is used during completion. Queues \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\) are used to store the chains in \({Q}_{\text {enq}}\) whose “bad” set uniform position is known at the time of detection. Queue \({Q}_{\text {mid}}\) is used to store new chains of the form \((x_5,x_6,5)\) that are enqueued during the completion of chains from \({Q}_{\text {all}}\). A set \(\mathsf{CompChains}\) is used to remember the chains that have been completed already. Finally, a set \(\mathsf{SimPChains}\) is used to hold chains of the form \((x_1,x_2,1)\) and \((x_9,x_{10},9)\) that are detected due to \(\textsc {P}/\textsc {P}^{-1}\) queries made by the simulator. This set is needed only for the purpose of analyzing the complexity of the simulator.
The variables used below are: Queues \({Q}_{\text {enq}},{Q}_{\text {all}},Q_{1},Q_{5},Q_{6},Q_{10},{Q}_{\text {mid}} \); Hashtables \(G_1,\ldots ,G_{10}\); Sets \(A^j_i := \emptyset \) for \(i = 1,\ldots ,10\) and \(j=1,\ldots ,q\) where q is the maximum number of queries made by the distinguisher, Sets \(\mathsf{CompChains}\) := \(\emptyset \) and \(\mathsf{SimPChains}:= \emptyset \). Initialize \(j:=0\). The procedure \(\textsc {F}(i,x)\) provides the interface to a distinguisher.

5 Proof of Indifferentiability
Let \(\textsf {Feistel}\) denote the 10-round Feistel construction, let \(\mathbf {F} \) be 10 independent random functions with domain and range \(\{0,1\}^n\), and let \(\mathbf {P} \) denote a random permutation on \(\{0,1\}^{2n}\). Let \(\mathbf {S} \) denote the simulator from the previous section. We prove:
Theorem 2
The probability that a distinguisher \(\mathbf {D} \) making at most q queries outputs 1 in an interaction with \((\mathbf {P},\mathbf {S} ^{\mathbf {P}})\) and the probability that it outputs 1 in an interaction with \((\mathsf{Feistel}^\mathbf {F},\mathbf {F})\) differ by at most \(O(q^{12}/2^n)\). Moreover, \(\mathbf {S} \) runs in time \(O(q^6)\) except with probability \(O(q^{12}/2^n)\).
For the rest of the paper, fix a distinguisher \(\mathbf {D} \) making at most q queries.
5.1 Proof Overview
Our proof structure utilizes four hybrid experiments \(H_1, \ldots , H_4\) as in the proof of indifferentiability of the 14-round Feistel network [1, 11]. Hybrid \(H_1\) denotes the scenario in which \(\mathbf {D} \) interacts with \((\mathbf {P},\mathbf {S} ^{\mathbf {P}})\), and \(H_4\) denotes the scenario in which \(\mathbf {D} \) interacts with \((\mathbf {\textsf {Feistel}}^\mathbf {F},\mathbf {F})\). To prove indifferentiability, we show that the difference between the probability \(\mathbf {D} \) outputs 1 in \(H_1\) and the probability \(\mathbf {D} \) outputs 1 in \(H_4\) is at most \(\text {poly}(q)/2^n\).
In \(H_2\), the random permutation \(\mathbf {P} \) is replaced with a two-sided random function \(\mathbf {R} \). Following [1, 11], we first bound the simulator complexity in hybrid \(H_2\) and use that to bound the simulator’s complexity in \(H_1\).
Next, we define certain “bad events” that can occur in an execution of \(H_2\), and show that these events occur with low probability. We then show that as long as these events do not occur in an execution of \(H_2\), then certain “good” properties hold; in particular, we can prove that for every call to \(\textsc {ForceVal} (x,\cdot ,j)\) that occurs in the execution, we have \(x \notin G_j\) before the call. If this is true, we say that “\(\textsc {ForceVal} \) does not overwrite.” This is the main technical part of the proof and can be found in Sect. 5.3.2.
In \(H_3\), the two-sided random function \(\mathbf {R} \) is replaced with the 10-round Feistel construction. The distinguisher interacts with  where \(\textsf {Feistel}^+\) is the \(\textsf {Feistel}\) construction with additional procedures
where \(\textsf {Feistel}^+\) is the \(\textsf {Feistel}\) construction with additional procedures  and
and  . Given the “good” properties that were proven in Sect. 5.3.2, we prove that \(H_2\) and \(H_3\) are indistinguishable. The proof follows exactly along the lines of the proof in [1, 11].
. Given the “good” properties that were proven in Sect. 5.3.2, we prove that \(H_2\) and \(H_3\) are indistinguishable. The proof follows exactly along the lines of the proof in [1, 11].
Finally, in \(H_4\), the distinguisher interacts with \((\textsf {Feistel}^\mathbf {F}, \mathbf {F})\) and hence accesses the random functions \(\mathbf {F} \) directly instead of through the simulator. We prove that \(H_3\) and \(H_4\) are indistinguishable similar to the proof of [1, 11].
Due to space constraints, we omit some of the proofs in the following sections. The omitted proofs can be found in the full version [3].
5.2 Indistinguishability of the First and Second Experiments
In \(H_2\), we replace the random permutation with the two-sided random function \(\mathbf {R}\), and \(\mathbf {D} \) interacts with  . The simulator \(\hat{\mathbf {S}}\) in \(H_2\) is exactly the same as the simulator \(\mathbf {S}\) described in Sect. 4.2 except that it implements procedures
. The simulator \(\hat{\mathbf {S}}\) in \(H_2\) is exactly the same as the simulator \(\mathbf {S}\) described in Sect. 4.2 except that it implements procedures

and

by calling the procedures \(\mathbf {R}\).

and \(\mathbf {R}\).

that are provided by \(\mathbf {R}\) (described below).
The two-sided function \(\mathbf {R}\) maintains a hashtable \(P\) containing elements of the form \((\downarrow ,x_0,x_1)\) and \((\uparrow ,x_{10},x_{11})\). Whenever \(\mathbf {R}.\textsc {P}(x_0,x_1)\) is queried, \(\mathbf {R}\) checks if \((\downarrow ,x_0,x_1) \in P\) and if so, answers accordingly. Otherwise, an independent uniform output \((x_{10},x_{11})\) is picked and \((\downarrow ,x_0,x_1)\) as well as \((\uparrow ,x_{10},x_{11})\) are added to \(P\), mapping to each other. In addition to \(\textsc {P}\) and \(\textsc {P}^{-1}\), \(\mathbf {R} \) contains the procedures  and
and  .Footnote 3
.Footnote 3  works as follows: If \((\downarrow ,x_0,x_1)\in P\), it returns true if \((\downarrow ,x_0,x_1)\) maps to \((x_{10},x_{11})\) for some value of \(x_{11} \in \{0,1\}^n\) and false otherwise. Procedure
works as follows: If \((\downarrow ,x_0,x_1)\in P\), it returns true if \((\downarrow ,x_0,x_1)\) maps to \((x_{10},x_{11})\) for some value of \(x_{11} \in \{0,1\}^n\) and false otherwise. Procedure  works as follows: If \((\uparrow ,x_{10},x_{11})\in P\), it returns true if \((\uparrow ,x_{10},x_{11})\) maps to \((x_{0},x_{1})\) for some value of \(x_{0} \in \{0,1\}^n\) and false otherwise. The pseudocode for the two-sided random function \(\mathbf {R} \), using hashtable \(P\), is as follows:
works as follows: If \((\uparrow ,x_{10},x_{11})\in P\), it returns true if \((\uparrow ,x_{10},x_{11})\) maps to \((x_{0},x_{1})\) for some value of \(x_{0} \in \{0,1\}^n\) and false otherwise. The pseudocode for the two-sided random function \(\mathbf {R} \), using hashtable \(P\), is as follows:
The proof of indistinguishability of \(H_1\) and \(H_2\) can be found in the full version [3]. In particular, we prove the following statements regarding the the indistinguishability of \(H_1\) and \(H_2\) and the simulator complexity.
Lemma 3
The probability that \(\mathbf {D} \) outputs 1 in \(H_{1}\) differs from the probability that it outputs 1 in \(H_2\) by at most \(\frac{2\cdot {10^{15}q^{12}}}{2^n}\cdot \)
Lemma 4
In \(H_1\), the simulator runs for at most \(O(q^6)\) steps and makes at most \(3.2 \times {(10q)}^6\) queries except with probability at most \(\frac{{10^{15}q^{12}}}{2^n}\cdot \)
We will prove some properties of \(H_2\) in the following section that will be useful to prove the indistinguishability of the second and third experiments.
5.3 Properties of \(H_2\)
We introduce some definitions and establish some properties of executions in \(H_2\). The definitions here follow closely along the lines of the definitions in [1, 11]. A partial chain is a triple \((x_{k},x_{k+1},k) \in \{0,1\}^n \times \{0,1\}^n \times \{0,\ldots ,10\}\). If \(C = (x_{k},x_{k+1},k)\) is a partial chain, we let \(C[1] = x_k\), \(C[2] = x_{k+1}\), and \(C[3] = k\).
Definition 5
Fix tables \(G = \hat{\mathbf {S}}.G\) and \(P= \mathbf {R}.P\) in an execution of \(H_2\), and let \(C = (x_{k},x_{k+1},k)\) be a partial chain. We define functions \(\mathsf{next}, \mathsf{prev}, \mathsf{val}^+, \mathsf{val}^-\), and \(\mathsf{val}\) as follows:

We say that \(\perp \notin G_i\) for \(i \in \{1,\ldots ,10\}\). So, if \(\mathsf{val}_i(C) \notin G_i\), then either \(\mathsf{val}_i(C) = \perp \) or \(\mathsf{val}_i(C) \ne \perp \) and \(\mathsf{val}_i(C) \notin G_i\).
Definition 6
For a given set of tables \(G, P\), two partial chains C, D are equivalent (denoted \(C \equiv D\)) if they are in the reflexive, transitive closure of the relations given by \(\mathsf{next}\) and \(\mathsf{prev}\).
So, two chains C and D are equivalent if \(C=D\), or if D can be obtained by applying \(\mathsf{next}\) and \(\mathsf{prev}\) finitely many times to C.
Definition 7
The set of table-defined chains contains all chains C for which \(\mathsf{next}(C) \ne \perp \) and \(\mathsf{prev}(C) \ne \perp \).
Definition 8
A chain \(C=(x_k,x_{k+1},k,\ell ,g,b)\) is called an enqueued chain if C is enqueued for completion. For such an enqueued chain, we define \(\mathsf{next}(C)\) as the procedure \(\mathsf{next}\) applied to the partial chain \((x_{k},x_{k+1},k)\) i.e. \(\mathsf{next}(C) := \mathsf{next}(x_k,x_{k+1},k)\). The procedures \(\mathsf{prev}\), \(\mathsf{val}^+\), \(\mathsf{val}^-\) and \(\mathsf{val}\) on an enqueued chain C are defined in a similar manner.
Definition 9
The set \({Q}^*_{\text {all}} \) contains chains that are enqueued in \({Q}_{\text {all}}\) but not in \(Q_{1}\), \(Q_{5}\), \(Q_{6}\), \(Q_{10}\).
Definition 10
We say a uniform assignment to \(G_k(x_k)\) occurs when the simulator sets \(G_k(x_k)\) through an assignment \(G_k(x_k) \leftarrow \{0,1\}^n\), i.e., a uniform value is chosen from the set of n-bit strings and \(G_k(x_k)\) is assigned that value.
A uniform assignment to \(G_k(x_k)\) occurs in line 94 of the simulator’s execution. In particular, if \(G_k(x_k)\) is set through a \(\textsc {ForceVal} (x_k,\cdot ,k)\) call, then it is not a uniform assignment.
Definition 11
We say a uniform assignment to \(P\) occurs in a call to \(\mathbf {R}.\textsc {P}(x_0,x_1)\) if \((\downarrow ,x_{0},x_{1}) \notin P\) when the call is made and \(P(\downarrow ,x_{0},x_{1})\) is set through the assignment \(P(\downarrow ,x_{0},x_{1}) := (x_{10},x_{11})\) where \((x_{10},x_{11})\) is chosen uniformly from the set of 2n-bit strings.
Similarly, it occurs in a call to \(\mathbf {R}.\textsc {P}^{-1}(x_{10},x_{11})\) if \((\uparrow ,x_{10},x_{11}) \notin P\) when the call is made and \(P(\uparrow ,x_{10},x_{11})\) is set through the assignment \(P(\uparrow ,x_{10},x_{11}):= (x_{0},x_{1})\) where \((x_{0},x_{1})\) is chosen uniformly from the set of 2n-bit strings.
A uniform assignment to \(P(\downarrow ,x_0,x_1)\) occurs in line 4 of \(\mathbf {R}\) in Fig. 1 and a uniform assignment to \(P(\uparrow ,x_{10},x_{11})\) occurs in line 15 of \(\mathbf {R}\) in Fig. 1.
In the following section, we define a set of “bad” events, and show that these occur with negligible probability. Following that, we analyze execution of the experiment assuming that none of these bad events occur.
In the remainder of the section, we let \(T = O(q^2)\) be an upper bound on the sizes of \(G_i\) and \(P\) as well as the upper bound on the number of enqueued chains and hence, the number of calls to the \(\textsc {Adapt} \) procedure in an execution of \(H_2\). The derivation of the bound on T and the proof of the lemmas below can be found in the full version [3].
5.3.1 Bad Executions
Definition 12
We say that event BadP occurs in \(H_2\) if either:
-
Immediately after choosing \((x_{10},x_{11})\) in a call to \(\mathbf {R}.\textsc {P}(\cdot ,\cdot )\), either \((\uparrow ,x_{10},x_{11}) \in P\) or \(x_{10} \in G_{10}\).
-
Immediately after choosing \((x_{0},x_{1})\) in a call to \(\mathbf {R}.\textsc {P}^{-1}(\cdot ,\cdot )\), either \((\downarrow ,x_0,x_1)\in P\) or \(x_{1} \in G_{1}\).
Lemma 13
The probability of event \(\mathsf{BadP}\) in \(H_2\) is at most \(2\, T^2/2^n\).
A partial chain \(C = (x_k,x_{k+1},k)\) that has been enqueued by our simulator may not get table-defined till it is completed since it is possible that \(x_k \in G_k\) while \(x_{k+1} \in A^j_{k+1}\) for some j but not in \(G_{k+1}\). Hence, we augment the definitions of BadlyHit and BadlyCollide given in [1, 11] to refer to interactions with enqueued chains and refer to the augmented definitions as \(\mathsf{BadlyHit^+}\) and \(\mathsf{BadlyCollide^+}\).
Definition 14
We say that event \(\mathsf{BadlyHit^+}\) occurs in \(H_2\) if either:
-
Immediately after a uniform assignment to \(G_k(x_k)\), there is a partial chain \((x_{k},x_{k+1},k)\) such that \(\mathsf{prev}(\mathsf{prev}(x_{k},x_{k+1},k)) \ne \perp \).
-
Immediately after a uniform assignment to \(G_k(x_k)\), there is a partial chain \((x_{k-1},x_k,k-1)\) such that \(\mathsf{next}(\mathsf{next}(x_{k-1},x_k,k-1)) \ne \perp \).
and the relevant partial chain is either table-defined or an enqueued chain in \({Q}_{\text {all}}\).
Lemma 15
The probability of event \(\mathsf{BadlyHit^+}\) in \(H_2\) is at most \(40\, T^3/2^n\).
Definition 16
We say that event \(\mathsf{BadlyCollide^+}\) occurs in \(H_2\) if a uniform assignment to \(G_i(x_i)\) is such that there exist two partial chains C and D such that for some \(\ell \in \{0,\ldots ,11\}\) and \(\sigma ,\rho \in \{+,-\}\) all of the following are true:
-
Immediately before the assignment, C and D are not equivalent.
-
Immediately before the assignment, \(\mathsf{val}_\ell ^\sigma (C) = \perp \) or \(\mathsf{val}_\ell ^\rho (D) = \perp \).
-
Immediately after the assignment, \(\mathsf{val}_\ell ^\sigma (C) = \mathsf{val}_\ell ^\rho (D) \ne \perp \).
and one of the following is true:
-
Immediately after the assignment, C and D are table-defined.
-
Immediately after the assignment, C is table-defined and D is a chain enqueued in \({Q}_{\text {all}}\).
-
C and D are chains enqueued in \({Q}_{\text {all}}\).
Lemma 17
The probability of event \((\mathsf{BadlyCollide^+}\wedge \lnot \mathsf{BadlyHit^+}\wedge \lnot \mathsf{BadP})\) in \(H_2\) is at most \(21160\, T^5/2^n\).
Definition 18
We say that event BadlyCollideP occurs in \(H_2\) if either:
-
A uniform assignment \(P(\downarrow ,x_0,x_1):= (x_{10},x_{11})\) is such that there exist partial chains C, D such that for some \(\sigma ,\rho \in \{+,-\}\) the following are all true:
-
Immediately before the assignment, C and D are not equivalent.
-
Immediately before the assignment, \(\mathsf{val}_{10}^\sigma (C) = \perp \) or \(\mathsf{val}_{10}^\rho (D) = \perp \).
-
Immediately after the assignment, \(\mathsf{val}_{10}^\sigma (C) = \mathsf{val}_{10}^\rho (D) = x_{10} \ne \perp \).
and one of the following conditions hold:
-
Before the assignment, C and D are chains in \({Q}^*_{\text {all}}\).
-
Immediately after the assignment, C and D are table-defined.
-
Before the assignment, C is a chain enqueued in \({Q}_{\text {all}}\) and immediately after the assignment, D is table-defined.
-
-
A uniform assignment \(P(\uparrow ,x_{10},x_{11}):= (x_{0},x_{1})\) is such that there exist partial chains C, D such that for some \(\sigma ,\rho \in \{+,-\}\) the following are all true:
-
Immediately before the assignment, C and D are not equivalent.
-
Immediately before the assignment, \(\mathsf{val}_{1}^\sigma (C) = \perp \) or \(\mathsf{val}_{1}^\rho (D) = \perp \).
-
Immediately after the assignment, \(\mathsf{val}_{1}^\sigma (C) = \mathsf{val}_{1}^\rho (D) = x_{1} \ne \perp \).
and one of the following conditions hold:
-
Before the assignment, C and D are chains in \({Q}^*_{\text {all}}\).
-
Immediately after the assignment, C and D are table-defined.
-
Before the assignment, C is a chain enqueued in \({Q}_{\text {all}}\) and immediately after the assignment, D is table-defined.
-
Lemma 19
The probability of event \(\mathsf{BadlyCollideP}\) in \(H_2\) is at most \(314\, T^5/2^n\).
Proof
Consider the case that after a uniform choice of \((x_0,x_1)\) leading to an assignment \(P(\uparrow ,x_{10},x_{11}):= (x_0,x_1)\), event BadlyCollideP occurs. The value \(\mathsf{val}_1^-(C)\) for a chain C does not change due to the assignment since it is a \(P(\uparrow ,x_{10},x_{11})\) assignment and \(\mathsf{val}_1^-(C)\) can change only due to a \(P(\downarrow ,x_0,x_1)\) assignment by definition of \(\mathsf{val}^-(\cdot )\).
Suppose that \(\mathsf{val}_1^+(C) = \perp \) and \(\mathsf{val}_1^-(D) \ne \perp \) before the assignment and after the assignment \(\mathsf{val}_1^+(C) = \mathsf{val}_1^-(D) = x_1\). The value \(\mathsf{val}_1^-(D)\) does not change due to the assignment as mentioned above. So, the probability that \(\mathsf{val}_1^+(C) = \mathsf{val}_1^-(D) = x_1\) is \(2^{-n}\).
Suppose that \(\mathsf{val}_1^+(C) = \mathsf{val}_1^+(D) = \perp \) before the assignment and after the assignment \(\mathsf{val}_1^+(C) = \mathsf{val}_1^+(D) = x_1\). For this to happen, \(\mathsf{val}_{10}(C) = \mathsf{val}_{10}(D) = x_{10}\) and \(\mathsf{val}_{11}(C) = \mathsf{val}_{11}(D) = x_{11}\) implying that C and D are equivalent chains. So, the probability of this event is 0.
Suppose that \(\mathsf{val}_1^+(C) = \perp \) and \(\mathsf{val}_1^+(D) \ne \perp \) before the assignment and after the assignment \(\mathsf{val}_1^+(C) = \mathsf{val}_1^+(D) = x_1\). Now, the value of \(\mathsf{val}_1^+(D)\) stays the same after the assignment (even if \(\mathsf{BadP}\) occurs). So, the probability that \(\mathsf{val}_1^+(C) = \mathsf{val}_1^+(D) = x_1\) is \(2^{-n}\).
The analysis for the other case follows similarly. There are at most T assignments of the form \(P(\uparrow ,x_{10},x_{11})\) or \(P(\downarrow ,x_0,x_1)\). There are at most \(11T^2\) possibilities for a chain to be table-defined before the assignment and T possibilities for a chain to be table-defined after the assignment but not before. There are at most T chains enqueued for completion in \({Q}_{\text {all}}\). So, the probability of event \(\mathsf{BadlyCollideP}\) is at most \(\left( T\cdot ({(11T^2+T)}^2 + T^2 + T\cdot {(11T^2 + T)})\cdot 2\right) \cdot 2^{-n}\).
Definition 20
We say event BadlyHitFV occurs in \(H_2\) if a uniform assignment to \(G_s(x_s)\) that occurs in a call \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\), for some \(s \in \{g,b\}\) one of the following happens (where we let \(C = (x_{\ell -2},x_{\ell -1},\ell -2)\)):
-
\(s = \ell +2\) and the following holds:
-
Immediately before the assignment, \(\mathsf{val}^-_{\ell +1}(C) = \perp \).
-
Immediately after the assignment, \(\mathsf{val}^-_{\ell +1}(C) \ne \perp \).
-
Immediately after the assignment, \(y := \mathsf{val}_{\ell -1}(C) \oplus \mathsf{val}^-_{\ell +1}(C)\) is such that \(x'_{\ell +1} \oplus x'_{\ell -1} = y\) for some \(x'_{\ell +1} \in G_{\ell +1}\) and \(x'_{\ell -1} \in G_{\ell -1}\).
-
-
\(s = \ell -1\) and the following holds:
-
Immediately before the assignment, \(\mathsf{val}^+_{\ell }(C) = \perp \).
-
Immediately after the assignment, \(\mathsf{val}^+_{\ell }(C) \ne \perp \).
-
Immediately after the assignment, \(y := \mathsf{val}_{\ell +2}(C) \oplus \mathsf{val}^+_{\ell }(C)\) is such that \(x'_{\ell +2} \oplus x'_{\ell } = y\) for some \(x'_{\ell +2} \in G_{\ell +2}\) and \(x'_{\ell } \in G_{\ell }\).
-
Lemma 21
The probability of event \(\mathsf{BadlyHitFV}\) in \(H_2\) is at most \(2\, T^3/2^n\).
Proof
Consider the first case where \(s = \ell +2\). Note that for a chain C with \(s = \ell +2\) the “value” at the adapt position \(\ell +1\) is set as \(\mathsf{val}_{\ell +1}(C) := \mathsf{val}_{\ell +3}(C) \oplus G_s(\mathsf{val}_s(C))\) where \(\mathsf{val}_{\ell +3}(C) \ne \perp \) is one of the arguments to \(\textsc {Adapt} \). Since the assignment to \(G_s(x_{s})\) happens inside the \(\textsc {Adapt} \) call, \(\mathsf{val}^-_{\ell +1}(C) = \perp \) until the assignment and \(\mathsf{val}^-_{\ell +1}(C) \ne \perp \) immediately after the assignment.
Now, \(y := \mathsf{val}_{\ell -1}(C) \oplus \mathsf{val}^-_{\ell +1}(C)\). Note that \(\mathsf{val}_{\ell -1}(C) \ne \perp \) since \(\mathsf{val}_{\ell -1}(C) = x_{\ell -1}\) is one of the arguments of the \(\textsc {Adapt} \) procedure. So, for \(y := \mathsf{val}_{\ell -1}(C) \oplus \mathsf{val}_{\ell +3}(C) \oplus G_s(\mathsf{val}_s(C))\) to be such that \(y = x'_{\ell -1} \oplus x'_{\ell +1}\) where \(x'_{\ell -1} \in G_{\ell -1}\) and \(x'_{\ell +1} \in G_{\ell +1}\), y needs to take one of \(T^2/2^n\) values. Note that there are at most T such calls to \(\textsc {Adapt} \) by assumption. So, the probability of the first case is at most \(T^3/2^n\). The analysis for the second case is analogous.
Definition 22
We say that event BadlyCollideFV occurs in \(H_2\) if a uniform assignment to \(G_s(x_s)\) that occurs in a call to \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\), for some \(s \in \{g,b\}\) the following happens (where we let \(C = (x_{\ell -2},x_{\ell -1},\ell -2)\) and D is a chain in \({Q}^*_{\text {all}}\)):
-
\(s = \ell +2\), and for some \((k,k') \in \{(\ell -1,\ell +1),(\ell +1,\ell -1)\}\) the following holds:
-
Immediately before the assignment, \(\mathsf{val}^-_{\ell +1}(C) = \perp \) and \(\mathsf{val}_{k}(D) \ne \perp \).
-
Immediately after the assignment, \(\mathsf{val}^-_{\ell +1}(C) \ne \perp \).
-
Immediately after the assignment, \(y := \mathsf{val}_{\ell -1}(C) \oplus \mathsf{val}^-_{\ell +1}(C)\) is such that \(x \oplus y = \mathsf{val}_{k}(D)\) for some \(x \in G_{k'}\).
-
-
\(s = \ell -1\), and for some \((k,k') \in \{(\ell ,\ell +2),(\ell +2,\ell )\}\) the following holds:
-
Immediately before the assignment, \(\mathsf{val}^+_{\ell }(C) = \perp \) and \(\mathsf{val}_k(D) \ne \perp \).
-
Immediately after the assignment, \(\mathsf{val}^+_{\ell }(C) \ne \perp \).
-
Immediately after the assignment, \(y := \mathsf{val}_{\ell +2}(C) \oplus \mathsf{val}^+_{\ell }(C)\) is such that \(x \oplus y = \mathsf{val}_k(D)\) for some \(x \in G_{k'}\).
-
Lemma 23
The probability of event \(\mathsf{BadlyCollideFV}\) in \(H_2\) is at most \(4\, T^3/2^n\).
Proof
Consider the first case where \(s = \ell +2\). Note that during the \(\textsc {Adapt} \) call the “value” at the adapt position \(\ell +1\) is set as \(\mathsf{val}_{\ell +1}(C) := \mathsf{val}_{\ell +3}(C) \oplus G_s(\mathsf{val}_s(C))\) where \(\mathsf{val}_{\ell +3}(C) \ne \perp \) is one of the arguments to \(\textsc {Adapt} \). Since the assignment to \(G_s(x_{s})\) happens inside the \(\textsc {Adapt} \) call, \(\mathsf{val}^-_{\ell +1}(C) = \perp \) until the assignment and \(\mathsf{val}^-_{\ell +1}(C) \ne \perp \) immediately after the assignment.
Now, \(y := \mathsf{val}_{\ell -1}(C) \oplus \mathsf{val}^-_{\ell +1}(C)\). Note that \(\mathsf{val}_{\ell -1}(C) \ne \perp \) since it is one of the arguments of \(\textsc {Adapt} \). Also note that if \(\mathsf{val}_k(D) \ne \perp \) before the assignment, then \(\mathsf{val}_k(D)\) does not change due to the assignment. Say \(k = \ell -1\) and \(k' = \ell +1\). So, for \(y := \mathsf{val}_{\ell -1}(C) \oplus \mathsf{val}_{\ell +3}(C) \oplus G_s(x_s)\) to be such that \(y = x \oplus \mathsf{val}_{\ell -1}(D)\) where \(x \in G_{\ell +1}\), the value y would have to take one of \(T^2/2^n\) values. (This is because T is the upper bound on the number of chains enqueued in \({Q}_{\text {all}}\) by assumption and on the size of \(G_{\ell +1}\).) Similarly for the case where \(k = \ell +1\) and \(k' = \ell -1\). So, for a single call to \(\textsc {Adapt} \) where \(s = \ell +2\), we have that the probability that the event occurs is \(2T^2/2^n\). There are at most T calls to \(\textsc {Adapt} \) by assumption and hence, the probability of the first case is at most \(2T^3/2^n\).
The analysis for the second case is analogous.
We say an execution of \(H_2\) is good if none of \(\mathsf{BadP}\), \(\mathsf{BadlyHit^+}\), \(\mathsf{BadlyCollide^+}\), \(\mathsf{BadlyCollideP}\), \(\mathsf{BadlyHitFV}\), or \(\mathsf{BadlyCollideFV}\) occur. Lemmas 13–23 imply:
Lemma 24
The probability that an execution of \(H_2\) is good is \(1 - O(T^5)/2^n\).
5.3.2 Properties of Good Executions
Notation. For a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\) that is enqueued for completion, the “adapt positions” are at \(\ell \), \(\ell +1\). These positions are those where the simulator uses \(\textsc {ForceVal} (\cdot ,\cdot ,\ell )\) and \(\textsc {ForceVal} (\cdot ,\cdot ,\ell +1)\) to force the values at \(G_{\ell }(\cdot )\) and \(G_{\ell +1}(\cdot )\). Also, for the chain C, the “set uniform” positions are at \(\ell -1\), \(\ell +2\). (These are the buffer zones that surround the adapt positions.) One of these “set uniform” positions is adjacent to the query that caused the chain to be enqueued and this position is denoted by g and referred to as the “good” set uniform position. The other “set uniform” position is referred to as the “bad” set uniform position. Note that \(g, b \in \{\ell -1, \ell +2\}\) and \(g \ne b\); Let a be the adapt position that is adjacent to “bad” set uniform position. So, if \(b=\ell -1\), then \(a=\ell \); Else, if \(b=\ell +2\), \(a=\ell +1\). Consider a call \(\textsc {Adapt} (x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\), if \(b = \ell -1\) define \(x_a = x_\ell \) as \(x_\ell : = x_{\ell -2} \oplus G_{\ell -1}(x_{\ell -1})\) if \(x_{\ell -1} \in G_{\ell -1}\), and \(x_\ell =\perp \) otherwise. Analogously, if \(b=\ell +2\), define \(x_a = x_{\ell +1} := x_{\ell +3} \oplus G_{\ell +2}(x_{\ell +2})\) if \(x_{\ell +2} \notin G_{\ell +2}\) and \(x_{\ell +1}=\perp \) otherwise.
Also, for a chain C enqueued in \(Q_{b}\) we say adapting is safe if just before the call to \(\textsc {Adapt} \) for C, we have \(x_g \notin G_g\) and \(x_a \notin G_a\). Analogously, for a chain C in \({Q}^*_{\text {all}}\) or \({Q}_{\text {mid}}\) we say adapting is safe if just before the call to \(\textsc {Adapt} \) for C, we have \(x_{\ell -1} \notin G_{\ell -1}\) and \(x_{\ell +2} \notin G_{\ell +2}\). Also, we loosely use the statement \(C \in \mathsf{CompChains}\) where \(C = (x_k,x_{k+1},k,\ell ,g,b)\) to mean that \((x_{k},x_{k+1},k) \in \mathsf{CompChains}\).
High-level Overview. The aim of this section is to prove that during a good execution of \(H_2\), every call to \(\textsc {ForceVal} (x,\cdot ,a)\) is such that \(x \notin G_a\), i.e., to prove that a \(\textsc {ForceVal} \) call does not “overwrite.”
To prove that \(\textsc {ForceVal} \) does not “overwrite,” we prove that for every call to \(\textsc {Adapt} \) that occurs during the completion of a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\), we have \(\mathsf{val}_g(C) \notin G_g\) before the call and if C is enqueued in \(Q_{b}\), \(\mathsf{val}_a(C) \notin G_a\) before the call; else, \(\mathsf{val}_b(C) \notin G_b\) before the call i.e. every call to \(\textsc {Adapt} \) is “safe”. In order to prove the above statements, we will prove that at the time a chain C is enqueued in \({Q}_{\text {all}}\), \(\mathsf{val}_g(C) = \perp \) and if C is a chain enqueued in \(Q_{b}\) for some \(b \in \{1,5,6,10\}\), then \(\mathsf{val}_b(C) \notin G_b\); else, \(\mathsf{val}_b(C) = \perp \) when C was enqueued. Similarly, if a chain C is enqueued in \({Q}_{\text {mid}}\), then just before the assignment that precedes C being enqueued occurs, we will prove that \(\mathsf{val}_g(C) = \perp \) and \(\mathsf{val}_b(C) = \perp \). We also need to prove properties of equivalent chains in order to prove that if a chain equivalent to C has been completed before C, then \(C \in \mathsf{CompChains}\) when it is dequeued. All of this put together will help us prove that \(\textsc {ForceVal} \) does not “overwrite” (Theorem 39). While the structure explained above is similar to the structure of the proof in [1, 11], the major difference is in how we prove the properties of chains at the time they are enqueued. This is due to the fact that we separate enqueueing from completion in our simulation.
Due to space constraints, we state some lemmas without proofs, and refer to the full version of our work for details [3].
Properties of Equivalent Chains
Lemma 25
Consider a good execution of \(H_2\). Suppose that at some point in the execution, two partial chains C and D are equivalent. Then there exists a sequence of partial chains \(C_1,\ldots ,C_r\) such that
-
\(C = C_1\) and \(D = C_r\), or else \(D = C_1\) and \(C = C_r\),
-
for \(r \ge 2\), \(C_i = \mathsf{next}(C_{i-1})\) and \(C_{i-1} = \mathsf{prev}(C_i)\) for all \(i \in \{2,\ldots ,r\}\),
-
for \(r \ge 3\), \(C_2,\ldots ,C_{r-1}\) is table-defined,
-
\(D = (\mathsf{val}^\rho _j(C),\mathsf{val}^\rho _{j+1}(C),j)\) where \(\mathsf{val}^\rho _{j}(C) \ne \perp \) and \(\mathsf{val}^\rho _{j+1}(C) \ne \perp \) for some \(\rho \in \{+,-\}\),
-
\(C = (\mathsf{val}^\sigma _{k}(D),\mathsf{val}^\sigma _{k+1}(D),k)\) where \(\mathsf{val}^\sigma _{k}(D) \ne \perp \) and \(\mathsf{val}^\sigma _{k+1}(D) \ne \perp \) for some \(\sigma \in \{+,-\}\).
Lemma 26
Consider some point in a good execution of \(H_2\) and assume that \(x \not \in G_j\) before every call to \(\textsc {ForceVal} (x,\cdot ,j)\) prior to this point in the execution. Then, if the partial chains \(C = (x_k,x_{k+1},k)\) with \(k \in \{1,5,9\}\) and \(D = (x'_m,x'_{m+1},m)\) with \(m \in \{1,5,9\}\) are equivalent at this point in the execution, then \(C \in \mathsf{CompChains}\) if and only if \(D \in \mathsf{CompChains}\).
Properties of Enqueued Chains
Recall that \(\{1,5,6,10\}\) are “bad” set uniform positions.
Lemma 27
Say a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\) is enqueued to be completed in \(Q_{b}\). Then at the time C is enqueued, \(\mathsf{val}_g(C) = \perp \) and \(\mathsf{val}_b(C) \notin G_b\).
Effects of a Call to ForceVal
For the following lemmas, note that \(g,b \in \{\ell -1,\ell +2\}\) and \(g \ne b\).
Lemma 28
In a good execution of \(H_2\), let \(x_{\ell -1} \notin G_{\ell -1}\) (respectively \(x_{\ell +2} \notin G_{\ell +2}\)) immediately before a call \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\). Then, before the call to \(\textsc {ForceVal} (x_{\ell },\cdot ,\ell )\) (respectively \(\textsc {ForceVal} (x_{\ell +1},\cdot ,\ell +1)\)) in that \(\textsc {Adapt} \) call, we have \(x_{\ell } \notin G_{\ell }\) (respectively \(x_{\ell +1} \notin G_{\ell +1}\)).
The lemma above immediately gives us the following corollary.
Corollary 29
Consider a call \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\) in a good execution of \(H_2\) and assume that adapting was safe for all chains C that were dequeued before this \(\textsc {Adapt} \) call. Then, before the call to \(\textsc {ForceVal} (x_{\ell },\cdot ,\ell )\) and \(\textsc {ForceVal} (x_{\ell +1},\cdot ,\ell +1)\) that occurs in \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\), we have \(x_{\ell } \notin G_{\ell }\) and \(x_{\ell +1} \notin G_{\ell +1}\) respectively.
Lemma 30
Suppose that \(x_{\ell -1} \notin G_{\ell -1}\) (respectively \(x_{\ell +2} \notin G_{\ell +2}\)) immediately before a call \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\) in a good execution of \(H_2\). Then, if C is a table-defined chain before the call to \(\textsc {Adapt} \), \(\mathsf{val}_i(C)\) for \(i \in \{1,\ldots ,10\}\) stays constant during the call to \(\textsc {ForceVal} (x_{\ell },\cdot ,\ell )\) (respectively \(\textsc {ForceVal} (x_{\ell +1},\cdot ,\ell +1)\)).
Lemma 31
Suppose that \(x_{\ell -1} \notin G_{\ell -1}\) (respectively \(x_{\ell +2} \notin G_{\ell +2}\)) immediately before a call \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\) in a good execution of \(H_2\). Then, if C is a chain enqueued in \({Q}_{\text {all}}\), \(\mathsf{val}_i(C)\) for \(i \in \{1,\ldots ,10\}\) stays constant during the call to \(\textsc {ForceVal} (x_{\ell },\cdot ,\ell )\) (respectively \(\textsc {ForceVal} (x_{\ell +1},\cdot ,\ell +1)\)) that occurs in the \(\textsc {Adapt} \) call.
Lemma 32
Consider a call to \(\textsc {Adapt} (Q,x_{\ell -2},x_{\ell -1},x_{\ell +2},x_{\ell +3},\ell ,g,b)\) in a good execution of \(H_2\) for some \(Q \in \{Q_{1},Q_{5},Q_{6},Q_{10}\}\). Assume that adapting was safe for all chains C that were dequeued from \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\) before this \(\textsc {Adapt} \) call. If \(x_{a} \notin G_{a}\) and \(x_g \notin G_g\) (where a is the adapt position adjacent to the “bad” set uniform position) before the \(\textsc {Adapt} \) call, then if C is a chain enqueued in \({Q}_{\text {all}}\), \(\mathsf{val}_i(C)\) for \(i \in \{1,\ldots ,10\}\) stays constant during the call to \(\textsc {ForceVal} (x_{a},\cdot ,a)\) that occurs in the \(\textsc {Adapt} \) call.
Additional Properties of Enqueued Chains
For the following lemma, if a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\) is enqueued in \({Q}_{\text {mid}}\), then the assignment \(G_i(x_i)\) that precedes C being enqueued happens either in lines 19, 149 or 152 of the simulator’s execution.
Lemma 33
Suppose that a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\) is enqueued in \({Q}_{\text {mid}}\) during a good execution of \(H_2\) such that no chain equivalent to C has been enqueued for completion so far. Suppose also that adapting has been safe for every chain dequeued from \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\) or \({Q}^*_{\text {all}}\) so far. Then \(\mathsf{val}_g(C) = \perp \) and \(\mathsf{val}_b(C) = \perp \) just before the assignment \(G_i(x_i)\) that precedes C being enqueued. Also, \(\mathsf{val}_9(C) = \mathsf{val}_2(C) = \perp \) just before the assignment \(G_i(x_i)\) that precedes C being enqueued.
Proof
Say a chain \(C = (x_5,x_6,5,2,4,1)\) is enqueued in \({Q}_{\text {mid}}\) with \(g=4\) and \(b=1\). Then, the assignment \(G_5(x_5)\) that precedes the enqueueing of C is such that \(x_5 \notin G_5\) before the assignment, by construction of the simulator. Otherwise,  is not called. Hence, \(\mathsf{val}^-_4(C) = \perp \) just before the assignment \(G_5(x_5)\) that precedes C being enqueued. Also, since \(\mathsf{val}^-_4(C) = \perp \), we have \(\mathsf{val}^-_1(C) = \perp \).
is not called. Hence, \(\mathsf{val}^-_4(C) = \perp \) just before the assignment \(G_5(x_5)\) that precedes C being enqueued. Also, since \(\mathsf{val}^-_4(C) = \perp \), we have \(\mathsf{val}^-_1(C) = \perp \).
Before we prove \(\mathsf{val}^+_4(C) = \perp \) and \(\mathsf{val}^+_1(C) = \perp \) (and hence, \(\mathsf{val}_4(C) = \perp \) and \(\mathsf{val}_1(C) = \perp \)), we make the following observation. If a partial chain \((x_5,x_6,5)\) is enqueued in \({Q}_{\text {mid}}\) such that no equivalent chain has been enqueued previously, by construction of the simulator, either (1) \(\mathsf{val}_5(D) = x_5\) for a chain D belonging to \({Q}^*_{\text {all}}\) where \(\mathsf{val}_5(D) = \perp \) when D was enqueued or (2) \(\mathsf{val}_6(E) = x_6\) for a chain E enqueued in \({Q}^*_{\text {all}}\) where \(\mathsf{val}_6(E) = \perp \) when E was enqueued or (3) both. In other words, either \(x_5 \notin G_5 \cup A^t_5\) or \(x_6 \notin G_6 \cup A^t_6\) or both when  in line 6 of the simulator’s execution after D’s \(t^{th}\) query.
in line 6 of the simulator’s execution after D’s \(t^{th}\) query.
Consider a chain \(C = (x_5,x_6,5,2,4,1)\) which was enqueued in \({Q}_{\text {mid}}\) such that no chain equivalent to C was enqueued previously. Such a chain C is enqueued in \({Q}_{\text {mid}}\), when \(x_6 \in G_6\), \(\mathsf{val}_5(C) = \mathsf{val}_5(D) = x_5\) and \(x_5 \in G_5\) right before C was enqueued (and not earlier) where D is a chain belonging to \({Q}^*_{\text {all}}\) and \(x_5 \in G_5\) due to the completion of D.
For \(\mathsf{val}_1(C) \ne \perp \) at the time of the assignment that precedes the enqueueing of C, we need \(\mathsf{val}^+_1(C) \ne \perp \). Then, in particular, we have that \(x_7 := \mathsf{val}_7(C) \in G_7\) and \(x_8 := \mathsf{val}_8(C) \in G_8\) (otherwise, \(\mathsf{val}^+_9(C) = \perp \) implying that \(\mathsf{val}^+_1(C) = \perp \)).
Consider the partial chains \(C = (x_5,x_6,5)\), \(C_1 = (x_6,x_7,6)\) and \(C_2 = (x_7,x_8,7)\). For \(\mathsf{val}^+_9(C) \ne \perp \) just before the assignment that precedes the enqueueing of C, we need (1) \(C_1 = \mathsf{next}(C)\), \(C_2 = \mathsf{next}(C_1)\) (and hence, \(x_6 \in G_6\) and \(x_7 \in G_7\)) and (2) \(x_5 = \mathsf{val}_5(D)\) for a chain D in \({Q}^*_{\text {all}}\) and (3) \(x_8 \in G_8\) or \(x_8 = \mathsf{val}_8(E)\) of a chain E enqueued in \({Q}_{\text {all}}\). Note that this condition is not true at the time the simulator finished enqueueing chains in \({Q}_{\text {all}}\) since we have either \(x_5 \notin G_5 \cup A_5^t\) or \(x_6 \notin G_6 \cup A_6^t\) or both. Hence, the conditions must have been met during the completion of chains in \({Q}_{\text {all}}\). Consider the last assignment that was made before all the above conditions were met.
Consider the case that when the last assignment (such that all the conditions listed above were met immediately after this assignment) happened, the chain \(C_1\) was already table-defined. Now, if the assignment was a \(\textsc {P}/\textsc {P}^{-1}\) assignment, then BadP occurred. It cannot be a \(\textsc {ForceVal} \) assignment since \(\textsc {ForceVal} \) does not change the value of a chain enqueued in \({Q}_{\text {all}}\) by Lemmas 31 and 32. If it were a uniform assignment to \(G_i(x_i)\), then, \(\mathsf{BadlyCollide^+}\) occurred.
Consider the case that when the last assignment (such that all the conditions listed above were met immediately after this assignment) happened, the chain \(C_1\) was not table-defined before the assignment but table-defined immediately after. Recall that if \(C_1 = (x_6,x_7,6)\) is table-defined then \(x_6 \in G_6\) and \(x_7 \in G_7\). So, the assignment was either to \(G_6(x_6)\) or \(G_7(x_7)\).
Consider the case that it set \(G_7(x_7)\). If this were a uniform assignment to \(G_7(x_7)\), then \(\mathsf{BadlyCollide^+}\) occurred since \(C_1 (\equiv C)\) and E are not equivalent as no chain equivalent to C has been enqueued previously. If this were a \(\textsc {ForceVal} \) assignment, then BadlyCollideFV occurred. This is because 7 is an adapt position only for partial chains that are either of the form (a) \(X = (x_9,x_{10},9)\) such that \((x_9,x_{10},9,6,8,5)\) belongs to \({Q}^*_{\text {all}}\). By assumption for chains in \({Q}^*_{\text {all}}\), we have \(\mathsf{val}_5(X) \notin G_5\) before the \(\textsc {Adapt} \) call for such a chain or, (b) \(Y = (x_1,x_2,1)\) such that \((x_1,x_2,1,7,9,6)\) is enqueued in \(Q_{6}\). In this case, the adapt position 7 is adjacent to the “bad” set uniform position 6. By assumption for chains enqueued in \(Q_{6}\), we have \(\mathsf{val}_9(Y) \notin G_9\) before the \(\textsc {Adapt} \) call for such a chain. Hence, BadlyCollideFV occurred due to the assignment \(G_5(\mathsf{val}_5(X))\) or \(G_9(\mathsf{val}_9(Y))\) that occurs in the \(\textsc {Adapt} \) call. The analysis for the case when \(G_6(x_6)\) is set is similar. So, the above conditions are not met for a chain C to be enqueued in \({Q}_{\text {mid}}\). Hence, for such a chain \(C = (x_5,x_6,5,2,4,1)\), \(\mathsf{val}^+_9(C) = \perp \) just before the assignment that caused C to be enqueued. Since \(\mathsf{val}^+_9(C) = \perp \) and \(\mathsf{val}^-_4(C) = \perp \) before the assignment, we have \(\mathsf{val}_4(C) = \perp \), \(\mathsf{val}_9(C) = \perp \) and \(\mathsf{val}_1(C) = \perp \) just before the assignment that precedes C being enqueued. The analysis for the case where \(C = (x_5,x_6,5,8,7,10)\) is analogous.
Lemma 34
Consider a good execution of \(H_2\). Just before the execution of line 27 during the simulator’s execution, if adapting was safe for every chain dequeued from \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\), \({Q}^*_{\text {all}}\) or \({Q}_{\text {mid}}\) so far, then it holds that:
-
i.
if \(x_9 \in G_9\), \(x_{10} \in G_{10}\), \(x_1 \in G_1\) such that
 , then \((x_9,x_{10},9) \in \mathsf{CompChains}\).
, then \((x_9,x_{10},9) \in \mathsf{CompChains}\). -
ii.
if \(x_1 \in G_1\), \(x_{2} \in G_{2}\), \(x_{10} \in G_{10}\) such that
 , then \((x_1,x_{2},1) \in \mathsf{CompChains}\).
, then \((x_1,x_{2},1) \in \mathsf{CompChains}\). -
iii.
if \(x_5 \in G_5\), \(x_6 \in G_6\), then \((x_5,x_6,5) \in \mathsf{CompChains}\).
Proof
We start by proving (i). For a triple \((x_9,x_{10},x_1)\), we say that “condition holds” if \((x_9,x_{10},x_1)\) is such that \(x_9 \in G_9\), \(x_{10} \in G_{10}\), \(x_1 \in G_1\) and  . Also, we refer to the partial chain \((x_9,x_{10},9)\) as the partial chain associated with the triple \((x_9,x_{10},x_1)\). So, our aim is to prove that for every triple \((x_9,x_{10},x_1)\) such that condition holds, the associated partial chain \((x_9,x_{10},9) \in \mathsf{CompChains}\). Assume that the lemma has held right before (and hence immediately after) line 27 of the simulator’s execution while answering the distinguisher’s \((t-1)^{th}\) query to \(\textsc {F}(\cdot ,\cdot )\). Let the distinguisher ask its \(t^{th}\) query \(\textsc {F}(k,x)\). The aim is to prove that at line 27 of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query to \(\textsc {F}(\cdot ,\cdot )\), if a triple \(T^* = (x_9,x_{10},x_1)\) is such that condition holds, then the partial chain \(C^* = (x_9,x_{10},9)\) associated with the triple is such that \(C^* \in \mathsf{CompChains}\). Note that the distinguisher could have made queries to \(\textsc {P}/\textsc {P}^{-1}\) between the \((t-1)^{th}\) and \(t^{th}\) queries to \(\textsc {F}(\cdot ,\cdot )\); but if those queries resulted in condition being true, then BadP occurred.
. Also, we refer to the partial chain \((x_9,x_{10},9)\) as the partial chain associated with the triple \((x_9,x_{10},x_1)\). So, our aim is to prove that for every triple \((x_9,x_{10},x_1)\) such that condition holds, the associated partial chain \((x_9,x_{10},9) \in \mathsf{CompChains}\). Assume that the lemma has held right before (and hence immediately after) line 27 of the simulator’s execution while answering the distinguisher’s \((t-1)^{th}\) query to \(\textsc {F}(\cdot ,\cdot )\). Let the distinguisher ask its \(t^{th}\) query \(\textsc {F}(k,x)\). The aim is to prove that at line 27 of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query to \(\textsc {F}(\cdot ,\cdot )\), if a triple \(T^* = (x_9,x_{10},x_1)\) is such that condition holds, then the partial chain \(C^* = (x_9,x_{10},9)\) associated with the triple is such that \(C^* \in \mathsf{CompChains}\). Note that the distinguisher could have made queries to \(\textsc {P}/\textsc {P}^{-1}\) between the \((t-1)^{th}\) and \(t^{th}\) queries to \(\textsc {F}(\cdot ,\cdot )\); but if those queries resulted in condition being true, then BadP occurred.
Suppose that there exists a triple \(T^*\) such that condition holds at line 27 of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query. If condition held at the end of simulator’s execution while answering the previous distinguisher query, then by assumption that the lemma has held so far, the partial chain \(C^*\) associated with the triple \(T^*\) is such that \(C^* \in \mathsf{CompChains}\). If condition held at the end of the simulator’s execution of the current query t (and not at the end of the previous query), we differentiate cases where the associated partial chain \(C^*\) was enqueued for completion during the simulator’s execution while answering the \(t^{th}\) query and when it’s not.
Consider the case where a chain equivalent to \(C^*\) was enqueued in \({Q}_{\text {all}}\) during the simulator’s execution while answering the distinguisher’s current query. If \(C^* = (x_9,x_{10},9)\) was enqueued during the \(t^{th}\) query, then \((x_9,x_{10},9) \in \mathsf{CompChains}\) by construction of the simulator. Note also that chains in \(\mathsf{SimPChains}\) are not enqueued for completion by the simulator. By definition of the set \(\mathsf{SimPChains}\), these chains are such that they are equivalent to a chain of the form \((x_5,x_6,5)\) that has been enqueued for completion. Since BadP does not occur and \(\textsc {ForceVal} \) does not overwrite, the equivalence holds when \((x_5,x_6,5) \in \mathsf{CompChains}\) and hence, by Lemma 26, such a chain in \(\mathsf{SimPChains}\) is placed in \(\mathsf{CompChains}\) as well. By the same argument, if a chain equivalent to \(C^*\) has been enqueued for completion, then too \(C^* \in \mathsf{CompChains}\) by the end of the simulator’s execution of the current query. So, if a chain equivalent to \(C^*\) was enqueued for completion or was in \(\mathsf{SimPChains}\) during the simulator’s execution while answering the current query t, then \(C^* \in \mathsf{CompChains}\).
Consider the case where no chain equivalent to \(C^*\) was enqueued in \({Q}_{\text {all}}\) and \(C^* \notin \mathsf{SimPChains}\) during the simulator’s execution while answering the distinguisher’s current query. We differentiate between the cases where (1) \(C = \mathsf{next}(C^*) \ne \perp \), \(\mathsf{next}(C) \ne \perp \) when  in line 6 of the simulator’s execution when answering the distinguisher’s \(t^{th}\) query and (2) when it’s not.
in line 6 of the simulator’s execution when answering the distinguisher’s \(t^{th}\) query and (2) when it’s not.
Consider the case when \(C = \mathsf{next}(C^*) \ne \perp \) and \(\mathsf{next}(C) \ne \perp \) at the time the simulator stops enqueueing chains in \({Q}_{\text {all}}\) i.e. when  in line 6 of the simulator’s execution when answering the distinguisher’s \(t^{th}\) query. This implies that \(x_{10} \in G_{10}\) and \((\uparrow ,x_{10},x_{11})\in P\) where \(x_{11} := x_9 \oplus G_{10}(x_{10})\) and hence, \(C = (x_{10},x_{11},10)\) is table-defined at the time the simulator stops enqueueing chains in \({Q}_{\text {all}}\). Since the triple \(T^*\) is such that the associated partial chain \(C^* = (x_9,x_{10},9)\) was not enqueued for completion and not in \(\mathsf{SimPChains}\), we have that either (a) \(x_9 \notin G_9 \cup A^t_9\) or (b) \(x_1 \notin G_1 \cup A^t_1\) when
in line 6 of the simulator’s execution when answering the distinguisher’s \(t^{th}\) query. This implies that \(x_{10} \in G_{10}\) and \((\uparrow ,x_{10},x_{11})\in P\) where \(x_{11} := x_9 \oplus G_{10}(x_{10})\) and hence, \(C = (x_{10},x_{11},10)\) is table-defined at the time the simulator stops enqueueing chains in \({Q}_{\text {all}}\). Since the triple \(T^*\) is such that the associated partial chain \(C^* = (x_9,x_{10},9)\) was not enqueued for completion and not in \(\mathsf{SimPChains}\), we have that either (a) \(x_9 \notin G_9 \cup A^t_9\) or (b) \(x_1 \notin G_1 \cup A^t_1\) when  in line 6. For the condition to be true, we need \(x_1 \in G_1\) and \(x_9 \in G_9\) and hence, we have that condition does not hold for the triple \(T^*\) when
in line 6. For the condition to be true, we need \(x_1 \in G_1\) and \(x_9 \in G_9\) and hence, we have that condition does not hold for the triple \(T^*\) when  in line 6. Consider the case where \(x_1 \notin G_1 \cup A^t_1\). For \(x_1 \in G_1\) to be true by the end of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query, it must be the case that \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) at some point for a chain D that has been enqueued in \({Q}_{\text {all}}\) or \({Q}_{\text {mid}}\). Before analyzing the case that \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) occurs, we make the following observations. Firstly, C and D are not equivalent as \(C \equiv C^*\) and no chain equivalent to \(C^*\) (including itself) has been enqueued. Secondly, for all chains D that have been enqueued in \({Q}_{\text {all}}\), \(\mathsf{val}_1(D) \ne x_1\) when enqueued since \(x_1 \notin G_1 \cup A^t_1\). Now, if \(\mathsf{val}_1(D) \ne x_1\) and \(\mathsf{val}_1(D) \ne \perp \), it cannot be that \(\mathsf{val}_1(D) = x_1\) at a later point since \(\textsc {ForceVal} \) does not overwrite and BadP does not occur. Hence, if \(\mathsf{val}_1(D) = x_1\) at a later point, then \(\mathsf{val}_1(D) = \perp \) when enqueued. Similarly, for all chains D that have been enqueued in \({Q}_{\text {mid}}\) \(\mathsf{val}_1(D) = \perp \) just before the assignment that precedes the enqueueing of D by Lemma 33. Since \(\mathsf{BadlyHit^+}\) and BadlyHitFV do not occur, \(\mathsf{val}_1(D) = \perp \) at the time D is enqueued. Now, if \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\), then this is during the completion of some chain E during the simulator’s execution while answering the distinguisher’s \(t^{th}\) query. Consider the last assignment before \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) was true. This cannot be a uniform assignment to \(G_i(x_i)\) since then \(\mathsf{BadlyCollide^+}\) occurred. This cannot be due to a uniform assignment to P since then BadP or BadlyCollideP occurred. This cannot be a \(\textsc {ForceVal} \) assignment since that would contradict Lemmas 30, 31 or 32. The analysis for the case where \(x_9 \notin G_9 \cup A^t_9\) when the simulator stops enqueueing chains in \({Q}_{\text {all}}\) is analogous. So, if C was table-defined when the simulator stops enqueueing chains in \({Q}_{\text {all}}\), then condition does not hold for the triple \(T^*\) at the end of the simulator’s execution of the current query.
in line 6. Consider the case where \(x_1 \notin G_1 \cup A^t_1\). For \(x_1 \in G_1\) to be true by the end of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query, it must be the case that \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) at some point for a chain D that has been enqueued in \({Q}_{\text {all}}\) or \({Q}_{\text {mid}}\). Before analyzing the case that \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) occurs, we make the following observations. Firstly, C and D are not equivalent as \(C \equiv C^*\) and no chain equivalent to \(C^*\) (including itself) has been enqueued. Secondly, for all chains D that have been enqueued in \({Q}_{\text {all}}\), \(\mathsf{val}_1(D) \ne x_1\) when enqueued since \(x_1 \notin G_1 \cup A^t_1\). Now, if \(\mathsf{val}_1(D) \ne x_1\) and \(\mathsf{val}_1(D) \ne \perp \), it cannot be that \(\mathsf{val}_1(D) = x_1\) at a later point since \(\textsc {ForceVal} \) does not overwrite and BadP does not occur. Hence, if \(\mathsf{val}_1(D) = x_1\) at a later point, then \(\mathsf{val}_1(D) = \perp \) when enqueued. Similarly, for all chains D that have been enqueued in \({Q}_{\text {mid}}\) \(\mathsf{val}_1(D) = \perp \) just before the assignment that precedes the enqueueing of D by Lemma 33. Since \(\mathsf{BadlyHit^+}\) and BadlyHitFV do not occur, \(\mathsf{val}_1(D) = \perp \) at the time D is enqueued. Now, if \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\), then this is during the completion of some chain E during the simulator’s execution while answering the distinguisher’s \(t^{th}\) query. Consider the last assignment before \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) was true. This cannot be a uniform assignment to \(G_i(x_i)\) since then \(\mathsf{BadlyCollide^+}\) occurred. This cannot be due to a uniform assignment to P since then BadP or BadlyCollideP occurred. This cannot be a \(\textsc {ForceVal} \) assignment since that would contradict Lemmas 30, 31 or 32. The analysis for the case where \(x_9 \notin G_9 \cup A^t_9\) when the simulator stops enqueueing chains in \({Q}_{\text {all}}\) is analogous. So, if C was table-defined when the simulator stops enqueueing chains in \({Q}_{\text {all}}\), then condition does not hold for the triple \(T^*\) at the end of the simulator’s execution of the current query.
Consider the case when either \(\mathsf{next}(C^*) = \perp \) or \(C = \mathsf{next}(C^*) \ne \perp \) and \(\mathsf{next}(C) = \perp \) at the time the simulator stops enqueueing chains in \({Q}_{\text {all}}\) i.e. when  in line 6 of the simulator’s execution when answering the distinguisher’s \(t^{th}\) query. Now if the triple \(T^* = (x_9,x_{10},x_1)\) is such that condition holds by the end of the simulator’s execution of the current query, then it must be the case that \(\mathsf{next}(C^*) \ne \perp \) and \(\mathsf{next}(\mathsf{next}(C^*)) \ne \perp \) by the end of the simulator’s execution. In particular, it means that the partial chain \(\mathsf{next}(C^*) = C = (x_{10},x_{11},10)\) where \(x_{11} := x_9 \oplus G_{10}(x_{10})\) is table-defined (with \(\mathsf{val}_1(C) = x_1\)) by the end of the simulator’s execution. Note that at the moment that C becomes table-defined either \(x_1 \notin G_1\) or \(x_9 \notin G_9\) as otherwise either BadP or \(\mathsf{BadlyHit^+}\) occurred. Furthermore, immediately before the assignment that causes C to be table-defined we have either \(\mathsf{val}_1(C) = \perp \) or \(\mathsf{val}_9(C) = \perp \) and immediately after the assignment, we have \(\mathsf{val}_9(C) \ne \perp \) and \(\mathsf{val}_1(C) \ne \perp \) by definition. Say \(\mathsf{val}_1(C) = \perp \) immediately before the assignment that caused C to be table-defined and \(\mathsf{val}_1(C) (= x_1) \ne \perp \) immediately after. For \(x_1 \in G_1\) to be true by the end of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query, it must be the case that \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) at some point for a chain D that has been enqueued in \({Q}_{\text {all}}\) or \({Q}_{\text {mid}}\). Consider the last assignment before \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) was true. The rest of the analysis proceeds similarly to the analysis above. The case when \(\mathsf{val}_9(C) = \perp \) immediately before the assignment that caused C to be table-defined and \(\mathsf{val}_9(C) (= x_9) \ne \perp \) immediately after follows in a similar fashion. So, if \(\mathsf{next}(C^*) = \perp \) or if \(\mathsf{next}(C^*) \ne \perp \) and \(\mathsf{next}(\mathsf{next}(C^*)) = \perp \) when the simulator stops enqueueing chains in \({Q}_{\text {all}}\), then too the condition does not hold for the triple \(T^*\) at the end of the simulator’s execution of the current query. Summarizing, if a chain equivalent to \(C^*\) was not enqueued in \({Q}_{\text {all}}\) and \(C^* \notin \mathsf{SimPChains}\) during the simulator’s execution while answering the distinguisher’s current query, then condition does not hold for the triple \(T^*\) at the end of the simulator’s execution of the current query.
in line 6 of the simulator’s execution when answering the distinguisher’s \(t^{th}\) query. Now if the triple \(T^* = (x_9,x_{10},x_1)\) is such that condition holds by the end of the simulator’s execution of the current query, then it must be the case that \(\mathsf{next}(C^*) \ne \perp \) and \(\mathsf{next}(\mathsf{next}(C^*)) \ne \perp \) by the end of the simulator’s execution. In particular, it means that the partial chain \(\mathsf{next}(C^*) = C = (x_{10},x_{11},10)\) where \(x_{11} := x_9 \oplus G_{10}(x_{10})\) is table-defined (with \(\mathsf{val}_1(C) = x_1\)) by the end of the simulator’s execution. Note that at the moment that C becomes table-defined either \(x_1 \notin G_1\) or \(x_9 \notin G_9\) as otherwise either BadP or \(\mathsf{BadlyHit^+}\) occurred. Furthermore, immediately before the assignment that causes C to be table-defined we have either \(\mathsf{val}_1(C) = \perp \) or \(\mathsf{val}_9(C) = \perp \) and immediately after the assignment, we have \(\mathsf{val}_9(C) \ne \perp \) and \(\mathsf{val}_1(C) \ne \perp \) by definition. Say \(\mathsf{val}_1(C) = \perp \) immediately before the assignment that caused C to be table-defined and \(\mathsf{val}_1(C) (= x_1) \ne \perp \) immediately after. For \(x_1 \in G_1\) to be true by the end of the simulator’s execution while answering the distinguisher’s \(t^{th}\) query, it must be the case that \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) at some point for a chain D that has been enqueued in \({Q}_{\text {all}}\) or \({Q}_{\text {mid}}\). Consider the last assignment before \(\mathsf{val}_1(D) = \mathsf{val}_1(C) = x_1\) was true. The rest of the analysis proceeds similarly to the analysis above. The case when \(\mathsf{val}_9(C) = \perp \) immediately before the assignment that caused C to be table-defined and \(\mathsf{val}_9(C) (= x_9) \ne \perp \) immediately after follows in a similar fashion. So, if \(\mathsf{next}(C^*) = \perp \) or if \(\mathsf{next}(C^*) \ne \perp \) and \(\mathsf{next}(\mathsf{next}(C^*)) = \perp \) when the simulator stops enqueueing chains in \({Q}_{\text {all}}\), then too the condition does not hold for the triple \(T^*\) at the end of the simulator’s execution of the current query. Summarizing, if a chain equivalent to \(C^*\) was not enqueued in \({Q}_{\text {all}}\) and \(C^* \notin \mathsf{SimPChains}\) during the simulator’s execution while answering the distinguisher’s current query, then condition does not hold for the triple \(T^*\) at the end of the simulator’s execution of the current query.
The proof of (ii) follows exactly along the lines of the proof of (i) given above.
The proof of (iii) is as follows. Let \(\mathbf {D} \) ask its \(t^{th}\) query \(\textsc {F}(k,x)\). Just before the simulator returns \(G_k(x)\) in line 27, let the lemma be false and let this be the first time that the lemma does not hold implying that there exists \(x_5 \in G_5\), \(x_6 \in G_6\) such that \((x_5,x_6,5) \notin \mathsf{CompChains}\).
If the lemma has held so far, in particular it has held right before (and immediately after) line 27 of the simulator’s execution while answering \(\mathbf {D} \)’s \((t-1)^{th}\) query to \(\textsc {F}(\cdot ,\cdot )\). Note that the distinguisher could have made queries to \(\textsc {P}/\textsc {P}^{-1}\) between the \((t-1)^{th}\) and \(t^{th}\) queries to \(\textsc {F}(\cdot ,\cdot )\); but those queries cannot result in \(x_5 \in G_5\) or \(x_6 \in G_6\).
So, \(x_5 \in G_5\), \(x_6 \in G_6\) such that \((x_5,x_6,5) \notin \mathsf{CompChains}\) happened during the simulator’s execution while answering \(\mathbf {D} \)’s \(t^{th}\) query. Now, if \((x_5,x_6,5)\) were enqueued for completion during the \(t^{th}\) query then \((x_5,x_6,5) \in \mathsf{CompChains}\). If a chain equivalent to \((x_5,x_6,5)\) were enqueued for completion during the \(t^{th}\) query, then \((x_5,x_6,5) \in \mathsf{CompChains}\). This is because equivalent chains are placed in \(\mathsf{CompChains}\) simultaneously since BadP does not occur and \(\textsc {ForceVal} \) does not overwrite. So, for \(x_5 \in G_5\), \(x_6 \in G_6\) such that \((x_5,x_6,5) \notin \mathsf{CompChains}\) to be true, the simulator did not enqueue this partial chain. (Note that chains of the type \((x_5,x_6,5)\) are not added to \(\mathsf{SimPChains}\)).
Let \(x_6 \in G_6\), and say an assignment occurs such that before the assignment \(x_5 \notin G_5\), but after the assignment \(x_5 \in G_5\) leading to the creation of a partial chain of the form \((x_5,x_6,5)\) with \(x_5 \in G_5, x_6 \in G_6\). (The analysis for the other case is analogous.) Such an assignment can happen only by completion of a chain in \(Q_{1}\), \(Q_{5}\), \(Q_{6}\), \(Q_{10}\) or completion of a chain in \({Q}^*_{\text {all}}\). We analyze these next.
Case 1: An assignment happens to \(G_5(x_5)\) during the completion of a chain C enqueued in \(Q_{b}\) where \(b \in \{1,5,6,10\}\) and \(x_6 \in G_6\) before this assignment. Now, if \(x_6 \in G_6\) before assignment causing \(x_5 \in G_5\), then either \(x_6 \in G_6\) before \(\mathbf {D}\) ’s t-th query or \(x_6 \in G_6\) due to the completion of a chain D enqueued in \(Q_{1}\), \(Q_{5}\), \(Q_{6}\), \(Q_{10}\) and dequeued before C. Again, by construction of the simulator, chains C that are enqueued in \(Q_{b}\) are such that either \(\mathsf{val}_5(C) \in A^t_5\) or \(\mathsf{val}_5(C) \in G_5\) at the time C was enqueued and similarly, chains D that are enqueued in \(Q_{b}\) are such that either \(\mathsf{val}_6(D) \in A^t_6\) or \(\mathsf{val}_6(D) \in G_6\) at the time D was enqueued. Since BadP does not occur and \(\textsc {ForceVal} \) does not overwrite, \(\mathsf{val}_5(C) = x_5 \in A^t_5\) (since \(x_5 \notin G_5\) before this assignment) and \(\mathsf{val}_6(D) = x_6 \in G_6 \cup A^t_6\). And so, \((x_5,x_6,5)\) is enqueued for completion by construction of simulator.
Case 2: An assignment happens to \(G_5(x_5)\) during the completion of a chain C in \({Q}^*_{\text {all}} \) and \(x_6 \in G_6\) before this assignment. If \(x_6 \in G_6 \cup A^t_6\) and \(x_5 \in A^t_5\) when the simulator enqueues chains in \({Q}_{\text {all}}\), then \((x_5,x_6,5)\) is enqueued for completion in \({Q}_{\text {all}}\). Else, \((x_5,x_6,5)\) is enqueued for completion in \({Q}_{\text {mid}}\).
This completes the proof.
Lemma 35
Consider a good execution of \(H_2\). If a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\) belongs to \({Q}^*_{\text {all}}\) such that at the time C is enqueued, adapting was safe for every chain dequeued from \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\), \({Q}^*_{\text {all}}\) or \({Q}_{\text {mid}}\) so far, then \(\mathsf{val}_b(C) = \perp \) and \(\mathsf{val}_g(C) = \perp \) at the time C is enqueued.
Proof
Say \(C = (x_9,x_{10},9,3,2,5)\) is enqueued where the query preceding the chain’s enqueueing is \(G_1(x_1)\) where \(\mathsf{val}_1(C) = x_1\). Then, by definition of simulator, \(x_1 \notin G_1\) as otherwise,  is not called. So, \(\mathsf{val}^+_2(C) = \perp \). Now, we claim that \(\mathsf{val}^-_5(C) \notin G_5\). This is because if \(\mathsf{val}^-_5(C)\in G_5\), then \(\mathsf{val}^-_6(C) \in G_6\) since otherwise, \(\mathsf{val}^-_5(C) = \perp \). This implies that the partial chain \((x_5,x_6,5)\) where \(x_5 = \mathsf{val}^-_5(C)\) and \(x_6 = \mathsf{val}^-_6(C)\) is such that \(x_5 \in G_5\) and \(x_6 \in G_6\). Hence, by Lemma 34, we have that \((x_5,x_6,5) \in \mathsf{CompChains}\) since no new \(G_i\) assignments have been issued between the moment the simulator returned the answer (line 27 of its execution) and the moment when a chain C is enqueued in \({Q}_{\text {all}}\). However, since \(\mathsf{BadP}\) does not occur, this means that \(x_1 \in G_1\) contradicting the first statement. Thus, we have that \(\mathsf{val}^-_5(C) \notin G_5\). Now, \(\mathsf{val}^+_5(C) = \perp \) since \(\mathsf{val}^+_2(C) = \perp \). So, \(\mathsf{val}_5(C) \notin G_5\).
is not called. So, \(\mathsf{val}^+_2(C) = \perp \). Now, we claim that \(\mathsf{val}^-_5(C) \notin G_5\). This is because if \(\mathsf{val}^-_5(C)\in G_5\), then \(\mathsf{val}^-_6(C) \in G_6\) since otherwise, \(\mathsf{val}^-_5(C) = \perp \). This implies that the partial chain \((x_5,x_6,5)\) where \(x_5 = \mathsf{val}^-_5(C)\) and \(x_6 = \mathsf{val}^-_6(C)\) is such that \(x_5 \in G_5\) and \(x_6 \in G_6\). Hence, by Lemma 34, we have that \((x_5,x_6,5) \in \mathsf{CompChains}\) since no new \(G_i\) assignments have been issued between the moment the simulator returned the answer (line 27 of its execution) and the moment when a chain C is enqueued in \({Q}_{\text {all}}\). However, since \(\mathsf{BadP}\) does not occur, this means that \(x_1 \in G_1\) contradicting the first statement. Thus, we have that \(\mathsf{val}^-_5(C) \notin G_5\). Now, \(\mathsf{val}^+_5(C) = \perp \) since \(\mathsf{val}^+_2(C) = \perp \). So, \(\mathsf{val}_5(C) \notin G_5\).
Since C is not enqueued in \(Q_{1}\),\(Q_{5}\),\(Q_{6}\),\(Q_{10}\), we have \(\mathsf{val}_5(C) = \perp \) when C is enqueued. So \(\mathsf{val}_2(C) = \perp \) and \(\mathsf{val}_5(C) = \perp \), where \(g=2\) and \(b=5\). The other cases are analogous.
ForceVal \((x,\cdot ,j)\) does not Overwrite \(G_j(x)\)
Lemma 36
Let \(C = (x_k,x_{k+1},k,\ell ,g,b)\) be a partial chain enqueued in \(Q_{1}\),\(Q_{5}\), \(Q_{6}\) or \(Q_{10}\) during a good execution of \(H_2\). At the moment \(C=(x_k,x_{k+1},k,\ell ,g,b)\) is dequeued, assume that adapting was safe for every chain \(C'\) in \({Q}^*_{\text {all}}\) or \({Q}_{\text {mid}}\) dequeued so far. Then,
-
At the moment \(C = (x_k,x_{k+1},k,\ell ,g,b)\) is dequeued, \(C \in \mathsf{CompChains}\), or
-
Just before the call to \(\textsc {Adapt} \) for C, \(\mathsf{val}_g(C) \notin G_g\) and \(\mathsf{val}_{a}(C) \notin G_{a}\) (where a is the adapt position adjacent to the “bad” set uniform position b).
Proof
Assume that the lemma has held until the moment that a chain \(C = (x_k,x_{k+1},k,\ell ,g,b)\) is dequeued. Note that if the lemma has held until now we have that for every call to \(\textsc {ForceVal} (x,\cdot ,j)\) so far, \(x \notin G_j\) by Corollary 29.
Consider the case that at the moment C was dequeued there is a chain D equivalent to C that was dequeued before C. Now, if D was dequeued before C, then \(D \in \mathsf{CompChains}\) by construction of the simulator. If C and D are equivalent chains such that \(D \in \mathsf{CompChains}\), then \(C \in \mathsf{CompChains}\) by Lemma 26.
Let us consider the case where no chain equivalent to C was dequeued before C was dequeued. Say \(C \notin \mathsf{CompChains}\) when dequeued. Note that if we prove \(\mathsf{val}_g(C) \notin G_g\) and \(\mathsf{val}_a(C) \notin G_a\) at the time C was dequeued, we have that \(\mathsf{val}_g(C) \notin G_g\) and \(\mathsf{val}_a(C) \notin G_a\) just before the call to \(\textsc {Adapt} \) for C since otherwise \(\mathsf{BadP}\) or \(\mathsf{BadlyHit^+}\) occurred.
By Lemma 27, we have that \(\mathsf{val}_g(C) = \perp \) at the time C was enqueued. If \(\mathsf{val}_g(C) \in G_g\) at the time C was dequeued, then this was due to the completion of a chain D which was enqueued in \(Q_{b'}\) where \(b' \in \{1,5,6,10\}\) due to the same distinguisher query as C and dequeued(and completed) before C such that \(\mathsf{val}_g(C) = \mathsf{val}_g(D) \ne \perp \).
Consider the last assignment that was made before \(\mathsf{val}_g(C) = \mathsf{val}_g(D) \ne \perp \) was true. This cannot have been a uniform assignment to \(G_i(x_i)\) since that implies that \(\mathsf{BadlyCollide^+}\) occurred. This is because C and D are not equivalent(by assumption) and C and D are both enqueued for completion in \({Q}_{\text {all}}\) and either \(\mathsf{val}_g(C) = \perp \) or \(\mathsf{val}_g(D) = \perp \) before the assignment(otherwise this is not the last assignment before \(\mathsf{val}_g(C) = \mathsf{val}_g(D) \ne \perp \)) and \(\mathsf{val}_g(C) = \mathsf{val}_g(D) \ne \perp \) after the assignment.
The assignment cannot have been of the form \(P(\downarrow ,x_0,x_1) = (x_{10},x_{11})\) or \(P(\uparrow ,x_{10},x_{11}) = (x_0,x_1)\) since then \(\mathsf{BadP}\) occurred. The assignment cannot have been a \(\textsc {ForceVal} \) query. This is because from Lemmas 32 and 31 we have that \(\textsc {ForceVal} \) does not change \(\mathsf{val}_i(C)\) for a chain C enqueued in \({Q}_{\text {all}}\) (including those enqueued in \(Q_{1},Q_{5},Q_{6},Q_{10}\)) during completion of chains in \(Q_{1},Q_{5},Q_{6},Q_{10}\).
Now, consider the argument for \(\mathsf{val}_a(C) \notin G_a\) when C is dequeued. By Lemma 27, we have that \(\mathsf{val}_b(C) \notin G_b\) and \(\mathsf{val}_g(C) = \perp \) at the time C was enqueued, implying that \(\mathsf{val}_a(C) = \perp \) when C was enqueued (where a is the adapt position adjacent to “bad” set uniform position). The argument for this case follows similar to the one above for \(\mathsf{val}_g(C)\).
Lemma 37
Consider a good execution of \(H_2\). Let \(C = (x_k,x_{k+1},k,\ell ,g,b)\) be a partial chain in \({Q}^*_{\text {all}}\). At the moment \(C=(x_k,x_{k+1},k,\ell ,g,b)\) is dequeued, assume that adapting was safe for every chain \(C'\) in \({Q}_{\text {mid}}\) dequeued so far. Then,
-
At the moment C is dequeued, \(C \in \mathsf{CompChains}\) or,
-
Just before the call to \(\textsc {Adapt} \) for C, \(\mathsf{val}_{\ell -1}(C) \notin G_{\ell -1}\) and \(\mathsf{val}_{\ell +2}(C) \notin G_{\ell +2}\).
Lemma 38
Consider a good execution of \(H_2\). Let \(C = (x_k,x_{k+1},k,\ell ,g,b)\) be a partial chain enqueued in \({Q}_{\text {mid}}\). Then,
-
At the moment C is dequeued, \(C \in \mathsf{CompChains}\), or
-
Just before the call to \(\textsc {Adapt} \) for C, \(\mathsf{val}_{\ell -1}(C) \notin G_{\ell -1}\) and \(\mathsf{val}_{\ell +2}(C) \notin G_{\ell +2}\).
Theorem 39
(No Overwrites). In a good execution of \(H_2\), for any call to \(\textsc {ForceVal} (x,\cdot ,j)\) we have \(x \notin G_j\) before the call.
Proof
Combining the result of Lemmas 36, 37 and 38 with Corollary 29, we have that for every call to \(\textsc {ForceVal} (x,\cdot ,j)\), \(x \notin G_j\) before the call.
5.4 Indistinguishability of \(H_2\) and \(H_4\)
Relying on the properties of good executions of \(H_2\) from the previous section, we prove that \(H_2\) and \(H_4\) are indistinguishable.
Lemma 40
The probability that a distinguisher \(\mathbf {D} \) outputs 1 in \(H_2\) differs at most by \(O(q^{10})/2^n\) from the probability that it outputs 1 in \(H_3\).
Lemma 41
The probability that a distinguisher outputs 1 in \(H_3\) differs by at most by \(O(q^{10})/2^n\) from the probability that it outputs 1 in \(H_4\).
This concludes the proof.
References
Coron, J.S., Holenstein, T., Künzler, R., Patarin, J., Seurin, Y., Tessaro, S.: How to build an ideal cipher: the indifferentiability of the feistel construction. J. Cryptology 29(1), 61–114 (2014)
Coron, J.-S., Patarin, J., Seurin, Y.: The random oracle model and the ideal cipher model are equivalent. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 1–20. Springer, Heidelberg (2008)
Dachman-Soled, D., Katz, J., Thiruvengadam, A.: 10-round Feistel is indifferentiable from an ideal cipher (2015). http://eprint.iacr.org/2015/876
Dai, Y., Steinberger, J.P.: Indifferentiability of 10-round Feistel networks (2015). http://eprint.iacr.org/2015/874
Dai, Y., Steinberger, J.P.: Indifferentiability of 8-round Feistel networks (2015). http://eprint.iacr.org/2015/1069
Dodis, Y., Puniya, P.: On the relation between the ideal cipher and the random oracle models. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 184–206. Springer, Heidelberg (2006)
Dodis, Y., Puniya, P.: Feistel networks made public, and applications. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 534–554. Springer, Heidelberg (2007)
Even, S., Mansour, Y.: A construction of a cipher from a single pseudorandom permutation. In: Imai, H., Rivest, R.L., Matsumoto, T. (eds.) ASIACRYPT 1991. LNCS, pp. 210–224. Springer, Heidelberg (1993)
Feistel, H.: Cryptography and computer privacy. Sci. Am. 228(5), 15–23 (1973)
Gentry, C., Ramzan, Z.: Eliminating random permutation oracles in the even-mansour cipher. In: Lee, P.J. (ed.) ASIACRYPT 2004. LNCS, vol. 3329, pp. 32–47. Springer, Heidelberg (2004)
Holenstein, T., Künzler, R., Tessaro, S.: The equivalence of the random oracle model and the ideal cipher model, revisited. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd ACM STOC. pp. 89–98. ACM Press, June 2011
Luby, M., Rackoff, C.: How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Comput. 17(2), 373–386 (1988)
Mandal, A., Patarin, J., Seurin, Y.: On the public indifferentiability and correlation intractability of the 6-round feistel construction. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 285–302. Springer, Heidelberg (2012)
Maurer, U.M., Renner, R.S., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004)
Ramzan, Z., Reyzin, L.: On the round security of symmetric-key cryptographic primitives. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 376–393. Springer, Heidelberg (2000)
Seurin, Y.: Primitives et Protocoles Cryptographiques à Sécurité Prouvée. PH.D. thesis, Versailles University (2009)
Seurin, Y.: A note on the indifferentiability of the 10-round Feistel construction (2011). http://eprint.iacr.org/2015/903
Yoneyama, K., Miyagawa, S., Ohta, K.: Leaky random oracle (extended abstract). In: Baek, J., Bao, F., Chen, K., Lai, X. (eds.) ProvSec 2008. LNCS, vol. 5324, pp. 226–240. Springer, Heidelberg (2008)
Acknowledgments
We thank Vanishree Rao for collaboration during the early stages of this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Dachman-Soled, D., Katz, J., Thiruvengadam, A. (2016). 10-Round Feistel is Indifferentiable from an Ideal Cipher. In: Fischlin, M., Coron, JS. (eds) Advances in Cryptology – EUROCRYPT 2016. EUROCRYPT 2016. Lecture Notes in Computer Science(), vol 9666. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49896-5_23
Download citation
DOI: https://doi.org/10.1007/978-3-662-49896-5_23
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49895-8
Online ISBN: 978-3-662-49896-5
eBook Packages: Computer ScienceComputer Science (R0)


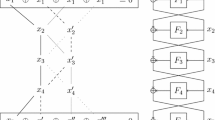



 , then
, then  , then
, then