Abstract
In this paper, we present two new adaptively secure identity-based encryption (IBE) schemes from lattices. The size of the public parameters, ciphertexts, and private keys are \(\tilde{O}(n^2 \kappa ^{1/d})\), \(\tilde{O}(n)\), and \(\tilde{O}(n)\) respectively. Here, n is the security parameter, \(\kappa \) is the length of the identity, and \(d\in \mathbb {N}\) is a flexible constant that can be set arbitrary (but will affect the reduction cost). Ignoring the poly-logarithmic factors hidden in the asymptotic notation, our schemes achieve the best efficiency among existing adaptively secure IBE schemes from lattices. In more detail, our first scheme is anonymous, but proven secure under the LWE assumption with approximation factor \(n^{\omega (1)}\). Our second scheme is not anonymous, but proven adaptively secure assuming the LWE assumption for all polynomial approximation factors.
As a side result, based on a similar idea, we construct an attribute-based encryption scheme for branching programs that simultaneously satisfies the following properties for the first time: Our scheme achieves compact secret keys, the security is proven under the LWE assumption with polynomial approximation factors, and the scheme can deal with unbounded length branching programs.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Background. Identity-based encryption (IBE) is an advanced form of public key encryption (PKE) where any string such as an email address can be used as a public key. The notion of IBE was proposed by Shamir in 1984 [42]. Since then, it took nearly 20 years for the first realizations of IBE [10, 18, 41] to appear. Boneh and Franklin [10] and Sakai, Ohgishi, and Kasahara [41] used groups equipped with efficiently computable bilinear maps to construct the first IBE. On the other hand, Cocks [18] used quadratic residue for a composite modulus. These constructions are only proven secure in the random oracle model. In subsequent works, pairing-based schemes in the standard model appeared [8, 9, 15, 47, 48]. While earlier works [8, 15] focus on the constructions that are only selectively secure, later works [9, 47, 48] focus on a much more realistic security, i.e., adaptive security.
Another important line of research is construction of IBE from lattices. The first lattice-based IBE was proposed in the seminal work by Gentry, Peikert, and Vaikuntanathan [25] in the random oracle model. Later, constructions in the standard model were proposed [1, 12, 16]. To achieve adaptive security in the lattice-based settings, we have to either rely on an analogue of Waters’ hash [47] or an admissible hash [9, 16]. In any case, we require \(O(\kappa )\) number of basic matrices in the public parameters (master public key), where \(\kappa \) is the bit length of the identities. This results in very large public parameters with size \(\tilde{O}(n^2\kappa )\). Here, n is the security parameter (dimension of the lattices). On the other hand, in the selectively secure variant of lattice IBE in [1], we only require small constant number of basic matrices in the public parameters. This stands in sharp contrast to pairing-based settings, in which we have adaptively secure IBE schemes [17, 31] that are as efficient as selectively secure ones [8], up to only small constant factors. A natural important question is:
Can we construct adaptively secure IBE schemes from lattices, which is as efficient as selectively secure ones? In particular, can we reduce the size of the public parameters?
Difficulties. A natural approach to achieve short public parameters in lattice based IBE schemes would be to mimic the technique for pairing based IBE schemes. However, all IBE schemes with short public parameters based on pairings are constructed using dual system encryption methodology [48], for which there is still no lattice analogue. The realization of the dual system encryption methodology in the lattice settings is an important open problem [38]. Another possible approach would be to use a technique from Naccache’s IBE scheme [36], as is done in [44]. Using this approach, we can obtain a scheme with the public parameters shorter by a factor of u, at the cost of \(2^u\)-loss in security. Therefore, using this approach, we are only allowed to reduce the size of public parameters up to logarithmic factor.
Our Contribution. Instead of taking the above approaches, we use a technique unique to the lattice setting. Namely, we use the fully homomorphic computation of trapdoors, which is recently devised in [11] to reduce the size of the public parameters. We obtain the following two different IBE schemes with trade-off between the security, efficiency, and underlying hardness assumptions. See Table 1 in Sect. 6 for the overview.
-
We propose an adaptively secure and anonymous IBE with asymptotically short parameters. In particular, the size of the public parameters, ciphertexts, and private keys are \(\tilde{O}(n^2 \kappa ^{1/d})\), \(\tilde{O}(n)\), and \(\tilde{O}(n)\) respectively. Here, \(d\in \mathbb {N}\) is a flexible constant which can be set arbitrary. Ignoring poly-logarithmic factors hidden in the asymptotic notation, our scheme achieves the best efficiency among all previous adaptively secure IBE schemes from lattices. The security of the scheme is proven under the LWE assumption with super-polynomial approximation factors.
-
We propose an adaptively secure IBE (without anonymity) that achieves asymptotically the same efficiency as the above scheme. The difference from the above scheme is that our scheme can be proven secure assuming the LWE assumption with all polynomial approximation factor. The assumption is weaker than the one used in the above scheme, but the sizes of the public parameters, ciphertexts, and private keys are larger than the above scheme by a super-constant factor.
In the second construction, different from lattice IBE schemes in the literature [1, 2, 12, 16], we have to rely on the LWE assumption for all polynomial approximation factors, rather than some fixed polynomial approximation factor (e.g., \(O(n^{3})\)). The interesting feature of the reduction is that the problem we reduce the security to varies according to the power of the adversary. More specifically, as the number of key extraction queries grows or as the advantage of the adversary drops, we would need the LWE assumption with larger approximation factor. This is somewhat similar to the security proof based on the q-type assumptions (e.g., [24]), in which the problem that the reduction algorithm solves depends on the number of key extraction queries made by the adversary. However, unlike the q-type assumptions, our assumptions enjoy reduction to the worst case lattice problems [13, 37, 40].
To present our schemes in a unified manner, we define the new notion of parametrized IBE (PIBE). The syntax of PIBE is the same as that of ordinary IBE except that it is parametrized by a variable c. As for the security, roughly speaking, we require the advantage of any adversary to be at most \(1{\slash }n^c\) if the number of key extraction queries is bounded by \(n^c\). In the case of c is a super-constant function, the notion of PIBE corresponds to that of (ordinary) IBE. We then construct a specific PIBE scheme from the LWE assumption. By setting c to be a super-constant function, we obtain our first IBE scheme. Our second IBE scheme is obtained by running several instances of the PIBE scheme in parallel with different values of c. This is captured as a generic conversion from PIBE to (ordinary) IBE.
We note that our IBE schemes might not be as efficient as previous adaptively secure lattice IBE schemes [1, 12] for a practical choice of parameters, due to the super-constant factors hidden in the asymptotic notation. However, we believe that our technique would be of theoretical interest. In particular, the security proof of our PIBE scheme is based on the traditional partitioning technique [47] with some novel ideas. In addition, our technique used in the generic construction of IBE from PIBE, inspired by [7], would be useful for other settings.
Other Application of Our Technique. As a side result, we show an application of our technique to attribute-based encryption (ABE). In particular, we obtain the first ABE scheme that simultaneously satisfies the following properties: an unbounded length branching program is usable as an attribute, the sizes of the private keys are compact, the security is proven under the LWE problem for all polynomial approximation factors. We obtain such a scheme by applying a simple conversion to the recent ABE scheme for branching programs by Gorbunov and Vinayagamurthy [28]. The idea for the conversion is similar in spirit to our PIBE-to-IBE conversion. We note that the original ABE scheme of [28] is either based on the super-polynomial LWE while dealing with unbounded length branching programs or based on the polynomial LWE while only dealing with bounded length branching programs. The details appear in the full version [50].
Related Works. We can obtain efficient PKE as well as IBE schemes over ideal lattices [22, 45]. By switching to the ring setting, we can generally reduce the size of the public parameters by an factor of O(n). However, we have to rely on the ring LWE (RLWE) assumption [33, 34], which is a stronger assumption than the LWE assumption.
The techniques for constructing IBE and signatures are somewhat similar and related. Indeed, we can obtain secure signature from (adaptively) secure IBE, via the Naor transformation [10]. A construction of short signature with short public parameters from weak assumptions has been an important research topic. This problem has been addressed by several previous works [4, 7, 23, 30, 32]. However, their techniques heavily depend on the fact that we can convert a non-adaptively secure signature scheme into adaptively secure (or equivalently, EUF-CMA secure) one by using chameleon hash functions [43]. There is no known analogue of the conversion in the setting of IBE. We also note that our technique of converting PIBE into IBE is similar to the “on the fly adaptation technique” in [21], which was used to improve the efficiency and the reduction cost of the Naor-Reingold PRF.
2 Overview of Our Technique
2.1 Overview of the Construction
We follow the general framework for constructing lattice-based IBE schemes, which is an abstraction of many existing schemes [1, 2, 16]. In the template, we associate each identity \(\mathsf {ID}\) with the following matrix:
where \(\mathbf {A}\in \mathbb {Z}_{q}^{n\times m}\) and \(\mathsf {H}(\cdot )\) is a function that maps an identity to a matrix in \(\mathbb {Z}_q^{n\times m'}\) for some \(n,m,m' \in \mathbb {N}\) and some prime number q. A ciphertext for an identity \(\mathsf {ID}\) includes a vector of the following form:
where \(\mathbf {s}\) is a random vector in \(\mathbb {Z}_q^{n}\) and \(\mathbf {x}_1 \in \mathbb {Z}_q^{m}\) and \(\mathbf {x}_2 \in \mathbb {Z}_q^{m'}\) are small error terms. A private key is a short vector \(\mathbf {e}\in \mathbb {Z}^{m+m'}\) that satisfies
for some fixed \(\mathbf {u}\in \mathbb {Z}_q^n\). In the adaptively secure variant of the IBE scheme in [1], the function \(\mathsf {H}(\mathsf {ID})\) is defined as
where \(\mathbf {B}_0,\mathbf {B}_1,\ldots , \mathbf {B}_\kappa \in \mathbb {Z}_q^{n\times m}\) are matrices that are included in the public parameters and \(\mathsf {ID}_i\) is the i-th bit of the bit string \(\mathsf {ID}\in \{ 0,1\}^\kappa \). We typically set \(\kappa = O(n)\) and require rather long public parameters \(\mathbf {B}_0,\mathbf {B}_1,\ldots , \mathbf {B}_\kappa \).
Our first idea is to use the technique called fully homomorphic trapdoor computation, which is introduced in [11], to reduce the size of the public parameters. Namely, we set \(\ell = \lceil \sqrt{\kappa } \rceil \) and the public parameters as matrices \(\mathbf {B}_{1,1}\ldots , \mathbf {B}_{1,\ell }, \mathbf {B}_{2,1}\ldots , \mathbf {B}_{2,\ell } \in \mathbb {Z}_q^{n\times m}\). We also introduce an injective map \(S: \{ 0,1 \}^\kappa \rightarrow 2^{ [\ell ] \times [\ell ] }\) that maps an identity to a subset of the set \( [\ell ] \times [\ell ]\). Then, we change the definition of the function as
where \(\mathbf {G}\) is a gadget matrix whose trapdoor is publicly known [35] and \(\mathbf {G}^{-1}\) is a deterministic functionFootnote 1 that maps a matrix in \(\mathbf {U}= \mathbb {Z}_q^{n\times m }\) to a matrix in \(\mathbf {V}= \{ 0,1 \}^{m\times m }\) such that \(\mathbf {G}\mathbf {V}= \mathbf {U}\). By this change, we are able to reduce the number of basic matrices from \(O(\kappa )\) to \(O( \sqrt{\kappa })\).Footnote 2
2.2 Overview of the Security Proof
We prove the security of the scheme under the LWE assumption. Let the input to the reduction algorithm be \(\mathbf {A}\in \mathbb {Z}_q^{n\times m }\) and \(\mathbf {v}\in \mathbb {Z}_{q}^m\). The task of the algorithm is to distinguish whether \(\mathbf {v}^\top = \mathbf {s}^\top \mathbf {A}+ \mathbf {x}^\top \mod q\) for some \(\mathbf {s}\in \mathbb {Z}_q^n\) and small \(\mathbf {x}\in \mathbb {Z}^m\), or, \(\mathbf {v}\) is a random vector. In the security proof, we pick random \(y_0, y_{1,1},\ldots , y_{1,\ell }, y_{2,1},\ldots , y_{2,\ell } \in \mathbb {Z}_q\) from certain domains, whose sizes grow proportion to the number of key extraction queries Q that the adversary makes (similarly to in [47]). Since we assume that Q is much smaller than q, these random values are bounded by some “small” polynomial. Then, the reduction algorithm picks \(\mathbf {R}_0, \mathbf {R}_{i,j} \overset{_{\tiny \text {\$}}}{\leftarrow }\{ -1,1\}^{m\times m}\) and embeds these values into the public parameters as
for \((i,j)\in \{1,2\} \times [1,\ell ]\). Then, we have
The reduction algorithm has a trapdoor for the matrix \(( \mathbf {A}\Vert \mathsf {H}(\mathsf {ID}))\) if \(\mathsf {F}_\mathbf {y}(\mathsf {ID}) \ne 0 \mod q\) and thus can simulate a private key for such an identity \(\mathsf {ID}\). (\(\mathbf {R}_\mathsf {ID}\) corresponds to the \(\mathbf {G}\)-trapdoor [35] of \((\mathbf {A}\Vert \mathsf {H}(\mathsf {ID}) )\)). On the other hand, the reduction algorithm expects the challenge identity \(\mathsf {ID}^\star \) to satisfy \(\mathsf {F}_\mathbf {y}(\mathsf {ID}^\star ) = 0\), for which it does not know the trapdoor. If these conditions are not satisfied, the reduction fails. We have to estimate the probability that it does not abort. In particular, we have to show that
is noticeable. Here, \(\mathsf {ID}_1,\ldots , \mathsf {ID}_Q\) are identities for which key extraction queries are made. By a similar analysis to [6, 47], to show a lower bound for the probability of (1), it suffices to show an upper bound for the following probability
for identities \(\mathsf {ID}^\star \) and \(\mathsf {ID}_i\) where \(\mathsf {ID}^\star \ne \mathsf {ID}_i\). To show an upper bound for (2), we first observe that
The value of \(y_0\) is clearly independent of the Event (B). Therefore, we can easily estimate the probability of Event (A) occurring, conditioned on that Event (B) occurs. Thus, it suffices to show an upper bound on the probability of Event (B) occurring. This can be accomplished by using the Schwartz-Zippel lemma.
Proof Continued. Based on the idea we have explained above, we can simulate key extraction queries with sufficiently high success probability. However, two problems remain in order to complete the security proof.
-
(C)
In the above discussion, we assumed that q is much larger than Q. Therefore, if q is bounded by some polynomial, so is Q. In such a setting, we can only prove “bounded” security, where the number of key extraction queries is bounded by a predetermined polynomial.
-
(D)
Furthermore, we are not able to generate a properly distributed challenge ciphertext, as we explain below.
Let us explain the problem (D). Assume that for the challenge identity \(\mathsf {ID}^\star \), we have \(\mathsf {F}_{\mathbf {y}}(\mathsf {ID}^\star ) = 0\) and thus \(\mathsf {H}(\mathsf {ID}^\star ) = \mathbf {A}\mathbf {R}_{\mathsf {ID}^\star }\). To prove security, we have to embed the LWE problem instance \(\mathbf {A}\) and \(\mathbf {v}\) into the challenge ciphertext, where \(\mathbf {v}^\top = \mathbf {s}^\top \mathbf {A}+ \mathbf {x}^\top \) or \(\mathbf {v}\) a random vector. A natural way to do this is to implicitly set \(\mathbf {x}_1=\mathbf {x}\) and \(\mathbf {x}_2 = \mathbf {R}_{\mathsf {ID}^\star }^\top \mathbf {x}\) and compute the challenge ciphertext as
The problem with this approach is that the vector \(\mathbf {x}_2\) is highly correlated to the value of \(\mathbf {R}_{\mathsf {ID}^\star }\), which includes the information of \(\mathbf {y}=(y_0, \{ y_{i,j} \}_{(i,j)\in [1,2]\times [1,\ell ] })\) and additionally \(\mathbf {R}_0,\mathbf {R}_{1,1}\ldots , \mathbf {R}_{1,\ell }, \mathbf {R}_{2,1}\ldots , \mathbf {R}_{2,\ell }\). While a similar (but simpler) problem is resolved in a previous work [1] using a generalized form of the leftover hash lemma [20], we are not able to do the same argument due to the additional correlation to \(\mathbf {y}\).
We can resolve the problem by a standard technique. Namely, we “smudge out” or “eat” the problematic term \(\mathbf {R}_{\mathsf {ID}^\star }^\top \mathbf {x}\) by adding a large enough term \(\mathbf {x}' \in \mathbb {Z}_q^{m}\) to it. This makes the error terms essentially statistically independent from \(\mathbf {R}_{\mathsf {ID}^\star }\). The size of the term \(\mathbf {x}'\) should be super-polynomially larger than the size of \(\mathbf {R}_{\mathsf {ID}^\star }^\top \mathbf {x}\), but it should be polynomially smaller than q. Therefore, the size of q should be super-polynomially large, which also resolves the problem (C) at the same time. Appropriately setting the parameters, we obtain our new adaptively secure and anonymous IBE scheme.
2.3 An Additional Idea
However, making q super-polynomially large is not quite desirable because of the following two reasons. Firstly, this would negatively impact the performance of the system. Secondly, since the error term (in our case \(\mathbf {x}\)) is super-polynomially smaller compared to q, the corresponding LWE problem becomes easier. While we are not able to resolve the first problem, we present an idea to avoid the second problem.
Our first observation is that for any constant \(c\in \mathbb {N}\), by making q and \(\mathbf {x}'\) sufficiently large (but polynomial size), we can show that any PPT adversary whose number of key extraction queries is bounded by \(n^c\) cannot break the security of IBE with advantage non-negligibly larger than \(1{\slash }n^c\). Of course, this is not sufficient because we need the adversary to have only negligible (rather than inverse of polynomial) advantage, even if the number of key extraction queries is unbounded.
In order to accomplish this, we prepare several instances of IBE scheme with different size of q. We call each instance of the IBE scheme as a sub-scheme. The number of sub-schemes is super-constant (rather than super-polynomial) and therefore the resulting scheme is still efficient. The size of q varies from very small polynomial to super-polynomial. Furthermore, we “glue” them so that an adversary must break the security of all of the sub-schemes, in order to break the resulting IBE scheme. This can easily be accomplished by splitting the message by k-out-of-k secret sharing scheme, and then encrypt them by each of the sub-schemes.
In the security proof, we assume an PPT adversary \(\mathcal {A}\) that breaks the resulting IBE scheme. Since \(\mathcal {A}\) is polynomial time and has non-negligible advantage, there exists some constant \(c\in \mathbb {N}\) such that the number of the key extraction queries that \(\mathcal {A}\) makes is smaller than \(n^c\) and \(\mathcal {A}\)’s advantage is non-negligibly larger than \(1{\slash }n^c\). Thus, there exists at least one sub-scheme whose size of q fits for \(\mathcal {A}\), and q is polynomial size. We transform the adversary A into another adversary \(\mathcal {B}\) that breaks the sub-scheme. Since q is polynomial size, we can reduce the security to the LWE assumption with polynomial approximation factor. Note that similar technique is used in [21] to improve the efficiency and the reduction cost of the Naor-Reingold PRF. There, the reduction algorithm chooses the target sub-scheme based on the number of queries that the adversary makes. In our reduction, we choose the target depending on the advantage of the adversary in addition to the number of key extraction queries.
To present our results in a unified and modular manner, we introduce the notion of PIBE. Roughly speaking, PIBE is an IBE scheme that is parametrized by a variable c. Our technique to avoid super-polynomial factor we discussed above can be generalized to be a generic conversion from PIBE to IBE. Furthermore, our scheme we discussed in the previous subsection also can be captured as a special case of PIBE, in that c is set to be a super-constant.
3 Preliminaries
Notation. We denote by [n] a set \(\{1,2,\ldots , n\}\) for any integer \(n\in \mathbb {N}\). We treat a vector as a column vector. If \(\mathbf {A}_1\) is \(n\times m\) and \(\mathbf {A}_2\) is \(n\times m'\) matrix, then \((\mathbf {A}_1 | \mathbf {A}_2 )\) denotes the \(n\times (m+ m')\) matrix formed by concatenating \(\mathbf {A}_1\) and \(\mathbf {A}_2\). We use similar notation for vectors. A function \(f: \mathbb {N} \rightarrow \mathbb {R}_{\ge 0}\) is said to be negligible, if for all c, there exists N such that \(f(n) < 1/n^c \) for all \(n> N\). We denote by \(\mathsf {negl}(n)\) a negligible function. We denote by \(x\overset{_{\tiny \text {\$}}}{\leftarrow }X\) the process of sampling a value x according to the distribution X. Similarly, for a finite set S, we denote by \(x\overset{_{\tiny \text {\$}}}{\leftarrow }S\) the process of sampling a value x according to the uniform distribution over S. Statistical distance between two random variables X and Y with support \(\varOmega \) is defined as \(\varDelta (X;Y) = \frac{1}{2} \sum _{s\in \varOmega }| \Pr [X=s] - \Pr [Y=s] |\). For ensembles of random variable \(\{ X(n) \}_{n\in \mathbb {N}}\) and \(\{ Y(n) \}_{n\in \mathbb {N}}\), we say that they are \(\mathsf {negl}(n)\)-close if \(\varDelta (X(n);Y(n))=\mathsf {negl}(n)\).
3.1 Identity-Based Encryption
Syntax. Let \(\mathcal {ID}\) be the ID space of the scheme. If a collision resistant hash function \(CRH: \{ 0,1 \}^* \rightarrow \mathcal {ID}\) is available, one can use an arbitrary string as an identity. An IBE scheme is defined by the following four algorithms.
-
\(\mathsf{Setup}(1^n)\rightarrow (\mathsf {mpk}, \mathsf {msk})\): The setup algorithm takes as input a security parameter \(1^n\) and outputs a master public key \(\mathsf {mpk}\) and a master secret key \(\mathsf {msk}\).
-
\(\mathsf{KeyGen}(\mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\rightarrow \mathsf {sk}_\mathsf {ID}\): The key generation algorithm takes as input the master public key \(\mathsf {mpk}\), the master secret key \(\mathsf {msk}\), and an identity \(\mathsf {ID}\in \mathcal {ID}\). It outputs a private key \(\mathsf {sk}_\mathsf {ID}\). We assume that \(\mathsf {ID}\) is implicitly included in \(\mathsf {sk}_\mathsf {ID}\).
-
\(\mathsf{Encrypt} (\mathsf {mpk}, \mathsf {ID}, \mathsf {M})\rightarrow C\): The encryption algorithm takes as input a master public key \(\mathsf {mpk}\), an identity \(\mathsf {ID}\in \mathcal {ID}\), and a message \(\mathsf {M}\), It outputs a ciphertext \(C\).
-
\(\mathsf{Decrypt}(\mathsf {mpk},\mathsf {sk}_\mathsf {ID}, C)\rightarrow \mathsf {M}\ or \bot \): The decryption algorithm takes as input the master public key \(\mathsf {mpk}\), a private key \(\mathsf {sk}_{\mathsf {ID}}\), and a ciphertext \(C\). It outputs the message \(\mathsf {M}\) or \(\bot \), which means that the ciphertext is not in a valid form.
Correctness. We require correctness of decryption: that is, for all n, all \(\mathsf {ID}\in \mathcal {ID}\), and all \(\mathsf {M}\) in the specified message space, \( \Pr [ \mathsf {Decrypt}(\mathsf {mpk}, \mathsf {sk}_\mathsf {ID}, \mathsf {Encrypt}(\mathsf {mpk}, \mathsf {ID},\mathsf {M}))= \mathsf {M}] = 1-\mathsf {negl}(n) \) holds, where the probability is taken over the randomness used in \((\mathsf {mpk},\mathsf {msk})\overset{_{\tiny \text {\$}}}{\leftarrow }\mathsf {Setup}(1^n)\), \(\mathsf {sk}_\mathsf {ID}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathsf {KeyGen}(\mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\), and \(\mathsf {Encrypt}(\mathsf {mpk},\mathsf {ID},\mathsf {M})\).
Security. We now define the security for an IBE scheme \(\varPi \). This security notion is defined by the following game between a challenger and an adversary \(\mathcal{A}\).
- Setup. At the outset of the game, the challenger runs \(\mathsf {Setup}(1^n)\rightarrow (\mathsf {mpk}, \mathsf {msk})\) and gives \(\mathsf {mpk}\) to \(\mathcal{A}\).
- Phase 1. \(\mathcal {A}\) may adaptively make key-extraction queries. If \(\mathcal {A}\) submits \(\mathsf {ID}\in \mathcal {ID}\) to the challenger, the challenger returns \(\mathsf {sk}_\mathsf {ID}\leftarrow \mathsf {KeyGen}(\mathsf {mpk},\mathsf {msk},\mathsf {ID})\).
- Challenge Phase. At some point, \(\mathcal {A}\) outputs a message \(\mathsf {M}\) and an identity \(\mathsf {ID}^\star \in \mathcal {ID}\), on which it wishes to be challenged. Then, the challenger picks a random coin \(\mathsf {coin}\overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1 \}\) and a random ciphertext \(C \overset{_{\tiny \text {\$}}}{\leftarrow }\mathcal {C}\) from the ciphertext space. If \(\mathsf {coin}= 0\), it runs \(\mathsf {Encrypt}(\mathsf {mpk},\mathsf {ID}^{\star },\mathsf {M})\rightarrow C^{\star }\) and gives the challenge ciphertext \(C^\star \) to \(\mathcal {A}\). If \(\mathsf {coin}= 1\), it sets the challenge ciphertext as \(C^\star = C\) and gives it to \(\mathcal {A}\).
- Phase 2. After the challenge query, \(\mathcal {A}\) may continue to make key-extraction queries, with the added restriction that \(\mathsf {ID}\ne \mathsf {ID}^\star \).
- Guess. Finally, \(\mathcal{A}\) outputs guess a \(\widehat{\mathsf {coin}}\) for \(\mathsf {coin}\). The advantage of \(\mathcal{A}\) is defined as \( \mathsf {Adv}^{\mathsf {IBE}}_{\mathcal{A},\varPi }= \left| \Pr [ \widehat{\mathsf {coin}} = \mathsf {coin}]-\frac{1}{2} \right| . \) We say that \(\varPi \) is adaptively anonymous, if the advantage of any PPT \(\mathcal {A}\) is negligible.
We also define adaptive security (without anonymity) for \(\varPi \) via a similar game to the above. To define adaptive security, we change the challenge phase as follows.
- Challenge Phase. \(\mathcal {A}\) outputs two messages \(\mathsf {M}_0\), \(\mathsf {M}_1\) and an identity \(\mathsf {ID}^\star \in \mathcal {ID}\), on which it wishes to be challenged. Then, the challenger picks a random coin \(\mathsf {coin}\overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1 \}\), runs \(\mathsf {Encrypt}(\mathsf {mpk},\mathsf {ID}^{\star },\mathsf {M}_\mathsf {coin})\rightarrow C^{\star }\), and gives the challenge ciphertext \(C^\star \) to \(\mathcal {A}\).
We also say that \(\varPi \) is adaptively secure, if the advantage of any PPT \(\mathcal {A}\) is negligible. We note that the adaptive anonymity implies the adaptive security. Namely, the former is a stronger security notion.
3.2 Lattice Preliminaries
For positive integers q, m, n, a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n\times m}\), and a vector \(\mathbf {u}\in \mathbb {Z}_q^m\), the m-dimensional integer lattice \(\varLambda _q^{\mathbf {u}}(\mathbf {A})\) is defined as \(\varLambda _q^{\mathbf {u}}(\mathbf {A})=\{ \mathbf {e}\in \mathbb {Z}^m: \mathbf {A}\mathbf {e}= \mathbf {u}\mod q \}\). \(\varLambda _q^{\bot }(\mathbf {A})\) denotes \(\varLambda _q^{\mathbf {0}}(\mathbf {A})\). Let \(D_{\varLambda ,\mathbf {c},\sigma }\) denote the discrete Gaussian distribution over \(\varLambda \) with center \(\mathbf {c}\) and parameter \(\gamma \). When \(\mathbf {c}\) is omitted, we set \(\mathbf {c}=\mathbf {0}\).
Matrix Norms. For a vector \(\mathbf {u}\), we let \(\Vert \mathbf {u}\Vert \) and \(\Vert \mathbf {u}\Vert _\infty \) denote its \(\ell _2\) and \(\ell _\infty \) norm respectively. For a matrix \(\mathbf {R}\le \mathbb {Z}^{k\times m }\) we denote three matrix norms:
-
\(\Vert \mathbf {R}\Vert \) denotes the \(\ell _2\) length of the longest column of \(\mathbf {R}\).
-
 denotes \(\Vert \tilde{\mathbf {R}} \Vert \) where \(\tilde{\mathbf {R}}\) is the result of applying Gram-Schmidt to the columns of \(\mathbf {R}\).
denotes \(\Vert \tilde{\mathbf {R}} \Vert \) where \(\tilde{\mathbf {R}}\) is the result of applying Gram-Schmidt to the columns of \(\mathbf {R}\). -
\(\Vert \mathbf {R}\Vert _2\) is the operator norm of \(\mathbf {R}\) defined as \(\Vert \mathbf {R}\Vert _2 = \sup _{\Vert \mathbf {x}\Vert =1} \Vert \mathbf {R}\mathbf {x}\Vert \).
We have that the following lemma holds [1].
Lemma 1
Let m, n, q be positive integers with \(m>n\), \(\mathbf {A}\in \mathbb {Z}_q^{n\times m}\) be a matrix, \(\mathbf {u}\in \mathbb {Z}_q^n\) be a vector, \(\mathbf {T}_\mathbf {A}\) be a basis for \(\varLambda _q^{\bot }(\mathbf {A})\), and  . Then we have
. Then we have  .
.
Trapdoor Generators and Related Operations
Lemma 2
Let \(n, m, q > 0\) be integers with q prime. There are polynomial time algorithms such that
-
1.
([3, 5]): \(\mathsf {TrapGen}(1^n, 1^m, q) \rightarrow (\mathbf {A}, \mathbf {T}_{\mathbf {A}})\)
a randomized algorithm that, when \(m \ge 6n\lceil \log q \rceil \), outputs a full rank matrix \(\mathbf {A}\in \mathbb {Z}_q^{n\times m}\) and a basis \(\mathbf {T}_\mathbf {A}\in \mathbb {Z}^{m\times m}\) for \(\varLambda _q^{\bot }(\mathbf {A})\) such that \(\mathbf {A}\) is \(\mathsf {negl}(n)\)-close to uniform and
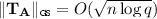 with all but negligible probability in n.
with all but negligible probability in n. -
2.
([16]): \(\mathsf {SampleLeft}(\mathbf {A},\mathbf {F},\mathbf {u}, \mathbf {T}_\mathbf {A}, \sigma ) \rightarrow \mathbf {e}\)
a randomized algorithm that, given a full rank matrix \(\mathbf {A}\in \mathbb {Z}_q^{n\times m}\), a matrix \(\mathbf {F}\in \mathbb {Z}_q^{n\times m}\), a vector \(\mathbf {u}\in \mathbb {Z}_q^n\), a basis \(\mathbf {T}_\mathbf {A}\) for \(\varLambda _q^{\bot }(\mathbf {A})\), and a Gaussian parameter
 , outputs a vector \(\mathbf {e}\in \mathbb {Z}^{2m}\) sampled from a distribution which is \(\mathsf {negl}(n)\)-close to \(D_{\varLambda _q^\mathbf {u}(\mathbf {A}|\mathbf {F}),\sigma }\).
, outputs a vector \(\mathbf {e}\in \mathbb {Z}^{2m}\) sampled from a distribution which is \(\mathsf {negl}(n)\)-close to \(D_{\varLambda _q^\mathbf {u}(\mathbf {A}|\mathbf {F}),\sigma }\). -
3.
([1]): \(\mathsf {SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}, y,\mathbf {u}, \mathbf {T}_{\mathbf {G}}, \sigma ) \rightarrow \mathbf {e}\) where \(\mathbf {F}= \mathbf {A}\mathbf {R}+ y \mathbf {G}\)
a randomized algorithm that, given a full rank matrix \(\mathbf {A}, \mathbf {G}\in \mathbb {Z}_q^{n\times m}\), \(y \in \mathbb {Z}_q{\backslash } \{ 0 \}\), a matrix \(\mathbf {R}\in \mathbb {Z}^{m\times m}\), a vector \(\mathbf {u}\in \mathbb {Z}_q^n\), a basis \(\mathbf {T}_{\mathbf {G}}\) for \(\varLambda _q^{\bot }(\mathbf {G})\), and a Gaussian parameter
 outputs a vector \(\mathbf {e}\in \mathbb {Z}^{2m}\) sampled from a distribution which is \(\mathsf {negl}(n)\)-close to \(D_{\varLambda _q^\mathbf {u}(\mathbf {A}|\mathbf {F}),\sigma }\).
outputs a vector \(\mathbf {e}\in \mathbb {Z}^{2m}\) sampled from a distribution which is \(\mathsf {negl}(n)\)-close to \(D_{\varLambda _q^\mathbf {u}(\mathbf {A}|\mathbf {F}),\sigma }\). -
4.
([35]): Let \(m > n \lceil \log q \rceil \). Then there is a fixed full-rank matrix \(\mathbf {G}\in \mathbb {Z}_q^{n\times m}\) such that the lattice \(\varLambda _q^{\bot }(\mathbf {G})\) has a publicly known basis \(\mathbf {T}_\mathbf {G}\in \mathbb {Z}^{m\times m}\) with
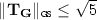 . Furthermore, there exists a deterministic polynomial-time algorithm \(\mathbf {G}^{-1}\) which takes the input \(\mathbf {U}\in \mathbb {Z}_q^{n\times m}\) and outputs \(\mathbf {R}= \mathbf {G}^{-1}(\mathbf {U})\) such that \(\mathbf {R}\in \{ 0,1 \}^{m\times m }\) and \(\mathbf {G}\mathbf {R}= \mathbf {U}\).
. Furthermore, there exists a deterministic polynomial-time algorithm \(\mathbf {G}^{-1}\) which takes the input \(\mathbf {U}\in \mathbb {Z}_q^{n\times m}\) and outputs \(\mathbf {R}= \mathbf {G}^{-1}(\mathbf {U})\) such that \(\mathbf {R}\in \{ 0,1 \}^{m\times m }\) and \(\mathbf {G}\mathbf {R}= \mathbf {U}\).
Note that in the above, we are abusing notation and \(\mathbf {G}^{-1}\) is not a matrix but rather a function. Namely, for any \(\mathbf {U}\) there are many choices of \(\mathbf {R}\) such that \(\mathbf {G}\mathbf {R}=\mathbf {U}\), and \(\mathbf {G}^{-1}(\mathbf {U})\) deterministically outputs a particular short matrix from this set. Since we have \(\Vert \mathbf {R}\Vert _2 \le m \) for any \(\mathbf {R}\in \{-1, 0,1 \}^{m\times m}\), \(\Vert \mathbf {G}^{-1}(\mathbf {U}) \Vert _{2} \le m\) holds for any \(\mathbf {U}\in \mathbb {Z}_q^{n\times m}\).
Learning with Errors. The learning with errors (LWE) problem was introduced by Regev who showed that solving it on the average is as hard as (quantumly) solving several standard lattice problems in the worst case.
Definition 1
(LWE). For an integers n, \(m=m(n)\), a prime integer \(q=q(n)>2\), an error distribution \(\chi = \chi (n)\) over \(\mathbb {Z}_q\), and an PPT algorithm \(\mathcal {A}\), an advantage for the learning with errors problem \(\mathsf {dLWE}_{n,m,q,\chi }\) of \(\mathcal {A}\) is defined as follows:
where  , \(\mathbf {x}\overset{_{\tiny \text {\$}}}{\leftarrow }\chi ^m\), \(\mathbf {v}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^m\). We say that \(\mathsf {dLWE}_{n,m,q,\chi }\) assumption holds if \(\mathsf {Adv}^{\mathsf {dLWE}_{n,m,q,\chi }}_{\mathcal {A}}\) is negligible for all PPT \(\mathcal {A}\).
, \(\mathbf {x}\overset{_{\tiny \text {\$}}}{\leftarrow }\chi ^m\), \(\mathbf {v}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^m\). We say that \(\mathsf {dLWE}_{n,m,q,\chi }\) assumption holds if \(\mathsf {Adv}^{\mathsf {dLWE}_{n,m,q,\chi }}_{\mathcal {A}}\) is negligible for all PPT \(\mathcal {A}\).
Let \(B = B(n)\in \mathbb {N}\). A family of distributions \(\chi = \{ \chi _n \}\) is called B-bounded if \( \Pr [\chi \in [-B,B]] =1. \) For any constant \(d>0\) and sufficiently large q, Regev [40] through a quantum reduction showed that taking \(\chi \) as a \(q/n^d\)-bounded (truncated) discretized Gaussian distribution, the \(\mathsf {dLWE}_{n,m,q,\chi }\) problem is as hard as approximating the worst-case \(\mathsf {GapSVP}\) to \(n^{O(d)}\) factors, which is believed to be hard. In subsequent works, (partial) dequantization of the Regev’s reduction were achieved [13, 37]. More generally, let \(\chi _{\max }<q\) be the bound on the noise distribution. The difficulty of the problem is measured by the ratio \(q/\chi _{\max }\). This ratio is always bigger than 1 and the smaller it is the harder the problem. The problem appears to remain hard even when \(q/\chi _{\max } < 2^{n^\epsilon }\) for some fixed \(\epsilon \) that is \(0< \epsilon < 1{\slash }2\).
3.3 Basic Facts
Injective Map. Let d and \(\kappa \) be some integers. Furthermore, let \(\ell \) be \(\ell = \lceil \kappa ^{1/d} \rceil \). Then, an element of \([1,\kappa ] \) can be written as an element of \([1,\ell ]^d\) using some canonical map. Furthermore, it is also possible to write a subset of \([1,\kappa ] \) as a subset of \([1,\ell ]^d\), by naturally extending the canonical map. By identifying a bit string in \(\{ 0,1 \}^\kappa \) with a subset of \([1,\kappa ]\) (for example, by regarding the former as the indicator vector of a subset of \([1,\kappa ]\)), we can define an efficiently computable injective map S that maps a bit string \(\mathsf {ID}\in \{ 0,1 \}^\kappa \) to a subset \(S(\mathsf {ID})\) of \([1,\ell ]^d\).
The following lemma can be shown by a simple calculation.
Lemma 3
(Smudging out Lemma). Let \(\mathbf {x}_0 \in \mathbb {Z}^m\) be a (fixed) vector such that \(\Vert \mathbf {x}_0 \Vert _\infty \le \delta \) and let \(\mathbf {x}\in \mathbb {Z}^m\) be a random vector that is chosen as \(\mathbf {x}\overset{_{\tiny \text {\$}}}{\leftarrow }[-B', B']^m\). Then, two distributions \(\mathbf {x}_0 + \mathbf {x}\) and \(\mathbf {x}\) are within statistical distance \({m\delta }/{B'}\).
As observed in [1, 40], the following lemma is obtained as a corollary to the (general) leftover hash lemma.
Lemma 4
(Leftover Hash Lemma). Let \(q\in \mathbb {N}\) be an odd prime and let \(m>(n+1)\log q + \omega (\log n)\). Let \(\mathbf {R}\overset{_{\tiny \text {\$}}}{\leftarrow }\{ -1,1 \}^{m\times m}\) and \(\mathbf {A}, \mathbf {A}' \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\) be uniformly random matrices. Then the distribution of \((\mathbf {A},\mathbf {A}\mathbf {R})\) is \(\mathsf {negl}(n)\)-close to the distribution of \((\mathbf {A},\mathbf {A}')\).
The following lemma is implicitly shown in [6].
Lemma 5
Let \(a_1,\ldots , a_n \in \mathbb {R}\) be real numbers such that \(| \sum ^n_{i=1} a_i | = \epsilon \) and \( \sum ^n_{i=1} | a_i | \le 1{\slash }2\). Furthermore, let \(\gamma _1,\ldots , \gamma _n \in \mathbb {R}\) be real numbers such that \(0 < \gamma _{\min } \le \gamma _i \le \gamma _{\max } \) for \(i\in [n]\). Then, we have \(| \sum ^n_{i=1} \gamma _i a_i | \ge \gamma _{\min }\epsilon - ( \gamma _{\max } - \gamma _{\min } )/2 \).
4 Parametrized IBE
In this section, we introduce the notion of parametrized IBE (PIBE), which is an slight extension of the ordinary notion of IBE. The syntax and the security notion for PIBE is almost the same, except that it is parametrized by an integer c. Roughly speaking, the larger c becomes, the more secure PIBE becomes. In particular, when c is super-constant in n, the security notion for PIBE corresponds to that for ordinary IBE. However, in our construction of PIBE in Sect. 5, in order to prove the security of the scheme for super-constant c, we need to assume super-polynomial LWE, which is a stronger assumption than the assumption that is needed for constant c. In this section, to base the scheme on a weaker assumption, we provide generic construction of adaptively secure IBE scheme from PIBE scheme that is secure only for constant c.
4.1 Definition of Parametrized IBE
Here, we define PIBE. The syntax of PIBE is the same as ordinary IBE except that the \(\mathsf {Setup}\) algorithm is parametrized by an integer \(c=c(n)\). Namely, \(\mathsf {Setup}\) takes as inputs \(1^n\) and \(1^c\) and outputs a master public key \(\mathsf {mpk}\) and a master secret key \(\mathsf {msk}\). Other algorithms, \(\mathsf {KeyGen}\), \(\mathsf {Encrypt}\), and \(\mathsf {Decrypt}\) are defined as in ordinary IBE. We require that these algorithms work within a time that is polynomial in n and c.
As for the security, we define advantage \(\mathsf {Adv}^{\mathsf {PIBE}}_{\mathcal{A},\varPi }\) of an adversary \(\mathcal {A}\) for a PIBE scheme \(\varPi \) via a game that is almost the same as that of an ordinary IBE scheme. The only difference is that \(\mathsf {mpk}\) and \(\mathsf {msk}\) are generated by \(\mathsf {Setup}(1^n,1^c)\) at the beginning of the game. The rest of the game is the same. We say that the scheme is c-adaptively anonymous, if for any PPT adversary \(\mathcal {A}\) such that \(Q(n)\le n^c{\slash }2 -1\),
holds for some negligible function \(\mathsf {negl}(n)\). Here \(Q=Q(n)\) is the upper bound for the number of key extraction queries made by \(\mathcal {A}\) during the game.
When c(n) is a constant, the c-adaptive anonymity is an weaker security notion than the adaptive anonymity for IBE, since it allows an adversary to have non-negligible advantage. Furthermore, there is a bound on the number of key extraction queries. On the other hand, when c(n) is super-constant, the security definition of c-adaptive anonymity corresponds to that of adaptive anonymity for (ordinary) IBE. More precisely, we have the following theorem.
Theorem 1
If \(\varPi =(\mathsf {Setup}, \mathsf {KeyGen},\mathsf {Encrypt},\mathsf {Decrypt})\) is \(c'\)-adaptively anonymous for some super constant function \(c'(n)=\omega (1)\) such that \(c'(n)< \mathsf {poly}(n)\), \(\varPi '=(\mathsf {Setup}', \mathsf {KeyGen},\mathsf {Encrypt},\mathsf {Decrypt})\) is adaptively anonymous (as an ordinary IBE) if we set \( \mathsf {Setup}'(1^n)=\mathsf {Setup}(1^n, 1^{c'(n)}). \)
Proof
Since \(c'(n) < \mathsf {poly}(n)\), \(\mathsf {Setup}'\), \(\mathsf {KeyGen}\), \(\mathsf {Encrypt}\), and \(\mathsf {Decrypt}\) run in polynomial time. In addition, since \(c'(n) = \omega (1)\) and thus \(n^{c'}\) is super-polynomial, there is no bound on the number of key extraction queries for the adversary in the \(c'\)-adaptive anonymity game. Furthermore, since \(1{\slash }n^{c'}\) is a negligible function, by Eq. (3), we have
for any adversary \(\mathcal {A}\). Thus, \(\varPi '\) defined as above is adaptively anonymous.
Comparison with Bounded Collusion IBE. Our notion of PIBE is similar to the notion of bounded collusion IBE [19] (also called k-resilient IBE [29]), in that adversaries only learn private keys of an a-priori bounded number of identities. The security requirement for the former is weaker than that for the latter, because we allow adversaries to have non-negligible advantages (in the case of c is a constant). On the other hand, we pose more severe requirement on the efficiency for the former. We require the algorithms of PIBE to work in polynomial time in c, rather than in \(n^c\). Because of this, existing bounded collusion IBE schemes [19, 26, 29, 46, 49] do not satisfy the requirement of PIBE.
4.2 IBE from PIBE
In this section, we show a conversion from a PIBE scheme \(\varPi =(\mathsf {PIBE}.\mathsf {Setup},\mathsf {PIBE}.\mathsf {KeyGen}, \mathsf {PIBE}.\mathsf {Encrypt},\mathsf {PIBE}.\mathsf {Decrypt})\) to an (ordinary) IBE scheme \(\varPi ' = (\mathsf {IBE}.\mathsf {Setup},\mathsf {IBE}.\mathsf {KeyGen}, \mathsf {IBE}.\mathsf {Encrypt},\mathsf {IBE}.\mathsf {Decrypt})\). In the following, let \(\eta (n)\) be any function such that \(\eta (n)=\omega (1)\) (e.g., \(\eta (n) = \log \log (n)\)). We also let the message space of \(\varPi \) and \(\varPi '\) be \(\{ 0,1\}^{\ell _M}\) for some \(\ell _M \in \mathbb {N}\).
-
\(\mathsf {IBE}.\mathsf {Setup}(1^n)\): It runs \(\mathsf {PIBE}.\mathsf {Setup}(1^n,1^i)\rightarrow (\mathsf {mpk}^{(i)}, \mathsf {msk}^{(i)} )\) for \(i= 1,\ldots , \eta \). It outputs
$$\begin{aligned} \mathsf {mpk}= ( \mathsf {mpk}^{(1)}, \mathsf {mpk}^{(2)}, \ldots , \mathsf {mpk}^{(\eta )} ) ~~ \text{ and } ~~ \mathsf {msk}= ( \mathsf {msk}^{(1)}, \mathsf {msk}^{(2)}, \ldots , \mathsf {msk}^{(\eta )} ). \end{aligned}$$ -
\(\mathsf {IBE}.\mathsf {KeyGen}(\mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\): It runs \(\mathsf {PIBE}.\mathsf {KeyGen}(\mathsf {mpk}^{(i)},\mathsf {msk}^{(i)},\mathsf {ID})\rightarrow \mathsf {sk}^{(i)}_{\mathsf {ID}} \) for \(i= 1,\ldots , \eta \). It outputs
$$\begin{aligned} \mathsf {sk}_\mathsf {ID}= ( \mathsf {sk}^{(1)}_{\mathsf {ID}},\mathsf {sk}^{(2)}_{\mathsf {ID}},\ldots , \mathsf {sk}^{(\eta )}_{\mathsf {ID}} ). \end{aligned}$$
-
\(\mathsf {Encrypt}(\mathsf {mpk}, \mathsf {ID}, \mathsf {M})\): To encrypt \(\mathsf {M}= \{ 0,1 \}^{\ell _M}\), it picks random \( \mathsf {M}^{(i)} \in \{ 0,1 \}^{\ell _M}\) for \(i\in [\eta ]\) subject to constraint that \(\mathsf {M}= \bigoplus _{i=1}^\eta \mathsf {M}^{(i)} \), where \(\bigoplus \) denotes bitwise exclusive or. Then it runs
$$\begin{aligned} \mathsf {PIBE}.\mathsf {Encrypt}( \mathsf {mpk}^{(i)}, \mathsf {ID}, \mathsf {M}^{(i)} ) \rightarrow C^{(i)} \qquad \text{ for } \quad i= 1,\ldots , \eta . \end{aligned}$$Finally, it outputs the ciphertext \(C=(C^{(1)},\ldots , C^{(\eta )})\).
-
\(\mathsf {Decrypt}(\mathsf {mpk}, \mathsf {sk}_\mathsf {ID}, C)\): It first parses the ciphertext and the private key as \(C\rightarrow (C^{(1)},\ldots , C^{(\eta )})\) and \(\mathsf {sk}_\mathsf {ID}\rightarrow (\mathsf {sk}_\mathsf {ID}^{(1)},\ldots , \mathsf {sk}_\mathsf {ID}^{(\eta )})\). Then, it runs
$$\begin{aligned} \mathsf {PIBE}.\mathsf {Decrypt}(\mathsf {mpk}^{(i)},\mathsf {sk}_\mathsf {ID}^{(i)},C^{(i)}) \rightarrow \mathsf {M}^{(i)} \qquad \text{ for } \quad i= 1,\ldots , \eta . \end{aligned}$$Finally, it outputs \(\mathsf {M}= \bigoplus _{i=1}^\eta \mathsf {M}^{(i)} \).
Correctness of the scheme can be shown very easily. The following theorem addresses the security of the scheme. Note that the resulting IBE scheme is not anonymous even if the original PIBE scheme is anonymous.
Theorem 2
Assume that PIBE \(\varPi \) is secure for all (constant) \(c \in \mathbb {N}\). Then, \(\varPi '\) is adaptively secure as an (ordinary, not parametrized) IBE scheme.
Proof
Assume an adversary \(\mathcal {A}\) that breaks \(\varPi '\) with non-negligible probability. Since \(\mathcal {A}\) is a PPT algorithm, there exist constants \(c' \in \mathbb {N}\) and \(c'' \in \mathbb {N}\) such that
-
The advantage \(\epsilon (n)\) of \(\mathcal {A}\) is greater than \(2/n^{c'}\) for infinitely many n.
-
The number Q(n) of key extraction queries that \(\mathcal {A}\) makes is bounded by \(n^{c''}{\slash }2 -1\).
Let \(i^\star \) be \(i^\star = c' + c''\). Then, we have
for infinitely many n. In particular, \(\epsilon /2(Q+1) - 1/n^{i^\star }\) cannot be bounded by any negligible function. To show the theorem, we construct an adversary \(\mathcal {B}\) against \(i^\star \)-adaptive anonymity of PIBE \(\varPi \) from \(\mathcal {A}\). In the following, we assume \(\eta \ge i^\star \). Since \(\eta (n) = \omega (1)\), this holds for sufficiently large n.
Setup. First, \(\mathsf {PIBE}.\mathsf {Setup}(1^n,1^{i^\star } )\rightarrow (\mathsf {mpk}^{(i^\star )}, \mathsf {msk}^{(i^\star )} )\) is run and \(\mathsf {mpk}^{(i^\star )}\) is given to \(\mathcal {B}\). Then, \(\mathcal {A}\) runs \(\mathsf {PIBE}.\mathsf {Setup}(1^n,1^i)\rightarrow (\mathsf {mpk}^{(i)}, \mathsf {msk}^{(i)} )\) for \(i= [1,\eta ]{\backslash } \{ i^\star \} \) and sets \(\mathsf {mpk}= ( \mathsf {mpk}^{(1)}, \mathsf {mpk}^{(2)}, \ldots , \mathsf {mpk}^{(\eta )} )\). \(\mathcal {B}\) keeps \(\mathsf {msk}^{(i)}\) for \(i\in [1,\eta ]{\backslash } \{ i^\star \}\) secret, and returns \(\mathsf {mpk}\) to \(\mathcal {A}\).
Phases 1 and 2. When \(\mathcal {A}\) makes a key extraction query for an identity \(\mathsf {ID}\), \(\mathcal {B}\) queries a private key for the same \(\mathsf {ID}\) to its challenger. Then, \(\mathsf {PIBE}.\mathsf {KeyGen}(\mathsf {mpk}^{(i^\star )},\mathsf {msk}^{(i^\star )}, \mathsf {ID})\rightarrow \mathsf {sk}^{(i^\star )}_{\mathsf {ID}} \) is run and \( \mathsf {sk}^{(i^\star )}_{\mathsf {ID}} \) is given to \(\mathcal {B}\). Then \(\mathcal {B}\) runs \(\mathsf {PIBE}.\mathsf {KeyGen}( \mathsf {mpk}^{(i)}, \mathsf {msk}^{(i^\star )}, \mathsf {ID})\rightarrow \mathsf {sk}^{(i)}_{\mathsf {ID}} \) for \(i\in [1,\eta ]{\backslash } \{ i^\star \}\) and returns \(\mathsf {sk}_\mathsf {ID}= ( \mathsf {sk}^{(1)}_{\mathsf {ID}},\ldots , \mathsf {sk}^{(\eta )}_{\mathsf {ID}} )\) to \(\mathcal {A}\).
Challenge. When \(\mathcal {A}\) makes a challenge query for \(( \mathsf {ID}^\star , \mathsf {M}_0, \mathsf {M}_1 ) \), \(\mathcal {B}\) first picks random \(\mathsf {M}^{(i)} \overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1 \}^{\ell _M}\) for \(i\in [1,\eta ]{\backslash } \{ i^\star \} \). Then, it sets
and runs \(\mathsf {PIBE}.\mathsf {Encrypt}( \mathsf {mpk}^{(i)}, \mathsf {ID}, \mathsf {M}^{(i)} ) \rightarrow C^{(i)}\) for \(i\in [1,\eta ]{\backslash } \{ i^\star \} \). Then, it picks random coin \(\mathsf {coin}' \overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1 \}\) and makes the challenge query for \((\mathsf {ID}^\star , \mathsf {M}^{(i^\star )}_{\mathsf {coin}'} )\) to its challenger. Then, the challenger picks a coin \(\mathsf {coin}\overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1 \}\) and returns \(C^\star \) to \(\mathcal {B}\). If \(\mathsf {coin}= 0\), we have \(\mathsf {PIBE}.\mathsf {Encrypt}(\mathsf {mpk}^{(i^\star )}, \mathsf {ID}^\star , \mathsf {M}^{(i^\star )}_{\mathsf {coin}'} ) \rightarrow C^\star \). Otherwise, \(C^\star \) is a random element of the ciphertext space. Given \(C^\star \), \(\mathcal {B}\) returns the challenge ciphertext
to \(\mathcal {A}\).
Guess. Finally, \(\mathcal {A}\) outputs a guess \( \widehat{\mathsf {coin}}\) for \(\mathsf {coin}'\). If \(\widehat{\mathsf {coin}}=\mathsf {coin}'\), \(\mathcal {B}\) outputs 0 as its guess for \(\mathsf {coin}\) and outputs 1 otherwise.
Analysis. We can see that \(\mathcal {B}\) is a valid adversary for the parametrized IBE \(\varPi \) since \(\mathcal {A}\) does not make a key extraction query for \(\mathsf {ID}^\star \). Furthermore, \(\mathcal {B}\) makes the same number of key extraction queries as \(\mathcal {A}\) and in particular, we have \(Q(n) < n^{i^\star }{\slash }2 -1\). It is easy to see that the view of the adversary \(\mathcal {A}\) corresponds to that in adaptive security game for IBE \(\varPi '\) when \(\mathsf {coin}=0\). It can also be seen that the view of the adversary is independent of \(\mathsf {coin}'\) when \(\mathsf {coin}=1\). Therefore, we have
Thus, by Eq. (4), \(\mathcal {B}\) is a successful attacker against the \(i^\star \)-adaptive anonymity of \(\varPi \).
More Efficient Conversion. In the above conversion, we run \(\eta \) instances of PIBE scheme in parallel. The number of instances can be reduced to \(O(\log \eta )\). We briefly sketch the construction and the security proof for it. Let us assume that \(\eta \) is a power of 2. In the setup algorithm of the variant, we run \(\mathsf {PIBE}.\mathsf {Setup}(1^n,1^i)\rightarrow (\mathsf {mpk}^{(i)}, \mathsf {msk}^{(i)} )\) for \(i=1,2,4,\ldots , 2^i, \ldots , 2^{\log \eta }(=\eta )\), instead of \(i=1,2,\ldots , \eta \). Other algorithms are defined similarly to the above. In the security proof, the target of the reduction algorithm is set to be \(i^\star \) such that \( 2^{i^\star - 1} \le c'+c'' < 2^{i^\star }.\)
5 Our Construction of PIBE from Lattices
Here, we show our constructions of PIBE from lattices. By setting the parameter c super-constant or applying the conversions in Sect. 4.2, we obtain IBE schemes that provide trade-off between the efficiency, security, and the underlying assumptions. (See Sect. 6 for the overview). In this section, we first introduce some functions that will be needed to describe our construction. Then, we show our construction of PIBE scheme for single-bit message space. We then prove the security of the scheme. Finally, we discuss extension of the scheme to the multi-bit variant.
5.1 Homomorphic Computation
Let d be a natural number. We introduce a function \(\mathsf {PubEval}_d\,{:}\,( \mathbb {Z}_{q}^{n\times m} )^d \rightarrow \mathbb {Z}_{q}^{n\times m} \) which takes a set of matrices \(\mathbf {B}_1, \mathbf {B}_2, \ldots , \mathbf {B}_d \in \mathbb {Z}_q^{n\times m}\) as inputs and outputs a matrix in \(\mathbb {Z}_{q}^{n\times m}\). The function is defined recursively as follows:
We have that the following lemma holds. The proof appears in the full version.
Lemma 6
Let \(\mathbf {A}\), \(\mathbf {B}_1,\ldots , \mathbf {B}_{d}\) be matrices in \(\mathbb {Z}_q^{n\times m}\) and \(\mathbf {R}_1,\ldots ,\mathbf {R}_{d}\) be matrices in \(\mathbb {Z}^{m\times m}\) such that \(\mathbf {B}_i = \mathbf {A}\mathbf {R}_i + y_i \mathbf {G}\) for \(i\in [d]\). Furthermore, we assume that \(\Vert \mathbf {R}_i \Vert _2 \le m\), \(| y_i |\le \delta \) for \(i \in [d]\), and \(\delta > m\). Then, there exists an efficient algorithm \(\mathsf {TrapEval}_d\) that takes \(\mathbf {R}_1, \ldots , \mathbf {R}_{d}, y_1,\ldots , y_d\) as inputs and outputs \(\mathbf {R}'\) such that
and \(\Vert \mathbf {R}' \Vert _2 \le m d \delta ^{d-1} .\)
5.2 Our Construction
In the following, we present our PIBE scheme. Let d be a (flexible) constant. In addition, let the identity space of the scheme be \(\mathcal {ID}= \{ 0,1 \}^{\kappa }\) for some \(\kappa \in \mathbb {N}\) and the message space be \(\{ 0,1 \}\). For our construction, we consider an efficiently computable injective map S that maps an identity \(\mathsf {ID}\in \{ 0,1 \}^\kappa \) to a subset \(S(\mathsf {ID})\) of \([1,\ell ]^d\), where \(\ell = \lceil \kappa ^{1/d} \rceil \). Such a map can be constructed easily as we explained in Sect. 3.3. We would typically set \(\kappa = O(n)\), and thus \(\ell = O(n^{1/d})\) in such a case.
-
\(\mathsf {Setup}(1^n,1^c)\): On input \(1^n\) and \(1^c\), it sets the parameters q, m, \(\sigma \), B, \(B'\), and a distribution \(\chi \) as specified in Sect. 5.3, where q is a prime number. Then, it picks random matrices \(\mathbf {B}_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\), \(\mathbf {B}_{i,j} \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\) for \((i,j)\in [d, \ell ]\) and a vector \(\mathbf {u}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^n\). It also picks \(\mathsf {TrapGen}(1^n, 1^m, q) \rightarrow (\mathbf {A},\mathbf {T}_\mathbf {A})\in \mathbb {Z}_q^{n\times m} \times \mathbb {Z}^{m\times m}\) such that
 . It finally outputs $$\begin{aligned} \mathsf {mpk}= (\mathbf {A}, \mathbf {B}_0, \{ \mathbf {B}_{i,j} \}_{(i,j)\in [d, \ell ] }, \mathbf {u}) \qquad \text{ and } \qquad \mathsf {msk}=\mathbf {T}_\mathbf {A}. \end{aligned}$$
. It finally outputs $$\begin{aligned} \mathsf {mpk}= (\mathbf {A}, \mathbf {B}_0, \{ \mathbf {B}_{i,j} \}_{(i,j)\in [d, \ell ] }, \mathbf {u}) \qquad \text{ and } \qquad \mathsf {msk}=\mathbf {T}_\mathbf {A}. \end{aligned}$$
In the following, we use a deterministic function \(\mathsf {H}{\,:\,}\mathcal {ID}\rightarrow \mathbb {Z}_q^{n\times m}\) that is defined as follows.
-
\(\mathsf {KeyGen}(\mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\): It first computes \(\mathsf {H}(\mathsf {ID})\) and picks \(\mathbf {e}\in \mathbb {Z}^{2m}\) such that
$$\begin{aligned} \bigl ( \mathbf {A}| \mathsf {H}(\mathsf {ID}) \bigr ) \cdot \mathbf {e}= \mathbf {u}\end{aligned}$$by running \(\mathsf {SampleLeft}(\mathbf {A},\mathsf {H}(\mathsf {ID}),\mathbf {u}, \mathbf {T}_\mathbf {A}, \sigma ) \rightarrow \mathbf {e}\). It returns \(\mathsf {sk}_\mathsf {ID}= \mathbf {e}\).
-
\(\mathsf {Encrypt}(\mathsf {mpk}, \mathsf {ID}, b)\): To encrypt a message \(b\in \{ 0,1 \}\), it picks \(\mathbf {s}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^n\), \(x_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\chi \), \(\mathbf {x}_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\chi ^m\), \(\mathbf {x}_2 \overset{_{\tiny \text {\$}}}{\leftarrow }[-B',B']^m\) and computes
$$\begin{aligned} \qquad c_0= \mathbf {s}^\top \mathbf {u}+ x_0 + b \cdot \lceil q/2 \rceil , \qquad \mathbf {c}^\top _1= \mathbf {s}^\top ( \mathbf {A}| \mathsf {H}(\mathsf {ID}) ) + ( \mathbf {x}_1^\top | \mathbf {x}_2^\top ). \end{aligned}$$Finally, it returns the ciphertext \(C=(c_0,\mathbf {c}_1)\).
-
\(\mathsf {Decrypt}(\mathsf {mpk},\mathsf {sk}_\mathsf {ID}, C)\): To decrypt a ciphertext \(C=(c_0,\mathbf {c}_1)\) using a private key \(\mathsf {sk}_\mathsf {ID}{:}= \mathbf {e}\), it first computes
$$\begin{aligned} w =c_0 - \mathbf {c}_1^\top \cdot \mathbf {e}\in \mathbb {Z}_q. \end{aligned}$$Then it returns 1 if \(| w - \lceil q/2 \rceil | < \lceil q/4 \rceil \) and 0 otherwise.
5.3 Correctness and Parameter Selection
When the cryptosystem is operated as specified, we have during decryption,
Lemma 7
Assuming \(B' >B\), the error term is bounded by \(O(B' \sigma m )\) with overwhelming probability.
Proof
Since \(\chi \) is B-bounded distribution, with overwhelming probability, we have
The second inequality above follows from Cauchy-Schwartz and the third inequality follows from Lemma 1.
Parameter Selection. Now, to satisfy the correctness requirement and make the security proof work, we need that
-
the error term is less than \(q{\slash }5\) with overwhelming probability (i.e., \(\varOmega ( B' \sigma m) < q\)),
-
that q is sufficiently large so that the simulation works (i.e., \(q > \varTheta ( \kappa (d n^c )^d )\)),
-
that \(\mathsf {TrapGen}\) can operate (i.e., \(m \ge 6 n \lceil \log q \rceil \)),
-
that the leftover hash lemma (Lemma 4) can be applied in the security proof (i.e., \(m=(n+1)\log q + \omega (\log n)\)),
-
that \(\sigma \) is sufficiently large so that \(\mathsf {SampleLeft}\) and \(\mathsf {SampleRight}\) work, (i.e., \(\sigma > O(\sqrt{n\log q}) \cdot \omega (\sqrt{ \log m } ) \) and \(\sigma > m ( 1 + \kappa d^{d} n^{c(d-1)} ) \cdot \omega ( \sqrt{\log m } ) \), where the latter condition turns out to be more restrictive),
-
that the “noise smudging step” in the security proof works (i.e., \(m^{5/2} ( 1 + \kappa d^{d} n^{c(d-1)} ) B/B' \le d/(\kappa +1)( dn^c )^{d+1}\). See Eq. (11)).
To satisfy the above requirements, we set the parameters as follows:
where \(c'\) is a constant such that \(\kappa = O( n^{c'} ) \). Typically, we would set \(c' = 1\).
5.4 Security Proof
The following theorem addresses the security of the scheme. The proof is based on the partitioning technique, similarly to [1, 6, 12, 47]. For simplicity, we opt to use the framework of [6] in our analysis, which does not require the artificial abort step [47]. The analysis with the artificial abort step is also possible, and it might lead to a scheme with slightly better efficiency (up to constant factors).
Theorem 3
The above scheme is c-adaptive anonymous assuming \(\mathsf {dLWE}_{n,m+1,q,\chi }\) is hard, where the ciphertext space is \(\mathcal {C}= \mathbb {Z}_q \times \mathbb {Z}_q^{2m}\).
Proof
Let \(\mathcal {A}\) be a PPT adversary that breaks c-adaptive anonymity of the scheme. In addition, let \(\epsilon = \epsilon (n)\) and \(Q = Q(n)\) be its advantage and the upper bound of the number of key extraction queries, respectively. Without loss of generality, we assume that \(\mathcal {A}\) always makes exactly Q key extraction queries. Let us define \(\tilde{c}\) as a constant that satisfies
where \(\mathsf {nonneg}(n)\) is some non-negligible function. We explain such \(\tilde{c}\) always exist. In the case of \(c=c(n)\) is a constant, we simply let \(\tilde{c}=c\). Let us consider the case of \(c(n)=\omega (1)\). Since \(\mathcal {A}\) is a PPT algorithm, there exists a constant \(c'\) such that \(Q(n) \le n^{c'}{\slash }2 - 1\). Furthermore, since \(\mathcal {A}\) breaks c-adaptive anonymity of the scheme and \(1{\slash }n^c\) is negligible, \(\epsilon /(Q+1)\) is non-negligible. Therefore, there exists a constant \(c''\) such that \(\epsilon /(Q+1) > 2/n^{c''}\) holds for infinitely many n. By setting \(\tilde{c}= \max \{ c',c'' \}\), we are done. We note that in any case, \(\tilde{c}(n) \le c(n)\) holds for sufficiently large n.
We show the security of the scheme via the following games. In each game, a value \(\mathsf {coin}' \in \{ 0,1 \}\) is defined. While it is set \(\mathsf {coin}' = \widehat{\mathsf {coin}}\) in the first game, these values might be different in the later games. In the following, we define \(X_i\) be the event that \(\mathsf {coin}' = \mathsf {coin}\).
-
\(\mathsf {Game}_{0}\): This is the real security game. Recall that since the ciphertext space is \(\mathcal {C}= \mathbb {Z}_q \times \mathbb {Z}_q^{2m}\), in the challenge phase, the challenge ciphertext is set as \(C^\star = (c_0, \mathbf {c}_1 )\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q\times \mathbb {Z}_q^{2m}\) if \(\mathsf {coin}= 1\). At the end of the game, \(\mathcal {A}\) outputs a guess \(\widehat{\mathsf {coin}}\) for \(\mathsf {coin}\). Finally, the challenger sets \(\mathsf {coin}' = \widehat{\mathsf {coin}}\). By the definition, we have
$$\begin{aligned} \left| \Pr [X_0] - \frac{1}{2} \right| = \left| \Pr [\mathsf {coin}' = \mathsf {coin}] - \frac{1}{2} \right| = \left| \Pr [\widehat{\mathsf {coin}} = \mathsf {coin}] - \frac{1}{2} \right| = \epsilon . \end{aligned}$$ -
\(\mathsf {Game}_{1}\): In this game, we change \(\mathsf {Game}_0\) so that the challenger performs the following additional step at the end of the game. First, the challenger picks \(\mathbf {y}=(y_0, \{ y_{i,j} \}_{(i,j)\in [d,\ell ]})\) as
$$\begin{aligned} y_0 \overset{_{\tiny \text {\$}}}{\leftarrow }[-(\kappa +1) (dn^{\tilde{c}} )^d +1, 0] \quad \text{ and } \quad y_{i,j} \overset{_{\tiny \text {\$}}}{\leftarrow }[1, dn^{\tilde{c}} ] \quad \text{ for } \quad (i,j)\in [d]\times [\ell ]. \end{aligned}$$We define a function \(\mathsf {F}_\mathbf {y}{\,:\,}\mathcal {ID}\rightarrow \mathbb {Z}_q\) as follows:
$$\begin{aligned} \mathsf {F}_\mathbf {y}(\mathsf {ID})= y_0 + \sum _{(j_1, \ldots , j_d)\in S(\mathsf {ID})} y_{1,j_1}\cdots y_{d,j_d}. \end{aligned}$$Then the challenger checks whether the following condition holds:
$$\begin{aligned} \mathsf {F}_\mathbf {y}(\mathsf {ID}^\star )=0 ~ \wedge ~ \mathsf {F}_\mathbf {y}(\mathsf {ID}_1) \ne 0 ~ \wedge ~ \mathsf {F}_\mathbf {y}(\mathsf {ID}_2) \ne 0 ~ \wedge ~ \cdots ~ \wedge ~ \mathsf {F}_\mathbf {y}(\mathsf {ID}_Q) \ne 0 \end{aligned}$$(7)where \(\mathsf {ID}^\star \) is the challenge identity, and \(\mathsf {ID}_1,\ldots , \mathsf {ID}_Q\) are identities for which \(\mathcal {A}\) has made key extraction queries. If it does not hold, the challenger ignores the output \(\widehat{\mathsf {coin}}\) of \(\mathcal {A}\), and sets \(\mathsf {coin}' \overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1\}\). In this case, we say that the challenger aborts. If condition (7) holds, the challenger sets \(\mathsf {coin}' = \widehat{\mathsf {coin}}\). As we will show in Lemma 8, we have
$$\begin{aligned} \left| \Pr [X_1] -\frac{1}{2} \right| \ge \frac{1}{\kappa +1} \cdot \left( \frac{1}{ dn^{\tilde{c}} } \right) ^d \cdot \left( \epsilon - \frac{Q}{n^{\tilde{c}}} \right) . \end{aligned}$$So as not to interrupt the proof of Theorem 3, we intentionally skip the proof for the time being.
-
\(\mathsf {Game}_{2}\): In this game, we change the way \(\mathbf {B}_0\) and \(\mathbf {B}_{i,j}\) are chosen. At the beginning of the game, the challenger picks \(\mathbf {R}_0, \mathbf {R}_{i,j} \overset{_{\tiny \text {\$}}}{\leftarrow }\{ -1, 1\}^{m\times m}\) for \((i,j)\in [d]\times [\ell ]\). It also picks \(\mathbf {y}\) as in \(\mathsf {Game}_1\). Then, \(\mathbf {A}\), \(\mathbf {B}_0\), and \(\mathbf {B}_{i,j}\) are defined as
$$\begin{aligned} \mathbf {B}_0=\mathbf {A}\mathbf {R}_0 + y_0 \mathbf {G}, \qquad \mathbf {B}_{i,j}=\mathbf {A}\mathbf {R}_{i,j} + y_{i,j} \mathbf {G}\end{aligned}$$(8)for \((i,j) \in [d] \times [\ell ]\). The rest of the game is the same as in \(\mathsf {Game}_1\). Then, we bound \(| \Pr [X_2]-\Pr [X_1] |\). By Lemma 4, the distributions
$$\begin{aligned} \bigl (\mathbf {A}, ~ \mathbf {A}\mathbf {R}_0+ y_0 \mathbf {G}, ~ \{ \mathbf {A}\mathbf {R}_{i,j}+y_{i,j}\mathbf {G}\} \bigr ) ~~ \text{ and } ~~ \bigl (\mathbf {A}, ~ \mathbf {B}_0, ~ \{ \mathbf {B}_{i,j} \} \bigr ) \end{aligned}$$are \(\mathsf {negl}(n)\)-close, where \(\mathbf {B}_0, \mathbf {B}_{i,j} \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\). Therefore, we have \(| \Pr [X_1] - \Pr [X_2] | = \mathsf {negl}(n).\)
Before describing the next game, we define \(\mathbf {R}_{\mathsf {ID}}\) for an identity \(\mathsf {ID}\in \mathcal {ID}\) as
Note that by Lemma 6, we have
for any \(\mathsf {ID}\in \mathcal {ID}\). The last inequality above follows from \(\tilde{c} \le c\).
-
\(\mathsf {Game}_{3}\): In this game, we change the way the challenge ciphertext is created when \(\mathsf {coin}=0\). If \(\mathsf {coin}=0\), to create the challenge ciphertext \(\mathsf {Game}_3\) challenger first picks \(\mathbf {s}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^n\), \(x_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\chi \), \(\mathbf {x}_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\chi ^m\), \(\mathbf {x}_2 \overset{_{\tiny \text {\$}}}{\leftarrow }[-B',B']^m\) and computes \(\mathbf {R}_{\mathsf {ID}^\star }\). Then, the challenge ciphertext \(C^\star = (c_0, \mathbf {c}_1)\) is computed as
$$\begin{aligned} c_0= \mathbf {s}^\top \mathbf {u}+ x_0 + b \cdot \lceil q/2 \rceil , \qquad \mathbf {c}_1^\top = \mathbf {s}^\top ( \mathbf {A}| \mathsf {H}(\mathsf {ID}^\star ) ) + ( \mathbf {x}_1^\top | \mathbf {x}_1^\top \mathbf {R}_{\mathsf {ID}^\star } + \mathbf {x}_2^\top ) \end{aligned}$$where \(b\in \{ 0,1\}\) is the message chosen by \(\mathcal {A}\).
We then proceed to bound \(| \Pr [X_3]-\Pr [X_2] |\). Since \(\mathbf {x}_1\) is chosen from a B-bounded distribution, we have
$$\begin{aligned} \Vert \mathbf {R}_{\mathsf {ID}^\star }^\top \mathbf {x}_1 \Vert _\infty \le \Vert \mathbf {R}_{\mathsf {ID}^\star }^\top \mathbf {x}_1 \Vert _2 \le \Vert \mathbf {R}_{\mathsf {ID}^\star }^\top \Vert _2 \cdot \Vert \mathbf {x}_1 \Vert \le m^{3/2} ( 1 + \kappa d^{d} n^{c(d-1)} ) B. \end{aligned}$$When all randomness other than \(\mathbf {x}_2\) in this game is fixed, the distributions \(\mathbf {x}_2\) and \( \mathbf {R}_{\mathsf {ID}^\star }^\top \cdot \mathbf {x}_1 + \mathbf {x}_2\) are within statistical distance
$$\begin{aligned} m \Vert \mathbf {R}^\top _{\mathsf {ID}^\star } \mathbf {x}_1 \Vert _{\infty }/B' = m^{5/2} ( 1 + \kappa d^{d} n^{c(d-1)} ) B/B' \le \frac{d}{\kappa +1} \cdot \left( \frac{1}{ dn^c } \right) ^{d+1} \end{aligned}$$(11)by Lemma 3. Averaging over all other randomness, we have that the distribution of the challenge ciphertext is within statistical distance \(d/(\kappa +1)( dn^c )^{d+1}\) from the previous game, when \(\mathsf {coin}=0\). In the case of \(\mathsf {coin}=1\), the view of \(\mathcal {A}\) is unchanged. Therefore, we conclude that the view of \(\mathcal {A}\) in this game is within statistical distance \(d/(\kappa +1)(dn^c )^{d+1}\) from the previous game. Thus, we have
$$\begin{aligned} | \Pr [X_2] - \Pr [X_3] | \le \frac{d }{\kappa +1 } \cdot \left( \frac{1}{dn^c} \right) ^{d+1}. \end{aligned}$$ -
\(\mathsf {Game}_{4}:\) Recall that in the previous game, the challenger aborts at the end of the game, if the condition (7) is not satisfied. In this game, we change the game so that the challenger aborts as soon as the abort condition becomes true. Since this is only a conceptual change, we have \( \Pr [X_3]=\Pr [X_4]. \)
-
\(\mathsf {Game}_{5}:\) In this game, we change the way the matrix \(\mathbf {A}\) is sampled. Namely, \(\mathsf {Game}_5\) challenger picks \(\mathbf {A}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\) instead of generating it with a trapdoor. By Lemma 2, this makes only negligible difference. Furthermore, we also change the way the key extraction queries are answered. When \(\mathcal {A}\) makes a key extraction query for an identity \(\mathsf {ID}\), the challenger first computes \(\mathbf {R}_\mathsf {ID}\) as in Eq. (9). By the definition of \(\mathbf {R}_\mathsf {ID}\), it holds that
$$\begin{aligned} \mathsf {H}(\mathsf {ID})=\mathbf {A}\cdot \left( \mathbf {R}_\mathsf {ID}+ \mathsf {F}_\mathbf {y}(\mathsf {ID})\mathbf {G}\right) . \end{aligned}$$If \(\mathsf {F}_\mathbf {y}(\mathsf {ID}) = 0\), it aborts, as the previous game. Otherwise, it runs
$$\begin{aligned} \mathsf {SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}_\mathsf {ID}, \mathsf {F}_\mathbf {y}(\mathsf {ID}),\mathbf {u}, \mathbf {T}_{\mathbf {G}}, \sigma ) \rightarrow \mathbf {e}, \end{aligned}$$and returns \(\mathbf {e}\) to \(\mathcal {A}\). Note that the private key was sampled as
$$\begin{aligned} \mathsf {SampleLeft}(\mathbf {A},\mathsf {H}(\mathsf {ID}),\mathbf {u}, \mathbf {T}_\mathbf {A}, \sigma ) \rightarrow \mathbf {e}\end{aligned}$$in the previous game. By Eq. (10) and the choice of \(\sigma \), the output distribution of \(\mathsf {SampleRight}\) is \(\mathsf {negl}(n)\)-close to \(D_{\varLambda _q^\mathbf {u}(\mathbf {A}|\mathsf {H}(\mathsf {ID}) ),\sigma }\). Similarly, by the choice of \(\sigma \), the output distribution of \(\mathsf {SampleLeft}\) is also \(\mathsf {negl}(n)\)-close to \(D_{\varLambda _q^\mathbf {u}(\mathbf {A}|\mathsf {H}(\mathsf {ID}) ),\sigma }\). Therefore, the above change alters the view of the adversary only negligibly. Thus, we have \( | \Pr [X_4] - \Pr [X_5] | = \mathsf {negl}(n). \)
-
\(\mathsf {Game}_{6}\): In this game, we change the way the challenge ciphertext is created when \(\mathsf {coin}=0\). If \(\mathsf {coin}=0\), to create the challenge ciphertext for the identity \(\mathsf {ID}^\star \) and the message b, \(\mathsf {Game}_6\) challenger first picks \(v_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q\), \(\mathbf {v}_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{m}\), \(\mathbf {x}_2 \overset{_{\tiny \text {\$}}}{\leftarrow }[-B', B']^m\) and computes \(\mathbf {R}_{\mathsf {ID}^\star }\). Then, it sets the challenge ciphertext \(C^\star = ( c_0,\mathbf {c}_1 )\) as
$$\begin{aligned} \qquad c_0= v_0 + b \cdot \lceil q/2 \rceil , \qquad \mathbf {c}_1^\top = ( \mathbf {v}_1^\top | \mathbf {v}_1^\top \mathbf {R}_{\mathsf {ID}^\star }) + ( \mathbf {0}_m^\top | \mathbf {x}_2^\top ). \end{aligned}$$As we will show in Lemma 9, assuming \(\mathsf {dLWE}_{n,m+1,q,\chi }\) is hard, we have \( |\Pr [X_5]-\Pr [X_6]|=\mathsf {negl}(n). \)
-
\(\mathsf {Game}_{7}\): In this game, we change the challenge ciphertext to be a random vector, regardless of whether \(\mathsf {coin}=0\) or \(\mathsf {coin}=1\). Namely, \(\mathsf {Game}_7\) challenger generates the challenge ciphertext \((c_0,\mathbf {c}_1)\) as \(c_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q\) and \(\mathbf {c}_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^m\). We now proceed to bound \(| \Pr [X_7] - \Pr [X_6] |\). Since \(\mathsf {Game}_6\) and \(\mathsf {Game}_7\) differ only in the creation of the challenge ciphertext when \(\mathsf {coin}= 0\), we focus on this case. First, it is easy to see that \(c_0\) is uniformly random over \(\mathbb {Z}_q\) in both of \(\mathsf {Game}_6\) and \(\mathsf {Game}_7\). We also have to show that the distribution of \(\mathbf {c}_1\) is \(\mathsf {negl}(n)\)-close to the uniform distribution over \(\mathbb {Z}_q^{2m}\). To see this, it suffices to show that \(( \mathbf {v}_1^\top | \mathbf {v}_1^\top \mathbf {R}_{\mathsf {ID}^\star } )\) is distributed statistically close to uniform distribution over \(\mathbb {Z}_q^{2m}\). Observe that the following distributions are \(\mathsf {negl}(n)\)-close:
$$\begin{aligned} (\mathbf {A}, \mathbf {A}\mathbf {R}_0, \mathbf {v}_1^\top , \mathbf {v}_1^\top \mathbf {R}_0) \approx (\mathbf {A}, \mathbf {A}', \mathbf {v}_1^\top , {\mathbf {v}'_1}^\top ) \approx (\mathbf {A}, \mathbf {A}\mathbf {R}_0, \mathbf {v}_1^\top , {\mathbf {v}'_1}^\top ), \end{aligned}$$(12)where \(\mathbf {A}, \mathbf {A}' \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\), \(\mathbf {R}_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\{ -1, 1 \}^{m \times m}\), \(\mathbf {v}_1, \mathbf {v}'_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^m\). It can be seen that the first and the second distributions are \(\mathsf {negl}(n)\)-close, by applying Lemma 4 for \(( \mathbf {A}^\top | \mathbf {v})^\top \in \mathbb {Z}_{(n+1)\times m}\) and \(\mathbf {R}_0\). It can also be seen that the second and the third distributions are \(\mathsf {negl}(n)\)-close, by applying the same lemma for \(\mathbf {A}\) and \(\mathbf {R}_0\). From the above, we have that the following distributions are statistically close:
$$\begin{aligned}&(\mathbf {A}, \mathbf {A}\mathbf {R}_0, \mathbf {v}_1, \mathbf {v}_1^\top \mathbf {R}_\mathsf {ID}^\star )\\= & {} \left( \mathbf {A}, \mathbf {A}\mathbf {R}_0, \mathbf {v}_1, \mathbf {v}_1^\top \left( \mathbf {R}_0 + \sum _{\begin{array}{c} (j_1, \ldots , j_d)\\ \in S(\mathsf {ID}) \end{array}} \mathsf {TrapEval}(\mathbf {R}_{1,j_1},\ldots , \mathbf {R}_{d,j_d}, y_{1,j_1}, \ldots , y_{d,j_d}) \right) \right) \\\approx & {} \left( \mathbf {A}, \mathbf {A}\mathbf {R}_0, \mathbf {v}_1, {\mathbf {v}'_1}^\top + \mathbf {v}_1^\top \left( \sum _{\begin{array}{c} (j_1, \ldots , j_d)\\ \in S(\mathsf {ID}) \end{array}} \mathsf {TrapEval}(\mathbf {R}_{1,j_1},\ldots , \mathbf {R}_{d,j_d}, y_{1,j_1}, \ldots , y_{d,j_d}) \right) \right) \\\approx & {} (\mathbf {A}, \mathbf {A}\mathbf {R}_0, \mathbf {v}_1, {\mathbf {v}'_1}^\top ) \end{aligned}$$where \(\mathbf {A}, \mathbf {A}' \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n\times m}\), \(\mathbf {R}_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\{ -1, 1 \}^{m \times m}\), \(\mathbf {v}_1, \mathbf {v}'_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^m\). The second and the third distributions above are \(\mathsf {negl}(n)\)-close by Eq. (12). Therefore, we may conclude that \( | \Pr [X_6] - \Pr [X_7] | = \mathsf {negl}(n). \)
Analysis. From the above, we have
The third inequality above follows from \(c \ge \tilde{c}\). Since the challenge ciphertext is independent from the value of \(\mathsf {coin}\) in \(\mathsf {Game}_7\), we have \(\Pr [X_7]=1{\slash }2\) and thus \(| \Pr [X_7] - 1/2 |=0\). Therefore, from inequality (13), \( \epsilon /(Q+1) < 1/n^{\tilde{c}} + \mathsf {negl}(n) \) follows. However, this contradicts to Eq. (6).
To complete the proof of Theorem 3, it remains to show Lemmas 8 and 9.
Lemma 8
For any PPT adversary \(\mathcal {A}\), we have
Proof
For a sequence of identities \(\mathbb {ID}=(\mathsf {ID}^\star , \mathsf {ID}_1,\ldots , \mathsf {ID}_Q) \in \mathcal {ID}^{Q+1}\), we define \(\gamma (\mathbb {ID})\) as
where the probability is taken over \(\mathbf {y}=(y_0, \{ y_{i,j} \}_{(i,j)\in [d,\ell ]})\), which is chosen as specified in \(\mathsf {Game}_1\). To show the lemma, we first show the following claim, which gives an upper and lower bounds for \(\gamma (\mathbb {ID})\).
Claim
For any \(\mathbb {ID}= (\mathsf {ID}^\star , \mathsf {ID}_1,\ldots , \mathsf {ID}_Q)\) such that \(\mathsf {ID}^\star \ne \mathsf {ID}_i\) for all \(i\in [Q]\),
Proof
Showing the upper bound of the probability is very easy. For any \(\{ y_{i,j} \}\), there exists exactly one \(y_0 \in [-(\kappa +1) (dn^{\tilde{c}} )^d +1, 0 ]\) such that \(\mathsf {F}_\mathbf {y}(\mathsf {ID}^\star ) = 0\), since for any \(\{ y_{i,j} \}_{(i,j)\in [d] \times [\ell ]}\) and \(\mathsf {ID}\), we have
Therefore, we have
We then proceed to show the lower bound.
It suffices to show an upper bound for \(\Pr [\mathsf {F}_\mathbf {y}(\mathsf {ID}^\star )=0 \wedge \mathsf {F}_\mathbf {y}(\mathsf {ID}_i)= 0] \). For \(i \in [Q]\), we have

In the above, we defined \(\mathsf {F}'_\mathbf {y}(\mathsf {ID}^\star , \mathsf {ID}_i)\) as
The last equation in Eq. (15) follows since \(y_0\) is independent from \(\mathsf {F}'_\mathbf {y}(\mathsf {ID}^\star , \mathsf {ID}_i)\). (Observe that \(y_0\) does not appear in the definition of \(\mathsf {F}'_\mathbf {y}(\mathsf {ID}^\star , \mathsf {ID}_i)\).)
We then finally bound \(\Pr _\mathbf {y}[\mathsf {F}'_\mathbf {y}(\mathsf {ID}^\star , \mathsf {ID}_i)= 0]\). Since \(\mathsf {ID}^\star \ne \mathsf {ID}_i\) and S is an injective map, we have \(S(\mathsf {ID}^\star )\ne S(\mathsf {ID}_i)\). Therefore, there exists \((j^\star _1,\ldots , j^\star _d) \in [\ell ]^d\) such that \((j^\star _1,\ldots , j^\star _d) \in S(\mathsf {ID}^\star ) \bigtriangleup S(\mathsf {ID}_i)\), where \(S(\mathsf {ID}^\star ) \bigtriangleup S(\mathsf {ID}_i)\) denotes the symmetric difference of \(S(\mathsf {ID}^\star )\) and \(S(\mathsf {ID}_i)\). Thus, \(\mathsf {F}'_{\mathbf {y}}(\mathsf {ID}^\star , \mathsf {ID}_i)\) is not a zero-polynomial when we regard it as a polynomial in indeterminates \(\{ y_{j,k} \}_{(j,k) \in [d]\times [\ell ]}\). Since each \(y_{j,k}\) is uniformly random over \([1, dn^{\tilde{c}} ]\) and \(\mathsf {F}'_\mathbf {y}(\mathsf {ID}^\star , \mathsf {ID}_i)\) is a polynomial with degree d, by the Schwartz-Zippel lemma, it follows that
By combining this with Eqs. (14) and (15), the claim follows.
We then proceed to show a lower bound for \(| \Pr [X_1]-1/2 |\). For \(\mathbb {ID}= (\mathsf {ID}^\star , \mathsf {ID}_1, \ldots , \mathsf {ID}_Q)\) such that \(\mathsf {ID}^\star \ne \mathsf {ID}_i \) for all \(i\in [Q]\), we define \(\gamma _{\max }\) and \(\gamma _{\min }\) as the largest and the smallest value of \(\gamma (\mathbb {ID})\) taken over all such \(\mathbb {ID}\), respectively. We define \(\mathsf {Q}(\mathbb {ID})\) as the event that \(\mathcal {A}\) chooses \(\mathsf {ID}^\star \) as its challenge identity and it makes key extraction queries for \(\mathsf {ID}_1,\ldots , \mathsf {ID}_Q\). We also define \(\mathsf {Abort}\) as the event that the challenger aborts. Then, we have
In the third equation above, we used the fact \(\sum _{\mathbb {ID}}\Pr [\mathsf {Q}(\mathbb {ID})] = 1\). The fourth equation above follows from the fact that the probability of the abort is \(\gamma (\mathbb {ID})\), when conditioned on \(\mathsf {Q}(\mathbb {ID})\) (regardless of the value of \(\widehat{\mathsf {coin}}\)). The last inequality above follows by Lemma 5, since we have
and
We complete the proof of Lemma 8 by observing
The last inequality follows from \(\epsilon \le 1{\slash }2\).
Lemma 9
For any PPT adversary \(\mathcal {A}\), there exists another PPT adversary \(\mathcal {B}\) such that
In particular, under the \(\mathsf {dLWE}_{n,m+1,q,\chi }\) assumption, we have \(| \Pr [X_5] - \Pr [X_6] | = \mathsf {negl}(n)\).
Proof
Suppose an adversary \(\mathcal {A}\) that has non-negligible advantage in distinguishing \(\mathsf {Game}_5\) and \(\mathsf {Game}_6\). We use \(\mathcal {A}\) to construct an LWE algorithm denoted \(\mathcal {B}\), which proceeds as follows.
Instance. \(\mathcal {B}\) is given the problem instance of LWE \((\mathbf {A}', \mathbf {v}' ) \in \mathbb {Z}_q^{n\times (m+1)} \times \mathbb {Z}_q^{m+1}\). Let the first column of \(\mathbf {A}'\) be \(\mathbf {u}\in \mathbb {Z}_q^n\) and the last m column be \(\mathbf {A}\in \mathbb {Z}_q^{n\times m}\). It also sets the first coefficient of \(\mathbf {v}'\) be \(v_0\) and the last m coefficients be \(\mathbf {v}_1\).
Setup. To construct master public key \(\mathsf {mpk}\), \(\mathcal {B}\) first picks \(\mathbf {y}\) as in \(\mathsf {Game}_1\). It also picks \(\mathbf {R}_0, \mathbf {R}_{i,j} \overset{_{\tiny \text {\$}}}{\leftarrow }\{ -1, 1\}^{m\times m}\) and sets \(\mathbf {B}_0\) and \(\mathbf {B}_{i,j}\) as Eq. (8). Finally, it returns \(\mathsf {mpk}= (\mathbf {A}, \mathbf {B}_0, \{ \mathbf {B}_{i,j} \}_{(i,j)\in [d, \ell ] }, \mathbf {u})\) to \(\mathcal {A}\). \(\mathcal {B}\) also picks a random bit \(\mathsf {coin}\overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1\}\) and keeps it secret.
Phases 1 and 2. When \(\mathcal {A}\) makes a key extraction query for \(\mathsf {ID}\), \(\mathcal {B}\) first computes \(\mathsf {F}_\mathbf {y}(\mathsf {ID})\). It aborts and sets \(\mathsf {coin}'\overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1\}\) if \(\mathsf {F}_\mathbf {y}(\mathsf {ID})=0\). Otherwise, \(\mathcal {B}\) generates the private key as in \(\mathsf {Game}_5\).
Challenge Query. When \(\mathcal {A}\) makes the challenge query for the challenge identity \(\mathsf {ID}^\star \) and the message b, \(\mathcal {B}\) first computes \(\mathsf {F}_\mathbf {y}(\mathsf {ID}^\star )\). Then, it aborts and sets \(\mathsf {coin}' \overset{_{\tiny \text {\$}}}{\leftarrow }\{ 0,1\}\) if \(\mathsf {F}_\mathbf {y}(\mathsf {ID}^\star )\ne 0\). Otherwise, it proceeds as follows. If \(\mathsf {coin}= 0\), it computes \(\mathbf {R}_{\mathsf {ID}^\star }\) and picks \(\mathbf {x}_2 \overset{_{\tiny \text {\$}}}{\leftarrow }[-B', B']^m\). Then, it sets the challenge ciphertext as
and returns \(C^\star = (c_0,\mathbf {c}_1)\) to \(\mathcal {A}\). In the case of \(\mathsf {coin}=1 \), \(\mathcal {B}\) picks \(c_0 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q\), \(\mathbf {c}_1 \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{2m}\) and returns the challenge ciphertext \(C^\star = (c_0,\mathbf {c}_1)\) to \(\mathcal {A}\).
Guess. At last, \(\mathcal {A}\) outputs its guess \(\widehat{\mathsf {coin}}\) (if the abort condition has not been satisfied). Then, \(\mathcal {B}\) sets \(\mathsf {coin}' = \widehat{\mathsf {coin}}\). Finally, \(\mathcal {B}\) outputs 1 if \(\mathsf {coin}' = \mathsf {coin}\) and 0 otherwise.
Analysis. We now show that \(\mathcal {B}\) perfectly simulates the view of \(\mathcal {A}\) in \(\mathsf {Game}_5\) if \((\mathbf {A}', \mathbf {v}')\) is a valid LWE sample (i.e., \({\mathbf {v}'}^\top = \mathbf {s}^\top \mathbf {A}' + \mathbf {x}^\top \) for \(\mathbf {s}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n}\) and \(\mathbf {x}\overset{_{\tiny \text {\$}}}{\leftarrow }\chi ^{m+1}\)), and \(\mathsf {Game}_6\) if \(\mathbf {v}' \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{m+1}\). Note that these games differ only in the generation of the challenge ciphertext in the case of \(\mathsf {coin}= 0\). Furthermore, it is easy to see that the simulation of the master public key, Phases 1 and 2, and the challenge ciphertext for the case of \(\mathsf {coin}= 1\) are perfect. Therefore, in the following, we focus on the generation of the challenge ciphertext in the case of \(\mathsf {coin}= 0\).
We first show that if \((\mathbf {A}',\mathbf {v}')\) is a valid LWE sample, i.e., \({\mathbf {v}'}^\top = \mathbf {s}^\top \mathbf {A}' + \mathbf {x}^\top \) for \(\mathbf {s}\overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{n}\) and \(\mathbf {x}\overset{_{\tiny \text {\$}}}{\leftarrow }\chi ^{m+1}\), the distribution of the challenge ciphertext corresponds to that of \(\mathsf {Game}_5\). Let us denote \(\mathbf {x}^\top = (x_0, \mathbf {x}_1^\top )\) and assume that \( \mathsf {F}_{\mathbf {y}}(\mathsf {ID}^\star ) = 0\) holds. Then, we have
The last equation follows because \( \mathsf {F}_{\mathbf {y}}(\mathsf {ID}^\star ) = 0\). Therefore, the challenge ciphertext is distributed as in \(\mathsf {Game}_5\) in this case. It is easy to see that the challenge ciphertext is distributed as in \(\mathsf {Game}_6\), if \(\mathbf {v}' \overset{_{\tiny \text {\$}}}{\leftarrow }\mathbb {Z}_q^{m+1}\).
Therefore, we have \( \mathsf {Adv}^{\mathsf {dLWE}_{n,m+1,q,\chi }}_{\mathcal {B}} = | \Pr [ X_5 ] - \Pr [ X_6 ] | \) as desired.
5.5 Multi-bit Encryption
Here, we explain that our scheme can be extended to deal with multi-bit messages without much increasing the sizes of public parameters and ciphertexts, similarly to [1, 39]. To modify the scheme so that it can encrypt messages with N-bit, we replace \(\mathbf {u}\in \mathbb {Z}_q^n\) in \(\mathsf {mpk}\) with \(\mathbf {u}_1,\ldots , \mathbf {u}_N \in \mathbb {Z}_q^n\). The component \(c_0 = \langle \mathbf {u}, \mathbf {s}\rangle + x_{0} + b \lceil \frac{q}{2}\rceil \) in the ciphertext is replaced with \(\mathbf {c}_0 = \{ \langle \mathbf {u}_i, \mathbf {s}\rangle + x_{0,i} + b_i \lceil \frac{q}{2}\rceil \}^N_{i=1} \) where \(x_{0,i} \overset{_{\tiny \text {\$}}}{\leftarrow }\chi \) and \(b_i \in \{ 0,1\}\) is the i-th bit of the message. Furthermore, the private key is changed to be short vectors \(\mathbf {e}_1,\ldots , \mathbf {e}_{N} \in \mathbb {Z}^m\) such that \(( \mathbf {A}| \mathsf {H}(\mathsf {ID}) ) \mathbf {e}_i = \mathbf {u}_i\) for \(i=1,\ldots , N\). We can prove the security for the variant from \(\mathsf {dLWE}_{n,m+N,q,\chi }\) by naturally extending the proof of Theorem 3.
As for the efficiency, the size of the master public key and the ciphertexts become \(O( ( \ell m + N ) n \log q )\) and \(O( ( m + N)\log q )\) respectively, and these are asymptotically the same as the case of single-bit encryption when \( N < O(m) \). The case of \(N > O(m) \) can also be handled without increasing the size of parameters, by employing the KEM-DEM approach. Namely, we encrypt a random ephemeral key of sufficient length (e.g., O(n)) by IBE and then encrypt the message by the ephemeral key using a symmetric cipher.
6 Comparisons and Discussions
From the PIBE scheme in Sect. 5, we can obtain the following new IBE schemes:
-
By setting \(c = \omega (1)\), we obtain adaptively anonymous IBE by Theorem 1. However, we have to rely on super-polynomial LWE assumption, namely, \(\mathsf {dLWE}_{n,m,q,\chi }\) with \(q/\chi _{\max } = n^{\omega (1)}\).
-
By applying PIBE-to-IBE conversion in Sect. 4.2 to our PIBE in Sect. 5, we obtain (non-anonymous) adaptively secure IBE from polynomial LWE. More precisely, the security of the scheme can be proven under the assumption that \(\mathsf {dLWE}_{n,m,q,\chi }\) is hard for all \(q/\chi _{\max } = \mathsf {poly}(n)\).
For concreteness, we would set \(c(n)=O(\log \log n)\) in the first construction, and \(c(n)=\log \log n\) and \(\eta (n) = \log \log n\) for the second construction. Ignoring poly-logarithmic factors hidden in the asymptotic notation \(\tilde{O}(\cdot )\), both of our schemes achieve the best efficiency among existing adaptively secure IBE schemes. See Table 1 for the comparison. Comparing in more details, ciphertexts and private keys of both of our schemes are longer than [1, 12] by a super-constant factor. This is because we need to use super polynomially large q. On the other hand, in both of our schemes, the sizes of master public keys are asymptotically smaller than [1, 12], even though we have to use larger q. This is because we require smaller number of basic matrices in the master public keys. Our first scheme is more efficient than our second scheme by super-constant factors, because the conversion in Sect. 4.2 incurs super-constant efficiency loss. We also note that our security reduction is very loose even compared to non-tight reduction of [1, 12]. The security degrades exponentially as d grows. Therefore, in order to have polynomial reduction, we have to set d to be a (possibly small) constant.
In the table, we compare IBE schemes from the LWE assumption in the standard model. \(|\mathsf {mpk}|\), \(|C|\), and \(|\mathsf {sk}_\mathsf {ID}|\) show the size of the master public keys, ciphertexts, and private keys, respectively. \(\kappa \) denotes the length of the identity (which corresponds to the output length of the collision resistant hash if we first hash the bit string representing identity in the scheme). \(d\in \mathbb {N}\) is a flexible constant, which can be set to be any value. “Anon?” shows whether the scheme is anonymous. “Selective\({\slash }\)Adaptive” shows whether the scheme is selectively secure or adaptively secure. “\(q/\chi _{\max }\)” for LWE assumption refers to the ratio of the modulus to the error size of the underlying LWE assumption used in the security reduction. “Fixed \(\mathsf {poly}(n)\)” means that the corresponding scheme is proven secure under the LWE assumption with \(q/\chi _{\max }\) being some fixed polynomial (e.g., \(n^3\)). “All \(\mathsf {poly}(n)\)” mean that we have to assume the LWE assumption for all polynomial \(q/\chi _{\max }\).
Notes
- 1.
Note that we are abusing the notation here. \(\mathbf {G}^{-1}\) is not an inverse matrix of \(\mathbf {G}\), but a function.
- 2.
For the sake of simplicity, we present a scheme that is a special case of our scheme in Sect. 5. More generally, we can further reduce the number of basic matrices from \(O( \sqrt{\kappa })\) to be \(O( \kappa ^{1/d})\) for any constant \(d \in \mathbb {N}\).
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010)
Agrawal, S., Boneh, D., Boyen, X.: Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 98–115. Springer, Heidelberg (2010)
Ajtai, M.: Generating hard instances of the short basis problem. In: Wiedermann, J., Van Emde Boas, P., Nielsen, M. (eds.) ICALP 1999. LNCS, vol. 1644, pp. 1–9. Springer, Heidelberg (1999)
Alperin-Sheriff, J.: Short signatures with short public keys from homomorphic trapdoor functions. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 236–255. Springer, Heidelberg (2015)
Alwen, J., Peikert, C.: Generating shorter bases for hard random lattices. In: STACS, pp. 75–86 (2009)
Bellare, M., Ristenpart, T.: Simulation without the artificial abort: simplified proof and improved concrete security for waters’ IBE scheme. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 407–424. Springer, Heidelberg (2009)
Böhl, F., Hofheinz, D., Jager, T., Koch, J., Seo, J.H., Striecks, C.: Practical signatures from standard assumptions. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 461–485. Springer, Heidelberg (2013)
Boneh, D., Boyen, X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004)
Boneh, D., Boyen, X.: Secure identity based encryption without random oracles. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 443–459. Springer, Heidelberg (2004)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001)
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014)
Boyen, X.: Lattice mixing and vanishing trapdoors: a framework for fully secure short signatures and more. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 499–517. Springer, Heidelberg (2010)
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: STOC, pp. 575–584 (2013)
Brakerski, Z., Vaikuntanathan, V.: Lattice-based FHE as secure as PKE. In: ITCS, pp. 1–12 (2014)
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. In: EUROCRYPT, pp. 255–271 (2003)
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010)
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013)
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) IMA 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001)
Dodis, Y., Katz, J., Xu, S., Yung, M.: Key-insulated public key cryptosystems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 65–82. Springer, Heidelberg (2002)
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Döttling, N., Schröder, D.: Efficient pseudorandom functions via on-the-fly adaptation. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 329–350. Springer, Heidelberg (2015)
Ducas, L., Lyubashevsky, V., Prest, T.: Efficient identity-based encryption over NTRU lattices. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 22–41. Springer, Heidelberg (2014)
Ducas, L., Micciancio, D.: Improved short lattice signatures in the standard model. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 335–352. Springer, Heidelberg (2014)
Gentry, C.: Practical identity-based encryption without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 445–464. Springer, Heidelberg (2006)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC, pp. 197–206 (2008)
Goldwasser, S., Lewko, A., Wilson, D.A.: Bounded-collusion IBE from key homomorphism. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 564–581. Springer, Heidelberg (2012)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: STOC, pp. 545–554 (2013)
Gorbunov, S., Vinayagamurthy, D.: Riding on asymmetry: efficient ABE for branching programs. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 549–573. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_23
Heng, S.-H., Kurosawa, K.: k-resilient identity-based encryption in the standard model. In: Okamoto, T. (ed.) CT-RSA 2004. LNCS, vol. 2964, pp. 67–80. Springer, Heidelberg (2004)
Hohenberger, S., Waters, B.: Short and stateless signatures from the RSA assumption. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 654–670. Springer, Heidelberg (2009)
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013)
Lyubashevsky, V., Micciancio, D.: Asymptotically efficient lattice-based digital signatures. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 37–54. Springer, Heidelberg (2008)
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010)
Lyubashevsky, V., Peikert, C., Regev, O.: A toolkit for ring-LWE cryptography. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 35–54. Springer, Heidelberg (2013)
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012)
Naccache, D.: Secure and practical identity-based encryption. IET Inf. Secur. 1(2), 59–64 (2007)
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem: extended abstract. In: STOC, pp. 333–342 (2009)
Peikert, C.: A decade of lattice cryptography. IACR Cryptology ePrint Archive, Report 2015/939
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: STOC, pp. 843–873 (2005)
Sakai, R., Ohgishi, K., Kasahara, M.: Cryptosystems based on pairing over elliptic curve. In: The 2000 Symposium on Cryptography and Information Security (2000). (in Japanese)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakely, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985)
Shamir, A., Tauman, Y.: Improved online/offline signature schemes. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 355–367. Springer, Heidelberg (2001)
Singh, K., Pandurangan, C., Banerjee, A.K.: Adaptively secure efficient lattice (H)IBE in standard model with short public parameters. In: Bogdanov, A., Sanadhya, S. (eds.) SPACE 2012. LNCS, vol. 7644, pp. 153–172. Springer, Heidelberg (2012)
Stehlé, D., Steinfeld, R., Tanaka, K., Xagawa, K.: Efficient public key encryption based on ideal lattices. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 617–635. Springer, Heidelberg (2009)
Tessaro, S., Wilson, D.A.: Bounded-collusion identity-based encryption from semantically-secure public-key encryption: generic constructions with short ciphertexts. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 257–274. Springer, Heidelberg (2014)
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005)
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009)
Yamada, S., Hanaoka, G., Kunihiro, N.: Two-dimensional representation of cover free families and its applications: short signatures and more. In: Dunkelman, O. (ed.) CT-RSA 2012. LNCS, vol. 7178, pp. 260–277. Springer, Heidelberg (2012)
Yamada, S.: Adaptively Secure Identity-Based Encryption from Lattices with Asymptotically Shorter Public Parameters. Cryptology ePrint Archive, Report/140 (2016). http://eprint.iacr.org/2016/140
Acknowledgement
The author would like to thank all members of the study group “Shin-Akarui-Angou-Benkyou-Kai” for fruitful discussion. In particular, the author thanks Shuichi Katsumata for his comments on improving the presentation, Goichiro Hanaoka and Jacob. C.N. Schuldt for their helpful advice in the rebuttal phase. The author also thanks the anonymous reviewers of Eurocrypt 2016 for their insightful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Yamada, S. (2016). Adaptively Secure Identity-Based Encryption from Lattices with Asymptotically Shorter Public Parameters. In: Fischlin, M., Coron, JS. (eds) Advances in Cryptology – EUROCRYPT 2016. EUROCRYPT 2016. Lecture Notes in Computer Science(), vol 9666. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49896-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-662-49896-5_2
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49895-8
Online ISBN: 978-3-662-49896-5
eBook Packages: Computer ScienceComputer Science (R0)


 denotes
denotes 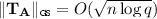 with all but negligible probability in n.
with all but negligible probability in n. , outputs a vector
, outputs a vector  outputs a vector
outputs a vector 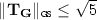 . Furthermore, there exists a deterministic polynomial-time algorithm
. Furthermore, there exists a deterministic polynomial-time algorithm  . It finally outputs
. It finally outputs