Multi-core Symbolic Bisimulation Minimisation

Abstract

Bisimulation minimisation alleviates the exponential growth of transition systems in model checking by computing the smallest system that has the same behavior as the original system according to some notion of equivalence. One popular strategy to compute a bisimulation minimisation is signature-based partition refinement. This can be performed symbolically using binary decision diagrams to allow models with larger state spaces to be minimised.

This paper studies strong and branching symbolic bisimulation for labeled transition systems, continuous-time markov chains, and interactive markov chains. We introduce the notion of partition refinement with partial signatures. We extend the parallel BDD library Sylvan to parallelize the signature refinement algorithm, and develop a new parallel BDD algorithm to refine a partition, which conserves previous block numbers and uses a parallel data structure to store block assignments. We also present a specialized BDD algorithm for the computation of inert transitions. The experimental evaluation, based on benchmarks from the literature, demonstrates a speedup of up to 95x sequentially. In addition, we find parallel speedups of up to 17x due to parallelisation with 48 cores. Finally, we present the implementation of these algorithms as a versatile tool that can be customized for bisimulation minimisation in various contexts.

The first author is supported by the NWO project MaDriD, grant nr. 612.001.101.

1 Introduction

One core challenge in model checking is the state space explosion problem. The space and time requirements of model checking increase exponentially with the size of the models. Bisimulation minimisation computes the smallest equivalent model (maximal bisimulation) under some notion of equivalence, which can significantly reduce the number of states. This technique is also used to abstract models from internal behavior, when only observable behavior is relevant.

The maximal bisimulation of a model is typically computed using partition refinement. Starting with an initially coarse partition (e.g. all states are equivalent), the partition is refined until states in each equivalence class can no longer be distinguished. The result is the maximal bisimulation with respect to the initial partition. Blom et al. [3] introduced a signature-based method for partition refinement, which assigns states to equivalence classes according to a characterizing signature. This method easily extends to various types of bisimulation.

Another well-known method to deal with very large state spaces is symbolic model checking, where sets of states are represented by their characteristic function, which is efficiently stored using binary decision diagrams (BDDs). In the literature, symbolic methods have been applied to bisimulation minimisation in several ways. Bouali and De Simone [5] refine the equivalence relation $R\subseteq S\times S$, by iteratively removing all “bad” pairs from R, i.e., pairs of states that are no longer equivalent. For strong bisimulation, Mumme and Ciardo [19] apply saturation-based methods to compute R. Wimmer et al. [25, 26] use signatures to refine the partition, represented by the assignment to equivalence classes $P:S\rightarrow C$. Symbolic bisimulation based on signatures has also been applied to Markov chains by Derisavi [11] and Wimmer et al. [23, 24].

The symbolic representation of the maximal bisimulation, when effective, often tends to be much larger than the original model. One particular application of symbolic bisimulation minimisation is as a bridge between symbolical models and explicit-state analysis algorithms. Such models can have very large state spaces that are efficiently encoded using BDDs. If the minimised model is sufficiently small, then it can be analyzed efficiently using explicit-state algorithms.

These techniques mainly reduce the memory requirements of model checking. To take advantage of computer systems with multiple processors, developing scalable parallel algorithms is the way forward. In [12, 14], we implemented the multi-core BDD package Sylvan, applying parallelism to symbolic model checking. Parallelization has also been applied to explicit-state bisimulation minimisation. Blom et al. [2, 3] introduced a parallel, signature-based algorithm for various types of bisimulation, especially strong and branching bisimulation. Also, [17] proposed a concurrent algorithm for bisimulation minimisation which combines signatures with the approach by Paige and Tarjan [20]. Recently, Wijs [22] implemented highly parallel strong and branching bisimilarity checking on GPGPUs. As far as we are aware, no earlier work combines symbolic bisimulation minimisation and parallelism.

In the current paper, we study bisimulation minimisation for labeled transition systems (LTSs), continuous-time Markov chains (CTMCs) and interactive Markov chains (IMCs), which combines the features of LTSs and CTMCs. These allow the analysis of quantitative properties, e.g. performance and dependability.

We concentrate on strong bisimulation and branching bisimulation. Strong bisimulation preserves both internal behavior ($\tau$-transitions) and observable behavior, while branching bisimulation abstracts from internal behavior. The advantage of branching bisimulation compared to other variations of weak bisimulation is that it preserves the branching structure of the LTS, thus preserving certain interesting properties such as CTL* without next-state operator [9].

The current paper contains the following contributions. We introduce the notion of partition refinement with partial signatures in Sect. 3. Section 4 discusses how we extend the multi-core BDD package Sylvan to parallelize signature-based partition refinement. In particular, we develop two specialized BDD algorithms. We implement a new refine algorithm, that refines a partition according to a signature, but maximally reuses the block number assignment of the previous partition (Sect. 4.3). This algorithm improves the operation cache use for the computation of the signatures of stable blocks, and enables partition refinement with partial signatures. We also present the inert algorithm, which, given a transition relation and a partition, removes all transitions that are not inert (Sect. 4.4). This algorithm avoids an expensive intermediate result reported in the literature [26]. Section 5 discusses experimental data based on benchmarks from the literature to demonstrate a speedup of up to 95x sequentially. In addition, we find parallel speedups of up to 17x due to parallelisation with 48 cores. Finally, we present the implementation of these algorithms as a versatile tool that can be customized for bisimulation minimisation in various contexts.

2 Preliminaries

We recall the basic definitions of partitions, of LTSs, of CTMCs, of IMCs, and of various bisimulations as in [3, 15, 25–27].

Definition 1

Given a set S, a partition $\pi$ of S is a subset $\pi \subseteq 2^S$ such that

$$\bigcup _{C\in \pi } C=S \qquad \text {and}\qquad \forall C,C'\in \pi :(C=C'\vee C\cap C'=\emptyset ).$$

If $\pi '$ and $\pi$ are two partitions, then $\pi '$ is a refinement of $\pi$, written $\pi '\sqsubseteq \pi$, if each block of $\pi '$ is contained in a block of $\pi$. The elements of $\pi$ are called equivalence classes or blocks. Each equivalence relation $\equiv$ is associated with a partition $\pi =S/\!\equiv$. In this paper, we use $\pi$ and $\equiv$ interchangeably.

Definition 2

A labeled transition system (LTS) is a tuple $(S,\textsf {Act},\rightarrow )$, consisting of a set of states S, a set of labels $\textsf {Act}$ that may contain the non-observable action $\tau$, and transitions $\rightarrow \,\subseteq S\times \textsf {Act}\times S$.

We write $s\overset{a}{\rightarrow }t$ for $(s,a,t)\!\in \,\rightarrow$. and $s\!\mathop {\nrightarrow }\limits ^{\tau }$ when s has no outgoing $\tau$-transitions. We use $\overset{a*}{\rightarrow }$ to denote the transitive reflexive closure of $\overset{a}{\rightarrow }$. Given an equivalence relation $\equiv$, we write for $\overset{a}{\rightarrow }\!\cap \!\equiv$, i.e., transitions between equivalent states, called inert transitions. We use for the transitive reflexive closure of .

Definition 3

A continuous-time Markov chain (CTMC) is a tuple $(S,\Rightarrow )$, consisting of a set of states S and Markovian transitions $\Rightarrow \,\subseteq S\times \mathbb {R}^{> 0}\times S$.

We write $s\overset{\lambda }{\Rightarrow }t$ for $(s,\lambda ,t)\!\in \,\Rightarrow$. The interpretation of $s\overset{\lambda }{\Rightarrow }t$ is that the CTMC can switch from s to t within d time units with probability $1\!-\!e^{-\lambda \cdot d}$. For a state s, let $\mathbf R (s)(s')=\sum \{\lambda \mid s\overset{\lambda }{\Rightarrow }s'\}$ be the rate to move from state s to state $s'$, and let $\mathbf R (s)(C)=\sum _{s'\in C} \mathbf R (s)(s')$ be the cumulative rate to reach a set of states $C\subseteq S$ from state s.

Definition 4

An interactive Markov chain (IMC) is a tuple ($S,\textsf {Act},\rightarrow ,\Rightarrow )$, consisting of a set of states S, a set of labels $\textsf {Act}$ that may contain the non-observable action $\tau$, transitions $\rightarrow \,\subseteq S\times \textsf {Act}\times S$, and Markovian transitions $\Rightarrow \,\subseteq S\times \mathbb {R}^{> 0}\times S$.

An IMC basically combines the features of an LTS and a CTMC. One feature of IMCs is the maximal progress assumption. Internal interactive transitions, i.e. $\tau$-transitions, can be assumed to take place immediately, while the probability that a Markovian transition executes immediately is zero. Therefore, we may remove all Markovian transitions from states that have outgoing $\tau$-transitions: $s\mathop {\rightarrow }\limits ^{\tau }$ implies $\mathbf R (s)(S)=0$. We call IMCs to which this operation has been applied maximal-progress-cut (mp-cut) IMCs.

For LTSs, strong and branching bisimulation are typically defined as follows [26]:

Definition 5

An equivalence relation $\equiv _{S}$ is a strong bisimulation on an LTS if for all states $s,t,s'$ with $s\equiv _{S}t$ and for all $s\overset{a}{\rightarrow }s'$, there exists a state $t'$ with $t\overset{a}{\rightarrow }t'$ and $s'\equiv _{S}t'$.

Definition 6

An equivalence relation $\equiv _{B}$ is a branching bisimulation on an LTS if for all states $s,t,s'$ with $s\equiv _{B}t$ and for all $s\overset{a}{\rightarrow }s'$, either

• $a=\tau$ and $s'\equiv _{B}t$, or

• there exist states $t',t''$ with $t\overset{\tau *}{\rightarrow }t'\overset{a}{\rightarrow }t''$ and $t\equiv _{B}t'$ and $s'\equiv _{B}t''$.

For CTMCs, strong bisimulation is defined as follows [11, 23]:

Definition 7

An equivalence relation $\equiv _{S}$ is a strong bisimulation on a CTMC if for all $(s,t)\in \;\equiv _{S}$ and for all classes $C\in S/\!\equiv _{S}$, $\mathbf R (s)(C)=\mathbf R (t)(C)$.

For mp-cut IMCs, strong and branching bisimulation are defined as follows [15, 27]:

Definition 8

An equivalence relation $\equiv _{S}$ is a strong bisimulation on an mp-cut IMC if for all $(s,t)\in \equiv _{S}$ and for all classes $C\in S/\!\equiv _{S}$

• $s\overset{a}{\rightarrow }s'$ for some $s'\in C$ implies $t\overset{a}{\rightarrow }t'$ for some $t'\in C$

• $\mathbf R (s)(C)=\mathbf R (t)(C)$

Definition 9

An equivalence relation $\equiv _{B}$ is a branching bisimulation on an mp-cut IMC if for all $(s,t)\in \equiv _{B}$ and for all classes $C\in S/\!\equiv _{B}$

• $s\overset{a}{\rightarrow }s'$ for some $s'\in C$ implies

  • $a=\tau$ and $(s,s')\in \,\equiv _{B}$, or

  • there exist states $t',t''\in S$ with $t \overset{\tau *}{\rightarrow } t'\overset{a}{\rightarrow }t''$ and $(t,t')\in \,\equiv _{B}$ and $t''\in C$.

• $\mathbf R (s)(C)>0$ implies

  • $\mathbf R (s)(C)=\mathbf R (t')(C)$ for some $t'\in S$ such that $t \overset{\tau *}{\rightarrow } t'\!\mathop {\nrightarrow }\limits ^{\tau }$ and $(t,t')\in \,\equiv _{B}$.

• $s\!\mathop {\nrightarrow }\limits ^{\tau }$ implies $t\overset{\tau *}{\rightarrow } t'\!\mathop {\nrightarrow }\limits ^{\tau }$ for some $t'$

3 Signature-Based Bisimulation

Blom and Orzan [3] introduced a signature-based approach to compute the maximal bisimulation of an LTS, which was further developed into a symbolic method by Wimmer et al. [26]. Each state is characterized by a signature, which is the same for all equivalent states in a bisimulation. These signatures are used to refine a partition of the state space until a fixed point is reached, which is the maximal bisimulation.

In the literature, multiple signatures are sometimes used that together fully characterize states, for example based on the state labels, based on the rates of continuous-time transitions, and based on the enabled interactive transitions. In the current paper, these multiple signatures are considered elements of a single signature that fully characterizes each state.

Definition 10

A signature $\sigma (\pi )(s)$ is a tuple of functions $f_i(\pi )(s)$, that together characterize each state s with respect to a partition $\pi$.

Two signatures $\sigma (\pi )(s)$ and $\sigma (\pi )(t)$ are equivalent, if and only if for all $f_i$, $f_i(\pi )(s)=f_i(\pi )(t)$.

The signatures of five bisimulations from Sect. 2 are known from the literature. For all actions $a\in \textsf {Act}$ and equivalence classes $C\in \pi$, we define

• $\mathbf T ({\pi })(s)=\{(a,C)\mid \exists s'\in C:s\overset{a}{\rightarrow }s'\}$

• 

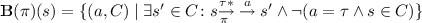
• $\mathbf R ^s({\pi })(s)=C\mapsto \mathbf R (s)(C)$

• 

The five bisimulations are associated with the following signatures:

Strong bisimulation for an LTS	(T)	[26]
Branching bisimulation for an LTS	(B)	[26]
Strong bisimulation for a CTMC	(R $^s$)	[23]
Strong bisimulation for an mp-cut IMC	(T, R $^s$)	[27]
Branching bisimulation for an mp-cut IMC		[27]

Functions $\mathbf T$ and $\mathbf B$ assign to each state s all actions a and equivalence classes $C\in \pi$, such that state s can reach C by an action a either directly ($\mathbf T$) or via any number of inert $\tau$-steps ($\mathbf B$). $\mathbf R ^s$ equals $\mathbf R$ but with the domain restricted to the equivalence classes $C\in \pi$, and represents the cumulative rate with which state s can go to states in C. $\mathbf R ^b$ equals $\mathbf R ^s$ for states $s\!\mathop {\nrightarrow }\limits ^{\tau }$, and takes the highest “reachable rate” for states with inert $\tau$-transitions. In branching bisimulation for mp-cut IMCs, the “highest reachable rate” is by definition the rate that all states ${s\!\overset{\tau }{\nrightarrow }}$ in C have. The element distinguishes time-convergent states from time-divergent states [27], and is independent of the partition.

For the bisimulations of Definitions 5–9, we state:

Lemma 1

A partition $\pi$ is a bisimulation, if and only if for all s and t that are equivalent in $\pi$, $\sigma (\pi )(s)=\sigma (\pi )(t)$.

For the above definitions it is fairly straightforward to prove that they are equivalent to the classical definitions of bisimulation. See e.g. [3, 26] for the bisimulations on LTSs and [27] for the bisimulations on IMCs.

3.1 Partition Refinement

The definition of signature-based partition refinement is as follows.

Definition 11

(Partition refinement with full signatures)

$$\begin{aligned} {{\mathrm{sigref}}}(\pi ,\sigma )&{\,}{:}{=}\, \{\{t\in S\mid \sigma (\pi )(s) = \sigma (\pi )(t)\}\mid s\in S\} \\ \pi ^0&{\,}{:}{=}\, \{S\} \\ \pi ^{n+1}&{\,}{:}{=}\, {{\mathrm{sigref}}}(\pi ^n, \sigma ) \\ \end{aligned}$$

The algorithm iteratively refines the initial coarsest partition $\{S\}$ according to the signatures of the states, until some fixed point $\pi ^{n+1}=\pi ^{n}$ is obtained. This fixed point is the maximal bisimulation for “monotone signatures”:

Definition 12

A signature is monotone if for all $\pi ,\pi '$ with $\pi \sqsubseteq \pi '$, whenever $\sigma (\pi )(s)=\sigma (\pi )(t)$, also $\sigma (\pi ')(s)=\sigma (\pi ')(t)$.

For all monotone signatures, the ${{\mathrm{sigref}}}$ operator is monotone: $\pi \sqsubseteq \pi '$ implies ${{\mathrm{sigref}}}(\pi ,\sigma )\sqsubseteq {{\mathrm{sigref}}}(\pi ',\sigma )$. Hence, following Kleene’s fixed point theorem, the procedure above reaches the greatest fixed point.

In Definition 11, the full signature is computed in every iteration. We propose to apply partition refinement using parts of the signature. By definition, $\sigma (\pi )(s)=\sigma (\pi )(t)$ if and only if for all parts $f_i(\pi )(s)=f_i(\pi )(t)$.

Definition 13

(Partition refinement with partial signatures)

$$\begin{aligned} {{\mathrm{sigref}}}(\pi ,f_i) {\,}{:}{=}\,&\{\{t\in S\mid f_i(\pi )(s) = f_i(\pi )(t) \wedge s \equiv _{\pi } t \}\mid s\in S\} \\ \pi ^0 {\,}{:}{=}\,&\{S\} \\ \pi ^{n+1} {\,}{:}{=}\,&{{\mathrm{sigref}}}(\pi ^n, f_i) \qquad ( \mathrm {select}\,\,\,f_i\in \sigma )\\ \end{aligned}$$

We always select some $f_i$ that refines the partition $\pi$. A fixed point is reached only when no $f_i$ refines the partition further: $\forall f_i\in \sigma :{{\mathrm{sigref}}}(\pi ^n, f_i)=\pi ^n$. The extra clause $s \equiv _{\pi } t$ ensures that every application of ${{\mathrm{sigref}}}$ refines the partition.

Theorem 1

If all parts $f_i$ are monotone, Definition 13 yields the greatest fixed point.

Proof

The procedure terminates since the chain is decreasing ($\pi ^{n+1}\sqsubseteq \pi ^n$), due to the added clause $s \equiv _{\pi } t$. We reach some fixed point $\pi ^n$, since $\forall f_i\in \sigma :{{\mathrm{sigref}}}(\pi ^n, f_i)=\pi ^n$ implies ${{\mathrm{sigref}}}(\pi ^n, \sigma )=\pi ^n$. Finally, to prove that we get the greatest fixed point, assume there exists another fixed point $\xi ={{\mathrm{sigref}}}(\xi ,\sigma )$. Then also $\xi ={{\mathrm{sigref}}}(\xi ,f_i)$ for all i. We prove that $\xi \sqsubseteq \pi ^n$ by induction on n. Initially, $\xi \sqsubseteq {S}=\pi ^0$. Assume $\xi \sqsubseteq \pi ^n$, then for the selected i, $\xi ={{\mathrm{sigref}}}(\xi ,f_i)\sqsubseteq {{\mathrm{sigref}}}(\pi ^n,f_i)=\pi ^{n+1}$, using monotonicity of $f_i$. $\square$

There are several advantages to this approach due to its flexibility. First, for any $f_i$ that is independent of the partition, refinement with respect to that $f_i$ only needs to be applied once. Furthermore, refinements can be applied according to different strategies. For instance, for the strong bisimulation of an mp-cut IMC, one could refine w.r.t. $\mathbf T$ until there is no more refinement, then w.r.t. $\mathbf R ^s$ until there is no more refinement, then repeat until neither $\mathbf T$ nor $\mathbf R ^s$ refines the partition. Finally, computing the full signature is the most memory-intensive operation in symbolic signature-based partition refinement. If the partial signatures are smaller than the full signature, then larger models can be minimised.

4 Symbolic Signature Refinement

This section describes the parallel decision diagram library Sylvan, followed by the (MT)BDDs and (MT)BDD operations required for signature-based partition refinement. We describe how we encode partitions and signatures for signature-based partition refinement. We present a new parallelized refine function that maximally reuses block numbers from the old partition. Finally, we present a new BDD algorithm that computes inert transitions, i.e., restricts a transition relation such that states s and $s'$ are in the same block.

4.1 Decision Diagram Algorithms in Sylvan

In symbolic model checking [7], sets of states and transitions are represented by their characteristic function, rather than stored individually. With states described by N Boolean variables, a set $S\subseteq \mathbb {B}^N$ can be represented by its characteristic function $f:\mathbb {B}^N\rightarrow \mathbb {B}$, where $S=\{s\mid f(s)\}$. Binary decision diagrams (BDDs) are a concise and canonical representation of Boolean functions [6].

An (ordered) BDD is a directed acyclic graph with leaves 0 and 1. Each internal node has a variable label $x_i$ and two outgoing edges labeled 0 and 1. Variables are encountered along each path according to a fixed variable ordering. Duplicate nodes and nodes with two identical outgoing edges are forbidden. It is well known that for a fixed variable ordering, every Boolean function is represented by a unique BDD.

In addition to BDDs with leaves 0 and 1, multi-terminal binary decision diagrams have been proposed [1, 8] with leaves other than 0 and 1, representing functions from the Boolean space $\mathbb {B}^N$ onto any finite set. For example, MTBDDs can have leaves representing integers (encoding $\mathbb {B}^N\rightarrow \mathbb {N}$), floating-point numbers (encoding $\mathbb {B}^N\rightarrow \mathbb {R}$) and rational numbers (encoding $\mathbb {B}^N\rightarrow \mathbb {Q}$). Partial functions are supported using a terminal leaf $\bot$.

Sylvan [12, 14] implements parallelized operations on decision diagrams using parallel data structures and work-stealing. Work-stealing [4, 13] is a load balancing method for task-based parallelism. Recursive operations, such as most BDD operations, implicitly form a tree of tasks. Independent subtasks are stored in queues and idle processors steal tasks from the queues of busy processors.

Algorithm 1 describes the implementation of a generic binary operation $\textsf {F}$. BDD operations mainly consist of consulting an operation cache, performing some recursive step, and creating new BDD nodes using a unique table. The operation cache is required to reduce the time complexity of BDD operations from exponential to polynomial in the size of the BDDs. Sylvan uses a single shared unique table for all BDD nodes and a single shared operation cache for all operations. To obtain high performance in a multi-core environment, the datastructures for the BDD nodes and the operation cache must be highly scalable. Sylvan implements several non-blocking datastructures to enable good speedups [14].

To compute symbolic signature-based partition refinement, several basic operations must be supported by the BDD package (see also [26]). Sylvan implements basic operations such as $\wedge$ and if-then-else, and existential quantification $\exists$. Negation $\lnot$ is performed in constant time using complement edges. To compute relational products of transition systems, there are operations relnext (to compute successors) and relprev (to compute predecessors and to concatenate relations), which combine the relational product with variable renaming. Similar operations are also implemented for MTBDDs. Sylvan is designed to support custom BDD algorithms. We present two new algorithms below.

4.2 Encoding of Signature Refinement

We implement symbolic signature refinement similar to [26]. Unlike [26], we do not refine the partition with respect to a single block, but with respect to all blocks simultaneously. We use a binary encoding with variables s for the current state, $s'$ for the next state, a for the action labels and b for the blocks. We order BDD variables a and b after s and $s'$, since this is required to efficiently replace signatures (a, b) by new block numbers b (see below). Variables s and $s'$ are interleaved, which is common in the context of transition systems.

Fig. 1.

Schematic overview of the BDDs in signature refinement

To perform symbolic bisimulation we represent a number of sets by their characteristic functions. See also Fig. 1.

• A set of states is represented by a BDD $\mathcal {S}(s)$;

• Transitions are represented by a BDD $\mathcal {T}(s,s',a)$;

• Markovian transitions are represented by an MTBDD $\mathcal {R}(s,s')$, with leaves containing rational numbers ($\mathbb {Q}$);

• Signatures $\mathbf T$ and $\mathbf B$ are represented by a BDD $\sigma _T(s,a,b)$;

• Signatures $\mathbf R ^s$ and $\mathbf R ^b$ are represented by an MTBDD $\sigma _R(s,b)$.

In the literature, three methods have been proposed to represent $\pi$.

• 1. As an equivalence relation, using a BDD $\mathcal {E}(s,s')=1$ iff $s\equiv _{\pi } s'$ [5, 19].

• 2. As a partition, by assigning each block a unique number, encoded with variables b, using a BDD $\mathcal {P}(s,b)=1$ iff $s\in C_b$ [11, 26, 27].

• 3. Using $k={\lceil }\log _2 n{\rceil }$ BDDs $\mathcal {P}_{0},\cdots ,\mathcal {P}_{k-1}$ such that $\mathcal {P}_i(s)=1$ iff $s\in C_b$ and the $i^\text {th}$ bit of b is 1. This requires significant time to restore blocks for the refinement procedure, but can require less memory [10].

We choose to use method 2, since in practice the BDD of $\mathcal {P}(s,b)$ is smaller than the BDD of $\mathcal {E}(s,s')$. Using $\mathcal {P}(s,b)$ also has the advantage of straight-forward signature computation. The logarithmic representation is incompatible with our approach, since we refine all blocks simultaneously. Their approach involves restoring individual blocks to the $\mathcal {P}(s,b)$ representation, performing a refinement step, and compacting the result to the logarithmic representation. Restoring all blocks simply computes the full $\mathcal {P}(s,b)$.

We represent Markovian transitions using rational numbers, since they offer better precision than floating-point numbers. The manipulation of floating-point numbers typically introduces tiny rounding errors, resulting in different results of similar computations. This significantly affects bisimulation reduction, often resulting in finer partitions than the maximal bisimulation [23].

4.3 The refine Algorithm

In this section, we present a new BDD algorithm to refine partitions according to a signature, which maximally preserves previously assigned block numbers.

Partition refinement consists of two steps: computing the signatures and computing the next partition. Given the signatures $\sigma _T$ and/or $\sigma _R$ for the current partition $\pi$, the new partition can be computed as follows.

Since the chosen variable ordering has variables $s,s'$ before a, b, each path in $\sigma$ ends in a (MT)BDD representing the signature for the states encoded by that path. For $\sigma _T$, every path that assigns values to s ends in a BDD on a, b. For $\sigma _R$, every path that assigns values to s ends in a MTBDD on b with rational leaves.

Wimmer et al. [26] present a BDD operation refine that “replaces” these sub-(MT)BDDs by the BDD representing a unique block number for each distinct signature. The result is the BDD of the next partition. They use a global counter and a hash table to associate each signature with a unique block number. This algorithm has the disadvantage that block number assignments are unstable. There is no guarantee that a stable block has the same block number in the next iteration. This has implications for the computation of the new signatures. When the block number of a stable block changes, cached results of signature computation in earlier iterations cannot be reused.

We modify the refine algorithm to use the current partition to reuse the previous block number of each state. This also allows refining a partition with respect to only a part of the signature, as described in Sect. 3. The modification is applied such that it can be parallelized in Sylvan. See Algorithm 2.

The algorithm has two input parameters: the (MT)BDD $\sigma$ which encodes the (partial) signature for the current partition, and the BDD $\mathcal {P}$ which encodes the current partition. The algorithm uses a global counter $\textsf {iter}$, which is the current iteration of partition refinement. This is necessary since the cached results of the previous iteration cannot be reused. It also uses and updates an array blocks, which contains the signature of each block in the new partition. This array is cleared between iterations of partition refinement.

The implementation is similar to other BDD operations, featuring the use of the operation cache (lines 2 and 15) and a recursion step for variables in s (lines 3–7), with the two recursive operations executed in parallel. refine simultaneously descends in $\sigma$ and $\mathcal {P}$ (lines 5–6), matching the valuation of $s_i$ in $\sigma$ and $\mathcal {P}$. Block assignment happens at lines 9–14. We rely on the well-known atomic operation compare_and_swap (cas), which atomically compares and modifies a value in memory. This is necessary so the algorithm is still correct when parallelized. We use cas to claim a block number for the signature (line 10). If the block number is already used for a different signature, then this block is being refined and we call a method search_or_insert to assign a new block number.

Different implementations of search_and_insert are possible. We implemented a parallel hash table that uses a global counter for the next block number when inserting a new pair $(\sigma , B)$, similar to [26]. An alternative implementation that performed better in our experiments integrates the blocks array with a skip list. A skip list is a probabilistic multi-level ordered linked list. See [21].

4.4 Computing Inert Transitions

To compute the set of inert $\tau$-transitions for branching bisimulation, i.e., , or more generally, to compute any inert transition relation $\rightarrow \!\cap \!\equiv$ where $\equiv$ is the equivalence relation corresponding to $\pi$ computed by $\mathcal {E}(s,s')=\exists b:\mathcal {P}(s,b) \wedge \mathcal {P}(s',b)$, the expression $\mathcal {T}(s,s') \wedge \exists b:\mathcal {P}(s,b) \wedge \mathcal {P}(s',b)$ must be computed. [26] writes that the intermediate BDD of $\exists b:\mathcal {P}(s,b) \wedge \mathcal {P}(s',b)$, obtained by first computing $\mathcal {P}(s',b)$ using variable renaming from $\mathcal {P}(s,b)$ and then $\exists b:\mathcal {P}(s,b) \wedge \mathcal {P}(s',b)$ using and_exists, is very large. This makes sense, since this intermediate result is indeed the BDD $\mathcal {E}(s,s')$, which we were avoiding by representing the partition using $\mathcal {P}(s,b)$.

The solution in [26] was to avoid computing $\mathcal {E}$ by computing the signatures and the refinement only with respect to one block at a time, which also enables several optimizations in [25].

Fig. 2.

Schematic overview of the BDDs in the inert algorithm

We present an alternative solution, which computes $\rightarrow \!\cap \!\equiv$ directly using a custom BDD algorithm. The inert algorithm takes parameters $\mathcal {T}(s,s')$ ($\mathcal {T}$ may contain other variables ordered after $s,s'$) and two copies of $\mathcal {P}(s,b)$: $\mathcal {P}^s$ and $\mathcal {P}^{s'}$. The algorithm matches $\mathcal {T}$ and $\mathcal {P}^s$ on valuations of variables s, and $\mathcal {T}$ and $\mathcal {P}^{s'}$ on valuations of variables $s'$. See Algorithm 3, and also Fig. 2 for a schematic overview. When in the recursive call all valuations to s and $s'$ have been matched, with $S_s,S_{s'}\subseteq S$ the sets of states represented by these valuations, then $\mathcal {T}$ is the set of actions that label the transitions between states in $S_s$ and $S_{s'}$, $\mathcal {P}^s$ is the block that contains all $S_s$ and $\mathcal {P}^{s'}$ is the block that contains all $S_{s'}$. Then if $\mathcal {P}^s\ne \mathcal {P}^{s'}$, the transitions are not inert and inert returns False, removing the transition from $\mathcal {T}$. Otherwise, $\mathcal {T}$ (which may still contain other variables ordered after $s,s'$, such as action labels), is returned.

5 Experimental Evaluation

5.1 Tool Support

We implemented multi-core signature-based partition refinement in a tool called SigrefMC, using the (MT)BDD-package Sylvan [12, 14]. The tool computes the same bisimulations as the original Sigref tool. SigrefMC LTSs, CTMCs and IMCs delivered in two input formats, the XML format used by the original Sigref tool, and the BDD format that the tool LTSmin [16] generates for various model checking languages. SigrefMC supports both the floating-point and the rational representation of rates in continuous-time transitions.

One of the design goals of this tool is to encourage researchers to extend it for their own file formats and notions of bisimulation, and to integrate it in other toolsets. Therefore, SigrefMC is freely available online¹ and licensed with the MIT license. Documentation is available and instructions for extending the tool for different input/output formats and types of bisimulation are included.

Table 1. Results for the benchmark experiments. Each data point is an average of at least 15 runs. The timeout was 3600 s.

5.2 Experiments

To study the improvements presented in the current paper, we compared our results (using the skip list variant of refine) to Sigref 1.5 [25] for LTS and IMC models, and to a version of Sigref used in [23] for CTMC models. For the CTMC models, we used Sigref with rational numbers provided by the GMP library and SigrefMC with rational number support by Sylvan. For the IMC models, version 1.5 of Sigref does not support the GMP library and the version used in [23] does not support IMCs. We used SigrefMC with floating points for a fairer comparison, but the tools give a slightly different number of blocks.

In the current paper, we restrict ourselves to the models presented in [23, 26] and an IMC model that is part of the distribution of Sigref. These models have been generated from PRISM benchmarks using a custom version of the PRISM toolset [18]. We refer to the literature for a description of these models.

We perform experiments on the three tools using the same 48-core machine, containing 4 AMD Opteron^TM 6168 processors with 12 cores each. We measure the runtimes for partition refinement using Sigref, SigrefMC with only 1 worker, and SigrefMC with 48 workers.

Note that apart from the new refine and inert algorithms presented in the current paper, there are several other differences. The first is that the original Sigref uses the CUDD implementation of BDDs, while SigrefMC obviously uses Sylvan, along with some extra BDD algorithms that avoid explicitly computing variable renaming of some BDDs. The second is that Sigref has several optimizations [25] that are not available in SigrefMC.

5.3 Results

See Table 1 for the results of these experiments. These results were obtained by repeating each benchmark at least 15 times and taking the average. The timeout was set to 3600 s. The column “States” shows the number of states before bisimulation minimisation, and “Blocks” the number of equivalence classes after bisimulation minimisation. We show the wallclock time using Sigref ($T_w$), using SigrefMC with 1 worker ($T_1$) and using SigrefMC with 48 workers ($T_{48}$). We compute the sequential speedup $T_w/T_1$, the parallel speedup $T_1/T_{48}$ and the total speedup $T_w/T_{48}$.

Fig. 3.

Time per iteration for Sigref and SigrefMC (1 worker), and the number of new blocks per iteration for strong bisimulation of the kanban04 LTS model.

Due to space constraints, we do not include all results, but restrict ourselves to larger models. We refer to the full experimental data that is available online². In the full set of results, excluding executions that take less than 1 s, SigrefMC is always faster sequentially and always benefits from parallelism.

The results show a clear advantage for larger models. One interesting result is for the p2p-7-5 model. This model is ideal for symbolic bisimulation with a large number of states ($2^{35}$) and very few blocks after minimisation (336). For this model, our tool is 95x faster sequentially and has a parallel speedup of 8x, resulting in a total speedup of 767x. The best parallel speedup of 17x was obtained for the kanban05 model.

In almost all experiments, the signature computation dominates with 70 %–99 % of the execution time sequentially. We observe that the refinement step sometimes benefits more from parallelism than signature computation, with speedups up to 29.9x. We also find that reusing block numbers for stable blocks causes a major reduction in computation time towards the end of the procedure. The kanban LTS models and the larger polling CTMC models are an excellent case study to demonstrate this. See Fig. 3.

6 Conclusions

Originally we intended to investigate parallelism in symbolic bisimulation minimisation. To our surprise, we obtained a much higher sequential speedup using specialized BDD operations, as demonstrated by the results in Table 1 and Fig. 3. The specialized BDD operations offer a clear advantage sequentially and the integration with Sylvan results in decent parallel speedups. Our best result had a total speedup of 767x. Similar to our experiments in symbolic reachability [14], further parallel speedups might be obtained by disjunctively partitioning the transition relations.