Abstract
This paper proposes a timed process algebra for wireless networks, an extension of the Algebra for Wireless Networks. It combines treatments of local broadcast, conditional unicast and data structures, which are essential features for the modelling of network protocols. In this framework we model and analyse the Ad hoc On-Demand Distance Vector routing protocol, and show that, contrary to claims in the literature, it fails to be loop free. We also present boundary conditions for a fix ensuring that the resulting protocol is indeed loop free.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In 2011 we developed the Algebra for Wireless Networks (AWN) [10], a process algebra particularly tailored for Wireless Mesh Networks (WMNs) and Mobile Ad Hoc Networks (MANETs). Such networks are currently being used in a wide range of application areas, such as public safety and mining. They are self-organising wireless multi-hop networks that provide network communication without relying on a wired backhaul infrastructure. A significant characteristic of such networks is that they allow highly dynamic network topologies, meaning that network nodes can join, leave, or move within the network at any moment. As a consequence routing protocols have constantly to check for broken links, and to replace invalid routes by better ones.
To capture the typical characteristics of WMNs and MANETs, AWN offers a unique set of features: conditional unicast (a message transmission attempt with different follow-up behaviour depending on its success), groupcast (communication to a specific set of nodes), local broadcast (messages are received only by nodes within transmission range of the sender), and data structure. We are not aware of any other process algebra that provides all these features, and hence could not use any other algebra to model certain protocols for WMNs or MANETs in a straightforward fashion.Footnote 1 Case studies [9–11, 15] have shown that AWN provides the right level of abstraction to model full IETF protocols, such as the Ad hoc On-Demand Distance Vector (AODV) routing protocol [29]. AWN has been employed to formally model this protocol—thereby eliminating ambiguities and contradictions from the official specification, written in English Prose—and to reason about protocol behaviour and provide rigorous proofs of key protocol properties such as loop freedom and route correctness.
However, AWN abstracts from time. Analysing routing protocols without considering timing issues is useful in its own right; for AODV it has revealed many shortcomings in drafts as well as in the standard (e.g., [3, 16, 19]). Including time in a formal analysis, however, will pave the way to analyse protocols that repeat some procedures every couple of time units; examples are OLSR [7] and B.A.T.M.A.N. [26]. Even for a reactive protocol such as AODV, which does not schedule tasks regularly, it has been shown that timing aspects are important: if timing parameters are chosen poorly, some routes are not established since data that is stored locally at network nodes expires too soon and is erased [6]. Besides such shortcomings in “performance”, also fundamental correctness properties like loop freedom can be affected by the treatment of time—as we will illustrate.
To enable time analyses of WMNs and MANETs, this paper proposes a Timed (process) Algebra for Wireless Networks (T-AWN), an extension of AWN. It combines AWN’s unique set of features, such as local broadcast, with time.
In this framework we model and analyse the AODV routing protocol, and show that, contrary to claims in the literature, e.g., [30], it fails to be loop free, as data required for routing can expire. We also present boundary conditions for a fix ensuring that the resulting protocol is loop free.
Design Decisions. Prior to the development of T-AWN we had to make a couple of decisions.
Intranode Computations. In wireless networks sending a packet from one node to another takes multiple microseconds. Compared to these “slow” actions, time spent for internal (intranode) computations, such as variable assignments or evaluations of expressions, is negligible. We therefore postulate that only transmissions from one node to another take time.
This decision is debatable for processes that can perform infinite sequences of intranode computations without ever performing a durational action. In this paper (and in all applications), we restrict ourselves to well-timed processes in the spirit of [27], i.e., to processes where any infinite sequence of actions contains infinitely many time steps or infinitely many input actions, such as receiving an incoming packet.
But, in the same spirit as T-AWN assigns time to internode communications, it is more or less straightforward to assign times to other operations as well.
Guaranteed Message Receipt and Input Enabledness. A fundamental assumption underlying the semantics of (T-)AWN is that any broadcast message is received by all nodes within transmission range [11, Sect. 1].Footnote 2 This abstraction enables us to interpret a failure of route discovery (as documented for AODV in [11, Sect. 9]) as an imperfection in the protocol, rather than as a result of a chosen formalism not ensuring guaranteed receipt.
A consequence of this design decision is that in the operational semantics of (T-)AWN a broadcast of one node in a network needs to synchronise with some (in)activity of all other nodes in the network [11, Sect. 11]. If another node is within transmission range of the broadcast, the broadcast synchronises with a receive action of that node, and otherwise with a non-arrive transition, which signals that the node is out of range for this broadcast [11, Sect. 4.3].
A further consequence is that we need to specify our nodes in such a way that they are input-enabled, meaning that in any state they are able to receive messages from any other node within transmission range.
Since a transmission (broadcast, groupcast, or unicast) takes multiple units of time, we postulate that another node can only receive a message if it remains within transmission range during the whole period of sending.Footnote 3 A possible way to model the receive action that synchronises with a transmission such as a broadcast is to let it take the same amount of time as the broadcast action. However, a process that is busy executing a durational receive action would fail to be input-enabled, for it would not be able to start receiving another message before the ongoing message receipt is finished. For this reason, we model the receipt of a message as an instantaneous action that synchronises with the very end of a broadcast action.Footnote 4
T-AWN Syntax. When designing or formalising a protocol in T-AWN, an engineer should not be bothered with timing aspects; except for functions and procedures that schedule tasks depending on the current time. Because of this, we use the syntax of AWN also for T-AWN; “extended” by a local timer now. Hence we can perform a timed analysis of any specification written in AWN, since they are also T-AWN specifications.
2 A Timed Process Algebra for Wireless Networks
In this section we propose T-AWN (Timed Algebra for Wireless Networks), an extension of the process algebra AWN [10, 11] with time. AWN itself is a variant of standard process algebras [2, 4, 18, 23], tailored to protocols in wireless mesh networks, such as the Ad-hoc on Demand Distance Vector (AODV) routing protocol. In (T-)AWN, a WMN is modelled as an encapsulated parallel composition of network nodes. On each node several sequential processes may be running in parallel. Network nodes communicate with their direct neighbours—those nodes that are in transmission range—using either broadcast, groupcast or unicast. Our formalism maintains for each node the set of nodes that are currently in transmission range. Due to mobility of nodes and variability of wireless links, nodes can move in or out of transmission range. The encapsulation of the entire network inhibits communications between network nodes and the outside world, with the exception of the receipt and delivery of data packets from or to clientsFootnote 5 of the modelled protocol that may be hooked up to various nodes.
In T-AWN we apply a discrete model of time, where each sequential process maintains a local variable now holding its local clock value—an integer. We employ only one clock for each sequential process. All sequential processes in a network synchronise in taking time steps, and at each time step all local clocks advance by one unit. For the rest, the variable now behaves as any other variable maintained by a process: its value can be read when evaluating guards, thereby making progress time-dependant, and any value can be assigned to it, thereby resetting the local clock.
In our model of a sequential process p running on a node, time can elapse only when p is transmitting a message to another node, or when p currently has no way to proceed—for instance, when waiting on input, or for its local clock to reach a specified value. All other actions of p, such as assigning values to variables, evaluating guards, communicating with other processes running on the same node, or communicating with clients of the modelled protocol hooked up at that node, are assumed to be an order of magnitude faster, and in our model take no time at all. Thus they are executed in preference to time steps.
2.1 The Syntax of T-AWN
The syntax of T-AWN is the same as the syntax of AWN [10, 11], except for the presence of the variable now of the new type TIME. This brings the advantage that any specification written in AWN can be interpreted and analysed in a timed setting. The rest of this Sect. 2.1 is almost copied verbatim from the original articles about AWN [10, 11].
A Language for Sequential Processes. The internal state of a process is determined, in part, by the values of certain data variables that are maintained by that process. To this end, we assume a data structure with several types, variables ranging over these types, operators and predicates. First order predicate logic yields terms (or data expressions) and formulas to denote data values and statements about them.Footnote 6 Our data structure always contains the types TIME, DATA, MSG, IP and  of time values, which we take to be integers (together with the special value \(\infty \)), application layer data, messages, IP addresses—or any other node identifiers—and sets of IP addresses. We further assume that there is a variable now of type TIME and a function \(\mathtt{newpkt}:\mathtt{DATA}\times \mathtt{IP}\rightarrow \mathtt{MSG}\) that generates a message with new application layer data for a particular destination. The purpose of this function is to inject data to the protocol; details will be given later.
of time values, which we take to be integers (together with the special value \(\infty \)), application layer data, messages, IP addresses—or any other node identifiers—and sets of IP addresses. We further assume that there is a variable now of type TIME and a function \(\mathtt{newpkt}:\mathtt{DATA}\times \mathtt{IP}\rightarrow \mathtt{MSG}\) that generates a message with new application layer data for a particular destination. The purpose of this function is to inject data to the protocol; details will be given later.
In addition, we assume a type SPROC of sequential processes, and a collection of process names, each being an operator of type \(\mathtt{TYPE}_1 \times \cdots \times \mathtt{TYPE}_n \rightarrow \mathtt{SPROC}\) for certain data types \(\mathtt{TYPE}_i\). Each process name X comes with a defining equation


in which, for each \(i=1,\ldots ,n\), \(\mathtt{var}_i\) is a variable of type \(\mathtt{TYPE}_i\) and p a guarded Footnote 7 sequential process expression defined by the grammar below. The expression p may contain the variables \(\mathtt{var}_i\) as well as X; however, all occurrences of data variables in \(p\) have to be bound. The choice of the underlying data structure and the process names with their defining equations can be tailored to any particular application of our language; our decisions made for modelling AODV are presented in Sect. 3. The process names are used to denote the processes that feature in this application, with their arguments \(\mathtt{var}_i\) binding the current values of the data variables maintained by these processes.
The sequential process expressions are given by the following grammar:


Here X is a process name, \(\textit{exp}_i\) a data expression of the same type as \(\mathtt{var}_i\), \(\varphi \) a data formula, \(\mathtt{var}\mathop {:=}\textit{exp}\) an assignment of a data expression exp to a variable var of the same type, dest, dests, data and ms data expressions of types IP,  , DATA and MSG, respectively, and \(\mathtt{msg}\) a data variable of type MSG.
, DATA and MSG, respectively, and \(\mathtt{msg}\) a data variable of type MSG.
The internal state of a sequential process described by an expression \(p\) in this language is determined by \(p\), together with a valuation \(\xi \) associating data values \(\xi (\mathtt{var})\) to the data variables var maintained by this process. Valuations naturally extend to \(\xi \) -closed data expressions—those in which all variables are either bound or in the domain of \(\xi \).
Given a valuation of the data variables by concrete data values, the sequential process  acts as \(p\) if \(\varphi \) evaluates to true, and deadlocks if \(\varphi \) evaluates to false. In case \(\varphi \) contains free variables that are not yet interpreted as data values, values are assigned to these variables in any way that satisfies \(\varphi \), if possible. The sequential process \(\mathbf [\![ \mathtt{var}:=\textit{exp}\mathbf ]\!] p\) acts as \(p\), but under an updated valuation of the data variable var. The sequential process \(p+q\) may act either as \(p\) or as \(q\), depending on which of the two processes is able to act at all. In a context where both are able to act, it is not specified how the choice is made. The sequential process \(\alpha .p\) first performs the action \(\alpha \) and subsequently acts as \(p\). The action \(\mathbf{broadcast }(\textit{ms})\) broadcasts (the data value bound to the expression) \(\textit{ms}\) to the other network nodes within transmission range, whereas \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).p\blacktriangleright q\) is a sequential process that tries to unicast the message \(\textit{ms}\) to the destination dest; if successful it continues to act as \(p\) and otherwise as \(q\). In other words, \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).p\) is prioritised over \(q\); only if the action \(\mathbf{unicast }({\textit{dest}},{\textit{ms}})\) is not possible, the alternative q will happen. It models an abstraction of an acknowledgment-of-receipt mechanism that is typical for unicast communication but absent in broadcast communication, as implemented by the link layer of relevant wireless standards such as IEEE 802.11 [20]. The process \(\mathbf{groupcast }({\textit{dests}},{\textit{ms}}).p\) tries to transmit ms to all destinations \(\textit{dests}\), and proceeds as \(p\) regardless of whether any of the transmissions is successful. Unlike unicast and broadcast, the expression groupcast does not have a unique counterpart in networking. Depending on the protocol and the implementation it can be an iterative unicast, a broadcast, or a multicast; thus groupcast abstracts from implementation details. The action \(\mathbf{send }(\textit{ms})\) synchronously transmits a message to another process running on the same network node; this action can occur only when this other sequential process is able to receive the message. The sequential process \(\mathbf{receive }(\mathtt{msg}).p\) receives any message m (a data value of type MSG) either from another node, from another sequential process running on the same node or from the client hooked up to the local node. It then proceeds as \(p\), but with the data variable \(\mathtt{msg}\) bound to the value m. The submission of data from a client is modelled by the receipt of a message \(\mathtt{newpkt}({\textit{d}},{\textit{dip}})\), where the function \(\mathtt{newpkt}\) generates a message containing the data \(\textit{d}\) and the intended destination \(\textit{dip}\). Data is delivered to the client by deliver(data).
acts as \(p\) if \(\varphi \) evaluates to true, and deadlocks if \(\varphi \) evaluates to false. In case \(\varphi \) contains free variables that are not yet interpreted as data values, values are assigned to these variables in any way that satisfies \(\varphi \), if possible. The sequential process \(\mathbf [\![ \mathtt{var}:=\textit{exp}\mathbf ]\!] p\) acts as \(p\), but under an updated valuation of the data variable var. The sequential process \(p+q\) may act either as \(p\) or as \(q\), depending on which of the two processes is able to act at all. In a context where both are able to act, it is not specified how the choice is made. The sequential process \(\alpha .p\) first performs the action \(\alpha \) and subsequently acts as \(p\). The action \(\mathbf{broadcast }(\textit{ms})\) broadcasts (the data value bound to the expression) \(\textit{ms}\) to the other network nodes within transmission range, whereas \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).p\blacktriangleright q\) is a sequential process that tries to unicast the message \(\textit{ms}\) to the destination dest; if successful it continues to act as \(p\) and otherwise as \(q\). In other words, \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).p\) is prioritised over \(q\); only if the action \(\mathbf{unicast }({\textit{dest}},{\textit{ms}})\) is not possible, the alternative q will happen. It models an abstraction of an acknowledgment-of-receipt mechanism that is typical for unicast communication but absent in broadcast communication, as implemented by the link layer of relevant wireless standards such as IEEE 802.11 [20]. The process \(\mathbf{groupcast }({\textit{dests}},{\textit{ms}}).p\) tries to transmit ms to all destinations \(\textit{dests}\), and proceeds as \(p\) regardless of whether any of the transmissions is successful. Unlike unicast and broadcast, the expression groupcast does not have a unique counterpart in networking. Depending on the protocol and the implementation it can be an iterative unicast, a broadcast, or a multicast; thus groupcast abstracts from implementation details. The action \(\mathbf{send }(\textit{ms})\) synchronously transmits a message to another process running on the same network node; this action can occur only when this other sequential process is able to receive the message. The sequential process \(\mathbf{receive }(\mathtt{msg}).p\) receives any message m (a data value of type MSG) either from another node, from another sequential process running on the same node or from the client hooked up to the local node. It then proceeds as \(p\), but with the data variable \(\mathtt{msg}\) bound to the value m. The submission of data from a client is modelled by the receipt of a message \(\mathtt{newpkt}({\textit{d}},{\textit{dip}})\), where the function \(\mathtt{newpkt}\) generates a message containing the data \(\textit{d}\) and the intended destination \(\textit{dip}\). Data is delivered to the client by deliver(data).
A Language for Parallel Processes. Parallel process expressions are given by the grammar
where \(\textit{SP}\) is a sequential process expression and \(\xi \) a valuation. An expression \(\xi ,p\) denotes a sequential process expression equipped with a valuation of the variables it maintains. The process \(P\mathbin {\langle \!\langle }Q\) is a parallel composition of P and Q, running on the same network node. An action \(\mathbf{receive }(\textit{m})\) of P synchronises with an action \(\mathbf{send }(\textit{m})\) of Q into an internal action \(\tau \), as formalised in Table 2. These receive actions of P and send actions of Q cannot happen separately. All other actions of P and Q, except time steps, including receive actions of Q and send actions of P, occur interleaved in \(P\mathbin {\langle \!\langle }Q\). Therefore, a parallel process expression denotes a parallel composition of sequential processes \(\xi ,P\) with information flowing from right to left. The variables of different sequential processes running on the same node are maintained separately, and thus cannot be shared.
Though \(\mathbin {\langle \!\langle }\) only allows information flow in one direction, it reflects reality of WMNs. Usually two sequential processes run on the same node: \(P \mathbin {\langle \!\langle }Q\). The main process P deals with all protocol details of the node, e.g., message handling and maintaining the data such as routing tables. The process Q manages the queueing of messages as they arrive; it is always able to receive a message even if P is busy. The use of message queueing in combination with \(\mathbin {\langle \!\langle }\) is crucial in order to create input-enabled nodes (cf. Sect. 1).
A Language for Networks. We model network nodes in the context of a wireless mesh network by node expressions of the form \(\textit{ip}:\textit{PP}:R\). Here \(\textit{ip} \in \mathtt{IP}\) is the address of the node, \(\textit{PP}\) is a parallel process expression, and \(R\subseteq \mathtt{IP}\) is the range of the node—the set of nodes that are currently within transmission range of \(\textit{ip}\).
A partial network is then modelled by a parallel composition \(\Vert \) of node expressions, one for every node in the network, and a complete network is a partial network within an encapsulation operator \([\_]\) that limits the communication of network nodes and the outside world to the receipt and the delivery of data packets to and from the application layer attached to the modelled protocol in the network nodes. This yields the following grammar for network expressions:
2.2 The Semantics of T-AWN
As mentioned in the introduction, the transmission of a message takes time. Since our main application assumes a wireless link and node mobility, the packet delivery time varies. Hence we assume a minimum time that is required to send a message, as well as an optional extra transmission time. In T-AWN the values of these parameters are given for each type of sending separately: LB, LG, and LU, satisfying \(\mathtt{LB},\mathtt{LG},\mathtt{LU} > 0\), specify the minimum bound, in units of time, on the duration of a broadcast, groupcast and unicast transmission; the optional additional transmission times are denoted by \(\mathtt{\Delta B}\), \(\mathtt{\Delta G}\) and \(\mathtt{\Delta U}\), satisfying \(\mathtt{\Delta B},\mathtt{\Delta G},\mathtt{\Delta U} \ge 0\). Adding up these parameters (e.g. \(\mathtt{LB} \) and \(\mathtt{\Delta B}\)) yields maximum transmission times. We allow any execution consistent with these parameters. For all other actions our processes can take we postulate execution times of 0.
Sequential Processes. The structural operational semantics of T-AWN, given in Tables 1, 2, 3 and 4, is in the style of Plotkin [31] and describes how one internal state can evolve into another by performing an action.
A difference with AWN is that some of the transitions are time steps. On the level of node and network expressions they are labelled “\(\mathrm{tick}\)” and the parallel composition of multiple nodes can perform such a transition iff each of those nodes can—see the third rule in Table 4. On the level of sequential and parallel process expressions, time-consuming transitions are labelled with wait actions from \(\mathcal {W}= \{\mathrm{w},\mathrm{ws},\mathrm{wr},\mathrm{wrs}\}\subseteq \text {Act}\) and transmission actions from \(\mathcal {R}\mathop {:}\mathcal {W}=\{R\mathop {:}w_1 \mid w_1 \mathbin \in \mathcal {W}\wedge R \subseteq \mathtt{IP}\}\subseteq \text {Act}\). Wait actions \(w_1\mathbin \in \mathcal {W}\) indicate that the system is waiting, possibly only as long as it fails to synchronise on a receive action (\(\mathrm{wr}\)), a send action (\(\mathrm{ws}\)) or both of those (\(\mathrm{wrs}\)); actions \(R\mathop {:}w_1\) indicate that the system is transmitting a message while the current transmission range of the node is \(R \subseteq \mathtt{IP}\). In the operational rule for choice (+) we combine any two wait actions \(w_1,w_2\in \mathcal {W}\) with the operator \(\wedge \), which joins the conditions under which these wait actions can occur.
\(\begin{array}{c|cccc} \wedge &{} \mathrm{w}&{} \mathrm{wr}&{} \mathrm{ws}&{} \mathrm{wrs}\\ \hline \mathrm{w}&{} \mathrm{w}&{} \mathrm{wr}&{} \mathrm{ws}&{} \mathrm{wrs}\\ \mathrm{wr}&{} \mathrm{wr}&{} \mathrm{wr}&{} \mathrm{wrs}&{} \mathrm{wrs}\\ \mathrm{ws}&{} \mathrm{ws}&{} \mathrm{wrs}&{} \mathrm{ws}&{} \mathrm{wrs}\\ \mathrm{wrs}&{} \mathrm{wrs}&{} \mathrm{wrs}&{} \mathrm{wrs}&{} \mathrm{wrs}\end{array}\)
In Table 1, which gives the semantics of sequential process expressions, a state is given as a pair \(\xi ,p\) of a sequential process expression p and a valuation \(\xi \) of the data variables maintained by p. The set \(\text {Act}\) of actions that can be executed by sequential and parallel process expressions, and thus occurs as transition labels, consists of  , \(\mathbf{send }(m)\), \(\mathbf{deliver }(\textit{d})\), \(\mathbf{receive }(m)\), durational actions \(w_1\) and \(R\mathop {:}w_1\), and internal actions \(\tau \), for each choice of \(R\subseteq \mathtt{IP}\), \(m \mathop {\in }\mathtt{MSG}\), \(\textit{d}\mathop {\in }\mathtt{DATA}\) and \(w_1\in \mathcal {W}\). Here
, \(\mathbf{send }(m)\), \(\mathbf{deliver }(\textit{d})\), \(\mathbf{receive }(m)\), durational actions \(w_1\) and \(R\mathop {:}w_1\), and internal actions \(\tau \), for each choice of \(R\subseteq \mathtt{IP}\), \(m \mathop {\in }\mathtt{MSG}\), \(\textit{d}\mathop {\in }\mathtt{DATA}\) and \(w_1\in \mathcal {W}\). Here  is the action of transmitting the message m, to be received by the set of nodes R, which is the intersection of the set of intended destinations with the nodes that are within transmission range throughout the transmission. We do not distinguish whether this message has been broadcast, groupcast or unicast—the differences show up merely in the value of R.
is the action of transmitting the message m, to be received by the set of nodes R, which is the intersection of the set of intended destinations with the nodes that are within transmission range throughout the transmission. We do not distinguish whether this message has been broadcast, groupcast or unicast—the differences show up merely in the value of R.
In Table 1 \(\xi [\mathtt{var}:= v]\) denotes the valuation that assigns the value v to the variable var, and agrees with \(\xi \) on all other variables. We use \(\xi [\mathtt{now} \mathord +\mathord {}\mathord +]\) as an abbreviation for \(\xi [\mathtt{now}:=\xi (\mathtt{now})\mathord +1]\), the valuation \(\xi \) in which the variable now is incremented by 1. This describes the state of data variables after 1 unit of time elapses, while no other changes in data occurred. The empty valuation \(\emptyset \) assigns values to no variables. Hence \(\emptyset [\mathtt{var}_i:=v_i]_{i=1}^n\) is the valuation that only assigns the values \(v_i\) to the variables \(\mathtt{var}_i\) for \(i=1,\ldots ,n\). Moreover, \(\xi (\textit{exp})\mathord \downarrow \), with exp a data expression, is the statement that \(\xi (\textit{exp})\) is defined; this might fail because exp contains a variable that is not in the domain of \(\xi \) or because exp contains a partial function that is given an argument for which it is not defined.
A state \(\xi ,r\) is unvalued, denoted by \(\xi (r)\mathord \uparrow \), if r has the form \(\mathbf{broadcast }(\textit{ms}).p\), \(\mathbf{groupcast }({\textit{dests}},{\textit{ms}}).p\), \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).p\), \(\mathbf{send }(\textit{ms}).p\), \(\mathbf{deliver }(\textit{data}).p\), \(\mathbf [\![ \mathtt{var}:=\textit{exp}\mathbf ]\!] p\,\) or \(\,X(\textit{exp}_1,\ldots ,\textit{exp}_n)\) with either \(\xi (\textit{ms})\) or \(\xi (\textit{dests})\) or \(\xi (\textit{dest})\) or \(\xi (\textit{data})\) or \(\xi (\textit{exp})\) or some \(\xi (\textit{exp}_i)\) undefined. From such a state no progress is possible. However, the sixth last line in Table 1 does allow time to progress. We use \(\xi (r)\mathord \downarrow \) to denote that a state is not unvalued.
Rule (rec) for process names in Table 1 is motivated and explained in [11, Sect. 4.1]. The variant (rec-w) of this rule for wait actions \(w_1\in \mathcal {W}\) has been modified such that the recursion is not yet unfolded while waiting. This simulates the behaviour of AWN where a process is only unwound if the first action of the process can be performed.
In the subsequent rules (grd) and (\(\lnot \)
grd) for variable-binding guards \([\varphi ]\), the notation \(\xi \mathop {\rightarrow }\limits ^{\varphi }\zeta \) says that \(\zeta \) is an extension of \(\xi \) that satisfies \(\varphi \): a valuation that agrees with \(\xi \) on all variables on which \(\xi \) is defined, and valuates the other variables occurring free in \(\varphi \), such that the formula \(\varphi \) holds under \(\zeta \). All variables not free in \(\varphi \) and not evaluated by \(\xi \) are also not evaluated by \(\zeta \). Its negation  says that no such extension exists, and thus that \(\varphi \) is false in the current state, no matter how we interpret the variables whose values are still undefined. If that is the case, the process \([\varphi ]p\) will idle by performing the action \(\mathrm{w}\) (of waiting) without changing its state, except that the variable now will be incremented.
says that no such extension exists, and thus that \(\varphi \) is false in the current state, no matter how we interpret the variables whose values are still undefined. If that is the case, the process \([\varphi ]p\) will idle by performing the action \(\mathrm{w}\) (of waiting) without changing its state, except that the variable now will be incremented.
Example 1
The process \(\mathbf [\![ \mathtt{timeout}:=\mathtt{now} +2\mathbf ]\!] [\mathtt{now} = \mathtt{timeout}] p\) first sets the variable timeout to 2 units after the current time. Then it encounters a guard that evaluates to false, and therefore takes a \(\mathrm{w}\)-transition, twice. After two time units, the guard evaluates to true and the process proceeds as p.
The process \(\mathbf{receive }(\mathtt{msg}).p\) can receive any message m from the environment in which this process is running. As long as the environment does not provide a message, this process will wait. This is indicated by the transition labelled \(\mathrm{wr}\) in Table 1. The difference between a \(\mathrm{wr}\)-and a \(\mathrm{w}\)-transition is that the former can be taken only when the environment does not synchronise with the \(\mathbf{receive }\)-transition. In our semantics any state with an outgoing \(\mathrm{wr}\)-transition also has an outgoing \(\mathbf{receive }\)-transition (see Theorem 1), which conceptually has priority over the \(\mathrm{wr}\)-transition. Likewise the transition labelled \(\mathrm{ws}\) is only enabled in states that also admit a \(\mathbf{send }\)-transition, and is taken only in a context where the \(\mathbf{send }\)-transition cannot be taken.
Rules (alt-l) and (alt-r), defining the behaviour of the choice operator for non-wait actions are standard. Rule (alt-w) for wait actions says that a process \(p+q\) can wait only if both p and q can wait; if one of the two arguments can make real progress, the choice process \(p+q\) always chooses this progress over waiting. This is a direct generalisation of the law \(p+\mathbf {0}=p\) of CCS [23]. As a consequence, a condition on the possibility of \(p\) or \(q\) to wait is inherited by \(p+q\). This gives rise to the transition label \(\mathrm{wrs}\), that makes waiting conditional on the environment failing to synchronising with a \(\mathbf{receive }\) as well as a \(\mathbf{send }\)-transition. In understanding the target \(\zeta ,p'{+}q'\) of this rule, it is helpful to realise that whenever  , then \(q= p\) and \(\zeta = \xi [\mathtt{now} \mathord +\mathord +]\); see Proposition 1.
, then \(q= p\) and \(\zeta = \xi [\mathtt{now} \mathord +\mathord +]\); see Proposition 1.
In order to give semantics to the transmission constructs (broadcast, groupcast, unicast), the language of sequential processes is extended with the auxiliary construct


with \(m\in \mathtt{MSG}\),  and \(\textit{dsts} \subseteq \mathtt{IP}\). This is a variant of the broadcast-, groupcast- and unicast-constructs, describing intermediate states of the transmission of message m. The argument dsts of *cast denotes those intended destinations that were not out of transmission range during the part of the transmission that already took place.
and \(\textit{dsts} \subseteq \mathtt{IP}\). This is a variant of the broadcast-, groupcast- and unicast-constructs, describing intermediate states of the transmission of message m. The argument dsts of *cast denotes those intended destinations that were not out of transmission range during the part of the transmission that already took place.
In a state \(\textit{dsts} \mathop {:}\mathbf{*cast }(\textit{m})[n,o].p \blacktriangleright q\) with \(n>0\) the transmission still needs between n and \(n\mathord +o\) time units to complete. If \(n=0\) the actual *cast-transition will take place; resulting in state p if the message is delivered to at least one node in the network (dsts is non-empty), and q otherwise.
Rule (gc) says that once a process commits to a groupcast-transmission, it is going to behave as \(\textit{dsts} \mathop {:}\mathbf{*cast }(m)[n,o]\) with time parameters \(n:=\mathtt{LG} \) and \(o:=\mathtt{\Delta G}\). The transmitted message m is calculated by evaluating the argument ms, and the transmission range dsts of this *cast is initialised by evaluating the argument dests, indicating the intended destinations of the groupcast. Rules (bc) and (uc) for broadcast and unicast are the same, except that in the case of broadcast the intended destinations are given by the set \(\mathtt{IP}\) of all possible destinations, whereas a unicast has only one intended destination. Moreover, only unicast exploits the difference in the continuation process depending on whether an intended destination is within transmission range. Subsequently, Rules (tr) and (tr-o) come into force; they allow time-consuming transmission steps to take place, each decrementing one of the time parameters n or o. Each time step of a transmission corresponds to a transition labelled \(R\mathop {:}\mathrm{w}\), where R records the current transmission range. Since sequential processes store no information on transmission ranges—this information is added only when moving from process expressions to node expressions—at this stage of the description all possibilities for the transmission range need to be left open, and hence there is a transition labelled \(R\mathop {:}\mathrm{w}\) for each choice of R.Footnote 8 When transitions for process expressions are inherited by node expressions, only one of the transitions labelled \(R\mathop {:}\mathrm{w}\) is going to survive, namely the one where R equals the transmission range given by the node expression (cf. Rule (n-t) in Table 3). Upon doing a transition \(R\mathop {:}\mathrm{w}\), the range dsts of the *cast is restricted to R. As soon as \(n\mathbin =0\), regardless of the value of o, the transmission is completed by the execution of the action \(\textit{dsts} \mathop {:}\mathbf{*cast }(m)\) (Rules (sc) and \(\lnot \)(sc)). Here the actual message m is passed on for synchronisation with receive-transitions of all nodes \(\textit{ip}\in \textit{dsts} \).
This treatment of message transmission is somewhat different from the one in AWN. There, the rule  describes the behaviour of the groupcast construct for sequential processes, and the rule
describes the behaviour of the groupcast construct for sequential processes, and the rule


lifts this behaviour from processes to nodes. In this last stage the groupcast-action is unified with the broadcast- and unicast-action into a *cast, at which occasion the range of the *cast is calculated as the intersection of the intended destinations D of the groupcast and the ones in transmission range R. In T-AWN, on the other hand, the conversion of groupcast to *cast happens already at the level of sequential processes.
Parallel Processes. Rules (p-al), (p-ar) and (p-a) of Table 2 are taken from AWN, and formalise the description of the operator \(\mathbin {\langle \!\langle }\) given in Sect. 2.1. Rule (p-w) stipulates under which conditions a process \(P\mathbin {\langle \!\langle }Q\) can do a wait action, and
\(\begin{array}{c|cccc} \mathbin {\langle \!\langle }&{} \mathrm{w}&{} \mathrm{wr}&{} \mathrm{ws}&{} \mathrm{wrs}\\ \hline \mathrm{w}&{} \mathrm{w}&{} \mathrm{wr}&{} \mathrm{w}&{} \mathrm{wr}\\ \mathrm{wr}&{} \mathrm{w}&{} \mathrm{wr}&{} - &{} - \\ \mathrm{ws}&{} \mathrm{ws}&{} \mathrm{wrs}&{} \mathrm{ws}&{} \mathrm{wrs}\\ \mathrm{wrs}&{} \mathrm{ws}&{} \mathrm{wrs}&{} - &{} - \end{array}\) of which kind. Here \(\mathbin {\langle \!\langle }\) is also a partial binary function on the set \(\mathcal {W}\), specified by the table on the right. The process \(P\mathbin {\langle \!\langle }Q\) can do a wait action only if both P and Q can do so. In case P can do a \(\mathrm{wr}\) or a \(\mathrm{wrs}\)-action, P can also do a receive and in case Q can do a \(\mathrm{ws}\) or a \(\mathrm{wrs}\), Q can also do a send. When both these possibilities apply, the receive of P synchronises with the send of Q into a \(\tau \)-step, which has priority over waiting. In the other 12 cases no synchronisation between P and Q is possible, and we do obtain a wait action. Since a receive-action of P that does not synchronise with Q is dropped, so is the corresponding side condition of a wait action of P. Hence (within the remaining 12 cases) a \(\mathrm{wr}\) of P is treated as a \(\mathrm{w}\), and a \(\mathrm{wrs}\) as a \(\mathrm{ws}\). Likewise a \(\mathrm{ws}\) of Q is treated as a \(\mathrm{w}\), and a \(\mathrm{wrs}\) as a \(\mathrm{wr}\). This leaves 4 cases to be decided. In all four, we have \(\mathrm{w}_1 \mathbin {\langle \!\langle }\mathrm{w}_2 = \mathrm{w}_1 \wedge \mathrm{w}_2\).
Time steps \(R\mathop {:}w_1\) are treated exactly like wait actions from \(\mathcal {W}\) (cf. Rules (p-tl), (p-tr) and (p-t)). If for instance P can do a \(R\mathop {:}\mathrm{w}\), meaning that it spends a unit of time on a transmission, while Q can do a \(\mathrm{wr}\), meaning that it waits a unit of time only when it does not receive anything from another source, the result is that \(P\mathbin {\langle \!\langle }Q\) can spend a unit of time transmitting something, but only as long as \(P\mathbin {\langle \!\langle }Q\) does not receive any message; if it does, the receive action of Q happens with priority over the wait action of Q, and thus occurs before P spends a unit of time transmitting.
Node and Network Expressions. The operational semantics of node and network expressions of Tables 3 and 4 uses transition labels tick,  , \(H\lnot K\mathop {:}\mathbf{arrive }(m)\), \(\textit{ip}\mathop {:}\mathbf{deliver }(\textit{d})\), \(\mathbf{connect }(\textit{ip},\textit{ip}')\), \(\mathbf{disconnect }(\textit{ip},\textit{ip}')\), \(\tau \) and \(\textit{ip}\mathop {:}\mathbf{newpkt }(\textit{d},\textit{dip})\). As before, \(m\in \mathtt{MSG}\), \(d\in \mathtt{DATA}\), \(R\subseteq \mathtt{IP}\), and \(\textit{ip},\textit{ip}'\in \mathtt{IP}\). Moreover, \(H,K\subseteq \mathtt{IP}\) are sets of IP addresses.
, \(H\lnot K\mathop {:}\mathbf{arrive }(m)\), \(\textit{ip}\mathop {:}\mathbf{deliver }(\textit{d})\), \(\mathbf{connect }(\textit{ip},\textit{ip}')\), \(\mathbf{disconnect }(\textit{ip},\textit{ip}')\), \(\tau \) and \(\textit{ip}\mathop {:}\mathbf{newpkt }(\textit{d},\textit{dip})\). As before, \(m\in \mathtt{MSG}\), \(d\in \mathtt{DATA}\), \(R\subseteq \mathtt{IP}\), and \(\textit{ip},\textit{ip}'\in \mathtt{IP}\). Moreover, \(H,K\subseteq \mathtt{IP}\) are sets of IP addresses.
The actions  are inherited by nodes from the processes that run on these nodes (cf. Rule (n-sc)). The action \(H\lnot K\mathop {:}\mathbf{arrive }(m)\) states that the message m simultaneously arrives at all addresses \(\textit{ip}\mathbin \in H\), and fails to arrive at all addresses \(\textit{ip}\mathbin \in K\). The rules of Table 4 let a
are inherited by nodes from the processes that run on these nodes (cf. Rule (n-sc)). The action \(H\lnot K\mathop {:}\mathbf{arrive }(m)\) states that the message m simultaneously arrives at all addresses \(\textit{ip}\mathbin \in H\), and fails to arrive at all addresses \(\textit{ip}\mathbin \in K\). The rules of Table 4 let a  -action of one node synchronise with an \(\mathbf{arrive }(m)\) of all other nodes, where this \(\mathbf{arrive }(m)\) amalgamates the arrival of message m at the nodes in the transmission range R of the
-action of one node synchronise with an \(\mathbf{arrive }(m)\) of all other nodes, where this \(\mathbf{arrive }(m)\) amalgamates the arrival of message m at the nodes in the transmission range R of the  , and the non-arrival at the other nodes. Rules (n-rcv) and (n-dis) state that arrival of a message at a node happens if and only if the node receives it, whereas non-arrival can happen at any time. This embodies our assumption that, at any time, any message that is transmitted to a node within range of the sender is actually received by that node. (Rule (n-dis) may appear to say that any node ip has the option to disregard any message at any time. However, the encapsulation operator (below) prunes away all such disregard transitions that do not synchronise with a cast action for which ip is out of range.)
, and the non-arrival at the other nodes. Rules (n-rcv) and (n-dis) state that arrival of a message at a node happens if and only if the node receives it, whereas non-arrival can happen at any time. This embodies our assumption that, at any time, any message that is transmitted to a node within range of the sender is actually received by that node. (Rule (n-dis) may appear to say that any node ip has the option to disregard any message at any time. However, the encapsulation operator (below) prunes away all such disregard transitions that do not synchronise with a cast action for which ip is out of range.)
The action \(\mathbf{send }(m)\) of a process does not give rise to any action of the corresponding node—this action of a sequential process cannot occur without communicating with a receive action of another sequential process running on the same node. Time-consuming actions \(w_1\) and \(R\mathop {:}w_1\), with \(w_1\in \mathcal {W}\), of a process are renamed into \(\mathrm{tick}\) on the level of node expressions.Footnote 9 All we need to remember of these actions is that they take one unit of time. Since on node expressions the actions \(\mathbf{send }(m)\) have been dropped, the side condition making the wait actions \(\mathrm{ws}\) and \(\mathrm{wrs}\) conditional on the absence of a send-action can be dropped as well. The priority of receive-actions over the wait action \(\mathrm{wr}\) can now also be dropped, for in the absence of send-actions, receive-actions are entirely reactive. A node can do a receive-action only when another node, or the application layer, casts a message, and in this case that other node is not available to synchronise with a \(\mathrm{tick}\)-transition.
Internal actions \(\tau \) and the action \(\textit{ip}\mathop {:}\mathbf{deliver }(\textit{d})\) are simply inherited by node expressions from the processes that run on these nodes (Rules (n- \(\tau \)) and (n-del)), and are interleaved in the parallel composition of nodes that makes up a network. Finally, we allow actions \(\mathbf{connect }(\textit{ip},\textit{ip}')\) and \(\mathbf{disconnect }(\textit{ip},\textit{ip}')\) for \(\textit{ip},\textit{ip}'\mathop \in \mathtt{IP}\) modelling a change in network topology. In this formalisation node \(\textit{ip}'\) may be in the range of node \(\textit{ip}\), meaning that \(\textit{ip}\) can send to \(\textit{ip}'\), even when the reverse does not hold. For some applications, in particular the one to AODV in Sect. 3, it is useful to assume that \(\textit{ip}'\) is in the range of \(\textit{ip}\) if and only if \(\textit{ip}\) is in the range of \(\textit{ip}'\). This symmetry can be enforced by adding the following rules to Table 3:


and replacing the rules in the third line of Table 4 for (dis)connect actions by


The main purpose of the encapsulation operator is to ensure that no messages will be received that have never been sent. In a parallel composition of network nodes, any action \(\mathbf{receive }(\textit{m})\) of one of the nodes ip manifests itself as an action \(H\lnot K\mathop {:}\mathbf{arrive }(\textit{m})\) of the parallel composition, with \(\textit{ip}\in H\). Such actions can happen (even) if within the parallel composition they do not communicate with an action  of another component, because they might communicate with a
of another component, because they might communicate with a  of a node that is yet to be added to the parallel composition. However, once all nodes of the network are accounted for, we need to inhibit unmatched arrive actions, as otherwise our formalism would allow any node at any time to receive any message. One exception however are those arrive actions that stem from an action \(\mathbf{receive }(\mathtt{newpkt}({\textit{d}},{\textit{dip}}))\) of a sequential process running on a node, as those actions represent communication with the environment. Here, we use the function \(\mathtt{newpkt}\), which we assumed to exist.Footnote 10 It models the injection of new data \(\textit{d}\) for destination dip.
of a node that is yet to be added to the parallel composition. However, once all nodes of the network are accounted for, we need to inhibit unmatched arrive actions, as otherwise our formalism would allow any node at any time to receive any message. One exception however are those arrive actions that stem from an action \(\mathbf{receive }(\mathtt{newpkt}({\textit{d}},{\textit{dip}}))\) of a sequential process running on a node, as those actions represent communication with the environment. Here, we use the function \(\mathtt{newpkt}\), which we assumed to exist.Footnote 10 It models the injection of new data \(\textit{d}\) for destination dip.
The encapsulation operator passes through internal actions, as well as delivery of data to destination nodes, this being an interaction with the outside world (Rule (e-a)).  -actions are declared internal actions at this level (Rule (e-sc)); they cannot be steered by the outside world. The connect and disconnect actions are passed through in Table 4 (Rule (e-a)), thereby placing them under control of the environment; to make them nondeterministic, their rules should have a \(\tau \)-label in the conclusion, or alternatively \(\mathbf{connect }(\textit{ip},\textit{ip}')\) and \(\mathbf{disconnect }(\textit{ip},\textit{ip}')\) should be thought of as internal actions. Finally, actions \(\mathbf{arrive }(m)\) are simply blocked by the encapsulation—they cannot occur without synchronising with a
-actions are declared internal actions at this level (Rule (e-sc)); they cannot be steered by the outside world. The connect and disconnect actions are passed through in Table 4 (Rule (e-a)), thereby placing them under control of the environment; to make them nondeterministic, their rules should have a \(\tau \)-label in the conclusion, or alternatively \(\mathbf{connect }(\textit{ip},\textit{ip}')\) and \(\mathbf{disconnect }(\textit{ip},\textit{ip}')\) should be thought of as internal actions. Finally, actions \(\mathbf{arrive }(m)\) are simply blocked by the encapsulation—they cannot occur without synchronising with a  —except for \(\{\textit{ip}\}\lnot K\mathop {:}\mathbf{arrive }(\mathtt{newpkt}({\textit{d}},{\textit{dip}}))\) with \(\textit{d}\in \mathtt{DATA}\) and \(\textit{dip}\in \mathtt{IP}\) (Rule (e-np)). This action represents new data d that is submitted by a client of the modelled protocol to node \(\textit{ip}\), for delivery at destination dip.
—except for \(\{\textit{ip}\}\lnot K\mathop {:}\mathbf{arrive }(\mathtt{newpkt}({\textit{d}},{\textit{dip}}))\) with \(\textit{d}\in \mathtt{DATA}\) and \(\textit{dip}\in \mathtt{IP}\) (Rule (e-np)). This action represents new data d that is submitted by a client of the modelled protocol to node \(\textit{ip}\), for delivery at destination dip.
Optional Augmentations to Ensure Non-blocking Broadcast. Our process algebra, as presented above, is intended for networks in which each node is input enabled [21], meaning that it is always ready to receive any message, i.e., able to engage in the transition \(\mathbf{receive }(m)\) for any \(m\in \mathtt{MSG}\)—in the default version of T-AWN, network expressions are required to have this property. In our model of AODV (Sect. 3) we will ensure this by equipping each node with a message queue that is always able to accept messages for later handling—even when the main sequential process is currently busy. This makes our model input enabled and hence non-blocking, meaning that no sender can be delayed in transmitting a message simply because one of the potential recipients is not ready to receive it.
In [10, 11] we additionally presented two versions of AWN without the requirement that all nodes need to be input enabled: one in which we kept the same operational semantics and simply accept blocking, and one were we added operational rules to avoid blocking, thereby giving up on the requirement that any broadcast message is received by all nodes within transmission range.
The first solution does not work for T-AWN, as it would give rise to time deadlocks, reachable states where time is unable to progress further.
The second solution is therefore our only alternative to requiring input enabledness for T-AWN. As in [10, 11], it is implemented by the addition of the rule


It states that a message may arrive at a node ip regardless whether the node is ready to receive it or not; if it is not ready, the message is simply ignored, and the process running on the node remains in the same state.
In [11, Sect. 4.5] also a variant of this idea is presented that avoids negative premises, yet leads to the same transition system. The same can be done to T-AWN in the same way, we skip the details and refer to [11, Sect. 4.5].
2.3 Results on the Process Algebra
In this section we list a couple of useful properties of our timed process algebra. In particular, we show that wait actions do not change the data state, except for the value of now. Moreover, we show the absence of time deadlocks: a complete network N described by T-AWN always admits a transition, independently of the outside environment. More precisely, either  , or
, or  or
or  . We also show that our process algebra admits a translation into one without data structure. The operational rules of the translated process algebra are in the de Simone format [33], which immediately implies that strong bisimilarity is a congruence, and yields the associativity of our parallel operators. Last, we show that T-AWN and AWN are related by a simulation relation. Due to lack of space, most of the proofs are omitted, they can be found in Appendix of [5].
. We also show that our process algebra admits a translation into one without data structure. The operational rules of the translated process algebra are in the de Simone format [33], which immediately implies that strong bisimilarity is a congruence, and yields the associativity of our parallel operators. Last, we show that T-AWN and AWN are related by a simulation relation. Due to lack of space, most of the proofs are omitted, they can be found in Appendix of [5].
Proposition 1
On the level of sequential processes, wait actions change only the value of the variable now, i.e.,  .
.
Proof Sketch
One inspects all rules of Table 1 that can generate w-steps, and then reasons inductively on the derivation of these steps.
Similarly, it can be observed that for transmission actions (actions from the set \(\mathcal {R}\mathop {:}\mathcal {W}\)) the data state does not change either; the process, however, changes. That means  for all \(rw \in \mathcal {R}\mathop {:}\mathcal {W}\). Furthermore, this result can easily be lifted to all other layers of our process algebra (with minor adaptations: for example on node expressions one has to consider \(\mathrm{tick}\) actions).
for all \(rw \in \mathcal {R}\mathop {:}\mathcal {W}\). Furthermore, this result can easily be lifted to all other layers of our process algebra (with minor adaptations: for example on node expressions one has to consider \(\mathrm{tick}\) actions).
To shorten the forthcoming definitions and properties we use the following abbreviations:
-
1.
 iff
iff  for some \(m\in \mathtt{MSG}\),
for some \(m\in \mathtt{MSG}\), -
2.
 iff
iff  for some \(m\in \mathtt{MSG}\),
for some \(m\in \mathtt{MSG}\), -
3.
 iff
iff  for some \(w_1\in \mathcal {W}\),
for some \(w_1\in \mathcal {W}\), -
4.
 iff
iff  for some \(a\in \text {Act}\) not of the forms above,
for some \(a\in \text {Act}\) not of the forms above,
where P is a parallel process expression—possibly incorporating the construct \(\textit{dsts} \mathop {:}\mathbf{*cast }(\textit{m})[n,o].p\), but never in a \(+\)-context. Note that the last line covers also transmission actions \(rw\in \mathcal {R}\mathop {:}\mathcal {W}\). The following result shows that the wait actions of a sequential process (with data evaluation) P are completely determined by the other actions P offers.
Theorem 1
Let P be a state of a sequential process.
-
1.
\(P{\mathop {\longrightarrow }\limits ^{\mathrm{w}}}\) iff
 .
. -
2.
\(P{\mathop {\longrightarrow }\limits ^{\mathrm{wr}}}\) iff
 .
. -
3.
\(P{\mathop {\longrightarrow }\limits ^{\mathrm{ws}}}\) iff
 .
. -
4.
\(P{\mathop {\longrightarrow }\limits ^{\mathrm{wrs}}}\) iff
 .
.
Proof Sketch
The proof is by structural induction. It requires, however, a distinction between guarded terms (as defined in Footnote 7) and unguarded ones.
We could equivalently have omitted all transition rules involving wait actions from Table 1, and defined the wait transitions for sequential processes as described by Theorem 1 and Proposition 1. That our transition rules give the same result constitutes a sanity check of our operational semantics.
Theorem 1 does not hold in the presence of unguarded recursion. A counterexample is given by the expression X() with \(X()\mathop {=}\limits ^{{ def}}X()\), for which we would have  .
.
Lemma 1
Let P be a state of a sequential or parallel process. If  for some \(R\subseteq \mathtt{IP}\) and \(w_1\mathbin \in \mathcal {W}\) then
for some \(R\subseteq \mathtt{IP}\) and \(w_1\mathbin \in \mathcal {W}\) then  for any \(R'\subseteq \mathtt{IP}\).
for any \(R'\subseteq \mathtt{IP}\).
Observation 1
Let P be a state of a sequential process. If  for some \(w_1\mathbin \in \mathcal {W}\) then \(w_1\) must be \(\mathrm{w}\) and all outgoing transitions of P are labelled \(R'\mathop :\mathrm{w}\).
for some \(w_1\mathbin \in \mathcal {W}\) then \(w_1\) must be \(\mathrm{w}\) and all outgoing transitions of P are labelled \(R'\mathop :\mathrm{w}\).
For N a (partial) network expression, or a parallel process expression, write  iff
iff  with a of the form
with a of the form  , \(\textit{ip}\mathop {:}\mathbf{deliver }(\textit{d})\) (or \(\mathbf{deliver }(\textit{d})\)) or \(\tau \)—an instantaneous non-blocking action. Hence, for a parallel process expression P,
, \(\textit{ip}\mathop {:}\mathbf{deliver }(\textit{d})\) (or \(\mathbf{deliver }(\textit{d})\)) or \(\tau \)—an instantaneous non-blocking action. Hence, for a parallel process expression P,  iff
iff  or
or  for \(w_1\mathbin \in \mathcal {W}\). Furthermore, write
for \(w_1\mathbin \in \mathcal {W}\). Furthermore, write  iff
iff  or
or  for some \(w_1\mathbin \in \mathcal {W}\). We now lift Theorem 1 to the level of parallel processes.
for some \(w_1\mathbin \in \mathcal {W}\). We now lift Theorem 1 to the level of parallel processes.
Theorem 2
Let P be a state of a parallel process.
-
1.
 iff
iff  .
. -
2.
 iff
iff 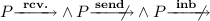 .
. -
3.
 iff
iff  .
. -
4.
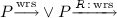 iff
iff  .
.
Corollary 1
Let P be a state of a parallel process. Then  iff
iff  . \(\square \)
. \(\square \)
Lemma 2
Let N be a partial network expression with L the set of addresses of the nodes of N. Then  , for any partition
, for any partition  of L into sets H and K, and any \(m\in \mathtt{MSG}\).
of L into sets H and K, and any \(m\in \mathtt{MSG}\).
Using this lemma, we can finally show one of our main results: an (encapsulated) network expression can perform a time-consuming action iff an instantaneous non-blocking action is not possible.
Theorem 3
Let N be a partial or complete network expression. Then  iff
iff  .
.
Proof
We apply structural induction on N. First suppose N is a node expression \(\textit{ip}\mathop :P\mathop :R\). Then  iff
iff  for some \(w_1\mathbin \in \mathcal {W}\). By Lemma 1 this is the case iff
for some \(w_1\mathbin \in \mathcal {W}\). By Lemma 1 this is the case iff  for some \(R'\subseteq \mathtt{IP}\) and \(w_1\mathbin \in \mathcal {W}\), i.e., iff
for some \(R'\subseteq \mathtt{IP}\) and \(w_1\mathbin \in \mathcal {W}\), i.e., iff  . Moreover
. Moreover  iff
iff  . Hence the claim follows from Corollary 1.
. Hence the claim follows from Corollary 1.
Now suppose N is a partial network expression \(M_1\Vert M_2\). In case  for \(i=1,2\) then
for \(i=1,2\) then  . By induction
. By induction  for \(i=1,2\), and hence
for \(i=1,2\), and hence  . Otherwise,
. Otherwise,  for \(i=1\) or 2. Now
for \(i=1\) or 2. Now  . In case
. In case  or
or  this follows from the third line of Table 4; if
this follows from the third line of Table 4; if  it follows from the first line, in combination with Lemma 2. By induction
it follows from the first line, in combination with Lemma 2. By induction  , and thus
, and thus  .
.
Finally suppose that N is a complete network expression [M]. By the rules of Table 4
 iff
iff  , and
, and  iff
iff  , so the claim follows from the case for partial network expressions. \(\square \)
, so the claim follows from the case for partial network expressions. \(\square \)
Corollary 2
A complete network N described by T-AWN always admits a transition, independently of the outside environment, i.e., \(\forall N, \exists a\) such that  and \(a \not \in \{\mathbf{connect }(\textit{ip},\textit{ip}'),\mathbf{disconnect }(\textit{ip},\textit{ip}'),\mathtt{newpkt}({\textit{d}},{\textit{dip}})\}\).
and \(a \not \in \{\mathbf{connect }(\textit{ip},\textit{ip}'),\mathbf{disconnect }(\textit{ip},\textit{ip}'),\mathtt{newpkt}({\textit{d}},{\textit{dip}})\}\).
More precisely, either  or
or  or
or  . \(\square \)
. \(\square \)
Our process algebra admits a translation into one without data structures (although we cannot describe the target algebra without using data structures). The idea is to replace any variable by all possible values it can take. The target algebra differs from the original only on the level of sequential processes; the subsequent layers are unchanged. A formal definition can be found in Appendix of [5]. The resulting process algebra has a structural operational semantics in the (infinitary) de Simone format, generating the same transition system—up to strong bisimilarity,  —as the original, which provides some results ‘for free’. For example, it follows that
—as the original, which provides some results ‘for free’. For example, it follows that  , and many other semantic equivalences, are congruences on our language.
, and many other semantic equivalences, are congruences on our language.
Theorem 4
Strong bisimilarity is a congruence for all operators of T-AWN.
This is a deep result that usually takes many pages to establish (e.g., [34]). Here we get it directly from the existing theory on structural operational semantics, as a result of carefully designing our language within the disciplined framework described by de Simone [33].
Theorem 5
\(\mathbin {\langle \!\langle }\) is associative, and \(\Vert \) is associative and commutative, up to  .
.
Proof
The operational rules for these operators fit a format presented in [8], guaranteeing associativity up to  . The details are similar to the case for AWN, as elaborated in [10, 11]; the only extra complication is the associativity of the operator \(\mathbin {\langle \!\langle }\) on \(\mathcal {W}\), as defined on Page 12, which we checked automatically by means of the theorem prover Prover9 [22]. Commutativity of \(\Vert \) follows by symmetry of the rules. \(\square \)
. The details are similar to the case for AWN, as elaborated in [10, 11]; the only extra complication is the associativity of the operator \(\mathbin {\langle \!\langle }\) on \(\mathcal {W}\), as defined on Page 12, which we checked automatically by means of the theorem prover Prover9 [22]. Commutativity of \(\Vert \) follows by symmetry of the rules. \(\square \)
Theorem 6
Each AWN process P, seen as a T-AWN process, can be simulated by the AWN process P. Likewise, each AWN network N, seen as a T-AWN network, can be simulated by the AWN network N.
Here a simulation refers to a weak simulation as defined in [14], but treating (dis)connect-actions as \(\tau \), and with the extra requirement that the data states maintained by related expressions are identical—except of course for the variables \(\mathtt{now} \), that are missing in AWN. Details can be found in Appendix of [5].
Thanks to Theorem 6, we can prove that all invariants on the data structure of a process expressed in AWN are still preserved when the process is interpreted as a T-AWN expression. As an application of this, an untimed version of AODV, formalised as an AWN process, has been proven loop free in [11, 15]; the same system, seen as a T-AWN expression—and thus with specific execution times associated to uni-, group-, and broadcast actions—is still loop free when given the operational semantics of T-AWN.
3 Case Study: The AODV Routing Protocol
Routing protocols are crucial to the dissemination of data packets between nodes in WMNs and MANETs. Highly dynamic topologies are a key feature of WMNs and MANETs, due to mobility of nodes and/or the variability of wireless links. This makes the design and implementation of robust and efficient routing protocols for these networks a challenging task. In this section we present a formal specification of the Ad hoc On-Demand Distance Vector (AODV) routing protocol. AODV [29] is a widely-used routing protocol designed for MANETs, and is one of the four protocols currently standardised by the IETF MANET working groupFootnote 11. It also forms the basis of new WMN routing protocols, including HWMP in the IEEE 802.11s wireless mesh network standard [20].
Our formalisation is based on an untimed formalisation of AODV [11, 15], written in AWN, and models the exact details of the core functionality of AODV as standardised in IETF RFC 3561 [29]; e.g., route discovery, route maintenance and error handling. We demonstrate how T-AWN can be used to reason about critical protocol properties. As major outcome we demonstrate that AODV is not loop free, which is in contrast to common belief. Loop freedom is a critical property for any routing protocol, but it is particularly relevant and challenging for WMNs and MANETs. We close the section by discussing a fix to the protocol and prove that the resulting protocol is indeed loop free.
3.1 Brief Overview
AODV is a reactive protocol, which means that routes are established only on demand. If a node S wants to send a data packet to a node D, but currently does not know a route, it temporarily buffers the packet and initiates a route discovery process by broadcasting a route request (RREQ) message in the network. An intermediate node A that receives the RREQ message creates a routing table entry for a route towards node S referred to as a reverse route, and re-broadcasts the RREQ. This is repeated until the RREQ reaches the destination node D, or alternatively a node that knows a route to D. In both cases, the node replies by unicasting a corresponding route reply (RREP) message back to the source S, via a previously established reverse route. When forwarding RREP messages, nodes create a routing table entry for node D, called the forward route. When the RREP reaches the originating node D, a route from S to D is established and data packets can start to flow. Both forward and reverse routes are maintained in a routing table at every node—details are given below. In the event of link and route breaks, AODV uses route error (RERR) messages to notify the affected nodes: if a link break is detected by a node, it first invalidates all routes stored in the node’s own routing table that actually use the broken link. Then it sends a RERR message containing the unreachable destinations to all (direct) neighbours using this route.
In AODV, a routing table consists of a list of entries—at most one for each destination—each containing the following information: (i) the destination IP address; (ii) the destination sequence number; (iii) the sequence-number-status flag—tagging whether the recorded sequence number can be trusted; (iv) a flag tagging the route as being valid or invalid—this flag is set to invalid when a link break is detected or the route’s lifetime is reached; (v) the hop count, a metric to indicate the distance to the destination; (vi) the next hop, an IP address that identifies the next (intermediate) node on the route to the destination; (vii) a list of precursors, a set of IP addresses of those 1-hop neighbours that use this particular route; and (viii) the lifetime (expiration or deletion time) of the route. The destination sequence number constitutes a measure approximating the relative freshness of the information held—a higher number denotes newer information. The routing table is updated whenever a node receives an AODV control message (RREQ, RREP or RERR) or detects a link break.
During the lifetime of the network, each node not only maintains its routing table, it also stores its own sequence number. This number is used as a local “timer” and is incremented whenever a new route request is initiated. It is the source of the destination sequence numbers in routing tables of other nodes.
Full details of the protocol are outlined in the request for comments (RFC) [29].
3.2 Route Request Handling Handled Formally
Our formal model consists of seven processes: \(\mathtt{AODV}\) reads a message from the message queue (modelled in process QMSG, see below) and, depending on the type of the message, calls other processes. Each time a message has been handled the process has the choice between handling another message, initiating the transmission of queued data packets or generating a new route request. \(\mathtt{NEWPKT}\) and \( \mathtt{PKT}\) describe all actions performed by a node when a data packet is received. The former process handles a newly injected packet. The latter describes all actions performed when a node receives data from another node via the protocol. \(\mathtt{RREQ}\) models all events that might occur after a route request message has been received. Similarly, \(\mathtt{RREP}\) describes the reaction of the protocol to an incoming route reply. \(\mathtt{RERR}\) models the part of AODV that handles error messages. The last process \(\mathtt{QMSG}\) queues incoming messages. Whenever a message is received, it is first stored in a message queue. When the corresponding node is able to handle a message, it pops the oldest message from the queue and handles it. An AODV network is an encapsulated parallel composition of node expressions, each with a different node address (identifier), and all initialised with the parallel composition \(\mathtt{AODV}(\dots )\mathbin {\langle \!\langle }\mathtt{QMSG}(\dots )\).
In this paper, we have room to present parts of the \(\mathtt{RREQ}\) process only, depicted in Process 4Footnote 12; the full formal specification of the entire protocol can be found in Appendix of [5]. There, we also discuss all differences between the untimed version of AODV, as formalised in [11, 15], and the newly developed timed version. These differences mostly consist of setting expiration times for routing table entries and other data maintained by AODV, and handling the expiration of this data.
A route discovery in AODV is initiated by a source node broadcasting a RREQ message; this message is subsequently re-broadcast by other nodes. Process 4 shows major parts of our process algebra specification for handling a RREQ message received by a node ip. The incoming message carries eight parameters, including hops, indicating how far the RREQ had travelled so far, rreqid, an identifier for this request, dip, the destination IP address, and sip, the sender of the incoming message; the parameters ip, sn and rt, storing the node’s address, sequence number and routing table, as well as rreqs and store, are maintained by the process RREQ itself.
Before handling the incoming message, the process first updates rreqs (Line 1), a list of (unique) pairs containing the originator IP address oip and a route request identifier rreqid received within the last PATH_DISCOVERY_TIME: the update removes identifiers that are too old. Based on this list, the node then checks whether it has recently received a RREQ with the same oip and rreqid.
If this is the case, the RREQ message is ignored, and the protocol continues to execute the main AODV process (Lines 3–4). If the RREQ is new (Line 5), the process updates the routing table by adding a “reverse route” entry to oip, the originator of the RREQ, via node sip, with distance hops+1 (Line 6). If there already is a route to oip in the node’s routing table rt, it is only updated with the new route if the new route is “better”, i.e., fresher and/or shorter and/or replacing an invalid route. The lifetime of this reverse route is updated as well (Line 7): it is set to the maximum of the currently stored lifetime and the minimal lifetime, which is determined by \(\mathtt{now} +2\cdot \mathtt{NET\_TRAVERSAL\_TIME}-2\cdot (\textit{hops}+1)\cdot \mathtt{NODE\_TRAVERSAL\_TIME}\) [29, Page 17]. The process also adds the message to the list of known RREQs (Line 8).
Lines 10–22 (only shown in Appendix of [5]) deal with the case where the node receiving the RREQ is the intended destination, i.e., dip=ip (Line 10).


Lines 23–45 deal with the case where the node receiving the RREQ is not the destination, i.e., \({\textit{dip}}\mathop {\ne }{\textit{ip}}\) (Line 23). The node can respond to the RREQ with a corresponding RREP on behalf of the destination node dip, if its route to dip is “fresh enough” (Line 26). This means that (a) the node has a valid route to dip, (b) the destination sequence number in the node’s current routing table entry \((\mathtt{sqn}({\textit{rt}},{\textit{dip}}))\) is greater than or equal to the requested sequence number to dip in the RREQ message, and (c) the node’s destination sequence number is trustworthy (\(\mathtt{sqnf}({\textit{rt}},{\!\textit{dip}})\mathbin =\mathtt{kno}\)). If these three conditions are met (Line 26), the node generates a RREP message, and unicasts it back to the originator node oip via the reverse route. Before unicasting the RREP message, the intermediate node updates the forward routing table entry to \(\textit{dip}\) by placing the last hop node (\(\textit{sip}\)) into the precursor list for that entry (Line 28). Likewise, it updates the reverse routing table entry to oip by placing the first hop \(\mathtt{nhop}({\textit{rt}},{\textit{dip}})\) towards \(\textit{dip}\) in the precursor list for that entry (Line 29). To generate the RREP message, the process copies the sequence number for the destination \(\textit{dip}\) from the routing table \(\textit{rt}\) into the destination sequence number field of the RREP message and it places its distance in hops from the destination (\(\mathtt{dhops}({\textit{rt}},{\textit{dip}})\)) in the corresponding field of the new reply (Line 31). The RREP message is unicast to the next hop along the reverse route back to the originator of the corresponding RREQ message. If this unicast is successful, the process goes back to the AODV routine (Line 32). If the unicast of the RREP fails, we proceed with Lines 33–40, in which a route error (RERR) message is generated and sent. This conditional unicast is implemented in our model with the (T-)AWN construct \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).P \blacktriangleright {Q}\). In the latter case, the node sends a RERR message to all nodes that rely on the broken link for one of their routes. For this, the process first determines which destination nodes are affected by the broken link, i.e., the nodes that have this unreachable node listed as a next hop in the routing table (not shown in the shortened specification). Then, it invalidates any affected routing table entries, and determines the list of precursors, which are the neighbouring nodes that have a route to one of the affected destination nodes via the broken link. Finally, a RERR message is sent via groupcast to all these precursors (Line 40).
If the node is not the destination and there is either no route to the destination \(\textit{dip}\) inside the routing table or the route is not fresh enough, the route request received has to be forwarded. This happens in Line 43. The information inside the forwarded request is mostly copied from the request received. Only the hop count is increased by 1 and the destination sequence number is set to the maximum of the destination sequence number in the RREQ packet and the current sequence number for \(\textit{dip}\) in the routing table. In case \(\textit{dip}\) is an unknown destination, \(\mathtt{sqn}({\textit{rt}},{\textit{dip}})\) returns the unknown sequence number 0.
To ensure that our time-free model from [11, 15] accurately captures the intended behaviour of AODV [29], we spent a long time reading and interpreting the RFC, inspecting open-source implementations, and consulting network engineers. We now prove that our timed version of AODV behaves similar to our original formal specification, and hence (still) captures the intended behaviour.
Theorem 7
The timed version of AODV (as sketched in this paper, and presented in [5]) is a proper extension of the untimed version (as presented in [11]). By this we mean that if all timing constants, such as ACTIVE_ROUTE_TIMEOUT, are set to \(\infty \), and the maximal number of pending route request retries RREQ_RETRIES is set to 1, then the (T-AWN) transition systems of both versions of AODV are weakly bisimilar.
Proof Sketch
First, one shows that the newly introduced functions, such as exp_rreqs and setTime_rt do not change the data state in case the time parameters equal \(\infty \); and hence lead to transitions of the form  . This kind of transitions are the ones that make the bisimulation weak, since they do not occur in the formal specification of [11]. Subsequently, one proves that all other transitions are basically identical.
. This kind of transitions are the ones that make the bisimulation weak, since they do not occur in the formal specification of [11]. Subsequently, one proves that all other transitions are basically identical.
3.3 Loop Freedom
Loop freedom is a critical property for any routing protocol, but it is particularly relevant and challenging for WMNs and MANETs. “A routing-table loop is a path specified in the nodes’ routing tables at a particular point in time that visits the same node more than once before reaching the intended destination” [12]. Packets caught in a routing loop can quickly saturate the links and have a detrimental impact on network performance.
For AODV and many other protocols sequence numbers are used to guarantee loop freedom. Such protocols usually claim to be loop free due to the use of monotonically increasing sequence numbers. For example, AODV “uses destination sequence numbers to ensure loop freedom at all times (even in the face of anomalous delivery of routing control messages), ...” [29]. It has been shown that sequence numbers do not a priori guarantee loop freedom [16]; for some plausible interpretationsFootnote 13 of different versions of AODV, however, loop freedom has been proven [3, 11, 15, 19, 25, 30, 34, 35]Footnote 14. With the exception of [3], all these papers consider only untimed versions of AODV. As mentioned in Sect. 1 untimed analyses revealed many shortcomings of AODV; hence they are necessary. At the same time, a timed analysis is required as well. [3] shows that the premature deletion of invalid routes, and a too quick restart of a node after a reboot, can yield routing loops. Since then, AODV has changed to such a degree that the examples of [3] do not apply any longer.
In [13], “it is shown that the use of a \(\mathtt{DELETE\_PERIOD}\) in the current AODV specification can result in loops”. However, the loop constructed therein at any time passes through at least one invalid routing table entry. As such, it is not a routing loop in the sense of [11, 15]—we only consider loops consisting of valid routing table entries, since invalid ones do not forward data packets. In a loop as in [13] data packets cannot be sent in circles forever.
It turns out that AODV as standardised in the RFC (and carefully formalised in Sect. 3.2 and the Appendix of [5]) is not loop free. A potential cause of routing loops, sketched in Fig. 1, is a situation where a node B has a valid routing table entry for a destination D (in Fig. 1 denoted  ), but the next hop C no longer has a routing table entry for D (\(D{:}-\)), valid or invalid. In such a case, C might search for a new route to D and create a new routing table entry pointing to B as next hop, or to a node A upstream from B. We refer to this scenario as a case of premature route expiration.
), but the next hop C no longer has a routing table entry for D (\(D{:}-\)), valid or invalid. In such a case, C might search for a new route to D and create a new routing table entry pointing to B as next hop, or to a node A upstream from B. We refer to this scenario as a case of premature route expiration.
A related scenario, which we also call premature route expiration, is when a node C sends a RREP message with destination D or a RREQ messages with originator D to a node B, but looses its route to D before that message arrives. This scenario can easily give rise to the scenario above.
Premature route expiration can be avoided by setting DELETE_PERIOD to \(\infty \), which is essentially the case in the untimed version of AODV (cf. Theorem 7). In that case, no routing table entry expires or is erased. Hence, the situation where C no longer has a routing table entry for D is prevented.
In [11] we studied 5184 possible interpretations of the AODV RFC [29], a proliferation due to ambiguities, contradictions and cases of underspecification that could be resolved in multiple ways. In 5006 of these readings of the standard, including some rather plausible ones, we found routing loops, even when excluding all loops that are due to timing issues [11, 16]. In [11, 15, 19] we have chosen a default reading of the RFC that avoids these loops, formalised it in AWN, and formally proved loop freedom, still assuming (implicitly) \(\mathtt{DELETE\_PERIOD}= \infty \).
After taking this hurdle, the present paper continues the investigation by allowing arbitrary values for time parameters and for RREQ_RETRIES; hence dropping the simplifying assumption that \(\mathtt{DELETE\_PERIOD}= \infty \).
One of our key results is that for the formalisation of AODV presented here, premature route expiration is the only potential source of routing loops. Under the assumption that premature route expiration does not occur, it turns out that, with minor modifications, the loop freedom proof of [11, 15] applies to our timed model of AODV as well. A proof of this result is presented in Appendix of [5]. There, we revisit all the invariants from [11] that contribute to the loop-freedom proof, and determine which of them are still valid in the timed setting, and how others need to be modified.
It is trivial to find an example where premature route expiration does occur in AODV, and a routing loop ensues. This can happen when a message spends an inordinate amount of time in the queue of incoming messages of a node. However, this situation tends not to occur in realistic scenarios. To capture this, we now make the assumption that the transmission time of a message plus the period it spends in the queue of incoming messages of the receiving node, is bounded by NODE_TRAVERSAL_TIME. We also assume that the period a route request travels through the network is bounded by NET_TRAVERSAL_TIME.
These assumptions eliminate the “trivial” counterexample mentioned above. As we show in Appendix of [5], we now almost can prove an invariant that essentially says that premature route expiration does not occur. Following the methodology from [11, 15, 19], we establish our invariants by showing that they hold in all possible initial states of AODV, and are preserved under the transitions of our operation semantics, which correspond to the line numbers in our process algebraic specification.
We said “almost”, because, as indicated in Appendix of [5], our main invariant is not preserved by five lines of our AODV specification. Additionally, we need to make the assumption that when a RREQ message is forwarded, the forwarding node has a valid routing table entry to the originator of the route request. This does not hold for our formalisation of AODV: in Process 4 no check is performed on \(\textit{oip}\), only the routing table to the destination node \(\textit{dip}\) has to satisfy certain conditions (Lines 23 and 41).
It turns out that for each of these failures we can construct an example of premature route expiration, and, by that, a counterexample to loop freedom.
However, if we skip all five offending lines (or adapt them in appropriate ways) and make a small change to process RREQ that makes the above assumption valid,Footnote 15 we obtain a proof of loop freedom for the resulting version of AODV. This follows immediately from the invariants established in Appendix of [5].
4 Conclusion
In this paper we have proposed T-AWN, a timed process algebra for wireless networks. We are aware that there are many other timed process algebras, such as timed CCS [24], timed CSP [28, 32], timed ACP [1], ATP [27] and TPL [17]. However, none of these algebras provides the unique set of features needed for modelling and analysing protocols for wireless networks (e.g. a conditional unicast).Footnote 16 These features are provided by (T-)AWN, though. Our treatment of time is based on design decisions that appear rather different from the ones in [1, 24, 27, 28, 32]. Our approach appears to be closest to [17], but avoiding the negative premises that play a crucial role in the operational semantics of [17].
We have illustrated the usefulness of T-AWN by analysing the Ad hoc On-Demand Distance Vector routing protocol, and have shown that, contrary to claims in the literature and to common belief, it fails to be loop free. We have also discussed boundary conditions for a fix ensuring that the resulting protocol is loop free.
Notes
- 1.
A comparison between AWN and other process algebras can be found in [11, Sect. 11].
- 2.
In reality, communication is only half-duplex: a single-interface network node cannot receive messages while sending and hence messages can be lost. However, the CSMA protocol used at the link layer—not modelled by (T-)AWN—keeps the probability of packet loss due to two nodes (within range) sending at the same time rather low.
- 3.
To be precise, we forgive very short interruptions in the connection between two nodes—those that begin and end within the same unit of time.
- 4.
Another solution would be to assume that a broadcast-receiving process can receive multiple messages in parallel. In case the process is meant to add incoming messages to a message queue (as happens in our application to AODV), one can assume that a message that is being received in parallel is added to that queue as soon as its receipt is complete. However, such a model is equivalent to one in which only the very last stage of the receipt action is modelled.
- 5.
The application layer that initiates packet sending and/or awaits receipt of a packet.
- 6.
As operators we also allow partial functions with the convention that any atomic formula containing an undefined subterm evaluates to false.
- 7.
An expression p is guarded if each call of a process name \(X(\textit{exp}_1,\ldots ,\textit{exp}_n)\) occurs with a subexpression
 , \(\mathbf [\![ \mathtt{var}:=\textit{exp}\mathbf ]\!] q\), \(\alpha .q\) or \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).q \blacktriangleright r\) of p.
, \(\mathbf [\![ \mathtt{var}:=\textit{exp}\mathbf ]\!] q\), \(\alpha .q\) or \(\mathbf{unicast }({\textit{dest}},{\textit{ms}}).q \blacktriangleright r\) of p. - 8.
Similar to \(\mathbf{receive }(\mathtt{msg}).p\) having a transition for each possible incoming message m.
- 9.
Rule (n-t) ensures that only those \(R\mathbin {:}w_1\)-transitions survive for which R is the current transmission range of the node.
- 10.
To avoid the function \(\mathtt{newpkt}\) we could have introduced a new primitive newpkt, which is dual to deliver.
- 11.
- 12.
The numbering scheme is consistent with the one in [5].
- 13.
By a plausible interpretation of a protocol standard written in English prose we mean an interpretation that fills the missing bits, and resolves ambiguities and contradictions occurring in the standard in a sensible and meaningful way.
- 14.
The proofs in [3, 30] are incorrect; the model of [34] does not capture the full behaviour of the routing protocol; and [35] is based on a subset of AODV that does not cover the “intermediate route reply” feature, a source of loops. In [25] a draft of a new version of AODV is modelled, without intermediate route reply. For a more detailed discussion see [15].
- 15.
The change basically introduces the test “\(\textit{oip}\in \mathtt{vD}(\textit{rt})\)” in Line 41 or 9 of Process 4.
- 16.
This is similar to the untimed situation. A detailed comparison between AWN and other process calculi for wireless networks is given in [11, Sect. 11.1]; this discussion can directly be transferred to the timed case.
References
Baeten, J., Bergstra, J.: Discrete time process algebra. Formal Aspects Comput. 8(2), 188–208 (1996). doi:10.1007/BF01214556
Bergstra, J.A., Klop, J.W.: Observation of strains: algebra of communicating processes. In: de Bakker, J.W., Hazewinkel, M., Lenstra, J.K. (eds) Mathematics and Computer Science, CWI Monograpph 1, pp. 89–138. North-Holland (2011)
Bhargavan, K., Obradovic, D., Gunter, C.A.: Formal verification of standards for distance vector routing protocols. J. ACM 49(4), 538–576 (2002). doi:10.1145/581771.581775
Bolognesi, T., Brinksma, E.: Introduction to the ISO Specification Language LOTOS. Comput. Netw. 14, 25–59 (1987). doi:10.1016/0169-7552(87)90085-7
Bres, E., van Glabbeek, R.J., Höfner, P.: A Timed Process Algebra for Wireless Networks with an Application in Routing. Technical Report 9145, NICTA (2016). http://nicta.com.au/pub?id=9145
Chiyangwa, S., Kwiatkowska, M.: A timing analysis of AODV. In: Steffen, M., Zavattaro, G. (eds.) FMOODS 2005. LNCS, vol. 3535, pp. 306–321. Springer, Heidelberg (2005). doi:10.1007/11494881_20
Clausen, T., Jacquet, P.: Optimized Link State Routing Protocol (OLSR). RFC 3626 (Experimental), Network Working Group (2003). http://www.ietf.org/rfc/rfc3626.txt
Cranen, S., Mousavi, M.R., Reniers, M.A.: A rule format for associativity. In: van Breugel, F., Chechik, M. (eds.) CONCUR 2008. LNCS, vol. 5201, pp. 447–461. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85361-9_35
Edenhofer, S., Höfner, P.: Towards a rigorous analysis of AODVv2 (DYMO). In: Rigorous Protocol Engineering (WRiPE 2012). IEEE (2012). doi:10.1109/ICNP.2012.6459942
Fehnker, A., van Glabbeek, R., Höfner, P., McIver, A., Portmann, M., Tan, W.L.: A process algebra for wireless mesh networks. In: Seidl, H. (ed.) Programming Languages and Systems. LNCS, vol. 7211, pp. 295–315. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28869-2_15
Fehnker, A., van Glabbeek, R.J., Höfner, P., McIver, A.K., Portmann, M., Tan, W.L.: A Process Algebra for Wireless Mesh Networks used for Modelling, Verifying and Analysing AODV. Technical report 5513, NICTA (2013). http://arxiv.org/abs/1312.7645
Garcia-Luna-Aceves, J.J.: A unified approach to loop-free routing using distance vectors or link states. In: SIGCOMM 1989, SIGCOMM Computer Communication Review 19(4), pp. 212–223. ACM Press (1989). doi:10.1145/75246.75268
Garcia-Luna-Aceves, J.J., Rangarajan, H.: A new framework for loop-free on-demand routing using destination sequence numbers. In: MASS 2004, pp. 426–435. IEEE (2004). doi:10.1109/MAHSS.2004.1392182
van Glabbeek, R.J.: The linear time - branching time spectrum II; the semantics of sequential systems with silent moves. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 66–81. Springer, Heidelberg (1993). doi:10.1007/3-540-57208-2_6
Glabbeek, R.J., Höfner, P., Portmann, M., Tan, W.L.: Modelling and Verifying the AODV Routing Protocol. Distributed Computing (2016) (to appear)
van Glabbeek, R.J., Höfner, P., Tan, W.L., Portmann, M.: Sequence numbers do not guarantee loop freedom –AODV can yield routing loops–. In: MSWiM 2013, pp. 91–100. ACM Press (2013). doi:10.1145/2507924.2507943
Hennessy, M., Regan, T.: A process algebra for timed systems. Inf. Comput. 117(2), 221–239 (1995). doi:10.1006/inco.1995.1041
Hoare, C.A.R.: Communicating Sequential Processes. Prentice Hall, Englewood Cliffs (1985)
Höfner, P., van Glabbeek, R.J., Tan, W.L., Portmann, M., McIver, A.K., Fehnker, A.: A Rigorous analysis of AODV and its variants. In: MSWiM 2012, pp. 203–212. ACM Press (2012). doi:10.1145/2387238.2387274
IEEE: IEEE Standard for Information Technology—Telecommunications and information exchange between systems—Local and metropolitan area networks —Specific requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications Amendment 10: Mesh Networking (2011). doi:10.1109/IEEESTD.2011.6018236
Lynch, N., Tuttle, M.: An introduction to input/output automata. CWI-Q. 2(3), 219–246 (1989). Centrum voor Wiskunde en Informatica, Amsterdam
McCune, W.W.: Prover9 and Mace4. http://www.cs.unm.edu/ mccune/prover9. Accessed 10 October 2015
Milner, R.: Communication and Concurrency. Prentice Hall, Upper Saddle River (1989)
Moller, F., Tofts, C.: A temporal calculus of communicating systems. In: Baeten, J.C.M., Klop, J.W. (eds.) CONCUR 1990. LNCS, vol. 458, pp. 401–415. Springer, Heidelberg (1990). doi:10.1007/BFb0039073
Namjoshi, K.S., Trefler, R.J.: Loop freedom in AODVv2. In: Graf, S., Viswanathan, M. (eds.) FORTE 2015. LNCS, vol. 9039, pp. 98–112. Springer, Heidelberg (2015). doi:10.1007/978-3-319-19195-9_7
Neumann, A., Aichele, M., Lindner, C., Wunderlich, S.: Better Approach To Mobile Ad-hoc Networking (B.A.T.M.A.N.). Internet-Draft (Experimental), Network Working Group (2008). http://tools.ietf.org/html/draft-openmesh-b-a-t-m-a-n-00
Nicollin, X., Sifakis, J.: The algebra of timed processes, ATP: theory and application. Inf. Comput. 114(1), 131–178 (1994). doi:10.1006/inco.1994.1083
Ouaknine, J., Schneider, S.: Timed CSP: a retrospective. Electronic Notes Theor. Comput. Sci. 162, 273–276 (2006). doi:10.1016/j.entcs.2005.12.093
Perkins, C.E., Belding-Royer, E.M., Das, S.: Ad hoc On-Demand Distance Vector (AODV) Routing. RFC 3561 (Experimental), Network Working Group (2003). http://www.ietf.org/rfc/rfc3561.txt
Perkins, C.E., Royer, E.M.: Ad-hoc on-demand distance vector routing. In: Mobile Computing Systems and Applications (WMCSA 1999), pp. 90–100. IEEE (1999). doi:10.1109/MCSA.1999.749281
Plotkin, G.D.: A structural approach to operational semantics. J. Logic Algebraic Program. 60–61, 17–139 (2004). doi:10.1016/j.jlap.2004.05.001. Originally appeared in (1981)
Reed, G., Roscoe, A.: A timed model for communicating sequential processes. In: Kott, L. (ed.) ICALP 1986. LNCS, vol. 226, pp. 314–323. Springer, Heidelberg (1986). doi:10.1007/3-540-16761-7_81
de Simone, R.: Higher-level synchronising devices in meije-SCCS. Theor. Comput. Sci. 37, 245–267 (1985). doi:10.1016/0304-3975(85)90093-3
Singh, A., Ramakrishnan, C.R., Smolka, S.A.: A process calculus for Mobile Ad Hoc Networks. Sci. Comput. Program. 75, 440–469 (2010). doi:10.1016/j.scico.2009.07.008
Zhou, M., Yang, H., Zhang, X., Wang, J.: The proof of AODV loop freedom. In: Wireless Communications & Signal Processing (WCSP 2009), IEEE (2009). doi:10.1109/WCSP.2009.5371479
Acknowledgement
NICTA is funded by the Australian Government through the Department of Communications and the Australian Research Council through the ICT Centre of Excellence Program.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bres, E., van Glabbeek, R., Höfner, P. (2016). A Timed Process Algebra for Wireless Networks with an Application in Routing. In: Thiemann, P. (eds) Programming Languages and Systems. ESOP 2016. Lecture Notes in Computer Science(), vol 9632. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49498-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-49498-1_5
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49497-4
Online ISBN: 978-3-662-49498-1
eBook Packages: Computer ScienceComputer Science (R0)




 iff
iff  for some
for some  iff
iff  for some
for some  iff
iff  for some
for some  iff
iff  for some
for some  .
. .
. .
. .
. iff
iff  .
. iff
iff 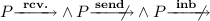 .
. iff
iff  .
.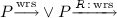 iff
iff  .
.

 ,
, 