Abstract
By integrating constructs from the \(\lambda \)-calculus and the \(\pi \)-calculus, in higher-order process calculi exchanged values may contain processes. This paper studies the relative expressiveness of \(\mathsf {HO}\pi \), the higher-order \(\pi \)-calculus in which communications are governed by session types. Our main discovery is that \(\mathsf {HO}\), a subcalculus of \(\mathsf {HO}\pi \) which lacks name-passing and recursion, can serve as a new core calculus for session-typed higher-order concurrency. By exploring a new bisimulation for \(\mathsf {HO}\), we show that \(\mathsf {HO}\) can encode \(\mathsf {HO}\pi \) fully abstractly (up to typed contextual equivalence) more precisely and efficiently than the first-order session \(\pi \)-calculus (\(\pi \)). Overall, under session types, \(\mathsf {HO}\pi \), \(\mathsf {HO} \), and \(\pi \) are equally expressive; however, \(\mathsf {HO}\pi \) and \(\mathsf {HO} \) are more tightly related than \(\mathsf {HO}\pi \) and \(\pi \).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Type-preserving compilations are important in the design of functional and object-oriented languages: type information has been used to, e.g., justify code optimizations and reason about programs [18, 21, 38]. A vast literature on expressiveness in concurrency theory also studies compilations (or encodings) [8, 10, 16, 26, 31]: they are used to transfer reasoning techniques across calculi, and to implement process constructs using simpler ones. In this work, we study relative expressiveness via type-preserving encodings for \(\mathsf {HO}\pi \), a higher-order process language that integrates message-passing concurrency with functional features. We consider source and target calculi coupled with session types [11] denoting interaction protocols. Building on untyped frameworks for relative expressiveness [10], we propose type preservation as a new criterion for precise encodings. We identify \(\mathsf {HO}\), a new core calculus for higher-order session concurrency without name passing. We show that \(\mathsf {HO}\) can encode \(\mathsf {HO}\pi \) precisely and efficiently. Requiring type preservation makes this encoding far from trivial: we crucially exploit advances on session type duality [2, 3] and recent characterisations of typed contextual equivalence [14]. We develop a full hierarchy of variants of \(\mathsf {HO}\pi \) based on precise encodings: our encodings are type-preserving and fully abstract up to typed behavioural equalities. Figure 1 illustrates this hierarchy; the variants of \(\mathsf {HO}\pi \) are explained next.
Encodability in higher-order sessions. Precise encodings are defined in Definition 15.
Context. In session-based concurrency, interactions are organised into sessions, basic communication units. Interaction patterns can then be abstracted as session types [11], against which specifications may be checked. Session type \(?(U) ; S\) (resp. \(!\langle U \rangle ; S\)) describes a protocol that first receives (resp. sends) a value of type U and then continues as protocol S. Also, given an index set I, types &\(\{l_i:S_i\}_{i \in I}\) and \(\oplus \{l_i:S_i\}_{i \in I}\) define, respectively, external and internal choice constructs for a labelled choice mechanism; types \(\mu \mathsf {t}.S\) and \(\texttt {end}\) denote recursive and completed protocols, respectively. In the \(\pi \)-calculus, session types describe the intended interactive behaviour of the names in a process [11].
Session-based concurrency has also been casted in higher-order process calculi which, by combining features from the \(\lambda \)-calculus and the \(\pi \)-calculus, enable the exchange of values that may contain processes [9, 22]. The higher-order calculus with sessions studied here, called \(\mathsf {HO}\pi \), can specify protocols involving code mobility: it includes constructs for synchronisation along shared names, session communication (value passing, labelled choice) along linear names, recursion, (first-order) abstractions and applications. That is, values in communications include names but also (first-order) abstractions—functions from name identifiers to processes. (In contrast, we rule out higher-order abstractions—functions from processes to processes.) Abstractions can be linear or shared; their types are denoted \(C\!\! \multimap \!\! \diamond \) and \(C\!\! \rightarrow \!\! \diamond \), respectively (C denotes a name). In \(\mathsf {HO}\pi \) we may have processes with a session type such as, e.g.,
S is the type of a server that offers (&) three different behaviours to a client: to upload a linear function, to download a shared function, or to quit the protocol. Following a client’s selection (\(\oplus \)), the server sends a message (\(\mathsf {ok}\) or \(\mathsf {bye}\)) before closing the session.
Expressiveness of \(\mathsf {HO}\pi \). We study the type-preserving, relative expressivity of \(\mathsf {HO}\pi \). As expected from known literature in the untyped setting [32], the first-order session \(\pi \)-calculus [11] (here denoted \(\pi \)) can encode \(\mathsf {HO}\pi \) preserving session types. In this paper, our main discovery is that \(\mathsf {HO}\pi \) without name-passing and recursion can serve as a core calculus for higher-order session concurrency.We call this core calculus \(\mathsf {HO}\). We show that \(\mathsf {HO}\) can encode \(\mathsf {HO}\pi \) more efficiently than \(\pi \). In addition, in the higher-order session typed setting, \(\mathsf {HO}\) offers more tractable bisimulation techniques than \(\pi \) (cf. Sect. 5.2).
Challenges and Contributions. We assess the expressivity of \(\mathsf {HO}\pi \), \(\mathsf {HO}\), and \(\pi \) as delineated by session types. We introduce type-preserving encodings: type information is used to define encodings and to retain the semantics of session protocols. Indeed, not only we require well-typed source processes are encoded into well-typed target processes: we demand that session type constructs (input, output, branching, select) used to type the source process are preserved by the typing of the target process. This criterion is included in our notion of precise encoding (Definition 15), which extends encodability criteria for untyped processes with full abstraction. Full abstraction results are stated up to two behavioural equalities that characterise barbed congruence: characteristic bisimilarity (\(\approx ^\texttt {C}\), defined in [14]) and higher-order bisimilarity (\(\approx ^\texttt {H}\)), introduced in this work. It turns out that \(\approx ^\texttt {H}\) offers more direct reasoning than \(\approx ^\texttt {C}\). Using precise encodings we establish strong correspondences between \(\mathsf {HO}\pi \) and its variants—see below.
One main contribution is an encoding of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) (Sect. 7.1). Since \(\mathsf {HO}\) lacks both name-passing and recursion, this encoding involves two key challenges:
-
a.
In known (typed) encodings of name-passing into process-passing [36] only the output capability of names can be sent—a received name cannot be used in later inputs. This is far too limiting in \(\mathsf {HO}\pi \), where session names may be passed around (delegation) and types describe interaction structures, rather than “loose” name capabilities.
-
b.
Known encodings of recursion in untyped higher-order calculi do not carry over to session typed calculi such as \(\mathsf {HO}\pi \), because linear abstractions cannot be copied/duplicated. Hence, the discipline of session types limits the possibilities for representing infinite behaviours—even simple forms, such as input-guarded replication.
Our encoding overcomes these two obstacles, as we discuss in Sect. 2.
Additional technical contributions include: (i) the encodability of \(\mathsf {HO}\) into \(\pi \) (Sect. 7.2); (ii) extensions of our encodability results to richer settings (Sect. 8); (iii) a non encodability result showing that shared names strictly add expressive power to session calculi (Sect. 7.4). In essence, (i) extends known results for untyped processes [32] to the session typed setting. Concerning (ii), we develop extensions of our encodings to
-
-
The extension of \(\mathsf {HO}\pi \) with higher-order abstractions (\(\mathsf {HO\pi ^{+}}\));
-
-
The extension of \(\mathsf {HO}\pi \) with polyadic name passing and abstraction (\(\mathsf {HO}\,{\widetilde{\pi }}\));
-
-
The super-calculus of \(\mathsf {HO\pi ^{+}}\) and \(\mathsf {HO}\,{\widetilde{\pi }}\) (\(\mathsf {HO}\,{\widetilde{\pi }}^{\,+}\)), equivalent to the calculus in [22].
Figure 1 summarises our encodability results: they connect \(\mathsf {HO}\pi \) with existing higher-order process calculi [22], and highlight the status of \(\mathsf {HO}\) as the core calculus for session concurrency. Finally, to our knowledge we are the first to prove the non encodability result (iii), exploiting session determinacy and typed equivalences.
Outline. Section 2 overviews key ideas of the precise encoding of \(\mathsf {HO}\pi \) into \(\pi \). Section 3 presents \(\mathsf {HO}\pi \) and its subcalculi (\(\mathsf {HO}\) and \(\pi \)); Sect. 4 summarises their session type system. Section 5 presents behavioural equalities for \(\mathsf {HO}\pi \): we recall definitions of barbed congruence and characteristic bisimilarity [14], and introduce higher-order bisimilarity. We show that these three typed relations coincide (Theorem 2). Section 6 defines precise encodings by extending encodability criteria for untyped processes. Section 7 gives precise encodings of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) and of \(\mathsf {HO}\pi \) into \(\pi \) (Theorems 3 and 4). Mutual encodings between \(\pi \) and \(\mathsf {HO}\) are derivable; all these calculi are thus equally expressive. Via empirical and formal comparisons between these two precise encodings, in Sect. 7.3 we establish that \(\mathsf {HO}\pi \) and \(\mathsf {HO}\) are more tightly related than \(\mathsf {HO}\pi \) and \(\pi \) (Theorem 5). Moreover, we prove the impossibility of encoding communication along shared names using linear names (Theorem 6). In Sect. 8 we show encodings of \(\mathsf {HO\pi ^{+}}\) and \(\mathsf {HO}\,{\widetilde{\pi }}\) into \(\mathsf {HO}\pi \) (Theorems 7 and 8). Section 9 collects concluding remarks and reviews related works. Omitted definitions and proofs are in [15].
2 Overview: Encoding Name Passing into Process Passing
A Precise Encoding of Name-Passing into Process-Passing. As mentioned above, our encoding of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) (Sect. 7.1) should (a) enable the communication of arbitrary names, as required to represent delegation, and (b) address the fact that linearity of session types limits the possibilities for representing infinite behaviour. To encode name passing into \(\mathsf {HO}\) we “pack” the name to be sent into an abstraction; upon reception, the receiver “unpacks” this object following a precise protocol on a fresh session:


Above, a, b are names and s and \(\overline{s}\) are linear session names (endpoints). Processes \(a !\langle V \rangle . P\) and \(a ?(x) . P\) denote output and input at a; abstractions and applications are denoted \(\lambda x.P\) and \((\lambda x.P)a\). Processes \((\nu \, s)(P)\) and \(\mathbf 0 \) represent hiding and inaction. Thus, following a communication on a, a (deterministic) reduction between s and \(\overline{s}\) guarantees that b is properly unpacked by means of abstraction passing and appropriate applications. Notice that the above encoding requires three extra reduction steps to mimic a name communication step in \(\mathsf {HO}\pi \). Also, an output action in the source process is translated into an output action in the encoded process (and similarly for input). This is key to ensure the preservation of session type operators mentioned above (cf. Definition 13).
As hinted at above, a challenge in encoding \(\mu X. P\) is preserving linearity of session names. Intuitively, we encode the recursion body P as an abstraction \(\lambda \tilde{x}.\,\big \lfloor \!\big \lfloor P\big \rfloor \!\big \rfloor ^{}_\sigma \) in which each session name of P (included in set \(\sigma \)) is converted into a name variable in \(\tilde{x}\). Since \(\lambda \tilde{x}.\,\big \lfloor \!\big \lfloor P\big \rfloor \!\big \rfloor ^{}_\sigma \) does not mention (linear) session names, we may embed it into a “duplicator” process which implements recursion using higher-order communication [40]. The encoding of the recursion variable X invokes this duplicator in a by-need fashion: it receives \(\lambda \tilde{x}.\,\big \lfloor \!\big \lfloor P\big \rfloor \!\big \rfloor ^{}_\sigma \) and uses two copies of it: one copy allows us to obtain P through the application of the session names of P; the other allows us to invoke the duplicator when needed. Interestingly, for this encoding to work we require non-tail recursive session types; this exploits recent advances on the theory of duality for session types [2, 3].
A Plausible Encoding That is Not Precise. Our notion of precise encoding (Definition 15) requires the translation of both process and types; it admits only process mappings that preserve session types and are fully abstract. Thus, our encodings not only exhibit strong behavioural correspondences, but also relate source and target processes with consistent communication structures described by session types. These requirements are demanding and make our developments far from trivial. In particular, requiring type preservation may rule out other plausible encoding strategies. To illustrate this point, consider the following alternative encoding of name-passing into \(\mathsf {HO} \):Footnote 1


Intuitively, the encoding of input takes the initiative by sending an abstraction containing the encoding of its continuation Q; the encoding of output applies this received value to name b. Hence, this mapping entails a “role inversion”: outputs are translated into inputs, and inputs are translated into outputs. Although fairly reasonable, we will see that the encoding \([\![\cdot ]\!]^u\) is not type preserving. Consequently, it is also not precise. Since individual prefixes (input, output, branching, select) represent actions in a structured communication sequence (i.e., a protocol abstracted by a session type), the encoding \([\![\cdot ]\!]^u\) would simply alter the meaning of the session protocol in the source language.
3 Higher-Order Session \(\pi \)-Calculi
We introduce the higher-order session \(\pi \) -calculus (\(\mathsf {HO}\pi \)). We define syntax, operational semantics, and its sub-calculi (\(\pi \) and \(\mathsf {HO}\)). A type system and behavioural equivalences are introduced in Sects. 4 and 5. Extensions of \(\mathsf {HO}\pi \) with higher-order abstractions and polyadicity (noted \(\mathsf {HO\pi ^{+}}\) and \(\mathsf {HO}\,{\widetilde{\pi }}\), respectively) are discussed in Sect. 8.
3.1 \(\mathsf {HO}\pi \): Syntax, Operational Semantics, and Subcalculi
Syntax. The syntax of \(\mathsf {HO}\pi \) is defined in Fig. 2. \(\mathsf {HO}\pi \) it is a subcalculus of the language studied in [22]. It is also a variant of the language that we investigated in [14], which includes higher-order value applications.
Names \(a,b,c, \dots \) (resp. \(s, \overline{s}, \dots \)) range over shared (resp. session) names. Names \(m, n, t, \dots \) are session or shared names. Dual endpoints are \(\overline{n}\) with \(\overline{\overline{s}} = s\) and \(\overline{a} = a\). Variables are denoted with \(x, y, z, \dots \), and recursive variables are denoted with \(X, Y \dots \). An abstraction \(\lambda x.\,P\) is a process P with name parameter x. Values V, W include identifiers \(u, v, \ldots \) and abstractions \(\lambda x.\,P\) (first- and higher-order values, resp.).
Process terms \(P, Q, \ldots \) include usual prefixes for sending/receiving values V. Processes \(u \triangleleft l . P\) and \(u \triangleright \{l_i: P_i\}_{i \in I}\) are the usual session processes for selecting and branching [11]. Process \(V\, {u}\) is the application which substitutes name u on the abstraction V. Typing ensures that V is not a name. Recursion \(\mu X. P\) binds the recursive variable \(X\) in P. Constructs for inaction \(\mathbf 0 \), parallel composition \(P_1 \;|\;P_2\), and name restriction \((\nu \, n) P\) are standard. Session name restriction \((\nu \, s) P\) simultaneously binds endpoints s and \(\overline{s}\) in P. Functions \(\texttt {fv}(P)\) and \(\texttt {fn}(P)\) denote the sets of free variables and names. We assume V in \(u !\langle V \rangle .{P}\) does not include free recursive variables \(X\). If \(\texttt {fv}(P) = \emptyset \), we call P closed.
Operational Semantics. The operational semantics of \(\mathsf {HO}\pi \) is defined in terms of a reduction relation, denoted \(\longrightarrow \) and given in Fig. 3 (top). We briefly describe the rules. Rule \({{[\mathrm {\small App}]}}\) defines name application. Rule \({{[\mathrm {\small Pass}]}}\) defines a shared interaction at n (with \(\overline{n}=n\)) or a session interaction. Rule \({{[\mathrm {\small Sel}]}}\) is the standard rule for labelled choice/selection. Other rules are standard \(\pi \)-calculus rules. Reduction is closed under structural congruence, noted \(\equiv \) (cf. Fig. 3, bottom). We assume the expected extension of \(\equiv \) to values V. We write \(\longrightarrow ^*\) for a multi-step reduction.
Subcalculi. As motivated in the introduction, we define two subcalculi of \(\mathsf {HO}\pi \):
-
The core higher-order session calculus, denoted \(\mathsf {HO}\), lacks recursion and name passing; its formal syntax is obtained from Fig. 2 by excluding constructs in
 .
. -
The session \(\pi \) -calculus, denoted \(\pi \), lacks higher-order communication but includes recursion; its formal syntax is obtained from Fig. 2 by excluding constructs in
 .
.
Let \(\mathsf {C} \in \{\mathsf {HO}\pi , \mathsf {HO}, \pi \}\). We write \(\mathsf {C} ^{-\mathsf {sh}}\) to denote the calculus \(\mathsf {C} \) without shared names: we delete a, b from n. In Sect. 7 we shall demonstrate that \(\mathsf {HO}\pi \), \(\mathsf {HO} \), and \(\pi \) have the same expressivity, and that \(\mathsf {C} \) is strictly more expressive than \(\mathsf {C} ^{-\mathsf {sh}}\).
4 Session Types for \(\mathsf {HO}\pi \)
We define a session type system for \(\mathsf {HO}\pi \) and state type soundness (Theorem 1), its main property. Our system distills the key features of [22, 23] and so it is simpler.
The syntax of types of \(\mathsf {HO}\pi \) follows. We write \(\diamond \) to denote the process type.


Value type U includes first-order types C and higher-order types L. Types \(C\!\! \rightarrow \!\! \diamond \) and \(C\!\! \multimap \!\! \diamond \) denote shared and linear higher-order types, respectively. Session types, denoted by S, follow the standard binary session type syntax [11], with the extension that carried types U may be higher-order. Shared channel types are denoted \(\langle S \rangle \) and \(\langle L \rangle \). Types of \(\mathsf {HO}\) exclude  from value types U; the types of \(\pi \) exclude
from value types U; the types of \(\pi \) exclude  and
and  . From each \(\mathsf {C} \in \{\mathsf {HO}\pi , \mathsf {HO}, \pi \}\), \(\mathsf {C} ^{-\mathsf {sh}}\) excludes shared name types (\(\langle S \rangle \) and \(\langle L \rangle \)), from name type C.
. From each \(\mathsf {C} \in \{\mathsf {HO}\pi , \mathsf {HO}, \pi \}\), \(\mathsf {C} ^{-\mathsf {sh}}\) excludes shared name types (\(\langle S \rangle \) and \(\langle L \rangle \)), from name type C.
We write \(S \ \mathsf {dual}\ S'\) if S is the dual of \(S'\). Intuitively, session type duality is obtained by dualising ! by ?, ? by !, \(\oplus \) by&, and&by \(\oplus \), including the fixed point construction. We use the co-inductive definition of duality given in [2].
We consider shared, linear, and session environments, denoted \(\varGamma \), \(\varLambda \), and \(\varDelta \), resp.:
\(\varGamma \) maps variables and shared names to value types, and recursive variables to session environments; it admits weakening, contraction, and exchange principles. \(\varLambda \) maps variables to linear higher-order types; \(\varDelta \) maps session names to session types. Both \(\varLambda \) and \(\varDelta \) are only subject to exchange. Domains of \(\varGamma , \varLambda \) and \(\varDelta \) are assumed pairwise distinct. \(\varDelta _1\cdot \varDelta _2\) is the disjoint union of \(\varDelta _1\) and \(\varDelta _2\). We focus on balanced session environments:
Definition 1
(Balanced). We say that a session environment \(\varDelta \) is balanced if whenever \(s: S_1, \overline{s}: S_2 \in \varDelta \) then \(S_1 \ \mathsf {dual}\ S_2\).
Given the above intuitions for environments, the typing judgements for values V and processes P are self-explanatory. They are denoted \(\varGamma ; \varLambda ; \varDelta \vdash V \triangleright U\) and \(\varGamma ; \varLambda ; \varDelta \vdash P \triangleright \diamond \).
Figure 4 gives selected typing rules; see [15] for a full account. The shared type \(C\!\! \rightarrow \!\! \diamond \) is derived using rule (Prom) only if the value has a linear type with an empty linear environment. Rule (EProm) allows us to freely use a shared type variable as linear. Abstraction values are typed with rule (Abs). Application typing is governed by rule (App): we expect the type C of an application name u to match the type of the application variable x (i.e., \(C\!\! \multimap \!\! \diamond \) or \(C\!\! \rightarrow \!\! \diamond \)). In rule (Send), the type U of value V should appear as a prefix in the session type \(!\langle U \rangle ; S\) of u. Rule (Rcv) is its dual. Rules (Req) and (Acc) type interaction along shared names; the type of the sent/received object (S and L, resp.) should match the type of the sent/received subject (\(\langle S \rangle \) and \(\langle L \rangle \), resp.).
Definition 2
We define the relation \(\longrightarrow \) on session environments as:
We state type soundness for \(\mathsf {HO}\pi \); it implies type soundness for \(\mathsf {HO}\), \(\pi \), and \(\mathsf {C} ^{-\mathsf {sh}}\).
Theorem 1
(Type Soundness).Suppose \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \) with \(\varDelta \) balanced. Then \(P \longrightarrow P'\) implies \(\varGamma ; \emptyset ; \varDelta ' \vdash P' \triangleright \diamond \) and \(\varDelta = \varDelta '\) or \(\varDelta \longrightarrow \varDelta '\) with \(\varDelta '\) balanced.
5 Behavioural Theory for \(\mathsf {HO}\pi \)
We first define reduction-closed, barbed congruence (\(\cong \), Definition 7) as the reference equivalence relation for \(\mathsf {HO}\pi \) processes. We then define two characterisations of \(\cong \): characteristic and higher-order bisimilarities (denoted \(\approx ^\texttt {C}\) and \(\approx ^\texttt {H}\), cf. Definitions 8 and 9).
5.1 Reduction-Closed, Barbed Congruence (\(\cong \))
We consider typed relations \(\mathfrak {R}\) that relate closed terms whose session environments are balanced and confluent:
Definition 3
(Session Environment Confluence). Let \(\longrightarrow ^*\) denote multi-step reduction as in Definition 2. We denote \(\varDelta _1 \rightleftharpoons \varDelta _2\) if there exists \(\varDelta \) such that \(\varDelta _1 \longrightarrow ^*\varDelta \) and \(\varDelta _2 \longrightarrow ^*\varDelta \).
Definition 4
(Typed Relation). We say that \(\varGamma ; \emptyset ; \varDelta _1 \vdash P \triangleright \diamond \ \mathfrak {R}\ \varGamma ; \emptyset ; \varDelta _2 \vdash Q \triangleright \diamond \) is a typed relation whenever P and Q are closed; \(\varDelta _1\) and \(\varDelta _2\) are balanced; and \(\varDelta _1 \rightleftharpoons \varDelta _2\). We write \(\varGamma ;\varDelta _1\vdash P\ \mathfrak {R}\ \varDelta _2\vdash Q\) for the typed relation \(\varGamma ; \emptyset ; \varDelta _1 \vdash P \triangleright \diamond \ \mathfrak {R}\ \varGamma ; \emptyset ; \varDelta _2 \vdash Q \triangleright \diamond \).
As usual, a barb \(\downarrow _{n}\) is an observable on an output prefix with subject n [20]. A weak barb \(\Downarrow _{n}\) is a barb after zero or more reduction steps. Typed barbs \(\downarrow _{n}\) (resp. \(\Downarrow _{n}\)) occur on typed processes \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \). When n is a session name we require that its dual endpoint \(\overline{n}\) is not present in the session environment \(\varDelta \):
Definition 5
(Barbs). Let P be a closed process. We define:
-
1.
\(P \downarrow _{n}\) if \(P \equiv (\nu \, \tilde{m})(n !\langle V \rangle . P_2 \;|\;P_3), n \notin \tilde{m}\).
-
2.
\(\varGamma ; \varDelta \vdash P \downarrow _{n}\) if \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \) with \(P \downarrow _{n}\) and \(\overline{n} \notin \texttt {dom}(\varDelta )\). \(\varGamma ; \varDelta \vdash P \Downarrow _{n}\) if \(P \longrightarrow ^* P'\) and \(\varGamma ; \varDelta ' \vdash P' \downarrow _{n}\).
To define a congruence relation, we introduce the family \({\mathbb {C}}\) of contexts:
Definition 6
(Context). A context \({\mathbb {C}}\) is defined as:
Notation \({\mathbb {C}}[P]\) replaces the hole \(-\) in \({\mathbb {C}}\) with P.
We define reduction-closed, barbed congruence [12].
Definition 7
(Barbed Congruence). Typed relation \(\varGamma ;\varDelta _1\vdash P\ \mathfrak {R}\ \varDelta _2\vdash Q\) is a reduction-closed, barbed congruence whenever:
-
1.
If \(P \longrightarrow P'\) then there exist \(Q', \varDelta _1'\), \(\varDelta _2'\) such that \(Q \longrightarrow ^* Q'\) and \(\varGamma ;\varDelta _1'\vdash P'\ \mathfrak {R}\ \varDelta _2'\vdash Q'\);
-
2.
If \(\varGamma ;\varDelta _1 \vdash P \downarrow _{n}\) then \(\varGamma ;\varDelta _2 \vdash Q \Downarrow _{n}\);
-
3.
For all \({\mathbb {C}}\), there exist \(\varDelta _1'',\varDelta _2''\) such that \(\varGamma ;\varDelta _1''\vdash {\mathbb {C}}[P]\ \mathfrak {R}\ \varDelta _2''\vdash {\mathbb {C}}[Q]\);
-
4.
The symmetric cases of 1 and 2.
The largest such relation is denoted with \(\cong \).
5.2 Two Equivalence Relations: \(\approx ^\texttt {C}\) and \(\approx ^\texttt {H}\)
A Typed Labelled Transition System. In [14] we have characterised reduction-closed, barbed congruence for \(\mathsf {HO}\pi \) via a typed relation called characteristic bisimilarity. Its definition uses a typed labelled transition system (LTS) informed by session types. Given a label \(\ell \) (a visible action or \(\tau \)), we write \(\varGamma ; \emptyset ; \varDelta \vdash P \mathop {\longmapsto }\limits ^{\ell } \varDelta ' \vdash P'\) to denote (strong) transitions. Weak transitions are as expected: we write  for the reflexive, transitive closure of \(\mathop {\longmapsto }\limits ^{\tau }\),
for the reflexive, transitive closure of \(\mathop {\longmapsto }\limits ^{\tau }\),  for
for  , and
, and  for
for  if \(\ell \not = \tau \) and
if \(\ell \not = \tau \) and  otherwise. Intuitively, the transitions of a typed process should be enabled by its associated typing:
otherwise. Intuitively, the transitions of a typed process should be enabled by its associated typing:
As an example of how types enable transitions, consider the rule for input:
This rule states that a session environment can input a value if such a value is typed with an input prefix and is either a name m, a characteristic value \([\!\!(U)\!\!]_{\mathsf {c}}\), or a trigger value (the abstraction \(\lambda {x}.\,t ?(y) . (y\, {{x}})\)). A characteristic value is the simplest process that inhabits a type (here, the type U carried by the input prefix). The above rule is used to limit the input actions that can be observed from a session input prefix. For more details on the typed LTS and the characteristic process definition see [14]. Moreover, we define a (first-order) trigger process:
The trigger process \(t \Leftarrow V \! : \! U\) is is defined as a process input prefixed on a fresh name t: it applies a value on the characteristic process \([\![?(U) ; \texttt {end}]\!]^{s}\) (see [14] for details).
Characterising \(\cong \). We define characteristic and higher-order bisimilarities. While higher-order bisimilarity is a new equality, characteristic bisimilarity was introduced in [14].
Definition 8
(Characteristic Bisimilarity). A typed relation \(\mathfrak {R}\) is called a characteristic bisimulation if for all \(\varGamma ;\varDelta _1\vdash P_1\ \mathfrak {R}\ \varDelta _2\vdash Q_1\)
-
1.
Whenever \(\varGamma ;\varDelta _1\vdash P_1\mathop {\longmapsto }\limits ^{(\nu \, \tilde{m_1}) n !\langle V_1: U \rangle }\varDelta _1'\vdash P_2\), there exist \(Q_2\), \(V_2\), \(\varDelta '_2\) such that
 and, for fresh t, $$\begin{aligned} \varGamma ; \varDelta ''_1 \vdash {(\nu \, \tilde{m_1})(P_2 \;|\;t \Leftarrow V_1 \! : \! U_1)} \ \mathfrak {R}\ \varDelta ''_2 \vdash {(\nu \, \tilde{m_2})(Q_2 \;|\;t \Leftarrow V_2 \! : \! U_2)} \end{aligned}$$
and, for fresh t, $$\begin{aligned} \varGamma ; \varDelta ''_1 \vdash {(\nu \, \tilde{m_1})(P_2 \;|\;t \Leftarrow V_1 \! : \! U_1)} \ \mathfrak {R}\ \varDelta ''_2 \vdash {(\nu \, \tilde{m_2})(Q_2 \;|\;t \Leftarrow V_2 \! : \! U_2)} \end{aligned}$$ -
2.
For all \(\varGamma ;\varDelta _1\vdash P_1\mathop {\longmapsto }\limits ^{\ell }\varDelta _1'\vdash P_2\) such that \(\ell \) is not an output, there exist \(Q_2\), \(\varDelta '_2\) such that
 and \(\varGamma ;\varDelta _1'\vdash P_2\ \mathfrak {R}\ \varDelta _2'\vdash Q_2\); and
and \(\varGamma ;\varDelta _1'\vdash P_2\ \mathfrak {R}\ \varDelta _2'\vdash Q_2\); and -
3.
The symmetric cases of 1 and 2.
The largest such bisimulation is called characteristic bisimilarity and denoted by \(\approx ^\texttt {C}\).
Interestingly, for reasoning about \(\mathsf {HO}\pi \) processes we can also exploit the simpler higher-order bisimilarity. We replace triggers as in (1) with higher-order triggers:
We may then define:
Definition 9
(Higher-Order Bisimilarity). Higher-order bisimilarity, denoted by \(\approx ^\texttt {H}\), is defined by replacing Clause (1) in Definition 8 with the following clause:
Whenever \(\varGamma ;\varDelta _1\vdash P_1\mathop {\longmapsto }\limits ^{(\nu \, \tilde{m_1}) n !\langle V_1 \rangle }\varDelta _1'\vdash P_2\) then there exist \(Q_2\), \(V_2\), \(\varDelta '_2\) such that
 and, for fresh t,
and, for fresh t,
\(\begin{array}{lrlll} \!\!\varGamma ; \varDelta ''_1 \vdash {(\nu \, \tilde{m_1})(P_2 t \hookleftarrow V_1)} \ \mathfrak {R}\ \varDelta ''_2 \vdash {(\nu \, \tilde{m_2})(Q_2 \;|\;t \hookleftarrow V_2)} \end{array}\)
We state the following important result, which attests the significance of \(\approx ^\texttt {H}\):
Theorem 2
Typed relations \(\cong \), \(\approx ^\texttt {H}\), and \(\approx ^\texttt {C}\) coincide for \(\mathsf {HO}\pi \) processes.
Proof
Coincidence of \(\cong \) and \(\approx ^\texttt {C}\) was established in [14]. Coincidence of \(\approx ^\texttt {H}\) with \(\cong \) and \(\approx ^\texttt {C}\) is a new result: see [15] for details. \(\square \)
Remark 1
(Comparison between \(\approx ^\texttt {H}\) and \(\approx ^\texttt {C}\) ). The key difference between \(\approx ^\texttt {H}\) and \(\approx ^\texttt {C}\) is in the trigger process considered. Because of the application in (2), \(\approx ^\texttt {H}\) cannot be used to reason about processes in \(\pi \). In contrast, \(\approx ^\texttt {C}\) is more general: it can uniformly input characteristic, first- or higher-order values. This convenience comes at a price: the definition of (1) requires information on the type of V; in contrast, the higher-order trigger (2) is more generic and simple, as it works independently of the given type.
An up-to technique. Processes that do not use shared names are deterministic. The following up-to technique, based on determinacy properties, will be useful in proofs (Sect. 7). Recall that \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau }\varDelta '\vdash P'\) denotes an internal (typed) transition.
Notation 1
(Deterministic Transitions). We distinguish two kinds of \(\tau \)-transitions: session transitions, noted \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau _{s}}\varDelta '\vdash P'\), and \(\beta \) -transitions, noted \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau _{\beta }}\varDelta '\vdash P'\). Intuitively, \(\mathop {\longmapsto }\limits ^{\tau _{s}}\) results from a session communication (i.e., synchronization between two dual endpoints), while \(\mathop {\longmapsto }\limits ^{\tau _{\beta }}\) results from an application. We write \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau _{d}}\varDelta '\vdash P'\) to denote a session transition or a \(\beta \)-transition. See [15] for definitions of \(\mathop {\longmapsto }\limits ^{\tau _{\beta }}\) and \(\mathop {\longmapsto }\limits ^{\tau _{s}}\).
We have the following determinacy property; see [15] for details.
Lemma 1
( \(\tau \) -Inertness). (1) Let \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau _{d}}\varDelta '\vdash P'\) be a deterministic transition, with balanced \(\varDelta \). Then \(\varGamma ; \varDelta \vdash P \cong \varDelta '\vdash P'\) with \(\varDelta \longrightarrow ^*\varDelta '\) balanced. (2) Let P be an \(\mathsf {HO}\pi ^{-\mathsf {sh}}\) process. Assume \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \). Then \(P \longrightarrow ^*P'\) implies \(\varGamma ; \varDelta \vdash P \cong \varDelta '\vdash P'\) with \(\varDelta \longrightarrow ^*\varDelta '\).
We use Lemma 1 to prove Theorem 6, the negative result stated in Sect. 7.4. This property also enables us to define the following up-to technique, useful in full abstraction proofs. We write  to denote a (possibly empty) sequence of deterministic steps \(\mathop {\longmapsto }\limits ^{\tau _{d}}\).
to denote a (possibly empty) sequence of deterministic steps \(\mathop {\longmapsto }\limits ^{\tau _{d}}\).
Lemma 2
(Up-to Deterministic Transition). Let \(\varGamma ;\varDelta _1\vdash P_1\ \mathfrak {R}\ \varDelta _2\vdash Q_1\) such that if whenever:
-
1.
\(\forall (\nu \, \tilde{m_1}) n !\langle V_1 \rangle \) such that \( \varGamma ;\varDelta _1\vdash P_1\mathop {\longmapsto }\limits ^{(\nu \, \tilde{m_1}) n !\langle V_1 \rangle }\varDelta _3\vdash P_3 \) implies that \(\exists Q_2, V_2\) such that
 and
and  and for fresh t: \( \varGamma ;\varDelta _1''\vdash (\nu \, \tilde{m_1})(P_2 \;|\;t \hookleftarrow V_1)\ \mathfrak {R}\ \varDelta _2''\vdash {(\nu \, \tilde{m_2})(Q_2 \;|\;t \hookleftarrow V_2)} \).
and for fresh t: \( \varGamma ;\varDelta _1''\vdash (\nu \, \tilde{m_1})(P_2 \;|\;t \hookleftarrow V_1)\ \mathfrak {R}\ \varDelta _2''\vdash {(\nu \, \tilde{m_2})(Q_2 \;|\;t \hookleftarrow V_2)} \). -
2.
\(\forall \ell \not = (\nu \, \tilde{m}) n !\langle V \rangle \) such that \( \varGamma ;\varDelta _1\vdash P_1\mathop {\longmapsto }\limits ^{\ell }\varDelta _3\vdash P_3 \) implies that \(\exists Q_2\)
such that
 and
and 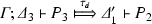 and \(\varGamma ;\varDelta _1'\vdash P_2\ \mathfrak {R}\ \varDelta _2'\vdash Q_2\).
and \(\varGamma ;\varDelta _1'\vdash P_2\ \mathfrak {R}\ \varDelta _2'\vdash Q_2\). -
3.
The symmetric cases of 1 and 2.
Then \(\mathfrak {R}\ \subseteq \ \approx ^\texttt {H}\).
6 Criteria for Typed Encodings
We define the formal notion of encoding by extending to a typed setting existing criteria for untyped processes (as in, e.g., [8, 10, 16, 24, 26, 27, 30, 41]). We first define a typed calculus parametrised by a syntax, operational semantics, and typing. Based on this definition, in Sects. 7 and 8 we define concrete instances of (higher-order) typed calculi.
Definition 10
(Typed Calculus). A typed calculus \(\mathcal {L}\) is a tuple \(\langle \mathsf {C}, \mathcal {T}, \mathop {\longmapsto }\limits ^{\tau }, \approx , \vdash \rangle \) where \(\mathsf {C} \) and \(\mathcal {T}\) are sets of processes and types, respectively; also, \(\mathop {\longmapsto }\limits ^{\tau }\), \(\approx \), and \(\vdash \) denote a transition system, a typed equivalence, and a typing system for \(\mathsf {C} \), respectively.
As we explain later, we write \(\mathop {\longmapsto }\limits ^{\tau }\) to denote an operational semantics defined in terms of \(\tau \)-transitions (to characterise reductions). Our notion of encoding considers mappings on both processes and types; these are denoted \([\![\cdot ]\!]\) and \((\!\!\langle \cdot \rangle \!\!)\), respectively:
Definition 11
(Typed Encoding). Consider typed calculi \(\mathcal {L}_1=\!\langle \mathsf {C} _1, \mathcal{{T}}_1, \mathop {\longmapsto }\limits ^{\tau }_1, \approx _1, \vdash _1 \rangle \) and \(\mathcal {L}_2=\langle \mathsf {C} _2, \mathcal{{T}}_2, \mathop {\longmapsto }\limits ^{\tau }_2, \approx _2, \vdash _2 \rangle \). Given mappings \([\![\cdot ]\!]: \mathsf {C} _1 \rightarrow \mathsf {C} _2\) and \((\!\!\langle \cdot \rangle \!\!): \mathcal{{T}}_1 \rightarrow \mathcal{{T}}_2\), we write \(\big \langle [\![\cdot ]\!], (\!\!\langle \cdot \rangle \!\!)\big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) to denote the typed encoding of \(\mathcal {L}_1\) into \(\mathcal {L}_2\).
Mapping \((\!\!\langle \cdot \rangle \!\!)\) extends to typing environments, e.g., \((\!\!\langle \varDelta \cdot u:S\rangle \!\!) = (\!\!\langle \varDelta \rangle \!\!) \cdot u:(\!\!\langle S\rangle \!\!)\). We introduce syntactic criteria for typed encodings. Let \(\sigma \) denote a substitution of names for names (a renaming, as usual). Given environments \(\varDelta \) and \(\varGamma \), we write \(\sigma (\varDelta )\) and \(\sigma (\varGamma )\) to denote the effect of applying \(\sigma \) on the domains of \(\varDelta \) and \(\varGamma \) (clearly, \(\sigma (\varGamma )\) concerns only shared names in \(\varGamma \): process and recursive variables in \(\varGamma \) are not affected by \(\sigma \)).
Definition 12
(Syntax Preservation). We say that typed encoding \(\big \langle [\![\cdot ]\!], (\!\!\langle \cdot \rangle \!\!)\big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) is syntax preserving if it is:
-
1.
Homomorphic wrt parallel, if \((\!\!\langle \varGamma \rangle \!\!); \emptyset ; (\!\!\langle \varDelta _1 \cdot \varDelta _2\rangle \!\!) \vdash _2 [\![P_1 \;|\;P_2]\!] \triangleright \diamond \) then \((\!\!\langle \varGamma \rangle \!\!); \emptyset ; (\!\!\langle \varDelta _1\rangle \!\!) \cdot (\!\!\langle \varDelta _2\rangle \!\!) \vdash _2 [\![P_1]\!] \;|\;[\![P_2]\!] \triangleright \diamond \).
-
2.
Compositional wrt restriction, if \((\!\!\langle \varGamma \rangle \!\!); \emptyset ; (\!\!\langle \varDelta \rangle \!\!) \vdash _2 [\![(\nu \, n)P]\!] \triangleright \diamond \) then \((\!\!\langle \varGamma \rangle \!\!); \emptyset ; (\!\!\langle \varDelta \rangle \!\!) \vdash _2 (\nu \, n)[\![P]\!] \triangleright \diamond \).
-
3.
Name invariant, if \((\!\!\langle \sigma (\varGamma )\rangle \!\!); \emptyset ; (\!\!\langle \sigma (\varDelta )\rangle \!\!) \vdash _2 [\![\sigma (P)]\!] \triangleright \diamond \) then \(\sigma ((\!\!\langle \varGamma \rangle \!\!)); \emptyset ; \sigma ((\!\!\langle \varDelta \rangle \!\!)) \vdash _2 \sigma ([\![P]\!]) \triangleright \diamond \), for any injective renaming of names \(\sigma \).
Homomorphism wrt parallel (used in, e.g., [26, 27]) expresses that encodings should preserve the distributed topology of source processes. This criterion is appropriate for both encodability and non encodability results; in our setting, it is induced by rules for typed composition. Compositionality wrt restriction is also supported by typing and is useful in our encodability results (Sect. 7). The name invariance criterion follows [10, 16].
We now state type preservation, a static criterion on the mapping \((\!\!\langle \cdot \rangle \!\!): \mathcal{{T}}_1 \rightarrow \mathcal{{T}}_2\): it ensures that type operators are preserved. The source and target languages that we consider here share five (session) type operators: input, output, recursion (binary operators); selection and branching (n-ary operators). Type preservation enables us to focus on mappings \((\!\!\langle \cdot \rangle \!\!)\) that always translate a type operator into itself. This is key to retain the meaning of structured protocols: as session types operators abstract communication behaviour, type preserving encodings help us maintain behaviour across translations.
Definition 13
(Type Preservation). The typed encoding \(\big \langle [\![\cdot ]\!], (\!\!\langle \cdot \rangle \!\!)\big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) is type preserving if for every k-ary type operator \(\texttt {op}\) in \(\mathcal{{T}}_1\) it holds that
Example 1
Following the discussion in Sect. 2, let \((\!\!\langle \cdot \rangle \!\!)_u\) be a mapping on session types such that \((\!\!\langle !\langle U \rangle ; S\rangle \!\!)_u = ?((\!\!\langle U\rangle \!\!)_u) ; (\!\!\langle S\rangle \!\!)_u\) and \((\!\!\langle ?(U) ; S\rangle \!\!)_u = !\langle (\!\!\langle U\rangle \!\!)_u \rangle ; (\!\!\langle S\rangle \!\!)_u\) (other type operators are translated homomorphically). That is, \((\!\!\langle \cdot \rangle \!\!)_u\) translates the output type operator into an input type operator (and viceversa). Therefore, \((\!\!\langle \cdot \rangle \!\!)_u\) does not satisfy type preservation.
Next we define semantic criteria for typed encodings:
Definition 14
(Semantic Preservation). Consider two typed calculi \(\mathcal {L}_1\) and \(\mathcal {L}_2\), defined as \(\mathcal {L}_1=\langle \mathsf {C} _1, \mathcal{{T}}_1, \mathop {\longmapsto }\limits ^{\tau }_1, \approx _1, \vdash _1 \rangle \) and \(\mathcal {L}_2=\langle \mathsf {C} _2, \mathcal{{T}}_2, \mathop {\longmapsto }\limits ^{\tau }_2, \approx _2, \vdash _2 \rangle \). We say that the encoding \(\big \langle [\![\cdot ]\!], (\!\!\langle \cdot \rangle \!\!)\big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) is semantic preserving if it satisfies the properties below.
-
1.
Type Soundness: if \(\varGamma ; \emptyset ; \varDelta \vdash _1 P \triangleright \diamond \) then \((\!\!\langle \varGamma \rangle \!\!); \emptyset ; (\!\!\langle \varDelta \rangle \!\!) \vdash _2 [\![P]\!] \triangleright \diamond \), for any P in \(\mathsf {C} _1\).
-
2.
Barb Preserving: if \(\varGamma ; \varDelta \vdash _1 P \downarrow _{n}\) then \((\!\!\langle \varGamma \rangle \!\!); (\!\!\langle \varDelta \rangle \!\!) \vdash _2 [\![P]\!] \Downarrow _{n}\).
-
3.
Operational Correspondence: If \(\varGamma ; \emptyset ; \varDelta \vdash _1 P \triangleright \diamond \) then
-
(a)
Completeness: If \(\varGamma ; \varDelta \vdash _{1} P \mathop {\longmapsto }\limits ^{\tau }_{1} \varDelta ' \vdash _{1} P' \) then \(\exists Q, \varDelta ''\) s.t.
(i)
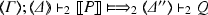 and (ii) \({(\!\!\langle \varGamma \rangle \!\!)};{(\!\!\langle \varDelta ''\rangle \!\!)}\vdash _2 {Q}{\approx _2} {(\!\!\langle \varDelta '\rangle \!\!)}\vdash _2 {[\![P']\!]}\).
and (ii) \({(\!\!\langle \varGamma \rangle \!\!)};{(\!\!\langle \varDelta ''\rangle \!\!)}\vdash _2 {Q}{\approx _2} {(\!\!\langle \varDelta '\rangle \!\!)}\vdash _2 {[\![P']\!]}\). -
(b)
Soundness: If
 then \(\exists P', \varDelta ''\) s.t.
then \(\exists P', \varDelta ''\) s.t.(i) \(\varGamma ; \varDelta \vdash _{1} P \mathop {\longmapsto }\limits ^{\tau }_{1} \varDelta '' \vdash _{1} P' \) and (ii) \({(\!\!\langle \varGamma \rangle \!\!)};{(\!\!\langle \varDelta ''\rangle \!\!)}\vdash _2 {[\![P']\!]}{\approx _2} {(\!\!\langle \varDelta '\rangle \!\!)}\vdash _2 {Q}\).
-
(a)
-
4.
Full Abstraction: \(\varGamma ; \varDelta \vdash _{1} P \approx _{1} \varDelta ' \vdash _{1} Q \) if and only if \((\!\!\langle \varGamma \rangle \!\!); (\!\!\langle \varDelta \rangle \!\!) \vdash _{2} [\![P]\!] \approx _{2} (\!\!\langle \varDelta '\rangle \!\!) \vdash _{2} [\![Q]\!] \).
Together with type preservation (Definition 13), type soundness is a distinguishing criterion in our notion of encoding. Barb preservation, related to success sensitiveness in [10], is convenient in our developments as all considered calculi have the same notion of barb. Operational correspondence, standardly divided into completeness and soundness, is also based on [10]; it relies on \(\tau \)-transitions (reductions). Completeness ensures that a step of the source process is mimicked by a step of its associated encoding; soundness is its converse. Above, operational correspondence is stated in generic terms. It is worth stressing that the operational correspondence statements for our encodings are tailored to the specifics of each encoding, and so they are actually stronger than the criteria given above (see Propositions 3, 6, 10, 13 and [15] for details). Finally, following [27, 32, 45], we consider full abstraction as an encodability criterion: this leads to stronger encodability results.
We introduce precise and minimal encodings. While we state strong positive encodability results in terms of precise encodings, to prove the non-encodability result in Sect. 7.4, we appeal to the weaker minimal encodings.
Definition 15
(Typed Encodings: Precise and Minimal). We say that the typed encoding \(\big \langle [\![\cdot ]\!], (\!\!\langle \cdot \rangle \!\!) \big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) is precise, if it is syntax, type, and semantic preserving (Definitions 12, 13, 14). We say that the encoding is minimal, if it is syntax preserving (Definition 12), barb preserving (Definition 14-2), and operationally complete (Definition 14-3(a)).
The following property will come in handy in Sect. 8:
Proposition 1
Let \(\big \langle [\![\cdot ]\!]^{1}, (\!\!\langle \cdot \rangle \!\!)^{1} \big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) and \(\big \langle [\![\cdot ]\!]^{2}, (\!\!\langle \cdot \rangle \!\!)^{2} \big \rangle : \mathcal {L}_2 \rightarrow \mathcal {L}_3\) be two precise encodings. Then their composition, denoted \(\big \langle [\![\cdot ]\!]^{2} \circ [\![\cdot ]\!]^{1}, (\!\!\langle \cdot \rangle \!\!)^{2} \circ (\!\!\langle \cdot \rangle \!\!)^{1} \big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_3\), is precise.
7 Expressiveness Results
We first present two precise encodings: (1) higher-order communication with recursion and name-passing (\(\mathsf {HO}\pi \)) into higher-order communication without name-passing nor recursion (\(\mathsf {HO}\)) (Sect. 7.1); and (2) \(\mathsf {HO}\pi \) into the first-order calculus with name-passing with recursion (\(\pi \)) (Sect. 7.2). We then compare these encodings (Sect. 7.3). Moreover, in Sect. 7.4 we state our impossibility result for shared/linear names. We consider the typed calculi (cf. Definition 10):
where: \(\mathcal{{T}}_1\), \(\mathcal{{T}}_2\), and \(\mathcal{{T}}_3\) are sets of types of \(\mathsf {HO}\pi \), \(\mathsf {HO} \), and \(\pi \), respectively. The typing \(\vdash \) is defined in Sect. 4. The LTSs follow the intuitions given in Sect. 5.2. Moreover, \(\approx ^\texttt {H}\) is as in Definition 9, and \(\approx ^\texttt {C}\) is as in Definitions 8.
7.1 From \(\mathsf {HO}\pi \) to \(\mathsf {HO}\)
\(\mathsf {HO} \) is expressive enough to precisely encode \(\mathsf {HO}\pi \). As discussed above, the main challenges are to encode (1) name passing and (2) recursion, for which we only use abstraction passing. As explained in Sect. 2, for (1), we pass an abstraction which enables to use the name upon application. For (2), we copy a process upon reception; passing around linear abstractions is delicate because they cannot be copied. To handle linearity, we define the following auxiliary mapping \(\big \lfloor \!\big \lfloor \cdot \big \rfloor \!\big \rfloor ^{}_\sigma \) from processes with free names to processes without free names (but with free variables instead):
Definition 16
(Auxiliary Mapping). Let \(|\!|\cdot |\!|: 2^{\mathcal {N}} \longrightarrow \mathcal {V}^\omega \) denote a map of sequences of lexicographically ordered names to sequences of variables, defined inductively as: \(|\!|\epsilon |\!| = \epsilon \) and \(|\!|n \cdot \tilde{m}|\!| = x_n \cdot |\!|\tilde{m}|\!|\). Also, let \(\sigma \) be a set of session names. Figure 5 defines an auxiliary mapping \(\big \lfloor \!\big \lfloor \cdot \big \rfloor \!\big \rfloor ^{}_\sigma : \mathsf {HO} \rightarrow \mathsf {HO} \).
Let P be an \(\mathsf {HO}\pi \) process with \(\texttt {fn}(P) = \{n_1, \cdots , n_k\}\). Intuitively, our encoding \([\![\cdot ]\!]^1_f\) exploits the abstraction \(\lambda x_1,\cdots , x_k.\,\big \lfloor \!\big \lfloor [\![P]\!]^1_f\big \rfloor \!\big \rfloor ^{}_\emptyset \), where \(|\!|n_j|\!| = x_j\), for all \(j \in \{1, \ldots , k\}\):
Definition 17
(Typed Encoding of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) ). Let f be a map from process variables to sequences of name variables. The typed encoding \(\big \langle [\![\cdot ]\!]^{1}_f, (\!\!\langle \cdot \rangle \!\!)^{1} \big \rangle : \mathcal {L}_{\mathsf {HO}\pi } \rightarrow \mathcal {L}_{\mathsf {HO}}\) is given in Fig. 6. Mapping \((\!\!\langle \cdot \rangle \!\!)^{1}\) on types homomorphically extends to environments \(\varDelta \) and \(\varGamma \), with \( (\!\!\langle \varGamma \cdot X:\varDelta _1\rangle \!\!)^{1} = (\!\!\langle \varGamma \rangle \!\!)^{1} \cdot z_X:(S_1,\ldots ,S_m,S^*)\!\! \rightarrow \!\! \diamond \) where \(S^*\) is defined as \(\mu \mathsf {t}.?((S_1,\ldots ,S_m,\mathsf {t})\!\! \rightarrow \!\! \diamond ) ; \texttt {end}\) provided that \(\varDelta _1 = \{n_i:S_i\}_{1\le i\le m}\).
Auxiliary mapping used to encode \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) (Definition 16).
Encoding of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) (Definition 17).
Note that \(\varDelta \) in \(X:\varDelta \) is mapped to a non-tail recursive session type with variable \(z_X\). Non-tail recursive session types were studied in [2, 3]; to our knowledge, this is the first application in the context of higher-order session types. For simplicity, we use polyadic name abstractions. A precise encoding of polyadicity into \(\mathsf {HO}\) is given in Sect. 8.
Key elements in Fig. 6 are encodings of name passing (\([\![u !\langle w \rangle . P]\!]^1_f\) and \([\![u ?(x) . P]\!]^1_f\)) and recursion (\([\![\mu X. P]\!]^1_f\) and \([\![X]\!]^1_f\)). As motivated in Sect. 2, a name w is passed as an input-guarded abstraction; on the receiver side, the encoding i) receives the abstraction; ii) applies to it a fresh endpoint s; iii) uses the dual endpoint \(\overline{s}\) to send the continuation P as an abstraction. Thus, name substitution is achieved via name application. As for recursion, to encode \(\mu X. P\) we first record a mapping from recursive variable X to process variable \(z_X\). Then, using \(\big \lfloor \!\big \lfloor \cdot \big \rfloor \!\big \rfloor ^{}_\sigma \) in Definition 16, we encode the recursion body P as a name abstraction in which free names of P are converted into name variables. (Notice that P is first encoded into \(\mathsf {HO}\) and then transformed using mapping \(\big \lfloor \!\big \lfloor \cdot \big \rfloor \!\big \rfloor ^{}_\sigma \).) Subsequently, this higher-order value is embedded in an input-guarded “duplicator” process. We encode X in such a way that it simulates recursion unfolding by invoking the duplicator in a by-need fashion. That is, upon reception, the \(\mathsf {HO}\) abstraction encoding P is duplicated: one copy is used to reconstitute the original recursion body P (through the application of \(\texttt {fn}(P)\)); another copy is used to re-invoke the duplicator when needed. We illustrate the encoding by means of an example.
Example 2
(The Encoding \([\![\cdot ]\!]^1_f\) At Work). Let \(P = \mu X. a !\langle m \rangle . X\) be an \(\mathsf {HO}\pi \) process. Its encoding into \(\mathsf {HO}\) is given next; notice that \(f = \emptyset \) and \(f' = X \rightarrow x_ax_m\).
That is, by writing V to denote the process
we would have
Next we illustrate the behaviour of \([\![P]\!]^1_f\); below \(\ell \) stands for \(a !\langle \lambda z.\,z ?(x) . (x\, {m}) \rangle \).
We now describe the properties of the encoding. Directly from Fig. 6 we may state:
Proposition 2
( \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) : Type Preservation). The encoding from \(\mathcal {L}_{\mathsf {HO}\pi }\) into \(\mathcal {L}_{\mathsf {HO}}\) (cf. Definition 17) is type preserving.
Now, we state operational correspondence with respect to reductions; the full statement (and proof) can be found in [15].
Proposition 3
( \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) : Operational Correspondence - Excerpt). Let P be an \(\mathsf {HO}\pi \) process such that \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \).
-
1.
Completeness: Suppose \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau }\varDelta '\vdash P'\). Then we have:
-
(a)
If
 then \(\exists R\) s.t.
then \(\exists R\) s.t.\((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash (\nu \, \tilde{m})([\![P_1]\!]^1_f \;|\;R)\), and
 .
. -
(b)
If
 then
then .
. -
(c)
If
 then
then\((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta '_1\rangle \!\!)^{1}\vdash [\![P']\!]^1_f\).
-
(a)
-
2.
Soundness: Suppose \((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta '\rangle \!\!)^{1}\vdash Q\). Then \(\varDelta ' = \varDelta \) and either
-
(a)
\(\exists P'\) s.t. \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau }\varDelta \vdash P'\), and \(Q = [\![P']\!]^{1}_f\).
-
(b)
\(\exists P_1, P_2, x, m, Q'\) s.t.
 , and
, and
-
(a)
Observe how we can explicitly distinguish the role of finite, deterministic reductions (\(\mathop {\longmapsto }\limits ^{\tau _{s}}\) and \(\mathop {\longmapsto }\limits ^{\tau _{\beta }}\), defined in Notation 1) in both soundness and completeness statements.
The typed operational correspondence given above is an important component in the proof of full abstraction, which we state next.
Proposition 4
( \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) : Full Abstraction). Let \(P_1, Q_1\) be \(\mathsf {HO}\pi \) processes.
\(\varGamma ;\varDelta _1\vdash P_1\approx ^\texttt {H}\varDelta _2\vdash Q_1\) if and only if \((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta _1\rangle \!\!)^{1}\vdash [\![P_1]\!]^1_f\approx ^\texttt {H}(\!\!\langle \varDelta _2\rangle \!\!)^{1}\vdash [\![Q_1]\!]^1_f\).
We may state the main result of this section. See [15] for details.
Theorem 3
(Precise Encoding of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) ). The encoding from \(\mathcal {L}_{\mathsf {HO}\pi }\) into \(\mathcal {L}_{\mathsf {HO}}\) (cf. Definition 17) is precise.
7.2 From \(\mathsf {HO}\pi \) to \(\pi \)
We now discuss the precise encodability of \(\mathsf {HO}\pi \) into \(\pi \); the non trivial issue is encoding higher-order communication, which is present in \(\mathsf {HO}\pi \) but not in \(\pi \). We closely follow Sangiorgi’s encoding [33, 36], which represents the exchange of a process with the exchange of a fresh trigger name. Trigger names may then be used to activate copies of the process, which becomes a persistent resource represented by an input-guarded replication. We cast this strategy in the setting of session-typed communications. In the presence of session names (which are linear and cannot be replicated), our approach uses replicated names as triggers for shared resources and non-replicated names for linear resources (cf. \([\![u !\langle \lambda x.\,Q \rangle . P]\!]^2\)).
Definition 18
(Typed Encoding of \(\mathsf {HO}\pi \) into \(\pi \) ). The typed encoding \(\big \langle [\![\cdot ]\!]^{2}, (\!\!\langle \cdot \rangle \!\!)^{2} \big \rangle : \mathcal {L}_{\mathsf {HO}\pi } \rightarrow \mathcal {L}_{\pi }\) is defined in Fig. 7.
Observe how \([\![(\lambda x.\,P)\, {u}]\!]^2\) naturally induces a name substitution. We describe key properties of this encoding. First, type preservation and operational correspondence:
Encoding of \(\mathsf {HO}\pi \) into \(\pi \) (Definition 18).
Proposition 5
( \(\mathsf {HO}\pi \) into \(\pi \): Type Preservation). The encoding from \(\mathcal {L}_{\mathsf {HO}\pi }\) into \(\mathcal {L}_{\pi }\) (cf. Definition 18) is type preserving.
Proposition 6
( \(\mathsf {HO}\pi \) into \(\pi \): Operational Correspondence - Excerpt). Let P be an \(\mathsf {HO}\pi \) process such that \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \).
-
1.
Completeness: Suppose \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\ell }\varDelta '\vdash P'\). Then either:
-
(a)
If \(\ell = \tau \) then one of the following holds:
-
-
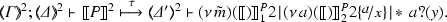
 for some \(P_1, P_2, Q\);
for some \(P_1, P_2, Q\); -
-

 , for some \(P_1, P_2, Q\);
, for some \(P_1, P_2, Q\); -
-
\((\!\!\langle \varGamma \rangle \!\!)^{2};(\!\!\langle \varDelta \rangle \!\!)^{2}\vdash [\![P]\!]^2\mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta '\rangle \!\!)^{2}\vdash {{[\![P']\!]^2 }} \)
-
-
-
(b)
If \(\ell = \tau _{\beta }\) then \((\!\!\langle \varGamma \rangle \!\!)^{2};(\!\!\langle \varDelta \rangle \!\!)^{2}\vdash [\![P]\!]^2\mathop {\longmapsto }\limits ^{\tau _{s}}(\!\!\langle \varDelta '\rangle \!\!)^{2}\vdash {{[\![P']\!]^2 }} \).
-
(a)
-
2.
Suppose \((\!\!\langle \varGamma \rangle \!\!)^{2}; (\!\!\langle \varDelta \rangle \!\!)^{2} \vdash [\![P]\!]^{2} \mathop {\longmapsto }\limits ^{\tau } (\!\!\langle \varDelta '\rangle \!\!)^{2} \vdash R \).
Then \(\exists P'\) such that \(P \mathop {\longmapsto }\limits ^{\tau } P'\) and \((\!\!\langle \varGamma \rangle \!\!)^{2};(\!\!\langle \varDelta '\rangle \!\!)^{2}\vdash [\![P']\!]^{2}\approx ^\texttt {H}(\!\!\langle \varDelta '\rangle \!\!)^{2}\vdash R\).
Exploiting the above properties (type preservation, typed operational correspondence), we can show that our typed encoding is fully abstract and precise.
Proposition 7
( \(\mathsf {HO}\pi \) to \(\pi \): Full Abstraction). Let \(P_1, Q_1\) be \(\mathsf {HO}\pi \) processes. \(\varGamma ;\varDelta _1\vdash P_1\approx ^\texttt {H}\varDelta _2\vdash Q_1\) if and only if \((\!\!\langle \varGamma \rangle \!\!)^{2};(\!\!\langle \varDelta _1\rangle \!\!)^{2}\vdash [\![P_1]\!]^2\approx ^\texttt {C}(\!\!\langle \varDelta _2\rangle \!\!)^{2}\vdash [\![Q_1]\!]^2\).
Theorem 4
(Precise Encoding of \(\mathsf {HO}\pi \) into \(\pi \) ). The encoding from \(\mathcal {L}_{\mathsf {HO}\pi }\) into \(\mathcal {L}_{\pi }\) (cf. Definition 18) is precise.
7.3 Comparing Precise Encodings
The precise encodings in Sects. 7.1 and 7.2 confirm that \(\mathsf {HO}\) and \(\pi \) constitute two important sources of expressiveness in \(\mathsf {HO}\pi \). This naturally begs the question: which of the two sub-calculi is more tightly related to \(\mathsf {HO}\pi \)? We argue, both empirically and formally, that when compared to \(\pi \), \(\mathsf {HO}\) is more economical and satisfies tighter correspondences.
Empirical Comparison: Reduction Steps. We first contrast the way in which (a) the encoding from \(\mathsf {HO}\pi \) to \(\mathsf {HO}\) (Sect. 7.1) translates processes with name passing; (b) the encoding from \(\mathsf {HO}\pi \) to \(\pi \) (Sect. 7.2) translates processes with abstraction passing. Consider the \(\mathsf {HO}\pi \) processes:
\(P_1\) features pure name passing (no abstraction-passing), whereas \(P_2\) involves pure abstraction passing (no name passing). In both cases, the intended communication on s leads to n usages of the communication object (name a in \(P_1\), abstraction \(\lambda x.\,P\) in \(P_2\)). Consider now the reduction steps from \(P_1\) and \(P_2\):


By considering the encoding of \(P_1\) into \(\mathsf {HO}\) we obtain:
Now, we encode \(P_2\) into \(\pi \):


Clearly, encoding \(P_1\) into \(\mathsf {HO}\) is more economical than encoding \(P_2\) into \(\pi \). Not only moving to a pure higher-order setting requires less reduction steps than in the first-order concurrency of \(\pi \); in the presence of shared names, moving to a first-order setting brings the need of setting up and handling replicated processes which will eventually lead to garbage (stuck) processes (cf. \(*\,b ?(y) . y ?(x) . P\) above). In contrast, the mechanism present in \(\mathsf {HO}\) works efficiently regardless of the linear or shared properties of the name that is “packed” into the abstraction. The use of \(\beta \)-transitions guarantees local synchronizations, which are arguably more economical than point-to-point, session synchronizations.
It is useful to move our comparison to a purely linear setting. Consider processes:


\(Q_1\) is a \(\pi \) process; \(Q_2\) is an \(\mathsf {HO}\) processs. If we consider their encodings into \(\mathsf {HO}\) and \(\pi \), respectively, we obtain:


In this case, the encoding \([\![\cdot ]\!]^2\) is more efficient, as it induces less reduction steps. Therefore, considering a fragment of \(\mathsf {HO}\pi \) without shared communications (linearity only) has consequences in terms of reduction steps. Notice that we prove that linear communications do not suffice to encode shared communications (Sect. 7.4).
Formal Comparison: Labelled Transition Correspondence. We now formally establish differences between \([\![\cdot ]\!]_f^1\) and \([\![\cdot ]\!]^2\). To this end, we introduce an extra encodability criterion: a form of operational correspondence for visible actions. Below we write \(\ell _1, \ell _2\) to denote actions different from \(\tau \) and \(\mathop {\longmapsto }\limits ^{\ell }\) to denote an LTS. As actions from different calculi may be different, we also consider a mapping on action labels, denoted \(\{\!\!\{\cdot \}\!\!\}\):
Definition 19
(Labelled Correspondence / Tight Encodings). Consider typed calculi \(\mathcal {L}_1\) and \(\mathcal {L}_2\), defined as \(\mathcal {L}_1=\langle \mathsf {C} _1, \mathcal{{T}}_1, \mathop {\longmapsto }\limits ^{{\ell _1}}_1, \approx _1, \vdash _1 \rangle \) and \(\mathcal {L}_2=\langle \mathsf {C} _2, \mathcal{{T}}_2, \mathop {\longmapsto }\limits ^{{\ell _2}}_2, \approx _2, \vdash _2 \rangle \). The encoding \(\big \langle [\![\cdot ]\!], (\!\!\langle \cdot \rangle \!\!)\big \rangle : \mathcal {L}_1 \rightarrow \mathcal {L}_2\) satisfies labelled operational correspondence if it satisfies:
-
1.
If \(\varGamma ; \varDelta \vdash _{1} P \mathop {\longmapsto }\limits ^{\ell _1}_{1} \varDelta ' \vdash _{1} P' \) then \(\exists Q\), \(\varDelta ''\), \(\ell _2\) s.t. (i)
 ;
;(ii) \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}\); (iii) \({(\!\!\langle \varGamma \rangle \!\!)};{(\!\!\langle \varDelta ''\rangle \!\!)}\vdash _2 {Q}{\approx _2}{(\!\!\langle \varDelta '\rangle \!\!)}\vdash _2 {[\![P']\!]}\).
-
2.
If
 then \(\exists P'\), \(\varDelta ''\), \(\ell _1\) s.t. (i) \(\varGamma ; \varDelta \vdash _{1} P \mathop {\longmapsto }\limits ^{\ell _1}_{1} \varDelta '' \vdash _{1} P' \); (ii) \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}\); (iii) \({(\!\!\langle \varGamma \rangle \!\!)};{(\!\!\langle \varDelta ''\rangle \!\!)}\vdash _2 {[\![P']\!]}{\approx _2}{(\!\!\langle \varDelta '\rangle \!\!)}\vdash _2 {Q}\).
then \(\exists P'\), \(\varDelta ''\), \(\ell _1\) s.t. (i) \(\varGamma ; \varDelta \vdash _{1} P \mathop {\longmapsto }\limits ^{\ell _1}_{1} \varDelta '' \vdash _{1} P' \); (ii) \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}\); (iii) \({(\!\!\langle \varGamma \rangle \!\!)};{(\!\!\langle \varDelta ''\rangle \!\!)}\vdash _2 {[\![P']\!]}{\approx _2}{(\!\!\langle \varDelta '\rangle \!\!)}\vdash _2 {Q}\).
A tight encoding is a typed encoding which is precise (Definition 15) and that also satisfies labelled operational correspondence as above.
We may formally state that \(\mathsf {HO}\pi \) and \(\mathsf {HO}\) are more closely related than \(\mathsf {HO}\pi \) and \(\pi \):
Theorem 5
( \(\mathsf {HO}\) Tightly Encodes \(\mathsf {HO}\pi \) ). While the encoding of \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) (Definition 17) is tight, the encoding of \(\mathsf {HO}\pi \) into \(\pi \) (Definition 18) is not tight.
To substantiate the above claim, we show that the encoding \([\![\cdot ]\!]^1_f\) enjoys labelled operational correspondence, whereas \([\![\cdot ]\!]^2\) does not. Consider the following mapping:
Then the following result, a complement of Proposition 3, holds:
Proposition 8
(Labelled Transition Correspondence, \(\mathsf {HO}\pi \) into \(\mathsf {HO}\) ). Let P be an \(\mathsf {HO}\pi \) process. If \(\varGamma ; \emptyset ; \varDelta \vdash P \triangleright \diamond \) then:
-
1.
Suppose \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\ell _1}\varDelta '\vdash P'\). Then we have:
-
(a)
If \( \ell _1 \in \{(\nu \, \tilde{m})n !\langle m \rangle , \,(\nu \, \tilde{m})n !\langle \lambda x.\,Q \rangle , \,s \oplus l, \,s \& l\}\) then \(\exists \ell _2\) s.t. \((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\ell _2}(\!\!\langle \varDelta '\rangle \!\!)^{1}\vdash [\![P']\!]^1_f\) and \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}^{1}\).
-
(b)
If \(\ell _1 = n ?\langle \lambda y.\,Q \rangle \) and
 then \(\exists \ell _2\) s.t.
then \(\exists \ell _2\) s.t.  and \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}^{1}\).
and \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}^{1}\). -
(c)
If \(\ell _1 = n ?\langle m \rangle \) and
 then \(\exists \ell _2\), R s.t. \((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\ell _2}(\!\!\langle \varDelta '\rangle \!\!)^{1}\vdash R\), with \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}^{1}\), and
then \(\exists \ell _2\), R s.t. \((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\ell _2}(\!\!\langle \varDelta '\rangle \!\!)^{1}\vdash R\), with \(\ell _2 = \{\!\!\{\ell _1\}\!\!\}^{1}\), and  .
.
-
(a)
-
2.
Suppose \((\!\!\langle \varGamma \rangle \!\!)^{1};(\!\!\langle \varDelta \rangle \!\!)^{1}\vdash [\![P]\!]^1_f\mathop {\longmapsto }\limits ^{\ell _2}(\!\!\langle \varDelta '\rangle \!\!)^{1}\vdash Q\). Then we have:
-
(a)
If \( \ell _2 \in \{(\nu \, \tilde{m})n !\langle \lambda z.\,\,z ?(x) . (x\, {m}) \rangle , \,(\nu \, \tilde{m}) n !\langle \lambda x.\,R \rangle , \,s \oplus l, \,s \& l\}\) then \(\exists \ell _1, P'\) s.t. \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\ell _1}\varDelta '\vdash P'\), \(\ell _1 = \{\!\!\{\ell _2\}\!\!\}^{1}\), and \(Q = [\![P']\!]^1_f\).
-
(b)
If \(\ell _2 = n ?\langle \lambda y.\,R \rangle \) then either:
-
(i)
\(\exists \ell _1, x, P', P''\) s.t.
 , \(\ell _1 = \{\!\!\{\ell _2\}\!\!\}^{1}\), \([\![P'']\!]^1_\emptyset = R\), and \(Q = [\![P']\!]^1_f\).
, \(\ell _1 = \{\!\!\{\ell _2\}\!\!\}^{1}\), \([\![P'']\!]^1_\emptyset = R\), and \(Q = [\![P']\!]^1_f\). -
(ii)
\(R \equiv y ?(x) . (x\, {m})\) and \(\exists \ell _1, z, P'\) s.t.
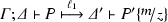 , \(\ell _1 = \{\!\!\{\ell _2\}\!\!\}^{1}\), and
, \(\ell _1 = \{\!\!\{\ell _2\}\!\!\}^{1}\), and 
-
(i)
-
(a)
The analog of Proposition 8 does not hold for the encoding of \(\mathsf {HO}\pi \) into \(\pi \). Consider the \(\mathsf {HO}\pi \) process:


with \(\lambda x.\,P\) being a linear value. We translate it into a \(\pi \) process:
The resulting processes have a mismatch both in the typing environment (\(\varDelta ' \not = (\!\!\langle \emptyset \rangle \!\!)^{2}\)) and in the actions that they can subsequently observe: the first process cannot perform any action, while the second process can perform actions of the encoding of \(\lambda x.\,P\).
7.4 A Negative Result
As most session calculi, \(\mathsf {HO}\pi \) includes communication on both shared and linear names. The former enables non determinism, unrestricted behaviour; the latter allows to represent deterministic, linear communication structures. The expressiveness of shared names is also illustrated by our encoding from \(\mathsf {HO}\pi \) into \(\pi \) (Fig. 7). This result begs the question: can we represent shared name interaction using session name interaction? It turns out that shared names add expressiveness to \(\mathsf {HO}\pi \): we prove the non existence of a minimal encoding (cf. Definition 15) of shared name interaction into linear interaction.
Theorem 6
There is no minimal encoding from \(\pi \) to \(\mathsf {HO}\pi ^{\mathsf {-sh}}\). Hence, for any \(\mathsf {C} _1,\mathsf {C} _2\in \{ \mathsf {HO}\pi , \mathsf {HO}, \pi \}\), there is no minimal encoding from \(\mathcal {L}_{\mathsf {C} _1}\) into \(\mathcal {L}_{\mathsf {C} _2^{-\mathsf {sh}}}\).
By Definitions 17 and 18 and Propositions 3 and 4, we have:
Corollary 1
Let \(\mathsf {C} _1,\mathsf {C} _2\in \{ \mathsf {HO}\pi , \mathsf {HO}, \pi \}\). There is a precise encoding of \(\mathcal {L}_{\mathsf {C} _1^{-\mathsf {sh}}}\) in \(\mathcal {L}_{\mathsf {C} _2^{-\mathsf {sh}}}\).
8 Extensions: Higher-Order Abstractions and Polyadicity
Here we extend \(\mathsf {HO}\pi \) in two directions: (i) \(\mathsf {HO\pi ^{+}}\) extends \(\mathsf {HO}\pi \) with higher-order applications/abstractions; (ii) \(\mathsf {HO}\,{\widetilde{\pi }}\) extends \(\mathsf {HO}\pi \) with polyadicity. In both cases, we detail the required modifications in syntax and types. Using encoding composability (Proposition 1), the two extensions may be combined into \(\mathsf {HO}\,{\widetilde{\pi }}^{\,+}\): the polyadic extension of \(\mathsf {HO\pi ^{+}}\).
\(\mathsf {HO}\pi \) with Higher-Order Abstractions ( \(\mathsf {HO\pi ^{+}} \) ) and with Polyadicity ( \(\mathsf {HO}\,{\widetilde{\pi }}\) ). We first introduce \(\mathsf {HO\pi ^{+}}\), the extension of \(\mathsf {HO}\pi \) with higher-order abstractions and applications. This is the calculus that we studied in [14]. The syntax of \(\mathsf {HO\pi ^{+}}\) is obtained from Fig. 2 by extending \(V\, {u}\) to \(V\, {W}\), where W is a higher-order value. As for the reduction semantics, we keep the rules in Fig. 3, except for \({{[\mathrm {\small App}]}}\) which is replaced by


The syntax of types is modified as follows: \( L \;\;{:}{:=}\;\;U\!\! \rightarrow \!\! \diamond \;\;\;|\;\;\;U\!\! \multimap \!\! \diamond . \) These types can be easily accommodated in the type system in Sect. 4: we replace C by U in [Abs] and C by \(U'\) in [App]. Subject reduction (Theorem 1) holds for \(\mathsf {HO\pi ^{+}}\) (cf. [14])
The calculus \(\mathsf {HO}\,{\widetilde{\pi }} \) extends \(\mathsf {HO}\pi \) with polyadic name passing \(\tilde{n}\) and \(\lambda \tilde{x}.\,Q\) in the syntax of values V. The operational semantics is kept unchanged, with the expected use of the simultaneous substitution  . The type syntax is extended to:
. The type syntax is extended to:


As in [22, 23], the type system for \(\mathsf {HO}\,{\widetilde{\pi }}\) disallows a shared name that directly carries polyadic shared names.
By combining \(\mathsf {HO\pi ^{+}}\) and \(\mathsf {HO}\,{\widetilde{\pi }}\) into a single calculus we obtain \(\mathsf {HO}\,{\widetilde{\pi }}^{\,+}\): the extension of \(\mathsf {HO}\pi \) allows both higher-order abstractions/aplications and polyadicity.
Precise Encodings of \(\mathsf {HO\pi ^{+}} \) and \(\mathsf {HO}\,{\widetilde{\pi }} \) into \(\mathsf {HO}\pi \). We give encodings of \(\mathsf {HO\pi ^{+}}\) into \(\mathsf {HO}\pi \) and into \(\mathsf {HO}\,{\widetilde{\pi }}\), and show that they are precise. We use encoding composition (Proposition 1) to encode \(\mathsf {HO}\,{\widetilde{\pi }}^{\,+}\) into \(\mathsf {HO}\) and \(\pi \). We consider the following typed calculi (cf. Definition 10):
-
-
\(\mathcal {L}_{\mathsf {HO\pi ^{+}}}=\langle \mathsf {HO\pi ^{+}}, \mathcal{{T}}_4, \mathop {\longmapsto }\limits ^{\ell }, \approx ^\texttt {H}, \vdash \rangle \), where \(\mathcal{{T}}_4\) is a set of types of \(\mathsf {HO\pi ^{+}} \); the typing \(\vdash \) is defined in Sect. 4 with extended rules [Abs] and [App].
-
-
\(\mathcal {L}_{\mathsf {HO}\,{\widetilde{\pi }}}=\langle \mathsf {HO}\,{\widetilde{\pi }}, \mathcal{{T}}_5, \mathop {\longmapsto }\limits ^{\ell }, \approx ^\texttt {H}, \vdash \rangle \), where \(\mathcal{{T}}_5\) is the set of types of \(\mathsf {HO}\,{\widetilde{\pi }} \); the typing \(\vdash \) is defined in in Sect. 4 with polyadic types.
First, the typed encoding \(\big \langle [\![\cdot ]\!]^{3}, (\!\!\langle \cdot \rangle \!\!)^{3}\big \rangle : \mathsf {HO\pi ^{+}} \rightarrow \mathsf {HO}\pi \) is defined in Fig. 8. It satisfies the following properties:
Proposition 9
( \(\mathsf {HO\pi ^{+}}\) into \(\mathsf {HO}\pi \): Type Preservation). The encoding from \(\mathcal {L}_{\mathsf {HO\pi ^{+}}}\) into \(\mathcal {L}_{\mathsf {HO}\pi }\) (cf. Fig. 8) is type preserving.
Proposition 10
(Operational Correspondence: From \(\mathsf {HO\pi ^{+}}\) to \(\mathsf {HO}\pi \) - Excerpt). Let P be an \(\mathsf {HO\pi ^{+}}\) process such that \(\varGamma ; \emptyset ; \varDelta \vdash P\).
-
1.
Completeness: \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\ell }\varDelta '\vdash P'\) implies
-
(a)
If \(\ell = \tau _{\beta }\) then \((\!\!\langle \varGamma \rangle \!\!)^{3};(\!\!\langle \varDelta \rangle \!\!)^{3}\vdash [\![P]\!]^3\mathop {\longmapsto }\limits ^{\tau }\varDelta ''\vdash R\) and \((\!\!\langle \varGamma \rangle \!\!)^{3};(\!\!\langle \varDelta '\rangle \!\!)^{3}\vdash [\![P']\!]^3\approx ^\texttt {H}\varDelta ''\vdash R\), for some R;
-
(b)
If \(\ell = \tau \) and \(\ell \not = \tau _{\beta }\) then \((\!\!\langle \varGamma \rangle \!\!)^{3};(\!\!\langle \varDelta \rangle \!\!)^{3}\vdash [\![P]\!]^3\mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta '\rangle \!\!)^{3}\vdash [\![P']\!]^3\).
-
(a)
-
2.
Soundness: \((\!\!\langle \varGamma \rangle \!\!)^{3};(\!\!\langle \varDelta \rangle \!\!)^{3}\vdash [\![P]\!]^3\mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta ''\rangle \!\!)^{3}\vdash Q\) implies either
-
(a)
\(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau }\varDelta '\vdash P'\) with \(Q \equiv [\![P']\!]^3\)
-
(b)
\(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau _{\beta }}\varDelta '\vdash P'\) and \((\!\!\langle \varGamma \rangle \!\!)^{3};(\!\!\langle \varDelta ''\rangle \!\!)^{3}\vdash Q\mathop {\longmapsto }\limits ^{\tau _{\beta }}(\!\!\langle \varDelta ''\rangle \!\!)^{3}\vdash [\![P']\!]^3\).
-
(a)
Proposition 11
(Full Abstraction. From \(\mathsf {HO\pi ^{+}}\) to \(\mathsf {HO}\pi \) ).
Let P, Q be \(\mathsf {HO\pi ^{+}}\) processes with \(\varGamma ; \emptyset ; \varDelta _1 \vdash P \triangleright \diamond \) and \(\varGamma ; \emptyset ; \varDelta _2 \vdash Q \triangleright \diamond \).
Then \(\varGamma ;\varDelta _1\vdash P\approx ^\texttt {H}\varDelta _2\vdash Q\) if and only if \((\!\!\langle \varGamma \rangle \!\!)^{3};(\!\!\langle \varDelta _1\rangle \!\!)^{3}\vdash [\![P]\!]^3\approx ^\texttt {H}(\!\!\langle \varDelta _2\rangle \!\!)^{3}\vdash [\![Q]\!]^3\)
Using the above propositions, Theorems 3 and 4, and Proposition 1, we derive the following:
Theorem 7
(Encoding \(\mathsf {HO\pi ^{+}}\) into \(\mathsf {HO}\pi \) ). The encoding from \(\mathcal {L}_{\mathsf {HO\pi ^{+}}}\) into \(\mathcal {L}_{\mathsf {HO}\pi }\) (cf. Fig. 8) is precise. Hence, the encodings from \(\mathcal {L}_{\mathsf {HO\pi ^{+}}}\) to \(\mathcal {L}_{\mathsf {HO}}\) and \(\mathcal {L}_{\pi }\) are also precise.
Second, we define the typed encoding \(\big \langle [\![\cdot ]\!]^{4}, (\!\!\langle \cdot \rangle \!\!)^{4}\big \rangle : \mathsf {HO}\,{\widetilde{\pi }} \rightarrow \mathsf {HO}\pi \) in Fig. 9. For simplicity, we give the dyadic case (tuples of length 2); the general case is as expected. The encoding of \(\mathsf {HO}\,{\widetilde{\pi }} \) satisfies the following properties:
Proposition 12
( \(\mathsf {HO}\,{\widetilde{\pi }}\) into \(\mathsf {HO}\pi \): Type Preservation). The encoding from \(\mathcal {L}_{\mathsf {HO}\,{\widetilde{\pi }}}\) into \(\mathcal {L}_{\mathsf {HO}\pi }\) (cf. Fig. 9) is type preserving.
Proposition 13
(Operational Correspondence: From \(\mathsf {HO}\,{\widetilde{\pi }}\) to \(\mathsf {HO}\pi \) - Excerpt). Let \(\varGamma ; \emptyset ; \varDelta \vdash P\).
-
1.
Completeness: \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\ell }\varDelta '\vdash P'\) implies
-
(a)
If \(\ell = \tau _{\beta }\) then \((\!\!\langle \varGamma \rangle \!\!)^{4};(\!\!\langle \varDelta \rangle \!\!)^{4}\vdash [\![P]\!]^4\mathop {\longmapsto }\limits ^{\tau _{\beta }} \mathop {\longmapsto }\limits ^{\tau _{s}} \mathop {\longmapsto }\limits ^{\tau _{s}}(\!\!\langle \varDelta '\rangle \!\!)^{4}\vdash [\![P']\!]^4\)
-
(b)
If \(\ell = \tau \) then \((\!\!\langle \varGamma \rangle \!\!)^{4};(\!\!\langle \varDelta \rangle \!\!)^{4}\vdash [\![P]\!]^4\mathop {\longmapsto }\limits ^{\tau }\mathop {\longmapsto }\limits ^{\tau } \mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta '\rangle \!\!)^{4}\vdash [\![P']\!]^4\)
-
(a)
-
2.
Soundness: \((\!\!\langle \varGamma \rangle \!\!)^{4};(\!\!\langle \varDelta \rangle \!\!)^{4}\vdash [\![P]\!]^4\mathop {\longmapsto }\limits ^{\ell }(\!\!\langle \varDelta _1\rangle \!\!)^{4}\vdash P_1\) implies
-
(a)
If \(\ell = \tau _{\beta }\) then \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau _{\beta }}\varDelta '\vdash P'\) and \((\!\!\langle \varGamma \rangle \!\!)^{4};(\!\!\langle \varDelta _1\rangle \!\!)^{4}\vdash P_1\mathop {\longmapsto }\limits ^{\tau _{s}} \mathop {\longmapsto }\limits ^{\tau _{s}}(\!\!\langle \varDelta '\rangle \!\!)^{4}\vdash (\!\!\langle P'\rangle \!\!)^{4}\)
-
(b)
If \(\ell = \tau \) then \(\varGamma ;\varDelta \vdash P\mathop {\longmapsto }\limits ^{\tau }\varDelta '\vdash P'\) and \((\!\!\langle \varGamma \rangle \!\!)^{4};(\!\!\langle \varDelta _1\rangle \!\!)^{4}\vdash P_1\mathop {\longmapsto }\limits ^{\tau } \mathop {\longmapsto }\limits ^{\tau } \mathop {\longmapsto }\limits ^{\tau }(\!\!\langle \varDelta '\rangle \!\!)^{4}\vdash (\!\!\langle P'\rangle \!\!)^{4}\)
-
(a)
Proposition 14
(Full Abstraction: From \(\mathsf {HO}\,{\widetilde{\pi }}\) to \(\mathsf {HO}\pi \) ). Let P, Q be \(\mathsf {HO}\,{\widetilde{\pi }}\) processes with \(\varGamma ; \emptyset ; \varDelta _1 \vdash P \triangleright \diamond \) and \(\varGamma ; \emptyset ; \varDelta _2 \vdash Q \triangleright \diamond \). Then we have:
\(\varGamma ;\varDelta _1\vdash P\approx ^\texttt {H}\varDelta _2\vdash Q\) if and only if \((\!\!\langle \varGamma \rangle \!\!)^{4};(\!\!\langle \varDelta _1\rangle \!\!)^{4}\vdash [\![P]\!]^4\approx ^\texttt {H}(\!\!\langle \varDelta _2\rangle \!\!)^{4}\vdash [\![Q]\!]^4\).
Using the above propositions, Theorems 3 and 4, and Proposition 1, we derive the following:
Theorem 8
(Encoding of \(\mathsf {HO}\,{\widetilde{\pi }}\) into \(\mathsf {HO}\pi \) ). The encoding from \(\mathcal {L}_{\mathsf {HO}\,{\widetilde{\pi }}}\) into \(\mathcal {L}_{\mathsf {HO}\pi }\) (cf. Fig. 9) is precise. Hence, the encodings from \(\mathcal {L}_{\mathsf {HO}\,{\widetilde{\pi }}}\) to \(\mathcal {L}_{\mathsf {HO}}\) and \(\mathcal {L}_{\pi }\) are also precise.
By combining Theorems 7 and 8, we can extend preciseness to the super-calculus \(\mathsf {HO}\,{\widetilde{\pi }}^{\,+} \).
9 Concluding Remarks and Related Work
We have thoroughly studied the expressivity of the higher-order \(\pi \)-calculus with sessions, here denoted \(\mathsf {HO}\pi \). Unlike most previous works, we have carried out our study in the setting of session types. Types not only delineate and enable encodings; they inform the techniques required to reason about such encodings. Our results cover a wide spectrum of features intrinsic to higher-order concurrency: pure process-passing (first- and higher-order abstractions), name-passing, polyadicity, linear/shared communication (cf. Fig. 1). Remarkably, the discipline embodied by session types turns out to be fundamental to show that all these languages are equally expressive, up to strong typed bisimilarities. Indeed, although our encodings may be used in an untyped setting, session type information is critical to establish key properties for preciseness, in particular full abstraction.
Related Work. There is a vast literature on expressiveness for process calculi; we refer to [28] and [29, Sect. 2.3] for surveys. Our study casts known results [32] into a session typed setting, and offers new encodability results. Our work stresses the view of “encodings as protocols”, namely session protocols which enforce linear and shared disciplines for names, a distinction little explored in previous works. This distinction enables us to obtain refined operational correspondence results (cf. Propositions. 3, 6, 10, 13). We showed that \(\mathsf {HO} \) suffices to encode the first-order session calculus [11], here denoted \(\pi \). To our knowledge, this is a new result; its significance is stressed by the demanding encodability criteria considered, in particular full abstraction up to typed bisimilarities (\(\approx ^\texttt {H}\)/\(\approx ^\texttt {C}\), cf. Propositions 4 and 7). This encoding is relevant in a broader setting, as known encodings of name-passing into higher-order calculi [4, 19, 36, 42, 44] require limitations in source/target languages, do not consider types, and/or fail to satisfy strong encodability criteria (see below). We also showed that \(\mathsf {HO} \) can encode \(\mathsf {HO}\pi \) and its extension with higher-order applications (\(\mathsf {HO\pi ^{+}} \)). Thus, all these calculi are equally expressive with fully abstract encodings (up to \(\approx ^\texttt {H}\)/\(\approx ^\texttt {C}\)). These appear to be the first results of this kind.
Early works on (relative) expressiveness appealed to different notions of encoding. Later on, proposals of abstract frameworks which formalise the notion of encoding and state associated syntactic/semantic criteria were put forward; recent proposals include [8, 10, 30, 31, 41]. Our formulation of precise encoding (Definition 15) builds upon existing proposals (e.g., [10, 16, 26]) to account for the session types associated to \(\mathsf {HO}\pi \).
Early expressiveness studies for higher-order calculi are [32, 39]; recent works include [4, 16, 17, 42, 43]. Due to the close relationship between higher-order process calculi and functional calculi, encodings of (variants of) the \(\lambda \)-calculus into the \(\pi \)-calculus (see, e.g., [1, 7, 33, 37, 46]) are also related. Sangiorgi’s encoding of the higher-order \(\pi \)-calculus into the \(\pi \)-calculus [32] is fully abstract with respect to reduction-closed, barbed congruence. We have shown in Sect. 7.2 that the analogue of Sangiorgi’s encoding for the session typed setting also satisfies full abstraction (up to \(\approx ^\texttt {H}\)/\(\approx ^\texttt {C}\), cf. Proposition 6). A basic form of input/output types is used in [35], where the encoding in [32] is casted in the asynchronous setting, with output and applications coalesced in a single construct. Building upon [35], a simply typed encoding for synchronous processes is given in [36]; the reverse encoding (i.e., first-order communication into higher-order processes) is also studied for an asynchronous, localised \(\pi \)-calculus (only the output capability of names can be sent around). The work [34] studies hierarchies for calculi with internal first-order mobility and with higher-order mobility without name-passing (similarly as the subcalculus \(\mathsf {HO}\)). The hierarchies are defined according to the order of types needed in typing. Via fully abstract encodings, it is shown that that name- and process-passing calculi with equal order of types have the same expressiveness.
Other related works are [4, 17, 19, 42]. The paper [4] gives a fully abstract encoding of the \(\pi \)-calculus into Homer, a higher-order calculus with explicit locations, local names, and nested locations. The paper [19] presents a reflective calculus with a “quoting” operator: names are quoted processes and represent the code of a process; name-passing is then a way of passing the code of a process. This reflective calculus can encode both first- and higher-order \(\pi \)-calculus. Building upon [40], the work [42] studies the (non)encodability of the untyped \(\pi \)-calculus into a higher-order \(\pi \)-calculus with a powerful name relabelling operator, which is essential to encode name-passing. The paper [44] defines an encoding of the (untyped) \(\pi \)-calculus without relabeling. This encoding is quite different from the one in Sect. 7.1: in [44] names are encoded using polyadic name abstractions (called pipes); guarded replication enables infinite behaviours. While our encoding satisfies full abstraction, the encoding in [44] does not: only divergence-reflection and operational correspondence (soundness and completeness) properties are established. Soundness is stated up-to pipe-bisimilarity, an equivalence tailored to the encoding strategy; the authors of [44] describe this result as “weak”.
A core higher-order calculus is studied in [17]: it lacks restriction, name passing, output prefix, and replication/recursion. Still, this subcalculus of \(\mathsf {HO}\) is Turing equivalent. The work [16] extends this core calculus with restriction, output prefix, and polyadicity; it shows that synchronous communication can encode asynchronous communication, and that process passing polyadicity induces an expressiveness hierarchy. The paper [43] complements [16] by studying the expressivity of second-order process abstractions. Polyadicity is shown to induce an expressiveness hierarchy; also, by adapting the encoding in [32], process abstractions are encoded into name abstractions. In contrast, here we give a fully abstract encoding of \(\mathsf {HO}\,{\widetilde{\pi }}^{\,+}\) into \(\mathsf {HO}\) that preserves session types; this improves [16, 43] by enforcing linearity disciplines on process behaviour. The focus of [16, 42–44] is on untyped, higher-order processes; they do not address communication disciplined by (session) type systems.
Within session types, the works [5, 6] encode binary sessions into a linearly typed \(\pi \)-calculus. While [6] gives an encoding of \(\pi \) into a linear calculus (an extension of [1]), the work [5] gives operational correspondence (without full abstraction) for the first- and higher-order \(\pi \)-calculi into [13]. By the result of [6], \(\mathsf {HO\pi ^{+}}\) is encodable into the linearly typed \(\pi \)-calculi. The syntax of \(\mathsf {HO}\pi \) is a subset of that in [22, 23]. The work [22] develops a higher-order session calculus with process abstractions and applications; it admits the type \(U=U_1 \rightarrow U_2 \dots U_n \rightarrow \diamond \) and its linear type \(U^1\) which corresponds to \(\tilde{U}\!\! \rightarrow \!\! \diamond \) and \(\tilde{U}\!\! \multimap \!\! \diamond \) in a super-calculus of \(\mathsf {HO\pi ^{+}} \) and \(\mathsf {HO}\,{\widetilde{\pi }} \). Our results show that the calculus in [22] is not only expressed but also reasoned in \(\mathsf {HO} \) via precise encodings (with a limited form of arrow types: \(C\!\! \rightarrow \!\! \diamond \) and \(C\!\! \multimap \!\! \diamond \)). The recent work [25] studies two encodings: from PCF with an effect system into a session-typed \(\pi \)-calculus, and its reverse. The reverse encoding is used to implement session channel passing in Concurrent Haskell. In future work we plan to use the core calculi studied in this paper to implement higher-order communication efficiently into Concurrent Haskell without losing its expressiveness.
Notes
- 1.
This encoding was suggested by a reviewer of a previous version of this paper.
References
Berger, M., Honda, K., Yoshida, N.: Sequentiality and the \(\pi \)-calculus. In: Abramsky, S. (ed.) TLCA 2001. LNCS, vol. 2044, pp. 29–45. Springer, Heidelberg (2001)
Bernardi, G., Dardha, O., Gay, S.J., Kouzapas, D.: On duality relations for session types. In: Maffei, M., Tuosto, E. (eds.) TGC 2014. LNCS, vol. 8902, pp. 51–66. Springer, Heidelberg (2014)
Bono, V., Padovani, L.: Typing copyless message passing. LMCS 8(1), 1–50 (2012)
Bundgaard, M., Hildebrandt, T.T., Godskesen, J.C.: A cps encoding of name-passing in higher-order mobile embedded resources. Theor. Comput. Sci. 356(3), 422–439 (2006)
Dardha, O., Giachino, E., Sangiorgi, D.: Session types revisited. In: Proceedings of PPDP 2012, pp. 139–150. ACM (2012)
Demangeon, R., Honda, K.: Full abstraction in a subtyped pi-calculus with linear types. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 280–296. Springer, Heidelberg (2011)
Fu, Y.: Variations on mobile processes. Theor. Comput. Sci. 221(1–2), 327–368 (1999)
Fu, Y., Lu, H.: On the expressiveness of interaction. Theor. Comput. Sci. 411(11–13), 1387–1451 (2010)
Gay, S.J., Vasconcelos, V.T.: Linear type theory for asynchronous session types. J. Funct. Program. 20(1), 19–50 (2010)
Gorla, D.: Towards a unified approach to encodability and separation results for process calculi. Inf. Comput. 208(9), 1031–1053 (2010)
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: Hankin, C. (ed.) ESOP 1998. LNCS, vol. 1381, p. 122. Springer, Heidelberg (1998)
Honda, K., Yoshida, N.: On reduction-based process semantics. TCS 151(2), 437–486 (1995)
Kobayashi, N., Pierce, B.C., Turner, D.N.: Linearity and the Pi-Calculus. TOPLAS 21(5), 914–947 (1999)
Kouzapas, D., Pérez, J.A., Yoshida, N.: Characteristic bisimulation for higher-order session processes. In: CONCUR 2015. LIPIcs, vol. 42, pp. 398–411, Dagstuhl, Germany (2015)
Kouzapas, D., Pérez, J.A., Yoshida, N.: Full version of this paper. Technical report, Imperial College / University of Groningen (2015). http://arxiv.org/abs/1502.02585
Lanese, I., Pérez, J.A., Sangiorgi, D., Schmitt, A.: On the expressiveness of polyadic and synchronous communication in higher-order process calculi. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6199, pp. 442–453. Springer, Heidelberg (2010)
Lanese, I., Pérez, J.A., Sangiorgi, D., Schmitt, A.: On the expressiveness and decidability of higher-order process calculi. Inf. Comput. 209(2), 198–226 (2011)
League, C., Shao, Z., Trifonov, V.: Type-preserving compilation of Featherweight Java. ACM Trans. Program. Lang. Syst. 24(2), 112–152 (2002)
Meredith, L.G., Radestock, M.: A reflective higher-order calculus. Electr. Notes Theor. Comput. Sci. 141(5), 49–67 (2005)
Milner, R., Sangiorgi, D.: Barbed bisimulation. In: Kuich, W. (ed.) ICALP 1992. LNCS, vol. 623, pp. 685–695. Springer, Heidelberg (1992)
Morrisett, J.G., Walker, D., Crary, K., Glew, N.: From system F to typed assembly language. ACM Trans. Program. Lang. Syst. 21(3), 527–568 (1999)
Mostrous, D., Yoshida, N.: Two session typing systems for higher-order mobile processes. In: Della Rocca, S.R. (ed.) TLCA 2007. LNCS, vol. 4583, pp. 321–335. Springer, Heidelberg (2007)
Mostrous, D., Yoshida, N.: Session typing and asynchronous subtying for higher-order \(\pi \)-Calculus. Inf. Comput. 241, 227–263 (2015)
Nestmann, U.: What is a “good” encoding of guarded choice? Inf. Comput. 156(1–2), 287–319 (2000)
Orchard, D., Yoshida, N.: Effects as sessions, sessions as effects. In: POPL. ACM (2016)
Palamidessi, C.: Comparing the expressive power of the synchronous and asynchronous pi-calculi. MSCS 13(5), 685–719 (2003)
Palamidessi, C., Saraswat, V.A., Valencia, F.D., Victor, B.: On the expressiveness of linearity vs persistence in the asychronous pi-calculus. Proc. LICS 2006, 59–68 (2006)
Parrow, J.: Expressiveness of process algebras. Electr. Notes Theor. Comput. Sci. 209, 173–186 (2008)
Pérez, J.A.: Higher-Order Concurrency: Expressiveness and Decidability Results. PhD thesis, University of Bologna (2010)
Peters, K., Nestmann, U., Goltz, U.: On distributability in process calculi. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 310–329. Springer, Heidelberg (2013)
Peters, K., van Glabbeek, R.J.: Analysing and comparing encodability criteria. In: Proceedings of EXPRESS/SOS. EPTCS, vol. 190, pp. 46–60 (2015)
Sangiorgi, D.: Expressing Mobility in Process Algebras: First-Order and Higher Order Paradigms. PhD thesis, University of Edinburgh (1992)
Sangiorgi, D.: The lazy lambda calculus in a concurrency scenario. In: 7th LICS Conference, pp. 102–109. IEEE Computer Society Press (1992)
Sangiorgi, D.: \(\pi \)-calculus, internal mobility and agent-passing calculi. TCS 167(2), 235–274 (1996)
Sangiorgi, D.: Asynchronous process calculi: the first- and higher-order paradigms. Theor. Comput. Sci. 253(2), 311–350 (2001)
Sangiorgi, D., Walker, D.: The \(\pi \)-Calculus: A Theory of Mobile Processes. Cambridge University Press, Cambridge (2001)
Sangiorgi, D., Xu, X.: Trees from functions as processes. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 78–92. Springer, Heidelberg (2014)
Shao, Z., Appel, A.W.: A type-based compiler for standard ML. In: Proceedings of PLDI 1995, pp. 116–129. ACM (1995)
Thomsen, B.: Calculi for Higher Order Communicating Systems. PhD thesis, Department of Computer Science, Imperial College (1990)
Thomsen, B.: Plain CHOCS: a second generation calculus for higher order processes. Acta Informatica 30(1), 1–59 (1993)
van Glabbeek, R.J.: Musings on encodings and expressiveness. In Proceedings of EXPRESS/SOS. EPTCS, vol. 89, pp. 81–98 (2012)
Xu, X.: Distinguishing and relating higher-order and first-order processes by expressiveness. Acta Informatica 49(7–8), 445–484 (2012)
Xu, X., Yin, Q., Long, H.: On the expressiveness of parameterization in process-passing. In: Tuosto, E., Ouyang, C. (eds.) WS-FM 2013. LNCS, vol. 8379, pp. 147–167. Springer, Heidelberg (2014)
Xu, X., Yin, Q., Long, H.: On the computation power of name parameterization in higher-order processes. In: Proceedings of ICE. EPTCS, vol. 189, pp. 114–127 (2015)
Yoshida, N.: Graph types for monadic mobile processes. In: Chandru, V., Vinay, V. (eds.) FSTTCS 1996. LNCS, vol. 1180, pp. 371–386. Springer, Heidelberg (1996)
Yoshida, N., Berger, M., Honda, K.: Strong normalisation in the pi -calculus. Inf. Comput. 191(2), 145–202 (2004)
Acknowledgments
We have benefited from feedback from the users of the Moca mailing list, in particular Greg Meredith and Xu Xian. We are grateful to the anonymous reviewers for their useful remarks and suggestions. This work has been partially sponsored by the Doctoral Prize Fellowship, EPSRC EP/K011715/1, EPSRC EP/K034413/1, and EPSRC EP/L00058X/1, EU project FP7-612985 UpScale, and EU COST Action IC1201 BETTY. Pérez is also affiliated to the NOVA Laboratory for Computer Science and Informatics (NOVA LINCS), Universidade Nova de Lisboa, Portugal.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Kouzapas, D., Pérez, J.A., Yoshida, N. (2016). On the Relative Expressiveness of Higher-Order Session Processes. In: Thiemann, P. (eds) Programming Languages and Systems. ESOP 2016. Lecture Notes in Computer Science(), vol 9632. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49498-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-662-49498-1_18
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49497-4
Online ISBN: 978-3-662-49498-1
eBook Packages: Computer ScienceComputer Science (R0)









 constructs,
constructs,  constructs.
constructs.

 .
. .
.

 and, for fresh t,
and, for fresh t,  and
and  and
and  and for fresh t:
and for fresh t:  and
and 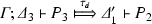 and
and 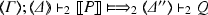 and (ii)
and (ii)  then
then 



 then
then  .
. then
then .
. then
then , and
, and


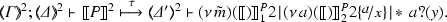
 for some
for some 
 , for some
, for some  ;
; then
then  then
then  and
and  then
then  .
. ,
, 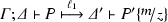 ,
, 




