Abstract
Direct Anonymous Attestation (DAA) is one of the most complex cryptographic algorithms that has been deployed in practice. In spite of this and the long body of work on the subject, there is still no fully satisfactory security definition for DAA. This was already acknowledged by Bernard et al. (IJIC’13) who showed that in existing models insecure protocols can be proved secure. Bernard et al. therefore proposed an extensive set of security games which, however, aim only at a simplified setting termed pre-DAA. In pre-DAA, the host platform that runs the TPM is assumed to be trusted. Consequently, their notion does not guarantee any security if the TPM is embedded in a potentially corrupt host which is a significant restriction. In this paper, we give a comprehensive security definition for full DAA in the form of an ideal functionality in the Universal Composability model. Our definition considers the host and TPM to be separate entities that can be in different corruption states. None of the existing DAA schemes satisfy our strong security notion. We therefore propose a realization that is based on a DAA scheme supported by the TPM 2.0 standard and prove it secure in our model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Direct Anonymous Attestation (DAA)
- Trusted Platform Module (TPM)
- Security Game
- Real-world Protocols
- Basename
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Direct Anonymous Attestation (DAA) allows a small chip, the Trusted Platform Module (TPM), that is embedded in a host computer to create attestations about the state of the host system. Such attestations, which can be seen as signatures on the current state under the TPM’s secret key, convince a remote verifier that the system is running on top of a certified hardware module and is using the correct software. A crucial feature of DAA is that it performs such attestations in a privacy-friendly manner. That is, the user of the host system can choose to create attestations anonymously ensuring that her transactions are unlinkable and do not leak any information about the particular TPM being used. User-controlled linkability is also allowed and is steered by a basename \(\texttt {bsn}\): attestations under a fresh or empty basename can not be linked whereas the repeated use of the same basename makes the corresponding transactions linkable.
DAA is one of the most complex cryptographic protocols deployed in practice. The Trusted Computing Group (TCG), the industry standardization group that designed the TPM, standardized the first DAA protocol in the TPM 1.2 specification in 2004 [23] and included support for multiple DAA schemes in the TPM 2.0 specification in 2014 [24]. Over 500 million computers with TPM chips have been soldFootnote 1, making DAA one of the largest deployments of such a complex cryptographic scheme. This sparked a strong interest in the research community in the security and efficiency of DAA schemes [3, 5–7, 14–18].
Direct Anonymous Attestation has recently also gained the attention of the FIDO alliance which aims at basing online authentication on strong cryptography rather than passwords. The FIDO approach is to choose a fresh key pair for every user account, to provide the public key to the service provider, and to re-authenticate via the corresponding secret key. Adding DAA to this approach allows one to prove that the secret key is properly stored on and protected by a trusted platform.
Existing Security Models. Interestingly, in spite of the large scale deployment and the long body of work on the subject, DAA still lacks a sound and comprehensive security model. There exist a number of security definitions using the simulation-based and property-based paradigms. Unfortunately all have rather severe shortcomings such as allowing completely broken schemes to be proven secure. This was recently discussed by Bernard et al. [3] who provided an analysis of existing security notions and also proposed a new DAA model. In a nutshell, the existing simulation-based models that capture the desired security properties in form of an ideal functionality either miss to treat signatures as concrete objects that can be output or stored by the verifier [5] or are unrealizable by any instantiation [14, 17]. The difficulty in defining a proper ideal functionality for the complex DAA setting might not be all that surprising considering the numerous (failed) attempts in modeling the much simpler standard signature scheme in the universal-composability framework [1, 13].
Another line of work therefore aimed at capturing the DAA requirements in the form of property-based security games [3, 7, 15] as a more intuitive way of modeling. However, the first attempts [7, 15] have missed to cover some of the expected security properties and also have made unconventional choices when defining unforgeability (the latter resulting in schemes being secure that use a constant value as signatures).
Realizing that the previous models were not sufficient, Bernard et al. [3] provided an extensive set of property-based security games. The authors consider only a simplified setting which they call pre-DAA. The simplification is that the host and the TPM are considered as single entity (the platform), thus they are both either corrupt or honest. For properties such as anonymity and non-frameability this is sufficient as they protect against a corrupt issuer and assume both the TPM and host to be honest. Unforgeability of a TPM attestation, however, should rely only on the TPM being honest but allow the host to be corrupt. This cannot be captured in their model. In fact, shifting the load of the computational work to the host without affecting security in case the host is corrupted is one of the main challenges when designing a DAA scheme. Therefore, a DAA security model should be able to formally analyze this setting of an honest TPM and a corrupt host.
This is also acknowledged by Bernard et al. [3] who, after proposing a pre-DAA secure protocol, argue how to obtain security in the full DAA context. Unfortunately, due to the absence of a full DAA security model, this argumentation is done only informally. We show that this argumentation is actually somewhat flawed: the given proof for unforgeability of the given pre-DAA proof can not be lifted (under the same assumptions) to the full DAA setting. This highlights the fact that an “almost matching” security model together with an informal argument of how to achieve the actually desired security does not provide sound guarantees beyond what is formally proved.
Thus still no satisfying security model for DAA exists to date. This lack of a sound security definition is not only a theoretic problem but it in fact has resulted in insecure schemes being deployed in practice. A DAA scheme that allows anyone to forge attestations (as it does not exclude the “trivial” TPM credential (1, 1, 1, 1)) has even been ISO standardized [18, 20].
Our Contributions. We tackle the challenge of formally defining Direct Anonymous Attestation and provide an ideal functionality for DAA in the Universal Composability (UC) framework [12]. Our functionality models the host and TPM as individual parties who can be in different corruption states and comprises all expected security properties such as unforgeability, anonymity, and non-frameability. The model also includes verifier-local revocation where a verifier, when checking the validity of a signature, can specify corrupted TPMs from which he no longer accepts signatures.
We choose to define a new model rather than addressing the weaknesses of one of the existing models. The latest DAA security model by Bernard et al. [3] seem to be the best starting point. However, as this model covers pre-DAA only, changing all these definitions to full DAA would require changes to almost every aspect of them. Furthermore, given the complexity of DAA, we believe that the simulation-based approach is more natural as one has a lower risk of overlooking some security properties. A functionality provides a full description of security and no oracles have to be defined as the adversary simply gets full control over corrupt parties. Furthermore, the UC framework comes with strong composability guarantees that allow for protocols to be analyzed individually and preserve that security when being composed with other protocols.
None of the existing DAA constructions [3, 6, 7, 16, 18] satisfy our security model. Therefore, we also propose a modified version of recent DAA schemes [3, 18] that are built from pairing-based Camenisch-Lysyanskaya signatures [9] and zero-knowledge proofs. We then rigorously prove that our scheme realizes our new functionality. By the universal composition theorem, this proves that our scheme can be composed in arbitrary ways without losing security.
Organization. The rest of this paper is structured as follows. We start with a detailed discussion of existing DAA models in Sect. 2, with a focus on the latest model by Bernard et al. [3]. Section 3 then presents our new definition in the form of an ideal functionality in the UC framework. Section 4 introduces the building blocks required for our DAA scheme, which is presented in Sect. 5. The latter section also contains a discussion why the existing DAA schemes could not be proven secure in our model. The proof that the new DAA scheme fulfills our definition of security is sketched in Sect. 6 (the complete proof is given in the full version of this paper).
2 Issues in Existing Security Models
In this section we briefly discuss why current security models do not properly capture the security properties one would expect from a DAA scheme. Some of the arguments were already pointed out by Bernard et al. [3], who provide a thorough analysis of the existing DAA security notions and also propose a new set of definitions. For the sake of completeness, we summarize and extend their findings and also give an assessment of the latest model by Bernard et al.
Before discussing the various security models and their limitation, we informally describe how DAA works and what are the desired security properties. In a DAA scheme, we have four main entities: a number of trusted platform module (TPM), a number of hosts, an issuer, and a number of verifiers. A TPM and a host together form a platform which performs the join protocol with the issuer who decides if the platform is allowed to become a member. After becoming a member, the TPM and host together can sign messages with respect to basenames \(\texttt {bsn}\). If a platform signs with \(\texttt {bsn}= \bot \) or a fresh basename, the signature must be anonymous and unlinkable. That is, any verifier can check that the signature stems from a legitimate platform via a deterministic verify algorithm, but the signature does not leak any information about the identity of the signer. Only when the platform signs repeatedly with the same basename \(\texttt {bsn}\ne \bot \), it will be clear that the resulting signatures were created by the same platform, which can be publicly tested via a (deterministic) link algorithm.
As usual one requires the typical completeness properties for signatures created by honest parties:
-
Completeness: When an honest platform successfully creates a signature on a message m w.r.t. a basename \(\texttt {bsn}\), an honest verifier will accept the signature.
-
Correctness of Link: When an honest platform successfully creates two signatures, \(\sigma _1\) and \(\sigma _2\), w.r.t. the same basename \(\texttt {bsn}\ne \bot \), an honest verifier running a link algorithm on \(\sigma _1\) and \(\sigma _2\) will output 1. To an honest verifier, it also does not matter in which order two signatures are supplied when testing linkability between the two signatures.
The more difficult part is to define the security properties that a DAA scheme should provide in the presence of malicious parties. These properties can be informally described as follows:
-
Unforgeability-1: When the issuer and all TPMs are honest, no adversary can create a signature on a message m w.r.t. basename \(\texttt {bsn}\) when no platform signed m w.r.t. \(\texttt {bsn}\).
-
Unforgeability-2: When the issuer is honest, an adversary can only sign in the name of corrupt TPMs. More precisely, if n TPMs are corrupt, the adversary can at most create n unlinkable signatures for the same basename \(\texttt {bsn}\ne \bot \).
-
Anonymity: An adversary that is given two signatures, w.r.t. two different basenames or \(\texttt {bsn}= \bot \), cannot distinguish whether both signatures were created by one honest platform, or whether two different honest platforms created the signatures.
-
Non-frameability: No adversary can create signatures on a message m w.r.t. basename \(\texttt {bsn}\) that links to a signature created by an honest platform, when this honest platform never signed m w.r.t. \(\texttt {bsn}\). We require this property to hold even when the issuer is corrupt.
2.1 Simulation-Based Models
A simulation-based security notion defines an ideal functionality, which can be seen as a central trusted party that receives inputs from all parties and provides outputs to them. Roughly, a protocol is called secure if its behavior is indistinguishable from the functionality.
The Brickell, Camenisch, and Chen Model [5]. DAA was first introduced by Brickell, Camenisch, and Chen [5] along with a simulation-based security model. This model has one procedure for signature generation and verification, meaning that a signature is generated for a specific verifier and will immediately be verified by that verifier. As the signature is never output to the verifier, he only learns that a message was correctly signed, but can neither forward signatures or verify them again. Clearly this limits the scenarios in which DAA can be applied.
Furthermore, linkability of signatures was not defined explicitly in the security model. In the instantiation it is handled by attaching pseudonyms to signatures, and when two signatures have the same pseudonym, they must have been created by the same platform.
The Chen, Morissey, and Smart Models [14, 17]. An extension to the model by Brickell et al. was later proposed by Chen, Morissey, and Smart [17]. It aims at providing linkability as an explicit feature in the functionality. To this end, the functionality is extended with a link interface that takes as input two signatures and determines whether they link or not. However, as discussed before, the sign and verify interfaces are interactive and thus signatures are never sent as output to parties, so it is not possible to provide them as input either. This was realized by the authors who thus proposed a new simulation-based model [14] that now separates the generation of signatures from their verification by outputting signatures. Unfortunately, the functionality models the signature generation in a too simplistic way: signatures are simply random values, even when the TPM is corrupt. Furthermore, the verify interface refuses all requests when the issuer is corrupt. Clearly, both these behaviours are not realizable by any protocol.
2.2 Property-Based Models
Given the difficulties in properly modeling signature-based ideal functionalities, there is also a line of work that captures DAA features via property-based definitions.
The Brickell, Chen, and Li Model [7]. The first paper is by Brickell, Chen, and Li [7], who define security games for anonymity, and “user-controlled traceability”. The latter aims to capture our unforgeability-1 and unforgeability-2 requirements. Unfortunately, this model has several major shortcomings that were already discussed in detail by Bernard et al. [3].
The first problem is that the game for unforgeability-1 allows insecure schemes to be considered secure. The adversary in the unforgeability-1 game has oracle access to the honest parties from whom he can request signatures on messages and basenames of his choice. The adversary then wins if he can come up with a valid signature that is not a previous oracle response. This last requirement allows trivially insecure schemes to pass the security game: assume a DAA scheme that outputs the hash of the TPM’s secret key gsk as signature, i.e., the signature is independent of the message. Clearly, this should be an insecure scheme as the adversary, after having seen one signature can provide valid signatures on arbitrary messages of his choice. However, it would actually be secure according to the unforgeability-1 game, as there reused signatures are not considered a forgery.
Another issue is that the game for unforgeability-2 is not well defined. The goal of the adversary is to supply a signature \(\sigma \), message m, basename \(\texttt {bsn}\ne \bot \), and a signer’s identity ID. The adversary wins if another signature “associated with the same ID” exists, but the signatures do not link. Firstly, there is no check on the validity of the supplied signature, which makes winning trivial for the adversary. Secondly, “another signature associated with the same ID” is not precisely defined, but we assume it to mean that the signature was the result of a signing query with that ID. However, then the adversary is limited to tamper with at most one of the signatures, whereas the second one is enforced to be honestly generated and unmodified. Thirdly, there is no check on the relation between the signature and the supplied ID. We expect that the intended behavior is that the supplied signature uses the key of ID, but there is no way to enforce this. Now an adversary can simply make a signing query with \((m, \texttt {bsn}, ID_1)\) giving \(\sigma \), and win the game with \((\sigma , m, \texttt {bsn}, ID_2)\).
The model further lacks a security game that captures the non-frameability requirement. This means a scheme with a link algorithm that always outputs 1 can be proven secure. Chen [15] extends the model to add non-frameability, but this extension inherits all the aforementioned problems from [7].
The Bernard et al. Model [3]. Realizing that the previous models are not sufficient, Bernard et al. [3] provide an extensive set of property-based security definitions covering all expected security requirements.
The main improvement is the way signatures are identified. An identify algorithm is introduced that takes a signature and TPM key, and outputs whether the key was used to create the signature, which is possible as signatures are uniquely identifiable if the secret key is known. In the game definitions, the keys of honest TPMs are known, allowing the challenger to identify which key was used to create the signature, solving the problems related to the imprecisely defined ID in the Brickell, Chen, and Li model.
However, the security games make a simplifying assumption, namely that the platform, consisting of a host and a TPM, is considered as one party. This approach, termed “pre-DAA”, suffices for anonymity and non-frameability, as there both the TPM and host have to be honest. However, for the unforgeability requirements it is crucial that the host does not have to be trusted. In fact, distributing the computational work between the TPM and the host, such that the load on the TPM is as small as possible and at the same time security does not require an honest host, is the main challenge in designing a DAA scheme. Therefore, a DAA security model must be able to formally analyze this setting of an honest TPM working with a corrupt host.
The importance of such full DAA security is also acknowledged by Bernard et al. [3]. After formally proving a proposed scheme secure in the pre-DAA model, the authors bring the scheme to the full DAA setting where the TPM and host are considered as separate parties. To obtain full DAA security, the host randomizes the issuer’s credential on the TPM’s public key. Bernard et al. then argue that this has no impact on the proven pre-DAA security guarantees, as the host does not perform any action involving the TPM secret key. While this is intuitively correct, it gives no guarantees whether the security properties are provably preserved in the full DAA setting.
Indeed, the proof of unforgeability of the pre-DAA scheme, which is proven under the DL assumption, does not hold in the full DAA setting as a corrupt host could notice the simulation used in the security proof. More precisely, in the Bernard et al. scheme, the host sends values (b, d) to the TPM which are the re-randomized part of the issuers credential and are supposed to have the form \(b^{gsk} = d\) with gsk being the TPM’s secret key. The TPM then provides a signature proof of knowledge (SPK) of gsk to the host. The pre-DAA proof relies on the DL assumption and places the unknown discrete logarithm of the challenge DL instance as the TPM key gsk. In the pre-DAA setting, the TPM then simulates the proof of knowledge of gsk for any input (b, d). This, however, is no longer possible in the full DAA setting. If the host is corrupt, he can send arbitrary values (b, d) with \(b^{gsk} \ne d\) to the TPM, but would expect the TPM to respond with a SPK only if (b, d) are properly set. Relying only on the DL assumption does not allow the TPM to check whether (b, d) are well-formed though, such that he would provide correct proofs for false statements. Thus, the unforgeability can no longer be proven under the DL assumption. Note that the scheme could still be proven secure using the stronger static DH assumption, but the point is that a proof of pre-DAA security and a seemingly convincing but informal argument to transfer the scheme to the full DAA setting does not guarantee security in the full DAA setting.
Another peculiarity of the Bernard et al. model is that it makes some rather strong yet somewhat hidden assumptions on the adversaries behavior. For instance, in the traceability game showing unforgeability of the credentials, the adversary must not only output the claimed forgery but also the secret keys of all TPMs. For a DAA protocol this implicitly assumes that the TPM secret key can be extracted from every signature. Similarly, in games such as non-frameability or anonymity that capture security against a corrupt issuer, the issuer’s key is generated honestly within the game, instead of being chosen by the adversary. For any realization this assumes either a trusted setup setting or an extractable proof of correctness of the issuer’s secret key.
In the scheme proposed in [3], none of these implicit assumptions hold though: the generation of the issuer key is not extractable or assumed to be trusted, and the TPM’s secret key cannot be extracted from every signature, as the rewinding would require exponential time. Note that these assumptions are indeed necessary to guarantee security for the proposed scheme. If the non-frameability game would allow the issuer to choose its own key, it could choose \(y = 0\) and win the game. Ideally, a security model should not impose such assumptions or protocol details. If it is necessary though, then the required assumptions should be made more explicit to avoid pitfalls in the protocol design.
3 A New Security Model for DAA
In this section we present our security model for DAA, which is defined as an ideal functionality \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) in the UC framework [12]. In UC, an environment \({\mathcal {E}} \) passes inputs and outputs to the protocol parties. The network is controlled by an adversary \({\mathcal {A}} \) that may communicate freely with \({\mathcal {E}} \). In the ideal world, the parties forward their inputs to the ideal functionality \({\mathcal {F}}\), which then (internally) performs the defined task and creates outputs that the parties forward to \({\mathcal {E}} \).
Roughly, a real-world protocol \(\varPi \) is said to securely realize a functionality \({\mathcal {F}}\), if the real world is indistinguishable from the ideal world, meaning for every adversary performing an attack in the real world, there is an ideal world adversary (often called simulator) \({\mathcal {S}} \) that performs the same attack in the ideal world. More precisely, a protocol \(\varPi \) is secure if for every adversary \({\mathcal {A}} \), there exists a simulator \({\mathcal {S}} \) such that no environment \({\mathcal {E}} \) can distinguish executing the real world with \(\varPi \) and \({\mathcal {A}} \), and executing the ideal world with \({\mathcal {F}}\) and \({\mathcal {S}} \).
3.1 Ideal Functionality \({{\mathcal {F}}}_{\mathsf{daa}}^{l}\)
We now formally define our ideal functionality \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\), for which we assume static corruptions, i.e., the adversary decides upfront which parties are corrupt and makes this information known to the functionality. The UC framework allows us to focus our analysis on a single protocol instance with a globally unique session identifier sid. Here we use session identifiers of the form \( sid = ({\mathcal {I}}, sid')\) for some issuer \({\mathcal {I}} \) and a unique string \( sid '\). To allow several sub-sessions for the join and sign related interfaces we use unique sub-session identifiers jsid and ssid. Our ideal functionality \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) is further parametrized by a leakage function \(l : \{0,1\}^* \rightarrow \{0,1\}^*\), that we need to model the information leakage that occurs in the communication between a host \({\mathcal {H}} _i\) and TPM \({\mathcal {M}} _j\).
We first briefly describe the main interfaces, then present the full functionality \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) and finally discuss in depth why \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) implements the desired security properties.
Setup. The \({\textsf {SETUP}}\) interface on input \( sid = ({\mathcal {I}}, sid')\) initiates a new DAA session for the issuer \({\mathcal {I}} \) and expects the adversary to provide a number of algorithms \((\textsf {ukgen}, \textsf {sig}, \textsf {ver}, \textsf {link}, \textsf {identify})\) that will be used inside the functionality.
-
 will be used to generate keys gsk for honest TPMs.
will be used to generate keys gsk for honest TPMs. -
 will also be used for honest TPMs and on input a key gsk, message m and basename \(\texttt {bsn}\), it outputs a signature \(\sigma \).
will also be used for honest TPMs and on input a key gsk, message m and basename \(\texttt {bsn}\), it outputs a signature \(\sigma \). -
\(f \leftarrow \textsf {ver}(\sigma , m, \texttt {bsn})\) will be used in the verify interface. On input a signature \(\sigma \), message m and basename \(\texttt {bsn}\), it outputs \(f = 1\) if the signature is valid, and \(f=0\) otherwise.
-
\(f \leftarrow \textsf {link}(\sigma , m, \sigma ', m', \texttt {bsn})\) will be used in the link interface. It takes two tuples \((\sigma , m)\), \((\sigma ', m')\), a basename \(\texttt {bsn}\) and outputs \(f = 1\) to indicate that both signature are generated by the same TPM and \(f=0\) otherwise.
-
\(f \leftarrow \textsf {identify}(\sigma , m, \texttt {bsn}, gsk)\) outputs \(f=1\) if \(\sigma \) is a signature of \( m, \texttt {bsn}\) under key gsk, and \(f=0\) otherwise. We will use \(\textsf {identify}\) in several places to ensure consistency, e.g., whenever a new key gsk is generated or provided by the adversary.
Note that the \(\textsf {ver}\) and \(\textsf {link}\) algorithms only assist the functionality for signatures that are not generated by \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) itself. For signatures generated by the functionality, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) will enforce correct verification and linkage using its internal records. While \(\textsf {ukgen}\) and \(\textsf {sig}\) are probabilistic algorithms, the other ones are required to be deterministic. The \(\textsf {link}\) algorithm also has to be symmetric, i.e., for all inputs it must hold that \(\textsf {link}(\sigma , m, \sigma ', m', \texttt {bsn}) \leftrightarrow \textsf {link}(\sigma ', m', \sigma , m, \texttt {bsn})\).
Join. When the setup is completed, a host \({\mathcal {H}} _j\) can request to join with a TPM \({\mathcal {M}} _i\) using the \(\textsf {JOIN}\) interface. Only if the issuer gives his approval through the \(\textsf {JOINPROCEED}\) interface, the join will complete and \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) stores \(\langle {\mathcal {M}} _i, {\mathcal {H}} _j, gsk \rangle \) in an internal list \(\texttt {Members} \). If the host or TPM are corrupt, gsk has to be provided by the adversary. If both are honest, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) stores \(gsk \leftarrow \bot \).
On the first glance, it might seem a bit surprising that we let the adversary also provide gsk when the host is corrupt but the TPM is honest. However we use gsk inside the functionality only to reflect the anonymity properties according to the set of corrupted parties. Only if the entire platform if honest, one can guarantee anonymity and then we enforce \(gsk \leftarrow \bot \). Note that gsk has in particular no impact on the unforgeability guarantees that are always enforced by \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) if \({\mathcal {M}} _i\) is honest.
Sign. Once a platform joined, the host \({\mathcal {H}} _j\) can call the \(\textsf {SIGN}\) interface to request a DAA signature from a TPM \({\mathcal {M}} _i\) for message m with respect to basename \(\texttt {bsn}\). If the issuer is honest, only platforms \(\langle {\mathcal {M}} _i, {\mathcal {H}} _j, gsk \rangle \in \texttt {Members} \) can sign. Then, the TPM is notified and has to give its explicit approval through the \(\textsf {SIGNPROCEED}\) interface. If the host or TPM are corrupt, the signature \(\sigma \) has to be input by the adversary. When both are honest, the signature is generated via the \(\textsf {sig}\) algorithm. Thereby, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) first chooses a fresh key gsk whenever an honest platform (honest host and honest TPM) wishes to sign under a new basename, which naturally enforces unlinkability and anonymity of those signatures. Every newly generated key is stored as \(\langle {\mathcal {M}} _i, \texttt {bsn}, gsk \rangle \) in a list \(\texttt {DomainKeys} \) and will be re-used whenever the honest platform wants to sign under the same \(\texttt {bsn}\) again. For honest platforms, the generated or adversarial provided signature is also stored as \(\langle \sigma , m, \texttt {bsn}, {\mathcal {M}} _i \rangle \) in a list \({\texttt {Signed}}\).
Verify. The verify interface \(\textsf {VERIFY}\) allows any party \({\mathcal {V}} \) to check whether \(\sigma \) is a valid signature on m with respect to \(\texttt {bsn}\). The functionality will use its internal records to determine whether \(\sigma \) is a proper signature. Here we also use the helper algorithm \(\textsf {identify}\) to determine which of the gsk values stored by \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) belongs to that signature. If the key belongs to an honest TPM, then an entry \(\langle \sigma , m, \texttt {bsn}, {\mathcal {M}} _i \rangle \in {\texttt {Signed}}\) must exist. For signatures of corrupt TPMs, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) checks that a valid signature would not violate any of the expected properties, e.g., whether the signature links to another signature by an honest TPM.
The interface also provides verifier-local revocation, as it excepts a revocations list \(\texttt {RL} \) as additional input which is a list of gsk’s from which the verifier does not accept signatures anymore. To ensure that this does not harm the anonymity of honest TPMs, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) ignores all honest \(gsk's\) for the revocation check.
If the \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) did find some reason why the signature should not be valid, it sets the output to \(f \leftarrow 0\). Otherwise, it determines the verification result f using the \(\textsf {ver}\) algorithm. Finally, the functionality keeps track of this result by adding \(\langle \sigma , m, \texttt {bsn}, \texttt {RL}, f \rangle \) to a list \(\texttt {VerResults} \).
Link. Any party \({\mathcal {V}} \) can use the \(\textsf {LINK}\) interface to learn whether two signature \((\sigma , m), (\sigma ', m')\) generated for the same basename \(\texttt {bsn}\) originate from the same TPM or not. Similarly as for verification, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) then first uses its internal records and helper functions to determine if there is any evidence for linkage or non-linkage. If such evidence is found, then the output bit f is set accordingly to 0 or 1. When the functionality has no evidence that the signatures must or must not belong together, it determines the linking result via the \(\textsf {link}\) algorithm.
The full definition of \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) is given in Figs. 1 and 2. To save on repeating and non-essential notation, we use the following conventions in our definition:
-
All requests other than the \({\textsf {SETUP}}\) are ignored until setup phase is completed. For such requests, \({\mathcal {F}}\) outputs \(\bot \) to the caller immediately.
-
Whenever the functionality performs a check that fails, it outputs \(\bot \) directly to the caller of the respective interface.
-
We require the \(\textsf {link}\) algorithm to be symmetric: \(\textsf {link}(\sigma , m, \sigma ', m', \texttt {bsn}) \leftrightarrow \textsf {link}(\sigma ', m', \sigma , m, \texttt {bsn})\). To guarantee this, whenever we write that \({\mathcal {F}}\) runs \(\textsf {link}(\sigma , m, \sigma ', m', \texttt {bsn})\), it runs \(\textsf {link}(\sigma , m, \sigma ', m', \texttt {bsn})\) and \(\textsf {link}(\sigma ', m', \sigma , m, \texttt {bsn})\). If the results are equal, it continues as normal with the result, and otherwise \({\mathcal {F}}\) outputs \(\bot \) to the adversary.
-
When \({\mathcal {F}}\) runs algorithms \(\textsf {sig}, \textsf {ver}, \textsf {identify}, \textsf {link}, \textsf {ukgen}\), it does so without maintaining state. This means all user keys have the same distribution, signatures are equally distributed for the same input, and \(\textsf {ver}\), \(\textsf {identify}\), and \(\textsf {link}\) invocations only depend on the current input, not on previous inputs.
We will further use two “macros” to determine if a gsk is consistent with the functionalities records or not. This is checked at several places in our functionality and also depends on whether the gsk belongs to an honest or corrupt TPM. The first macro \(\textsf {CheckGskHonest}\) is used when the functionality stores a new TPM key gsk that belongs to an honest TPM, and checks that none of the existing valid signatures are identified as belonging to this TPM key. The second macro \(\textsf {CheckGskCorrupt}\) is used when storing a new gsk that belongs to a corrupt TPM, and checks that the new gsk does not break the identifiability of signatures, i.e., it checks that there is no other known TPM key \(gsk'\), unequal to gsk, such that both keys are identified as the owner of a signature. Both functions output a bit b where \(b=1\) indicates that the new gsk is consistent with the stored information, whereas \(b=0\) signals an invalid key. Formally, the two macros are defined as follows.
The setup and join related interfaces of \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\). (The roman numbers are labels for the different checks made within the functionality and will be used as references in the detailed analysis in Sect. 3.2 )
3.2 Detailed Analysis of \({{\mathcal {F}}}_{\mathsf{daa}}^{l}\)
We now argue that our functionality enforces the desired unforgeability, anonymity and non-frameability properties we informally introduced in Sect. 2.
In terms of completeness and correctness, we further have to add to three more properties: consistency of verify and link, and consistency of link. These properties are trivially achieved for property-based definitions, where one simply requires the algorithms to be deterministic, and the link algorithm to be symmetric. In a simulation-based definition, however, the behavior of a functionality may depend on its state, which is why we explicitly show that we achieve these properties.
We start with the security related properties unforgeability, anonymity and non-frameability, and then discuss the correctness and consistency properties.
Unforgeability. We consider two unforgeability properties, depending on all TPMs being honest or some of them being corrupt. The issuer is of course always honest when aiming at unforgeability. Firstly, if all TPMs are honest, an adversary cannot create a signature on a message m with respect to basename \(\texttt {bsn}\) when no honest TPM signed m with respect to \(\texttt {bsn}\). By Check (x), the signature must trace to some TPMs gsk. As we assumed all TPMs to be honest, Check (xi) will reject any signature on messages not signed by that TPM.
Secondly, when some TPMs are corrupt, an adversary cannot forge signatures with more distinct ‘identities’ than there are corrupt TPMs. More precisely, when the adversary corrupted n TPMs, he cannot create more than n unlinkable signatures for the same \(\texttt {bsn}\ne \bot \), and when no honest TPM signed under \(\texttt {bsn}\) too. We show that for any \(n+1\) signatures \(\{\sigma _i, m_i, \texttt {bsn}\}_{0 \ge i \ge n}\), we cannot have that all signatures verify, \(m_i\) was not signed with respect to \(\texttt {bsn}\) by an honest TPMs, and every pair of signatures is unlinkable.
If all signatures verify, by Check (x), each of the \(n+1\) signatures must trace to exactly one pair \(({\mathcal {M}} _i, gsk_i)\). Given the fact that no honest TPM signed \(m_i\) with respect to \(\texttt {bsn}\), by Check (xi), we must have that every TPM in the list of tracing \(({\mathcal {M}} _i, gsk_i)\) pairs is corrupt. Furthermore, we know that all \(({\mathcal {M}} _i, gsk_i)\) come from \(\texttt {Members} \), as only honest TPMs occur in \(\texttt {DomainKeys} \). Since the issuer is honest, Check (ii) enforces that every TPM can join at most once, i.e., there can be at most n pairs \(({\mathcal {M}} _i, gsk_i)\) of corrupt TPMs in \(\texttt {Members} \). Thus, the traced list of \(({\mathcal {M}} _i, gsk_i)\) pairs must contain at least one duplicate entry. By Check (xvi), the two signatures that trace to the same gsk must link, showing that the adversary cannot forge more than n unlinkable signatures with a single \(\texttt {bsn}\ne \bot \).
Anonymity. Anonymity of signatures created by an honest TPM \({\mathcal {M}} _i\) and host \({\mathcal {H}} _j\) is guaranteed by \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) due to the random choice of gsk for every signature. More precisely, if the platform is honest, our functionality does not store any unique gsk for the pair \(({\mathcal {M}} _i,{\mathcal {H}} _j)\) in \(\texttt {Members} \), but leaves the key unassigned. Whenever a new signature is requested for an unused basename \(\texttt {bsn}\), \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) first draws a fresh key \(gsk \leftarrow \textsf {ukgen}\) under which it then creates the signature using the \(\textsf {sig}\) algorithm. The combination of basename and key is stored as \(\langle {\mathcal {M}} _i, \texttt {bsn}, gsk \rangle \) in a list \(\texttt {DomainKeys} \), and gsk is re-used whenever \({\mathcal {M}} _i\) wishes to sign under the same \(\texttt {bsn}\ne \bot \) again.
That is, two signatures with different basenames or with basename \(\texttt {bsn}= \bot \) are distributed in exactly the same way for all honest platforms, independent of whether the signatures are created for the same platform or for two distinct platforms.
Verifier-local revocation is enabled via the revocation list attribute \(\texttt {RL} \) in the \(\textsf {VERIFY}\) interface and allows to “block” signatures of exposed gsk’s. This revocation feature should not be exploitable to trace honest users, though, as that would clearly break anonymity. To this end, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) ignores \(gsk \in \texttt {RL} \) in the revocation test when the key belongs to an honest TPM (Check (xii)).
Note that the anonymity property dictated the use of the \(\textsf {sig}\) algorithm in \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\). We only use the algorithm if the platform is honest though, whereas for corrupt platforms the simulator is allowed to provide the signature (which then could depend on the identity of the signer). This immediately reflects that anonymity is only guaranteed if both the TPM and host are honest.
Non-frameability. An honest platform \(({\mathcal {M}} _i, {\mathcal {H}} _j)\) cannot be framed, meaning that no one can create signatures on messages that the platform never signed but that link to signatures the platform did create. Note that this definition also crucially relies on both \({\mathcal {M}} _i, {\mathcal {H}} _j\) being honest. Intuitively, one might expect that only the TPM \({\mathcal {M}} _i\) is required to be honest, and the host could be corrupt. However, that would be unachievable. We can never control the signatures that a corrupt \({\mathcal {H}} _j\) outputs. In particular, the host could additionally run a corrupt TPM that joined as well, and create signatures using the corrupt TPM’s key instead of using \({\mathcal {M}} _i\)’s contribution. The resulting signature can not be protected from framing, as it uses a corrupt TPM’s key. Thus, for a meaningful non-frameability guarantee, the host has to be honest too. The issuer can of course be corrupt.
We now show that when an honest platform \(({\mathcal {M}} _i, {\mathcal {H}} _j)\) created a signature \(\sigma \) on message m and under basename \(\texttt {bsn}\), then no other signature \(\sigma '\) on some \(m'\) links to \(\sigma \) when \(({\mathcal {M}} _i, {\mathcal {H}} _j)\) never signed \(m'\) with respect to \(\texttt {bsn}\). The first requirement in \(\textsf {LINK}\) is that both signatures must be valid (Check (xiv)). By completeness (discussed below) we know that \(\sigma , m, \texttt {bsn}\) generated by the honest platform is valid, and that it traces to some key gsk. If the second signature \(\sigma ', m', \texttt {bsn}\) is valid too, we know by the Check (xi) in the \(\textsf {VERIFY}\) interface that the signature cannot trace to the same gsk, because \(({\mathcal {M}} _i, {\mathcal {H}} _j)\) has never signed \(m', \texttt {bsn}'\). Finally, by Check (xv) that ensures that the output of \(\textsf {identify}\) must be consistent for \(all \) used keys, the output of \(\textsf {LINK}\) is set to \(f \leftarrow 0\).
Completeness. The functionality guarantees completeness, i.e., when an honest platform successfully creates a signature, this signature will be accepted by honest verifiers. More precisely, when honest TPM \({\mathcal {M}} _i\) with honest host \({\mathcal {H}} _j\) signs m with respect to \(\texttt {bsn}\) resulting in a signature \(\sigma \), a verifier will accept \((\sigma , m, \texttt {bsn})\). To show this, we argue that the four checks the functionality makes (Check (ix), Check (x), Check (xi), and Check (xii)) do not set f to 0, and that \(\textsf {ver}\) will accept the signature.
Check (ix) will not trigger, as by Check (viii) there was no honest TPM other than \({\mathcal {M}} _i\) with a key matching this signature yet and, by Check (iv), Check (iv), and Check (v), gsk values matching \(\sigma \) cannot be added to \(\texttt {Members} \) and \(\texttt {DomainKeys} \).
Check (x) will not trigger as we have an entry \(\langle {\mathcal {M}} _i, \texttt {bsn}, gsk \rangle \in \texttt {DomainKeys} \), and by Check (vii) we know this one matches \(\sigma \).
In Check (xi), \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) finds all honest TPMs that have a key matching this signature, and checks whether they signed m with respect to \(\texttt {bsn}\). By Check (viii), at the time of signing there were no other TPMs with keys matching this signature and, by Check (iii) and Check (v), no honest TPM can get a key matching this signature. The only honest TPM with a matching key is \({\mathcal {M}} _i\), but as he honestly signed m with respect to \(\texttt {bsn}\), we have an entry \(\langle \sigma , m, \texttt {bsn}, {\mathcal {M}} _i \rangle \in {\texttt {Signed}}\) ensuring that the check does not trigger.
The revocation test Check (xii) does not trigger as by Check (vii) we know that honest TPM \({\mathcal {M}} _i\) has a key matching this signature.
As all previous checks did not apply, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) sets the verification outcome using the \(\textsf {ver}\) algorithm, we now show that \(\textsf {ver}\) will accept the signature. \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) checked that \(\textsf {ver}\) accepts the signature in Check (vi), and by Check (i) and the fact that \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) does not maintain state for the algorithms, the verification algorithm output only depends on its input, so \(\textsf {ver}\) outputs 1 and \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) accepts the signature.
Correctness of Link. If an honest platform signs multiple times with the same basename, the resulting signatures will link. Let platform \(({\mathcal {M}} _i\), \({\mathcal {H}} _j)\) sign messages \(m_1\) and \(m_2\) with basename \(\texttt {bsn}\ne \bot \), resulting in signatures \(\sigma _1\) and \(\sigma _2\) respectively. By completeness, both signatures verify, so Check (xiv) does not trigger. By Check (vii), both signatures identify to some gsk, which results in Check (xvi) setting the signatures as linked.
Consistency of Verify. This property ensures that calling the \(\textsf {VERIFY}\) interface with the same input multiple times gives the same result every time. To prevent the functionality from becoming unnecessarily complex, we only enforce consistency for valid signatures. That is, whenever a signature was accepted, it will remain valid, whereas an invalid signature could become valid at a later time.
Suppose a signature \(\sigma \) on message m with basename \(\texttt {bsn}\) was verified successfully with revocation list \(\texttt {RL} \). We now show that in any future verification with the same \(\texttt {RL} \) will lead to the same result. To show this, we argue that the four checks the functionality makes (Check (ix), Check (x), Check (xi), and Check (xii)) do not set f to 0, and that \(\textsf {ver}\) will accept the signature.
Check (ix) makes sure that at most one key gsk matches the signature \(\sigma \), meaning that for at most one gsk we have \(\textsf {identify}(\sigma , m, \texttt {bsn}, gsk) = 1\). This check does not cause rejection of the signature, as the signature previously verified, and by Check (ix) we have that at most one gsk matched the signature at that time. After that, the signature was placed in \(\texttt {VerResults} \), which means Check (iii), Check (iv), and Check (v) prevent adding gsk values that match \(\sigma \), so the number of matching gsk values has not changed and Check (ix) still passes.
Check (x) does not apply. If \({\mathcal {I}} \) is corrupt, the check trivially does not trigger. If \({\mathcal {I}} \) is honest, from the previous verification we have that there was precisely one key matching, and as argued for the previous check, no matching gsk values can be added, so we must still have precisely one matching gsk.
To show that Check (xi) does not apply, we must show that for every honest TPM that has a key matching this signature, that TPM has signed m with respect to \(\texttt {bsn}\). As the check previously passed, so we know that at that point for any matching \({\mathcal {M}} _i\) there is a satisfying entry in \({\texttt {Signed}}\). No new TPMs matching this signature can be found, as Check (iii) and Check (v) prevent honest TPMs from registering a key that matches an existing signature.
Check (xii), the revocation check, did not reject \(\sigma \) in the previous verification. By the fact that \(\textsf {identify}\) is deterministic Check (i) and executed without maintaining state, it will not do so now.
As the four checks \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) makes did not apply, \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) uses the verification algorithm \(\textsf {ver}\). Since the signature was previously accepted, by Check (xiii) \(\textsf {ver}\) must have accepted the signature. By the fact that \(\textsf {ver}\) is deterministic (Check (i)) and executed without maintaining state, it will also accept now.
Consistency of Link. We also want to ensure that calling the \(\textsf {LINK}\) interface with the same input multiple times gives the same result every time. Here we guarantee consistency for both outputs \(f \in \{0,1\}\) i.e., if \(\textsf {LINK}\) outputs f for some input \((\sigma , m, \sigma ', m', \texttt {bsn})\), the result will always be f.
Suppose we have signatures \(\sigma \) and \(\sigma '\) on messages m and \(m'\) respectively, both with respect to basename \(\texttt {bsn}\), that have been linked with output \(f \in \{0,1\}\) before. We now show that the same result f will be given in future queries, by showing that Check (xiv) will not cause an output of \(\bot \), and by showing that Check (xv), Check (xvi), and the \(\textsf {link}\) algorithm are consistent.
\({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) will not output \(\bot \), as by the previous output \(f \ne \bot \) we know that the verification of both signatures must have passed. As \(\textsf {VERIFY}\) is consistent for valid signatures, this test in Check (xiv) will pass again.
Check (xv) and Check (xvi) are consistent. They depend on the gsk values in \(\texttt {Members} \) and \(\texttt {DomainKeys} \) that match the signatures and are retrieved via the deterministic \(\textsf {identify}\) algorithm. The matching gsk values cannot have changed as Check (iii), Check (iv), and Check (v) prevent conflicting gsk values to be added to these lists. The \(\textsf {link}\) algorithm used to in the final step is deterministic by Check (i). Thus, Link will consistently generate the same output bit f.
Symmetry of Link. The link interface is symmetric, i.e., it does not matter whether one gives input \((\textsf {LINK}, \sigma , m, \sigma ', m', \texttt {bsn})\) or \((\textsf {LINK}, \sigma ', m', \sigma , m, \texttt {bsn})\). Both signatures are verified, the order in which this happens does not change the outcome. Next \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) finds matching keys for the signatures, and as \(\textsf {identify}\) is executed without state, it does not matter whether it first tries to match \(\sigma \) or \(\sigma '\). The next checks are based on the equality of the \(b_i\) and \(b_i'\) values, which clearly is symmetric. Finally \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) uses the \(\textsf {link}\) algorithm, which is enforced to be symmetric as \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) will abort as soon as it detects \(\textsf {link}\) not being symmetric.
4 Building Blocks
In this section we introduce the building blocks for our construction. Apart from standard building blocks such as pairing-based CL-signatures [9] and zero-knowledge proofs, we also provide a new functionality \({{\mathcal {F}}_{\textsf {auth*}}} \) that captures the semi-authenticated channel that is present in the DAA setting.
4.1 Bilinear Maps
Let \(\mathbb {G}_1\), \(\mathbb {G}_2\) and \( \mathbb {G}_T\) be groups of prime order q. A map \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) must satisfy bilinearity, i.e., \(e(g_1^x,g_2^y)=e(g_1,g_2)^{xy}\); non-degeneracy, i.e., for all generators \(g_1 \in \mathbb {G}_1\) and \(g_2 \in \mathbb {G}_2\), \(e(g_1,g_2)\) generates \( \mathbb {G}_T\); and efficiency, i.e., there exists an efficient algorithm \(\mathcal {G}(1^\tau )\) that outputs the bilinear group \((q,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e,g_1,g_2)\) and an efficient algorithm to compute e(a, b) for any \(a \in \mathbb {G}_1\), \(b \in \mathbb {G}_2\). If \(\mathbb {G}_1 = \mathbb {G}_2\) the map is called symmetric, otherwise the map is called asymmetric.
4.2 Camenisch-Lysyanskaya Signature
We now recall the pairing-based Camenisch-Lysyanskaya (CL) signature scheme [9] that allows for efficient proofs of signature possession and is the basis for the DAA scheme we extend. The scheme uses a bilinear group \((q,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e,g_1,g_2)\) that is available to all algorithms.
-
Key generation. The key generation algorithm chooses
 and
and  , and sets \(sk \leftarrow (x,y)\), \(pk \leftarrow (X, Y)\), where \(X \leftarrow g_2^x\) and \(Y \leftarrow g_2^y\).
, and sets \(sk \leftarrow (x,y)\), \(pk \leftarrow (X, Y)\), where \(X \leftarrow g_2^x\) and \(Y \leftarrow g_2^y\). -
Signature. On input a message m and secret key \(sk = (x,y)\), choose a random
 , and output the signature \(\sigma \leftarrow (a,a^y,a^{x+mxy})\).
, and output the signature \(\sigma \leftarrow (a,a^y,a^{x+mxy})\). -
Verification. On input a public key \(pk = (X,Y)\), message m, and purported signature \(\sigma = (a,b,c)\), output 1 if the following verification equations hold, and 0 otherwise: \(a \ne 1_{\mathbb {G}_1}, e(a,Y) = e(g_1,b) \) and \(e(X,a) \cdot e(X,b)^m = e(g_1,c)\).
This signature scheme is existentially unforgeable against a chosen-message attack (EUF-CMA) under the LRSW assumption [21], which is proven in [9]. Certain schemes [3, 18], including ours, add a fourth element \(d = b^m\) to the signature, which allows more efficient proofs of knowledge of a message signed by a signature. This extended CL signature is as secure as the original CL signature: Any adversary that can create a standard CL forgery (a, b, c) on message m can forge an extended CL signature by adding \(d = b^m\). Any adversary that can create an extended CL forgery (a, b, c, d) on m can forge a standard CL signature, by adding \(d = b^m\) to the signing oracle outputs, and omitting d from the final forgery.
4.3 Proof Protocols
When referring to the zero-knowledge proofs of knowledge of discrete logarithms and statements about them, we will follow the notation introduced by Camenisch and Stadler [11] and formally defined by Camenisch, Kiayias, and Yung [8].
For instance, \( PK \{(a, b, c): y=g^a h^b \wedge \tilde{y}=\tilde{g}^a \tilde{h}^c \}\) denotes a “zero-knowledge Proof of Knowledge of integers a, b and c such that \(y=g^{a}h^{b}\) and \(\tilde{y}=\tilde{g}^{a}\tilde{h}^{c}\) holds,” where \(y, g, h, \tilde{y}, \tilde{g}\) and \(\tilde{h}\) are elements of some groups \(\mathbb {G}=\langle {g}\rangle =\langle {h}\rangle \) and \(\tilde{\mathbb {G}}=\langle \tilde{g} \rangle =\langle \tilde{h} \rangle \). Given a protocol in this notation, it is straightforward to derive an actual protocol implementing the proof [8]. Indeed, the computational complexities of the proof protocol can be easily derived from this notation: for each term \(y=g^{a}h^{b}\), the prover and the verifier have to perform an equivalent computation, and to transmit one group element and one response value for each exponent.
\( SPK \) denotes a signature proof of knowledge, that is a non-interactive transformation of a proof with the Fiat-Shamir heuristic [19] in the random oracle model [2]. From these non-interactive proofs, the witness can be extracted by rewinding the prover and programming the random oracle. Alternatively, these proofs can be extended to be online-extractable, by verifiably encrypting the witness to a public key defined in the common reference string (CRS). Now a simulator controlling the CRS can extract the witness without rewinding by decrypting the ciphertext. A practical instantiation is given by Camenisch and Shoup [10] using Paillier encryption, secure under the DCR assumption [22].
4.4 Semi-Authenticated Channels via \({{\mathcal {F}}_{\textsf {auth*}}} \)
In the join protocol of DAA, it is crucial that the TPM and issuer authenticate to each other, such that only authentic TPMs can create signatures. This is not an ordinary authenticated channel, as all communication is channeled via the host, that can read the messages, block the communication, or append messages. There exist several sub-protocols and setup settings in the DAA context that provide this type of special authenticated channels, of which an overview is given by Bernard et al. [3]. These constructions require the TPM to have a key pair, the endorsement key, of which the public part is known to the issuer. In practice, the TPM manufacturer certifies the public key using traditional PKI, allowing an issuer to verify that this public key indeed belongs to a certain TPM. If the endorsement key is a key for a signature scheme, the TPM can send an authenticated message to the issuer by signing the message. If a public key encryption key is used, this can be used to exchange a MAC key to authenticate later messages.
We design a functionality \({{\mathcal {F}}_{\textsf {auth*}}} \) modeling the desired channel, which allows us to rather use the abstract functionality in the protocol design instead of a concrete sub-protocol. Then, any protocol that securely realizes \({{\mathcal {F}}_{\textsf {auth*}}} \) can be used for the initial authentication.
The functionality must capture the fact that the sender S sends a message containing an authenticated and an unauthenticated part to the receiver R, while giving some forwarder F (this role will be played by the host) the power to block the message or replace the unauthenticated part, and giving the adversary the power to replace the forwarder’s message and block the communication. We capture these requirements in \({{\mathcal {F}}_{\textsf {auth*}}} \), defined in Fig. 3.
Clearly we can realize this functionality using the endorsement key and a signature scheme or public key encryption scheme.
5 Construction
In this section, we present our DAA scheme that securely implements \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\). While our scheme is similar to previous constructions [3, 6, 7, 16, 18], it required several modifications in order to fulfill all of our desired security guarantees. We give a detailed discussion of the changes with respect to previous versions in Sect. 5.2.
The high-level idea of our DAA scheme is as follows. In the join protocol, a platform, consisting of a TPM \({\mathcal {M}} _i\) and host \({\mathcal {H}} _j\), receives a credential (a, b, c, d) from the issuer \({\mathcal {I}} \) which is a Camenisch-Lysyanskaya signature [9] on some TPM chosen secret \( gsk \). After joining, the platform can sign any message m w.r.t. some basename \(\texttt {bsn}\). To this end, the host first randomizes the credential (a, b, c, d) to \((a' = a^r, b'= b^r, c' = c^r, d' = d^r)\) for a random r and then lets the TPM \({\mathcal {M}} _i\) create a signature proof of knowledge (SPK) on m showing that \(b'^{ gsk } = d'\). To obtain user-controlled linkability for basenames \(\texttt {bsn}\ne \bot \), pseudonyms are attached to the signature. Pseudonyms are similar to BLS signatures [4] on the basename and have the form \(\texttt {nym}= H_1(\texttt {bsn})^{ gsk }\) for some hash function \(H_1\). Whenever a basename \(\texttt {bsn}\ne \bot \) is used, the SPK generated by the TPM also proves that the pseudonym is well-formed.
5.1 Our DAA Protocol \(\varPi _{\textsf {daa}}\)
We now present our DAA scheme in detail, and also give a simplified overview of the join and sign protocols in Figs. 4 and 5 respectively.
We assume that a common reference string functionality \({\mathcal {F}_{\mathsf{crs}}^{D}}\) and a certificate authority functionality \({{\mathcal {F}}_{\textsf {ca}}} \) are available to all parties. The later allows the issuer to register his public key, and \({\mathcal {F}_{\mathsf{crs}}^{D}}\) is used to provide all entities with the system parameters comprising a security parameter \(\tau \), a bilinear group \(\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T\) of prime order q with generators \(g_1, g_2\) and bilinear map e, generated via \(\mathcal {G}(1^\tau )\). We further use a random oracle \(H_1 : \{0,1\}^* \rightarrow \mathbb {G}_1\).
For the communication between the TPM and issuer (via the host) in the join protocol, we use our semi-authenticated channel \({{\mathcal {F}}_{\textsf {auth*}}} \) introduced in Sect. . For all communication between a host and TPM we assume the secure message transmission functionality \({\mathcal {F}_{\mathsf{smt}}^{l}}\) (enabling authenticated and encrypted communication). In practice, \({\mathcal {F}_{\mathsf{smt}}^{l}}\) is naturally guaranteed by the physical proximity of the host and TPM forming the platform, i.e., if both are honest an adversary can neither alter nor read their internal communication. To make the protocol more readable, we simply say that \({\mathcal {H}} _i\) sends a message to, or receives a message from \({\mathcal {M}} _j\), instead of explicitly calling \({\mathcal {F}_{\mathsf{smt}}^{l}}\) with sub-session IDs etc. For definitions of the standard functionalities \({\mathcal {F}_{\mathsf{crs}}^{D}}, {{\mathcal {F}}_{\textsf {ca}}} \) and \({\mathcal {F}_{\mathsf{smt}}^{l}}\) we refer to [12, 13].
In the description of the protocol, we assume that parties call \({\mathcal {F}_{\mathsf{crs}}^{D}}\) and \({{\mathcal {F}}_{\textsf {ca}}} \) to retrieve the necessary key material whenever they use a public key of another party. Further, if any of the checks in the protocol fails, the protocol ends with a failure message \(\bot \). The protocol also outputs \(\bot \) whenever a party receives an input or message it does not expect (e.g., protocol messages arriving in the wrong order.)
Setup. In the setup phase, the issuer \({\mathcal {I}} \) creates a key pair of the CL-signature scheme and registers the public key with \({{\mathcal {F}}_{\textsf {ca}}} \).
-
1.
\({\mathcal {I}} \) upon input \(({\textsf {SETUP}}, sid )\) generates his key pair:
-
Check that \( sid = ({\mathcal {I}}, sid ')\) for some \( sid '\).
-
Choose
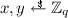 , and set \(X \leftarrow g_2^x, Y \leftarrow g_2^y\). Initiate \(\mathcal {L}_\textsf {JOINED}\leftarrow \emptyset \).
, and set \(X \leftarrow g_2^x, Y \leftarrow g_2^y\). Initiate \(\mathcal {L}_\textsf {JOINED}\leftarrow \emptyset \). -
Prove that the key is well-formed in
 .
. -
Register the public key \((X, Y, \pi )\) at \({{\mathcal {F}}_{\textsf {ca}}} \), and store the secret key as (x, y).
-
Output \(({\textsf {SETUPDONE}}, sid )\).
-
Join. The join protocol runs between the issuer \({\mathcal {I}} \) and a platform, consisting of a TPM \({\mathcal {M}} _i\) and a host \({\mathcal {H}} _j\). The platform authenticates to the issuer and, if the issuer allows, obtains a credential that subsequently enables the platform to create signatures. To distinguish several join sessions that might run in parallel, we use a unique sub-session identifier jsid that is given as input to all parties.
-
1.
\({\mathcal {H}} _j\) upon input \((\textsf {JOIN}, sid , jsid, {\mathcal {M}} _i)\) parses \( sid = ({\mathcal {I}}, sid ')\) and sends the message \((\textsf {JOIN}, sid , jsid)\) to \({\mathcal {I}} \).
-
2.
\({\mathcal {I}} \) upon receiving \((\textsf {JOIN}, sid , jsid)\) from a party \({\mathcal {H}} _j\) chooses a fresh nonce \(n \leftarrow \{0,1\}^{\tau }\) and sends (sid, jsid, n) back to \({\mathcal {H}} _j\).
-
3.
\({\mathcal {H}} _j\) upon receiving \(( sid , jsid, n)\) from \({\mathcal {I}} \), sends (sid, jsid, n) to \({\mathcal {M}} _i\).
-
4.
\({\mathcal {M}} _i\) upon receiving \(( sid , jsid, n)\) from \({\mathcal {H}} _j\), generates its secret key:
-
Check that no completed key record exists.
-
Choose
 and store the key as \((sid, {\mathcal {H}} _j, gsk , \bot )\).
and store the key as \((sid, {\mathcal {H}} _j, gsk , \bot )\). -
Set \(Q \leftarrow g_1^{ gsk }\) and compute
 .
. -
Send \((Q, \pi _1)\) via the host to \({\mathcal {I}} \) using \({{\mathcal {F}}_{\textsf {auth*}}} \), i.e., invoke \({{\mathcal {F}}_{\textsf {auth*}}} \) on input \((\textsf {SEND}, ({\mathcal {M}} _i, {\mathcal {I}}, sid ), jsid, (Q, \pi _1), {\mathcal {H}} _j)\).
-
-
5.
\({\mathcal {H}} _j\) upon receiving \((\textsf {APPEND}, ({\mathcal {M}} _i, {\mathcal {I}}, sid ), jsid, Q, \pi _1)\) from \({{\mathcal {F}}_{\textsf {auth*}}} \), forwards the message to \({\mathcal {I}} \) by sending \((\textsf {APPEND}, ({\mathcal {M}} _i, {\mathcal {I}}, sid ), jsid, {\mathcal {H}} _j)\) to \({{\mathcal {F}}_{\textsf {auth*}}} \). It also keeps state as (jsid, Q).
-
6.
\({\mathcal {I}} \) upon receiving \((\textsf {SENT}, ({\mathcal {M}} _i, {\mathcal {I}}, sid ), jsid, (Q, \pi _1), {\mathcal {H}} _j)\) from \({{\mathcal {F}}_{\textsf {auth*}}} \) verifies \(\pi _1\) and checks that \({\mathcal {M}} _i \notin \mathcal {L}_\textsf {JOINED}\). It stores \((jsid, Q, {\mathcal {M}} _i, {\mathcal {H}} _j)\) and outputs \((\textsf {JOINPROCEED}, sid , jsid, {\mathcal {M}} _i)\).
The join session is then completed when the issuer receives an explicit input telling him to proceed with join session jsid.
-
1.
\({\mathcal {I}} \) upon input \((\textsf {JOINPROCEED}, sid , jsid)\) generates the CL credential:
-
Retrieve the record \((jsid, Q, {\mathcal {M}} _i, {\mathcal {H}} _j)\) and add \({\mathcal {M}} _i\) to \(\mathcal {L}_\textsf {JOINED}\).
-
Choose \(r \leftarrow {\mathbb {Z}} _q\) and compute \(a \leftarrow g_1^r\), \(b \leftarrow a^y\), \(c \leftarrow a^{x} \cdot Q^{rxy}\), \(d \leftarrow Q^{ry}\).
-
Prove correctness of the signature in
 .
. -
Send the credential (a, b, c, d) to the host \({\mathcal {H}} _j\) by giving \({{\mathcal {F}}_{\textsf {auth*}}} \) input \((\textsf {SEND}, ({\mathcal {I}}, {\mathcal {M}} _i, sid ), jsid, (b, d, \pi _2), (a, c), {\mathcal {H}} _j)\).
-
-
2.
\({\mathcal {H}} _j\) upon receiving \((\textsf {APPEND}, ({\mathcal {I}}, {\mathcal {M}} _i, sid ), jsid, (b, d, \pi _2), (a, c))\) from \({{\mathcal {F}}_{\textsf {auth*}}} \) verifies the credential (a, b, c, d) and forwards \((b,d, \pi _2)\) to \({\mathcal {M}} _i\):
-
Retrieve (jsid, Q) and verify \(\pi _2\) w.r.t. Q.
-
Verify the credential as \(a \ne 1\), \(e(a, Y) = e(b, g_2)\), and \(e(c, g_2) = e(a \cdot d, X)\).
-
Send \((\textsf {APPEND}, ({\mathcal {I}}, {\mathcal {M}} _i, sid ), jsid, \bot )\) to \({{\mathcal {F}}_{\textsf {auth*}}} \).
-
-
3.
\({\mathcal {M}} _i\) upon receiving \((\textsf {SENT}, ({\mathcal {I}}, {\mathcal {M}} _i, sid ), jsid, (b, d, \pi _2), \bot )\) from \({{\mathcal {F}}_{\textsf {auth*}}} \), completes the join:
-
Retrieve the record \((sid, {\mathcal {H}} _j, gsk , \bot )\) and verify \(\pi _2\) with respect to \(Q \leftarrow g_1^{ gsk }.\)
-
Complete the record to \((sid, {\mathcal {H}} _j, gsk ,(b, d))\) and send \((jsid, \textsf {JOINED})\) to \({\mathcal {H}} _j\).
-
-
4.
\({\mathcal {H}} _j\) upon receiving \((jsid, \textsf {JOINED})\) from \({\mathcal {M}} _i\) stores \((sid, {\mathcal {M}} _i, (a,b,c,d))\) and outputs \((\textsf {JOINED}, sid , jsid)\).
Sign. The sign protocol runs between a TPM \({\mathcal {M}} _i\) and a host \({\mathcal {H}} _j\). After joining, together they can sign a message m with respect to basename \(\texttt {bsn}\). Again, we use a unique sub-session identifier ssid to allow for multiple sign sessions.
-
1.
\({\mathcal {H}} _j\) upon input \((\textsf {SIGN}, sid , ssid, {\mathcal {M}} _i, m, \texttt {bsn})\) re-randomizes the CL-credential:
-
Retrieve the join record \((sid,{\mathcal {M}} _i, (a,b,c,d))\).
-
Choose
 and set \((a', b', c', d') \leftarrow (a^r, b^r, c^r, d^r)\).
and set \((a', b', c', d') \leftarrow (a^r, b^r, c^r, d^r)\). -
Send \((ssid, m, \texttt {bsn}, r)\) to \({\mathcal {M}} _i\) and store \((ssid, (a', b', c', d'))\)
-
-
2.
\({\mathcal {M}} _i\) upon receiving \((ssid, m, \texttt {bsn}, r)\) from \({\mathcal {H}} _j\) asks for permission to proceed.
-
Check that a complete join record \(( sid , {\mathcal {H}} _j, gsk , (b,d))\) exists.
-
Store \((ssid, m, \texttt {bsn}, r)\) and output \((\textsf {SIGNPROCEED}, sid , ssid, m, \texttt {bsn})\).
-
The signature is completed when \({\mathcal {M}} _i\) gets permission to proceed for ssid.
-
1.
\({\mathcal {M}} _i\) upon input \((\textsf {SIGNPROCEED}, sid , ssid)\) computes the SPK and \(\texttt {nym}\):
-
Retrieve records \(( sid , {\mathcal {H}} _j, gsk , (b,d))\) and \((ssid, m, \texttt {bsn}, r)\).
-
Compute \(b' \leftarrow b^r, d' \leftarrow d^r\).
-
If \(\texttt {bsn}= \bot \), set \(\texttt {nym}= \bot \) and compute
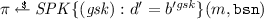 .
. -
If \(\texttt {bsn}\ne \bot \), set \(\texttt {nym}= H_1(\texttt {bsn})^{ gsk }\) and compute the SPK on (m,bsn) as
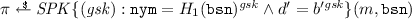 .
. -
Send \((ssid, \pi , \texttt {nym})\) to \({\mathcal {H}} _j\).
-
-
2.
\({\mathcal {H}} _j\) upon receiving \((ssid, \pi , \texttt {nym})\) from \({\mathcal {H}} _j\), retrieves \((ssid, (a', b', c', d'))\) and outputs \((\textsf {SIGNATURE}, sid , ssid, (a', b', c', d', \pi , \texttt {nym}))\).
Verify. The verify algorithm allows everyone to check whether signature \(\sigma \) on message m with respect to basename \(\texttt {bsn}\) is valid, i.e., stems from a certified TPM. To test whether the signature originates from a TPM that did get corrupted, the verifier can pass a revocation list \(\texttt {RL} \) to the algorithm. This list contains the keys of corrupted TPMs he no longer wishes to accept signatures from.
-
1.
\({\mathcal {V}} \) upon input \((\textsf {VERIFY}, sid , m, \texttt {bsn}, \sigma , \texttt {RL})\) verifies the signature:
-
Parse \(\sigma \) as \((a, b, c, d, \pi , \texttt {nym})\).
-
Verify \(\pi \) with respect to \((m, \texttt {bsn})\) and \(\texttt {nym}\) (if \(\texttt {bsn}\ne \bot )\).
-
Check that \(a \ne 1, b \ne 1\), \(e(a, Y) = e(b, g_2)\) and \(e(c, g_2) = e(a \cdot d, X)\).
-
For every \( gsk _i \in \texttt {RL} \), check that \(b^{ gsk _i} \ne d\).
-
If all tests pass, set \(f \leftarrow 1\), otherwise \(f \leftarrow 0\).
-
Output \((\textsf {VERIFIED}, sid , f)\).
-
Link. With the link algorithm, anyone can test whether two signatures \((\sigma , m)\), \((\sigma ', m')\) that were generated for the same basename \(\texttt {bsn}\ne \bot \), stem from the same TPM.
-
1.
\({\mathcal {V}} \) upon input \((\textsf {LINK}, sid , \sigma , m, \sigma ', m', \texttt {bsn})\) verifies the signatures and compares the pseudonyms contained in \(\sigma , \sigma '\):
-
Check that \(\texttt {bsn}\ne \bot \) and that both signatures \(\sigma , \sigma '\) are valid.
-
Parse the signatures as \((a, b, c, d, \pi , \texttt {nym}) \leftarrow \sigma \), \((a', b', c', d', \pi ', \texttt {nym}') \leftarrow \sigma '\).
-
If \(\texttt {nym}= \texttt {nym}'\), set \(f \leftarrow 1\), otherwise \(f \leftarrow 0\).
-
Output \((\textsf {LINK}, sid , f)\).
-
5.2 Differences with Previous Schemes
The proposed scheme is very similar to previous DAA schemes using the CL signature. For each part of the protocol, we now show the weaknesses of previous schemes and the way our solution overcomes them.
Setup. In our scheme, the issuer is required to prove knowledge of the issuer secret key. Previous works let the challenger generate the issuer key in the security game for anonymity, which allowed the simulator to use the issuer private key in the security reduction. This implicitly assumes that the issuer private key is extractable, but none of the schemes actually realized this. We therefore add a SPK proof \(\pi \) to the issuer’s public key from which the simulator can extract the issuer secret key.
Join. In the join protocol, we reintroduced a proof \(\pi _1\) by the TPM, that was present in many previous works but omitted in the scheme by Bernard et al. [3]. Additionally, our scheme contains the proof \(\pi _2\) by the issuer, which was introduced by Bernard et al.
Many previous schemes [6, 7, 16, 18] let the TPM prove knowledge of the discrete log of \(g^{ gsk }\) in the join protocol. Bernard et al. removed this proof by reducing the forgery of a credential to the security of a blind signature scheme, and in the unforgeability game requiring the adversary to output all secret keys. This assumes that all these secrets are extractable which, if extraction by rewinding is used, would require exponential time. We realize efficient extraction by adding the TPM’s proof of knowledge of gsk to the join protocol and allowing only a logarithmic number of simultaneous join sessions.
Bernard et al. let the issuer compute d and required the issuer to prove that he correctly formed the credential, which none of the previous works did. We also use this proof as it allows to simulate a TPM without knowing the secret key \( gsk \). This is required in our reduction where we use the unknown discrete logarithm of a DL or DDH instance as the key of a TPM.
Sign. We change the communication between the TPM and host to prevent the TPM from leaking information about its secret key \( gsk \) to the host, and we only use pseudonyms when required.
Chen, Page, and Smart [18] let the host send a randomized b value of the credential to the TPM, which responded with \(d = b^{ gsk }\). This gives information to the host that cannot be simulated without knowing \( gsk \), which prevents a proof of unforgeability under the DL assumption, and requires the stronger static DH assumption. The scheme by Bernard et al. [3] has a similar problem: The host sends (b, d) to the TPM, and the TPM responds with a proof proving that \(b^{ gsk } = d\). Now the TPM should only output a valid proof for valid inputs, i.e., when \(b^{ gsk } = d\). A simulator mimicking a TPM in the security proof, however, cannot decide this when reducing to the DL problem, a stronger assumption is required to prove unforgeability in their scheme.
We apply the fix by Xi et al. [25], in which the host sends the randomness r used to randomize the credential. This does not give the host any new information on \( gsk \), which is why we can prove unforgeability under the DL assumption.
Some schemes [6, 7, 16, 18] always attached a pseudonym to signatures to support revocation, even when the basename \(\texttt {bsn}\) was equal to \(\bot \). However, we can perform the revocation check on the credential: \(b^{ gsk } \mathop {=}\limits ^{?} d\), so the pseudonym can be omitted when \(\texttt {bsn}= \bot \) for a more efficient scheme.
Verify. We add a check \(a \ne 1_{\mathbb {G}_1}\) to the verification algorithm, which many of the previous schemes [6, 7, 16, 18] are lacking. Without this check, schemes tolerate a trivial issuer credential \((1_{\mathbb {G}_1},1_{\mathbb {G}_1},1_{\mathbb {G}_1},1_{\mathbb {G}_1})\) that allows anyone to create valid DAA signatures, which clearly breaks unforgeability. Note that [18] has been ISO standardized [20] with this flaw.
The verification algorithm also checks \(b \ne 1_{\mathbb {G}_1}\), which is not present in any of the previous schemes. A credential with \(b = 1_{\mathbb {G}_1}\) leads to \(d = 1_{\mathbb {G}_1}\), and lets any \( gsk \) match the credential, which is undesirable as we no longer have a unique matching \( gsk \). An adversarial issuer can create such credentials by choosing its secret key \(y = 0\). This case is “excluded” by the non-frameability property of Bernard et al. [3] which assumes that even a corrupt issuer creates his keys honestly, so \(y = 0\) will occur with negligible probability only. We avoid such an assumption and simply add the check \(b \ne 1_{\mathbb {G}_1}\).
6 Security Proof Sketch
Theorem 1
The protocol \(\varPi _{\textsf {daa}}\) presented in Sect. 5 securely realizes \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) in the \(({{\mathcal {F}}_{\textsf {auth*}}}, {{\mathcal {F}}_{\textsf {ca}}}, {\mathcal {F}_{smt}^{l}}, {\mathcal {F}_{crs}^{D}})\)-hybrid model using random oracles and static corruptions, if the DL and DDH assumptions hold, the CL signature [9] is unforgeable, and the proofs-of-knowledge are online extractable.
As CL signatures are unforgeable under the LRSW assumption [21], and we can instantiate the SPKs to be online extractable under the DCR assumption [22], we obtain the following corollary:
Corollary 1
The protocol \(\varPi _{\textsf {daa}}\) presented in Sect. 5 instantiated with online extractable proofs securely realizes \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) in the \(({{\mathcal {F}}_{\textsf {auth*}}}, {{\mathcal {F}}_{\textsf {ca}}}, {\mathcal {F}_{smt}^{l}}, {\mathcal {F}_{crs}^{D}})\)-hybrid model using random oracles and static corruptions under the DL, DDH, LRSW, and DCR assumptions.
Instead of relying on online extractable SPKs one could also use extraction by rewinding, which would yield a more efficient scheme. However, one needs to take special care that the rewinding does not require exponential time in the security proof. The only SPK we constantly have to extract from in our security proof is \(\pi _1\) used in the join protocol. Thus, we can avoid the exponential blow-up by letting the issuer limit the number of simultaneous join sessions to be logarithmic in the security parameter. Since we keep the way in which the simulator extracts witnesses abstract in the proof of Theorem 1, the very same simulator proves the scheme with extraction by rewinding secure. Note though, that the UC framework does not allow rewinding at all, i.e., this only proves the instantiation using extraction by rewinding secure in a stand-alone fashion, but one cannot claim composability guarantees.
To show that no environment \({\mathcal {E}} \) can distinguish the real world, in which it is working with \(\varPi _{\textsf {daa}}\) and adversary \({\mathcal {A}} \), from the ideal world, in which it uses \({\mathcal {F}_{\textsf {daa}}^{l}}\) with simulator \({\mathcal {S}} \), we use a sequence of games. We start with the real world protocol execution. In the next game we construct one entity \({\mathcal {C}} \) that runs the real world protocol for all honest parties. Then we split \({\mathcal {C}} \) into two pieces, a functionality \({\mathcal {F}}\) and a simulator \({\mathcal {S}} \), where \({\mathcal {F}}\) receives all inputs from honest parties and sends the outputs to honest parties. We start with a useless functionality, and gradually change \({\mathcal {F}}\) and update \({\mathcal {S}} \) accordingly, to end up with the full \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) and a satisfying simulator. This strategy is depicted in Fig. 6.
Due to space constraints, we present the complete security proof including all intermediate functionalities and simulators in the full paper. Here an overview of the game hops is given, along with an explanation how we can show indistinguishability between the games.
Game 1: This is the real world protocol.
Game 2: One entity \({\mathcal {C}} \) now receives all inputs and simulates the real world protocol for honest parties. Since \({\mathcal {C}} \) gets all inputs, it can simply run the real world protocol. It also simulates all hybrid functionalities, but does so honestly, so \({\mathcal {E}} \) does not see any difference. By construction, this is equivalent to the previous game.
Game 3: We now split \({\mathcal {C}} \) into \({\mathcal {F}}\) and \({\mathcal {S}} \). \({\mathcal {F}}\) receives all inputs, and simply forwards them to \({\mathcal {S}} \). \({\mathcal {S}} \) simulates the real world protocol and sends the outputs it generated to \({\mathcal {F}}\), who then outputs it to \({\mathcal {E}} \). This game only restructures the previous game.
Game 4: In the next step, we let the next intermediate \({\mathcal {F}}\) handle the setup related interfaces. \({\mathcal {S}} \) now has to give algorithms to \({\mathcal {F}}\), that will be used to verify, link, and identify signatures. Note that the \(\textsf {sig}\) algorithm must contain the issuer private key from the real world, so \({\mathcal {S}} \) must be able to get those values.
When \({\mathcal {I}} \) is honest, \({\mathcal {S}} \) will receive a message from \({\mathcal {F}}\) asking for the algorithms, which informs \({\mathcal {S}} \) what is happening and allows him to start simulating the issuer. Because \({\mathcal {S}} \) is simulating the issuer, it knows the secret keys, and can set the algorithms accordingly.
When \({\mathcal {I}} \) is corrupt, \({\mathcal {S}} \) knows when to simulate the setup as it simulates \({{\mathcal {F}}_{\textsf {ca}}} \) and it notices the issuer registering a key. Because the public key includes a proof of knowledge of the secret key, \({\mathcal {S}} \) can extract the secret key and define the algorithms accordingly. As \({\mathcal {I}} \) is corrupt, \({\mathcal {S}} \) can send inputs to \({\mathcal {F}}\) on the issuer’s behalf, and performs the setup procedure giving \({\mathcal {F}}\) the correct algorithms.
Game 5: \({\mathcal {F}}\) now performs the verify and link queries, rather than forwarding them to \({\mathcal {S}} \). Because verify and link do not involve network traffic, the simulator does not have to simulate network traffic, we must only make sure the output does not change.
\({\mathcal {F}}\) executes the algorithms that \({\mathcal {S}} \) supplied, and \({\mathcal {S}} \) supplied them in such a way that they are equivalent to the real world algorithms. \({\mathcal {F}}\) does not perform checks yet, so the outcome will clearly be equivalent.
Game 6: In this step we change \({\mathcal {F}}\) to handle to join-related interfaces, meaning it will receive the inputs and generate the outputs. We must make sure that \({\mathcal {F}}\) outputs the same values as the real world did. As the join interfaces do not output crypto values, but only output messages like start and complete, we only have to make sure that whenever the real world protocol would reach a certain output the functionality also allows that output, and vice versa. The first direction we achieve by removing all checks from \({\mathcal {F}}\), such that it will always proceed. We introduce these checks further on in the proof. The other direction we achieve as before every output, \({\mathcal {F}}\) sends a message to \({\mathcal {S}} \) and requires a response. When the real world protocol would not proceed, \({\mathcal {S}} \) simply does not respond to \({\mathcal {F}}\), such that \({\mathcal {F}}\) will also not proceed.
Furthermore, as \({\mathcal {A}} \) and \({\mathcal {E}} \) can communicate freely, \({\mathcal {S}} \) must make sure that \({\mathcal {A}} \) sees the right messages between every input and output. \({\mathcal {S}} \) is activated before every output, and in that activation must simulate the network traffic \({\mathcal {A}} \) expects to see. If \({\mathcal {S}} \) can figure out which inputs were send to \({\mathcal {F}}\), it can do so by simulating the real world protocol with the same input. When the host is honest, \({\mathcal {F}}\) upon receiving the first input from the host informs \({\mathcal {S}} \) of the full input, making the simulation easy. When the host is corrupt but the TPM is honest, \({\mathcal {S}} \) simulating the TPM will receive a message over a secure channel from the host, by which it learns that host wants to join with the TPM, again giving \({\mathcal {S}} \) the full input. Only when the TPM and host are corrupt and the issuer is honest, \({\mathcal {S}} \) is missing information: It cannot determine the identity of the host, as the host does not authenticate towards the issuer in the real world. This does not matter for the real world simulation, as \({\mathcal {S}} \) only has to simulate the honest issuer, for which it does know the input.
Finally, \({\mathcal {S}} \) must call \({\mathcal {F}}\) on behalf of corrupt parties. For inputs it can derive, \({\mathcal {S}} \) simply sends the input on behalf of the corrupt party to \({\mathcal {F}}\). The only input it cannot derive is the identity of the host when only the issuer is honest. Then, \({\mathcal {S}} \) simply chooses an arbitrary corrupt host and uses that as input to \({\mathcal {F}}\). This will only result in a different host in \(\texttt {Members} \), but \({\mathcal {F}}\) never uses this identity when the corresponding TPM is corrupt.
Later in the proof, we need to know the gsk value of every TPM when \({\mathcal {I}} \) is honest. \({\mathcal {S}} \) can extract the key from the proof \(\pi _1\) and submits it to \({\mathcal {F}}\).
Game 7, 8, 9, 10: Over the next four game hops, we transform \({\mathcal {F}}\) such that it handles the signing queries instead of forwarding the inputs and outputs. As in the previous step, \({\mathcal {S}} \) receives a message from \({\mathcal {F}}\) before every output, such that it can block any output that would not happen in the real world. We remove all checks from \({\mathcal {F}}\) such that it does not block any output that could happen in the real world, and we add these checks later on in the proof.
\({\mathcal {S}} \) can easily simulate the network traffic when the TPM or the host is corrupt, as it sees the message and basename sent over a secure channel in the real world. When both the TPM and host are honest, \({\mathcal {F}}\) only informs \({\mathcal {S}} \) of the leakage of the message and basename, \(l(m, \texttt {bsn})\). In this scenario, \({\mathcal {S}} \) only has to simulate the network traffic, and as all messages between the TPM and host are sent over a secure channel, it picks a message and basename with the same leakage which is sufficient to simulate the messages.
When the TPM or the host is corrupt, \({\mathcal {S}} \) is allowed to supply the signature, which it can take from the real world simulation, making it output the same as the real world. When both the TPM and the host are honest, \({\mathcal {F}}\) creates the signatures anonymously: It chooses a new gsk per basename, or per signature when \(\texttt {bsn}= \bot \). This difference is indistinguishable under the DDH assumption.
The reduction uses the fact that we can simulate a TPM knowing only \(h = g_1^{gsk}\), but not gsk itself. A TPM uses gsk to set Q in the join protocol, to do proofs \(\pi _1\) in the join protocol and \(\pi \) in signing, and to compute pseudonyms. In simulation, we set \(Q \leftarrow h\) and we simulate the proofs. For pseudonyms, the power over the random oracle is used. \({\mathcal {S}} \) chooses \(H_1(\texttt {bsn}) = g_1^{r}\) for  , and now it can set \(\texttt {nym}\leftarrow h^r = H_1(\texttt {bsn})^{gsk}\) without knowing gsk. Note that the proof the issuer makes in the join protocol helps simulating the TPM without knowing gsk: With this proof the TPM does not have to use gsk to check \(b^{gsk} \mathop {=}\limits ^{?} d\), it can simply verify the proof.
, and now it can set \(\texttt {nym}\leftarrow h^r = H_1(\texttt {bsn})^{gsk}\) without knowing gsk. Note that the proof the issuer makes in the join protocol helps simulating the TPM without knowing gsk: With this proof the TPM does not have to use gsk to check \(b^{gsk} \mathop {=}\limits ^{?} d\), it can simply verify the proof.
Suppose an environment can distinguish a signature by an honest party with the gsk it joined with from a signature by the same party but with a different gsk. Then we show we can break DDH instance \(\alpha , \beta , \gamma \) by simulating the join and the first signature using the unknown \(log_{g_1}(\alpha )\) as gsk, and for the second signature we use the unknown \(log_{\beta }(\gamma )\) as gsk. If the environment notices a difference, we know that \(log_{g_1}(\alpha ) \ne log_{\beta }(\gamma )\), solving the DDH problem.
Game 11: In this game we let \({\mathcal {F}}\) additionally check the validity of every new gsk that is generated or received in the join and sign interface.
\({\mathcal {F}}\) now checks that \(\textsf {CheckGskCorrupt}(gsk) = 1\), which prevents the adversary from choosing keys that will lead to two distinct gsk values matching one signature. This will never fail, as in our protocol for every valid signature there exists only a single gsk with \(\textsf {identify}(\sigma , m, \texttt {bsn}, gsk)\).
For keys of honest TPMs, \({\mathcal {F}}\) verifies that \(\textsf {CheckGskHonest}(gsk) = 1\), which prevents the registration of keys for which there already are matching signatures. Because keys for honest TPMs are chosen uniformly at random from an exponentially large group and every signature as one matching key, the chance that a signature using that key already exists is negligible.
Game 12: We now add checks on honestly generated signatures to \({\mathcal {F}}\). After creating a signature, \({\mathcal {F}}\) checks whether the signature verifies and matches the right key. As \({\mathcal {S}} \) supplied proper algorithms, these checks will obviously always succeed.
It also checks no one else already has a key that matches this signature. If this fails, we can solve the DL problem: We simulate a TPM using the unknown discrete logarithm of a DL instance as key like before. If a matching gsk is found, then we solve the DL problem.
Game 13, 14, 15, 16: In these four game hops, we let \({\mathcal {F}}\) perform the four checks that are done by \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) in the verification interface and show that this does not change the verification outcome.
The first check prevents multiple gsk values matching one signature, but as \(\textsf {identify}\) considers the discrete log relation between b and d from the credential, and \(b \ne 1\), there exists only one \(gsk \in {\mathbb {Z}} _q\) such that \(b^{gsk} = d\).
If the issuer is honest, the second check prevents signing with credentials that were not issued by the issuer. We can reduce this to the unforgeability of the CL signature. The signing oracle is now used to create credentials, and when a credential is verified that was not signed by the issuer, it must be a forgery.
\({\mathcal {F}}\) prevents signatures that use the key and credential of an honest TPM, but are signing messages that this TPM never signed. We can reduce this to the DL problem. Again we simulate a TPM using the unknown discrete logarithm of the problem instance. When a signature is verified that signs a message that the TPM never signed, we know that the proof \(\pi \) is not simulated, so we can extract gsk from it, breaking the DL assumption.
The last check prevents revocation of honest TPMs. This too we can reduce to the DL problem. We simulate the TPM using the DL instance, and if a matching key is placed on the revocation list, this must be the discrete logarithm of the problem instance.
Game 17: We now let \({\mathcal {F}}\) perform all the checks \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\) makes for link inputs. If it notices a key that matches one signature but not the other, \({\mathcal {F}}\) states the signatures are not linked. If it notices one key that matches both signatures, it outputs that the signatures are linked. This output is always the same as the output \(\textsf {link}\) gives: If there is a gsk that matches one signature but not the other, by soundness of \(\pi \) we have that the pseudonyms are not based on the same gsk. As \(H_1(\texttt {bsn})\) generates \(\mathbb {G}_1\) with overwhelming probability, the pseudonyms differ and \(\textsf {link}\) would output 0. If there is a gsk that matches both signatures, by soundness of \(\pi \) we have that the pseudonyms are based on the same gsk and must be equal, resulting in \(\textsf {link}\) outputting 1.
Now \({\mathcal {F}}\) is equal to \({{\mathcal {F}}_{\mathsf{daa}}^{l}}\), concluding our proof sketch.
References
Backes, M., Hofheinz, D.: How to break and repair a universally composable signature functionality. In: Zhang, K., Zheng, Y. (eds.) ISC 2004. LNCS, vol. 3225, pp. 61–72. Springer, Heidelberg (2004)
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM CCS (1993)
Bernhard, D., Fuchsbauer, G., Ghadafi, E., Smart, N., Warinschi, B.: Anonymous attestation with user-controlled linkability. Int. J. Inf. Secur. 12(3), 219–249 (2013)
Boneh, D., Lynn, B., Shacham, H.: Short signatures from the weil pairing. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 514–532. Springer, Heidelberg (2001)
Brickell, E., Camenisch, J., Chen, L.: Direct anonymous attestation. In: ACM CCS (2004)
Brickell, E., Chen, L., Li, J.: A new direct anonymous attestation scheme from bilinear maps. In: Lipp, P., Sadeghi, A.-R., Koch, K.-M. (eds.) Trust 2008. LNCS, vol. 4968, pp. 166–178. Springer, Heidelberg (2008)
Brickell, E., Chen, L., Li, J.: Simplified security notions of direct anonymous attestation and a concrete scheme from pairings. Int. J. Inf. Secur. 8(5), 315–330 (2009)
Camenisch, J., Kiayias, A., Yung, M.: On the portability of generalized schnorr proofs. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 425–442. Springer, Heidelberg (2009)
Camenisch, J.L., Lysyanskaya, A.: Signature schemes and anonymous credentials from bilinear maps. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 56–72. Springer, Heidelberg (2004)
Camenisch, J.L., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer, Heidelberg (2003)
Camenisch, J.L., Stadler, M.A.: Efficient group signature schemes for large groups. In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 410–424. Springer, Heidelberg (1997)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. ePrint Archive Report 2000/067 (2000)
Canetti, R.: Universally composable signatures, certification and authentication. ePrint Archive, Report 2003/239 (2003)
Chen, L., Morrissey, P., Smart, N.: DAA: fixing the pairing based protocols. ePrint Archive, Report 2009/198 (2009)
Chen, L.: A DAA scheme requiring less TPM resources. In: Bao, F., Yung, M., Lin, D., Jing, J. (eds.) Inscrypt 2009. LNCS, vol. 6151, pp. 350–365. Springer, Heidelberg (2010)
Chen, L., Morrissey, P., Smart, N.P.: Pairings in trusted computing (invited talk). PAIRING (2008)
Chen, L., Morrissey, P., Smart, N.P.: On proofs of security for DAA schemes. In: Baek, J., Bao, F., Chen, K., Lai, X. (eds.) ProvSec 2008. LNCS, vol. 5324, pp. 156–175. Springer, Heidelberg (2008)
Chen, L., Page, D., Smart, N.P.: On the design and implementation of an efficient DAA scheme. In: Gollmann, D., Lanet, J.-L., Iguchi-Cartigny, J. (eds.) CARDIS 2010. LNCS, vol. 6035, pp. 223–237. Springer, Heidelberg (2010)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987)
International Organization for Standardization: ISO/IEC 20008–2: Information technology - Security techniques - Anonymous digital signatures - Part 2: Mechanisms using a group public key (2013)
Lysyanskaya, A., Rivest, R.L., Sahai, A., Wolf, S.: Pseudonym systems (extended abstract). In: Heys, H.M., Adams, C.M. (eds.) SAC 1999. LNCS, vol. 1758, pp. 184–199. Springer, Heidelberg (2000)
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999)
Trusted Computing Group: TPM main specification version 1.2 (2004)
Trusted Computing Group: Trusted platform module library specification, family “2.0” (2014)
Xi, L., Yang, K., Zhang, Z., Feng, D.: DAA-related APIs in TPM 2.0 revisited. In: Holz, T., Ioannidis, S. (eds.) Trust 2014. LNCS, vol. 8564, pp. 1–18. Springer, Heidelberg (2014)
Acknowledgements
This work was supported by the European Commission through the Seventh Framework Programme, under grant agreements #321310 for the PERCY grant and #318424 for the project FutureID.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Camenisch, J., Drijvers, M., Lehmann, A. (2016). Universally Composable Direct Anonymous Attestation. In: Cheng, CM., Chung, KM., Persiano, G., Yang, BY. (eds) Public-Key Cryptography – PKC 2016. PKC 2016. Lecture Notes in Computer Science(), vol 9615. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49387-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-662-49387-8_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49386-1
Online ISBN: 978-3-662-49387-8
eBook Packages: Computer ScienceComputer Science (R0)





 will be used to generate keys gsk for honest TPMs.
will be used to generate keys gsk for honest TPMs. will also be used for honest TPMs and on input a key gsk, message m and basename
will also be used for honest TPMs and on input a key gsk, message m and basename 

 and
and  , and sets
, and sets  , and output the signature
, and output the signature 


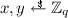 , and set
, and set  .
. and store the key as
and store the key as  .
. .
. and set
and set 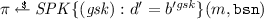 .
.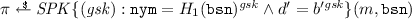 .
.
