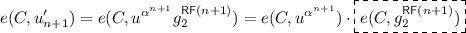1 Introduction

In identity-based encryption (IBE) [5, 27], ciphertexts and secret keys are associated with identities, and decryption is possible only when the identities match. IBE has been studied extensively over the last decade, with a major focus on obtaining constructions that simultanously achieve short parameters and full adaptive security under static assumptions in the standard model. This was first achieved in the works of Lewko and Waters [23, 29], which also introduced the powerful dual system encryption methodology. The design of the Lewko-Waters IBE and the underlying proof techniques have since had a profound impact on both attribute-based encryption and pairing-based cryptography.

1.1 Our Contributions

In this work, we obtain the first efficiency improvement to the Lewko-Waters IBE in composite-order bilinear groups. We present an adaptively secure and anonymous identity-based encryption (IBE) scheme with essentially optimal parameters: the ciphertext overhead and the secret key are one group element each, and decryption only requires one pairing; this improves upon the Lewko-Waters IBE [23] in three ways: shorter parameters, faster decryption, and anonymity. Via Naor’s transformation, we obtain a fully secure signature scheme where the signature is again only one group element. We stress that we achieve all of these improvements while relying on the same computational subgroup assumptions as in the Lewko-Waters IBE, notably in composite-order groups whose order is the product of three primes. We refer to Fig. 1 for a comparison with prior works.

The Lewko-Waters IBE has played a foundational role in recent developments of IBE and more generally attribute-based encryption (ABE). Indeed, virtually all of the state-of-the-art prime-order IBE schemes in [2, 22] —along with the subsequent extensions to ABE [1, 12, 24, 30]— follow the basic design and proof strategy introduced in the Lewko-Waters IBE. For this reason, we are optimistic that our improvement to the Lewko-Waters IBE will lead to further advances in IBE and ABE. In fact, our improved composite-order IBE already hints at the potential of a more efficient prime-order IBE that subsumes all known schemes; we defer further discussion to Sect. 1.3.

We also present a selectively secure broadcast encryption scheme for n users where the ciphertext overhead is two group elements (independent of the number of recipients) and the user private key is a single group element.Footnote 1 To the best of our knowledge, this is the first broadcast encryption scheme to achieve constant-size ciphertext overhead, constant-size user private keys and linear-size public parameters under static assumptions; previously, such schemes were only known under q-type assumptions [6].

1.2 Our Techniques

The starting point of our constructions is the Déjà Q framework introduced by Chase and Meiklejohn [10]; this is an extension of Waters’ dual system techniques to eliminate the use of q-type assumptions in settings beyond the reach of previous techniques. These settings include deterministic primitives such as pseudo-random functions (PRF) and —quite remarkably— schemes based on the inversion framework [4, 8, 26]. However, the Déjà Q framework is also limited in that it cannot be applied to advanced encryption systems such as identity-based and broadcast encryption, where certain secret exponents appear in both ciphertexts and secret keys on both sides of the pairing. We show how to overcome this limitation using several simple ideas.

IBE Overview. We describe our IBE scheme and the security proof next. We present a simplified variant of the constructions, suppressing many details pertaining to randomization and subgroups. Following the Lewko-Waters IBE [23], we rely on composite-order bilinear groups whose order N is the product of three primes \(p_1,p_2,p_3\). We will use the subgroup \(G_{p_1}\) of order \(p_1\) for functionality, and the subgroup \(G_{p_2}\) of order \(p_2\) in the proof of security. The third subgroup corresponding to \(p_3\) is used for additional randomization.

Recall that the Lewko-Waters IBE has the following form:

$$ \mathsf {mpk}:= (g,g^\beta ,g^\gamma ,e(g,u)), \; \mathsf {ct}_\mathsf {id}:= (g^s, g^{(\beta +\gamma \mathsf {id})s}, e(g,u)^s \cdot m), \; \mathsf {sk}_\mathsf {id}:= (u \cdot g^{(\beta +\gamma \mathsf {id})r}, g^r))$$

Our IBE scheme has the following form:

$$ \mathsf {mpk}:= (g,g^\alpha ,e(g,u)), \; \mathsf {ct}_\mathsf {id}:= (g^{(\alpha +\mathsf {id})s}, e(g,u)^s \cdot m), \; \mathsf {sk}_\mathsf {id}:= (u^{\frac{1}{\alpha +\mathsf {id}}})$$

Note that our scheme uses the “exponent inversion” framework [8], which has traditionally eluded a proof of security under static assumptions. In both schemes, g, u are random group elements of order \(p_1\), and \(\alpha ,\beta ,\gamma \) are random exponents over \(\mathbb {Z}_N\). It is easy to see that decryption in our scheme only requires a single pairing to compute \(e(g^{(\alpha +\mathsf {id})s}, u^{\frac{1}{\alpha +\mathsf {id}}}) = e(g,u)^s\).

Fig. 1.
figure 1

Comparison amongst adaptively secure IBEs in composite-order bilinear groups \(e: G_N \times G_N \rightarrow G_T\).

Full size image

IBE Security Proof. We rely on the same assumption as the Lewko-Waters IBE in [23], namely the \((p_1\mapsto p_1p_2)\)-subgroup assumption, which asserts that random elements of order \(p_1\) and those of order \(p_1p_2\) are computationally indistinguishable. In the proof of security, we rely on the assumption to introduce random \(G_{p_2}\)-components to the ciphertext and the secret keys.

We begin with the secret keys. We introduce a random \(G_{p_2}\)-component to the secret key \(\mathsf {sk}_\mathsf {id}\) following the Déjà Q framework [10] as follows:

$$\begin{aligned} \mathsf {sk}_\mathsf {id}= u^{\frac{1}{\alpha +\mathsf {id}}} \;\mathop {\longrightarrow }\limits ^{{\small \text{ subgroup }}}\; u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_1}{\alpha +\mathsf {id}}} \;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\; u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_1}{\alpha _1+\mathsf {id}}}, \end{aligned}$$
(1)

where \(\alpha _1 \leftarrow \mathbb {Z}_N\). In the first transition, we use the \((p_1\mapsto p_1p_2)\)-subgroup assumption which says that \(u \approx _c u g_2^{r_1}, r_1 \leftarrow _\mathrm{{R}}\mathbb {Z}_N\), where \(g_2\) is a generator of order \(p_2\). In the second transition, we use the Chinese Reminder Theorem (CRT), which tell us \(\alpha \mod p_1\) and \(\alpha \mod p_2\) are independently random values, so we may replace \(\alpha \mod p_2\) with \(\alpha _1 \mod p_2\) for a fresh \(\alpha _1 \leftarrow _\mathrm{{R}}\mathbb {Z}_N\); this is fine as long as the challenge ciphertext and \(\mathsf {mpk}\) reveal no information about \(\alpha \mod p_2\), as is the case here. We may then repeat this transition q more times:

$$\begin{aligned} \begin{array}{ccccc} u^{\frac{1}{\alpha +\mathsf {id}}} &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ subgroup }}}\;&{} u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_1}{\alpha +\mathsf {id}}} &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\;&{} u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_1}{\alpha _1+\mathsf {id}}}\\ &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ subgroup }}}\;&{} u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_2}{\alpha +\mathsf {id}}} g_2^{\frac{r_1}{\alpha _1+\mathsf {id}}} &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\;&{} u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_2}{\alpha _2+\mathsf {id}} +\frac{r_1}{\alpha _1+\mathsf {id}}}\\ &{}\longrightarrow &{}\cdots &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\;&{} u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\frac{r_{q+1}}{\alpha _{q+1}+\mathsf {id}} + \cdots + \frac{r_2}{\alpha _2+\mathsf {id}} +\frac{r_1}{\alpha _1+\mathsf {id}}} \end{array} \end{aligned}$$

where \(r_1,\ldots ,r_{q+1},\alpha _1,\ldots ,\alpha _{q+1} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\), and q is an upper bound on the number of key queries made by the adversary.Footnote 2

Next, we show that for distinct \(x_1,\ldots ,x_q\), the following matrix

$$\begin{aligned} \begin{pmatrix} \frac{1}{\alpha _1+x_1} &{} \frac{1}{\alpha _1+x_2} &{} \cdots &{} \frac{1}{\alpha _1 + x_q}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{1}{\alpha _q+x_1} &{} \frac{1}{\alpha _q+x_2} &{} \cdots &{} \frac{1}{\alpha _q + x_q} \end{pmatrix} \end{aligned}$$
(2)

is invertible with overwhelming probability over \(\alpha _1,\ldots ,\alpha _{q} \leftarrow _\mathrm{{R}}\mathbb {Z}_p\). We provide an explicit formula for the determinant of this matrix in Sect. 3.1; this is the only place in the proof where we crucially exploit the “exponent inversion” structure. We can then replace

$$\begin{aligned} \mathsf {id}\mapsto \frac{r_{q+1}}{\alpha _{q+1}+\mathsf {id}} + \cdots + \frac{r_2}{\alpha _2+\mathsf {id}} +\frac{r_1}{\alpha _1+\mathsf {id}} \end{aligned}$$

by a truly random function \(\mathsf {RF}(\cdot )\). Indeed, \(\mathsf {sk}_\mathsf {id}\) can now be written as \(u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\mathsf {RF}(\mathsf {id})}\), which have independently random \(G_{p_2}\)-components.

So far, what we have done is the same as the use of Déjà Q framework for showing that \(x \mapsto u^{\frac{1}{x+\alpha }}\) yields a PRF [10] (the explicit formula for the matrix determinant is new), and this is where the similarity ends. At this point, we still need to hide the message m in the ciphertext \((g^{(\alpha +\mathsf {id})s},e(g,u)^s \cdot m)\). Towards this goal, we want to introduce a \(G_{p_2}\)-component into the ciphertext, which will then interact with newly random \(G_{p_2}\)-component in the keys to generate extra statistical entropy to hide m. At the same time, we need to ensure that the ciphertext still hides \(\alpha \mod p_2\) so that we may carry out the transition of the secret keys in (1). Indeed, naively applying the \((p_1\mapsto p_1p_2)\)-subgroup assumption to \(g^s\) in the ciphertext would leak \(\alpha \mod p_2\).

To circumvent this difficulty, note that we can rewrite the ciphertext in terms of \(\mathsf {sk}_\mathsf {id}\) as

$$\begin{aligned} \mathsf {ct}_\mathsf {id}= (g^{(\alpha +\mathsf {id})s}, e(g^{(\alpha +\mathsf {id})s},\mathsf {sk}_\mathsf {id}) \cdot m) \end{aligned}$$

Moreover, as long as \(\alpha +\mathsf {id}\ne 0\), we can replace \((\alpha +\mathsf {id})s\) with s without changing the distribution, which allows us to rewrite the challenge ciphertext as

$$\begin{aligned} \mathsf {ct}_\mathsf {id}= (g^{s}, e(g^{s},\mathsf {sk}_\mathsf {id}) \cdot m). \end{aligned}$$

This means that the challenge ciphertext leaks no information about \(\alpha \) except through \(\mathsf {sk}_\mathsf {id}\). In addition, the challenge ciphertext also leaks no information about \(\mathsf {id}\), which allows us to prove anonymity. In contrast, the Lewko-Waters IBE is not anonymous, and anonymous variants there-of in [9, 31] requires the use of 4 primes and additional assumptions.

We can now apply the \((p_1\mapsto p_1p_2)\)-subgroup assumption to the ciphertext to replace \(g^s\) with \(g^s g_2^{r'}\). Now, the ciphertext distribution is completely independent of \(\alpha \) except what is leaked through \(\mathsf {sk}_\mathsf {id}\), so we can apply the secret key transitions as before, at the end of which the challenge ciphertext is given by:

Recall that we only allow the adversary to request for secret keys corresponding to identities different from \(\mathsf {id}\), which means those keys leak no information about \(\mathsf {RF}(\mathsf {id})\). We can then use the \(\log p_2\) bits of entropy from \(\mathsf {RF}(\mathsf {id})\) over \(G_{p_2}\) to hide m; this requires modifying the original scheme so that an encryption of m is given by \((g^{(\alpha +\mathsf {id})s}, \mathsf {H}(e(g,u)^s) \cdot m)\), where \(\mathsf {H}\) denotes a strong randomness extractor whose seed is specified in \(\mathsf {mpk}\).

Broadcast Encryption. By rewriting the challenge ciphertext in terms of \(\mathsf {sk}_\mathsf {id}\) in order to hide \(\alpha \), our technique for IBE seems inherently limited to IBE. We show how to extend our techniques to broadcast encryption in Sect. 4; however, we only achieve selective and not adaptive security. We briefly note that our broadcast encryption scheme is derived from Boneh-Gentry-Waters (BGW) scheme [6] based on the q-DBDHE assumption. This is the first scheme to asymptotically match the parameters of the BGW broadcast encryption scheme under static assumptions.

1.3 Discussion

Comparison with Déjà Q Framework [10]. The core of the Déjà Q framework is a beautiful technique which translates linear independence (and thus computational independence in the generic group model) amongst a set of monomials “in the exponent” into statistical independence, upon which security can be established using a purely information-theoretic argument. There are however three caveats to the prior instantiation in [10]: first, these monomials must appear on the same side of the pairing, which means the techniques cannot be applied to advanced encryption primitives where the same term often appears in the ciphertext and the secret key on both sides of the pairing; second, the statistical independence only holds within certain subgroups, and another subgroup assumption was used to spread this localized entropy over the entire group; third, the prior instantiation is limited to asymmetric composite-order groups. In this work, we showed how to overcome all of these three caveats.

In particular, we rely only on the \((p_1 \mapsto p_1p_2)\)-subgroup assumption and eliminated the additional use of the \((p_2 \mapsto p_1p_2)\)-subgroup assumption. This technique can also be applied to the PRF in [10]. We note that while simulating subgroup decisional assumptions in composite-order groups using the k-LIN assumption in prime-order groups, we can simulate the \((p_1 \mapsto p_1p_2)\)-subgroup assumption using \(k+1\) group elements whereas simulating both subgroup assumption requires 2k group elements.

Candidate Prime-Order IBE. As noted earlier, our composite-order IBE scheme constitutes the first evidence for an adaptively IBE based on SXDH with two group elements in the ciphertext and in the secret keys and constant-size public parameters, which would be a significant improvement over the state of the art, subsuming a long series of incomparable constructions, and giving us adaptive security at essentially the same cost as selective security! Moreover, such a IBE would in turn also yield a fully secure signature scheme based on SXDH with two group elements in the signature and constant-size public key. The optimism comes from combining our composite-order IBE scheme with the huge success we have had in converting composite-order schemes to prime-order ones [12, 15, 22, 25]. In fact, we present a concrete candidate for a prime-order IBE in Sect. 3.3; we stress that we do not have a security proof for the scheme. We note that an improved SXDH-based signature scheme would likely yield further improvements to other related primitives, such as group signatures and structure-preserving signatures. These applications further motivate the open problem highlighted in [10] of finding prime-order analogues for the Déjà Q framework.

Perspective. We presented new constructions of “optimal” IBE and signatures and new IBE candidates that improve upon a long line of work; moreover, we achieve these via an extended Déjà Q framework which avoid the limitations of widely used techniques. We are optimistic and excited about challenges and possibilities that lie ahead.

2 Preliminaries

Notation. We denote by \(s \leftarrow _\mathrm{{R}}S\) the fact that s is picked uniformly at random from a finite set S. By PPT, we denote a probabilistic polynomial-time algorithm. Throughout, we use \(1^\lambda \) as the security parameter.

2.1 Composite-Order Bilinear Groups and Cryptographic Assumptions

We instantiate our system in composite-order bilinear groups, which were introduced in [7] and used in [21, 23, 24]. A generator \(\mathcal {G}\) takes as input a security parameter \(\lambda \) and outputs a description \(\mathbb {G}:=(N,G,G_T,e)\), where N is product of distinct primes of \(\Theta (\lambda )\) bits, G and \(G_T\) are cyclic groups of order N, and \(e:G\times G \rightarrow G_T\) is a non-degenerate bilinear map. We require that the group operations in G and \(G_T\) as well the bilinear map e are computable in deterministic polynomial time. We consider bilinear groups whose orders N are products of three distinct primes \(p_1,p_2,p_3\) (that is, \(N = p_1p_2p_3\)). We can write \(G = G_{p_1}G_{p_2}G_{p_3}\) where \(G_{p_1},G_{p_2},G_{p_3}\) are subgroups of G of order \(p_1,p_2\) and \(p_3\) respectively. In addition, we use \(G_{p_i}^*\) to denote \(G_{p_i} \setminus \{1\}\). We will often write \(g_1,g_2,g_3\) to denote random generators for the subgroups \(G_{p_1},G_{p_2},G_{p_3}\).

Cryptographic Assumptions. Our construction relies on the following two decisional subgroup assumptions (also known as subgroup hiding assumptions). We define the following two advantage functions:

The decisional subgroup assumptions assert that that for all PPT adversaries \(\mathcal {A}\), the advantages \({{\mathsf {Adv}}^{\textsc {sd1}}_{\mathcal {G},\mathcal {A}}(\lambda )}\) and \({{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}}(\lambda )}\) are negligible functions in \(\lambda \).

2.2 Anonymous Identity-Based Encryption

We define identity-based encryption (IBE) in the framework of key encapsulation. An identity-based encryption scheme consists of four algorithms \((\mathsf {Setup}, \mathsf {Enc}, \mathsf {KeyGen}, \mathsf {Dec})\):

  • \(\mathsf {Setup}(1^\lambda )\rightarrow (\mathsf {mpk}, \mathsf {msk})\). The setup algorithm gets as input the security parameter \(\lambda \) and outputs the public parameter \(\mathsf {mpk}\), and the master key \(\mathsf {msk}\). All the other algorithms get \(\mathsf {mpk}\) as part of its input.

  • \(\mathsf {Enc}(\mathsf {mpk},\mathsf {id})\rightarrow (\mathsf {ct}, \kappa )\). The encryption algorithm gets as input \(\mathsf {mpk}\) and an identity \(\mathsf {id}\in \{0,1\}^\lambda \). It outputs a ciphertext \(\mathsf {ct}\) and a symmetric key \(\kappa \in \{0,1\}^\lambda \).

  • \(\mathsf {KeyGen}(\mathsf {msk},\mathsf {id})\rightarrow \mathsf {sk}_\mathsf {id}\). The key generation algorithm gets as input \(\mathsf {msk}\) and an identity \(\mathsf {id}\in \{0,1\}^\lambda \). It outputs a secret key \(\mathsf {sk}_\mathsf {id}\).

  • \(\mathsf {Dec}(\mathsf {sk}_\mathsf {id},\mathsf {ct}) \rightarrow \kappa \). The decryption algorithm gets as input \(\mathsf {sk}_\mathsf {id}\) and \(\mathsf {ct}\). It outputs a symmetric key \(\kappa \).

Correctness. We require that for all \(\mathsf {id}\in \{0,1\}^\lambda \),

$$\begin{aligned} \Pr [(\mathsf {ct},\kappa ) \leftarrow \mathsf {Enc}(\mathsf {mpk},\mathsf {id});\; \mathsf {Dec}(\mathsf {sk}_\mathsf {id},\mathsf {ct}) = \kappa )]= 1, \end{aligned}$$

where the probability is taken over \((\mathsf {mpk},\mathsf {msk}) \leftarrow \mathsf {Setup}(1^\lambda )\) and the coins of \(\mathsf {Enc}\).

Security Definition. We require pseudorandom ciphertexts against adaptively chosen plaintext and identity attacks, which implies both anonymity and adaptive security. For a stateful adversary \(\mathcal {A}\), we define the advantage function

$$\begin{aligned} {{\mathsf {Adv}}^{\textsc {a-ibe}}_{\mathcal {A}}(\lambda )} := \Pr \left[ b = b' : \begin{array}{l} (\mathsf {mpk},\mathsf {msk}) \leftarrow \mathsf {Setup}(1^\lambda );\\ \mathsf {id}^* \leftarrow \mathcal {A}^{\mathsf {KeyGen}(\mathsf {msk},\cdot )}(\mathsf {mpk});\\ b \leftarrow _\mathrm{{R}}\{0,1\}; \mathsf {ct}_1 \leftarrow _\mathrm{{R}}\mathcal {C}; \kappa _1 \leftarrow _\mathrm{{R}}\{0,1\}^\lambda ;\\ (\mathsf {ct}_0,\kappa _0) \leftarrow \mathsf {Enc}(\mathsf {mpk},\mathsf {id}^*);\\ b' \leftarrow \mathcal {A}^{\mathsf {KeyGen}(\mathsf {msk},\cdot )}(\mathsf {ct}_b,\kappa _b) \end{array}\right] - \frac{1}{2} \end{aligned}$$

with the restriction that all queries \(\mathsf {id}\) that \(\mathcal {A}\) makes to \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\) satisfies \(\mathsf {id}\ne \mathsf {id}^*\), and where \(\mathsf {ct}_1 \leftarrow _\mathrm{{R}}\mathcal {C}\) denotes a random element from the ciphertext space.Footnote 3 An identity-based encryption (IBE) scheme is adaptively secure and anonymous if for all PPT adversaries \(\mathcal {A}\), the advantage \({{\mathsf {Adv}}^{\textsc {a-ibe}}_{\mathcal {A}}(\lambda )}\) is a negligible function in \(\lambda \).

2.3 Broadcast Encryption

A broadcast encryption scheme consists of three algorithms \((\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\):

  • \(\mathsf {Setup}(1^\lambda ,1^n)\rightarrow (\mathsf {mpk}, (\mathsf {sk}_1,\ldots ,\mathsf {sk}_n))\). The setup algorithm gets as input the security parameter \(\lambda \) and \(1^n\) specifying the number of users and outputs the public parameter \(\mathsf {mpk}\), and secret keys \(\mathsf {sk}_1,\ldots ,\mathsf {sk}_n\).

  • \(\mathsf {Enc}(\mathsf {mpk},\Gamma )\rightarrow (\mathsf {ct}_\Gamma , \kappa )\). The encryption algorithm gets as input \(\mathsf {mpk}\) and a subset \(\Gamma \subseteq [n]\). It outputs a ciphertext \(\mathsf {ct}_\Gamma \) and a symmetric key \(\kappa \in \{0,1\}^\lambda \). Here, \(\Gamma \) is public given \(\mathsf {ct}_\Gamma \).

  • \(\mathsf {Dec}(\mathsf {mpk},\mathsf {sk}_y,\mathsf {ct}_\Gamma ) \rightarrow \kappa \). The decryption algorithm gets as input \(\mathsf {mpk},\mathsf {sk}_y\) and \(\mathsf {ct}_\Gamma \). It outputs a symmetric key \(\kappa \).

Correctness. We require that for all \(\Gamma \subseteq [n]\) and all \(y \in [n]\) for which \(y \in \Gamma \),

$$\begin{aligned} \Pr [(\mathsf {ct}_\Gamma ,\kappa ) \leftarrow \mathsf {Enc}(\mathsf {mpk},\Gamma );\; \mathsf {Dec}(\mathsf {mpk},\mathsf {sk}_y,\mathsf {ct}_\Gamma ) = \kappa )]= 1, \end{aligned}$$

where the probability is taken over \((\mathsf {mpk},(\mathsf {sk}_1,\ldots ,\mathsf {sk}_n)) \leftarrow \mathsf {Setup}(1^\lambda ,1^n)\) and the coins of \(\mathsf {Enc}\).

Security Definition. For a stateful adversary \(\mathcal {A}\), we define the advantage function

$$\begin{aligned} {{\mathsf {Adv}}^{\textsc {s-bce}}_{\mathcal {A}}(\lambda )} := \Pr \left[ b = b' : \begin{array}{l} \Gamma ^* \leftarrow \mathcal {A}(1^\lambda );\\ (\mathsf {mpk},(\mathsf {sk}_1,\ldots ,\mathsf {sk}_n)) \leftarrow \mathsf {Setup}(1^\lambda );\\ b \leftarrow _\mathrm{{R}}\{0,1\}; \kappa _1 \leftarrow _\mathrm{{R}}\{0,1\}^\lambda ;\\ (\mathsf {ct}_{\Gamma ^*},\kappa _0) \leftarrow \mathsf {Enc}(\mathsf {mpk},\Gamma ^*);\\ b' \leftarrow \mathcal {A}(\mathsf {ct}_{\Gamma ^*},\kappa _b,\{\mathsf {sk}_y : y \notin \Gamma ^*\}) \end{array}\right] - \frac{1}{2} \end{aligned}$$

A broadcast encryption scheme is selectively secure if for all PPT adversaries \(\mathcal {A}\), the advantage \({{\mathsf {Adv}}^{\textsc {s-bce}}_{\mathcal {A}}(\lambda )}\) is a negligible function in \(\lambda \).

3 Identity-Based Encryption

We present an adaptively secure and anonymous IBE scheme in Fig. 2, and a fully secure signature scheme in Fig. 3. The schemes here refer to symmetric composite-order bilinear groups; we present the variant for asymmetric composite-bilinear groups in Sect. A. The schemes and the proofs are the same as in the overview in the introduction (Sect. 1.2), except the secret keys in both the scheme and the proof have an extra random \(G_{p_3}\)-component and we will use the \((p_1p_3\mapsto N)\)-subgroup assumption to switch the secret keys.

Comparison with Prior Schemes. We recall several IBE and signature schemes in the inversion framework which share a similar structure to our IBE and signature scheme. All of these schemes require an additional scalar in the key/signature, and both of the IBE schemes require an additional group element in the ciphertext.

  • BB \(_2\) IBE [4]. The BB\(_2\) IBE is selectively secure under the q-DBDHI assumption:

    $$\begin{aligned} \mathsf {ct}_\mathsf {id}:= (g^{(\alpha +\mathsf {id})s}, g^{\beta s}, e(g,u)^s \cdot m), \; \mathsf {sk}_\mathsf {id}:= (u^{\frac{1}{\alpha +\mathsf {id}+\beta r}},r) \end{aligned}$$

  • Gentry’s IBE [18]. Gentry’s IBE is adaptively secure and anonymous under the q-ADBDHE assumption:

    $$ \mathsf {ct}_\mathsf {id}:= (g^{(\alpha +\mathsf {id})s}, e(g,g)^s, e(g,u)^s \cdot m), \; \mathsf {sk}_\mathsf {id}:= ((u \cdot g^{-r})^{\frac{1}{\alpha +\mathsf {id}}},r)$$

  • Boneh-Boyen Signatures [3, 10]. The Déjà Q analogue [10] of the Boneh-Boyen signatures is given by:

    $$\begin{aligned} \mathsf {pk}:= (g,g^\alpha ,g^\beta ,e(g,u)), \; \sigma := (u^{\frac{1}{\alpha +M+\beta r}},r) \in \mathbb {G}_N \times \mathbb {Z}_N. \end{aligned}$$

    Our signature scheme in Fig. 3 is simpler and shorter, and the scheme can be also be instantiated in symmetric composite-order groups. In fact, our signature scheme may be viewed as applying the Déjà Q framework to the Boneh-Boyen weak signatures, which both “upgrades” the security from weak to full, and removes the use of q-type assumptions.

3.1 Core Lemma

The following lemma is implicit in the analysis of the PRF in [10, Theorem 4.2, Eq. 8].

Lemma 1

Fix a prime p and define \(\mathsf {F}^q_{r_1,\ldots ,r_q,\alpha _1,\ldots ,\alpha _q} : \mathbb {Z}_p \rightarrow \mathbb {Z}_p\) to be

$$\begin{aligned} \mathsf {F}^q_{r_1,\ldots ,r_q,\alpha _1,\ldots ,\alpha _q}(x) := \sum _{i=1}^q \frac{r_i}{\alpha _i + x} \end{aligned}$$

Then, for any (possibly unbounded) adversary \(\mathcal {A}\) that makes at most q queries, we have

$$\begin{aligned} \Bigl | \Pr _{r_1,\ldots ,r_q,\alpha _1,\ldots ,\alpha _q \leftarrow _\mathrm{{R}}\mathbb {Z}_p} \bigl [ \mathcal {A}^{\mathsf {F}^q_{r_1,\ldots ,r_q,\alpha _1,\ldots ,\alpha _q}(\cdot )}(1^q) = 1\bigr ] - \Pr \bigl [\mathcal {A}^{\mathsf {RF}(\cdot )}(1^q) = 1\bigr ]\Bigr | \le \frac{q^2}{p} \end{aligned}$$

where \(\mathsf {RF}: \mathbb {Z}_p \rightarrow \mathbb {Z}_p\) is a truly random function.

The proof in [10] directly rewrites the function \(\mathsf {F}^q_{r_1,\ldots ,r_q,\alpha _1,\ldots ,\alpha _q}\) with a common denominator and then relates the numerator to the Lagrange interpolating polynomial for an appropriate choice of q points. We sketch an alternative proof which better explains the choice of the function \((\alpha ,\mathsf {id}) \mapsto \frac{1}{\alpha +\mathsf {id}}\). We first consider the case where the queries \(x_1,\ldots ,x_q\) made by \(\mathcal {A}\) are chosen non-adaptively. WLOG, we may assume that these queries are distinct. Then, it suffices to show that the following matrix

$$\begin{aligned} \begin{pmatrix} \frac{1}{\alpha _1+x_1} &{} \frac{1}{\alpha _1+x_2} &{} \cdots &{} \frac{1}{\alpha _1 + x_q}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{1}{\alpha _q+x_1} &{} \frac{1}{\alpha _q+x_2} &{} \cdots &{} \frac{1}{\alpha _q + x_q} \end{pmatrix} \end{aligned}$$

is invertible with overwhelming probability over \(\alpha _1,\ldots ,\alpha _{q} \leftarrow _\mathrm{{R}}\mathbb {Z}_p\). (Such a statement follows from the proof in [10] but was not pointed out explicitly.) As it turns out, we can write the determinant of this matrix explicitly as:

$$\begin{aligned} \frac{\Pi _{1 \le i < j \le q} (x_i-x_j)(\alpha _i-\alpha _j)}{\Pi _{1 \le i,j \le q} (\alpha _i+x_j)} \end{aligned}$$

which is non-zero as long as \(\alpha _1,\ldots ,\alpha _q\) are distinct, \(x_1,\ldots ,x_q\) are distinct, and the \(\alpha _i+x_j\)’s are all non-zero.

That is, we want to show that

$$\begin{aligned} \Pi _{1 \le i,j \le q} (\alpha _i+x_j) \cdot \det \begin{pmatrix} \frac{1}{\alpha _1+x_1} &{} \frac{1}{\alpha _1+x_2} &{} \cdots &{} \frac{1}{\alpha _1 + x_q}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{1}{\alpha _q+x_1} &{} \frac{1}{\alpha _q+x_2} &{} \cdots &{} \frac{1}{\alpha _q + x_q} \end{pmatrix} = \Pi _{1 \le i < j \le q} (x_i-x_j)(\alpha _i-\alpha _j) \end{aligned}$$

Using the standard formula for the determinant of the matrix, we can write the determinant above as a sum of inverses of homogenous polynomials of degree q in \(x_1,\ldots ,x_q,\alpha _1,\ldots ,\alpha _q\). Upon multiplying by \(\Pi _{1 \le i,j \le q} (\alpha _i+x_j)\), we would “clear the denominators” to obtain a homogeneous polynomial P in \(x_1,\ldots ,x_q,\alpha _1,\ldots ,\alpha _q\) of degree \(q^2-q\). Moreover, the matrix has two equal rows (resp. columns) whenever we have \(\alpha _i = \alpha _j\) (resp. \(x_i = x_j\)); when this happens, the matrix has determinant 0 and thus P vanishes. Therefore, the polynomial P must be a multiple of \(\Pi _{1 \le i < j \le q} (x_i-x_j)(\alpha _i-\alpha _j)\), which also has degree \(q^2-q\). This means that P must be a constant multiple of \(\Pi _{1 \le i < j \le q} (x_i-x_j)(\alpha _i-\alpha _j)\), and it is easy to check that the constant is 1.

To handle adaptive queries, observe that this corresponds to building the matrix one column at a time. As long as the partial selection of columns have full rank, the output of F is uniformly random, which then completely hides \(\alpha _1,\ldots ,\alpha _q\). Therefore, the probability that \(\alpha _1,\ldots ,\alpha _q\) are distinct, and that \(\alpha _i+x_j\)’s are all non-zero is at least \(1-q^2/p\), even for adaptive choices of distinct \(x_1,\ldots ,x_q\).

Fig. 2.
figure 2

Adaptively secure anonymous IBE w.r.t. a composite-order bilinear group \(\mathbb {G}\). Here, \(\mathsf {H}: G_T \rightarrow \{0,1\}^\lambda \) is drawn from a family of pairwise-independent hash functions. In asymmetric groups, randomization with \(R_3\) in \(\mathsf {KeyGen}\) is not necessary (i.e., \(\mathsf {KeyGen}\) is deterministic).

Full size image
Fig. 3.
figure 3

Fully secure signature scheme, obtained by applying Naor’s transformation to the IBE scheme in Fig. 2. In asymmetric groups, randomization with \(R_3\) in \(\mathbf {sign}\) is not necessary (i.e., \(\mathbf {sign}\) is deterministic).

Full size image

3.2 Our IBE Scheme

Theorem 1

The scheme in Fig. 2 is an adaptively secure anonymous IBE under the decisional subgroup assumption in \(\mathbb {G}\).

Proof

Correctness follows readily from the equation

$$\begin{aligned} e(g_1^{(\alpha +\mathsf {id})s},u^{\frac{1}{\alpha +\mathsf {id}}}R_3) = e(g_1,u)^s. \end{aligned}$$

We show that for any adversary \(\mathcal {A}\) that makes at most q queries against the IBE, there exist adversaries \(\mathcal {A}_1,\mathcal {A}_2\) whose running times are essentially the same as that of \(\mathcal {A}\), such that

$${{\mathsf {Adv}}^{\textsc {a-ibe}}_{\mathcal {A}}(\lambda )} \le {{\mathsf {Adv}}^{\textsc {sd1}}_{\mathcal {G},\mathcal {A}_1}(\lambda )} + (q+1) \cdot {{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}_2}(\lambda )} + 2^{-\Omega (\lambda )}$$

We proceed via a series of games and we use \(\mathsf {Adv}_i\) to denote the advantage of \(\mathcal {A}\) in Game i.

  • Game 0. This is the real experiment as defined in Sect. 2.2. We will also make the following simplifying assumptions:

    • – We never encounter an identity \(\mathsf {id}\) such that \(\mathsf {id}= \alpha \mod p_1\); such an identity constitutes the discrete log of \(g_1^\alpha \) and trivially breaks the subgroup assumption.

    • – The adversary’s queries \(\mathsf {id}_1,\ldots ,\mathsf {id}_q \in \mathbb {Z}_N\) are distinct, since we can perfectly randomize the secret key \(\mathsf {sk}_\mathsf {id}= u^{\frac{1}{\alpha +\mathsf {id}}}R_3\) given \(g_3\) (we can add \(g_3\) to \(\mathsf {mpk}\) without affecting the security proof).

    • – \(\mathsf {id}_1,\ldots ,\mathsf {id}_q\) are distinct mod \(p_2\); given \(\mathsf {id}_i \ne \mathsf {id}_j \in \mathbb {Z}_N\) such that \(\mathsf {id}_i = \mathsf {id}_j \mod p_2\), computing gcd\((\mathsf {id}_i-\mathsf {id}_j,N)\) would allow us to factor N.

    We can incorporate these simplifying assumptions by introducing an extra hybrid before Game 1 that aborts if the first or third condition is violated, and that uses randomization to handle repeated key queries.

  • Game 1. We change \((\mathsf {ct}_0,\kappa _0) \leftarrow _\mathrm{{R}}\mathsf {Enc}(\mathsf {mpk},\mathsf {id}^*)\) as follows: pick \(C \leftarrow _\mathrm{{R}}G_{p_1}\), output

    $$\begin{aligned} (\mathsf {ct}_0,\kappa _0) := (C, H(e(C,\mathsf {sk}_{\mathsf {id}^*}))). \end{aligned}$$

    We claim that \(\mathsf {Adv}_0 = \mathsf {Adv}_1\). This follows readily from the following two observations:

    1. i.

      for all \(\mathsf {id}\), \(e(g_1,u)^s = e(g_1^{(\alpha +\mathsf {id})s},u^{\frac{1}{\alpha +\mathsf {id}}}) = e(g_1^{(\alpha +\mathsf {id})s},\mathsf {sk}_\mathsf {id})\);

    2. ii.

      if \(\alpha +\mathsf {id}\ne 0\), \(g_1^{(\alpha +\mathsf {id})s}\) and C are identically distributed.

  • Game 2. We change the distribution of C in \((\mathsf {ct}_0,\kappa _0)\) from \(C \leftarrow _\mathrm{{R}}G_{p_1}\) to \(C \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}\). We now construct \(\mathcal {A}_1\) for which

    $$\begin{aligned} \mathsf {Adv}_0 - \mathsf {Adv}_1 \le {{\mathsf {Adv}}^{\textsc {sd1}}_{\mathcal {G},\mathcal {A}_1}(\lambda )}. \end{aligned}$$

    \(\mathcal {A}_1\) on input \((g_1,g_3,C)\) where either \(C \leftarrow _\mathrm{{R}}G_{p_1}\) or \(C \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}\), simulates the experiment in Game 1 with the adversary \(\mathcal {A}\) as follows: runs \(\mathsf {Setup}(\mathbb {G})\) honestly to obtain \((\alpha ,u)\), then uses \((\alpha ,u)\) to answer all key queries honestly and to compute \((\mathsf {ct},\kappa _0)\) as \((C, H(e(C,\mathsf {sk}_{\mathsf {id}^*})))\).

  • Game 3. We change the distribution of \(\mathsf {sk}_\mathsf {id}\) from \(u^{\frac{1}{\alpha +\mathsf {id}}}R_3\) to \(u^{\frac{1}{\alpha +\mathsf {id}}}g_2^{\sum _{i=1}^{q+1}\frac{r_i}{\alpha _i+\mathsf {id}}} R_3\), where \(r_1,\ldots ,r_{q+1},\alpha _1,\ldots ,\alpha _{q+1} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\), as outlined in Sect. 1.1. We proceed via a series of sub-games 3.j.0 and 3.j.1 for \(j=1,2,\ldots ,q+1\), where

    • – In Sub-Game 3.j.0, \(\mathsf {sk}_\mathsf {id}\) is given by \(u^{\frac{1}{\alpha +\mathsf {id}}}g_2^{\frac{r_j}{\alpha +\mathsf {id}}+\sum _{i=1}^{j-1}\frac{r_i}{\alpha _i+\mathsf {id}}}R_3\);

    • – In Sub-Game 3.j.1, \(\mathsf {sk}_\mathsf {id}\) is given by \(u^{\frac{1}{\alpha +\mathsf {id}}}g_2^{\sum _{i=1}^{j}\frac{r_i}{\alpha _i+\mathsf {id}}}R_3\). Game 2 corresponds to Sub-Game 3.0.1, and Game 3 corresponds to Sub-Game \(3.q+1.1\).

    First, observe that \(\mathsf {Adv}_{3.j.0} = \mathsf {Adv}_{3.j.1}\). This follows readily from the fact that \(\alpha \mod p_2\) is completely hidden given \(\mathsf {mpk}\) and the challenge ciphertext, and therefore we may replace \(\alpha \mod p_2\) with \(\alpha _j \mod p_2\). Next, for \(j=1,\ldots ,q+1\), we construct \(\mathcal {A}_2\) for which

    $$\begin{aligned} \mathsf {Adv}_{3.(j-1).1} - \mathsf {Adv}_{3.j.0} \le {{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}_2}(\lambda )}. \end{aligned}$$

    \(\mathcal {A}_2\) on input \((\mathbb {G},g_1,g_{\{2,3\}},g_3,C,T)\) where \(C \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}\) and either \(T = u R_3 \leftarrow _\mathrm{{R}}G_{p_1}G_{p_3}\) or \(T = u g_2^{r_j} R_3 \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}G_{p_3}\), simulates the experiment in Game 3 with the adversary \(\mathcal {A}\) as follows:

    • – picks \(\alpha \leftarrow _\mathrm{{R}}\mathbb {Z}_N\) and publishes \(\mathsf {mpk}:= (g_1,g_1^\alpha ,e(g_1,T),H)\), where \(e(g_1,T) = e(g_1,u)\);

    • – picks \(\alpha _1,\ldots ,\alpha _{j-1},r_1,\ldots ,r_{j-1} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\);

    • – simulates \(\mathsf {KeyGen}\) on input \(\mathsf {id}\) by choosing \(R'_3 \leftarrow _\mathrm{{R}}G_{p_3}\) and outputting \(T^{\frac{1}{\alpha +\mathsf {id}}} g_{2,3}^{\sum _{i=1}^{j-1}\frac{r_i}{\alpha _i+\mathsf {id}}} R'_3\)

    • – uses C to compute \((\mathsf {ct}_0,\kappa _0)\);

    Observe that if \(T = uR_3\), then this is exactly Game 3.\(j-1\).1, and if \(T = ug_2^{r_j}R_3\), then this is exactly Game 3.j.0. It follows readily that

    $$\begin{aligned} \mathsf {Adv}_{2} - \mathsf {Adv}_{3} \le (q+1) \cdot {{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}_2}(\lambda )}. \end{aligned}$$

  • Game 4. We replace \(\sum _{i=1}^{q+1}\frac{r_i}{\alpha _i+\mathsf {id}}\) in \(\mathsf {sk}_\mathsf {id}\) with \(\mathsf {RF}(\mathsf {id})\) where \(\mathsf {RF}: \mathbb {Z}_N \rightarrow \mathbb {Z}_{p_2}\) is a truly random function; that is, \(\mathsf {sk}_\mathsf {id}\) is now given by \(u^{\frac{1}{\alpha +\mathsf {id}}} g_2^{\mathsf {RF}(\mathsf {id})} R_3\). It follows readily from Lemma 1 that

    $$\begin{aligned} \mathsf {Adv}_3 - \mathsf {Adv}_4 \le O(q^2/p_2). \end{aligned}$$

  • Game 5. We replace \(\kappa _0 = \mathsf {H}(e(C,\mathsf {sk}_{\mathsf {id}^*}))\) with \(\kappa _0 \leftarrow _\mathrm{{R}}\{0,1\}^\lambda \). Observe that the quantity (from which \(\kappa _0\) is derived)

    has \(\log p_2 = \Theta (\lambda )\) bits of min-entropy coming from \(\mathsf {RF}(\mathsf {id}^*)\), since \(\mathsf {id}^* \notin \{\mathsf {id}_1,\ldots ,\mathsf {id}_q\}\); this holds as long as the \(G_{p_2}\)-component of C is not 1, which happens with probability \(1-1/p_2\). Then, by the left-over hash lemma, \(\kappa _0 = \mathsf {H}(e(C,\mathsf {sk}_{\mathsf {id}^*}))\) is \(2^{-\Omega (\lambda )}\)-close to the uniform distribution over \(\{0,1\}^\lambda \), even given \(\mathsf {ct}_0 = C\).

In Game 5, the joint distribution of \((\kappa _0,\mathsf {ct}_0)\) is uniformly random over \(\{0,1\}^\lambda \times \mathcal {C}\), where \(\mathcal {C}:= G_{p_1}G_{p_2}\). Therefore, the view of the adversary \(\mathcal {A}\) is statistically independent of the challenge bit b. Hence, \(\mathsf {Adv}_5=0\). This completes the proof.    \(\square \)

Fig. 4.
figure 4

Candidate IBE in prime-order bilinear groups under the \(k\)-LIN assumption, following the Diffie-Hellman framework and notation in [13]. Here, \(\mathbf {A},\mathbf {B}\in \mathbb {Z}_p^{k\times (k+1)}\) denote the matrices for the \(k\)-LIN assumptions in \(G_1\) and \(G_2\) respectively. Both the keys and the ciphertext contain \(k+1\) group elements, i.e. 2 elements under SXDH = 1-LIN.

Full size image

3.3 A Candidate Prime-Order Scheme

In Fig. 4, we present a candidate prime-order scheme obtained by applying the transformation in [12] to our composite-order IBE scheme; concretely, the transformation was used to obtain prime-order dual-system ABE schemes starting from composite-order ones based on the same decisional subgroup assumptions as used in this work. The ciphertext and secret keys in the candidate scheme contain \(k+1\) group elements, which is a substantial improvement over the state-of-the-art, c.f. Fig. 5. Applying Naor’s transformation then yields a signature scheme with signature size \(k+1\) group elements. In contrast, a scheme that uses both the \((p_1 \mapsto p_1p_2)\)-subgroup and \((p_2 \mapsto p_1p_2)\)-subgroup assumptions as in [10] would likely require at least 2k group elements, which is another reason to eliminate the use of the \((p_2 \mapsto p_1p_2)\)-subgroup assumption.

We stress that we do not have a proof of security for this scheme. The main technical difficulties arise from having to understand the matrix inverse \((\mathbf {W}+ \mathsf {id}\mathbf {I}_{k+1})^{-1}\) for general matrices \(\mathbf {W}\). For this specific scheme, it appears that we can completely recover \(\mathbf {W}\in \mathbb {Z}_p^{k \times k}\) given \((\mathbf {W}+\mathsf {id}\mathbf {I}_{k+1})^{-1}\mathbf {B}\in \mathbb {Z}_p^k\) for many choices of \(\mathsf {id}\), which ruins parameter-hiding in the secret key space. On the other hand, in the composite-order scheme, given \(\frac{1}{\alpha +\mathsf {id}} \mod p_1\) for an unbounded number of \(\mathsf {id}\) still completely hides \(\alpha \mod p_2\). Nonetheless, we conjecture that a more judicious choice of a matrix distribution for \(\mathbf {W}\) would yield a variant of this scheme which is adaptively secure under the k-linear assumption. We quickly point out here that diagonal matrices don’t work.

Fig. 5.
figure 5

Comparison amongst adaptively secure IBEs from standard assumptions in prime-order bilinear groups. We refer to both groups of prime order p with pairing \(e: G_1 \times G_2 \rightarrow G_T\). We included the candidate scheme in Fig. 4 for comparison, and we stress that we do not have a proof of security for the scheme.

Full size image

4 Broadcast Encryption

In broadcast encryption [14], a sender broadcasts encrypted content in such a way that only a specified set of authorized receivers may decrypt the message. In this section, we present a selectively secure broadcast encryption scheme for n users, where the ciphertext overhead and the secret keys are a constant number of group elements, and security is based on the decisional subgroup assumption in composite-order groups. Previous dual-system broadcast encryption schemes [16, 19, 29] achieve adaptive security under static assumptions, but never better than a (t, n / t)-type trade-off between ciphertext overhead and key size [17].

4.1 Overview

We begin with an informal description of the scheme, ignoring randomization in the \(G_{p_3}\)-subgroup. The scheme is derived from the Boneh-Gentry-Waters (BGW) broadcast encryption scheme [6], which is also selectively secure under the q-DBDHE assumption. The public parameters in our scheme are given by

$$\mathsf {mpk}:= (g_1^\gamma , g_1^\alpha , g_1^{\alpha ^2},\ldots ,g_1^{\alpha ^n}, u^\alpha , u^{\alpha ^2},\ldots ,u^{\alpha ^n}, u^{\alpha ^{n+2}},\ldots ,u^{\alpha ^{2n}})$$

The ciphertext for a subset \(\Gamma \subseteq [n]\) and the key for a user \(y \in [n]\) are given by

$$ \mathsf {ct}_\Gamma := (g_1^s, g_1^{(\gamma + \sum _{k \in \Gamma } \alpha ^k)s}, e(g_1,u^{\alpha ^{n+1}})^s \cdot m), \; \mathsf {sk}_y := u^{\alpha ^{n-y+1}\gamma }$$

Decryption proceeds analogously to the BGW scheme, and requires a judicious choice of pairing-product equation to recover \(e(g_1,u^{\alpha ^{n+1}})^s\). We note that \(u^{\alpha ^{n+1}}\) is omitted from \(\mathsf {mpk}\). Indeed, given \(g_1^s\) and \(\mathsf {mpk}\), it is easy to compute \(e(g_1,u^{\alpha ^k})^s\) for any \(k \ne n+1\). We also note that the BGW scheme uses \(u=g_1\).

To establish security, we will introduce random \(G_{p_2}\)-components to the 2n terms \(u^{\alpha },u^{\alpha ^2},\ldots ,u^{\alpha ^{2n}}\) (including \(u^{\alpha ^{n+1}}\)), and the extra entropy from \(u^{\alpha ^{n+1}}\) will be used to hide the message m. That is, we apply the Déjà Q framework to the set of 2n linearly independent monomials \(\{ \alpha , \alpha ^2, \ldots , \alpha ^{2n} \}\), as encoded “in the exponent of u” in the secret keys. To achieve this, we proceed as follows:

$$\begin{aligned} \begin{array}{ccccc} u^{\alpha ^k} &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ subgroup }}}\;&{} u^{\alpha ^k} g_2^{r_1 \alpha ^k} &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\;&{} u^{\alpha ^k} g_2^{r_1 \alpha _1^k}\\ &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ subgroup }}}\;&{} u^{\alpha ^k} g_2^{r_2 \alpha ^k} g_2^{r_1 \alpha _1^k} &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\;&{} u^{\alpha ^k} g_2^{r_2 \alpha _2^k +r_1 \alpha _1^k}\\ &{}\longrightarrow &{}\cdots &{}\;\mathop {\longrightarrow }\limits ^{{\small \text{ CRT }}}\;&{} u^{\alpha ^k} g_2^{r_{2n}\alpha _{2n}^k + \cdots + r_2 \alpha _2^k +r_1 \alpha _1^k} \end{array} \end{aligned}$$

where \(r_1,\ldots ,r_{2n},\alpha _1,\ldots ,\alpha _{2n} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\). We can then replace

$$\begin{aligned} k \mapsto r_{2n}\alpha _{2n}^k + \cdots + r_2 \alpha _2^k +r_1 \alpha _1^k \end{aligned}$$

by a truly random function \(\mathsf {RF}(\cdot )\). As with the IBE scheme, we need to avoid leaking \(\alpha \mod p_2\) in the ciphertext in order to carry out the transformation to the secret keys above. That is, we need to eliminate all occurrences of \(\alpha \) in the polynomial \(\gamma + \sum _{k \in \Gamma } \alpha ^k\) which shows up in the ciphertext. Unfortunately, we do not know a transformation to the ciphertext distribution analogous to that for the IBE. Instead, we will need to settle for selective security where the adversary announces the subset \(\Gamma \) at the very beginning, so that we can use \(\gamma \) as a one-time pad. We will then select \(\tilde{\gamma }\) at random (which is treated as a known scalar) and program \(\gamma \) so that \(\tilde{\gamma } = \gamma + \sum _{k \in \Gamma } \alpha ^k\). We can then rewrite the ciphertext and key as

$$ \mathsf {ct}_\Gamma := (g^s, g^{\tilde{\gamma }s}, e(g,u^{\alpha ^{n+1}})^s \cdot m), \; \mathsf {sk}_y := (u^{\alpha ^{n-y+1}\tilde{\gamma } - \sum _{k \in \Gamma } \alpha ^{n+1-y+k}})$$

Now, the monomials in \(\alpha \) only show up on the same side of the pairing in both the ciphertext and the secret keys in the exponents of u. As in the security proof for the BGW scheme, we will later use the fact that the monomial \(\alpha ^{n+1}\) does not show up in any \(\mathsf {sk}_y\) for which \(y \notin \Gamma \). We note that in the proof of security, the distribution of \(\mathsf {mpk}\) changes, which is quite unusual for a proof based on the dual system methodology.

Fig. 6.
figure 6

Broadcast encryption w.r.t. a composite-order bilinear group \(\mathbb {G}\). Here, \(\mathsf {H}: G_T \rightarrow \{0,1\}^\lambda \) is drawn from a family of pairwise-independent hash functions.

Full size image

4.2 Our Broadcast Encryption Scheme

Theorem 2

The scheme in Fig. 6 is a selectively secure broadcast encryption scheme under the decisional subgroup assumption in \(\mathbb {G}\).

Proof

Correctness follows readily from the fact that for all \(y \in \Gamma \),

$$\begin{aligned} e\bigl (g_1^{(\gamma +\sum _{k \in \Gamma } \alpha ^k)s},u^{\alpha ^{n-y+1}}\bigr ) \cdot e\bigl (g_1^{s},u^{\alpha ^{n-y+1}\gamma } \prod _{k \in \Gamma , k \ne y} u^{\alpha ^{n+1+(k-y)}}\bigr ) = e(g_1,u^{\alpha ^{n+1}})^s. \end{aligned}$$

Note that for all \(k \ne y\), \(n+1+(k-y) \in \{2,\ldots ,n,n+2,\ldots ,2n\}\), which means we can compute \(u^{\alpha ^{n+1+(k-y)}}\) given \(\mathsf {mpk}\). Next, we show that for any adversary \(\mathcal {A}\) against the broadcast encryption scheme, there exist adversaries \(\mathcal {A}_1,\mathcal {A}_2\) whose running times are essentially the same as that of \(\mathcal {A}\), such that

$${{\mathsf {Adv}}^{\textsc {s-bce}}_{\mathcal {A}}(\lambda )} \le {{\mathsf {Adv}}^{\textsc {sd1}}_{\mathcal {G},\mathcal {A}_1}(\lambda )} + 2n \cdot {{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}_2}(\lambda )} + 2^{-\Omega (\lambda )}$$

We proceed via a series of games and we use \(\mathsf {Adv}_i\) to denote the advantage of \(\mathcal {A}\) in Game i.

  • Game 0. This is the real experiment as defined in Sect. 2.3.

  • Game 1. Pick \((\alpha ,\tilde{\gamma },u) \leftarrow _\mathrm{{R}}\mathbb {Z}_N^2 \times G_{p_1}\) and set \(\gamma := \tilde{\gamma } - \sum _{k \in \Gamma ^*} \alpha ^k\), where \(\Gamma ^*\) is the selective challenge output by \(\mathcal {A}\). Then,

    • – compute \(u'_1,\ldots ,u'_{2n}\) as in the honest \(\mathsf {Setup}\);

    • – compute \(\mathsf {mpk}\) as in the honest \(\mathsf {Setup}\).

    • – compute \(\mathsf {ct}_{\Gamma ^*} = (g_1^s,(g_1^s)^{\tilde{\gamma }})\) and \(\kappa _0 = \mathsf {H}(e(g_1^s,u'_{n+1}))\);

    • – simulate \(\{ \mathsf {sk}_y : y \notin \Gamma ^* \}\) using \(\tilde{\gamma }\) and \((u'_1,\ldots ,u'_n,u'_{n+2},\ldots ,u'_{2n})\), by computing

      $$\begin{aligned} \mathsf {sk}_y = (u'_{n-y+1})^{\tilde{\gamma }} \cdot \bigl (\prod _{k \in \Gamma ^*, k \ne y} u'_{n+1+(k-y)}\bigr )^{-1} \cdot R_{3,y} \end{aligned}$$

    Clearly, Game 0 and 1 are identically distributed, so \(\mathsf {Adv}_0 = \mathsf {Adv}_1\).

  • Game 2. We change the distribution of \((\mathsf {ct}_{\Gamma ^*},\kappa _0)\) by replacing \(g_1^s\) with \(C \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}\), that is

    $$\begin{aligned} (\mathsf {ct}_{\Gamma ^*}, \kappa _0) := ((C,C^{\tilde{\gamma }}),\,\mathsf {H}(e(C,u'_{n+1})) \end{aligned}$$

    It is straight-forward to construct \(\mathcal {A}_1\) (following the proof for Theorem 1) for which

    $$\begin{aligned} \mathsf {Adv}_1 - \mathsf {Adv}_2 \le {{\mathsf {Adv}}^{\textsc {sd1}}_{\mathcal {G},\mathcal {A}_1}(\lambda )}. \end{aligned}$$

  • Game 3. We change the distribution of \(u'_1,\ldots ,u'_{2n}\) from \(u^{\alpha ^k}R'_{3,k}\) to \(u^{\alpha ^k}g_2^{\sum _{i=1}^{2n}r_i \alpha _i^k} R'_{3,k}\), where \(r_1,\ldots ,r_{2n},\alpha _1,\ldots ,\alpha _{2n} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\), as outlined in Sect. 4.1; this in turn affects the distribution of \(\mathsf {mpk}, \kappa _0\) and \(\{ \mathsf {sk}_y : y \notin \Gamma ^* \}\). We proceed via a series of sub-games 3.j.0 and 3.j.1 for \(j=1,2,\ldots ,2n\), where

    • – In Sub-Game 3.j.0, \(u'_k\) is given by \(u^{\alpha ^k}g_2^{r_j\alpha ^k+\sum _{i=1}^{j-1}r_i \alpha _i^k}R'_{3,k}\) for \(k=1,\ldots ,2n\);

    • – In Sub-Game 3.j.1, \(u'_k\) is given by \(u^{\alpha ^k}g_2^{\sum _{i=1}^{j}r_i \alpha _i^k}R'_{3,k}\) for \(k=1,\ldots ,2n\). Game 2 corresponds to Sub-Game 3.0.1, and Game 3 corresponds to Sub-Game 3.2n.1.

    First, observe that \(\mathsf {Adv}_{3.j.0} = \mathsf {Adv}_{3.j.1}\) as before. Next, for \(j=1,\ldots ,2n\), we construct \(\mathcal {A}_2\) for which

    $$\begin{aligned} \mathsf {Adv}_{3.(j-1).1} - \mathsf {Adv}_{3.j.0} \le {{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}_2}(\lambda )}. \end{aligned}$$

    \(\mathcal {A}_2\) on input \((g_1,g_{\{2,3\}},g_3,C,T)\) where \(C \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}\) and either \(T = u R'_{3,k} \leftarrow _\mathrm{{R}}G_{p_1}G_{p_3}\) or \(T = u g_2^{r_j} R'_{3,k} \leftarrow _\mathrm{{R}}G_{p_1}G_{p_2}G_{p_3}\), simulates the experiment in Game 2 with the adversary \(\mathcal {A}\) as follows:

    • – picks \(\alpha ,\alpha _1,\ldots ,\alpha _{j-1},r_1,\ldots ,r_{j-1} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\);

    • – for \(k=1,\ldots ,2n\), computes \(u'_k\) by choosing \(R'_{3,k} \leftarrow _\mathrm{{R}}G_{p_3}\) and outputting \(T^{\alpha ^k} g_{2,3}^{\sum _{i=1}^{j-1}r_i \alpha _i^k} R'_{3,k}\)

    • – proceed as in Game 2 using \(\alpha ,u'_1,\ldots ,u'_{2n}\) as computed above to compute \(\mathsf {mpk}\) and \(\{ \mathsf {sk}_y : y \notin \Gamma ^* \}\), and using C as provided and \(u'_{n_1}\) as computed above to compute \((\mathsf {ct}_{\Gamma ^*},\kappa _0)\).

    Observe that if \(T = uR'_{3,k}\), then this is exactly Game 3.\(j-1\).1, and if \(T = ug_2^{r_j}R'_{3,k}\), then this is exactly Game 3.j.0. It follows readily that

    $$\begin{aligned} \mathsf {Adv}_{2} - \mathsf {Adv}_{3} \le 2n \cdot {{\mathsf {Adv}}^{\textsc {sd2}}_{\mathcal {G},\mathcal {A}_2}(\lambda )}. \end{aligned}$$

  • Game 4. We replace \(\sum _{i=1}^{2n}r_i \alpha _i^k\) in \(u'_k\) with \(\mathsf {RF}(k)\) where \(\mathsf {RF}: [2n] \rightarrow \mathbb {Z}_{p_2}\) is a truly random function; that is, \(u'_k\) is now given by \(u^{\alpha ^k} g_2^{\mathsf {RF}(k)} R'_{3,k}\), for \(k=1,\ldots ,2n\). Now, we exploit the fact that the Vandermonde matrix

    $$\begin{aligned} \begin{pmatrix} \alpha _1 &{} \alpha _2 &{} \cdots &{} \alpha _{2n}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \alpha _1^{2n} &{} \alpha _2^{2n} &{} \cdots &{} \alpha _{2n}^{2n} \end{pmatrix} \end{aligned}$$

    is invertible as long as \(\alpha _1,\ldots ,\alpha _{2n} \mod p_2\) are distinct, which happens with overwhelming probability over \(\alpha _1,\ldots ,\alpha _{2n} \leftarrow _\mathrm{{R}}\mathbb {Z}_N\). It follows readily that

    $$\begin{aligned} \mathsf {Adv}_3 - \mathsf {Adv}_4 \le O(n^2/p_2). \end{aligned}$$

  • Game 5. We replace \(\kappa _0 = \mathsf {H}(e(C,u'_{n+1}))\) with \(\kappa _0 \leftarrow _\mathrm{{R}}\{0,1\}^\lambda \). First, recall from Game 1 that \(\{ \mathsf {sk}_y : y \notin \Gamma ^*\}\) only depend on \(u'_1,\ldots ,u'_n,u'_{n+2},\ldots ,u'_{2n}\); therefore, they only depend on \(\mathsf {RF}(1),\ldots ,\mathsf {RF}(n),\mathsf {RF}(n+2),\ldots ,\mathsf {RF}(2n)\) and do not reveal any information about \(\mathsf {RF}(n+1)\). Then, the quantity (from which \(\kappa _0\) is derived)

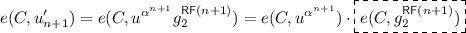
    has \(\log p_2 = \Theta (\lambda )\) bits of min-entropy coming from \(\mathsf {RF}(n+1)\); this holds as long as the \(G_{p_2}\)-component of C is not 1, which happens with probability \(1-1/p_2\). Then, by the left-over hash lemma, \(\kappa _0 = \mathsf {H}(e(C,u'_{n+1}))\) is \(2^{-\Omega (\lambda )}\)-close to the uniform distribution over \(\{0,1\}^\lambda \).

In Game 5, both \(\kappa _0,\kappa _1\) are uniformly random over \(\{0,1\}^\lambda \). Therefore, the view of the adversary \(\mathcal {A}\) is statistically independent of the challenge bit b. Hence, \(\mathsf {Adv}_5=0\). This completes the proof.    \(\square \)