Abstract
Error correcting codes, though powerful, are only applicable in scenarios where the adversarial channel does not introduce “too many” errors into the codewords. Yet, the question of having guarantees even in the face of many errors is well-motivated. Non-malleable codes, introduced by Dziembowski et al. (ICS 2010), address precisely this question. Such codes guarantee that even if an adversary completely over-writes the codeword, he cannot transform it into a codeword for a related message. Not only is this a creative solution to the problem mentioned above, it is also a very meaningful one. Indeed, non-malleable codes have inspired a rich body of theoretical constructions as well as applications to tamper-resilient cryptography, CCA2 encryption schemes and so on.
Another remarkable variant of error correcting codes were introduced by Katz and Trevisan (STOC 2000) when they explored the question of decoding “locally”. Locally decodable codes are coding schemes which have an additional “local decode” procedure: in order to decode a bit of the message, this procedure accesses only a few bits of the codeword. These codes too have received tremendous attention from researchers and have applications to various primitives in cryptography such as private information retrieval. More recently, Chandran et al. (TCC 2014) explored the converse problem of making the “re-encoding” process local. Locally updatable codes have an additional “local update” procedure: in order to update a bit of the message, this procedure accesses/rewrites only a few bits of the codeword.
At TCC 2015, Dachman-Soled et al. initiated the study of locally decodable and updatable non-malleable codes, thereby combining all the important properties mentioned above into one tool. Achieving locality and non-malleability is non-trivial. Yet, Dachman-Soled et al. provide a meaningful definition of local non-malleability and provide a construction that satisfies it. Unfortunately, their construction is secure only in the computational setting.
In this work, we construct information-theoretic non-malleable codes which are locally updatable and decodable. Our codes are non-malleable against \(\mathcal {F}_{\textsf {half}}\), the class of tampering functions where each function is arbitrary but acts (independently) on two separate parts of the codeword. This is one of the strongest adversarial models for which explicit constructions of standard non-malleable codes (without locality) are known. Our codes have \(\mathcal {O}(1)\) rate and locality \(\mathcal {O}(\lambda )\), where \(\lambda \) is the security parameter. We also show a rate 1 code with locality \(\omega (1)\) that is non-malleable against bit-wise tampering functions. Finally, similar to Dachman-Soled et al., our work finds applications to information-theoretic secure RAM computation.
B. Kanukurthi—Research supported in part by a start-up grant from the Indian Institute of Science and in part by a grant from the Ministry of Communications and Information Technology, Government of India.
S. Raghuraman—Research done while this author was at Indian Institute of Science and Microsoft Research, India.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Non-malleable Codes. The notion of error correcting codes allow a sender to encode a message \(s \in \{0,1\}^k\) into a codeword \(C \in \{0,1\}^n\) such that a receiver can then decode the original message s from a tampered codeword \(\tilde{C} = f(C)\). Naturally, s cannot be recovered from arbitrarily tampered codewords, and hence traditional error correcting codes (for the Hamming distance metric) require that the tampering function f be such that \(\tilde{C} = C + \varDelta \), with \(\varDelta \in \{0,1\}^n\) and the Hamming weight of \(\varDelta \) is \(\le \delta n\) (for some constant \(0<\delta <1\)). While powerful, error correcting codes provide no guarantees for larger classes of tampering functions. In light of this, Dziembowski et al. [19], introduced the notion of non-malleable codes. Informally, non-malleable codes are codes such that for all messages \(s \in \{0,1\}\), and for all f in the class of tampering functions \(\mathcal {F}\), \(\textsf {Dec}(f(\textsf {Enc}(s)))\) is either s or is unrelated to s. A little thought reveals that even in this case, \(\mathcal {F}\) cannot be arbitrary – for example, if \(\mathcal {F}\) includes the function \(\textsf {Enc}(\textsf {Dec}(\cdot )+1)\), then the output of \(\textsf {Dec}(f(\textsf {Enc}(s)))\) would be \(s+1\) and clearly related to s. A rich line of work has explored the largest possible class of tampering functions \(\mathcal {F}\) for which non-malleable codes can be constructed. Existential results [12, 19, 22], are known for large classes of tampering functions (essentially any function family whose size is less than \(\mathcal {F}_{\textsf {all}}\), the class of all functions). The works of [4, 5, 13] construct explicit non-malleable codes against the class of tampering functions \(\mathcal {F}_{\textsf {bit}}\) (i.e., functions that operate on every bit of the codeword separately) and \(\mathcal {F}_{\textsf {pertperm}}\) (i.e., functions that can perturb or permute bits of the codeword), while the works of [1, 2, 10, 18] construct such codes against the class of tampering functions \(\mathcal {F}_{\textsf {half}}\) (i.e., functions that operate independently on two halves of the codeword). Non-malleable codes have found many applications in cryptography, such as in tamper resilient cryptography [3, 26] and in constructing CCA secure encryption schemes [15].
Codes with Locality. Locally decodable codes (introduced formally by Katz and Trevisan [25]), are a class of error correcting codes, where every bit of the message can be decoded by reading only a few bits of the corrupted codeword. These codes have a wide range of applications and several constructions of such codes are known (see Yekhanin’s survey [32] for further details). Locally updatable codes (introduced by Chandran et al. [8]) are error correcting codes with the property that in order to obtain a codeword of message \(s'\) from a codeword of message s (where s and \(s'\) differ only in one bit), one only needs to modify a few bits of the codeword.
Locally Updatable/Decodable Non-malleable Codes. A natural question to ask is whether we can construct non-malleable codes that can be locally decoded and updated. Indeed, Dachman-Soled et al. [16] consider the above question and show how to construct locally updatable/decodable non-malleable codes. Combining local decodability with non-malleability is challenging: indeed, local decodability gives us a way to read a bit of the message by only reading a few bits of the codeword. If these bits were precisely the ones which are tampered, then how can non-malleability be guaranteed? In particular, it is likely that these bits are not accessed while decoding some other bits of the message. At its core, the challenge is that the adversary could tamper the codeword in such a manner that decoding some of the bits of the message could return \(\perp \), while the others may not. While this can be detected via a “global” decode, locally it will be undetected, thus resulting in a weak form of malleability. Dachman-Soled et al. capture these challenges by requiring that this weak form of malleability is all that the adversary will be able to accomplish. To be more specific, they show that their construction satisfies a (slightly) weaker form of non-malleability – in this, given a codeword \(C = \textsf {Enc}(s), s \in \{0,1\}^k\), an adversary may come up with a mauled codeword \(\tilde{C}\) such that \(\textsf {Dec}(i,\tilde{C}) = s_i\) for \(i \in [I]\), for some \([I] \subseteq [k]\) and \(\textsf {Dec}(i,\tilde{C}) = \bot \) for \(i \notin [I]\). Otherwise, the standard definition of non-malleability holds.
Dachman-Soled et al. present a construction that is non-malleable in the split-state adversarial model and requires the adversary to be computationally bounded. Given the rich body of work in constructing information-theoretic non-malleable codes and local codes (individually), we believe the question of building local, non-malleable codes in the information-theoretic setting is very well motivated. This is the question which we investigate in this work.
1.1 Results
-
1.
We construct a locally updatable and locally decodable non-malleable code that is non-malleable against the tampering class \(\mathcal {F}_{\textsf {half}}\), which denotes the class of tampering functions that operate independently on two different parts of the codeword, but can otherwise be arbitrary. Our code has constant rate and a decode/update locality of \(\mathcal {O}(\lambda )\), where \(\lambda \) is the security parameter.
-
2.
We can also obtain such non-malleable codes against the tampering class \(\mathcal {F}_{\textsf {bit}}\). In this case, our code has rate 1 and decode/update locality \(\omega (1)\).
-
3.
The work of Dachman-Soled et al. [16] showed how to use a local non-malleable code that is also leakage-resilient [26] to construct a protocol for secure RAM computation that remains secure when the adversary can tamper and leak from memory. In a similar way, we show how to use a leakage-resilient version of our code to construct an information-theoretic protocol for secure RAM computation that remains secure when the adversary can tamper and leak from memoryFootnote 1.
1.2 Techniques
Overview of [16]. Before we describe our techniques, we begin with a description of how Dachman-Soled et al. [16] construct their locally decodable/updatable non-malleable code. The idea is as follows: to encode a message \(s \in \{0,1\}^k\), pick a key \(\textsf {key}\) to a symmetric key encryption scheme and compute the codeword as \((\textsf {Enc}_{\textsf {NM}}(\textsf {key}), \textsf {AEnc}_\textsf {key}(1,s_1), \cdots , \textsf {AEnc}_\textsf {key}(1,s_1))\), where \(\textsf {Enc}_{\textsf {NM}}(\cdot )\) denotes a standard non-malleable code, \(\textsf {AEnc}_\textsf {key}(\cdot )\) denotes an authenticated encryption with key \(\textsf {key}\), and \(s_i\) denotes the \(i^{\text {th}}\) bit of s (\(i \in [k]\)). Now, suppose \(\textsf {Enc}_{\textsf {NM}}\) is a non-malleable code against a tampering function class \(\mathcal {F}_{\textsf {NM}}\), then the claim is that the above construction is non-malleable against the tampering function class \(\mathcal {F}\) of the form \((f_1,f_2)\), where \(f_1 \in \mathcal {F}_{\textsf {NM}}\) and \(f_2\) is any polynomial-time computable function. To see why this is true, consider the following two cases: (a) the tampering function \(f \in \mathcal {F}\) is such that f does not tamper with \(\textsf {Enc}_{\textsf {NM}}(\textsf {key})\); (b) the tampering function \(f \in \mathcal {F}\) is such that f tampers with \(\textsf {Enc}_{\textsf {NM}}(\textsf {key})\). In the first case, note that the function \(f_2\) does not have any information about the key \(\textsf {key}\), and hence by the security of the authenticated encryption scheme, we have that any polynomial-time computable \(f_2\) cannot tamper the authenticated encryptions of the \(s_i\) values to any related messageFootnote 2. In the second case, note that by the non-malleability of \(\textsf {Enc}_{\textsf {NM}}(\cdot )\), we have that \(f_1\) can only compute an encoding of \(\textsf {key'}\) such that \(\textsf {key'}\) is unrelated to \(\textsf {key}\). Since \(\textsf {key'}\) will be used to authenticate and decrypt the ciphertexts in the other part of the codeword, this essentially means that the output of the decode algorithm will be unrelated to s. Choosing \(\textsf {Enc}_{\textsf {NM}}\) to be the non-malleable code of Aggarwal et al. [1], gives a local non-malleable code that is secure against \(\mathcal {F}_{\textsf {split+poly}}^3\), which denotes the class of tampering functions that operate independently on three parts of the codeword, and additionally constrains the third function to be polynomial-time computable.
Challenges. A first attempt to convert the above code into an information-theoretically secure one is to use an information-theoretic authenticated encryption \(\textsf {ITAEnc}_{\textsf {itkey}}\) instead of \(\textsf {AEnc}_{\textsf {key}}\) above. We could follow a similar idea – encode \(\textsf {itkey}\) using a non-malleable encoding and encrypt\(+\)authenticate every bit of the message. Unfortunately, this idea quickly runs into trouble – for the information-theoretic authenticated encryption to be secure, we require the size of \(\textsf {itkey}\) to be proportional to the message and hence \(|\textsf {itkey}|\) must be proportional to k Footnote 3. Now, if we encode \(\textsf {itkey}\) as a whole using a non-malleable code, we have lost all locality (since we would require locality of k to even decode the code and retrieve \(\textsf {itkey}\)). On the other hand, if we encode every part of \(\textsf {itkey}\) separately, then an adversary can always replace one of these parts with a (sub)key of his choice and appropriately replace the ciphertext to obtain a codeword that decodes to \(s_i\) in a few indices and decodes to (independent) \(\tilde{s}_j\) in other indices (this violates the non-malleability definition from [16]). It seems that, in order to succeed, we must use an information-theoretic locally decodable code to encode \(\textsf {itkey}\), thereby running into a circular problem!
Another approach that one might consider is to start with an information-theoretic non-malleable code and somehow make that code “local”. Typical constructions of non-malleable codes make use of error-correcting codes with certain independence guarantees “across states”. This independence is exploited to get non-malleability. Unfortunately, this approach doesn’t yield any benefit as the locality of an error correcting code is orthogonal to its independence. Indeed, it is easy to see that a locally decodable code with locality r, necessarily has independence less than r.
Construction of Local Non-malleable Codes. To explain how we overcome these challenges, we explore the construction using (information-theoretic) authenticated encryption in more detail. The construction non-malleably encodes a \(\textsf {itkey}\) and uses it to authentically encrypt the message block-wise. Non-malleability dictates that \(|\textsf {itkey}| \ge k\) and this ruins locality. This tradeoff between non-malleability and locality is our main challenge. Our main observation is that this approach of using authenticated encryption is an overkill. In particular, we have existing constructions of non-malleable codes in the split-state model which we could use as a building block, except that it is unclear how to use them.
Consider this (insecure) construction: split the message s into k / t blocks each of size t, for some parameter t. Encode the message s as \((\textsf {Enc}_{\textsf {NM}}(s_1, \cdots , s_t), \cdots , \textsf {Enc}_{\textsf {NM}}(s_{k-t+1}, \cdots , s_k))\). To decode a bit \(s_i\), decode \(\textsf {Enc}_{\textsf {NM}}(s_{\lceil \frac{i}{t}\rceil }, \cdots , s_{\lceil \frac{i}{t}\rceil +t})\) and recover \(s_i\) appropriately. Let each block of the encoding be stored on separate states i.e., increase the number of states to 2k / t. It is easy to see that this construction is not secure against \(\mathcal {F}_{\textsf {split}}^{2k/t}\). Indeed, an adversary can always replace one block, say the first block, with an encoding of a known message, say all zeroes. Even though \(\textsf {Enc}_{\textsf {NM}}(0^{t})\) is independent of \(s_1,\cdots ,s_t\), the new message is related to the underlying message as a whole. The main problem is that an adversary is allowed to tamper certain parts of the encoding independently and still create a “globally related” codeword.
This brings us to the following question: how can we combine non-malleable encodings of different blocks of messages, so that the resulting construction is non-malleable? The answer lies in preventing such isolated tampering or at least detecting it when it happens. To do this, we simply tie together all the encodings by using \(\textsf {itkey}\) to provide consistency across blocks. If an adversary changes one block independently, either it is detected or he needs to change all blocks to something independent. This use of \(\textsf {itkey}\), as randomness that allows for consistency checks across blocks, and not as an encryption key, allows us to keep \(\textsf {itkey}\) short and achieve locality.
In retrospect, all our constructions are remarkably simple. We first give an overview of our non-malleable construction that is secure against \(\mathcal {F}_{\textsf {split}}^{2k/t+2}\) (i.e., the class of tampering functions that operate independently on \(2k/t+2\) parts of the codeword, for some chosen parameter t and message length k). We will discuss how to reduce the number of states later. The idea is as follows: to authenticate a part of the message, we will pick a random value r and encode it twice in 2 different states – once on its own and once with a message. In other words, to encode a message \(s \in \{0,1\}^k\), split s into \(\frac{k}{t}\) parts, each of length t, as before. Now, pick \(\frac{k}{t}\) random \(r_i\) values (each \(r_i\) being of length \(\lambda \)). These \(r_i\) values correspond to the key \(\textsf {itkey}\) above.
Encode the message s as \((\textsf {Enc}_{\textsf {NM}}(r_1,\cdots ,r_{\frac{k}{t}}),\textsf {Enc}_{\textsf {NM}}(r_1, s_1, \cdots , s_t), \) \(\cdots , \textsf {Enc}_{\textsf {NM}}(r_{\frac{k}{t}}, s_{k-t+1}, \cdots , s_k))\). To decode a bit \(s_i\), decode \(\textsf {Enc}_{\textsf {NM}}(r_1,\cdots ,r_{\frac{k}{t}})\) to obtain \(r_{\lceil \frac{i}{t}\rceil }\); then decode \(\textsf {Enc}_{\textsf {NM}}(r_{\lceil \frac{i}{t}\rceil }, s_{\lceil \frac{i}{t}\rceil }, \cdots , s_{\lceil \frac{i}{t}\rceil +t})\). Now, check if the r values encoded in both these codewords match and if so, output \(s_i\). The claim then is that if \(\textsf {Enc}_{\textsf {NM}}(\cdot )\) is non-malleable against a tampering function class \(\mathcal {F}_{\textsf {NM}}\), then the above construction is non-malleable against a tampering function class \(\mathcal {F}\) of the form \((f_0,f_1,\cdots ,f_{k})\), where \(f_i \in \mathcal {F}_{\textsf {NM}}, 0 \le i \le k\). At a very high level, to see why this is true, again consider two cases: (a) if the adversary does not maul the first component of the codeword, then if he mauls any other component of the codeword, the decode algorithm will output \(\bot \) (except with probability \(2^{-\lambda }\)) as he must get “guess” an \(r_i\) value encoded in a different state; (b) if the adversary mauls the first component of the codeword, then he must maul all other components of the codeword (as otherwise the decode algorithm will output \(\bot \)) and by the non-malleability of the underlying code, the new codeword will be independent of the \(s_i\) values. We note that the r in our construction plays a role similar to the one played by the secret label L in the leakage and tamper-resilient RAM computation construction of Faust et al. [21]. While this indeed gives us a construction of a locally decodable/encodable non-malleable code, the locality of the code is \(t+\frac{k}{t}\) (and is thus minimized with \(t = \sqrt{k}\)); also, using the \(\mathcal {F}_{\textsf {half}}\) code from Aggarwal et al. [1] this gives us a construction that is non-malleable against \(\mathcal {F}_{\textsf {split}}^{\sqrt{k}}\).
We now show how to reduce the number of states. Suppose \(\textsf {Enc}_{\textsf {NM}}(\cdot )\) is non-malleable against the tampering class \(\mathcal {F}_{\textsf {half}}\), then \(\textsf {Enc}_{\textsf {NM}}(\cdot )\) has the form (L, R) and hence our above construction has the form \((L_0,R_0, L_1, R_1, \cdots , L_t, R_t)\). In such a case, we show that the codeword can be written as \((C_1,C_2,C_3,C_4) = ([L_0],[R_0],[L_1,\cdots ,L_t],[R_1,\cdots ,R_t])\) and that this construction is non-malleable against \(\mathcal {F}_{\textsf {split}}^4\). While this code is secure against a larger class of tampering function, it still has locality \(t+\frac{k}{t}\). However, we then show that a single r value can be reused across the encodings (instead of \(\frac{k}{t}\) different \(r_i\) values) as long as we encode the \(s_i\) values with indices, and moreover that this r value does not even have to be encoded using a non-malleable code (as long as it is hidden). This can be accomplished by simply secret sharing r into \(r_L, r_R\) and storing them separately. In other words, our final construction has the form \(([r_L, L_1,\cdots ,L_k],[r_R, R_1,\cdots ,R_k])\), where \((L_i, R_i) = \textsf {Enc}_{\textsf {NM}}(r, i, s_i)\) and \(r_L \oplus r_R = r\). Instantiating the \(\textsf {Enc}_{\textsf {NM}}(\cdot )\) with the code of [1] gives us our first result, while instantiating it with the code of [13] gives us our second result.
Tamper and Leakage-Resilient RAM Computation. In order to obtain a protocol for secure RAM computation that is tamper and leakage resilient, Dachman-Soled et al. [16] require the local non-malleable code to tolerate many-time leakage (i.e., the adversary can obtain an unbounded amount of leakage throughout the course of the protocol, but is bounded by the amount of leakage that can be obtained in between successive updates to the memory that will “refresh” the encoding). The challenge is to obtain such a construction even though the update algorithm is local and only updates a small part of the codeword. In their work, [16] do this by computing a Merkle hash of the ciphertexts and by encoding this Merkle hash along with the symmetric key \(\textsf {key}\) and by computing a fresh encoding of \(\textsf {key}\) together with the root of the Merkle Hash everytime. However, intuitively, obtaining such a guarantee seems a contradictary task for us – information theoretically, if we do not bound the total amount of leakage, and only refresh a part of the encoding, then the adversary over time can learn information about the various parts of the codeword (and hence the message itself, thereby defeating non-malleability). We show that by compromising on the leakage bound tolerated, and by using the information-theoretic leakage-resilient non-malleable codes of Aggarwal et al. [3], we can achieve both information-theoretic leakage/tamper-resilience along with locality, by periodically refreshing “different” parts of the codeword. We note here, that leakage and tamper-resilient RAM computation has also been studied by Faust et al. [21] in a model different from Dachman-Soled et al. [16] (and our work). In the model of Faust et al. [21], they allow an adversary to obtain and store past codewords and use that to tamper with the later encodings; on the other hand, they assume a tamper and leak-free component. Faust et al. [21] use continuous non-malleable codes [20], to obtain their construction. They show that if the underlying continuous non-malleable code is information-theoretic, then their final construction is also information-theoretic; however, no information-theoretic construction of continuous non-malleable codes are known. Furthermore, that construction would require a tamper/leak free component; in our case, as in [16], the memory of the RAM can be completely subjected to leakage and tampering.
1.3 Organization of the Paper
In Sect. 2, we present the formal definition of non-malleable coding schemes with locality. As a stepping stone towards our main construction, in Sect. 3, we present a construction of a non-malleable coding scheme with \(\widetilde{\mathcal {O}}(\sqrt{k})\) locality against \(\mathcal {F}_{\textsf {split}}^{4}\) adversaries. We present our main result namely, a constant rate non-malleable coding scheme with \(\mathcal {O}(\lambda )\) locality against \(\mathcal {F}_{\textsf {half}}\), in Sect. 4. Section 5 contains our constructions which are also locally updatable and leakage-resilient. Finally, Sect. 6 presents the application of our non-malleable codes to secure RAM computation.
2 Preliminaries
2.1 Notation
We say that two probability distributions \(\mathcal {X}\) and \(\mathcal {Y}\) are \(\epsilon \)-close if their statistical distance is \(\le \epsilon \) and this is denoted by \(\mathcal {X} \approx _{\epsilon } \mathcal {Y}\). The formal definition is given below.
Definition 1
Let \(\mathcal {X}, \mathcal {Y}\) be two probability distributions over some set S. Their statistical distance is
We say that \(\mathcal {X}\) and \(\mathcal {Y}\) are \(\epsilon \)-close if \(\mathbf {SD}\left( {\mathcal {X}, \mathcal {Y}} \right) \le \epsilon \) and this is denoted by \(\mathcal {X} \approx _{\epsilon } \mathcal {Y}\).
For a sequence \(x = \left( x_{1}, \ldots , x_{n}\right) \) and set \(S \subseteq [n]\), we use \(x\vert _{S}\) to denote the subsequence of \(x_{i}\) values where \(i \in S\). For any string y and \(i \in [|y|]\), we use \(y_{i}\) to denote the \(i^{th}\) bit of y. The security parameter is denoted by \(\lambda \). We use \(\widetilde{\mathcal {O}}\left( \cdot \right) \) to denote asymptotic estimates that hide poly-logarithmic factors in the involved parameter.
2.2 Definitions
Definition 2
(Coding schemes). A coding scheme consists of a pair of functions \(\textsf {Enc}: \{0, 1\}^{k} \rightarrow \{0, 1\}^{n}\) and \(\textsf {Dec}: \{0, 1\}^{n} \rightarrow \{0, 1\}^{k} \cup \{\perp \}\) where k is the message length, n is the block length and \(k < n\).
-
1.
The encoder \(\textsf {Enc}\) takes as input a message \(s \in \{0, 1\}^{k}\) and outputs a codeword \(c = \textsf {Enc}(s)\).
-
2.
The decoder \(\textsf {Dec}\) when given a correct (untampered) codeword as input, outputs the corresponding message. The correctness requirement is that for all \(s\in \{0,1\}^{k}, \textsf {Dec}(\textsf {Enc}(s)) = s\), with probability 1.
The rate of the coding scheme is the ratio k / n. A coding scheme is said to have relative distance \(\delta \) (or minimum distance \(\delta n\)), for some \(\delta \in [0, 1)\), if for every \(s \in \{0, 1\}^{k}\) the following holds. Let \(X := \textsf {Enc}\left( s\right) \). Then, for any \(\varDelta \in \{0, 1\}^{n}\) of Hamming weight at most \(\delta n\), \(\textsf {Dec}\left( X + \varDelta \right) = s\) with probability 1. Standard error correcting codes, as defined above, are only applicable in settings where the adversarial channel cannot make too many (i.e., more than \(\delta n\)) errors. Non-malleable codes, introduced by Dziembowski et al. [19], provide a meaningful guarantee in situations where the adversarial channel may completely overwrite the codeword. Informally, a coding scheme is said to be non-malleable if an adversary cannot transform the codeword of a message s into a codeword of a related message \(s'\). Note that such codes do not focus on error-tolerance and, therefore, the parameter \(\delta \) is set to 0.
Definition 3
(Non-malleable codes [19]). A coding scheme \(\left( \textsf {Enc}, \textsf {Dec}\right) \) with message length k and block length n is said to be non-malleable with error \(\epsilon \) (also called exact security) with respect to a family \(\mathcal {F}\) of tampering functions acting on \(\{0, 1\}^{n}\) (i.e., each \(f \in \mathcal {F}\) maps \(\{0, 1\}^{n}\) to \(\{0, 1\}^{n}\)) if for every \(f \in \mathcal {F}\) there is a simulator \(\mathcal {S}\) such that for all \(s \in \{0, 1\}^{k}\), we have

where \(\mathbf{Tamper }_{s}^{f}\) is the output of the tampering experiment defined by
In this work, we focus on information-theoretic non-malleable codes i.e., the \(\approx _{\epsilon }\) is measured by statistical distance. Our goal is to design information-theoretic non-malleable codes which are also local. Locally decodable codes (LDCs), introduced by Katz and Trevisan [25] are a class of error correcting codes, where every bit of the message can be probabilistically decoded by reading only a few bits of the (possibly corrupted) codeword. We now state the formal definition.
Definition 4
(Local Decodability [25]). A coding scheme \(\left( \textsf {Enc}, \textsf {Dec}\right) \) with message length k and block length n is said to be \(\left( r, \delta , \epsilon \right) \)-locally decodable if there exists a randomized decoding algorithm \(\textsf {Dec}\) such that the following properties hold.
-
1.
For all \(s \in \{0, 1\}^{k}\), \(i \in [k]\) and all vectors \(y \in \{0, 1\}^{n}\) such that the Hamming distance between \(\textsf {Enc}\left( s\right) \) and y is not more than \(\delta n\),
$$ \Pr [\textsf {Dec}\left( y, i\right) = s_{i}] \ge 1 - \epsilon , $$where the probability is taken over the random coin tosses of the algorithm \(\textsf {Dec}\).
-
2.
\(\textsf {Dec}\) reads at most r coordinates of y.
Dachman-Soled et al. [16] introduced and designed codes which combine non-malleability and locality. While their coding scheme is in the computational setting, their definition is applicable even for the information-theoretic setting by simply using the appropriate notion of “closeness”.
Definition 5
(Local Decodability and Non-malleability, LDNMC [16]). A coding scheme \(\left( \textsf {Enc}, \textsf {Dec}\right) \) with message length k and block length n is said to be a \(\left( r, \epsilon _{1}, \epsilon _{2}\right) \)-locally decodable non-malleable coding scheme with respect to a family \(\mathcal {F}\) of tampering functions acting on \(\{0, 1\}^{n}\) if it is \(\left( r, 0, \epsilon _{1}\right) \)-locally decodable and if for every \(f \in \mathcal {F}\) there is a simulator \(\mathcal {S}\) such that for all \(s \in \{0, 1\}^{k}\), we have
where \(\mathbf{Tamper }_{s}^{f}\) is the output of the tampering experiment defined by
and \(\mathbf{Ideal }_{\mathcal {S}, s}\) is defined as
-
1.
\(\left( \mathcal {I}, s^{*}\right) \leftarrow \mathcal {S}^{f\left( \cdot \right) }\left( 1^{\lambda }\right) \), where \(\mathcal {I} \subseteq [k]\) and \(s^{*} \in \{0, 1, \perp \}^{k}\).
-
2.
If \(\mathcal {I} = [k]\), then \(\tilde{s} = s^{*}\). Otherwise, \(\tilde{s}\vert _{\mathcal {I}} =\ \perp \) and \(\tilde{s}\vert _{\overline{\mathcal {I}}} = s\vert _{\overline{\mathcal {I}}}\), where \(\overline{\mathcal {I}}\) denotes the complement of the set \(\mathcal {I}\).
-
3.
Output \(\tilde{s}\).
Dachman-Soled et al. apply local NMCs to the problem of secure RAM computation. Towards this end, they require NMCs that are also locally updatable. Locally updatable and decodable error correcting codes were formalized in the work of Chandran et al. [8]. Informally, such codes allow for a bit of the underlying message to be updated by rewriting just a few bits of the codeword. In the context of non-malleable codes, which do not require error-tolerance, a weaker definition [16] of local updatability suffices, which we present next.
Definition 6
(Local Decodability and Updatability [8, 16]). A coding scheme \(\left( \textsf {Enc}, \textsf {Dec}, \textsf {Update}\right) \) with message length k and block length n is said to be \(\left( r_{1}, r_{2}, \delta , \epsilon \right) \)-locally decodable and updatable if it is \(\left( r_{1}, \delta , \epsilon \right) \)-locally decodable and there exists a randomized algorithm \(\textsf {Update}\) such that:
-
1.
For all \(s \in \{0, 1\}^{k}\), \(i \in [k]\), \(s_{i}' \in \{0, 1, \perp \}\) and all vectors \(y \in \{0, 1\}^{n}\) such that the Hamming distance between \(\textsf {Update}^{C}\left( i, s_{i}'\right) \) and y is not more than \(\delta n\), where \(C = \textsf {Enc}\left( s\right) \),
$$ \Pr [\textsf {Dec}\left( y, i\right) = s_{i}'] \ge 1 - \epsilon , $$where the probability is taken over the random coin tosses of the algorithm \(\textsf {Dec}\).
-
2.
\(\textsf {Update}\) reads and changes at most \(r_{2}\) coordinates of y.
Remarks. We note that the above definition can be extended in a straight-forward manner to account for the decoding of a codeword which has been updated multiple times as opposed to once (as above). Additionally, although we focus on the case of correcting zero errors in the codeword, we can modify our construction to get a construction that tolerates errors and is also non-malleable, by simply encoding each “state” of our non-malleable codeword using an LDC. This would reduce the error-tolerance of the code (by a fraction equal to the number of states) and the rate of the obtained code would now depend on the rate of the LDC. It suffices however here to discuss the case of correcting zero errors in the codeword.
Similar to [16], we also construct locally decodable/updatable leakage resilient non-malleable codes and use them to construct information-theoretic tamper and leakage resilient RAM computation. We refer the reader to the full version of this paper for details on these primitives.
3 Non-malleable Codes with \(\widetilde{\mathcal {O}}(\sqrt{k})\) Locality Against \(\mathcal {F}_{\textsf {split}}^{4}\)
In this section, we describe a construction of a locally updatable/decodable non-malleable code that is non-malleable against the tampering function class \(\mathcal {F}_{\textsf {split}}^{4}\) (i.e., the tampering function class that operates independently on 4 parts of the codeword), with locality \(\widetilde{\mathcal {O}}(\sqrt{k})\), where k is the length of the message being encoded. The motivation for presenting this construction is two-fold: first, it has ideas which will lead to our main construction described in Sect. 4; second, this construction will be used to achieve the application to secure RAM computation. We remark that the four parts of the codeword seen by a 4-state adversary from the class \(\mathcal {F}_{\textsf {split}}^{4}\) need not be of equal sizes (in fact, they are not in this construction). We specify how a codeword is broken into 4 parts in the proof of Theorem 2. If one is so particular on requiring all parts to be of equal length, we note that it is trivial to achieve this via padding, although this would affect the rate of the final coding scheme (by at most a constant factor).
Recall that \(\lambda \) denotes the security parameter; t denotes a parameter that will be set appropriately later on. Let \(\textsf {NMC} = \left( \textsf {Enc}_{\textsf {NM}}, \textsf {Dec}_{\textsf {NM}}\right) \) be a non-malleable coding scheme on strings of length \(\lambda k/t\) and \(\textsf {NMC}' = \left( \textsf {Enc}_{\textsf {NM}}', \textsf {Dec}_{\textsf {NM}}'\right) \) be a non-malleable coding scheme on strings of length \(\lambda + t\). We assume without loss of generality that t divides k. We define the following coding scheme:
-
1.
\(\textsf {Enc}\left( s\right) \): On input \(s \in \{0, 1\}^{k}\), the algorithm splits s into k / t blocks, say \(\textsf {s}_{1}, \ldots , \textsf {s}_{k/t}\) of size t each. Then, the algorithm chooses k / t random strings \(r_{1}, \ldots , r_{k/t} \in \{0, 1\}^{\lambda }\), and computes \(c = \textsf {Enc}_{\textsf {NM}}\left( r_{1} \Vert \ldots \Vert r_{k/t}\right) \) and \(e_{i} = \textsf {Enc}_{\textsf {NM}}'\left( r_{i} \Vert \textsf {s}_{i}\right) \) for \(i \in [k/t]\). The algorithm finally outputs the codeword \(C = \left( c, e_{1}, \ldots , e_{k/t}\right) \).
-
2.
\(\textsf {Dec}\left( C, i\right) \): On input \(i \in [k]\), the algorithm reads the first and \(\left( \lceil i/t \rceil + 1\right) \)th block of C, retrieving \(c, e_{\lceil i/t \rceil }\). Then it runs \(r_{1} \Vert \ldots \Vert r_{k/t} := \textsf {Dec}_{\textsf {NM}}\left( c\right) \). If the decoding algorithm outputs \(\perp \), the algorithm outputs \(\perp \). Otherwise, it computes \(r_{\lceil i/t \rceil }^{*} \Vert \textsf {s}_{\lceil i/t \rceil } = \textsf {Dec}_{\textsf {NM}}'\left( e_{\lceil i/t \rceil }\right) \). If the decoding algorithm outputs \(\perp \), the algorithm outputs \(\perp \). If \(r_{\lceil i/t \rceil }^{*} \ne r_{\lceil i/t \rceil }\), the algorithm outputs \(\perp \). Otherwise, the algorithm outputs \(s_{i}\) from \(\textsf {s}_{\lceil i/t \rceil }\).
We instantiate this construction by instantiating the non-malleable codes NMC and \(\textsf {NMC}'\). A natural and strong class of functions which we may assume the schemes are non-malleable against is the class of split-state adversaries, \(\mathcal {F}_{\textsf {half}}\), that tamper two partsFootnote 4 of the codeword independently, that is, \(f \in \mathcal {F}_{\textsf {half}}\) iff \(f : \{0, 1\}^{n}\) can be written as \(f\left( c_{1}, c_{2}\right) = \left( f_{1}\left( c_{1}\right) , f_{2}\left( c_{2}\right) \right) \) for \(f_{1}\), \(f_{2} : \{0, 1\}^{n/2} \rightarrow \{0, 1\}^{n/2}\). The following result is known.
Theorem 1
[1]. Let \(\mathcal {F}_{\textsf {half}}\) be the function family of split-state adversaries over \(\{0, 1\}^{n}\). Let \(\epsilon > 0\) be an arbitrary value and \(k, n > 0\) be integers such that \(k/n \le \gamma \), for some constant \(\gamma \). Then there exists a non-malleable code with respect to \(\mathcal {F}_{\textsf {half}}\), with k-bit source-messages and n-bit codewords, and exact security \(\epsilon \).
We now show the local-decodability and non-malleability of the above scheme instantiated using the non-malleable code in Lemma 1.
Theorem 2
Assume that NMC, \(\textsf {NMC}'\) be non-malleable coding schemes of rate \(1/\gamma \), and exact security \(\epsilon > 0\), which is non-malleable against split-state adversaries. Then the above coding scheme is a \(\left( \left( \lambda \left( 1 + k/t\right) + t\right) \gamma , 0, k\left( \epsilon + 2^{-\lambda }\right) /t\right) \)-locally decodable non-malleable coding scheme which is non-malleable against the tampering class \(\mathcal {F}_{\textsf {split}}^4\), for any \(t \le k\). The rate of the code is \(1/\gamma '\), where \(\gamma ' = \lambda \gamma /t + \left( 1 + \lambda /t\right) \gamma \).
Proof
Clearly the decoding algorithm reads \(\left( \lambda \left( 1 + k/t\right) + t\right) \gamma \) positions of the codeword since \(|c| = \lambda \gamma k/t\) and \(|e_{i}| = \left( \lambda + t\right) \gamma \). Also, since the decoding algorithm is deterministic, the error probability in the local decoding procedure is 0. This justifies the first two parameters of the coding scheme.
The underlying non-malleable codes \(\textsf {NMC}\) and \(\textsf {NMC}'\) are non-malleable against split-state adversaries and let \(L_{0}, R_{0}\) be the parts of c viewed by the two states corresponding to the split-state adversary for c, and let \(L_{i}, R_{i}\) be the parts of \(e_{i}\) viewed by the two states corresponding to the split-state adversary for \(e_{i}\), for all \(i \in [k/t]\). We define how a codeword is split into four parts – the four-state adversaries against which the above scheme is non-malleable consists of adversaries which are arbitrary functions over \(L_{0}\), \(R_{0}\), \(L_{1} \Vert \ldots \Vert L_{k/t}\) and \(R_{1} \Vert \ldots \Vert R_{k/t}\).
To show the theorem, for any suitable four-state adversary \(f = \left( f_{1}, f_{2}, f_{3}, f_{4}\right) \) as described above, which we denote as \(f_{1}\left( L_{0}\right) \), \(f_{2}\left( R_{0}\right) \), \(f_{3}\left( L_{1}, \ldots , L_{k/t}\right) \) and \(f_{4}\left( R_{1}, \ldots , R_{k/t}\right) \), we need to construct a simulator \(\mathcal {S}\). We describe the simulator with oracle access to f.
-
1.
Let \(\mathcal {S}'\) be the simulator for the non-malleable code NMC, and \(\mathcal {S}''\) for \(\textsf {NMC}'\). Now \(\mathcal {S}^{f\left( \cdot \right) }\) simulates \(\mathcal {S}'\) once and \(\mathcal {S}''\) k / t times to obtain simulated codewords c and \(e_{i}\) for all \(i \in [k/t]\). Note that the simulator described for the code instantiated from Lemma 1 does not need oracle access to the tampering function to produce simulated codewords assuming a super-polynomial message space, which is the case since the messages are of length \(\lambda k/t\) and \(\lambda + t\) respectively, where \(0 \le t \le k\). Let \(C = \left( c, e_{1}, \ldots , e_{k/t}\right) \).
-
2.
\(\mathcal {S}^{f\left( \cdot \right) }\) then computes \(\tilde{C} = f\left( C\right) \), where \(\tilde{C} = \left( \tilde{c}, \tilde{e}_{1}, \ldots , \tilde{e}_{k/t}\right) \).
-
3.
Let \(L_{i}, R_{i}\) be the parts of \(\tilde{e}_{i}\) viewed by the two states corresponding to the split-state adversary for \(e_{i}\), for all \(i \in [k/t]\). Let \(f'_{i} = f_{3}\big (L_{1}, \ldots , L_{i - 1}, \cdot ,\) \( L_{i + 1}, \ldots , L_{k/t}\big )\) and \(f''_{i} = f_{4}\left( R_{1}, \ldots , R_{i - 1}, \cdot , R_{i + 1}, \ldots , R_{k/t}\right) \) for all \(i \in [k/t]\). Now \(\mathcal {S}^{f\left( \cdot \right) }\) simulates \(\mathcal {S}'^{f_{1}\left( \cdot \right) , f_{2}\left( \cdot \right) }\) with \(\tilde{c}\) and \(\mathcal {S}''^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) with \(\tilde{e}_{i}\) for each \(i \in [k/t]\) internally. \(\mathcal {S}'\) returns an output \(r' = r_{1}' \Vert \ldots \Vert r_{k/t}'\), where
 and \(\mathcal {S}''\) returns an output
and \(\mathcal {S}''\) returns an output 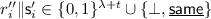 for each \(i \in [k/t]\).
for each \(i \in [k/t]\). -
4.
Set \(\mathcal {I} = \emptyset \).
-
(a)
If \(r' =\ \perp \), then set \(\mathcal {I} = [k]\) and \(s^{*}_{i} =\ \perp \) for all \(i \in [k]\).
-
(b)
If
 , then, for each \(i \in [k]\), check if
, then, for each \(i \in [k]\), check if  . If so, set \(\mathcal {I} = \mathcal {I} \cup \{j : \left( i - 1\right) t + 1 \le j \le it\}\) and \(s^{*}_{j} =\ \perp \) for all j such that \(\left( i - 1\right) t + 1 \le j \le it\).
. If so, set \(\mathcal {I} = \mathcal {I} \cup \{j : \left( i - 1\right) t + 1 \le j \le it\}\) and \(s^{*}_{j} =\ \perp \) for all j such that \(\left( i - 1\right) t + 1 \le j \le it\). -
(c)
Otherwise, if
 , set \(\mathcal {I} = [k]\). Let \(s' = \textsf {s}_{1}' \Vert \ldots \Vert \textsf {s}_{k/t}'\). For each \(i \in [k]\),
, set \(\mathcal {I} = [k]\). Let \(s' = \textsf {s}_{1}' \Vert \ldots \Vert \textsf {s}_{k/t}'\). For each \(i \in [k]\),-
i.
If \(r_{\lceil i/t \rceil }'' \Vert \textsf {s}_{\lceil i/t \rceil }' =\ \perp \) or
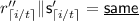 , then set \(s^{*}_{i} =\ \perp \).
, then set \(s^{*}_{i} =\ \perp \). -
ii.
Otherwise, check if \(r'_{\lceil i/t \rceil } = r''_{\lceil i/t \rceil }\). If so, set \(s^{*}_{i} = s'_{i}\), otherwise set \(s^{*}_{i} =\ \perp \).
-
i.
-
(a)
-
5.
Output \(\left( \mathcal {I}, s^{*}\right) \).
The above simulator now defines \(\mathbf{Ideal }_{\mathcal {S}, s}\). We must now show that \(\mathbf{Tamper }_{s}^{f} \approx _{\epsilon '} \mathbf{Ideal }_{\mathcal {S}, s}\) for some negligible \(\epsilon '\). We proceed through a series of hybrids of the form \(\mathbf{Ideal }_{\mathcal {S}_{j}, s}\) for \(j \in [k/t]\), which is the same as \(\mathbf{Ideal }_{\mathcal {S}_{j - 1}, s}\) except that it randomly chooses an \(r_{i} \in \{0, 1\}^{\lambda }\), and generates \(e_{i} = \textsf {Enc}_{\textsf {NM}}'\left( r_{i} \Vert \textsf {s}_{i}\right) \) for \(i = j\) and obtains \(r''_{i} \Vert \textsf {s}'_{i} = \textsf {Dec}_{\textsf {NM}}'\left( g_{i}\left( e_{i}\right) \right) \) for \(i = j\), where \(g_{i} = \left( f'_{i}, f''_{i}\right) \); if \(r''_{i} \Vert \textsf {s}'_{i} = r_{i} \Vert \textsf {s}_{i}\), it outputs  . This is to say that it obtains codewords and performs decoding as in the real experiment for index j (as well). Note that \(\mathbf{Ideal }_{\mathcal {S}, s} \equiv \mathbf{Ideal }_{\mathcal {S}_{0}, s}\).
. This is to say that it obtains codewords and performs decoding as in the real experiment for index j (as well). Note that \(\mathbf{Ideal }_{\mathcal {S}, s} \equiv \mathbf{Ideal }_{\mathcal {S}_{0}, s}\).
Lemma 1
For all \(j \in [k/t]\), \(\mathbf{Ideal }_{\mathcal {S}_{j - 1}, s} \approx _{\epsilon } \mathbf{Ideal }_{\mathcal {S}_{j}, s}\).
Proof
Let \(\mathcal {A} = \left( \mathcal {A}_{1}, \mathcal {A}_{2}, \mathcal {A}_{3}, \mathcal {A}_{4}\right) \) be a four-state adversary that can distinguish between the outputs of the experiments \(\mathbf{Ideal }_{\mathcal {S}_{j - 1}, s}\) and \(\mathbf{Ideal }_{\mathcal {S}_{j}, s}\) for some \(j \in [k/t]\), with an advantage of \(\alpha \). We describe a split-state adversary \(\mathcal {B} = \left( \mathcal {B}_{1}, \mathcal {B}_{2}\right) \) (where \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) operate independently on two halves of the underlying codeword) that can break the non-malleability of the scheme \(\textsf {NMC}'\) with the same advantage \(\alpha \). However, since \(\textsf {NMC}'\) is non-malleable against split-state adversaries with exact security \(\epsilon \), \(\alpha \le \epsilon \), which completes the proof.
Let \(\mathcal {C}\) be the challenger for the scheme \(\textsf {NMC}'\). \(\mathcal {B}\), using \(\mathcal {A}\), executes as follows. First, \(\mathcal {A}\) chooses a message \(s \in \{0, 1\}^{k}\) on which he will distinguish between the outputs of the experiments \(\mathbf{Ideal }_{\mathcal {S}_{j - 1}, s}\) and \(\mathbf{Ideal }_{\mathcal {S}_{j}, s}\), and sends it to \(\mathcal {B}_{1}\), which then splits s into k / t blocks, say \(\textsf {s}_{1}, \ldots , \textsf {s}_{k/t}\) of size t each. \(\mathcal {B}_{1}\) randomly chooses \(r_{i} \in \{0, 1\}^{\lambda }\), where \(\lambda \) is the security parameter, for all \(i \in [j]\). It then generates \(e_{i} = \textsf {Enc}_{\textsf {NM}}'\left( r_{i} \Vert \textsf {s}_{i}\right) \) for \(i \in [j - 1]\). Let \(\mathcal {S}'\) be the simulator for the non-malleable code NMC, and \(\mathcal {S}''\) for \(\textsf {NMC}'\) (on all indices but j). Now, \(\mathcal {B}_{1}\) simulates \(\mathcal {S}'\) once and \(\mathcal {S}''\) \(k/t - j\) times to obtain simulated codewords c and \(e_{i}\) for all \(i \in \{j + 1, \ldots , k/t\}\). \(\mathcal {B}_{1}\) then sends the message \(r_{j} \Vert \textsf {s}_{j}\) to the challenger \(\mathcal {C}\).
\(\mathcal {C}\) then either computes \(e_{j} = \textsf {Enc}_{\textsf {NM}}'\left( r_{j} \Vert \textsf {s}_{j}\right) \), or uses the simulator \(\mathcal {S}''\) to obtain a simulated codeword \(e_{j}\). It then splits \(e_{j}\) into two parts \(L_{j}\), \(R_{j}\) and sends \(L_{j}\) to \(\mathcal {B}_{1}\) and \(R_{j}\) to \(\mathcal {B}_{2}\) respectively. \(\mathcal {B}_{1}\) splits c into two parts, \(L_{0}\) and \(R_{0}\), and \(e_{i}\) into two parts, \(L_{i}\) and \(R_{i}\), for each \(i \in [k/t] \backslash \{j\}\). \(\mathcal {B}_{1}\) then sends across \(L_{0}\) to \(\mathcal {A}_{1}\), \(R_{0}\) to \(\mathcal {A}_{2}\), \(L_{i}\), for all \(i \in [k/t]\), to \(\mathcal {A}_{3}\), and \(R_{i}\), for all \(i \in [k/t] \backslash \{j\}\), to \(\mathcal {A}_{4}\), and \(\mathcal {B}_{2}\) sends across \(R_{j}\) to \(\mathcal {A}_{4}\). \(\mathcal {A}\) then chooses its four-state tampering function \(f = \left( f_{1}, f_{2}, f_{3}, f_{4}\right) \), and computes \(\tilde{L}_{0} = f_{1}\left( L_{0}\right) \), \(\tilde{R}_{0} = f_{2}\left( R_{0}\right) \), \(\tilde{L} = f_{3}\left( L_{1}, \ldots , L_{k/t}\right) \) and \(\tilde{R} = f_{4}\left( R_{1}, \ldots , R_{k/t}\right) \). It then parses \(\tilde{L}\) as \(\tilde{L} = \left( \tilde{L}_{1}, \ldots , \tilde{L}_{k/t}\right) \) and \(\tilde{R}\) as \(\tilde{R} = \left( \tilde{R}_{1}, \ldots , \tilde{R}_{k/t}\right) \). \(\mathcal {A}_{1}\), \(\mathcal {A}_{2}\), \(\mathcal {A}_{3}\) and \(\mathcal {A}_{4}\) also determine the descriptions of the functions \(f_{1}\), \(f_{2}\), \(f'_{i} = f_{3}\left( L_{1}, \ldots , L_{i - 1}, \cdot , L_{i + 1}, \ldots , L_{k/t}\right) \) and \(f''_{i} = f_{4}\left( R_{1}, \ldots , R_{i - 1}, \cdot , R_{i + 1}, \ldots , R_{k/t}\right) \), respectively, for all \(i \in \{j + 1, \ldots , k/t\}\). Then, \(\mathcal {A}_{1}\) sends across \(\tilde{L}_{0}\) and the description of the function \(f_{1}\) to \(\mathcal {B}_{1}\), \(\mathcal {A}_{2}\) sends across \(\tilde{R}_{0}\) and the description of the function \(f_{2}\) to \(\mathcal {B}_{1}\), \(\mathcal {A}_{3}\) sends across \(\tilde{L}_{i}\), for all \(i \in [k/t]\), and the descriptions of the functions \(f'_{i}\), for all \(i \in \{j + 1, \ldots , k/t\}\), to \(\mathcal {B}_{1}\), and \(\mathcal {A}_{4}\) sends across \(\tilde{R}_{i}\), for all \(i \in [k/t] \backslash \{j\}\), and the descriptions of the functions \(f''_{i}\), for all \(i \in \{j + 1, \ldots , k/t\}\), to \(\mathcal {B}_{1}\), and \(\tilde{R}_{j}\) to \(\mathcal {B}_{2}\).
\(\mathcal {B}_{1}\) then computes \(r''_{i} \Vert \textsf {s}'_{i} = \textsf {Dec}_{\textsf {NM}}'\left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for \(i \in [j - 1]\); if \(r''_{i} \Vert \textsf {s}'_{i} = r_{i} \Vert \textsf {s}_{i}\), it renames the output \(r''_{i} \Vert \textsf {s}'_{i}\) as  . \(\mathcal {B}_{1}\) then simulates \(\mathcal {S}'^{f_{1}\left( \cdot \right) , f_{2}\left( \cdot \right) }\) with \(\tilde{c} = \left( \tilde{L}_{0}, \tilde{R}_{0}\right) \) and \(\mathcal {S}''^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) with \(\tilde{e}_{i} = \left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for each \(i \in \{j + 1, \ldots , k/t\}\), to obtain \(r' = r_{1}' \Vert \ldots \Vert r_{k/t}'\), where
. \(\mathcal {B}_{1}\) then simulates \(\mathcal {S}'^{f_{1}\left( \cdot \right) , f_{2}\left( \cdot \right) }\) with \(\tilde{c} = \left( \tilde{L}_{0}, \tilde{R}_{0}\right) \) and \(\mathcal {S}''^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) with \(\tilde{e}_{i} = \left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for each \(i \in \{j + 1, \ldots , k/t\}\), to obtain \(r' = r_{1}' \Vert \ldots \Vert r_{k/t}'\), where  and
and  for each \(i \in \{j + 1, \ldots , k/t\}\). \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) then send across \(\tilde{L}_{j}\) and \(\tilde{R}_{j}\) respectively to \(\mathcal {C}\). \(\mathcal {C}\) then responds back with
for each \(i \in \{j + 1, \ldots , k/t\}\). \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) then send across \(\tilde{L}_{j}\) and \(\tilde{R}_{j}\) respectively to \(\mathcal {C}\). \(\mathcal {C}\) then responds back with  to \(\mathcal {B}_{1}\), by either running the real decode algorithm or by simulation (in coherence with the way it generated the codeword to begin with).
to \(\mathcal {B}_{1}\), by either running the real decode algorithm or by simulation (in coherence with the way it generated the codeword to begin with).
\(\mathcal {B}_{1}\) then defines variables \(\mathcal {I}\) and \(s^{*}\), and sets \(\mathcal {I} = \emptyset \).
-
1.
If \(r' =\ \perp \), then it sets \(\mathcal {I} = [k]\) and \(s^{*}_{i} =\ \perp \) for all \(i \in [k]\).
-
2.
If
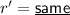 , then, for each \(i \in [k]\), it checks if
, then, for each \(i \in [k]\), it checks if 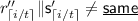 . If so, it sets \(\mathcal {I} = \mathcal {I} \cup \{\beta : \left( i - 1\right) t + 1 \le \beta \le it\}\) and \(s^{*}_{\beta } =\ \perp \) for all \(\beta \) such that \(\left( i - 1\right) t + 1 \le \beta \le it\).
. If so, it sets \(\mathcal {I} = \mathcal {I} \cup \{\beta : \left( i - 1\right) t + 1 \le \beta \le it\}\) and \(s^{*}_{\beta } =\ \perp \) for all \(\beta \) such that \(\left( i - 1\right) t + 1 \le \beta \le it\). -
3.
Otherwise, if
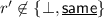 , it sets \(\mathcal {I} = [k]\). Let \(s' = \textsf {s}_{1}' \Vert \ldots \Vert \textsf {s}_{k/t}'\). For each \(i \in [k]\),
, it sets \(\mathcal {I} = [k]\). Let \(s' = \textsf {s}_{1}' \Vert \ldots \Vert \textsf {s}_{k/t}'\). For each \(i \in [k]\),-
(a)
If \(r_{\lceil i/t \rceil }'' \Vert \textsf {s}_{\lceil i/t \rceil }' =\ \perp \) or
 , then it sets \(s^{*}_{i} =\ \perp \).
, then it sets \(s^{*}_{i} =\ \perp \). -
(b)
Otherwise, it checks if \(r'_{\lceil i/t \rceil } = r''_{\lceil i/t \rceil }\). If so, it sets \(s^{*}_{i} = s'_{i}\), otherwise it sets \(s^{*}_{i} =\ \perp \).
-
(a)
Finally, \(\mathcal {B}_{1}\) defines \(\tilde{s}\) as follows. If \(\mathcal {I} = [k]\), then it sets \(\tilde{s} = s^{*}\). Otherwise, it sets \(\tilde{s}\vert _{\mathcal {I}} =\ \perp \) and \(\tilde{s}\vert _{\overline{\mathcal {I}}} = s\vert _{\overline{\mathcal {I}}}\), where \(\overline{\mathcal {I}}\) denotes the complement of the set \(\mathcal {I}\). Then, \(\mathcal {B}_{1}\) sends across \(\tilde{s}\) to \(\mathcal {A}\). \(\mathcal {A}\) then replies back with a bit b to \(\mathcal {B}_{1}\), where \(b = 0\) denotes that the experiment run was \(\mathbf{Ideal }_{\mathcal {S}_{j}, s}\), and \(b = 1\) denotes that the experiment run was \(\mathbf{Ideal }_{\mathcal {S}_{j - 1}, s}\), which \(\mathcal {B}_{1}\) forwards to \(\mathcal {C}\).
Note that if the challenger \(\mathcal {C}\) sent across a simulated codeword for \(e_{j}\), then the experiment is identical to \(\mathbf{Ideal }_{\mathcal {S}_{j - 1}, s}\), while if \(\mathcal {C}\) sent across a real codeword for the message \(r_{j} \Vert \textsf {s}_{j}\) for \(e_{j}\), then the experiment is identical to \(\mathbf{Ideal }_{\mathcal {S}_{j}, s}\). Hence, since \(\mathcal {A}\) is able to distinguish between the outputs of the two experiments with advantage \(\alpha \), so can \(\mathcal {B}\) between the outputs of the experiments \(\mathbf{Tamper }_{r_{j} \Vert \textsf {s}_{j}}^{\left( f_{j}', f_{j}''\right) }\) and \(\mathbf{Ideal }_{\mathcal {S}'', r_{j} \Vert \textsf {s}_{j}}\) as defined in Definition 3, where \(f'_{j} = f_{3}\left( L_{1}, \ldots , L_{j - 1}, \cdot , L_{j + 1}, \ldots , L_{k/t}\right) \) and \(f''_{j} = f_{4}\left( R_{1}, \ldots , R_{j - 1}, \cdot , R_{j + 1}, \ldots , R_{k/t}\right) \). Since \(\mathcal {B}\) is a valid split-state adversary for the scheme \(\textsf {NMC}'\), as mentioned before, \(\alpha \le \epsilon \), which completes the proof. \(\square \)
We define \(\mathbf{Ideal }_{\mathcal {S}^{\dag }, s}\), which is the same as \(\mathbf{Ideal }_{\mathcal {S}_{k/t}, s}\) except that the first two components of the codeword are generated using an actual encoding (i.e., \(\textsf {Enc}_{\textsf {NM}}\left( r_{1} \Vert \ldots \Vert r_{k/t}\right) \)) and the decoding is done using the real decoding algorithm; i.e., \(r' = \textsf {Dec}_{\textsf {NM}}\left( \left( f_{1}, f_{2}\right) \left( \textsf {Enc}_{\textsf {NM}}\left( r_{1} \Vert \ldots \Vert r_{k/t}\right) \right) \right) \). If \(r' = r_{1} \Vert \ldots \Vert r_{k/t}\), it outputs  .
.
Lemma 2
\(\mathbf{Ideal }_{\mathcal {S}_{k/t}, s} \approx _{\epsilon } \mathbf{Ideal }_{\mathcal {S}^{\dag }, s}\).
Proof
Let \(\mathcal {A} = \left( \mathcal {A}_{1}, \mathcal {A}_{2}, \mathcal {A}_{3}, \mathcal {A}_{4}\right) \) be a four-state adversary who can distinguish between the outputs of the experiments \(\mathbf{Ideal }_{\mathcal {S}_{k/t}, s}\) and \(\mathbf{Ideal }_{\mathcal {S}^{\dag }, s}\) with an advantage of \(\alpha \). We describe a split-state adversary \(\mathcal {B} = \left( \mathcal {B}_{1}, \mathcal {B}_{2}\right) \) (where \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) do not communicate with each other) who can break the non-malleability of the the scheme \(\textsf {NMC}\) with the same advantage \(\alpha \). However, since \(\textsf {NMC}\) is non-malleable against split-state adversaries with exact security \(\epsilon \), \(\alpha \le \epsilon \), which completes the proof.
Let \(\mathcal {C}\) be the challenger for the scheme \(\textsf {NMC}\). \(\mathcal {B}\), using \(\mathcal {A}\), executes as follows. First, \(\mathcal {A}\) chooses a message \(s \in \{0, 1\}^{k}\) on which he will distinguish between the outputs of the experiments \(\mathbf{Ideal }_{\mathcal {S}_{k/t}, s}\) and \(\mathbf{Ideal }_{\mathcal {S}^{\dag }, s}\), and sends it to \(\mathcal {B}_{1}\), which then splits s into k / t blocks, say \(\textsf {s}_{1}, \ldots , \textsf {s}_{k/t}\) of size t each. \(\mathcal {B}_{1}\) randomly chooses \(r_{i} \in \{0, 1\}^{\lambda }\), where \(\lambda \) is the security parameter, for all \(i \in [k/t]\). It then generates \(e_{i} = \textsf {Enc}_{\textsf {NM}}'\left( r_{i} \Vert \textsf {s}_{i}\right) \) for \(i \in [k/t]\). \(\mathcal {B}_{1}\) then sends the message \(r_{1} \Vert \ldots \Vert r_{k/t}\) to the challenger \(\mathcal {C}\).
\(\mathcal {C}\) then either computes \(c = \textsf {Enc}_{\textsf {NM}}\left( r_{1} \Vert \ldots \Vert r_{k/t}\right) \), or uses the simulator \(\mathcal {S}'\) to obtain a simulated codeword c, where \(\mathcal {S}'\) is the simulator for the non-malleable code NMC. It then splits c into two parts \(L_{0}\), \(R_{0}\) and sends \(L_{0}\) to \(\mathcal {B}_{1}\) and \(R_{0}\) to \(\mathcal {B}_{2}\) respectively. \(\mathcal {B}_{1}\) splits \(e_{i}\) into two parts, \(L_{i}\) and \(R_{i}\), for each \(i \in [k/t]\). \(\mathcal {B}_{1}\) then sends across \(L_{0}\) to \(\mathcal {A}_{1}\), \(L_{i}\), for all \(i \in [k/t]\), to \(\mathcal {A}_{3}\), and \(R_{i}\), for all \(i \in [k/t]\), to \(\mathcal {A}_{4}\), and \(\mathcal {B}_{2}\) sends across \(R_{0}\) to \(\mathcal {A}_{2}\). \(\mathcal {A}\) then chooses its four-state tampering function \(f = \left( f_{1}, f_{2}, f_{3}, f_{4}\right) \), and computes \(\tilde{L}_{0} = f_{1}\left( L_{0}\right) \), \(\tilde{R}_{0} = f_{2}\left( R_{0}\right) \), \(\tilde{L} = f_{3}\left( L_{1}, \ldots , L_{k/t}\right) \) and \(\tilde{R} = f_{4}\left( R_{1}, \ldots , R_{k/t}\right) \). It then parses \(\tilde{L}\) as \(\tilde{L} = \left( \tilde{L}_{1}, \ldots , \tilde{L}_{k/t}\right) \) and \(\tilde{R}\) as \(\tilde{R} = \left( \tilde{R}_{1}, \ldots , \tilde{R}_{k/t}\right) \). Then, \(\mathcal {A}_{1}\) sends across \(\tilde{L}_{0}\) to \(\mathcal {B}_{1}\), \(\mathcal {A}_{2}\) sends across \(\tilde{R}_{0}\) to \(\mathcal {B}_{2}\), \(\mathcal {A}_{3}\) sends across \(\tilde{L}_{i}\), for all \(i \in [k/t]\), to \(\mathcal {B}_{1}\), and \(\mathcal {A}_{4}\) sends across \(\tilde{R}_{i}\), for all \(i \in [k/t]\), to \(\mathcal {B}_{1}\).
\(\mathcal {B}_{1}\) then computes \(r''_{i} \Vert \textsf {s}'_{i} = \textsf {Dec}_{\textsf {NM}}'\left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for \(i \in [k/t]\); if \(r''_{i} \Vert \textsf {s}'_{i} = r_{i} \Vert \textsf {s}_{i}\), it renames the output \(r''_{i} \Vert \textsf {s}'_{i}\) \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) then send across \(\tilde{L}_{0}\) and \(\tilde{R}_{0}\) respectively to \(\mathcal {C}\). \(\mathcal {C}\) then responds back with  to \(\mathcal {B}_{1}\), by either running the real decode algorithm or by simulation (in coherence with the way it generated the codeword to begin with).
to \(\mathcal {B}_{1}\), by either running the real decode algorithm or by simulation (in coherence with the way it generated the codeword to begin with).
\(\mathcal {B}_{1}\) then defines variables \(\mathcal {I}\) and \(s^{*}\), and sets \(\mathcal {I} = \emptyset \).
-
1.
If \(r' =\ \perp \), then it sets \(\mathcal {I} = [k]\) and \(s^{*}_{i} =\ \perp \) for all \(i \in [k]\).
-
2.
If
 , then, for each \(i \in [k]\), it checks if
, then, for each \(i \in [k]\), it checks if  . If so, it sets \(\mathcal {I} = \mathcal {I} \cup \{\beta : \left( i - 1\right) t + 1 \le \beta \le it\}\) and \(s^{*}_{\beta } =\ \perp \) for all \(\beta \) such that \(\left( i - 1\right) t + 1 \le \beta \le it\).
. If so, it sets \(\mathcal {I} = \mathcal {I} \cup \{\beta : \left( i - 1\right) t + 1 \le \beta \le it\}\) and \(s^{*}_{\beta } =\ \perp \) for all \(\beta \) such that \(\left( i - 1\right) t + 1 \le \beta \le it\). -
3.
Otherwise, if
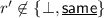 , it sets \(\mathcal {I} = [k]\). Let \(s' = \textsf {s}_{1}' \Vert \ldots \Vert \textsf {s}_{k/t}'\). For each \(i \in [k]\),
, it sets \(\mathcal {I} = [k]\). Let \(s' = \textsf {s}_{1}' \Vert \ldots \Vert \textsf {s}_{k/t}'\). For each \(i \in [k]\),-
(a)
If \(r_{\lceil i/t \rceil }'' \Vert \textsf {s}_{\lceil i/t \rceil }' =\ \perp \) or
 , then it sets \(s^{*}_{i} =\ \perp \).
, then it sets \(s^{*}_{i} =\ \perp \). -
(b)
Otherwise, it checks if \(r'_{\lceil i/t \rceil } = r''_{\lceil i/t \rceil }\). If so, it sets \(s^{*}_{i} = s'_{i}\), otherwise it sets \(s^{*}_{i} =\ \perp \).
-
(a)
Finally, \(\mathcal {B}_{1}\) defines \(\tilde{s}\) as follows. If \(\mathcal {I} = [k]\), then it sets \(\tilde{s} = s^{*}\). Otherwise, it sets \(\tilde{s}\vert _{\mathcal {I}} =\ \perp \) and \(\tilde{s}\vert _{\overline{\mathcal {I}}} = s\vert _{\overline{\mathcal {I}}}\), where \(\overline{\mathcal {I}}\) denotes the complement of the set \(\mathcal {I}\). Then, \(\mathcal {B}_{1}\) sends across \(\tilde{s}\) to \(\mathcal {A}\). \(\mathcal {A}\) then replies back with a bit b to \(\mathcal {B}_{1}\), where \(b = 0\) denotes that the experiment run was \(\mathbf{Ideal }_{\mathcal {S}^{\dag }, s}\), and \(b = 1\) denotes that the experiment run was \(\mathbf{Ideal }_{\mathcal {S}_{k/t}, s}\), which \(\mathcal {B}_{1}\) forwards to \(\mathcal {C}\).
Note that if the challenger \(\mathcal {C}\) sent across a simulated codeword for c, then the experiment is identical to \(\mathbf{Ideal }_{\mathcal {S}_{k/t}, s}\), while if \(\mathcal {C}\) sent across a real codeword for the message \(r_{1} \Vert \ldots \Vert r_{k/t}\) for c, then the experiment is identical to \(\mathbf{Ideal }_{\mathcal {S}^{\dag }, s}\). Hence, since \(\mathcal {A}\) is able to distinguish between the outputs of the two experiments with advantage \(\alpha \), so can \(\mathcal {B}\) between the outputs of the experiments \(\mathbf{Tamper }_{r_{1} \Vert \ldots \Vert r_{k/t}}^{\left( f_{1}, f_{2}\right) }\) and \(\mathbf{Ideal }_{\mathcal {S}', r_{1} \Vert \ldots \Vert r_{k/t}}\) as defined in Definition 3. Since \(\mathcal {B}\) is a valid split-state adversary for the scheme \(\textsf {NMC}\), as mentioned before, \(\alpha \le \epsilon \), which completes the proof. \(\square \)
Lemma 3
\(\mathbf{Ideal }_{\mathcal {S}^{\dag }, s} \approx _{k\left( \epsilon + 2^{-\lambda }\right) /t} \mathbf{Tamper }^{f}_{s}\).
Proof
The only difference between the two experiments is step 4 of the simulator, which is the decoding step. In particular, differences only lie in steps 4(b) and 4(c)i where  .
.
In step 4(b),  while
while  . By the non-malleability of \(\textsf {NMC}'\), \(r''_{i} \Vert \textsf {s}'_{i}\) is independent of \(r_{i} \Vert \textsf {s}_{i}\), in particular, \(r''_{i}\) is independent of \(r_{i}\). Further, the split state adversaries see nothing else which has information about \(r_{i}\) (since the \(r_{i}\)’s are all random). Hence, the probability that \(r''_{i} = r_{i}\) is atmost \(2^{-\lambda }\), and with probability \(1 - 2^{-\lambda }\), even the real decoding algorithm outputs \(\perp \). Hence, for each \(i \in [k/t]\), the output distributions of the two experiments differ only by \(\epsilon + 2^{-\lambda }\).
. By the non-malleability of \(\textsf {NMC}'\), \(r''_{i} \Vert \textsf {s}'_{i}\) is independent of \(r_{i} \Vert \textsf {s}_{i}\), in particular, \(r''_{i}\) is independent of \(r_{i}\). Further, the split state adversaries see nothing else which has information about \(r_{i}\) (since the \(r_{i}\)’s are all random). Hence, the probability that \(r''_{i} = r_{i}\) is atmost \(2^{-\lambda }\), and with probability \(1 - 2^{-\lambda }\), even the real decoding algorithm outputs \(\perp \). Hence, for each \(i \in [k/t]\), the output distributions of the two experiments differ only by \(\epsilon + 2^{-\lambda }\).
In step 4(c)i. when  ,
,  . By the non-malleability of NMC, \(r'_{i}\) is independent of \(r_{i}\) and the split state adversaries see nothing else which has information about \(r_{i}\) (since the r’s are all different and random). Hence, the probability that \(r''_{i} = r'_{i}\) is atmost \(2^{-\lambda }\), and with probability \(1 - 2^{-\lambda }\), even the real decoding algorithm outputs \(\perp \). Hence, for each \(i \in [k/t]\), the output distributions of the two experiments differ only by \(\epsilon + 2^{-\lambda }\). \(\square \)
. By the non-malleability of NMC, \(r'_{i}\) is independent of \(r_{i}\) and the split state adversaries see nothing else which has information about \(r_{i}\) (since the r’s are all different and random). Hence, the probability that \(r''_{i} = r'_{i}\) is atmost \(2^{-\lambda }\), and with probability \(1 - 2^{-\lambda }\), even the real decoding algorithm outputs \(\perp \). Hence, for each \(i \in [k/t]\), the output distributions of the two experiments differ only by \(\epsilon + 2^{-\lambda }\). \(\square \)
Combining all the hybrids, we see that \(\mathbf{Tamper }_{s}^{f} \approx _{\epsilon '} \mathbf{Ideal }_{\mathcal {S}, s}\) for \(\epsilon ' = \mathcal {O}\left( k\left( \epsilon + 2^{-\lambda }\right) /t\right) \). This completes the proof of non-malleability of the scheme. \(\square \)
Corollary 1
For all k, there exists an explicit construction of a \(\big (\widetilde{\mathcal {O}}\big (\sqrt{k}\big ), 0,\) \(\nu \big (\lambda \big )\big )\)-locally decodable non-malleable coding scheme over k-bit messages with constant rate (for some negligible function \(\nu \left( \cdot \right) \)) which is non-malleable against four-state adversaries.
Proof
This follows by choosing \(t = \sqrt{k}\) and using constant-rate non-malleable codes non-malleable against split state adversaries (from [1]) in Theorem 2. \(\square \)
4 Non-malleable Codes with \(\mathcal {O}(\lambda )\) Locality Against \(\mathcal {F}_{\textsf {half}}\)
We now present our construction of LDNMC with \(\mathcal {O}(\lambda )\) locality and against \(\mathcal {F}_{\textsf {half}}\). The key behind this improvement in locality is that we use just one random string r across all encodings instead of multiple r’s as in the previous construction. Somewhat surprisingly, not only are we able to use this idea to build a non-malleable code, we are also able to secure it against a stronger adversarial model, i.e., \(\mathcal {F}_{\textsf {half}}\). Before we present this construction, for ease of exposition, we present a construction that is non-malleable against \(\mathcal {F}_{\textsf {split}}^3\) (and then show how to reduce the number of states to 2). Let \(\textsf {NMC} = \left( \textsf {Enc}_{\textsf {NM}}, \textsf {Dec}_{\textsf {NM}}\right) \) be a non-malleable coding scheme on strings of length \(\log k + \lambda + 1\), where \(\lambda \) is the security parameter. The construction works as follows:
-
1.
\(\textsf {Enc}\left( s\right) \): On input \(s \in \{0, 1\}^{k}\), the algorithm chooses a random string \(r \in \{0, 1\}^{\lambda }\) and computes \(e_{i} = \textsf {Enc}_{\textsf {NM}}\left( i, r \Vert s_{i}\right) \) for \(i \in [k]\). The algorithm finally outputs the codeword \(C = \left( r, e_{1}, \ldots , e_{k}\right) \).
-
2.
\(\textsf {Dec}\left( C, i\right) \): On input \(i \in [k]\), the algorithm reads the first and \(\left( i + 1\right) \)th block of C, retrieving \(r, e_{i}\). Then it computes \(i^{*}, r^{*} \Vert s_{i} = \textsf {Dec}_{\textsf {NM}}\left( e_{i}\right) \). If the decoding algorithm outputs \(\perp \), the algorithm outputs \(\perp \). If \(r^{*} \ne r\) or \(i^{*} \ne i\), the algorithm outputs \(\perp \). Otherwise, the algorithm outputs \(s_{i}\).
In order to prove the security of this construction, we digress and consider a modified construction which ignores r and merely encodes each bit of s along with its index i.e., \(\textsf {Enc}(s) = \{e_{i} = \textsf {Enc}_{\textsf {NM}}\left( i, s_{i}\right) \}_{i \in [k]}\). A quick inspection reveals that this does not satisfy our definition of non-malleability. Indeed, an adversary could replace \(e_{1}\) with an encoding of a bit \(s'_1\) of his choosing and leave all other \(e_i\)s the same. In other words, he can copy some bits of the encoding and replace the rest with encodings of bits chosen independently by him. While this construction is not non-malleable in the standard sense, we can show that the above mauling really is all that the adversary can do.
4.1 Quoted Non-malleability
To formalize this intuition, we introduce a new notion of non-malleability which we call “Quoted Non-malleability.” This definition is similar in spirit to the definition “unquoted” CCA security (UCCA) defined in Myers and Shelat [27].
Definition 7
(Quoted-non-malleability, QNMC). A coding scheme \(\left( \textsf {Enc}, \textsf {Dec}\right) \) with message length k and block length n is said to be quoted-non-malleable with error \(\epsilon \) with respect to a family \(\mathcal {F}\) of tampering functions acting on \(\{0, 1\}^{n}\) if for every \(f \in \mathcal {F}\) there is a simulator \(\mathcal {S}\) such that for all \(s \in \{0, 1\}^{k}\), we have
where \(\mathbf{QTamper }_{s}^{f}\) is the output of the tampering experiment definedFootnote 5 by
and \(\mathbf{QIdeal }_{\mathsf {S}, s}\) is defined by

We now prove that the construction with the randomness r, i.e. \(C = \left( r, \{e_{i} = \textsf {Enc}_{\textsf {NM}}\left( i, r \Vert s_{i}\right) \}_{i \in [k]}\right) \) is quoted non-malleable.
Theorem 3
Assume that NMC is a non-malleable coding scheme of exact security \(\epsilon \), which is non-malleable against split-state adversaries. Then the above coding scheme is a quoted-non-malleable coding scheme with exact security \(k\epsilon \) which is non-malleable against three-state adversaries.
Proof
The underlying non-malleable code \(\textsf {NMC}\) is non-malleable against split-state adversaries and let \(L_{i}, R_{i}\) be the parts of \(e_{i}\) viewed by the two states corresponding to the split-state adversary for \(e_{i}\), for all \(i \in [k]\). The three-state adversaries against which the above scheme is non-malleable consists of adversaries which are arbitrary functions over r, \(L_{1} \Vert \ldots \Vert L_{k}\) and \(R_{1} \Vert \ldots \Vert R_{k}\).
To show the theorem, for any function suitable three-state adversary \(f = \left( f_{1}, f_{2}, f_{3}\right) \) as described above, which we denote as \(f_{1}\left( r\right) \), \(f_{2}\left( L_{1}, \ldots , L_{k}\right) \) and \(f_{3}\left( R_{1}, \ldots , R_{k}\right) \), we need to construct a simulator \(\mathsf {S}\). We describe the simulator with oracle access to f.
-
1.
\(\mathsf {S}^{f\left( \cdot \right) }\) first chooses a random string \(r \in \{0, 1\}^{\lambda }\).
-
2.
Let \(\mathcal {S}'\) be the simulator for the non-malleable code NMC. Now \(\mathcal {S}^{f\left( \cdot \right) }\) simulates \(\mathcal {S}'\) k times to obtain simulated codewords \(e_{i}\) for all \(i \in [k]\). Let \(C = \left( r, e_{1}, \ldots , e_{k}\right) \).
-
3.
Next \(\mathsf {S}^{f\left( \cdot \right) }\) obtains \(r' = f_{1}\left( r\right) \), where \(r' \in \{0, 1\}^{\lambda }\).
-
4.
Let \(L_{i}, R_{i}\) be the parts of \(e_{i}\) viewed by the two states corresponding to the split-state adversary for \(e_{i}\), for all \(i \in [k]\). Let \(f'_{i} = f_{2}\left( L_{1}, \ldots , L_{i - 1}, \cdot , L_{i + 1}, \ldots , L_{k}\right) \) and \(f''_{i} = f_{3}\left( R_{1}, \ldots , R_{i - 1}, \cdot , R_{i + 1}, \ldots , R_{k}\right) \) for all \(i \in [k]\). Now \(\mathsf {S}^{f\left( \cdot \right) }\) simulates \(\mathcal {S'}^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) internally. At some point, \(\mathcal {S}'\) returns an output
 .
. -
5.
For each \(i \in [k]\),
-
(a)
if \(\left( i', r_{i}'' \Vert s_{i}'\right) =\ \perp \), then set \(\overline{s}_{i} =\ \perp \).
-
(b)
if
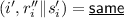 ,
,-
i.
if \(r' \ne r\), then set \(\overline{s}_{i} =\ \perp \).
-
ii.
otherwise, set
 .
.
-
i.
-
(c)
otherwise,
-
i.
if \(r' = r''_{i}\) and \(i' = i\), then set \(\overline{s}_{i} = s'_{i}\).
-
ii.
otherwise, set \(\overline{s}_{i} =\ \perp \).
-
i.
-
(a)
-
6.
Output \(\overline{s}\).
The above simulator defines \(\mathbf{QIdeal }_{\mathsf {S}, s}\). We must now show that \(\mathbf{QTamper }_{s}^{f} \approx _{\epsilon '} \mathbf{QIdeal }_{\mathsf {S}, s}\) for some \(\epsilon '\). We proceed through a series of hybrids of the form \(\mathbf{QIdeal }_{\mathsf {S}_{j}, s}\) for \(j \in [k]\), which is the same as \(\mathbf{QIdeal }_{\mathsf {S}_{j - 1}, s}\) except that it generates \(e_{i} = \textsf {Enc}_{\textsf {NM}}\left( i, r \Vert s_{i}\right) \) for \(i = j\) and it obtains \(\left( i', r''_{i} \Vert s'_{i}\right) = \textsf {Dec}_{\textsf {NM}}\left( g_{i}\left( e_{i}\right) \right) \) for \(i = j\), where \(g_{i} = \left( f'_{i}, f''_{i}\right) \). If \(\left( i', r''_{i} \Vert s'_{i}\right) = \left( i, r \Vert s_{i}\right) \), it outputs  . Note that \(\mathbf{QIdeal }_{\mathsf {S}, s} \equiv \mathbf{QIdeal }_{\mathsf {S}_{0}, s}\) and \(\mathbf{QTamper }_{s}^{f} \equiv \mathbf{Ideal }_{\mathsf {S}_{k}, s}\).
. Note that \(\mathbf{QIdeal }_{\mathsf {S}, s} \equiv \mathbf{QIdeal }_{\mathsf {S}_{0}, s}\) and \(\mathbf{QTamper }_{s}^{f} \equiv \mathbf{Ideal }_{\mathsf {S}_{k}, s}\).
Lemma 4
For all \(j \in [k]\), \(\mathbf{QIdeal }_{\mathsf {S}_{j - 1}, s} \approx _{\epsilon } \mathbf{QIdeal }_{\mathsf {S}_{j}, s}\).
Proof
Let \(\mathcal {A} = \left( \mathcal {A}_{1}, \mathcal {A}_{2}, \mathcal {A}_{3}\right) \) be a three-state adversary who can distinguish between the outputs of the experiments \(\mathbf{QIdeal }_{\mathcal {S}_{j - 1}, s}\) and \(\mathbf{QIdeal }_{\mathcal {S}_{j}, s}\) for some \(j \in [k]\), with an advantage of \(\alpha \). We describe a split-state adversary \(\mathcal {B} = \left( \mathcal {B}_{1}, \mathcal {B}_{2}\right) \) (where \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) do not communicate with each other) who can break the non-malleability of the the scheme \(\textsf {NMC}\) with the same advantage \(\alpha \). However, since \(\textsf {NMC}\) is non-malleable against split-state adversaries with exact security \(\epsilon \), \(\alpha \le \epsilon \), which completes the proof.
Let \(\mathcal {C}\) be the challenger for the scheme \(\textsf {NMC}\). \(\mathcal {B}\), using \(\mathcal {A}\), executes as follows. First, \(\mathcal {A}\) chooses a message \(s \in \{0, 1\}^{k}\) on which he will distinguish between the outputs of the experiments \(\mathbf{QIdeal }_{\mathcal {S}_{j - 1}, s}\) and \(\mathbf{QIdeal }_{\mathcal {S}_{j}, s}\), and sends it to \(\mathcal {B}_{1}\). \(\mathcal {B}_{1}\) randomly chooses \(r \in \{0, 1\}^{\lambda }\), where \(\lambda \) is the security parameter. It then generates \(e_{i} = \textsf {Enc}_{\textsf {NM}}\left( i, r \Vert s_{i}\right) \) for \(i \in [j - 1]\). Let \(\mathcal {S}'\) be the simulator for the non-malleable code \(\textsf {NMC}\) (on all indices but j). Now, \(\mathcal {B}_{1}\) simulates \(\mathcal {S}'\) \(k - j\) times to obtain simulated codewords \(e_{i}\) for all \(i \in \{j + 1, \ldots , k\}\). \(\mathcal {B}_{1}\) then sends the message \(\left( j, r \Vert s_{j}\right) \) to the challenger \(\mathcal {C}\).
\(\mathcal {C}\) then either computes \(e_{j} = \textsf {Enc}_{\textsf {NM}}\left( j, r \Vert s_{j}\right) \), or uses the simulator \(\mathcal {S}'\) to obtain a simulated codeword \(e_{j}\). It then splits \(e_{j}\) into two parts \(L_{j}\), \(R_{j}\) and sends \(L_{j}\) to \(\mathcal {B}_{1}\) and \(R_{j}\) to \(\mathcal {B}_{2}\) respectively. \(\mathcal {B}_{1}\) splits \(e_{i}\) into two parts, \(L_{i}\) and \(R_{i}\), for each \(i \in [k] \backslash \{j\}\). \(\mathcal {B}_{1}\) then sends across r to \(\mathcal {A}_{1}\), \(L_{i}\), for all \(i \in [k]\), to \(\mathcal {A}_{2}\), and \(R_{i}\), for all \(i \in [k] \backslash \{j\}\), to \(\mathcal {A}_{3}\), and \(\mathcal {B}_{2}\) sends across \(R_{j}\) to \(\mathcal {A}_{3}\). \(\mathcal {A}\) then chooses its three-state tampering function \(f = \left( f_{1}, f_{2}, f_{3}\right) \), and computes \(\tilde{r} = f_{1}\left( r\right) \), \(\tilde{L} = f_{2}\left( L_{1}, \ldots , L_{k}\right) \) and \(\tilde{R} = f_{3}\left( R_{1}, \ldots , R_{k}\right) \). It then parses \(\tilde{L}\) as \(\tilde{L} = \left( \tilde{L}_{1}, \ldots , \tilde{L}_{k}\right) \) and \(\tilde{R}\) as \(\tilde{R} = \left( \tilde{R}_{1}, \ldots , \tilde{R}_{k}\right) \). \(\mathcal {A}_{2}\) and \(\mathcal {A}_{3}\) also determine the descriptions of the functions \(f'_{i} = f_{2}\left( L_{1}, \ldots , L_{i - 1}, \cdot , L_{i + 1}, \ldots , L_{k}\right) \) and \(f''_{i} = f_{3}\left( R_{1}, \ldots , R_{i - 1}, \cdot , R_{i + 1}, \ldots , R_{k}\right) \), respectively, for all \(i \in \{j + 1, \ldots , k\}\). Then, \(\mathcal {A}_{1}\) sends across \(\tilde{r}\) to \(\mathcal {B}_{1}\), \(\mathcal {A}_{2}\) sends across \(\tilde{L}_{i}\), for all \(i \in [k]\), and the descriptions of the functions \(f'_{i}\), for all \(i \in \{j + 1, \ldots , k\}\), to \(\mathcal {B}_{1}\), and \(\mathcal {A}_{3}\) sends across \(\tilde{R}_{i}\), for all \(i \in [k] \backslash \{j\}\), and the descriptions of the functions \(f''_{i}\), for all \(i \in \{j + 1, \ldots , k\}\), to \(\mathcal {B}_{1}\), and \(\tilde{R}_{j}\) to \(\mathcal {B}_{2}\).
\(\mathcal {B}_{1}\) then computes \(\left( i', r''_{i} \Vert s'_{i}\right) = \textsf {Dec}_{\textsf {NM}}\left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for \(i \in [j - 1]\); if \(\left( i', r''_{i} \Vert s'_{i}\right) = \left( i, r \Vert s_{i}\right) \), it renames the output \(\left( i', r''_{i} \Vert s'_{i}\right) \) as  . \(\mathcal {B}_{1}\) then simulates \(\mathcal {S}'^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) with \(\tilde{e}_{i} = \left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for each \(i \in \{j + 1, \ldots , k\}\), to obtain
. \(\mathcal {B}_{1}\) then simulates \(\mathcal {S}'^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) with \(\tilde{e}_{i} = \left( \tilde{L}_{i}, \tilde{R}_{i}\right) \) for each \(i \in \{j + 1, \ldots , k\}\), to obtain  for each \(i \in \{j + 1, \ldots , k\}\). \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) then send across \(\tilde{L}_{j}\) and \(\tilde{R}_{j}\) respectively to \(\mathcal {C}\). \(\mathcal {C}\) then responds back with
for each \(i \in \{j + 1, \ldots , k\}\). \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\) then send across \(\tilde{L}_{j}\) and \(\tilde{R}_{j}\) respectively to \(\mathcal {C}\). \(\mathcal {C}\) then responds back with  to \(\mathcal {B}_{1}\), by either running the real decode algorithm or by simulation (in coherence with the way it generated the codeword to begin with).
to \(\mathcal {B}_{1}\), by either running the real decode algorithm or by simulation (in coherence with the way it generated the codeword to begin with).
\(\mathcal {B}_{1}\) then defines the variable \(\overline{s}\). For each \(i \in [k]\),
-
1.
if \(\left( i', r_{i}'' \Vert s_{i}'\right) =\ \perp \), then it sets \(\overline{s}_{i} =\ \perp \).
-
2.
if
 ,
,-
(a)
if \(\tilde{r} \ne r\), then it sets \(\overline{s}_{i} =\ \perp \).
-
(b)
otherwise, it sets
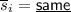 .
.
-
(a)
-
3.
otherwise,
-
(a)
if \(\tilde{r} = r''_{i}\) and \(i' = i\), then it sets \(\overline{s}_{i} = s'_{i}\).
-
(b)
otherwise, it sets \(\overline{s}_{i} =\ \perp \).
-
(a)
Finally, \(\mathcal {B}_{1}\) defines \(\tilde{s}\) as follows. For each \(i \in [k]\), if  , set \(\tilde{s}_{i} = s_{i}\), otherwise set \(\tilde{s}_{i} = \overline{s}_{i}\). Then, \(\mathcal {B}_{1}\) sends across \(\tilde{s}\) to \(\mathcal {A}\). \(\mathcal {A}\) then replies back with a bit b to \(\mathcal {B}_{1}\), where \(b = 0\) denotes that the experiment run was \(\mathbf{QIdeal }_{\mathcal {S}_{j}, s}\), and \(b = 1\) denotes that the experiment run was \(\mathbf{QIdeal }_{\mathcal {S}_{j - 1}, s}\), which \(\mathcal {B}_{1}\) forwards to \(\mathcal {C}\).
, set \(\tilde{s}_{i} = s_{i}\), otherwise set \(\tilde{s}_{i} = \overline{s}_{i}\). Then, \(\mathcal {B}_{1}\) sends across \(\tilde{s}\) to \(\mathcal {A}\). \(\mathcal {A}\) then replies back with a bit b to \(\mathcal {B}_{1}\), where \(b = 0\) denotes that the experiment run was \(\mathbf{QIdeal }_{\mathcal {S}_{j}, s}\), and \(b = 1\) denotes that the experiment run was \(\mathbf{QIdeal }_{\mathcal {S}_{j - 1}, s}\), which \(\mathcal {B}_{1}\) forwards to \(\mathcal {C}\).
Note that if the challenger \(\mathcal {C}\) sent across a simulated codeword for \(e_{j}\), then the experiment is identical to \(\mathbf{QIdeal }_{\mathcal {S}_{j - 1}, s}\), while if \(\mathcal {C}\) sent across a real codeword for the message \(\left( j, r \Vert s_{j}\right) \) for \(e_{j}\), then the experiment is identical to \(\mathbf{QIdeal }_{\mathcal {S}_{j}, s}\). Hence, since \(\mathcal {A}\) is able to distinguish between the outputs of the two experiments with advantage \(\alpha \), so can \(\mathcal {B}\) between the outputs of the experiments \(\mathbf{Tamper }_{\left( j, r \Vert s_{j}\right) }^{\left( f_{j}', f_{j}''\right) }\) and \(\mathbf{Ideal }_{\mathcal {S}', \left( j, r \Vert s_{j}\right) }\) as defined in Definition 3, where \(f'_{j} = f_{2}\left( L_{1}, \ldots , L_{j - 1}, \cdot , L_{j + 1}, \ldots , L_{k}\right) \) and \(f''_{j} = f_{3}\left( R_{1}, \ldots , R_{j - 1}, \cdot , R_{j + 1}, \ldots , R_{k}\right) \). Since \(\mathcal {B}\) is a valid split-state adversary for the scheme \(\textsf {NMC}\), as mentioned before, \(\alpha \le \epsilon \), which completes the proof. \(\square \)
Combining all the hybrids, we see that \(\mathbf{QTamper }_{s}^{f} \approx _{\epsilon '} \mathbf{QIdeal }_{\mathsf {S}, s}\) for \(\epsilon ' = k\epsilon \). This completes the proof of quoted-non-malleability of the scheme. \(\square \)
4.2 Achieving Full Non-malleability
Recall that our ultimate goal is to construct a coding scheme which is non-malleable against split-state adversaries. As the theorem below states, we can show that the quoted non-malleable construction from the previous subsection is itself fully non-malleable. As a careful reader may have observed, the proof of quoted non-malleability does not use the randomness of r at all. Indeed, the construction, as we alluded to earlier, is quoted non-malleable even without using r in the encoding. Yet this randomness is precisely what makes the construction (fully) non-malleable. We first show how the construction from Sect. 4 is non-malleable against 3-state adversaries and then show how to modify the construction to achieve security against \(\mathcal {F}_{\textsf {half}}\).
Theorem 4
Assume that NMC is a non-malleable coding scheme of rate \(1/\gamma \) and exact security \(\epsilon \), which is non-malleable against split-state adversaries. Then the coding scheme from Sect. 4 is a \(\left( \lambda + \left( \lambda + \log k + 1\right) \gamma , 0, k\left( \epsilon + 2^{-\lambda }\right) \right) \)-locally decodable non-malleable coding scheme which is non-malleable against three-state adversaries. The rate of the code is \(1/\gamma '\), where \(\gamma ' = \lambda /k + \left( \lambda + \log k + 1\right) \gamma \).
Proof
Clearly the decoding algorithm reads \(\lambda + \left( \lambda + \log k + 1\right) \gamma \) positions of the codeword since \(|r| = \lambda \) and \(|e_{i}| = \left( \lambda + \log k + 1\right) \gamma \). Also, since the decoding algorithm is deterministic, the error probability in the local decoding procedure is 0. This justifies the first two parameters of the coding scheme.
The underlying non-malleable code \(\textsf {NMC}\) is non-malleable against split-state adversaries and let \(L_{i}, R_{i}\) be the parts of \(e_{i}\) viewed by the two states corresponding to the split-state adversary for \(e_{i}\), for all \(i \in [k]\). The three-state adversaries against which the above scheme is non-malleable consists of adversaries which are arbitrary functions over r, \(L_{1} \Vert \ldots \Vert L_{k}\) and \(R_{1} \Vert \ldots \Vert R_{k}\).
To show the theorem, for any function suitable three-state adversary \(f = \left( f_{1}, f_{2}, f_{3}\right) \) as described above, which we denote as \(f_{1}\left( r\right) \), \(f_{2}\left( L_{1}, \ldots , L_{k}\right) \) and \(f_{3}\left( R_{1}, \ldots , R_{k}\right) \), we need to construct a simulator \(\mathcal {S}\). We describe the simulator with oracle access to f.
-
1.
\(\mathsf {S}^{f\left( \cdot \right) }\) first chooses a random string \(r \in \{0, 1\}^{\lambda }\).
-
2.
Let \(\mathcal {S}'\) be the simulator for the non-malleable code NMC. Now \(\mathcal {S}^{f\left( \cdot \right) }\) simulates \(\mathcal {S}'\) k times to obtain simulated codewords \(e_{i}\) for all \(i \in [k]\). Note that the simulator described for the code instantiated from Lemma 1 does not need oracle access to the tampering function to produce simulated codewords assuming a super-polynomial message space, which is the case since the messages are of length \(\log k + \lambda + 1\). Let \(C = \left( r, e_{1}, \ldots , e_{k}\right) \).
-
3.
Next \(\mathsf {S}^{f\left( \cdot \right) }\) obtains \(r' = f_{1}\left( r\right) \), where \(r' \in \{0, 1\}^{\lambda }\).
-
4.
Let \(L_{i}, R_{i}\) be the parts of \(e_{i}\) viewed by the two states corresponding to the split-state adversary for \(e_{i}\), for all \(i \in [k]\). Let \(f'_{i} = f_{2}\left( L_{1}, \ldots , L_{i - 1}, \cdot , L_{i + 1}, \ldots , L_{k}\right) \) and \(f''_{i} = f_{3}\left( R_{1}, \ldots , R_{i - 1}, \cdot , R_{i + 1}, \ldots , R_{k}\right) \) for all \(i \in [k]\). Now \(\mathsf {S}^{f\left( \cdot \right) }\) simulates \(\mathcal {S'}^{f'_{i}\left( \cdot \right) , f''_{i}\left( \cdot \right) }\) internally. At some point, \(\mathcal {S}'\) returns an output
 .
. -
5.
Set \(\mathcal {I} = \emptyset \).
-
(a)
If \(r' = r\), then, for each \(i \in [k]\),
-
i.
if \(\left( i', r_{i}'' \Vert s_{i}'\right) =\ \perp \), then set \(\mathcal {I} = \mathcal {I} \cup \{i\}\) and \(s^{*}_{i} =\ \perp \).
-
ii.
otherwise, if
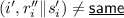 , then set \(\mathcal {I} = \mathcal {I} \cup \{i\}\) and \(s^{*}_{i} =\ \perp \).
, then set \(\mathcal {I} = \mathcal {I} \cup \{i\}\) and \(s^{*}_{i} =\ \perp \).
-
i.
-
(b)
Otherwise, set \(\mathcal {I} = [k]\). For each \(i \in [k]\),
-
i.
if \(\left( i', r_{i}'' \Vert s_{i}'\right) =\ \perp \) or
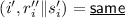 , then set \(s^{*}_{i} =\ \perp \).
, then set \(s^{*}_{i} =\ \perp \). -
ii.
otherwise,
-
A.
if \(r' = r''_{i}\) and \(i' = i\), then set \(s^{*}_{i} = s'_{i}\).
-
B.
otherwise, set \(s^{*}_{i} =\ \perp \).
-
A.
-
i.
-
(a)
-
6.
Output \(\left( \mathcal {I}, s^{*}\right) \).
We first note that for the construction in Sect. 4, \(\mathbf{QTamper }_{s}^{f} \equiv \mathbf{Tamper }_{s}^{f}\), by definition. Hence, we only need to show the indistinguishability of \(\mathbf{QIdeal }_{\mathsf {S}, s}\) and \(\mathbf{Ideal }_{\mathcal {S}, s}\), where \(\mathcal {S}\) is the simulator described above and \(\mathsf {S}\) is the simulator described in the proof of Theorem 3.
Lemma 5
\(\mathbf{QIdeal }_{\mathsf {S}, s} \approx _{2^{-\lambda }k} \mathbf{Ideal }_{\mathcal {S}, s}\).
Proof
The only difference between the two experiments is step 5, which is the decoding step. In particular, differences only lies in step 5(a)ii of the simulator \(\mathcal {S}\).
In step 4(a)ii,  , and note that \(r''_{i}\) is generated by the simulator \(\mathcal {S}'\) without any knowledge of r. Hence, \(r''_{i}\) is independent of r. Hence, the probability that \(r''_{i} = r\) is atmost \(2^{-\lambda }\), and with probability \(1 - 2^{-\lambda }\), even the decoding step in the simulator \(\mathsf {S}\) in the proof of Theorem 3 outputs \(\perp \). Hence, for each \(i \in [k]\), the output distributions of the two experiments differ only by \(2^{-\lambda }\). \(\square \)
, and note that \(r''_{i}\) is generated by the simulator \(\mathcal {S}'\) without any knowledge of r. Hence, \(r''_{i}\) is independent of r. Hence, the probability that \(r''_{i} = r\) is atmost \(2^{-\lambda }\), and with probability \(1 - 2^{-\lambda }\), even the decoding step in the simulator \(\mathsf {S}\) in the proof of Theorem 3 outputs \(\perp \). Hence, for each \(i \in [k]\), the output distributions of the two experiments differ only by \(2^{-\lambda }\). \(\square \)
Combining this hybrid with the proof of Theorem 3, we see that \(\mathbf{Tamper }_{s}^{f} \approx _{\epsilon '} \mathbf{Ideal }_{\mathcal {S}, s}\) for \(\epsilon ' = k\left( \epsilon + 2^{-\lambda }\right) \). This completes the proof of non-malleability of the scheme. \(\square \)
Reducing States to 2. The proof of Theorem 4 crucially relies on the secrecy of r (from the adversaries in states 2 and 3 above). This contributes to making the number of states to be 3. However, secrecy of r can also be preserved by simply secret sharing r into \(r = r_L \oplus r_R\). The final encoding is as follows: \(\textsf {Enc}\left( s\right) = ([r_L,L_1,\cdots ,L_k],[r_R,R_1,\cdots ,R_k])\), where \(r_L \oplus r_R = r\) for a random \(r \in \{0, 1\}^{\lambda }\) and \(e_{i} = \textsf {Enc}_{\textsf {NM}}\left( i, r \Vert s_{i}\right) = (L_i, R_i)\) for \(i \in [k]\). This gives us a construction that is non-malleable against \(\mathcal {F}_{\textsf {half}}\). Additionally, note that it is straight-forward to modify the construction to split s into blocks of size t as opposed to single bits (similar to the construction in Sect. 3) to obtain the following theorem, the proof of which is given in the full version of this paper.
Theorem 5
Assume that NMC is a non-malleable coding scheme of rate \(1/\gamma \) and exact security \(\epsilon \), which is non-malleable against split-state adversaries. Then there is an efficient \(\left( \lambda + \left( \lambda + \log \left( k/t\right) + t\right) \gamma , 0, k\left( \epsilon + 2^{-\lambda }\right) /t\right) \)-locally decodable non-malleable coding scheme which is non-malleable against \(\mathcal {F}_{\textsf {half}}\). The rate of the code is \(1/\gamma '\), where \(\gamma ' = \lambda /k + \left( 1 + \lambda /t + \log \left( k/t\right) /t\right) \gamma \).
Corollary 2
Assuming \(\lambda \ge \log k\), there exists an explicit construction of a \(\left( \mathcal {O}\left( \lambda \right) , 0, \nu \left( \lambda \right) \right) \)-locally decodable non-malleable coding scheme over k-bit messages with constant rate (for some negligible function \(\nu (\cdot )\)) which is non-malleable against \(\mathcal {F}_{\textsf {half}}\).
Proof
This follows by choosing \(t = \lambda \) and using constant-rate non-malleable codes non-malleable against \(\mathcal {F}_{\textsf {half}}\) (from the work of Aggarwal et al. [1]) in Theorem 5. \(\square \)
Corollary 3
There exists an explicit construction of a \(\left( \omega (1), 0, \nu (\lambda )\right) \)-locally decodable non-malleable coding scheme with rate 1 (for a negligible function \(\nu (\cdot )\)) which is non-malleable against the tampering function class \(\mathcal {F}_{\textsf {bit}}\).
Proof
The proof of this corollary follows by instantiating \(\textsf {Enc}_{\textsf {NM}}\) in Theorem 4 with the rate 1 non-malleable coding scheme from [13] that is non-malleable against \(\mathcal {F}_{\textsf {bit}}\) and by splitting the k-bit input message into blocks of size \(\omega (1)\) each and encoding these bits together. \(\square \)
5 Updatability and Security Against Continual Attacks
We now show how to modify the construction from Sect. 3 to get a code that is leakage and tamper-resilient against continual attacks. Note that if codewords are not periodically refreshed, then an adversary that obtains leakage that is unbounded, can, over time, leak one codeword completely and then tamper the codeword based on this codeword. At a high level, to prevent this, we must refresh codewords periodically (even if they are not updated). We do this, by cycling through the codewords that encode all \(s_i\) values one-by-one and “refresh” them. Of course, if the encoder and decoder maintain state, they can perform this refreshing in a cyclic manner. However, in order to perform this refresh in a stateless manner, we maintain a counter that is encoded along with all the \(r_i\) values. This ensures that we refresh all codewords periodically. Additionally, for technical reasons (that we describe later), we refresh codewords everytime we decode a particular index. By lowering the threshold of leakage tolerated in every “round”, we ensure that our construction remains secure. We describe our construction (and the security) in more detail in the full version [9] of this paper.
6 Applications of Local Non-malleable Codes
Similar to the work of Dachman-Soled et al. [16], our locally updatable/decodable leakage-resilient non-malleable codes can be used in the construction of secure RAM computation protocols. At a very high level, if the memory and program code are encoded using a local leakage-resilient non-malleable code (that is resilient to tampering from the family \(\mathcal {F}\) and leakage from the family \(\mathcal {G}\)) and the resulting codeword is then accessed through an oblivious RAM (ORAM) [23, 24, 28, 29] protocol, one can show that the resulting protocol is a protocol for secure RAM computation that is secure against tampering of the memory from the same tampering family \(\mathcal {F}\) and leakage from the same family \(\mathcal {G}\). Now, if we instantiate the non-malleable code with our information-theoretic non-malleable code from Sect. 5, and instantiate the ORAM protocol with an ORAM that has information-theoretic guarantees [6, 14, 17, 31], then one can show that the resulting RAM computation protocol has information-theoretic security. Of course, information-theoretic RAM protocols assume the existence of ideal encryption and our final compiler will make the same assumption. However, if the compiler is applied in the context of information-theoretic secure multi-party computation [7, 11], then one can obtain an information-theoretic secure RAM computation protocol that is resilient to tampering from the class \(\mathcal {F}\) and leakage from the class \(\mathcal {G}\) (by replacing the ideal encryption with secret sharing [30]).
For further details of ORAM compilers, tamper/leakage resilient (information-theoretic) RAM computation, our construction and results, we refer the reader to the full version of this paper.
Notes
- 1.
Of course, in the case of single party RAM computation, our protocol is information-theoretic modulo the encryption that is used in the underlying oblivious RAM (ORAM) protocol; in the case of secure multi-party computation, we obtain a tamper and leakage resilient information-theoretic secure computation protocol.
- 2.
Of course, the adversary can always copy certain ciphertexts and have them decode to \(s_i\) and maul other indices to decode to \(\bot \), but as noted earlier, this is allowed by their definition of non-malleability.
- 3.
One might think that we only require authentication and hence could use a shorter key; however non-malleable codes inherently imply that the underlying message be hidden, thus forcing us to use a key as long as the message.
- 4.
While we define these two parts to be of equal length, as remarked earlier, there is no such requirement.
- 5.
Note that in this definition, we abuse notation mildly by allowing \(\textsf {Dec}\) to take the index i as input, in addition to \(\tilde{C}\). The output of \(\textsf {Dec}(\cdot ,i)\) is in \(\{0,1\}\bigcup {\perp }\). Since the definition of quoted non-malleability makes sense without locality, one can think of \(\textsf {Dec}(\cdot ,\cdot )\) as simply running the actual decode algorithm and simply outputting the \(i^{th}\) bit (or \(\perp \) if the decoding fails).
References
Aggarwal, D., Dodis, Y., Kazana, T., Obremski, M.: Non-malleable reductions and applications. In: Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, Portland, OR, USA, 14–17 June 2015, pp. 459–468 (2015)
Aggarwal, D., Dodis, Y., Lovett, S.: Non-malleable codes from additive combinatorics. In: Symposium on Theory of Computing, STOC 2014, New York, NY, USA, 31 May–03 June 2014, pp. 774–783 (2014)
Aggarwal, D., Dziembowski, S., Kazana, T., Obremski, M.: Leakage-resilient non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 398–426. Springer, Heidelberg (2015)
Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M.: Explicit non-malleable codes against bit-wise tampering and permutations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 538–557. Springer, Heidelberg (2015)
Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M.: A rate-optimizing compiler for non-malleable codes against bit-wise tampering and permutations. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 375–397. Springer, Heidelberg (2015)
Ajtai, M.: Oblivious RAMs without cryptographic assumptions. In: Proceedings of the 42nd ACM Symposium on Theory of Computing, STOC 2010, Cambridge, Massachusetts, USA, 5–8 June 2010, pp. 181–190 (2010)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: Proceedings of the 20th Annual ACM Symposium on Theory of Computing, Chicago, Illinois, USA, 2–4 May 1988, pp. 1–10 (1988)
Chandran, N., Kanukurthi, B., Ostrovsky, R.: Locally updatable and locally decodable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 489–514. Springer, Heidelberg (2014)
Chandran, N., Kanukurthi, B., Raghuraman, S.: Information-theoretic local non-malleable codes and their applications. Cryptology ePrint Archive, Report 2015 (2015). http://eprint.iacr.org/
Chattopadhyay, E., Zuckerman, D.: Non-malleable codes against constant split-state tampering. In: 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, Philadelphia, PA, USA, 18–21 October 2014, pp. 306–315 (2014)
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: Proceedings of the 20th Annual ACM Symposium on Theory of Computing, Chicago, Illinois, USA, 2–4 May 1988, pp. 11–19 (1988)
Cheraghchi, M., Guruswami, V.: Capacity of non-malleable codes. In: Innovations in Theoretical Computer Science, ITCS 2014, Princeton, NJ, USA, 12–14 January 2014, pp. 155–168 (2014)
Cheraghchi, M., Guruswami, V.: Non-malleable coding against bit-wise and split-state tampering. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 440–464. Springer, Heidelberg (2014)
Chung, K.-M., Liu, Z., Pass, R.: Statistically-secure ORAM with \(\tilde{O}(\log ^2 n)\) overhead. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 62–81. Springer, Heidelberg (2014)
Coretti, S., Maurer, U., Tackmann, B., Venturi, D.: From single-bit to multi-bit public-key encryption via non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 532–560. Springer, Heidelberg (2015)
Dachman-Soled, D., Liu, F.-H., Shi, E., Zhou, H.-S.: Locally decodable and updatable non-malleable codes and their applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 427–450. Springer, Heidelberg (2015)
Damgård, I., Meldgaard, S., Nielsen, J.B.: Perfectly secure oblivious RAM without random oracles. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 144–163. Springer, Heidelberg (2011)
Dziembowski, S., Kazana, T., Obremski, M.: Non-malleable codes from two-source extractors. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 239–257. Springer, Heidelberg (2013)
Dziembowski, S., Pietrzak, K., Wichs, D.: Non-malleable codes. In: Innovations in Computer Science, ICS 2010, Tsinghua University, Beijing, China, 5–7 January 2010, pp. 434–452 (2010)
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: Continuous non-malleable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 465–488. Springer, Heidelberg (2014)
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: A tamper and leakage resilient von Neumann architecture. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 579–603. Springer, Heidelberg (2015)
Faust, S., Mukherjee, P., Venturi, D., Wichs, D.: Efficient non-malleable codes and key-derivation for poly-size tampering circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 111–128. Springer, Heidelberg (2014)
Goldreich, O.: Towards a theory of software protection and simulation by oblivious RAMs. In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing, New York, USA, pp. 182–194 (1987)
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious RAMs. J. ACM 43(3), 431–473 (1996)
Katz, J., Trevisan, L.: On the efficiency of local decoding procedures for error-correcting codes. In: Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 21–23 May 2000, pp. 80–86 (2000)
Liu, F.-H., Lysyanskaya, A.: Tamper and leakage resilience in the split-state model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 517–532. Springer, Heidelberg (2012)
Myers, S., Shelat, A.: Bit encryption is complete. In: 50th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2009, Atlanta, Georgia, USA, 25–27 October 2009, pp. 607–616 (2009)
Ostrovsky, R.: An efficient software protection scheme. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 610–611. Springer, Heidelberg (1990)
Ostrovsky, R.: Efficient computation on oblivious RAMs. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, Baltimore, Maryland, USA, 13–17 May 1990, pp. 514–523 (1990)
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Stefanov, E., van Dijk, M., Shi, E., Fletcher, C.W., Ren, L., Yu, X., Devadas, S.: Path ORAM: an extremely simple oblivious RAM protocol. In: 2013 ACM SIGSAC Conference on Computer and Communications Security, CCS 2013, Berlin, Germany, 4–8 November 2013, pp. 299–310 (2013)
Yekhanin, S.: Locally decodable codes. Found. Trends Theoret. Comput. Sci. 6(3), 139–255 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Chandran, N., Kanukurthi, B., Raghuraman, S. (2016). Information-Theoretic Local Non-malleable Codes and Their Applications. In: Kushilevitz, E., Malkin, T. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9563. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49099-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-662-49099-0_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49098-3
Online ISBN: 978-3-662-49099-0
eBook Packages: Computer ScienceComputer Science (R0)



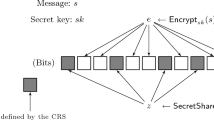

 and
and 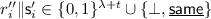 for each
for each  , then, for each
, then, for each  . If so, set
. If so, set  , set
, set 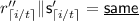 , then set
, then set 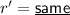 , then, for each
, then, for each 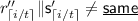 . If so, it sets
. If so, it sets 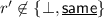 , it sets
, it sets  , then it sets
, then it sets  , then, for each
, then, for each  . If so, it sets
. If so, it sets 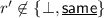 , it sets
, it sets  , then it sets
, then it sets  .
.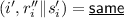 ,
, .
.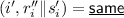 ,
,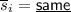 .
. .
.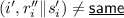 , then set
, then set 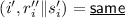 , then set
, then set 