Non-Malleable Encryption: Simpler, Shorter, Stronger

Abstract

In a seminal paper, Dolev et al. [15] introduced the notion of non-malleable encryption (NM-CPA). This notion is very intriguing since it suffices for many applications of chosen-ciphertext secure encryption (IND-CCA), and, yet, can be generically built from semantically secure (IND-CPA) encryption, as was shown in the seminal works by Pass et al. [29] and by Choi et al. [9], the latter of which provided a black-box construction. In this paper we investigate three questions related to NM-CPA security:

• 1. Can the rate of the construction by Choi et al. of NM-CPA from IND-CPA be improved?

• 2. Is it possible to achieve multi-bit NM-CPA security more efficiently from a single-bit NM-CPA scheme than from IND-CPA?

• 3. Is there a notion stronger than NM-CPA that has natural applications and can be achieved from IND-CPA security?

We answer all three questions in the positive. First, we improve the rate in the scheme of Choi et al. by a factor $\mathcal {O}(\lambda )$, where $\lambda$ is the security parameter. Still, encrypting a message of size $\mathcal {O}(\lambda )$ would require ciphertext and keys of size $\mathcal {O}(\lambda ^2)$ times that of the IND-CPA scheme, even in our improved scheme. Therefore, we show a more efficient domain extension technique for building a $\lambda$-bit NM-CPA scheme from a single-bit NM-CPA scheme with keys and ciphertext of size $\mathcal {O}(\lambda )$ times that of the NM-CPA one-bit scheme. To achieve our goal, we define and construct a novel type of continuous non-malleable code (NMC), called secret-state NMC, as we show that standard continuous NMCs are not enough for the natural “encode-then-encrypt-bit-by-bit” approach to work.

Finally, we introduce a new security notion for public-key encryption that we dub non-malleability under (chosen-ciphertext) self-destruct attacks (NM-SDA). After showing that NM-SDA is a strict strengthening of NM-CPA and allows for more applications, we nevertheless show that both of our results—(faster) construction from IND-CPA and domain extension from one-bit scheme—also hold for our stronger NM-SDA security. In particular, the notions of IND-CPA, NM-CPA, and NM-SDA security are all equivalent, lying (plausibly, strictly?) below IND-CCA security.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Several different security notions for public-key encryption (PKE) have been proposed. The most basic one is that of indistinguishability under chosen-plaintext attacks (IND-CPA) [21], which requires that an adversary with no decryption capabilities be unable to distinguish between the encryption of two messages. Although extremely important and useful for a number of applications, in many cases IND-CPA security is not sufficient. For example, consider the simple setting of an electronic auction, where the auctioneer U publishes a public key $\mathsf {pk}$, and invites several participants $P_1,\ldots , P_q$ to encrypt their bids $b_i$ under $\mathsf {pk}$. As was observed in the seminal paper of Dolev et al. [15], although IND-CPA security of encryption ensures that $P_1$ cannot decrypt a bid of $P_2$ under the ciphertext $e_2$, it leaves open the possibility that $P_1$ can construct a special ciphertext $e_1$ which decrypts to a related bid $b_1$ (e.g., $b_1=b_2+1$). Hence, to overcome such “malleability” problems, stronger forms of security are required.

The strongest such level of PKE security is indistinguishability under chosen-ciphertext attacks (IND-CCA), where the adversary is given unrestricted, adaptive access to a decryption oracle (modulo not being able to ask on the “challenge ciphertext”). This notion is sufficient for most natural applications of PKE, and several generic [5, 15, 25, 28, 31] and concrete [13, 14, 22, 24] constructions of IND-CCA secure encryption schemes are known by now. Unfortunately, all these constructions either rely on specific number-theoretic assumptions, or use much more advanced machinery (such as non-interactive zero-knowledge proofs or identity-based encryption) than IND-CPA secure encryption. Indeed, despite numerous efforts (e.g., a partial negative result [20]), the relationship between IND-CPA and IND-CCA security remains unresolved until now. This motivates the study of various “middle-ground” security notions between IND-CPA and IND-CCA, which are sufficient for applications, and, yet, might be constructed from simpler basic primitives (e.g., any IND-CPA encryption).

One such influential notion is non-malleability under chosen-plaintext attacks (NM-CPA), originally introduced by Dolev et al. [15] with the goal of precisely addressing the auction example above, by demanding that an adversary not be able to maul ciphertexts to other ciphertexts encrypting related plaintexts. As was later shown by Bellare and Sahai [4] and by Pass et al. [30], NM-CPA is equivalent to security against adversaries with access to a non-adaptive decryption oracle, meaning that the adversary can only ask one “parallel” decryption query. Although NM-CPA appears much closer to IND-CCA than IND-CPA security, a seminal result by Pass et al. [29] showed that one can generically build NM-CPA encryption from any IND-CPA-secure scheme, and Choi et al. [9] later proved that this transformation can also be achieved via a black-box construction. Thus, NM-CPA schemes can be potentially based on weaker assumptions than IND-CCA schemes, and yet suffice for important applications.

Our Work. We investigate three questions related to NM-CPA security:

• 1. Can the efficiency of the construction by Choi et al. of NM-CPA from IND-CPA be improved?

• 2. Is it possible to achieve multi-bit NM-CPA security more efficiently from a single-bit NM-CPA scheme than from IND-CPA?

• 3. Is there a notion stronger than NM-CPA that has natural applications and can be achieved from IND-CPA security?

We answer all three questions positively. We start with Question 3, as it will also allow us to achieve stronger answers for Questions 1 and 2. In a recent paper, Coretti et al. [10] introduced a new middle-ground security notion for encryption—termed indistinguishability under (chosen-ciphertext) self-destruct attacks (IND-SDA) in this paper¹—where the adversary gets access to an adaptive decryption oracle, which, however, stops decrypting after the first invalid ciphertext is submitted. Applying this notion to the auction example above, it means that the auctioneer can reuse the secret key for subsequent auctions, as long as all the encrypted bids are valid. Unfortunately, if an invalid ciphertext is submitted, even the results of the current auction should be discarded, as IND-SDA security is not powerful enough to argue that the decryptions of the remaining ciphertexts are unrelated w.r.t. prior plaintexts.

Motivated by the above, we introduce a new security notion that we dub non-malleability under (chosen-ciphertext) self-destruct attacks (NM-SDA). This notion (see Definition 3) naturally combines NM-CPA and IND-SDA, by allowing the adversary to ask many adaptive “parallel” decryption queries (i.e., a query consists of many ciphertexts) up to the point when the first invalid ciphertext is submitted. In such a case, the whole parallel decryption query containing an invalid ciphertext is still answered in full, but no future decryption queries are allowed. By being stronger (as we show below) than both NM-CPA and IND-SDA, NM-SDA security appears to be a strongest natural PKE security notion that is still weaker (as we give evidence below) than IND-CCA—together with q-bounded CCA-secure PKE [12], to which it seems incomparable. In particular, it seems to apply better to the auction example above: First, unlike with basic NM-CPA, the auctioneer can reuse the same public key $\mathsf {pk}$, provided no invalid ciphertexts were submitted. Second, unlike IND-SDA, the current auction can be safely completed, even if some ciphertexts are invalid. Compared to IND-CCA, however, the auctioneer will still have to change its public key for subsequent auctions if some of the ciphertexts are invalid. Still, one can envision situations where parties are penalized for submitting such malformed ciphertexts, in which case NM-SDA security might be practically sufficient, leading to an implementation under (potentially) lesser computational assumptions as compared to using a full-blown IND-CCA PKE.

Having introduced and motivated NM-SDA security, we provide a comprehensive study of this notion, and its relationship to other PKE security notions. The prior notions of NM-CPA and IND-SDA are incomparable, meaning that there are (albeit contrived) schemes that satisfy the former but not the latter notion and vice versa. This is shown in the full version of this work and implies that NM-SDA security is strictly stronger than either of the two other notions.

We turn to Question 2 above and answer it affirmatively even for our stronger notion of NM-SDA security; indeed, our security proof is easily seen to carry over to the simpler case of NM-CPA security. Finally, we also simultaneously answer Questions 1 and 3, by presenting a generalization of the Choi et al. [9] construction from IND-CPA encryption which: (a) allows us to improve the plaintext-length to ciphertext-length rate by a factor linear in the security parameter as compared to the construction of [9] (which is a special case of our abstraction, but with sub-optimal parameters); (b) generically achieves NM-SDA security (with or without the efficiency improvement). We detail these results below.

Domain Extension. For several security notions in public-key cryptography, is is known that single-bit public-key encryption implies multi-bit public-key encryption. For IND-CPA, this question is simple [21], since the parallel repetition of a single-bit scheme (i.e., encrypting every bit of a message separately) yields an IND-CPA secure multi-bit scheme. For the other notions considered in this paper, i.e., for NM-CPA, IND-SDA, and NM-SDA, as well as for IND-CCA, the parallel repetition (even using independent public keys) is not a scheme that achieves the same security level as the underlying single-bit scheme. However, Coretti et al. [10] provide a single-to-multi-bit transformation for IND-SDA security based on non-malleable codes [17] (see below), and Myers and Shelat [27], as well as Hohenberger et al. [23], provide (much) more complicated such transformations for IND-CCA security. To complement these works, we answer the question of domain extension for NM-SDA and NM-CPA in the affirmative. In particular we show the following result:

Theorem 1

(Informal). Let $\lambda$ be the security parameter. Then there is a black-box construction of a $\lambda$-bit NM-SDA (resp. NM-CPA) PKE scheme from a single-bit NM-SDA (resp. NM-CPA) PKE scheme, making $\mathcal {O}(\lambda )$ calls to the underlying single-bit scheme.²

The proof of Theorem 1 can be found in Sect. 4. Our approach follows that for IND-SDA [10] and combines single-bit PKE with so-called non-malleable codes (NMCs), introduced by Dziembowski et al. [17]. Intuitively, NMCs protect encoded messages against a tampering adversary, which tampers with the codeword by means of applying functions $f$ from a particular function class $\mathcal F$ to it, in the sense that the decoding results in either the original message or a completely unrelated value.

Our construction has the following simple structure (see also Fig. 4): The plaintext $m$ is first encoded using an appropriate non-malleable code into an encoding $c$, which is in turn encrypted bit-by-bit (under independent public keys) with the single-bit NM-SDA scheme.³ The fact that NM-SDA security guarantees that an attacker can either leave a ciphertext intact or replace it, which results in an unrelated message, translates to the following capability of an adversary w.r.t. decryption queries: It can either leave a particular bit of the encoding unchanged, or fix it to 0 or to 1. Therefore, the tamper class against which the non-malleable code must be resilient is the class $\mathcal F_\mathsf {set}$ of functions that tamper with each bit of an encoding individually and can either leave it unchanged or set it to a fixed value.

The main new challenge for our construction is to deal with the parallel decryption queries: in order for the combined scheme to be NM-SDA secure, the NMC needs to be resilient against parallel tamper queries as well. Unfortunately, we show that no standard non-malleable code (as originally defined by Dziembowski et al. [17] and Faust et al. [18]) can achieve this notion (see Sect. 4.6). Fortunately, we observe that the NMC concept can be extended to allow the decoder to make use of (an initially generated) secret state, which simply becomes part of the secret key in the combined scheme. This modification of NMCs—called secret-state NMCs—allows us to achieve resilience against parallel tampering and may be of independent interest. This reduces our question to building a secret-state non-malleable code resilient against continuous parallel tampering attacks from $\mathcal F_\mathsf {set}$. We construct such a code in Sect. 4.3, by combining the notion of linear error-correcting secret sharing (see [17]) with the idea of a secret “trigger set” [9]. This construction forms one of the main technical contributions of our work.

Fig. 1.

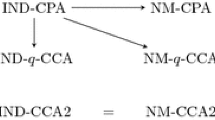
Diagram of the main relationships between the security notions considered in this paper. $X\rightarrow Y$ means that X implies Y; $X \nrightarrow Y$ indicates a separation between X and Y. Notions with the same color are equivalent under black-box transformations; notions with different colors are not known to be equivalent.

NM-SDA from IND-CPA. Next, we show:

Theorem 2

(Informal). There exists a black-box construction of an NM-SDA-secure PKE scheme from an IND-CPA-secure PKE.

Hence, the notions of IND-CPA, NM-CPA, IND-SDA, and NM-SDA security are all equivalent, lying (plausibly, strictly?) below IND-CCA security. See Fig. 1.

The proof of Theorem 2 appears in Sect. 5. In fact, we show that a generalization of the construction by Choi et al. already achieves NM-SDA security (rather than only NM-CPA security). Our proof much follows the pattern of the original one, except for one key step in the proof, where a brand new proof technique is required. Intuitively, we need to argue that no sensitive information about the secret “trigger set” is leaked to the adversary, unless one of the ciphertexts is invalid. This rather general technique (for analyzing security of so called “parallel stateless self-destruct games”) may be interesting in its own right (e.g., it is also used in the security proof of our non-malleable code in Sect. 4), and is detailed in Sect. 6.

Along the way, we also manage to slightly abstract the transformation of [9], and to re-phrase it in terms of certain linear error-correcting secret-sharing schemes (LECSSs) satisfying a special property (as opposed to using Reed-Solomon codes directly as an example of such a scheme). Aside from a more modular presentation (which gives a more intuitive explanation for the elegant scheme of Choi et al. [9]), this also allows us to instantiate the required LECSS more efficiently and thereby improve the rate of the transformation of [9] by a factor linear in the security parameter (while also arguing NM-SDA, instead of NM-CPA, security), giving us the positive answer to Question 1.⁴

2 Preliminaries

This section introduces notational conventions and basic concepts that we use throughout the work.

Bits and Symbols. Let $\ell \in \mathbb N$. For any multiple $m = t \ell$ of $\ell$, an m-bit string $x = (x[1],\ldots ,x[m]) = (x_{1},\ldots ,x_{t})$ can be seen as composed of its bits $x[j]$ or its symbols $x_{i} \in \{0,1\}^{\ell }$. For two m-bit strings x and y, denote by $d_\mathsf {H}(x,y)$ their hamming distance as the number of symbols in which they differ.

Oracle Algorithms. Oracle algorithms are algorithms that can make special oracle calls. An algorithm A with an oracle O is denoted by $A(O)$. Note that oracle algorithms may make calls to other oracle algorithms (e.g., $A(B(O))$).

Distinguishers and Reductions. A distinguisher is an (possibly randomized) oracle algorithm $D (\cdot )$ that outputs a single bit. The distinguishing advantage on two (possibly stateful) oracles $S$ and $T$ is defined by

$$ \varDelta ^{ D }(S,T)\quad :=\quad |{\mathsf P[ D (S)= 1]} - {\mathsf P[ D (T)= 1]}|, $$

where probabilities are over the randomness of $D$ as well as $S$ and $T$, respectively.

Reductions between distinguishing problems are modeled as oracle algorithms as well. Specifically, when reducing distinguishing two oracles $U$ and $V$ to distinguishing $S$ and $T$, one exhibits an oracle algorithm $R(\cdot )$ such that $R(U)$ behaves as $S$ and $R(V)$ as $T$; then, $\varDelta ^{ D }(S,T)= \varDelta ^{ D }(R(U),R(V)) = \varDelta ^{ D (R(\cdot ))}(U,V)$.

Linear Error-Correcting Secret Sharing. The following notion of a linear error-correcting secret sharing, introduced by Dziembowski et al. [17], is used in several places in this paper.

Definition 1

(Linear error-correcting sharing scheme). Let $n\in \mathbb N$ be a security parameter and $\mathbb F$ a field of size $L= 2^\ell$ for some $\ell \in \mathbb N$. A $(k,n,\delta ,\tau )$ linear error-correcting secret sharing (LECSS) over $\mathbb F$ is a pair of algorithms $(\mathsf {E},\mathsf {D})$, where $\mathsf {E}: \mathbb F^k\rightarrow \mathbb F^n$ is randomized and $\mathsf {D}: \mathbb F^n\times \mathbb N\rightarrow \mathbb F^k\cup {\{\bot \}}$ is deterministic, with the following properties:

• Linearity: For any vectors $w$ output by $\mathsf {E}$ and any $c\in \mathbb F^n$,

  $$ \mathsf {D}(w+ c) = {\left\{ \begin{array}{ll} \bot &{} \text {if}\,\, \mathsf {D}(c) = \bot , \, \text {and} \\ \mathsf {D}(w) + \mathsf {D}(c) &{} \text {otherwise.} \end{array}\right. } $$

• Minimum distance: For any two codewords $w,w'$ output by $\mathsf {E}$, $d_\mathsf {H}(w,w') \ge \delta n$.

• Error correction: It is possible to efficiently correct up to $\delta n/2$ errors, i.e., for any $x\in \mathbb F^k$ and any $w$ output by $\mathsf {E}(x)$, if $d_\mathsf {H}(c,w) \le t$ for some $c\in \mathbb F^n$ and $t < \delta n/2$, then $\mathsf {D}(c,t) = x$.

• Secrecy: The symbols of a codeword are individually uniform over $\mathbb F$ and and $\tau n$-wise independent (over the randomness of $\mathsf {E}$).

This paper considers various instantiations of LECSSs, which are described in Sects. 4.5 and 5.3, where they are used.

One-time Signatures. A digital signature scheme (DSS) is a triple of algorithms $\varSigma = (KG,S,V)$, where the key-generation algorithm $KG$ outputs a key pair $(\mathsf {sk},\mathsf {vk})$, the (probabilistic) signing algorithm $S$ takes a message $m$ and a signing key $\mathsf {sk}$ and outputs a signature $s\leftarrow S_{\mathsf {sk}}(m)$, and the verification algorithm takes a verification key $\mathsf {vk}$, a message $m$, and a signature $s$ and outputs a single bit $V_{\mathsf {vk}}(m,s)$. A (strong) one-time signature (OTS) scheme is a digital signature scheme that is secure as long as an adversary only observes a single signature. More precisely, OTS security is defined using the following game $G^{\varSigma ,\mathsf {ots}}$ played by an adversary $A$: Initially, the game generates a key pair $(\mathsf {sk},\mathsf {vk})$ and hands the verification key $\mathsf {vk}$ to $A$. Then, $A$ can specify a single message $m$ for which he obtains a signature $s\leftarrow S_{\mathsf {vk}}(m)$. Then, the adversary outputs a pair $(m',s')$. The adversary wins the game if $(m',s') \ne (m,s)$ and $V_{\mathsf {vk}}(m',s') = 1$. The advantage of $A$ is the probability (over all involved randomness) that $A$ wins the game, and is denoted by $\varGamma ^{ A }(G^{\varSigma ,\mathsf {ots}})$.

Definition 2

A DSS scheme $\varSigma$ is a $(t,\varepsilon )$ -strong one-time signature scheme if for all adversaries $A$ with running time at most $t$, $\varGamma ^{ A }(G^{\varSigma ,\mathsf {ots}}) \le \varepsilon$.

3 Non-Malleability Under Self-Destruct Attacks

A public-key encryption (PKE) scheme with message space $\mathcal {M}\subseteq \{0,1\}^*$ and ciphertext space $\mathcal {C}$ is defined as three algorithms $\varPi = (KG,E,D)$, where the key-generation algorithm $KG$ outputs a key pair $(\mathsf {pk},\mathsf {sk})$, the (probabilistic) encryption algorithm $E$ takes a message $m\in \mathcal {M}$ and a public key $\mathsf {pk}$ and outputs a ciphertext $c\leftarrow E_{\mathsf {pk}}(m)$, and the decryption algorithm takes a ciphertext $c\in \mathcal {C}$ and a secret key $\mathsf {sk}$ and outputs a plaintext $m\leftarrow D_{\mathsf {sk}}(c)$. The output of the decryption algorithm can be the special symbol $\bot$, indicating an invalid ciphertext. A PKE scheme is correct if $m= D_{\mathsf {sk}}(E_{\mathsf {pk}}(m))$ (with probability 1 over the randomness in the encryption algorithm) for all messages $m$ and all key pairs $(\mathsf {pk},\mathsf {sk})$ generated by $KG$.

Security notions for PKE schemes in this paper are formalized using the distinguishing game $G^{\varPi ,q,p}_{b}$, depicted in Fig. 2: The distinguisher (adversary) is initially given a public key and then specifies two messages $m_0$ and $m_1$. One of these, namely $m_b$, is encrypted and the adversary is given the resulting challenge ciphertext. During the entire game, the distinguisher has access to a decryption oracle that allows him to make at most $q$ decryption queries, each consisting of at most $p$ ciphertexts. Once the distinguisher specifies an invalid ciphertext, the decryption oracle self-destructs, i.e., no further decryption queries are answered.

The general case is obtained when both $q$ and $p$ are arbitrary (denoted by $q= p= *$), which leads to our main definition of non-malleability under (chosen-ciphertext) self-destruct attacks (NM-SDA). For readability, set $G^{\varPi ,{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{b} := G^{\varPi ,*,*}_{b}$ for $b \in \{0,1\}$. Formally, NM-SDA is defined as follows:

Definition 3

(Non-malleability under self-destruct attacks). A public-key encryption scheme $\varPi$ is $(t,q,p,\varepsilon )$ -NM-SDA-secure if for all distinguishers $D$ with running time at most $t$ and making at most $q$ decryption queries of size at most $p$ each, $\varDelta ^{ D }(G^{\varPi ,{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{0},G^{\varPi ,{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{1}) \quad \le \quad \varepsilon$.

Fig. 2.

Distinguishing game $G^{\varPi ,q,p}_{b}$, where $b \in \{0,1\}$, used to define security of a PKE scheme $\varPi = (KG,E,D)$. The numbers $q,p\in \mathbb N$ specify the maximum number of decryption queries and their size, respectively. The command $\mathbf {self-destruct}$ results in all future decryption queries being answered by $\bot$.

All other relevant security notions in this paper can be derived as special cases of the above definition, by setting the parameters $q$ and $p$ appropriately.

Chosen-Plaintext Security (IND-CPA). In this variant, the distinguisher is not given access to a decryption oracle, i.e., $q= p= 0$. For readability, set $G^{\varPi ,{\mathsf {ind}}\text {-}{\mathsf {sda}}}_{b} := G^{\varPi ,0,0}_{b}$ for $b \in \{0,1\}$ in the remainder of this paper. We say that $\varPi$ is $(t,\varepsilon )$-IND-CPA-secure if it is, in fact, $(t,0,0,\varepsilon )$-NM-SDA-secure.

Non-malleability (NM-CPA). A scheme is non-malleable under chosen-plaintext attacks [29], if the adversary can make a single decryption query consisting of arbitrarily many ciphertexts, i.e., $q= 1$ and $p$ arbitrary (denoted by $p= *$). Similarly to above, set $G^{\varPi ,{\mathsf {nm}}\text {-}{\mathsf {cpa}}}_{b} := G^{\varPi ,1,*}_{b}$ for $b \in \{0,1\}$. We say that $\varPi$ is $(t,p,\varepsilon )$-NM-CPA-secure if it is, in fact, $(t,1,p,\varepsilon )$-NM-SDA-secure.⁵

Indistinguishability Under Self-Destruct Attacks (IND-SDA). This variant, introduced in [10], allows arbitrarily many queries to the decryption oracle, but each of them may consist of a single ciphertext only, i.e., $q$ arbitrary (denoted by $q= *$) and $p= 1$. Once more, set $G^{\varPi ,{\mathsf {ind}}\text {-}{\mathsf {sda}}}_{b} := G^{\varPi ,*,1}_{b}$. We say that $\varPi$ is $(t,q,\varepsilon )$-IND-SDA-secure if it is, in fact, $(t,q,1,\varepsilon )$-NM-SDA-secure.

Chosen-Ciphertext Security (IND-CCA). The standard notion of IND-CCA security can be obtained as a strengthening of NM-SDA where $q= *$, $p= 1$, and the decryption oracle never self-destructs. We do not define this notion formally, as it is not the main focus of this paper.

Asymptotic Formulation. To allow for concise statements, sometimes we prefer to use an asymptotic formulation instead of stating concrete parameters. More precisely, we will say that a PKE scheme $\varPi$ is X-secure for $\text {X}\in \{\text {IND-CPA}, \text {NM-CPA}, \text {IND-SDA}, \text {NM-SDA}\}$ if for all efficient adversaries the advantage $\varepsilon$ in the distinguishing game is negligible in the security parameter.

Non-malleable CPA vs. Indistinguishable SDA. We provide a separation between the notions of NM-CPA and IND-SDA security; a corresponding theorem and proof can be found in the full version of this work. Given such a separation, our notion of NM-SDA security (see Definition 3) is strictly stronger than either of the two other notions.

4 Domain Extension

This section contains one of our main technical results. We show how single-bit NM-SDA PKE can be combined with so-called secret-state non-malleable codes resilient against continuous parallel tampering, which we believe is an interesting notion in its own right, to achieve multi-bit NM-SDA-secure PKE. We construct such a code and prove its security. In the full version of this paper, we additionally show that no code without secret state can achieve security against parallel tampering unconditionally.⁶

Fig. 3.

Distinguishing game ($R_{\mathcal F},S_{\mathcal F,\mathsf {sim}})$ used to define non-malleability of a secret-state coding scheme $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$. The command $\mathbf {self-destruct}$ has the effect that all future queries are answered by $\bot$.

4.1 A New Flavor of Non-Malleable Codes

Non-malleable codes were introduced by Dziembowski et al. [17]. Intuitively, they protect encoded messages in such a way that any tampering with the codeword causes the decoding to either output the original message or a completely unrelated value. The original notion can be extended to include the aforementioned secret state in the decoder as follows:

Definition 4

(Code with secret state). A $(k,n)$ -code with secret state (CSS) is a triple of algorithms $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$, where the (randomized) state-generation algorithm $\mathrm {Gen}$ outputs a secret state $s$ from some set $\mathcal S$, the (randomized) encoding algorithm $\mathrm {Enc}$ takes a $k$-bit plaintext $x$ and outputs an $n$-bit encoding $c\leftarrow \mathrm {Enc}(x)$, and the (deterministic) decoding algorithm $\mathrm {Dec}$ takes an encoding as well as some secret state $s\in \mathcal S$ and outputs a plaintext $x\leftarrow \mathrm {Dec}(c,s)$ or the special symbol $\bot$, indicating an invalid encoding.

Tampering attacks are captured by functions $f$, from a certain function class $\mathcal F$, that are applied to an encoding. The original definition by [17] allows an attacker to apply only a single tamper function. In order to capture continuous parallel attacks, the definition below permits the attacker to repeatedly specify parallel tamper queries, each consisting of several tamper functions. The process ends as soon as one of the tamper queries leads to an invalid codeword.

The non-malleability requirement is captured by considering a real and an ideal experiment. In both experiments, an attacker is allowed to encode a message of his choice. In the real experiment, he may tamper with an actual encoding of that message, whereas in the ideal experiment, the tamper queries are answered by a (stateful) simulator. The simulator is allowed to output the special symbol $\mathsf {same}$, which the experiment replaces by the originally encoded message. In either experiment, if a component of the answer vector to a parallel tamper query is the symbol $\bot$, a self-destruct occurs, i.e., all future tamper queries are answered by $\bot$. The experiments are depicted in Fig. 3.

Definition 5

(Non-malleable code with secret state). Let $q,p\in \mathbb N$ and $\varepsilon > 0$. A CSS $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$ is $(\mathcal F,q,p,\varepsilon )$ -non-malleable if the following properties are satisfied:

• Correctness: For each $x\in \{0,1\}^k$ and all $s\in \mathcal S$ output by $\mathrm {Gen}$, correctness means $\mathrm {Dec}(\mathrm {Enc}(x),s) = x$ with probability 1 over the randomness of $\mathrm {Enc}$.

• Non-Malleability: There exists a (possibly stateful) simulator $\mathsf {sim}$ such that for any distinguisher $D$ asking at most $q$ parallel queries, each of size at most $p$, $\varDelta ^{ D }(R_{\mathcal F},S_{\mathcal F,\mathsf {sim}}) \le \varepsilon$.

We remark that for codes without secret state (as the ones considered in [17]), one obtains the standard notion of non-malleability [17] by setting $q= p= 1$, and continuous non-malleability [18] by letting $p= 1$ and $q$ arbitrary (i.e., $q= *$).

4.2 Combining Single-Bit PKE and Non-Malleable Codes

Our construction of a multi-bit NM-SDA-secure PKE scheme $\varPi '$ from a single-bit NM-SDA-secure scheme $\varPi$ and a secret-state non-malleable $(k,n)$-code follows the approach of [10]: It encrypts a $k$-bit message $m$ by first computing an encoding $c= (c[1],\ldots ,c[n])$ of $m$ and then encrypting each bit $c[j]$ under an independent public key of $\varPi$; it decrypts by first decrypting the individual components and then decoding the resulting codeword using the secret state of the non-malleable code; the secret state is part of the secret key. The scheme is depicted in detail in Fig. 4.

Intuitively, NM-SDA security (or CCA security in general) guarantees that an attacker can either leave a message intact or replace it by an independently created one. For our construction, which separately encrypts every bit of an encoding of the plaintext, this translates to the following of an adversary w.r.t. decryption queries: It can either leave a particular bit of the encoding unchanged or fix it to 0 or to 1. Therefore, the tamper class against which the non-malleable code must be resilient is the class $\mathcal F_\mathsf {set}\subseteq {\{f\mid f: \{0,1\}^{n}\rightarrow \{0,1\}^{n}\}}$ of functions that tamper with each bit of an encoding individually and can either leave it unchanged or set it to a fixed value. More formally, $f\in \mathcal F_\mathsf {set}$ can be characterized by $(f[1],\ldots ,f[n])$, where $f[j]: \{0,1\}\rightarrow \{0,1\}$ is the action of $f$ on the ${j}^\text {th}$ bit and $f[j] \in {\{\mathsf {zero},\mathsf {one},\mathsf {keep}\}}$ with the meaning that it either sets the ${j}^\text {th}$ bit to 0 ($\mathsf {zero}$) or to 1 ($\mathsf {one}$) or leaves it unchanged ($\mathsf {keep}$).

Before stating the theorem about the security of our construction $\varPi '$, it needs to be pointed out that it achieves only the so-called replayable variant of NM-SDA security. The notion of replayable CCA (RCCA) security (in general) was introduced by Canetti et al. [6] to deal with the fact that for many applications (full) CCA security is unnecessarily strict. Among other things, they provide a MAC-based generic transformation of RCCA-secure schemes into CCA-secure ones, which we can also apply in our setting (as we show) to obtain a fully NM-SDA-secure scheme $\varPi ''$.

Theorem 3

Let $q,p\in \mathbb N$ and $\varPi$ be a $(t+t_\mathsf{1bit},q,p,\varepsilon _\mathsf{1bit})$-NM-SDA-secure 1-bit PKE scheme, $(T,V)$ a $(t+t_\mathsf{mac},1,qp,\varepsilon _\mathsf{mac})$-MAC, and $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$ a $(\mathcal F_\mathsf {set},q,p,\varepsilon _\mathsf{nmc})$-non-malleable $(k,n)$-code with secret state. Then, $\varPi ''$ is $(t,q,p,\varepsilon )$-NM-SDA-secure PKE scheme with $\varepsilon = 2(3 (n\varepsilon _\mathsf{1bit}+ \varepsilon _\mathsf{nmc}) + qp\cdot 2^{-\ell } + \varepsilon _\mathsf{mac})$, where $t_\mathsf{1bit}$ and $t_\mathsf{mac}$ are the overheads incurred by the corresponding reductions and $\ell$ is the length of a verification key for the MAC.

Fig. 4.

The $k$-bit PKE scheme $\varPi '= (KG',E',D')$ built from a 1-bit PKE scheme $\varPi = (KG,E,D)$ and a $(k,n)$-coding scheme with secret state $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$.

The full proof of Theorem 3 can be found in the full version; here we only provide a sketch. We stress that an analogous statement as the one of the above theorem works for domain extension of NM-CPA, i.e., for constructing a multi-bit NM-CPA scheme out of a single-bit NM-CPA scheme. The proof is very similar to the one of Theorem 3 and therefore omitted.

Proof

(Sketch). The proof considers a series of $n$ hybrid experiments. In very rough terms, the ${i}^\text {th}$ hybrid generates the challenge ciphertext by computing an encoding $c= (c[1],\ldots ,c[n])$ of the challenge plaintext and by replacing the first i bits $c[i]$ of $c$ by random values $\tilde{c}[i]$ before encrypting the encoding bit-wise, leading to the challenge $(c_{1}^*,\ldots ,c_{n}^*)$. Moreover, when answering decryption queries $(c_{1}',\ldots ,c_{n}')$, if $c_{j}' = c_{j}^*$ for $j \le i$, the ${i}^\text {th}$ hybrid sets the outcome of $c_{j}'$’s decryption to be the corresponding bit $c[j]$ of the original encoding $c$, whereas if $c_{j}' \ne c_{j}^*$, it decrypts normally (then it decodes the resulting $n$-bit string normally). This follows the above intuition that a CCA-secure PKE scheme guarantees that if a decryption query is different from the challenge ciphertext, then the plaintext contained in it must have been created independently of the challenge plaintext. The indistinguishability of the hybrids follows from the security of the underlying single-bit scheme $\varPi$.

In the ${n}^\text {th}$ hybrid, the challenge consists of $n$ encryptions of random values. Thus, the only information about the encoding of the challenge plaintext that an attacker gets is that leaked through decryption queries. But in the ${n}^\text {th}$ hybrid there is a 1-to-1 correspondence between decryption queries and the tamper function $f= (f[1],\ldots ,f[n])$ applied to the encoding of the challenge plaintext: The case $c_{j}' = c_{j}^*$ corresponds to $f[j] = \mathsf {keep}$, and the case $c_{j}' \ne c_{j}^*$ corresponds to $f[j] = \mathsf {zero}$ or $f[j] = \mathsf {one}$, depending on whether $c_{j}'$ decrypts to $\mathsf {zero}$ or to $\mathsf {one}$. This allows a reduction to the security of the non-malleable code.    $\square$

4.3 Non-Malleable Code Construction

It remains to construct a non-malleable code (with secret state) resilient against parallel tampering. The intuition behind our construction is the following: If a code has the property (as has been the case with previous schemes secure against (non-parallel) bit-wise tampering) that changing a single bit of a valid encoding results in an invalid codeword, then the tamper function that fixes a particular bit of the encoding and leaves the remaining positions unchanged can be used to determine the value of that bit; this attack is parallelizable, and thus a code of this type cannot provide security against parallel tampering. A similar attack is also possible if the code corrects a fixed (known) number of errors. To circumvent this issue, our construction uses a—for the lack of a better word—“dynamic” error-correction bound: The secret state (initially chosen at random) determines the positions of the encoding in which a certain amount of errors is tolerated.

Construction. Let $\mathbb F= {{\mathrm{GF}}}(2)$ and $\alpha > 0$. Let $(\mathsf {E},\mathsf {D})$ be a $(k,n,\delta ,\tau )$-LECSS (cf. Definition 1) with minimum distance $\delta$ and secrecy $\tau$ over $\mathbb F$ such that:⁷

• Minimum distance: $\delta > 1/4 + 2 \alpha$ and $\delta /2 > 2\alpha$.

• Constant rate: $k/n= \varOmega (1)$.

• Constant secrecy: $\tau = \varOmega (1)$.

In the following, we assume that $\alpha \ge \tau$, an assumption that can always be made by ignoring some of the secrecy. Consider the following $(k,n)$-code with secret state $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$:

• $\mathrm {Gen}$: Choose a subset $T$ of $[n]$ of size $\tau n$ uniformly at random and output it.

• $\mathrm {Enc}(x)$ for $x\in \{0,1\}^{k}$: Compute $c= \mathsf {E}(x)$ and output it.

• $\mathrm {Dec}(c,T)$ for $c\in \{0,1\}^{n}$: Find codeword $w= (w[1],\ldots ,w[n])$ with $d_\mathsf {H}(w,c)\le \alpha n$. If no such $w$ exists, output $\bot$. If $w[j] \ne c[j]$ for some $j \in T$, output $\bot$ as well. Otherwise, decode $w$ to its corresponding plaintext $x$ and output it.

We prove the following theorem:

Theorem 4

For all $q,p\in \mathbb N$, $(k,n)$-code $(\mathrm {Gen},\mathrm {Enc},\mathrm {Dec})$ based on a $(k,n,\delta ,\tau )$-LECSS satisfying the three conditions above is $(\mathcal F_\mathsf {set},q,p,\varepsilon _\mathsf{nmc})$-non-malleable with $\varepsilon _\mathsf{nmc}= p( \mathcal {O}(1) \cdot e^{-\tau n/ 16} + e^{-\tau ^2 n/ 4} ) + pe^{-\tau ^2 n}$.

Instantiating the Construction. Section 4.5 details how a LECSS satisfying the above properties can be constructed by combining high-distance binary codes with a recent result by Cramer et al. [11] in order to “add” secrecy. The resulting LECSS has secrecy $\tau = \varOmega (1)$ and rate $\rho = \varOmega (1)$ (cf. Corollary 1 in Sect. 4.5). The secrecy property depends on the random choice of a universal hash function. Thus, the instantiated code can be seen as a construction in the CRS model. When combined with the single-bit PKE as described above, the description of the hash function can be made part of the public key.

By combining Theorems 3, and 4, and Corollary 1, we obtain a 1-to-$k$-bit black-box domain extension for NM-SDA (and NM-CPA) making $\mathcal {O}(k)$ calls to the underlying 1-bit scheme, therefore establishing Theorem 1.⁸

4.4 Proof of the Non-Malleable Code Construction

For the proof of Theorem 4, fix $q,p\in \mathbb N$ and a distinguisher $D$ making at most $q$ tamper queries of size $p$ each. Set $\mathcal F:= \mathcal F_\mathsf {set}$ for the rest of the proof. In the following, we assume that $\alpha \ge \tau$, an assumption that can always be made by ignoring some of the secrecy. The goal is to show $\varDelta ^{ D }(R_{\mathcal F},S_{\mathcal F,\mathsf {sim}}) \le \varepsilon _\mathsf{nmc}= p( \mathcal {O}(1) \cdot e^{-\tau n/ 16} + e^{-\tau ^2 n/ 4} ) + pe^{-\tau ^2 n}$ for a simulator $\mathsf {sim}$ to be determined.

On a high level, the proof proceeds as follows: First, it shows that queries that interfere with too many bits of an encoding and at the same time do not fix enough bits (called middle queries below) are rejected with high probability. The effect of the remaining query types (called low and high queries) on the decoding process can always be determined from the query itself and the bits of the encoding at the positions indexed by the secret trigger set $T$. Since the size of $T$ is $\tau n$, these symbols are uniformly random and independent of the encoded message, which immediately implies a simulation strategy for $\mathsf {sim}$.

Tamper-Query Types. Recall that $f\in \mathcal F_\mathsf {set}$ is characterized by $(f[1],\ldots ,f[n])$, where $f[j]: \{0,1\}\rightarrow \{0,1\}$ is the action of $f$ on the ${j}^\text {th}$ bit, for $f[j] \in {\{\mathsf {zero},\mathsf {one},\mathsf {keep}\}}$, with the meaning that it either sets the ${j}^\text {th}$ bit to 0 ($\mathsf {zero}$) or to 1 ($\mathsf {one}$) or leaves it unchanged ($\mathsf {keep}$). Define $A(f)$ to be the set of all indices j such that $f[j] \in {\{\mathsf {zero},\mathsf {one}\}}$, and let $q(f):= |A(f)|$. Moreover, let $\mathsf {val}(\mathsf {zero}) := 0$ and $\mathsf {val}(\mathsf {one}) := 1$.

A tamper query $f$ is a low query if $q(f)\le \tau n$, a middle query if $\tau n< q(f)< (1-\tau ) n$, and a high query if $q(f)\ge (1-\tau ) n$.

Analyzing Query Types. The following lemma states that an isolated middle query is rejected with high probability.

Lemma 1

Let $f\in \mathcal F_\mathsf {set}$ be a middle query. Then, for any $x\in \{0,1\}^{k}$,

$$ {\mathsf P[\mathrm {Dec}(f(\mathrm {Enc}(x))) \ne \bot ]} \quad \le \quad \mathcal {O}(1) \cdot e^{-\tau n/ 16} + e^{-\tau ^2 n/ 4} $$

where the probability is over the randomness of $\mathrm {Enc}$ and the choice of the secret trigger set $T$.

Proof

Fix $x\in \{0,1\}^{k}$ and a middle query $f= (f[1],\ldots ,f[n])$. Suppose first that $q(f)\ge n/2$. Define $\mathcal W:= \{w\in \mathbb F^n\mid \text {w is codeword} \wedge \exists r: d_\mathsf {H}(f(\mathsf {E}(x;r)),w) \le \alpha n\}$, where r is the randomness of $\mathsf {E}$. That is, $\mathcal W$ is the set of all codewords that could possibly be considered while decoding an encoding of x tampered with via $f$. Consider two distinct codewords $w,w' \in \mathcal W$. From the definition of $\mathcal W$ it is apparent that $w[j] \ne \mathsf {val}(f[j])$ for at most $\alpha n$ positions $j \in A(f)$ (and similarly for $w'$), which implies that $w$ and $w'$ differ in at most $2 \alpha n$ positions $j \in A(f)$. Therefore, $w$ and $w'$ differ in at least $(\delta -2\alpha )n$ positions $j \notin A(f)$.

For $w\in \mathcal W$, let $\tilde{w}$ be the projection of $w$ onto the unfixed positions $j \notin A(f)$ and set $\tilde{\mathcal W}:= {\{\tilde{w}\mid w\in \mathcal W\}}$. The above distance argument implies that $|\mathcal W| = |\tilde{\mathcal W}|$. Moreover, $\tilde{\mathcal W}$ is a binary code with block length $n- q(f)$ and relative distance at least

$$ \frac{(\delta -2\alpha )n}{n- q(f)} \ge \frac{(\delta -2\alpha )n}{n/2} = 2\delta -4\alpha > 1/2, $$

where the last inequality follows from the fact that $\delta$ and $\alpha$ are such that $\delta - 2\alpha > 1/4$. Therefore, by the Plotkin bound (a proof can, e.g., be found in [26, p. 41]),⁹

$$ |\mathcal W| = |\tilde{\mathcal W}| \le \mathcal {O}(1). $$

Denote by $c= (c[1],\ldots ,c[n])$ and $\tilde{c}= (\tilde{c}[1],\ldots ,\tilde{c}[n])$ the (random variables corresponding to the) encoding $c= \mathrm {Enc}(x)$ and the tampered encoding $\tilde{c}= f(c)$, respectively. For an arbitrary ($n$-bit) codeword $w\in \mathcal W$,

$$\begin{aligned} \mathbf {E}[d_\mathsf {H}(\tilde{c},w)] \quad =\quad \sum _{j=1}^n\mathbf {E}[d_\mathsf {H}(\tilde{c}[j],w[j])] \quad \ge \quad \sum _{j \in J} \mathbf {E}[d_\mathsf {H}(\tilde{c}[j],w[j])], \end{aligned}$$

where $J\subseteq [n]$ is the set containing the indices of the first $\tau n$ bits not fixed by $f$. Note that by the definition of middle queries, there are at least that many, i.e., $|J| = \tau n$.

Observe that for $j \in J$, $d_\mathsf {H}(\tilde{c}[j],w[j])$ is an indicator variable with expectation $\mathbf {E}[d_\mathsf {H}(\tilde{c}[j],w[j])] \ge \frac{1}{2}$, since $c[j]$ is a uniform bit. Thus, $\mathbf {E}[d_\mathsf {H}(\tilde{c},w)] \ge \frac{\tau n}{2}$.

Additionally, $(d_\mathsf {H}(\tilde{c}[j],w[j]))_{j \in J}$ are independent. Therefore, using a standard Chernoff bound, for $\varepsilon > 0$

$$ {\mathsf P[d_\mathsf {H}(\tilde{c},w)\quad <\quad (1-\varepsilon ) \tau n/2]} \quad \le \quad e^{-\tau \varepsilon ^2 n/ 4}. $$

Therefore, the probability that there exists $w\in \mathcal W$ for which the above does not hold is at most $|\mathcal W| \cdot e^{-\tau \varepsilon ^2 n/ 4} \le \mathcal {O}(1) \cdot e^{-\tau \varepsilon ^2 n/ 4}$, by a union bound.

Suppose now that $d_\mathsf {H}(\tilde{c},w)\ge (1-\varepsilon ) \tau n/2$ for all codewords $w\in \mathcal W$. Then, over the choice of $T$,¹⁰

$$ {\mathsf P[\forall j \in T: d_\mathsf {H}(\tilde{c}[j],w[j]) = 0]} \quad \le \quad (1 - (1-\varepsilon ) \tau / 2)^{\tau n} \quad \le \quad e^{-(1-\varepsilon )\tau ^2 n/ 2}. $$

The lemma now follows by setting $\varepsilon := \frac{1}{2}$.

If $q(f)< n/2$ an analogous argument can be made for the difference $d:= c- \tilde{c}$ between the encoding and the tampered codeword, as such a query $f$ fixes at least half of the bits of $d$ (to 0, in fact) and $\mathsf {D}(d) \ne \bot$ implies $\mathsf {D}(\tilde{c}) \ne \bot$.    $\square$

It turns out that low and high queries always result in $\bot$ or one other value.

Lemma 2

Low queries $f\in \mathcal F_\mathsf {set}$ can result only in $\bot$ or the originally encoded message $x\in \{0,1\}^{k}$. High queries $f\in \mathcal F_\mathsf {set}$ can result only in $\bot$ or one other value $x_{f}\in \{0,1\}^{k}$, which solely depends on $f$. Furthermore, $x_{f}$, if existent, can be found efficiently given $f$.

Proof

The statement for low queries is trivial, since a low query $f$ cannot change the encoding beyond the error correction bound $\alpha n$.

Consider now a high query $f$ and the following efficient procedure:

• 1. Compute $\tilde{c}_{f}\leftarrow f(0^n)$.

• 2. Find codeword $w_{f}$ with $d_\mathsf {H}(w_{f},\tilde{c}_{f}) \le 2 \alpha n$ (this is possible since $2 \alpha < \delta /2$).

• 3. Output $w_{f}$ or $\bot$ if none exists.

Consider an arbitrary encoding $c$ and let $\tilde{c}\leftarrow f(c)$ be the tampered encoding. Assume there exists $w$ with $d_\mathsf {H}(w,\tilde{c})\le \alpha n$. Since a high query $f$ fixes all but $\tau n$ bits, $d_\mathsf {H}(\tilde{c},\tilde{c}_{f}) \le \tau n\le \alpha n$, and, thus, $d_\mathsf {H}(w,\tilde{c}_f) \le 2 \alpha n$, by the triangle inequality. Hence, $w= w_{f}$.

In other words, if the decoding algorithm $\mathrm {Dec}$ on $\tilde{c}$ finds a codeword $w= w_{f}$, one can find it using the above procedure, which also implies that high queries can only result in $\bot$ or one other message $x_{f}= \mathsf {D}(w_{f})$.    $\square$

Handling Middle Queries. Consider the hybrid game $H_1$ that behaves as $R_{\mathcal F}$, except that it answers all middle queries by $\bot$.

Lemma 3

$\varDelta ^{ D }(R_{\mathcal F},H_1)\quad \le \quad p( \mathcal {O}(1) \cdot e^{-\tau n/ 16} + e^{-\tau ^2 n/ 4} )$.

The proof of Lemma 3 follows a generic paradigm, at whose core is the so-called self-destruct lemma, which deals with the indistinguishability of hybrids with the self-destruct property and is explained in detail in Sect. 6. Roughly, this lemma applies whenever the first hybrid (in this case $R_{\mathcal F}$) can be turned into the second one (in this case $H_1$) by changing (“bending”) the answers to a subset (the “bending set”) of the possible queries to always be $\bot$, and when additionally non-bent queries have a unique answer (cf. the statement of Lemma 10). Intuitively, the lemma states that parallelism and adaptivity do not help distinguish (much) in such cases, which allows using Lemma 1.

Proof

The lemma is proved conditioned on the message $x$ encoded by $D$. To use the self-destruct lemma, note first that both $R_{\mathcal F}$ and $H_1$ answer parallel tamper queries in which each component is from the set $\mathcal X:= \mathcal F$ by vectors whose components are in $\mathcal Y:= \{0,1\}^{k}\cup {\{\bot \}}$. Moreover, both hybrids use as internal randomness a uniformly chosen element from $\mathcal R:= \{0,1\}^{\rho }\times \mathcal S$, where $\rho$ is an upper bound on the number of random bits used by $\mathrm {Enc}$ and $\mathcal S$ is the set of all $\tau n$-subsets $T$ of $[n]$. $R_{\mathcal F}$ answers each component of a query $f\in \mathcal X$ by

$$ g(f,(r,T)) \quad :=\quad \mathrm {Dec}(f(\mathrm {Enc}(x;r)),T). $$

Define $\mathcal B\subseteq \mathcal X$ to be the set of all middle queries; $H_1$ is the $\mathcal B$-bending of $R_{\mathcal F}$ (cf. Definition 7).

Observe that queries $f\notin \mathcal B$ are either low or high queries. For low queries $f$, the unique answer is $y_{f}= x$, and for high queries $f$, $y_{f}= x_{f}$ (cf. Lemma 2). Thus, by Lemmas 10 and 1,

$$ \varDelta ^{ D }(R_{\mathcal F},H_1)\quad \le \quad p\cdot \max _{f\in \mathcal B} {\mathsf P[g(f,(r,T)) \ne \bot ]} \quad \le \quad p( \mathcal {O}(1) \cdot e^{-\tau n/ 16} + e^{-\tau ^2 n/ 4} ), $$

where the probability is over the choice of $(r,T)$.    $\square$

Handling High Queries. Consider the following hybrid game $H_2$: It differs from $H_1$ in the way it decodes high queries $f$. Instead of applying the normal decoding algorithm to the tampered codeword $\tilde{c}$, it proceeds as follows:

• 1. Find $w_{f}$ (as in the proof of Lemma 2).

• 2. If $w_{f}$ does not exist, return $\bot$.

• 3. If $\tilde{c}[j] = w_{f}[j]$ for all $j \in T$, return $\mathrm {Dec}(w)$. Otherwise, return $\bot$.

Lemma 4

$\varDelta ^{ D }(H_1,H_2)\quad \le \quad pe^{-\tau ^2 n}$.

Proof

The lemma is proved conditioned on the message $x$ encoded by $D$ and the randomness $r$ of the encoding. For the remainder of the proof, $r$ is therefore considered fixed inside $H_1$ and $H_2$. The proof, similarly to that of Lemma 3, again uses the self-destruct lemma.

Set $\mathcal X:= \mathcal F$ and $\mathcal Y:= \{0,1\}^{k}\cup {\{\bot \}}$. However, this time, let $\mathcal R:= \mathcal S$. For $f\in \mathcal X$ and $T\in \mathcal R$, define

$$ g(f,T) \quad :=\quad \mathrm {Dec}(\tilde{c},T), $$

where $\tilde{c}:= f(\mathrm {Enc}(x;r))$. The bending set $\mathcal B\subseteq \mathcal X$ is the set of all high queries $f$ such that $w_{f}$ exists and $d_\mathsf {H}(w_{f},\tilde{c}) > \alpha n$.¹¹ It is readily verified that $H_2$ is a parallel stateless self-destruct game (cf. Definition 6) that behaves according to $g$, and that $H_1$ is its $\mathcal B$-bending.

Consider a query $f\notin \mathcal B$. If $f$ is a low query, the unique answer is $y_{f}= x$; if it is a middle query, $y_{f}= \bot$; if it is a high query, $y_{f}= x_{f}$ (cf. Lemma 2). Therefore,

$$ \varDelta ^{ D }(H_1,H_2)\quad \le \quad \max _{f\in \mathcal B} {\mathsf P[g(f,T) \ne \bot ]} \quad \le \quad pe^{-\tau ^2 n}, $$

where the first inequality follows from Lemma 10 and the second one from the fact that $d_\mathsf {H}(x_{f},\tilde{c}) > \tau n$ for queries $f\in \mathcal B$, and therefore the probability over the choice of $T$ that it is accepted is at most $(1 - \tau )^{\tau n} \le e^{-\tau ^2 n}$.    $\square$

Simulation. By analyzing hybrid $H_2$, one observes that low and high queries can now be answered knowing only the query itself and the symbols of the encoding indexed by the secret trigger set $T\in \mathcal S$.

Lemma 5

Consider the random experiment of distinguisher $D$ interacting with $H_2$. There is an efficiently computable function $\mathrm {Dec}': \mathcal F_\mathsf {set}\times \mathcal S\times \{0,1\}^{\tau n} \rightarrow \{0,1\}^{k}\cup {\{\mathsf {same},\bot \}}$ such that for any low or high query $f$, any fixed message $x$, any fixed encoding $c$ thereof, and any output $T$ of $\mathrm {Gen}$,

$$ \left[ \mathrm {Dec}'(f,T,(c[j])_{j \in T})\right] _{\mathsf {same}/x} \quad =\quad \mathrm {Dec}(f(c)), $$

where $\left[ \cdot \right] _{\mathsf {same}/x}$ is the identity function except that $\mathsf {same}$ is replaced by $x$ and where $(c[j])_{j \in T}$ are the symbols of $c$ specified by $T$.

Proof

Consider a low query $f$. Due to the error correction, $\mathrm {Dec}(f(c))$ is the message originally encoded if no bit indexed by $T$ is changed and $\bot$ otherwise. Which one is the case can clearly be efficiently computed from $f$, $T$, and $(c[j])_{j \in T}$.

For high queries $f$ the statement follows by inspecting the definition of $H_2$ and Lemma 2.    $\square$

In $H_2$, by the $\tau n$-secrecy of the LECSS, the distribution of the symbols indexed by $T$ is independent of the message $x$ encoded by $D$. Moreover, the distribution of $T$ is trivially independent of $x$. This suggests the following simulator $\mathsf {sim}$: Initially, it chooses a random subset $T$ from $\left( {\begin{array}{c}[n]\\ \tau n\end{array}}\right)$ and chooses $\tau n$ random symbols $(c[j])_{j \in T}$. Every component $f$ of any tamper query is handled as follows: If $f$ is a low or a high query, the answer is $\mathrm {Dec}'(f,T,(c[j])_{j \in T})$; if $f$ is a middle query, the answer is $\bot$. This implies:

Lemma 6

$H_2\equiv S_{\mathcal F,\mathsf {sim}}$.

Proof

(Theorem 4 ). From Lemmas 3, 4, and 6 and a triangle inequality.    $\square$

4.5 LECSS for the Non-Malleable Code

Let $\mathbb F= {{\mathrm{GF}}}(2)$ and $\alpha > 0$. In this section we show how to construct a $(k,n,\delta ,\tau )$-LECSS $(\mathsf {E},\mathsf {D})$ (cf. Definition 1 in Sect. 2) with minimum distance $\delta$ and secrecy $\tau$ over $\mathbb F$ and the following properties (as required in Sect. 4.3):

• Minimum distance: $\delta > 1/4 + 2 \alpha$ and $\delta /2 > 2\alpha$.

• Constant rate: $k/n= \varOmega (1)$.

• Constant secrecy: $\tau = \varOmega (1)$.

The construction combines high-distance binary codes with a recent result by Cramer et al. [11], which essentially allows to “add” secrecy to any code of sufficient rate.

Let $\mathcal C$ be a $(n,l)$-code with rate $R= \frac{l}{n}$ over $\mathbb F$. In the following we write $\mathcal C(x)$ for the codeword corresponding to $x \in \mathbb F^l$ and $\mathcal C^{-1}(c,e)$ for the output of the efficient error-correction algorithm attempting to correct up to e errors on c, provided that $e < \delta n/ 2$;¹² the output is $\bot$ if there is no codeword within distance e of c.

Adding Secrecy. Let $l$ be such that $k< l< n$. The construction by [11] combines a surjective linear universal hash function $\mathsf h: \mathbb F^l\rightarrow \mathbb F^k$ with $\mathcal C$ to obtain a LECSS $(\mathsf {E},\mathsf {D})$ as follows:¹³

• $\mathsf {E}(x)$ for $x\in \{0,1\}^{k}$: Choose $s\in \{0,1\}^{l}$ randomly such that $\mathsf h(s) = x$ and output $c= \mathcal C(s)$.

• $\mathsf {D}(c,e)$ for $c\in \{0,1\}^{n}$ and $e < \delta n / 2$: Compute $s = \mathcal C^{-1}(c,e)$. If $s = \bot$, output $\bot$. Otherwise, output $x = \mathsf h(s)$.

The resulting LECSS has rate $\rho = \frac{k}{ln}$ and retains all distance and error-correction properties of $\mathcal C$. Additionally, if $R$ is not too low, the LECSS has secrecy. More precisely, Cramer et al. prove the following theorem:

Theorem 5

([11]). Let $\tau > 0$ and $\eta > 0$ be constants and $\mathcal H$ be a family of linear universal hash functions $\mathsf h: \mathbb F^l\rightarrow \mathbb F^k$. Given that $R\ge \rho + \eta + \tau + h(\tau )$, there exists a function $\mathsf h\in \mathcal H$ such that $(\mathsf {E},\mathsf {D})$ achieves secrecy $\tau$. Moreover, such a function $\mathsf h$ can be chosen randomly with success probability $1 - 2^{-\eta n}$.

The version of the above theorem presented in [11] does not claim that any $\tau n$ bits of an encoding are uniform and independent but merely that they are independent of the message encoded. Yet, by inspecting their proof, it can be seen that uniformity is guaranteed if $\tau n\le l- k$, which is the case if and only if $\tau \le \frac{l}{n}- \frac{k}{n}= R- \rho$, which is clearly implied by the precondition of the theorem.

Zyablov Bound. For code $\mathcal C$, we use concatenated codes reaching the Zyablov bound:

Theorem 6

For every $\delta < 1/2$ and all sufficiently large $n$, there exists a code $\mathcal C$ that is linear, efficiently encodable, of distance at least $\delta n$, allows to efficiently correct up to $\delta n/ 2$ errors, and has rate

$$ R\ge {\max \limits _{0\le r\le {1- h(\delta + \varepsilon )}}} r \left( 1 - \frac{\delta }{h^{-1}(1 - r) - \varepsilon } \right) , $$

for $\varepsilon > 0$ and where $h(\cdot )$ is the binary entropy function.

The Zyablov bound is achieved by concatenating Reed-Solomon codes with linear codes reaching the Gilbert-Varshamaov bound (which can be found by brute-force search in this case). Alternatively, Shen [32] showed that the bound is also reached by an explicit construction using algebraic geometric codes.

Choice of Parameters. Set $\alpha := 1/200$ and $\delta := 1/4 + 2 \alpha + \varepsilon$ for $\varepsilon := 1/500$, say. Then, $\delta - 2 \alpha > 1/4$, as required. Moreover, the rate of the Zyablov code with said distance $\delta$ can be approximated to be $R\ge 0.0175$. Setting, $\tau := 1/1000$ yields $\tau + h(\tau ) \le 0.0125$, leaving a possible rate for the LECSS of up to $\rho \approx 0.005 - \eta$. Hence:

Corollary 1

For any $\alpha > 0$ there exists a $(k,n,\delta ,\tau )$-LECSS $(\mathsf {E},\mathsf {D})$ with the following properties:

• Minimum distance: $\delta > 1/4 + 2 \alpha$ and $\delta /2 > 2\alpha$.

• Constant rate: $k/n= \varOmega (1)$.

• Constant secrecy: $\tau = \varOmega (1)$.

4.6 Impossibility for Codes Without State

We show that codes without secret state (as, e.g., the ones in [1, 2, 7, 10, 16, 17, 19]) cannot achieve (unconditional) non-malleability against parallel tampering. Specifically, we prove the following theorem:

Theorem 7

Let $\mathcal F:= \mathcal F_\mathsf {set}$. Let $(\mathrm {Enc},\mathrm {Dec})$ be a $(k,n)$-code without secret state and noticeable rate. There exists a distinguisher $D$ asking a single parallel tampering query of size $n^6$ such that, for all simulators $\mathsf {sim}$ and all $n$ large enough, $\varDelta ^{ D }(R_{\mathcal F},S_{\mathcal F,\mathsf {sim}}) \ge 1/2.$

The above impossibility result requires that the rate of the code not be too small (in fact $n= o(2^{k/6})$ suffices, see the full version for the exact parameters). The distinguisher $D$ is inefficient, so it might still be possible to construct a non-malleable code against parallel tampering with only computational security. We leave this as an interesting open question for future research.

Here, we outline an attack for the case where $\mathrm {Dec}$ is deterministic. A full proof and a generalization to the setting where $\mathrm {Dec}$ uses (independent) randomness for (each) decoding is in the full version.

Proof

(Sketch). A possible attack works as follows: There exists an (inefficient) extraction algorithm that, by suitably tampering with an encoding in the real experiment $R_{\mathcal F}$, is able to recover the original plaintext with high probability. Since (modulo some technicalities) this is not possible in the ideal experiment $S_{\mathcal F,\mathsf {sim}}$ (for any simulator $\mathsf {sim}$), this constitutes a distinguishing attack.

For simplicity, suppose that the decoding algorithm $\mathrm {Dec}$ is deterministic. The extraction relies on the fact that for any position $i \in [n]$ with relevance in the decoding, there exist two codewords $c_i'$ and $c_i''$ with $\mathrm {Dec}(c_i') \ne \mathrm {Dec}(c_i'')$ and differing in position i only. From the result of a tamper query fixing all but the ${i}^\text {th}$ position to correspond with the bits of $c_i'$ (or $c_i''$) one can therefore infer the value of the ${i}^\text {th}$ bit of the encoding. This extraction is an independent process for every (relevant) position and thus parallelizable. In other words, a single parallel tamper query can be used to recover every relevant position of an encoding (from which the original message can be computed by filling the non-relevant positions with arbitrary values and applying the decoding algorithm).    $\square$

5 Construction from CPA Security

In this section we show that NM-SDA security can be achieved in a black-box fashion from IND-CPA security. Specifically, we prove that a generalization using LECSS (cf. Sect. 2) of the scheme by Choi et al. [9] (dubbed the CDMW construction in the remainder of this section) is NM-SDA secure. Using a constant-rate LECSS allows to improve the rate of the CDMW construction from $\varOmega (1/\lambda ^2)$ to $\varOmega (1/\lambda )$, where $\lambda$ is the security parameter. This abstraction might also give a deeper understanding of the result of [9]. The main difficulty in the analysis is to extend their proof to deal with adaptively chosen parallel decryption queries (with self-destruct).

5.1 The CDMW Construction

The CDMW construction uses a randomized Reed-Solomon code, which is captured as a special case by the notion of a linear error-correcting secret sharing (LECSS) $(\mathsf {E},\mathsf {D})$ (cf. Sect. 2). For ease of description, we assume that the decoding algorithm returns not only the plaintext $x$ but also the corresponding codeword $w$, i.e., $(x,w) \leftarrow \mathsf {D}(c,e)$, where $e \in \mathbb N$ specifies the number of errors to correct; moreover, the output is $(x,w) = (\bot ,\bot )$ if $c$ is not within distance e of any codeword.

The LECSS has to satisfy an additional property, which is that given a certain number of symbols chosen uniformly at random and independently and a plaintext $x$, one can efficiently produce an encoding that matches the given symbols and has the same distribution as $\mathsf {E}(x)$. It is described in more detail in the proof of Lemma 9, where it is needed.¹⁴

Let $\varPi = (KG,E,D)$ be a PKE scheme with message space $\mathcal {M}= \{0,1\}^{\ell }$ (we assume $\ell = \varOmega (\lambda )$), and let $\varSigma = (KG^\mathsf {ots},S,V)$ be a one-time signature scheme with verification keys of length $\kappa = \mathcal {O}(\lambda )$. Moreover, let $\alpha > 0$ be any constant and $(\mathsf {E},\mathsf {D})$ a $(k,n,\delta ,\tau )$-LECSS over ${{\mathrm{GF}}}(2^\ell )$ with $\delta > 2\alpha$.

The CDMW construction (cf. Fig. 5), to encrypt a plaintext $m\in \{0,1\}^{k\ell }$, first computes an encoding $(c_{1},\ldots ,c_{n})\leftarrow \mathsf {E}(m)$ and then creates the $(\kappa \times n)$-matrix $\mathbf C$ in which this encoding is repeated in every row. For every entry $\mathbf C_{ij}$ of this matrix, there are two possible public keys $\mathsf {pk}^{b}_{i,j}$; which of them is used to encrypt the entry is determined by the ${i}^\text {th}$ bit $v[i]$ of the verification key $\mathsf {verk}= (v[1],\ldots ,v[\kappa ])$ of a freshly generated key pair for $\varSigma$. In the end, the encrypted matrix $\mathbf E$ is signed using $\mathsf {verk}$, producing a signature $\sigma$. The ciphertext is $(\mathbf E,\mathsf {verk},\sigma )$.

The decryption first verifies the signature. Then, it decrypts all columns indexed by a set $T\subset [n]$, chosen as part of the secret key, and checks that each column consists of a single value only. Finally, it decrypts the first row and tries to find a codeword with relative distance at most $\alpha$. If so, it checks whether the codeword matches the first row in the positions indexed by $T$. If all checks pass, it outputs the plaintext corresponding to the codeword; otherwise it outputs $\bot$.

In the remainder of this section, we sketch the proof of the following theorem, which implies Theorem 2.

Fig. 5.

The CDMW PKE scheme $\varPi '$ based on a CPA-secure scheme $\varPi$ [9].

Theorem 8

Let $t\in \mathbb N$ and $\varPi$ be a $(t+t_\mathsf {cpa},\varepsilon _\mathsf {cpa})$-IND-CPA-secure PKE scheme, $\alpha > 0$, $(\mathsf {E},\mathsf {D})$ a $(k,n,\delta ,\tau )$-LECSS with $\delta > 2\alpha$, and $\varSigma$ a $(t+t_\mathsf {ots},\varepsilon _\mathsf {ots})$-secure OTS scheme with verification-key length $\kappa$. Then, for any $q,p\in \mathbb N$, PKE scheme $\varPi '$ is $(t,q,p,\varepsilon )$-NM-SDA-secure with

$$ \varepsilon \quad =\quad (1-\tau )\kappa n\cdot \varepsilon _\mathsf {cpa}+ 2 \cdot \varepsilon _\mathsf {ots}+ 4 \cdot p(1-\tau )^{\alpha n}, $$

where $t_\mathsf {cpa}$ and $t_\mathsf {ots}$ represent the overhead incurred by corresponding reductions.

Instantiating the Construction. Note that the security proof below does not use the linearity of the LECSS. The CDMW construction can be seen as using a Reed-Solomon-based LECSS with rate $\mathcal {O}(1/\kappa )$. If the construction is instantiated with a constant-rate LECSS, the final rate improves over CDMW by a factor of $\varOmega (\kappa ) = \varOmega (\lambda )$. More concretely, assuming a constant-rate CPA encryption, a ciphertext of length $\mathcal {O}(\lambda ^3)$ can encrypt a plaintext of length $\varOmega (\lambda ^2)$ as compared to $\varOmega (\lambda )$ for plain CDMW. As shown in Sect. 5.3, the LECSS can be instantiated with constructions based on Reed-Solomon or algebraic geometric codes (which also satisfy the additional property mentioned above), both with constant rate. Among the constant-rate codes, algebraic geometric codes allow to choose the parameters optimally also for shorter plaintexts.

5.2 Security Proof of the CDMW Construction

The proof follows the original one [9]. The main change is that one needs to argue that, unless they contain invalid ciphertexts, adaptively chosen parallel queries do not allow the attacker to obtain useful information, in particular on the secret set $T$. This is facilitated by using the self-destruct lemma (cf. Sect. 6). The proof proceeds in three steps using two hybrid games $H_{b}$ and $H_{b}'$:

• The first hybrid $H_{b}$ gets rid of signature forgeries for the verification key used to create the challenge ciphertext. The indistinguishability of the hybrid from $G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{b}$ follows from the security of the OTS scheme and requires only minor modifications compared to the original proof.

• The second hybrid $H_{b}'$ uses an alternative decryption algorithm. The indistinguishability of $H_{b}'$ and $H_{b}$ holds unconditionally; this step requires new techniques compared to the original proof.

• Finally, the distinguishing advantage between $H_{0}'$ and $H_{1}'$ is bounded by a reduction to the IND-CPA security of the underlying scheme $\varPi$; the reduction again resembles the one in [9].

Dealing with Forgeries. For $b \in \{0,1\}$, hybrid $H_{b}$ behaves as $G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{b}$ but generates the signature key pair $(\mathsf {sigk}^*,\mathsf {verk}^*)$ used for the challenge ciphertext initially and rejects any decryption query $(\mathbf E',\sigma ',\mathsf {verk}')$ if $\mathsf {verk}' = \mathsf {verk}^*$.

Lemma 7

For $b \in \{0,1\}$, there exists a reduction $R'_{b}(\cdot )$ such that for all distinguishers $D$, $\varDelta ^{ D }(G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{b},H_{b}) \le \varGamma ^{R'_{b}( D )}(G^{\varSigma ,\mathsf {ots}})$.

Proof

$R'_{b}(\cdot )$ is a standard reduction to the unforgeability of $\varSigma$.    $\square$

Alternative Decryption Algorithm. For $b \in \{0,1\}$, hybrid $H_{b}'$ behaves as $H_{b}$ but for the way it answers decryption queries $(\mathbf E',\sigma ',\mathsf {verk}')$: As before, it first verifies the signature $\sigma '$ and checks that each column of $\mathbf E'$ consists of encryptions of a single value. Then, it determines the first position i at which $\mathsf {verk}'$ and $\mathsf {verk}^*$ differ, i.e., where $v'[i] \ne v^*[i]$. It decrypts the ${i}^\text {th}$ row of $\mathbf E$ and checks if there is a codeword $w$ within distance $2\alpha n$.¹⁵ If such $w$ does not exist or else if $w$ does not match the first row in a position indexed by $T$, the check fails. Otherwise, the plaintext corresponding to $w$ is output.

Lemma 8

For $b \in \{0,1\}$ and all distinguishers $D$, $\varDelta ^{ D }(H_{b},H_{b}') \le 2 \cdot p(1-\tau )^{\alpha n}.$

The proof of Lemma 8 shows that the original and alternative decryption algorithms are indistinguishable not just for a single parallel query (as is sufficient for NM-CPA) but even against adaptively chosen parallel queries (with self-destruct). It is the main technical contribution of this section.

At the core of the proof is an analysis of how different types of encoding matrices $\mathbf C$ are handled inside the two decryption algorithms. To that end, one can define two games $B$ and $B'$ (below) that capture the behaviors of the original and the alternative decryption algorithms, respectively. The proof is completed by bounding $\varDelta ^{}(B,B')$ (for all distinguishers) and showing the existence of a wrapper $W_{b}$ such that $W_{b}(B)$ behaves as $H_{b}$ and $W_{b}(B')$ as $H_{b}'$ (also below). This proves the lemma since $\varDelta ^{ D }(H_{b},H_{b}') = \varDelta ^{ D }(W_{b}(B),W_{b}(B')) = \varDelta ^{ D (W_{b}(\cdot ))}(B,B')$.

The games $B$ and $B'$ behave as follows: Both initially choose a random size-$\tau$ subset of $[n]$. Then, they accept parallel queries with components $(\mathbf C,i)$ for $\mathbf C\in \mathbb F^{\kappa \times n}$ and $i \in [\kappa ]$. The answer to each component is computed as follows:

• 1. Both games check that all columns indexed by $T$ consist of identical entries.

• 2. Game $B$ tries to find a codeword $w$ with distance less than $\alpha n$ from the first row (regardless of i), whereas $B'$ tries to find $w$ within $2\alpha n$ of row i. Then, if such a $w$ is found, both games check that it matches the first row of $\mathbf C$ in the positions indexed by $T$.

• 3. If all checks succeed, the answer to the (component) query is $w$; otherwise, it is $\bot$.

Both games then output the answer vector and implement the self-destruct, i.e., if any of the answers is $\bot$, all future queries are answered by $\bot$.

Claim

For $b \in \{0,1\}$ and all distinguishers $D$, $\varDelta ^{ D }(B,B') \le 2 \cdot p(1-\tau )^{\alpha n}.$

Encoding Matrices. Towards a proof of Claim 5.2, consider the following partition of the set of encoding matrices $\mathbf C$ (based on the classification in [9]):

• 1. There exists a codeword $w$ within $\alpha n$ of the first row of $\mathbf C$, and all rows have distance at most $\alpha n$.

• 2.

  • (a) There exist two rows in $\mathbf C$ with distance greater than $\alpha n$.

  • (b) The rest; in this case the first row differs in more than $\alpha n$ positions from any codeword.

Observe that queries $(\mathbf C,i)$ with $\mathbf C$ of type 1 are treated identically by both $B$ and $B'$: A codeword $w$ within $\alpha n$ of the first row of $\mathbf C$ is certainly found by $B$; since all rows have distance at most $\alpha n$, $w$ is within $2\alpha n$ of row i and thus also found by $B'$. Furthermore, note that if $\mathbf C$ is of type 2b, it is always rejected by $B$ (but not necessarily by $B'$).

Consider the hybrids $C$ and $C'$ that behave as $B$ and $B'$, respectively, but always reject all type-2 queries. Since type-1 queries are treated identically, $C$ and $C'$ are indistinguishable. Moreover:

Claim

For all distinguishers $D$, $\varDelta ^{ D }(B,C)\le p(1-\tau )^{\alpha n}$ and $\varDelta ^{ D }(C',B')\le p(1-\tau )^{\alpha n}$.

The proof of Claim 5.2 follows a generic paradigm, at whose core is the so-called self-destruct lemma, which deals with the indistinguishability of hybrids with the self-destruct property and is explained in detail in Sect. 6. Roughly, this lemma applies whenever the first hybrid (in this case $B$ resp. $B'$) can be turned into the second one (in this case $C$ resp. $C'$) by changing (“bending”) the answers to a subset (the “bending set”) of the possible queries to always be $\bot$, and when additionally non-bent queries have a unique answer (cf. the statement of Lemma 10). Intuitively, the lemma states that parallelism and adaptivity do not help distinguish (much) in such cases.

Proof

To use the self-destruct lemma, note that $B$, $C$, $C'$, and $B'$ all answer queries from $\mathcal X:= \mathbb F^{\kappa \times n} \times [\kappa ]$ by values from $\mathcal Y:= \mathbb F^n$. Moreover, note that they use as internal randomness a uniformly chosen element $T$ from the set $\mathcal R:= \left( {\begin{array}{c}[n]\\ \tau n\end{array}}\right)$ of size-$\tau n$ subsets of $[n]$.

Consider first $B$ and $C$. Let $g: \mathcal X\times \mathcal R\rightarrow \mathcal Y$ correspond to how $B$ answers queries $(\mathbf C,i)$ (see above). Let $\mathcal B$ be the set $\mathcal B$ of all type-2a-queries. Then, $C$ is its $\mathcal B$-bending (cf. Definition 7). Observe that queries $x= (\mathbf C,i) \notin \mathcal B$ are either of type 1 or 2b. For the former, the unique answer $y_{x}$ is the codeword $w$ within $\alpha n$ of the first row of $\mathbf C$; for the latter, $y_{x}$ is $\bot$. Therefore, using the self-destruct lemma (Lemma 10), for all distinguishers $D$, $\varDelta ^{ D }(B,C)\le p\cdot \max _{(\mathbf C,i) \in \mathcal B} {\mathsf P[g((\mathbf C,i),T) \ne \bot ]}$, where the probability is over the choice of $T$. Since type-2a queries have two rows with distance greater than $\alpha n$, the probability over the choice of $T$ that this remains unnoticed is at most $(1-\tau )^{\alpha n}$.

For the second part of the claim, consider $B'$ and $C'$. Now, let $g: \mathcal X\times \mathcal R\rightarrow \mathcal Y$ correspond to how $B'$ answers queries $(\mathbf C,i)$ (see above again), and let $\mathcal B$ be the set $\mathcal B$ of all type-2-queries. Then, $C'$ is the $\mathcal B$-bending of $B'$.

Note that all queries $x= (\mathbf C,i) \notin \mathcal B'$ are of type 1, and the unique answer $y_{x}$ is the codeword $w$ within $2\alpha n$ of row i of $\mathbf C$. Therefore, using Lemma 10 again, for all distinguishers $D$, $\varDelta ^{ D }(B',C')\le p\cdot \max _{(\mathbf C,i) \in \mathcal B'} {\mathsf P[g'((\mathbf C,i),T) \ne \bot ]}$, where the probability is again over the choice of $T$. Since type-2a queries have two rows with distance greater than $\alpha n$ and in type-2b queries the first row differs in more than $\alpha n$ positions from any codeword, the probability over the choice of $T$ that this remains unnoticed is at most $(1-\tau )^{\alpha n}$.    $\square$

Proof

(Claim 5.2). The proof follows using the triangle inequality:

$$\begin{aligned} \varDelta ^{ D }(B,B')\le \varDelta ^{ D }(B,C)+ \varDelta ^{ D }(C,C')+ \varDelta ^{ D }(C',B')\le 2 \cdot p(1-\tau )^{\alpha n}.\quad \square \end{aligned}$$

Wrapper. It remains to show that there exists a wrapper $W_{b}$ such that $W_{b}(B)$ behaves as $H_{b}$ and $W_{b}(B')$ as $H_{b}'$. The construction of $W_{b}$ is straight forward: $H_{b}$ and $H_{b}'$ generate all keys and the challenge in the identical fashion; therefore, $W_{b}$ can do it the same way. $W_{b}$ answers decryption queries $(\mathbf E',\mathsf {verk}',\sigma ')$ by first verifying the signature $\sigma '$ and rejecting queries if $\sigma '$ is invalid or if $\mathsf {verk}'$ is identical to the verification key $\mathsf {verk}^*$ chosen for the challenge, decrypting the entire matrix $\mathbf E'$ to $\mathbf C'$ and submitting $(\mathbf C',i)$ to the oracle (either $B$ or $B'$), where i is the first position at which $\mathsf {verk}'$ and $\mathsf {verk}^*$ differ, and decoding the answer $w$ and outputting the result or simply forwarding it if it is $\bot$. Moreover, $W_{b}$ implements the self-destruct. By inspection it can be seen that $W_{b}(B)$ implements the original decryption algorithm and $W_{b}(B')$ the alternative one.

Reduction to IND-CPA Security. We prove:

Lemma 9

There exists a reduction $R(\cdot )$ such that for all distinguishers $D$,

$$ \varDelta ^{ D }(H_{0}',H_{1}') \quad =\quad (1-\tau )\kappa n\cdot \varDelta ^{ D (R(\cdot ))}({ G }^{{\mathsf {ind}}\text {-}{\mathsf {cpa}}}_{\varPi }0,{ G }^{{\mathsf {ind}}\text {-}{\mathsf {cpa}}}_{\varPi }1). $$

Proof

(Sketch). The proof is a straight-forward generalization of the original proof by [9]; the only difference is that it needs to process multiple parallel decryption queries and implement the self-destruct feature appropriately. For ease of exposition, we describe the reduction to a many-public-key version of the CPA game for $\varPi$.¹⁶

Reduction $R(\cdot )$ initially chooses the secret set $T$ and creates the challenge OTS key pair with verification key $\mathsf {verk}^* = (v^*[1],\ldots ,v^*[\kappa ])$ and all key pairs $(\mathsf {pk}^{b}_{i,j},\mathsf {sk}^{b}_{i,j})$ with $j \in T$ or $b \ne v^*[i]$. The remaining $(1-\tau )\kappa n$ key pairs are generated by the CPA game.

Recall that the LECSS is assumed to satisfy the following property: Given $\tau n$ symbols $(c_{i})_{i \in T}$ chosen uniformly at random and independently and any plaintext $x\in \mathbb F^k$, one can efficiently sample symbols $(c_{i})_{i \notin T}$ such that $(c_{1},\ldots ,c_{n})$ has the same distribution as $\mathsf {E}(x)$. Using this fact, $R(\cdot )$ creates the challenge for $m_0$ and $m_1$ as follows: It picks the random symbols $(c_{i})_{i \in T}$ and completes them to two full encodings $c_{m_{0}}$ and $c_{m_{1}}$ with the above procedure, once using $m_0$ and once using $m_1$ as the plaintext. Let $\mathbf C_{m_{0}}$ and $\mathbf C_{m_{1}}$ be the corresponding matrices (obtained by copying the encodings $\kappa$ times). Observe that the two matrices match in the columns indexed by $T$. These entries are encrypted by $R(\cdot )$, using the public key $\mathsf {pk}^{b}_{i,j}$ for entry (i, j) for which $b \ne v^*[i]$. Denote by $\mathbf C_{m_{0}}'$ and $\mathbf C_{m_{1}}'$ the matrices $\mathbf C_{m_{0}}$ and $\mathbf C_{m_{1}}$ with the columns in $T$ removed. The reduction outputs $(\mathsf {chall},\mathbf C_{m_{0}}',\mathbf C_{m_{1}}')$ to its oracle and obtains the corresponding ciphertexts, which it combines appropriately with the ones it created itself to form the challenge ciphertext.

Finally, since the reduction knows all the secret keys $\mathsf {pk}^{b}_{i,j}$ with $b \ne v^*[i]$, it can implement the alternative decryption algorithm (and the self-destruct).    $\square$

Overall Proof. Finally, one obtains:

Proof

(Theorem  8 ). Let $t_\mathsf {cpa}$ be the overhead caused by reduction $R(\cdot )$ and $t_\mathsf {ots}$ the larger of the overheads caused by $R'_{0}(\cdot )$ and $R'_{1}(\cdot )$. Moreover, let $D$ be a distinguisher with running time at most $t$. Using the triangle inequality, and Lemmas 7, 8, and 9,

$$\begin{aligned} \varDelta ^{ D }(G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{0},G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{1})\quad \le \quad&\ \varDelta ^{ D }(G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{0},H_{0}) + \varDelta ^{ D }(H_{0},H_{0}') \\&+ \varDelta ^{ D }(H_{0}',H_{1}') + \varDelta ^{ D }(H_{1}',H_{1})\\&+ \varDelta ^{ D }(H_{1},G^{\varPi ',{\mathsf {nm}}\text {-}{\mathsf {sda}}}_{1}) \\ \le \quad&\ \varGamma ^{ D (R'_{0}(\cdot ))}(G^{\varSigma ,\mathsf {ots}}) + 2 \cdot p(1-\tau )^{\alpha n} \\&+ (1-\tau )\kappa n\cdot \varDelta ^{ D (R(\cdot ))}({ G }^{{\mathsf {ind}}\text {-}{\mathsf {cpa}}}_{\varPi }0,{ G }^{{\mathsf {ind}}\text {-}{\mathsf {cpa}}}_{\varPi }1) \\&+ 2 \cdot p(1-\tau )^{\alpha n} + \varGamma ^{ D (R'_{1}(\cdot ))}(G^{\varSigma ,\mathsf {ots}}) \\ \le \quad&\ \varepsilon _\mathsf {ots}+ 2 \cdot p(1-\tau )^{\alpha n} \\&+ (1-\tau )\kappa n\cdot \varepsilon _\mathsf {cpa}+ 2 \cdot p(1-\tau )^{\alpha n} + \varepsilon _\mathsf {ots}. \end{aligned}$$

   $\square$

5.3 LECSS for the CDMW Construction

In this section we show how to instantiate the LECSS used for the CDMW construction in Sect. 5. Let $\mathbb F$ be a finite field of size $L= 2^\ell$, where $\ell$ is the plaintext length of the IND-CPA scheme used in the construction. Then, there are the following variants of a $(k,n,\delta ,\tau )$-LECSS:

• CDMW Reed-Solomon codes: The original CDMW construction can be seen as using a Reed-Solomon-based LECSS with rate $\varTheta (1/\lambda )$, which is suboptimal (see next item).

• Constant-Rate Reed-Solomon codes: Cheraghchi and Guruswami [8] provide a LECSS based on a construction by Dziembowski et al. [17] and on Reed-Solomon (RS) codes with $\ell = \varTheta (\log n)$. One can show that it achieves the following parameters (not optimized): $\alpha = 1/8$, $\tau = 1/8$ and rate $k/n\ge 1/4$ (i.e., all constant).

• Algebraic geometric codes: Using algebraic geometric (AG) codes, Cramer et al. [12] provide a LECSS with $\ell = \mathcal {O}(1)$ and still constant error correction, secrecy, and rate (but with worse concrete constants than Reed-Solomon codes).

Note that asymptotically, RS and AG codes are equally good: both have constant rate, distance, and secrecy. However, since with AG codes $\ell$ is constant (i.e., they work over an alphabet of constant size), the minimal plaintext length can be shorter than with RS codes.

6 A General Indistinguishability Paradigm

A recurring issue in this paper are proofs that certain self-destruct games answering successive parallel decryption/tampering queries are indistinguishable. We formalize such games as parallel stateless self-destruct games.

Definition 6

An oracle $U$ is a parallel stateless self-destruct (PSSD) game if

• it accepts parallel queries in which each component is from some set $\mathcal X$ and answers them by vectors with components from some set $\mathcal Y$,

• $\bot \in \mathcal Y$,

• there is a function $g: \mathcal X\times \mathcal R\rightarrow \mathcal Y$ such that every query component $x\in \mathcal X$ is answered by $g(x,r)$, where $r\in \mathcal R$ is the internal randomness of $U$, and

• the game self-destructs, i.e., after the first occurrence of $\bot$ in an answer vector all further outputs are $\bot$.

A PSSD game can be transformed into a related one by “bending” the answers to some of the queries $x\in \mathcal X$ to the value $\bot$. This is captured by the following definition:

Definition 7

Let $U$ be a PSSD game that behaves according to $g$ and let $\mathcal B\subseteq \mathcal X$. The $\mathcal B$ -bending of $U$, denoted by $U'$, is the PSSD game that behaves according to $g'$, where

$$ g'(x,r) \quad =\quad {\left\{ \begin{array}{ll} \bot &{} \text {if} \,\, x\in \mathcal B, \\ g(x,r) &{} \text {otherwise.} \end{array}\right. } $$

The self-destruct lemma below states that in order to bound the distinguishing advantage between a PSSD and its bending, one merely needs to analyze a single, non-parallel query, provided that all non-bent queries $x$ can only be answered by a unique value $y_{x}$ or $\bot$.

Lemma 10

Let $U$ be a PSSD game and $U'$ its $\mathcal B$-bending for some $\mathcal B\subseteq \mathcal X$. If for all $x\notin \mathcal B$ there exists $y_{x}\in \mathcal Y$ such that ${\{g(x,r) \mid r\in \mathcal R\}} = {\{y_{x},\bot \}}$, then, for all distinguishers $D$, $\varDelta ^{ D }(U,U') \le p\cdot \max _{x\in \mathcal B} {\mathsf P[g(x,R) \ne \bot ]}$, where the probability is over the choice of $R$.

Proof

Fix a distinguisher $D$ and denote by $R$ and $R'$ the random variables corresponding to the internal randomness of $U$ and $U'$, respectively. Call a value $x\in \mathcal X$ dangerous if $x\in \mathcal B$ and a query dangerous if it contains a dangerous value.

In the random experiment corresponding to the interaction between $D$ and $U$, define the event $E$ that the first dangerous query contains a dangerous value $X$ with $g(X,R) \ne \bot$ and that the self-destruct has not been provoked yet. Similarly, define the event $E'$ for the interaction between $D$ and $U'$ that the first dangerous query contains a dangerous value $X'$ with $g(X',R') \ne \bot$ and that the self-destruct has not been provoked yet.¹⁷

Clearly, $U$ and $U'$ behave identically unless $E$ resp. $E'$ occur. Thus, it remains to bound ${\mathsf P[E]} = {\mathsf P[E']}$. To that end, note that adaptivity does not help in provoking $E$. For any distinguisher $D$, there exists a non-adaptive distinguisher $\tilde{ D }$ such that whenever $D$ provokes $E$, so does $D '$. $D '$ proceeds as follows: First, it interacts with $D$ only. Whenever $D$ asks a non-dangerous query, $D '$ answers every component $x\notin \mathcal B$ by $y_{x}$. As soon as $D$ specifies a dangerous query, $D '$ stops its interaction with $D$ and sends all queries to $U$.

Fix all randomness in experiment $D '(U)$, i.e., the coins of $D$ (inside $D '$) and the randomness $r$ of $U$. Suppose $D$ would provoke $E$ in the direct interaction with $U$. In such a case, all the answers by $D '$ are equal to the answers by $U$, since, by assumption, the answers to components $x\notin \mathcal B$ in non-dangerous queries are $y_{x}$ or $\bot$ and the latter is excluded if $E$ is provoked. Thus, whenever $D$ provokes $E$, $D '$ provokes it as well.

The success probability of non-adaptive distinguishers $D$ is upper bounded by the probability over $R$ that their first dangerous query provokes $E$, which is at most $p\cdot \max _{x\in \mathcal B} {\mathsf P[g(x,R) \ne \bot ]}$.    $\square$