A Synthetic Indifferentiability Analysis of Interleaved Double-Key Even-Mansour Ciphers

Abstract

Iterated Even-Mansour scheme (IEM) is a generalization of the basic 1-round proposal (ASIACRYPT ’91). The scheme can use one key, two keys, or completely independent keys.

Most of the published security proofs for IEM against relate-key and chosen-key attacks focus on the case where all the round-keys are derived from a single master key. Whereas results beyond this barrier are relevant to the cryptographic problem whether a secure blockcipher with key-size twice the block-size can be built by mixing two relatively independent keys into IEM and iterating sufficiently many rounds, and this strategy actually has been used in designing blockciphers for a long-time.

This work makes the first step towards breaking this barrier and considers IEM with Interleaved Double independent round-keys:

$$\begin{aligned} \text {IDEM}_r((k_1,k_2),m)=k_i\oplus (P_r(\ldots k_1\oplus P_2(k_2\oplus P_1(k_1\oplus m))\ldots )), \end{aligned}$$

where $i=2$ when r is odd, and $i=1$ when r is even. As results, this work proves that 15 rounds can achieve (full) indifferentiability from an ideal cipher with $O({q^{8}}/{2^n})$ security bound. This work also proves that 7 rounds is sufficient and necessary to achieve sequential-indifferentiability (a notion introduced at TCC 2012) with $O({q^{6}}/{2^n})$ security bound, so that $\text {IDEM}_{7}$ is already correlation intractable and secure against any attack that exploits evasive relations between its input-output pairs.

D. Lin—A full version is available [GL15b].

1 Introduction

Blockciphers are arguably the most important primitives in cryptography. A blockcipher $\textsf {BC}[\kappa ,n]:\{0,1\}^{\kappa } \times \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ maps a $\kappa$-bit key K and an n-bit input x to an n-bit output y. For each key K, the map $\textsf {BC}[\kappa ,n](K,\cdot )$ is a permutation, and is efficiently invertible.

Most of the existing blockcipher designs can be roughly split into two families, namely Feistel ciphers and substitution-permutation networks. The latter are known as the structure of AES, and can be generalized as key-alternating ciphers [DR02]/iterated Even-Mansour ciphers (IEM for short). An r-round IEM cipher $\text {IEM}_r$ consists of r fixed n-bit permutations $P_i$ separated by key addition

$$\begin{aligned} \text {IEM}_r(K,m)=k_r\oplus P_r(\ldots k_2\oplus P_2(k_1\oplus P_1(k_0\oplus m))\ldots ). \end{aligned}$$

The single round Even-Mansour (the case $r=1$) was developed in 1991 [EM93] in an attempt to turn a single permutation into a family of permutations (blockcipher). $\text {IEM}_1$ has been proved pseudorandom when the underlying permutation is random and public while the keys are secret. Since then, a soar of studies on IEM has been witnessed (especially in the recent half decade), for instance, on minimization [DKS13, CLL+14], on pseudorandomness [BKL+12, Ste12, LPS12, CS14], on related-key (RK) security [FP15, CS15], and on attacks (notable examples include [DKS13, DDKS15, DDKS14]). The pseudorandomness results showed that IEM is provably secure in traditional single secret key settings.

Indifferentiability of IEM. The studies on indifferentiability and sequential-indifferentiability (seq-indifferentiability) of $\text {IEM}$ are mainly motivated by further validating the SPN-based blockcipher design methodology by proving $\text {IEM}$ secure against known-key and chosen-key (CK) attacks, in which the adversary knows and chooses keys and tries to exhibit non-randomness. Roughly speaking, indifferentiability of IEM means that IEM can be as secure as an ideal cipher [MRH04], whereas seq-indifferentiability of IEM implies that IEM is correlation intractable [CGH04], and there is no relation between the inputs and outputs of IEM that can be exploited by an attack (even a chosen-key one) [MPS12]. Here the ideal cipher $\mathbf {IC}[\kappa ,n]:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^n$ is taken randomly from the set of $(2^{n}!)^{2^{\kappa }}$ possible choices of $\textsf {BC}[\kappa ,n]$. In this work, $\mathbf {IC}[2n,n]$ will be referred by $\mathbf {E}$.

As to (seq-)indifferentiability, we have been aware of four works: [ABD+13],  [LS13], [CS15], and [Ste15]. [ABD+13] showed that $\text {IEM}_5$ is indifferentiable from $\mathbf {IC}[\kappa ,n]$, if the round-key is derived from a preimage-aware key derivation function (KDF). On the other hand, [LS13] and [CS15] concentrated on single-key EM ($\text {SEM}$) in which the user-provided n-bit master key is directly used at each round: [LS13] proved that $\text {SEM}_{12}$ (12-round SEM; similarly for $\text {SEM}_{4}$ and $\text {SEM}_9$) is indifferentiable, while [CS15] proved that $\text {SEM}_{4}$ is seq-indifferentiable. In [Ste15], Steinberger proved the indifferentiability of $\text {SEM}_9$. Results on $\text {SEM}$ are closer to concrete designs, since they can be easily generalized to the case where each round-key is derived by an efficiently invertible permutation.

Problem: Even-Mansour with Two Keys. Existing works on provable security of IEM in RK and CK settings almost all focus on the SEM context: [LS13] (ASIACRYPT 2013), [FP15] (FSE 2015), [CS15] (EUROCRYPT 2015) (except for those considered random oracle modeled KDF, e.g. [ABD+13]). This work makes the first step towards breaking this barrier and considers the following problem: can we obtain an ideal cipher by mixing two independent keys into IEM and iterating enough rounds? (a problem left open by Lampe and Seurin (LS) [LS13])¹. This problem is far from being trivial because all the works on SEM (in RK and CK settings) crucially rely on the correlation between all round-keys, so that they cannot be directly generalized to double-key case. Also, the independence between round-keys may bring in weakness – the most extreme case is IEM with completely independent round-keys, which is vulnerable to trivial related-key attacks. This problem is also practical since the idea is really used in existing designs such as AES-256 [DR02], Serpent [ABK98], and LED-128 [GPPR11] – note that they (certainly) mix the keys into the state by lightweight and efficient operations and iterate, rather than use some very complex hash function to seal the 2n key bits first. The intuition is that by iterating enough rounds, such designs will be “secure”; but the fact that the diffusion of the 2n key bits is relatively slow brings in doubts (e.g. doubts on AES-256 [KHP07, BDK+10]). The fact that among the three AES variants, AES-256 was the first that is theoretically broken [BK09] seems to support such doubts, and this attack raises a problem whether there exists a $\textsf {BC}[2n,n]$ design behaving like $\mathbf {IC}[2n,n]$;² due to this, it is necessary to either validate (using a security proof) or negate (using a generic attack) this intuitive methodology.

To dig out a solution, note that using one key in the first n / 2 rounds while using the other in the last n / 2 rounds is trivially insecure [LS13]. Instead, a (seemingly) more promising approach to mixing two keys into IEM is the idea behind LED-128 [GPPR11], that is, interleaving the xoring of them: we name it interleaved double-key Even-Mansour cipher ($\text {IDEM}$ for short; see Fig. 1 for an illustration). More formally, the r-round variant is written as follows:

$$\begin{aligned} \text {IDEM}_{r}((k_1,k_2),m)=k_{t}\oplus P_{r}(\ldots k_2\oplus P_3(k_1\oplus P_2(k_2\oplus P_1(k_1\oplus m)))), \end{aligned}$$

where $t=2$ when r is odd, and $t=1$ when r is even. LS viewed $\text {IDEM}$ as a promising solution to the problem mentioned before, and gave an extremely preliminary analysis, which led to the conjecture that 15 rounds is sufficient to achieve indifferentiability; but no concrete proof exists. Moreover, the provable security of $\text {IDEM}$ with shorter rounds has not been considered yet.

Contributions. We give the first indifferentiability proof for 15-round $\text {IDEM}$. This is the first main result of this work. Interestingly, this matches LS’s conjecture, but the proof is obtained by an approach quite different from they expected.

To obtain security guarantees for shorter round cases, we prove that $\text {IDEM}_7$ is seq-indifferentiable from $\mathbf {IC}[2n,n]$; therefore, $\text {IDEM}_7$ is also correlation intractable in the random permutation model [MPS12], and resists all attacks that exploit evasive relation between its inputs and outputs. We also find a sequential distinguisher against $\text {IDEM}_6$ (which is actually an easy extension of LS’s attack against $\text {SEM}_3$ [LS13]), so that 7 rounds is also necessary. All the results are summarized by the following informal theorem.

Theorem. For the construction IDEM based on completely independent random permutations, 6 rounds is not (seq-)indifferentiable; 7 rounds is seq- indifferentiable from $\mathbf {IC}[2n,n]$ with $O({q^{6}}/{2^n})$ security bound, and is also correlation intractable in the random permutation model; 15 rounds is indifferentiable from $\mathbf {IC}[2n,n]$ with $O({q^{8}}/{2^n})$ security bound.

Due to the independence between the two n-bit round keys, at current time, we are not sure whether the results can be generalized to $\text {IEM}$ with “very general” key schedules; however, for the first time, these results indeed validate the (seemingly long standing) design principle to some extent in the open-key model, i.e. a secure blockcipher $\textsf {BC}[2n,n]$ can be built from key-alternating ciphers without using very complex KDFs, or even without any KDF. Especially, they show that the intuition behind the key schedule of LED-128 is sound. However, they certainly cannot provide direct security guarantee for LED-128 – in fact, as theoretical results, they do not guarantee the security of ANY concrete blockcipher. As already mentioned, whether there exist some designs that “behave like” $\mathbf {IC}[2n,n]$ have to be supported by more (cryptanalysis) works.

Techniques. To prove indifferentiability and seq-indifferentiability, one first builds a simulator to mimic the behaviors of all the underlying permutations. Taking $\text {IDEM}_{15}$ as an example, consider a sequence of pairs of input and output (IO for short) $(x_1,y_1),\ldots ,(x_{15},y_{15})$ (called a computation path/chain) of the 15 permutations simulated by the simulator, which satisfies $y_i\oplus x_{i+1}=k_2$ when i is odd, and $y_i\oplus x_{i+1}=k_1$ when i is even. The simulator should ensure that each such chain simulated by it matches the ideal cipher $\mathbf {E}$, i.e. $\mathbf {E}((k_1,k_2),x_1\oplus k_1)=y_{15}\oplus k_2$. The basic idea to reach this goal is Coron et al.’s simulation via chain completion technique [CHK+14], which has achieved success in (weaker) indifferentiability proofs for a variety of idealized blockciphers. It requires the simulator $\mathbf {S}$ to detect partial computation chains formed by the queries of the distinguisher, and completes the chains in advance by querying the ideal cipher $\mathbf {E}$, such that $\mathbf {S}$ is ready for answering queries in the future. To simulate answers that are consistent with $\mathbf {E}$, $\mathbf {S}$ has to use the answer from $\mathbf {E}$ to define some simulated answers; this action is called adaptation.

Detect Chains. To detect the so-called partial chains, note that the construction IDEM has the following property: given 4 values of 3 permutations $y_i$, $x_{i+1}$, $y_{i+1}$, and $x_{i+2}$ (namely, an output of $P_i$, a pair of IO of $P_{i+1}$, and an input to $P_{i+2}$), the two associated keys can be derived as $k=y_i\oplus x_{i+1}$ and $k'=y_{i+1}\oplus x_{i+2}$, and it is possible to move forward and backward along the path. By this, at some place, using three rounds for chain detection is necessary – this idea has already appeared in [LS13].

Overall Strategy of the Simulators. As to the overall strategy, the simulator used to prove seq-indifferentiability of $\text {IDEM}_7$ is quite close to those for 6-round Feistel [MPS12] and $\text {SEM}_4$ [CS15]: the simulator detects partial chains at the three middle round of $\text {IDEM}_7$, completes them forward or backward, and finally adapts them at the first or last round – depending on concrete contexts.

On the other hand, the simulator used to prove the indifferentiability of $\text {IDEM}_{15}$ is motivated by Steinberger’s illustration of indifferentiability proof for $\text {SEM}_9$ [Ste15]. The overall strategy requires detecting chains both at the two sides and at the middle – which is similar to several previous works (e.g. [CHK+14]). The core idea in this part is a so-called “pureness” property which is different from [CHK+14]: the simulator may fall into a recursive chain completion process; however, during each such recursive completion process, all the partial chains are to be adapted at the same round; as a consequence, when a partial chain is to be completed, its extending is necessarily due to simulator defining new simulated answers to random ones rather than the adaptation of some other chains, so that the “endpoints” of this chain are always random. Whereas in the context of $\text {IDEM}$, to uniquely specify a chain requires at least 3 values of 3 consecutive permutations, so that the adversary has more freedom to choose values and make different chains collide. With this in mind, we arrange two rounds to surround each adaptation zone to ensure different chains diverge in the adaptation zone; following an old convention [CHK+14], we call them buffer rounds.³ For a more detailed overview of the simulator, we refer to Sect. 3.1.

In the indifferentiability proof for $\text {IDEM}_{15}$, we used an active-chain-oriented bad events define strategy, which is motivated by the analysis of $\text {IDEM}_{7}$: we directly define some bad events to be with respect to the chains that are active during the completion process. This helps us achieving the $O({q^{8}}/{2^n})$ indifferentiability security bound in spite of the complex character of $\text {IDEM}$. Albeit loose, this bound has been quite well-looking compared to similar (full) indifferentiability proofs for idealized blockciphers (the best non-flawed one(s) among them reached the level of $O({q^{10}}/{2^n})$ [ABD+13]).

Summary: What are Inherited and What are Novel? Technically speaking, we inherit the simulation via chain completion technique, the randomness mapping argument, and the basic idea for simulator termination argument from [CHK+14]; we also inherit (and adapt) the overall frameworks of Steinberger (which dates back to Seurin [Seu09]) and Cogliati et al. [CS15] (which dates back to Mandal et  al. [MPS12]). Our novelties mainly lie in the proof for $\text {IDEM}_{15}$: first, we use a bad event to establish a slightly tighter bound on the size of the history ($O(q^2/2^n)$) and the simulator’s complexity; second, we define the bad events to be so-called active-chain-oriented, so that the probability can be very low ($O(q^6/2^n)$). They two together enable to establish the $O(q^8/2^n)$ security bound.

Organization. Section 2 presents preliminaries. Section 3 contains the first main result – the indifferentiability of $\text {IDEM}_{15}$, and the proof sketch. Section 4 contains the second main result – the seq-indifferentiability of $\text {IDEM}_{7}$. Section 5 concludes. Due to page constraints, the full proofs of the two main results have to be deferred to the full version of this paper [GL15b].

2 Preliminaries and Notations

This work focuses on $\textsf {BC}[2n,n]$, say, blockciphers with n-bit blocks and 2n-bit keys. Throughout the remaining, the n-bit round-keys are denoted by lower-case letters, i.e. $k_1$ and $k_2$, while the 2n-bit master key is interchangeably denoted by the capital letter K or the concatenation $(k_1,k_2)$ (as the reader has seen).

An n-bit random permutation is a permutation that is uniformly selected from all $(2^n)!$ possible choices. In this work, the notation $\mathbf {P}=(\mathbf {P}_1,\ldots ,\mathbf {P}_j)$ is used to denote a tuple of random permutations ($j=15$ in the context of $\text {IDEM}_{15}$, and $j=7$ in the context of $\text {IDEM}_7$), and we let $\mathbf {P}$ provide a unified interface, i.e. $\mathbf {P}.\text {P}(i,\delta ,z):=\{1,\ldots ,j\} \times \{+,-\}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$, i indicates the index, $\delta \in \{+,-\}$ indicates direct query or inverse query, and $z\in \{0,1\}^n$ is the queries value). On the other hand, the interface of the ideal cipher $\mathbf {E}$ is $\mathbf {E}.\text {E}(\delta ,K,z):=\{+,-\}\times \{0,1\}^{2n}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$.

Indifferentiability. The indifferentiability framework [MRH04] addresses the idealized construction in settings where the underlying parameters are exposed to the adversary. For concreteness, consider $\text {IDEM}_{15}^{\mathbf {P}}$: a distinguisher $\mathbf {D}^{\text {IDEM}_{15}^{\mathbf {P}},\mathbf {P}}$ with oracle access to the cipher and the underlying primitives is trying to distinguish $\text {IDEM}_{15}^{\mathbf {P}}$ from $\mathbf {E}$. Then the formal definition is as follows.

Definition 1

(Indifferentiability). The idealized blockcipher $\text {IDEM }_{15}^{\mathbf {P}}$ with oracle access to ideal primitives $\mathbf {P}$ is said to be statistically and strongly $(q,\sigma ,t,\varepsilon )$-indifferentiable from an ideal cipher $\mathbf {E}$ if there exists a simulator $\mathbf {S}^{\mathbf {E}}$ s.t. $\mathbf {S}$ makes at most $\sigma$ queries to $\mathbf {E}$, runs in time at most t, and for any distinguisher $\mathbf {D}$ which issues at most q queries, it holds

$$\begin{aligned} \left| Pr[ \mathbf {D}^{\text {IDEM }_{15}^{\mathbf {P}}, \mathbf {P}} = 1] - Pr[ \mathbf {D}^{\mathbf {E}, \mathbf {S}^{\mathbf {E}}} = 1] \right| \le \varepsilon \end{aligned}$$

Such a result means that $\text {IDEM}_{15}^{\mathbf {P}}$ can safely replace $\mathbf {E}$ in most “natural” settings – although this belief does not necessarily hold when the resource of the adversary is limited [RSS11, DGHM13]. Since introduced, indifferentiability framework has been applied to various constructions, including variants of Merkle-Damgård, Feistel [CHK+14], Sponge [BDPVA08], and IEM [ABD+13, LS13].

To formally define seq-indifferentiability, we first specify a restricted distinguisher class, namely the sequential distinguisher (seq-distinguisher) [MPS12]. Consider $\text {IDEM}_7^{\mathbf {P}}$ and ${D}^{\text {IDEM}_7^{\mathbf {P}},\mathbf {P}}$. D is sequential if it issues queries in a specific order: (1) queries the underlying primitives $\mathbf {P}$ as it wishes; (2) queries $\text {IDEM}_7^{\mathbf {P}}$ as it wishes; (3) outputs, and cannot query $\mathbf {P}$ again. This order is illustrated in the italic numbers in Fig. 3. We then define the notion total oracle query cost of D, which equals the total number of queries received by $\mathbf {P}$ (from D or $\text {IDEM}_7^{\mathbf {P}}$) when D interacts with $(\text {IDEM}_7^{\mathbf {P}},\mathbf {P})$ [MPS12]. Then, the definition of seq-indifferentiability can be obtained by tweaking the definition of (full) indifferentiability by restricting the distinguisher to the range of sequential ones, and replacing the query cost of the distinguisher by the total oracle query cost.

Definition 2

(Seq-indifferentiability). The idealized blockcipher $\text {IDEM }_7^{\mathbf {P}}$ with oracle access to ideal primitives $\mathbf {P}$ is said to be statistically and strongly $(q,\sigma ,t,\varepsilon )$-seq-indifferentiable from an ideal cipher $\mathbf {E}$ if there exists a simulator $\mathcal {S}^{\mathbf {E}}$ s.t. $\mathcal {S}$ makes at most $\sigma$ queries to $\mathbf {E}$, runs in time at most t, and for any sequential distinguisher D of total oracle query cost at most q, it holds

$$\begin{aligned} \left| Pr[ D ^{\text {IDEM }_7^{\mathbf {P}}, \mathbf {P}} = 1] - Pr[ D ^{\mathbf {E}, \mathcal {S}^{\mathbf {E}}} = 1] \right| \le \varepsilon \end{aligned}$$

Sequential-indifferentiability implies correlation intractability [MPS12, CS15].

3 Indifferentiability for 15-Round IDEM

We prove the first main theorem of this paper in this section, which is:

Theorem 1

The 15-round Even-Mansour cipher IDEM $_{15}$ from fifteen independent random permutations $\mathbf {P}=(\mathbf {P}_1,\ldots ,\mathbf {P}_{15})$ and two n-bit keys $(k_1,k_2)$ alternatively xored is strongly and statistically $(q,\sigma ,t,\varepsilon )$-indifferentiable from an ideal cipher $\mathbf {IC}[2n,n]$, where $\sigma =2^{10}\cdot q^{8}$, $t=O({q^{8}})$, and $\varepsilon \le \frac{2^{11}\cdot q^{8}}{2^{n}}+\frac{2^{14}\cdot q^6}{2^n} =O(\frac{q^{8}}{2^n})$.

As usual, we first present the simulator, then sketch the proof.

3.1 The Simulator

To build the simulator, we borrow a variant of the explicit randomness technique [CHK+14] from [CS15], that is, letting the simulator $\mathbf {S}$ query $\mathbf {P}$ as explicit randomness. We denote by $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ the simulator for IDEM$_{15}$ which takes $\mathbf {P}$ as randomness source and interacts with $\mathbf {E}$. $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ provides an interface $\mathbf {S}.\textsc {P}(i,\delta ,z)$ ($i\in \{1,\ldots ,15\}$) which is exactly the same as $\mathbf {P}$. As argued [ABD+13, CS15], using such explicit randomness is actually equivalent to lazily sampling in advance before the experiment.

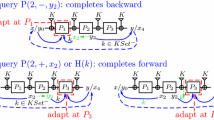
We now give a high-level overview of the simulator $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ (depicted in Fig. 1 (left)). $\mathbf {S}$ maintains a history for each simulated permutation under the form of fifteen sets $P_1,\ldots ,P_{15}$. Each of the sets has entries in the form of (x, y) for $x,y\in \{0,1\}^n$. $\mathbf {S}$ will ensure that for any $z\in \{0,1\}^n$ and $i\in \{1,\ldots ,15\}$, there is at most one $z'\in \{0,1\}^n$ such that $(z,z')\in P_i$, and vice versa; once such consistency cannot be kept, $\mathbf {S}$ aborts (will be discussed later). By this, the sets $\{P\}=\{P_1,\ldots ,P_{15}\}$ are expected to define fifteen partial permutations, and we denote by $P_i^{+}$ ($P_i^{-}$, resp.) the (time-dependent) set of all n-bit values x (y, resp.) satisfying that $\exists z\in \{0,1\}^n$ s.t. $(x,z)\in P_i$ ($(z,y)\in P_i$, resp.); denote by $P_i^{+}(x)$ ($P_i^{-}(y)$, resp.) the corresponding value of z (as mentioned the uniqueness of z is ensured by $\mathbf {S}$).

Queries that have already appeared in the history will be instantly answered with the contents in $\{P\}$. Upon a new query $\mathbf {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(i,\delta ,z)$, $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ queries $\mathbf {P}$ to draw $z'=\mathbf {P}.\textsc {P}(i,\delta ,z)$ as the answer and calls a procedure $\textsc {ForceVal}(z,z',\delta ,i)$ to add z and $z'$ to $P_i$ – inside this procedure, if $z'$ is found already in $P_i^{\overline{\delta }}$, $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ aborts due to the broken consistency (as mentioned). Then, if $(i,\delta )\in \{(2,+),(6,-),(10,+),(14,-)\}$ it satisfies the chain detection conditions, so that $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ enqueues and completes chains formed by previous queries to ensure that it is ready to simulate answers consistent with those of $\mathbf {E}$ in the future.

The cases $(i,\delta )$ equals $(2,+)$ and $(14,-)$ are similar: taking the former $\textsc {P}(2,+,x_2)$ as an example, $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ considers all tuples $(x_1,y_1,x_{14},y_{14},x_{15},y_{15})$ such that $(x_j,y_j)\in P_{j}$ for $j\in \{1,14,15\}$, recovers two keys $k_2:=y_1\oplus x_2$ and $k_1:=y_{14}\oplus x_{15}$, computes $y_0:=x_1\oplus k_1$ and $x_{16}:=y_{15}\oplus k_2$, checks whether $\mathbf {E}.\textsc {E}(+,(k_1,k_2),y_0)=x_{16}$ via an inner procedure $\mathbf {S}.\textsc {Check}$ and enqueues a 5-tuple $(y_0,k_1,k_2,0,4)$ into a queue ChainQueue when this is the case. In this tuple, the 4-th value 0 informs $\mathbf {S}$ that the first value of the tuple is $y_0$, and the last value 4 describes that when completing the chain characterized by the tuple $(y_0,k_1,k_2,0)$, $\mathbf {S}$ should add the adapted pair to $P_4$ to ensure consistency with $\mathbf {E}$. The action towards answering new query $\textsc {P}(14,-,y_{14})$ is symmetric: $\mathbf {S}$ considers all tuples $(x_1,y_1,x_{2},y_{2},x_{15},y_{15})$ such that $(x_j,y_j)\in P_{j}$ for $j\in \{1,2,15\}$, recovers the two keys, calls $\mathbf {S}.\textsc {Check}$ and enqueues $(y_0,k_1,k_2,0,12)$ into ChainQueue when $\textsc {Check}$ returns true. The chain represented by this 5-tuple will be adapted at $P_{12}$, which is different from the case $(i,\delta )=(2,+)$.

The other two cases $\textsc {P}(6,-,y_6)$ and $\textsc {P}(10,+,x_{10})$ are similar by symmetry: in each case, $\mathbf {S}$ considers all tuples $(x_7,y_7,x_{8},y_{8},x_{9},y_{9})$ such that $(x_j,y_j)\in P_{j}$ for $j\in \{7,8,9\}$, computes $k_1:=y_8\oplus x_9$ and $k_2:=y_7\oplus x_8$, checks whether $x_7\oplus k_1=y_6\wedge y_9\oplus k_2\in P_{10}^+$ (in case $\textsc {P}(6,-,y_6)$) or $x_7\oplus k_1\in P_6^-\wedge y_9\oplus k_2=x_{10}$ (in case $\textsc {P}(10,+,x_{10})$), and enqueues $(y_7,k_1,k_2,7,l)$ into ChainQueue when this is the case, where $l=4$ in case $\textsc {P}(6,-,y_6)$ and $l=12$ in case $\textsc {P}(10,+,x_{10})$.

After enqueuing, $\mathbf {S}$ starts an execution of $\textsc {RecursiveCompletion}$, during which it continues taking the tuples out of ChainQueue and completing the associated partial chains till ChainQueue is empty again. More clearly, for each chain C dequeued from the queue, $\mathbf {S}$ evaluates in the $\text {IDEM}_{15}$ computation path both forward and backward and queries $\mathbf {E}$ once to “wrap” around, until obtaining $x_l$ (when moving forward) or $y_{l}$ (when moving backward). $\mathbf {S}$ then calls $\textsc {ForceVal}(x_l,y_{l},\bot ,l)$ to add $(x_l,y_{l})$ to $P_l$ as a newly defined pair of IO, so that the entire computation path is consistent with the answers of $\mathbf {E}$. Inside this call to $\textsc {ForceVal}$, if $x_{l}\in P_l^+$ or $y_{l}\in P_l^-$ before they are to be added, $\mathbf {S}$ aborts (also as mentioned).

During the completion of a chain, $\mathbf {S}$ adds new entries to $P_i$ which are necessary for its evaluation. Such new values also trigger new chains to be enqueued when they satisfy the chain detection conditions mentioned before. For this, note that $\mathbf {S}$ continues dequeuing and completing chains till ChainQueue is empty again. To avoid re-completing the same chain, $\mathbf {S}$ maintains a set CompSet to keep a record of what it has completed, and a chain C dequeued from the queue will be completed only if $C\notin CompSet$. After all the works above are finished, $\mathbf {S}$ answers the original query with $P_i^{\delta }(z)$.

Note that throughout the process, the entries in $\mathbf {S}.\{P\}$ are never overwritten; once $\mathbf {S}$ finds itself unable to maintain consistency any more, $\mathbf {S}$ just aborts.

The pseudocode of $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ and a modified simulator $\widetilde{S}^{\widetilde{E}^{\mathbf {E}},\mathbf {P}}$ (please see Sect. 3.2) is presented as follows. When a line has a boxed variant next to it, $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ uses the original code, whereas $\widetilde{S}^{\widetilde{E}^{\mathbf {E}},\mathbf {P}}$ uses the boxed one.

Fig. 1.

(left) $\text {IDEM}_{15}$ with the zones where the simulator detects chains and adapts them; (right) $\text {IDEM}_{7}$ and how the simulator for sequential indifferentiability works.

3.2 The Key Points of the Proof

As in previous works, for any fixed, deterministic,⁴ and computationally unbounded distinguisher $\mathbf {D}$, we first show that the complexity of $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ is polynomial except with negligible probability, then show that the simulated system $\varSigma _{1}(\mathbf {E},\mathbf {S}^{\mathbf {E},\mathbf {P}})$ and the real system $\varSigma _{3}(\text {IDEM}_{15}^{\mathbf {P}},\mathbf {P})$ are indistinguishable.

Intermediate System. The proof uses an intermediate system $\varSigma _2(\widetilde{E}^{\mathbf {E}},\widetilde{S}^{\widetilde{E}^{\mathbf {E}},\mathbf {P}})$ which consists of two modified constructions $\widetilde{E}^{\mathbf {E}}$ and $\widetilde{S}^{\widetilde{E}^{\mathbf {E}},\mathbf {P}}$. $\widetilde{E}^{\mathbf {E}}$ can be seen as an ideal cipher $\mathbf {E}$ enhanced with a history maintaining mechanism and a Check procedure. More clearly, $\widetilde{E}^{\mathbf {E}}$ offers the same interface as $\mathbf {E}$, relays the answers of $\mathbf {E}$ except that it uses a set ES to keep the history of these queries. The entries in ES are of the form $(x,y,(k_1,k_2))$. $\widetilde{E}^{\mathbf {E}}$ provides an additional interface Check to $\widetilde{S}$; upon a call to $\textsc {Check}(x,y,K)$, $\widetilde{E}^{\mathbf {E}}$ checks whether $(x,y,K)\in ES$ and answers accordingly. On the other hand, the modified simulator $\widetilde{S}^{\widetilde{E}^{\mathbf {E}},\mathbf {P}}$ shares the same main strategy with $\mathbf {S}^{\mathbf {E},\mathbf {P}}$ except that it queries $\widetilde{E}^{\mathbf {E}}$ – particularly, it calls $\widetilde{E}^{\mathbf {E}}.\textsc {Check}$ whenever necessary. The code of $\widetilde{S}$ is presented along with $\mathbf {S}$ in Sect. 3.1. The three systems are depicted in Fig. 2.

Since all the entries of ES actually come from (an ideal cipher) $\mathbf {E}$, ES always defines a partial cipher, and we use a notation system similar to that for $\{P\}$. More clearly, we denote by $ES^{+}$ the set of tuples (K, x) s.t. $\exists y:(x,y,K)\in ES$, and denote by $ES^{+}(K,x)$ the corresponding y. Similarly for $ES^{-}$ and $ES^{-}(K,y)$. Finally, denote by $|\widetilde{E}.ES|$ the size of $\widetilde{E}.ES$.

Fig. 2.

Systems used in the indifferentiability proof for $\text {IDEM}_{15}$.

Complexity of $\widetilde{{\varvec{S}}}$ in $\varvec{\varSigma _2,}$ and Transition from $\varvec{\varSigma _1}$ to $\varvec{\varSigma _2}$ . The starting point is the same as [CHK+14]: the number of “external” chains $(y_0,k_1,k_2,0)$ completed by $\widetilde{S}$ is bounded by the number of queries of $\mathbf {D}$ to $\widetilde{E}$, which is at most q; by this, for $i\in \{6,7,8,9,10\}$, $P_i$ consists of entries due to $\mathbf {D}$’s queries and $\widetilde{S}$ completing chains $(y_0,k_1,k_2,0)$, so that $|P_i|\le 2q$.

Then the argument deviates from [CHK+14]: by construction, $\widetilde{S}$ enqueues a “middle” chain $(y_7,k_1,k_2,7,l)$ only if there are 5 entries $(x_i,y_i)\in P_i$ for $i=6,7,8,9,10$ s.t. $y_6=x_{7}\oplus y_8\oplus x_{9}$ and $y_7\oplus x_{8}\oplus y_9=x_{10}$. Consider a bad event BadLockMid, which happens in $\mathbf {D}^{\varSigma _2}$ if any call to $\textsc {InnerP}$ creates a new pair of 3-tuples $((x_{7},y_{7}),(x_{8},y_{8}),(x_{9},y_{9}))\!\!\in P_7\times P_8\times P_9$ and $((x_{7}',y_{7}'),(x_{8}',y_{8}'),(x_{9}',y_{9}'))\in P_7\times P_8\times P_9$ such that $x_{7}\oplus y_{8}\oplus x_{9}=x_{7}'\oplus y_{8}'\oplus x_{9}'$ and $y_{7}\oplus x_{8}\oplus y_{9}=y_{7}'\oplus x_{8}'\oplus y_{9}'$. Taking all possibilities into consideration, its overall probability is at most $\frac{2^7\cdot q^6}{2^n}+\frac{2^6\cdot q^4}{2^n}+\frac{2^5\cdot q^4}{2^n}\le \frac{2^8\cdot q^6}{2^n}$; and conditioned on $\lnot \textsf {BadLockMid}$, each pair $(y_6,x_{10})\in P_6^-\times P_{10}^+$ corresponds to at most one tuple $((x_{7},y_7),(x_{8},y_8),(x_{9},y_9))\in P_7\times P_8\times P_9$ s.t. $y_6=x_{7}\oplus y_8\oplus x_{9}$ and $y_7\oplus x_{8}\oplus y_9=x_{10}$, hence $\widetilde{S}$ enqueues at most $|P_6|\cdot |P_{10}|\le 4q^2$ “middle” chains $(y_7,k_1,k_2,7,l)$. By this, each $|P_i|$ is bounded to $O(q^2)$, $|\widetilde{E}.ES|$ to $5q^2$, and $\widetilde{S}$ issues at most $(5q^2)^4$ queries to $\widetilde{E}.\textsc {Check}$.

The rest part of the first transition is very close to [CHK+14] (and is almost the same as [GL15a]): for two executions $\mathbf {D}^{\varSigma _{1}}$ and $\mathbf {D}^{\varSigma _2}$ which share the same random primitives $(\mathbf {E},\mathbf {P})$, conditioned on $\lnot \textsf {BadLockMid}$, if the first $(5q^2)^4$ calls to $\mathbf {S}.\textsc {Check}$ in $\mathbf {D}^{\varSigma _{1}}$ obtain the same answers as the first $(5q^2)^4$ calls to $\widetilde{E}.\textsc {Check}$ in $\mathbf {D}^{\varSigma _2}$ ($Pr\ge 1-1250q^8/2^n$), then $\mathbf {D}$ outputs the same in $\mathbf {D}^{\varSigma _{1}}$ and $\mathbf {D}^{\varSigma _2}$.

Lemma 1

For any distinguisher $\mathbf {D}$ which issues at most q queries, it holds:

• (i) $| Pr[\mathbf {D}^{ \varSigma _{1}(\mathbf {E},\mathbf {S}) } = 1] - Pr[\mathbf {D}^{\varSigma _2(\widetilde{E},\widetilde{S})} = 1] | \le \frac{2^{11}\cdot q^{8}}{2^{n}};$

• (ii) during the execution $\mathbf {D}^{\varSigma _{1}(\mathbf {E},\mathbf {S})}$, with probability at least $1- \frac{2^{11}\cdot q^{8}}{2^{n}}$, $\mathbf {S}$ issues at most $2^{10}\cdot q^{8}$ queries to $\mathbf {E}$, and runs in time at most $O(q^{8})$.

The most difficult part of the proof is the transition from $\varSigma _2$ to $\varSigma _3$, which will be presented in the next paragraph.

Transition from $\varvec{\varSigma _2}$ to $\varvec{\varSigma _3}$ : Non-abortion Argument for $\widetilde{{\varvec{S}}}$ . ${\widetilde{S}}$ is built with the expectation that if it does not abort, then the outputs of $\varSigma _2$ and $\varSigma _3$ are indistinguishable; we will see that this intuition is true, so that the first (and actually core) step of the transition is to show that the abort probability of $\widetilde{S}$ is negligible. For this, we introduce several notions and (improbable) bad events, then show that if neither of them happens, then $\widetilde{S}$ does not abort.

Random Assignments. Similarly to [LS13], we use the notion random forward assignment in set $P_i$ (random backward assignment in set $P_i$, resp.) to refer to line 62 inside any execution of $\textsc {ForceVal}(z,z',+,i)$ (line 61 inside any execution of $\textsc {ForceVal}(z,z',-,i)$, resp.), and use the notion random forward (backward, resp.) assignment in set ES to refer to any operation sequence $z':=\mathbf {E}.\textsc {E}(+,K,z)$ ($z':=\mathbf {E}.\textsc {E}(-,K,z)$, resp.) and then adding z and $z'$ to ES. We also use random assignments to indifferently refer to the forward or backward case.

Partial Chains. In this paper, the partial chains are characterized by 4-tuples $(y_i, k_1, k_2, i)\in \{0,1\}^{n}\times \{0,1\}^{n}\times \{0,1\}^{n}\times \{0,\ldots ,15\}$. Besides this notion, we borrow two helper functions $val_{l}^{+}$ and $val_{l}^{-}$ from previous works: w.r.t. the values in the given sets ES and $\{P\}$, $val_{l}^{+}$ and $val_{l}^{-}$ take a partial chain as input, and evaluate forward and backward respectively (wrap around through ES if necessary) until obtaining the corresponding input value $x_l$ to $P_l$ and input value $y_l$ to $P_l^{-1}$ respectively, or the evaluation is blocked by some missed entry (in the sets), and return $x_l$ and $y_l$ respectively in the former case while $\bot$ in the latter case. Based on $val_{l}^{+}$ and $val_{l}^{-}$, we borrow (and redefine) the notion of equivalent partial chains: w.r.t. $\{P\}$ and $\widetilde{E}.ES$, two partial chains $C=(y_i,k_1,k_2,i)$ and $D=(y_j,k_1,k_2,j)$ (with the same keys) are equivalent (denoted $C\equiv D$) if $y_i=val_i^-(D)$ or $y_j=val_j^-(C)$.⁵

Bad Events, and Non-abortion. A random answer from $\mathbf {P}$ or $\mathbf {E}$ is bad if it collides with some value relevant to the “active” chains. To specify such “active” chains, we define a notion history for partial chains $\mathcal {CH}$ from the sets ES and $\{P_7,P_8,P_9\}$ at the moment where the random answer is drawn: $\mathcal {CH}$ is the union of two sets $\mathcal {ECH}$ and $\mathcal {MCH}$, where $\mathcal {ECH}$ includes all the tuples $(y_0,k_1,k_2,0)$ with $((k_1,k_2),y_0)\in ES^+$, and $\mathcal {MCH}$ includes all $(y_7,k_1,k_2,7)$ with $y_7\in P_7^-$, $x_8=y_7\oplus k_2\in P_8^+$, and $x_9=P_8^+(x_8)\oplus k_1\in P_9^+$. By the complexity analysis, conditioned on $\lnot \textsf {BadLockMid}$, $|\mathcal {CH}|\le 5q^2+(2q)^3\le 13q^3$.

We then list the bad events (more precisely, their ideas). Due to space constraints, we have to defer their formal definitions to the full version [GL15b].

• BadHitAdapt: an answer from $\mathbf {P}$ collides with a previous adapted value;

• BadE: an answer from $\mathbf {E}$ collides with a value in $P_1$ or $P_{15}$ xored the key, i.e. $\mathbf {E}.\textsc {E}(-,(k_1,k_2),x_{16})\oplus k_1\in P_{1}^+$, or $\mathbf {E}.\textsc {E}(+,(k_1,k_2),y_0)\oplus k_2\in P_{15}^-$;

• BadP: extension of some chain C meets an old P-tuple after a random assignment in $\{P\}$ with the same direction, i.e. $\exists C\in \mathcal {CH}$ s.t. for more than one value i, $val_i^{+}(C)$ ($val_i^{-}(C)$, resp.) differs after a random forward (backward, resp.) assignment in $\{P\}$ from before the assignment;

• BadInvP: some chain C extends after a random assignment in $\{P\}$ with the opposite direction, i.e. $\exists C\in \mathcal {CH}$ s.t. for some value i, $val_i^{+}(C)$ ($val_i^{-}(C)$, resp.) differs after a random backward (forward, resp.) assignment in $\{P\}$ from before the assignment;

• BadMidP: a random assignment in $P_7$, $P_8$, or $P_9$ creates a new 5-tuple $(y_6, (x_7,y_7),(x_8,y_8),(x_9,y_9),x_{10})\in P_6^-\times P_7 \times P_8 \times P_9 \times P_{10}^+$ such that $y_6\oplus x_7=y_8\oplus x_9$ and $y_7\oplus x_8=y_9\oplus x_{10}$;

• BadlyCollide (a term from [CHK+14]): two chains C, $D\in \mathcal {CH}$ that are not equivalent suddenly satisfies $val_i^{\delta }(C)=val_i^{\delta }(D)$ after a random assignment.

The overall probability (the event BadLockMid included) cumulates to $\frac{2^{13.4}\cdot q^6}{2^n}$.

We call a pair of primitive (E,P) a good $\varSigma _2$ -tuple if none of the bad events above (BadLockMid included) happens during the execution $D^{\varSigma _2(\widetilde{E}^{\mathbf {E}},\widetilde{S}^{\widetilde{E}^{\mathbf {E}},\mathbf {P}})}$, and call $D^{\varSigma _2}$ with good $\varSigma _2$-tuples good $\varSigma _2$ executions. During good $\varSigma _2$ executions, $\widetilde{S}$ never aborts due to calls to $\textsc {ForceVal}(x_i,y_i,+,i)$/$\textsc {ForceVal}(x_i,y_i,-,i)$, as otherwise $\textsf {BadHitAdapt}$ happens. We then proceed to argue that $\widetilde{S}$ never aborts due to calls to $\textsc {ForceVal}(x_l,y_l,\bot ,l)$ (i.e. adaptations: $l\in \{4,12\}$), to complete the non-abortion argument.

Lemma 2

In a good execution $\overline{D}^{\varSigma _2}$, before any call to $\textsc {ForceVal}(x_l,y_l,\bot ,l)$ ($l\in \{4,12\}$), $x_l\notin P^+_l\wedge y_{l}\notin P_l^-$ must hold.

Proof

The proof flow is very similar to [CHK+14], while some ideas slightly deviate. Let’s sketch the flow: wlog consider a call $\textsc {ForceVal}(x_4,y_4,\bot ,4)$, and suppose that it is made during an execution of $\textsc {Complete}(C,4)$. We argue that $val^{+}_{4}(C)\notin P_4^+$ right before the call to $\textsc {ForceVal}(x_4,y_4,\bot ,4)$, and the argument for $val^{-}_{4}(C)\notin P_4^-$ is similar by symmetry. The ideas are as follows:

First, before C is enqueued, $val^{+}_{3}(C)=\bot$ (this implies $val^{+}_{4}(C)=\bot \notin P_4^+$): if $C=(y_0,k_1,k_2,0)$ is enqueued by $\textsc {InnerP}(2,+,x_2)$, then $val^{+}_{3}(C)=\bot$ is clear; if $C=(y_7,k_1,k_2,7)$ is enqueued by $\textsc {InnerP}(6,-,y_6)$, then if $val^{+}_{3}(C)\ne \bot$, a chain $(y_0,k_1,k_2,0)$ equivalent to C must have been previously enqueued and completed due to the call to $\textsc {InnerP}(2,+,val^+_2(C))$, and C would have been in CompletedSet when C is dequeued, as a consequence the purported call to $\textsc {ForceVal}(x_4,y_4,\bot ,4)$ would not happen.

Second, if $val_{4}^{+}(C)\in P^+_4$ when C is dequeued, it can only be that for another chain D enqueued before C is enqueued and dequeued after C is enqueued, it holds $val_{4}^{+}(D)=val_{4}^{+}(C)\ne \bot$ so that $val_{4}^{+}(C)$ was added to $P^+_4$ during D’s completion.

Then, we argue that $val_{4}^{+}(D)=val_{4}^{+}(C)\ne \bot$ is not possible for any such chain D, so that when C is dequeued, either $val_{4}^{+}(C)=\bot$, or $val_{4}^{+}(C)\ne \bot \wedge val_{4}^{+}(C)\notin P^+_4$. To argue about this, we exclude the possibility for each of the following cases:

• (i) if $val^+_{2}(C)\ne val^+_{2}(D)$ at some point, then $val^{+}_{3}(C)\ne val^{+}_{3}(D)$. Otherwise, consider the last assignment before $val^{+}_{3}(C)=val^{+}_{3}(D)\ne \bot$ holds. This assignment happens earliest right before C is enqueued, at which point both C and D have been in $\mathcal {CH}$ (by construction and definition). Then:

  • it cannot have been in ES, otherwise BadE happens;

  • it cannot have been a random backward assignment in $\{P\}$, otherwise BadInvP happens;

  • it cannot have been a random forward assignment in $\{P\}$, otherwise BadlyCollide happens;

  • it cannot have been due to a previous adaptation, since by construction, when C is enqueued, all the chains in ChainQueue are to be adapted at $P_4$ which is the same as C, so that it cannot be that $val^{+}_{3}(C)=\bot$ or $val^{+}_{3}(D)=\bot$ due to a missed entry in $P_{12}$ which is later added by an adaptation in this period.

  Then a similar discussion further establishes $val^{+}_{4}(C)\ne val^{+}_{4}(D)$;

• (ii) if $val^+_{2}(C)=val^+_{2}(D)\ne \bot$ while $val^+_{3}(C)\ne val^+_{3}(D)$ at some point, then similarly to Case (i), $val^{+}_{4}(C)\ne val^{+}_{4}(D)$ will hold;

• (iii) if $val^{+}_{2}(C)=val^{+}_{2}(D)\ne \bot$ and $val^{+}_{3}(C)=val^+_{3}(D)\ne \bot$, then $val^{+}_{4}(C)\ne val^{+}_{4}(D)$ otherwise $C\equiv D$ and $C\in CompletedSet$ when C is dequeued.

Finally, after C is dequeued, if $val_{4}^{+}(C)=\bot$, then since $\lnot \textsf {BadP}$, it can only be changed non-empty by a random forward assignment in $P_3$ which occurs during the completion of C, after which $val_{4}^{+}(C)\notin P_4^+$. These complete the proof.    $\square$

The Rest Part. During $\mathbf {D}^{\varSigma _2}$, if $\widetilde{S}$ does not abort, then the answers are consistent with some $\varSigma _3$ executions. By a randomness mapping argument [CHK+14], the advantage of $\mathbf {D}$ in distinguishing $\varSigma _2$ and $\varSigma _3$ is bounded.

Lemma 3

For any distinguisher $\mathbf {D}$ which issues at most q queries, it holds:

$$\begin{aligned} \left| Pr[\mathbf {D}^{\varSigma _3(\text {IDEM }_{15},\mathbf {P})}=1]-Pr[\mathbf {D}^{\varSigma _2(\widetilde{E},\widetilde{S})}=1] \right| \le \frac{2^{14}\cdot q^6}{2^n} . \end{aligned}$$

4 Seq-indifferentiability for 7-Round $\text {IDEM}$

According to [LS13, ABD+13], there is a seq-distinguisher for $\text {SEM}_3$. Consider $\text {IDEM}_6$. If we fix the key $k_2$ to an arbitrary value, then the construction is reduced to a 3-round single-key Even-Mansour. By this, a seq-distinguisher for $\text {IDEM}_6$ is easily obtained.

It is natural to ask whether the additional n-bit key offers more freedom to the adversary and enable to attack more than this trivial $2\times 3$ rounds. The second main result – also the main theorem of this section – provides a negative answer, and is as follows:

Theorem 2

The 7-round Even-Mansour cipher $\text {IDEM }_7$ from seven independent random permutations $\mathbf {P}=(\mathbf {P}_1,\ldots ,\mathbf {P}_{7})$ and two n-bit keys $(k_1,k_2)$ alternatively xored is strongly and statistically $(q,\sigma ,t,\varepsilon )$-seq-indifferentiable from $\mathbf {E}$, where $\sigma =q^{3}$, $t=O(q^3)$, and $\varepsilon \le \frac{27q^6}{2^n}=O(\frac{q^{6}}{2^n})$.

Proof

The proof is much simpler than that of Theorem 1, since there is no recursive chain completion. In the following, we first present the simulator, then sketch the proof. The full proof is deferred to the full version [GL15b].

Simulator for IDEM $_7$. To make a distinction from the notations used in Sect. 3, we denote by $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ the simulator for $\text {IDEM}_7$ with access to $\mathbf {E}$ and $\mathbf {P}$. Similarly to $\mathbf {S}^{\mathbf {E},\mathbf {P}}$, $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ also offers an interface $\textsc {P}(i,\delta ,z)$ where $(i,\delta ,z)\in \{1,\ldots ,7\}\times \{+,-\}\times \{0,1\}^n$ and maintains a set $P_i$ for each i to keep the already defined pairs of IO. The other notations $P_i^{+}$, $P_i^{-}$, and $|P_i|$ are all similar to those introduced in the context of $\text {IDEM}_{15}$. $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ uses an additional set ES to maintain the history of its queries to $\mathbf {E}$, which is similar to the set of $\widetilde{E}^{\mathbf {E}}$ introduced in Sect. 3. We also use the notations $ES^{+}$, $ES^{-}$, and |ES| similar to Sect. 3.

Upon a query to $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(i,\delta ,z)$, $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ calls an inner procedure $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}^{in}$, and $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}^{in}$ answers with $P_i^{\delta }(z)$ if $x\in P_i^{\delta }$, or queries $\mathbf {P}.\mathrm {P}(i,\delta ,z)$ to obtain the answer $z'$ and adds z and $z'$ to $P_i$ if $z'\notin P_i^{\overline{\delta }}$ while aborts otherwise.

The chain completing mechanism of $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ is much simpler than that of $\mathbf {S}^{\mathbf {E},\mathbf {P}}$, and is somehow close to that appeared in [CS15]: $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ completes the potential partial chains upon receiving a new query $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(i,\delta ,x)$ with $i\in \{3,4,5\}$. More clearly, when the query is of the form $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(3,+,x)$, $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(4,-,y)$, or $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(5,+,x)$, $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ considers all newly created tuples $(x_3,x_4,x_5)\in P_3^{+}\times P_4^{+}\times P_5^{+}$, and computes $k_1:=P_4^+(x_4)\oplus x_5$, $k_2:=P_3^+(x_3)\oplus x_4$. $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ then evaluates in $\text {IDEM}_7$ both backward and forward until obtaining the corresponding $y_7$ and $x_7$, that is, computing the following values by calling $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}^{in}$ and querying $\mathbf {E}$, in the order: (1) $y_2:=x_3\oplus k_1$; (2) $y_1:=\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}^{in}(2,-,y_2)\oplus k_2$; (3) $y_0:=\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}^{in}(1,-,y_1)\oplus k_1$; (4) $y_7:=\mathbf {E}.\textsc {E}(+,(k_1,k_2),y_0)\oplus k_2$; (5) $x_6:=P_5^+(x_5)\oplus k_2$; (6) $x_7:=\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}^{in}(6,+,x_6)\oplus k_1$. $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ finally aborts if $x_7\in P_7^{+}$ or $y_7\in P_7^{-}$, otherwise adds $(x_7,y_7)$ to $P_7$ as a newly defined pair of IO.

When the query is $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(3,-,y)$, $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(4,+,x)$, or $\mathcal {S}^{\mathbf {E},\mathbf {P}}.\textsc {P}(5,-,y)$, $\mathcal {S}^{\mathbf {E},\mathbf {P}}$ considers all newly created tuples $(x_3,x_4,x_5)\in P_3^{+}\times P_4^{+}\times P_5^{+}$, computes $k_1$ and $k_2$, evaluates in $\text {IDEM}_7$ both forward and backward until obtaining the corresponding $x_1$ and $y_1$, and finally adds $(x_1,y_1)$ to $P_1$ or aborts if $x_1\in P_1^{+}$ or $y_1\in P_1^{-}$. The strategy is illustrated in Fig. 1 (right).

To simplify the reasoning, we introduce a modified simulator $\mathcal {T}^{\mathbf {E},\mathbf {P}}$, which is obtained by embedding two early abort conditions into $\mathcal {S}^{\mathbf {E},\mathbf {P}}$:

• (i) when a chain C is to be adapted at $P_1$ ($P_7$, resp.), right after the assignment (lines 13 or 16 in the code below) inside the call to $\textsc {P}^{in}$ which led to C being detected, if the value $y_2$ ($x_6$, resp.) corresponding to C has been in $P_2^-$ ($P_6^+$, resp.), then $\mathcal {T}$ aborts. This is captured by the procedure $\textsc {CheckFreeBuffer}$;

• (ii) right after an assignment in $P_3$, $P_4$, or $P_5$ (lines 13/16), $\mathcal {T}$ aborts if the assignment creates a “lock” in the middle three rounds: for $(i,j)\in \{(3,4),(4,5)\}$, if $\exists (x_i,y_i),(x_i',y_i')\in P_i$ and $(x_j,y_j),(x_j',y_j')\in P_j$ such that $x_i\oplus y_j=x_i'\oplus y_j'$ and $y_i\oplus x_j=y_i'\oplus x_j'$. This is captured by the procedure $\textsc {CheckLock}$. This situation is harmful for the procedure $\textsc {CompChain}$ in some cases.

With all the above in mind, we have the pseudocode of $\mathcal {S}$ and $\mathcal {T}$ as follows. Note that the underlined lines only exist in $\mathcal {T}$ (say, $\mathcal {S}$ does not early abort).

Intermediate System $\varSigma _2'$. Denote by $\varSigma _1'(\mathbf {E},\mathcal {S}^{\mathbf {E},\mathbf {P}})$ the simulated system, and by $\varSigma _3'({\text {IDEM}}_7^{\mathbf {P}},\mathbf {P})$ the real system. As a quite standard first step, we introduce an intermediate system $\varSigma _2'(\text {IDEM}_7^{\mathcal {T}^{\mathbf {E},\mathbf {P}}},\mathcal {T}^{\mathbf {E},\mathbf {P}})$, in which the cipher $\text {IDEM}_7$ calls the interfaces of $\mathcal {T}$ to compute (as done in [MPS12, CS15]). The three systems involved in this proof are depicted in Fig. 3.

Fig. 3.

Systems used in the seq-indifferentiability proof for $\text {IDEM}_7$. The number in

and italic illustrates the order of the queries/actions (of the sequential distinguisher) (Color figure online).

Complexity of $\mathcal {S}$/$\mathcal {T}$. By construction, for $i\in \{3,4,5\}$, $|P_i|$ can be enlarged by at most 1 only if $\mathcal {S}$/$\mathcal {T}$ receives a query $\textsc {P}(i,\delta ,\cdot )$. Hence for any seq-distinguisher D of total oracle query cost at most q, $\mathcal {S}$/$\mathcal {T}$ completes at most $|P_3|\cdot |P_4|\cdot |P_5|\le q^3$ chains, and queries $\mathbf {E}$ at most $q^3$ times (say, $|ES|\le q^3$).

The running time of $\mathcal {S}$ is clearly dominated by the executions of $\textsc {CompChain}$, the number of which is $O(q^3)$. Therefore, $\mathcal {S}$ runs in time $O(q^3)$.

Indistinguishability of Outputs. We first upper bound the abort probability of $\mathcal {T}$. Consider the two early abort conditions first:

• (i) The overall probability that $\mathcal {T}$ aborts during $\textsc {CheckFreeBuffer}$ is at most $\frac{2q^6}{2^n-q}$;

• (ii) The overall probability that $\mathcal {T}$ aborts during $\textsc {CheckLock}$ is at most $\frac{2q^4}{2^n-q}$;

Then the two types of main abortions of $\mathcal {T}$ are as follows:

• (i) a random answer from $\mathbf {P}_1$ or $\mathbf {P}_7$ collides with a previously added adapted value. The overall probability is at most $\frac{4q^6}{2^n-2q^3}$;

• (ii) $\mathcal {T}$ aborts due to adaptations. The overall probability is at most $\frac{5q^6}{2^n-2q^3}$; this is obtained by carefully analyzing each case. A key point is that the buffer rounds ensure that any two chains completed during the same call to $\textsc {P}^{in}$ will diverge at the adaptation round – the case is slightly similar to $\text {IDEM}_{15}$.

These cumulate to $\frac{26q^6}{2^n}$ (assuming $q^3<\frac{2^n}{4}$). For a tuple $(\mathbf {E},\mathbf {P})$, if $\mathcal {T}$ does not abort in $\varSigma _2'(\text {IDEM}_7^{\mathcal {T}^{\mathbf {E},\mathbf {P}}},\mathcal {T}^{\mathbf {E},\mathbf {P}})$, then $\mathcal {S}$ does not abort in $\varSigma _1'(\mathbf {E},\mathcal {S}^{\mathbf {E},\mathbf {P}})$; and then the final bound $\frac{27q^6}{2^n}=\frac{26q^6}{2^n}+\frac{q^6}{2^n}$ is obtained by a randomness mapping argument, where the statistical distance $\frac{q^6}{2^n}$ is due to $|ES|\le q^3$ random values from $\mathbf {E}$.   $\square$

5 Conclusion

As a first step towards understanding the security of iterated Even-Mansour with key-length larger than the block-size, this work analyzes (seq-)indifferentiability of Even-Mansour with two independent round-keys alternatively xored, and proves that 7 rounds is necessary and sufficient to achieve sequential indifferentiability while 15 rounds is sufficient to achieve full indifferentiability.