Abstract
We introduce a novel concept of dual-system simulation-sound non-interactive zero-knowledge (NIZK) proofs. Dual-system NIZK proof system can be seen as a two-tier proof system. As opposed to the usual notion of zero-knowledge proofs, dual-system defines an intermediate partial-simulation world, where the proof simulator may have access to additional auxiliary information about the word, for example a membership bit, and simulation of proofs is only guaranteed if the membership bit is correct. Further, dual-system NIZK proofs allow a quasi-adaptive setting where the CRS can be generated based on language parameters. This allows for the further possibility that the partial-world CRS simulator may have access to additional trapdoors related to the language parameters. We show that for important hard languages like the Diffie-Hellman language, such dual-system proof systems can be given which allow unbounded partial simulation soundness, and which further allow transition between partial simulation world and single-theorem full simulation world even when proofs are sought on non-members. The construction is surprisingly simple, involving only two additional group elements for general linear-subspace languages in asymmetric bilinear pairing groups.
As a direct application we give a short keyed-homomorphic CCA-secure encryption scheme. The ciphertext in this scheme consists of only six group elements (under the SXDH assumption) and the security reduction is tight. An earlier scheme of Libert et al. based on their efficient unbounded simulation-sound QA-NIZK proofs only provided a loose security reduction, and further had ciphertexts almost twice as long as ours.
We also show a single-round universally-composable password authenticated key-exchange (UC-PAKE) protocol which is secure under adaptive corruption in the erasure model. The single message flow only requires four group elements under the SXDH assumption.
This is the shortest known UC-PAKE even without considering adaptive corruption. The latest published scheme which considered adaptive corruption, by Abdalla et al [ABB+13], required non-constant (more than 10 times the bit-size of the password) number of group elements.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Since the introduction of simulation-sound non-interactive zero-knowledge proofs (NIZK) in [Sah99] (based on the concept of non-malleability [DDN91]), simulation-soundness has become an essential cryptographic tool. While the idea of zero-knowledge simulation [GMR89] brought rigor to the concept of semantic security, simulation-soundness of some form is usually implicit in most cryptographic applications. While the original construction of [Sah99] was rather inefficient, the advent of pairing based cryptography, and in particular Groth-Sahai NIZK proofs [GS08], has led to much more efficient simulation-sound NIZK constructions. Pairing-based cryptography has also led to efficient construction of powerful primitives where simulation-soundness is not very explicit.
It has been shown that different forms of simulation-soundness suffice for many applications. Indeed, the original application (CCA2-secure encryption) considered in [Sah99] only required what is known as single-theorem simulation-soundness (also known as one-time simulation-soundness). However, many other cryptographic constructions are known only using unbounded simulation-sound NIZK proofs. In this paper, we introduce the concept of dual-system simulation-sound NIZK proofs, which lie somewhere in between one-time and unbounded simulation-sound NIZK proofs. The aim is to show that this weaker concept suffices for constructions where unbounded simulation-soundness was being used till now. We also show that in many applications this new concept of dual-system simulation soundness is implicit, in the sense that although we cannot get a generic construction from a NIZK proof, we can use the underlying ideas of the dual-system simulation-sound NIZK proofs.
Indeed, our novel definition is inspired by the dual-system identity-based encryption (IBE) scheme of Waters [Wat09], where such a concept was implicit, and led to the first IBE scheme which was fully-secure under static and standard assumptions. So without further ado, we jump straight into the main idea of the new concept. In dual-system simulation-sound NIZK proof systems we will consider three worlds: the real-world, the partial-simulation world, and the one-time full-simulation world. The real world consists of a common-reference string (CRS), an efficient prover \({\mathsf{P}}\), and an efficient verifier \({\mathsf{V}}\). The concept of completeness and soundness of \({\mathsf{P}}\) and \({\mathsf{V}}\) with respect to a witness-relation R is well-understood. The full-simulation world is also standard, and it includes two simulators: a CRS simulator and a proof simulator. The proof simulator is a zero-knowledge simulator in the sense that it can simulate proofs even without access to the witness. In order to achieve this, the CRS simulator generates the CRS in a potentially different way and produces a trapdoor for the proof simulator. The partial-simulation world we consider also has a CRS simulator, and a proof simulator, but this proof simulator is allowed partial access to the witness (or some other auxiliary information) about the member on which the proof is sought.
At this point, we also bring in the possibility of the CRS being generated as a function of the language or witness-relation under consideration. The recent quasi-adaptive NIZK (QA-NIZK) proofs of [JR13] allow this possibility for distributions of witness-relations. The CRS in the real and the full-simulation world is generated based on a language parameter generated according to some distribution. Now we consider the possibility that in the partial-simulation world, the CRS simulator actually generates the language parameter itself. In other words, the CRS simulator has access to the “witness” of the language parameter. For example, the CRS simulator may know the discrete-logs of the language parameters. This leads to the possibility that in the partial simulation world the proof simulator may have access to additional trapdoors which makes simulation and/or simulation soundness easier to achieve.
In this paper, we will only define and consider dual-system simulation sound QA-NIZK proofs (called DSS-QA-NIZK), where the only auxiliary information that the partial proof simulator gets is a single bit which is called the membership bit. The membership bit indicates whether the word on which the proof is sought is in the language or not. We show that we can achieve unbounded partial-simulation soundness for important languages like the Diffie-Hellman language by relatively simple constructions. The constructions also allow one-time full-ZK simulation, and hence form a DSS-QA-NIZK for the Diffie-Hellman language. We actually give a general construction for arbitrary languages which allow smooth and universal\(_2\) projective hash proofs [CS02] and have QA-NIZKs for the language augmented with such a hash proof. We show that for linear subspace languages (over bilinear groups), like the Diffie-Hellman and decisional-linear (DLIN) languages, the requirements for the general construction are easy to obtain. Thus, for all such languages, under the standard and static SXDH assumption in bilinear pairing groups, we get a DSS-QA-NIZK proof of only two group elements.
Table 1 summarizes comparison among existing schemes and ours. DSS is weaker than unbounded simulation soundness, and although incomparable with one time simulation soundness, it seems to enjoy better properties. Consistent with this, we observe that the proof sizes also place in the middle of the shortest known OTSS-NIZKs [ABP15, KW15] and the shortest known USS-NIZKs [KW15] for linear subspaces.
Applications. We now give the main idea as to why such a construction is useful. The security of most applications is shown by reduction to a hard language. However, a particular application may have a more complex language for which the NIZK proofs are required, and the security proof may require soundness of the NIZK system while proofs of many elements (real or fake) of such a complex language are being simulated. The idea is that multiple simulations of such elements can be performed in a partial-simulation manner (i.e. it is always possible to supply the correct membership-bit), and full simulation is only required of one member at a time, on which the hardness assumption can then be invoked.
Keyed-Homomorphic CCA-secure Encryption. As a first application we consider the keyed-homomorphic CCA-secure encryption scheme notion of [EHO+13]. In such an encryption scheme, a further functionality called Eval is available which using a key can homomorphically combine valid ciphertexts. The scheme should provide IND-CCA2 security when this Eval key is unavailable to the adversary, and should continue to enjoy IND-CCA1 security when the Eval key is exposed to the adversary. Emura et al. also gave constructions for such a scheme, albeit schemes which are not publicly verifiable, and further satisfying a weaker notion than CCA1-security when Eval key is revealed. Recently, Libert et al. gave a publicly-verifiable construction which is more efficient and also CCA1-secure when Eval key is revealed. Their construction is based on a new and improved unbounded simulation-sound QA-NIZK for linear subspace languages. We show in this paper that a DSS-QA-NIZK for the Diffie-Hellman language suffice, and leads to a much improved construction. While the construction in [LPJY14], under the SXDH assumption, requires nine group elements in one group, and two more in the other plus a one-time signature key pair, our construction only requires six group elements in any one of the bilinear groups. Further, while the earlier construction was loose (i.e. loses a factor quadratic in number of Eval calls), our reduction is tight.
UC Password-Authenticated Key Exchange (UC-PAKE). The UC-PAKE ideal functionality was introduced in [CHK+05] where they also gave a three-round construction. In [KV11] a single-round construction for UC-PAKE was given using Groth-Sahai NIZK proofs along with unbounded simulation-soundness construction of [CCS09] (also see [JR12]). Later [BBC+13] gave a UC-PAKE construction based on novel trapdoor smooth projective hash functions, but secure only under static corruption; each message consisted of six group elements in one group, and another five elements in the other group (under the SXDH assumption).
In this paper, we construct a a single-round construction based on dual-system simulation-soundness which is UC-secure under adaptive corruption (in the erasure model), and which has only a total of four group elements in each message. The key is generated in the target group. The construction is not a black-box application of the DSS-QA-NIZK for the Diffie-Hellman language, but uses its underlying idea as well as the various component algorithms of the DSS-QA-NIZK. The main idea of the construction is given in more detail in Sect. 6.2.
To the best of our knowledge, this is the shortest known UC-PAKE, even without considering adaptive corruption. The first UC-PAKE to consider adaptive corruption was by Abdalla, Chevalier and Pointcheval [ACP09], which was a two round construction. Recently, Abdalla et al [ABB+13] also constructed a single round protocol, which required a non-constant (more than 10 times the bit-size of the password) number of group elements in each flow. Comparison with existing UC-PAKEs is given in Table 2.
Identity-Based Encryption (IBE). In the full version of this paper [JR14b], we show that the recent efficient dual-system IBE [JR13] (inspired by the original dual-system IBE of Waters [Wat09]) can also be obtained using the ideas of DSS-QA-NIZK. While the construction is not black-box and utilizes additional “smoothness” and “single-pairing-product test” properties of the verifier, it along with the other two applications clearly demonstrate the power and utility of the new notion, which we expect will find many more applications.
2 Preliminaries: Quasi-Adaptive NIZK Proofs
A witness relation is a binary relation on pairs of inputs, the first called a word and the second called a witness. Note that each witness relation R defines a corresponding language L which is the set of all x for which there exists a witness w, such that R(x, w) holds.
We will consider Quasi-Adaptive NIZK proofs [JR13] for a probability distribution \(\mathcal{D}\) on a collection of (witness-) relations \(\mathcal{{R}}= \{R_\rho \}\) (with corresponding languages \(L_\rho \)). Recall that in a quasi-adaptive NIZK, the CRS can be set after the language parameter has been chosen according to \(\mathcal{D}\). Please refer to [JR13] for detailed definitions.
Definition 1
([JR13]) We call \(({\mathsf{pargen}},{\mathsf{crsgen}},{\mathsf{prover}},{\mathsf{ver}})\) a (labeled) quasi-adaptive non-interactive zero-knowledge (QA-NIZK) proof system for witness-relations \(\mathcal{{R}}_\lambda = \{R_\rho \}\) with parameters sampled from a distribution \(\mathcal{D}\) over associated parameter language \(\mathsf{Lpar}\), if there exist simulators \({\mathsf{crs-sim}}, {\mathsf{sim}}\) such that for all non-uniform PPT adversaries \({\mathcal{A}_1, \mathcal{A}_2, \mathcal{A}_3}\) we have (in all of the following probabilistic experiments, the experiment starts by setting \({\lambda }\) as \({\lambda \leftarrow {\mathsf{pargen}}(1^m)}\), and choosing \({\rho }\) as \({\rho \leftarrow \mathcal{D}_\lambda }\)):
-
Quasi-Adaptive Completeness:

-
Quasi-Adaptive Soundness:

-
Quasi-Adaptive Zero-Knowledge:
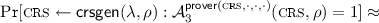
 , where \({\mathsf{sim^*}}(\textsc {crs}, {\mathsf{trap}}, x,w, {{ l}}) = {\mathsf{sim}}(\textsc {crs}, {\mathsf{trap}}, x, {{ l}})\) for \((x,w)\in R_\rho \) and both oracles (i.e. \({\mathsf{prover}}\) and \({\mathsf{sim^*}}\)) output failure if \((x,w)\not \in R_\rho \).
, where \({\mathsf{sim^*}}(\textsc {crs}, {\mathsf{trap}}, x,w, {{ l}}) = {\mathsf{sim}}(\textsc {crs}, {\mathsf{trap}}, x, {{ l}})\) for \((x,w)\in R_\rho \) and both oracles (i.e. \({\mathsf{prover}}\) and \({\mathsf{sim^*}}\)) output failure if \((x,w)\not \in R_\rho \).
The QA-NIZK is called a statistical zero-knowledge QA-NIZK if the view of adversary \(\mathcal{A}_3\) above in the two experiments is statistically indistinguishable.
3 Dual-System Simulation-Soundness
To define dual-system simulation soundness of QA-NIZK proofs, we will consider three worlds: the real-world, the partial-simulation world, and the one-time (or single theorem) full-simulation world. While the real-world and the full-simulation world should be familiar from earlier definitions of NIZK proof systems, the partial-simulation world leads to interesting possibilities. To start with, in the partial simulation world, one would like the proof simulator to have access to partial or complete witness of the wordFootnote 1. Finally, in the quasi-adaptive setting, the language parameters may actually be generated by the CRS simulator and hence the simulator may have access to, say, the discrete logs of the language parameters, which can serve as further trapdoors.
Rather than considering these general settings, we focus on a simple partial-simulation setting, where (a) the CRS simulator can generate the language parameters itself and (b) the proof simulator when invoked with a word x is given an additional bit \(\beta \), which we call the membership bit, that represents the information whether x is indeed a member or not.
The partial simulation world is required to be unbounded simulation-sound, and hopefully this should be easier to prove than usual unbounded simulation-soundness (given that its simulators have additional information). We also allow the partial simulation world to be sound with respect to a private verifier (this concept has been considered earlier in [JR12]), and this further leads to the possibility of easier and/or simpler constructions. A surprising property achievable under such a definition is that one can go back and forth between the partial-simulation world and the one-time full-simulation world even when simulating fake tuples.
Definition 2
\({\mathbf {(Dual-System\,Non-Interactive\,Proofs).}}\) A Dual-system non-interactive proof system consists of PPT algorithms defined in three worlds as follows:
-
Real World consisting of:
-
–
A pair of CRS generators \(({\mathsf{K}}_0, {\mathsf{K}}_1)\), where \({\mathsf{K}}_0\) takes a unary string and produces an ensemble parameter \(\lambda \). (The ensemble parameter \(\lambda \) is used to sample a witness-relation parameter \(\rho \) using \(\mathcal{D}_\lambda \) in the security definition.) PPT algorithm \({\mathsf{K}}_1\) uses \(\rho \) (and \(\lambda \)) to produce the real-world CRS \(\psi \).
-
–
A prover \({\mathsf{P}}\) that takes as input a CRS, a language member and its witness, a label, and produces a proof.
-
–
A verifier \({\mathsf{V}}\) that takes as input a CRS, a word, a label, and a proof, and outputs a single bit.
-
–
-
Partial-Simulation World consisting of:
-
–
A semi-functional CRS simulator \({\mathsf{sfK}}_1\) that takes ensemble parameter \(\lambda \) as input and produces a witness relation parameter \(\rho \), a semi-functional CRS \(\sigma \), as well as two trapdoors \(\tau \) and \(\eta \). The first trapdoor is used by the proof simulator, and the second by the private verifier.
-
–
A semi-functional simulator \({\mathsf{sfSim}}\) that takes a CRS, a trapdoor \(\tau \), a word, a membership-bit \(\beta \), and a label, to produce a proof.
-
–
A private verifier \({\mathsf{pV}}\) that takes a CRS, a trapdoor \(\eta \), a word, a label, and a proof and outputs a single bit.
-
–
-
One-time Full Simulation World consisting of:
-
–
A one-time full-simulation CRS generator \({\mathsf{otfK}}_1\), that takes as input the ensemble parameter \(\lambda \), the witness relation parameter \(\rho \) to produce a CRS and three trapdoors \(\tau \), \(\tau _1\) and \(\eta \).
-
–
A one-time full simulator \({\mathsf{otfSim}}\) that takes as input a CRS, a trapdoor \(\tau _1\), a word, a label, and produces a proofFootnote 2.
-
–
A semi-functional verifier \({\mathsf{sfV}}\) that takes as input a CRS, a trapdoor \(\eta \), a word, a label, a proof and outputs a bit. The adversaries also have access to the semi-functional simulator.
-
–
Definition 3
(DSS-QA-NIZK). The definition of the real-world components of a dual-system non-interactive proof to be complete and (computationally) sound are same as in QA-NIZK Definition 1. Such a proof system is called a dual-system simulation-sound quasi-adaptive NIZK (DSS-QA-NIZK) for a collection of witness relations \(\mathcal{{R}}_\lambda = \{R_\rho \}\), with parameters sampled from a distribution \(\mathcal{D}\), if its real-world components are complete and (computationally) sound, and if for all non-uniform PPT adversaries \(\mathcal{A} = (\mathcal{A}_0, \mathcal{A}_1, \mathcal{A}_2, \mathcal{A}_3, \mathcal{A}_4)\) all of the following properties are satisfied (in all of the following probabilistic experiments, the experiment starts by setting \(\lambda \) as \(\lambda \leftarrow {\mathsf{K}}_0(1^m)\)):
-
(Composable) Partial-ZK:
$$\begin{aligned}&\Pr [ \rho \leftarrow \mathcal{D}_\lambda ; \sigma \,\leftarrow \, {\mathsf{K}}_1(\lambda ,\rho ): {\mathcal{A}}_0(\sigma , \rho ) = 1] \approx \\&\Pr [ (\rho , \sigma , \tau , \eta ) \leftarrow {\mathsf{sfK}}_1(\lambda ): {\mathcal{A}}_0(\sigma , \rho ) = 1], \end{aligned}$$and
$$\begin{aligned} \Pr [(\rho , \sigma , \tau , \eta ) \leftarrow {\mathsf{sfK}}_1(\lambda ): \, {\mathcal{A}}_1^{\;{\mathsf{P}}(\sigma , \cdot ,\cdot , \cdot ), \;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \;{\mathsf{V}}(\sigma , \cdot , \cdot , \cdot )}(\sigma , \rho ) = 1] \,\approx \\ \Pr [(\rho , \sigma , \tau , \eta ) \leftarrow {\mathsf{sfK}}_1(\lambda ): \, {\mathcal{A}}_1^{\;{\mathsf{sfSim^*}}(\sigma ,\tau , \cdot , \cdot , \cdot ), \;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \;{\mathsf{pV}}(\sigma , \eta , \cdot , \cdot , \cdot )}(\sigma , \rho ) = 1], \end{aligned}$$where \({\mathsf{sfSim^*}}(\sigma , \tau , x, w, {{ l}})\) is defined to be \({\mathsf{sfSim}}(\sigma , \tau , x, \beta =1, {{ l}})\) (i.e. witness is dropped, and membership-bit \(\beta =1\)), and the experiment aborts if either a call to the first oracle (i.e. \({\mathsf{P}}\) and \({\mathsf{sfSim^*}}\)) is with \((x,w, {{ l}})\) s.t. \(\lnot R_\rho (x,w)\), or call to the second oracle is with an \((x, \beta , {{ l}})\) s.t. \(x \not \in L_\rho \) or \(\beta =0\).
-
Unbounded Partial-Simulation Soundness:
$$\begin{aligned} \Pr&\left[ \begin{array}{c} (\rho , \sigma , \tau , \eta ) \leftarrow {\mathsf{sfK}}_1(\lambda ); \, (x,{{ l}}, \pi )\leftarrow {\mathcal{A}}_2^{\;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \; {\mathsf{pV}}(\sigma , \eta , \cdot , \cdot , \cdot )}(\sigma , \rho ):\,\\ ((x \not \in L_\rho ) \,\vee \, {\mathsf{V}}(\sigma , x, {{ l}}, \pi )=0) \,\wedge \, {\mathsf{pV}}(\sigma ,\eta ,x, {{ l}}, \pi )=1 \end{array} \right] \approx 0. \end{aligned}$$ -
One-time Full-ZK:
$$\begin{aligned} \Pr&\left[ \begin{array}{c} (\rho , \sigma , \tau , \eta ) \leftarrow {\mathsf{sfK}}_1(\lambda ); (x^*,{{ l}}^*, \beta ^*,s) \leftarrow \, {\mathcal{A}}_3^{\;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \;{\mathsf{pV}}(\sigma , \eta , \cdot , \cdot , \cdot )}(\sigma , \rho ); \\ \pi ^* \leftarrow {\mathsf{sfSim}}(\sigma , \tau , x^*,\beta ^*, {{ l}}^*): {\mathcal{A}}_4^{\;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \;{\mathsf{pV}}(\sigma , \eta , \cdot , \cdot , \cdot )}(\pi ^*,s) = 1 \end{array} \right] \\ \approx \Pr&\left[ \begin{array}{c} \rho \leftarrow \mathcal{D}_\lambda ;\, (\sigma , \tau , \tau _1, \eta ) \leftarrow {\mathsf{otfK}}_1(\lambda ,\rho ); \\ (x^*, {{ l}}^*, \beta ^*, s) \leftarrow {\mathcal{A}}_3^{\;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \;{\mathsf{sfV}}(\sigma , \eta , \cdot , \cdot , \cdot )}(\sigma , \rho );\;\; \\ \pi ^* \leftarrow {\mathsf{otfSim}}(\sigma ,\tau _1, x^*, {{ l}}^*): {\mathcal{A}}_4^{\;{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot ), \;{\mathsf{sfV}}(\sigma , \eta , \cdot , \cdot , \cdot )}(\pi ^*,s) = 1 \end{array} \right] \!, \\ \end{aligned}$$where the experiment aborts if either in the call to the first oracle, or in the \((x^*, \beta ^*)\) produced by \({\mathcal{A}}_3\), the membership-bit provided is not correct for \(L_\rho \), or if \(\langle x^*, {{ l}}^*, \pi ^* \rangle \) is queried to \({\mathsf{sfV}}/{\mathsf{pV}}\). Here s is a state variable.
The three worlds and the properties of a DSS-QA-NIZK are depicted in Fig. 1.
Remark 1. In the partial-simulation soundness definition, there is no restriction of \(x, {{ l}}, \pi \) being not the same as that obtained from a call to the first oracle \({\mathsf{sfSim}}\).
Remark 2. Note that in the partial-ZK definition, the calls to the prover are restricted to ones satisfying the relation. However, the calls to the simulator \({\mathsf{sfSim}}\) in the one-time full-ZK definition are only restricted to having the correct membership bit \(\beta \).
Remark 3. It can be shown that \({\mathsf{sfSim}}\) generated proofs on words (whether members or not) are accepted by real-world verifier \({\mathsf{V}}\) (with semi-functional CRS). Of course, the private verifier \({\mathsf{pV}}\) will even reject proofs generated by \({\mathsf{sfSim}}\) on non-language words. This justifies the name “semi-functional simulator”. See [JR14b] for a precise claim and proof.
It can also be shown that the semi-functional verifier \({\mathsf{sfV}}\) is still complete, i.e. it accepts language members and proofs generated on them by \({\mathsf{P}}(\sigma , \cdot , \cdot , \cdot )\) (with \(\sigma \) generated by \({\mathsf{otfK}}_1\)). As opposed to \({\mathsf{P}}\) and \({\mathsf{pV}}\), it may no longer be sound. This justifies the name “semi-functional verifier” a la Waters’ dual-system IBE construction. However, if the one-time full-ZK property holds statistically, it can be shown that the semi-functional verifier is sound in the one-time full-simulation world. See [JR14b] for a precise statement.
Remark 4. The composable partial-ZK and unbounded partial-simulation soundness imply that that the system is true-simulation-sound (cf. true-simulation extractable [Har11]) w.r.t. the semi-functional simulator, as stated below.
Lemma 1
(true-simulation-soundness) For a DSS-QA-NIZK, for all PPT \({\mathcal{A}}\),
\( \Pr \left[ \begin{array}{c} (\rho , \sigma , \tau , \eta ) \leftarrow {\mathsf{sfK}}_1(\lambda );\, (x, {{ l}}, \pi ) \leftarrow {\mathcal{A}}^{{\mathsf{sfSim}}(\sigma , \tau , \cdot , \cdot , \cdot )}\;(\sigma , \rho ): \\ \, (x \not \in L_\rho ) \,\wedge \, {\mathsf{V}}(\sigma , x, {{ l}}, \pi )=1\end{array}\right] \,\approx 0,\) where the experiment aborts if \({\mathcal{A}}\) calls the oracle with some \((y, \beta , {{ l}})\), s.t. \(y \not \in L_\rho \) or \(\beta =0\).
4 DSS-QA-NIZK for Linear Subspaces
In this section we show that languages that are linear subspaces of vector spaces of hard bilinear groups have very short dual-system simulation sound QA-NIZK. In fact, under the Symmetric-eXternal Diffie-Hellman (SXDH) assumption, such proofs only require two group elements, regardless of the subspace. It was shown in [JR14a] that such subspaces have a QA-NIZK proof of just one group element (under the SXDH assumption). Our construction essentially shows that with one additional group element, one can make the QA-NIZK dual-system simulation-sound. We will actually show a more general construction which is more widely applicable, and does not even refer to bilinear groups or linear subspaces. Informally speaking, the requirement for such a general construction for parameterized languages is that each language has a 2-universal projective hash proof system and the augmented language with this hash proof attached has a QA-NIZK proof system with statistical zero-knowledge. A few other properties of the QA-NIZK are required for this construction, and we show that such properties already hold for the construction of [JR14a]. Since for linear subspaces, 2-universal projective hash proofs are rather easy to obtain, the general construction along with the QA-NIZK of [JR14a] allows us to obtain a short DSS-QA-NIZK for linear subspaces. Apart from abstracting the main ideas involved in the DSS-QA-NIZK construction for linear subspaces, the general construction’s wider applicability also allows us to extend our results to linear subspaces with tags.
We start this section by briefly reviewing projective hash proofs [CS02], and their extensions to distributions of languages, as they are extensively used in the rest of the section.
Projective Hash Proof System. For a language L, let X be a superset of L and let \(H = (H_k)_{k \in K}\) be a collection of (hash) functions indexed by K with domain X and range another set \(\Pi \). The hash function family is generalized to a notion of projective hash function family if there is a set S of projection keys, and a projection map \(\alpha : \, K \rightarrow S\), and further the action of \(H_k\) on subset L of X is completely determined by the projection key \(\alpha (k)\). Finally, the projective hash function family is defined to be \(\mathbf {\epsilon }\)-\({\mathbf {universal_2}}\) is for all \(s\in S\), \(x, x^* \in X\), and \(\pi , \pi ^* \in \Pi \) with \(x \not \in L \cup \{x^*\}\), the following holds:
A projective hash function family is called \(\mathbf {\epsilon }\)-smooth if for all \(x \in X \setminus L\), the statistical difference between the following two distributions is \(\epsilon \): sample k uniformly from K and \(\pi '\) uniformly from \(\Pi \); the first distribution is given by the pair \((\alpha (k), H_k(x))\) and the second by the pair \((\alpha (k), \pi ')\). For languages defined by a witness-relation R, the projective hash proof family constitutes a projective hash proof system (PHPS) if \(\alpha \), \(H_k\), and another public evaluation function \(\hat{H}\) that computes \(H_k\) on \(x \in L\), given a witness of x and only the projection key \(\alpha (k)\), are all efficiently computable. An efficient algorithm for sampling the key \(k \in K\) is also assumed.
The above notions can also incorporate labels. In an extended PHPS, the hash functions take an additional input called label. The public evaluation algorithm also takes this additional input called label. All the above notions are now required to hold for each possible value of label. The extended PHPS is now defined to be \(\mathbf {\epsilon }\)-\({\mathbf {universal_2}}\) is for all \(s\in S\), \(x, x^* \in X\), all labels \({{ l}}\) and \({{ l}}^*\), and \(\pi , \pi ^* \in \Pi \) with \(x \not \in L\) and \((x, {{ l}}) \ne (x^*, {{ l}}^*)\), the following holds: \( \Pr [H_k(x, {{ l}})\,=\,\pi \) | \(H_k(x^*, {{ l}}^*)\) \(=\) \(\pi ^* \, \wedge \) \(\alpha (k) = s]\) \(\, \le \,\) \(\epsilon . \)
Since, we are interested in distributions of languages, we extend the above definition to distribution of languages. So consider a parametrized class of languages \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\) with the parameters coming from an associated parameter language \(\mathsf{Lpar}\). Assume that all the languages in this collection are subsets of X. Let H as above be a collection of hash functions from X to \(\Pi \). We say that the hash family is a projective hash family if for all \(L_\rho \), the action of \(H_k\) on \(L_\rho \) is determined by \(\alpha (k)\). Similarly, the hash family is \(\epsilon \)-universal\(_2\) (\(\epsilon \)-smooth) for \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\) if for all languages \(L_\rho \) the \(\epsilon \)-universal\(_2\) (resp. \(\epsilon \)-smooth) property holds.
Intuition for the Construction. The main idea of the construction is to first attach (as a proof component) a universal\(_2\) and smooth projective hash proof T. The DSS-QA-NIZK is then just \((T, \pi )\), where \(\pi \) is a QA-NIZK proof of the original language augmented with hash proof T. So, why should this work? First note that the smooth projective hash function is a designated-verifier NIZK, and hence this component T is used in private verification. Secondly, since it is universal\(_2\), its soundness will hold even when the Adversary gets to see the projection key \(\alpha (k)\) plus one possibly fake hash proof (i.e. \(H_k(x)\), where x not in the language).
We will assume in our general construction that the parameterized language is such that the simulator can sample the language parameters along with auxiliary information that allows it to easily verify a language member. For example, this auxiliary information can be discrete logs of the language parameters. The idea of obtaining partial-ZK and unbounded partial-simulation soundness is then pretty simple. The proof simulation of T is easy to accomplish given the hash keys and, crucially, the correct membership-bit. In fact, if the membership-bit is false, T can just be set randomly (by smoothness). The simulation of \(\pi \) part of the proof is done using the QA-NIZK simulation trapdoor. The private verification is done as conjunction of three separate checks: (a) using the auxiliary information, (b) using the hash proof and (c) using the real-world verifier.
Now, in the one-time full simulation, the auxiliary information is not available, but the semi-functional verifier can still use hash keys. Further, we can have one bad use of keys (in full simulation of one proof. Since the oracle calls to semi-functional simulator \({\mathsf{sfSim}}\) are restricted to having correct membership-bit, they do not yield any additional information about the hash keys.
Requirements of the General Construction. Consider a parameterized class of languages \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\), and a probability distribution \(\mathcal{D}\) on \(\mathsf{Lpar}\). Assume that this class has a projective hash proof system as above. Let \(R_\rho \) be the corresponding witness relation of \(L_\rho \). Now consider the augmented witness-relation \({R^{*}_{\rho ,s}}\) defined as follows (for \(\rho \in \mathsf{Lpar}\) and \(s \in S\)):
Note, the witness remains the same for the augmented relation. Since H is a projective hash function, it follows that for \(s = \alpha (k)\), the corresponding augmented language is \({L^{*}_{\rho , s}} = \{ (x, T, {{ l}}) ~|~ x\in L_\rho \, \wedge \, T \mathop {=}\limits ^{?}H_k(x, {{ l}}) \}.\) Let the distribution \(\mathcal{D}'\) on pairs \((\rho , s)\) be defined by sampling \(\rho \) according to \(\mathcal{D}\) and sampling k uniformly from K, and setting \(s= \alpha (k)\). We remark that the language parameters of the augmented language include projection keys s (instead of keys k) because it is crucial that the CRS simulator in the quasi-adaptive NIZK gets only the projection key s (and not k).
We will also assume that the distribution \(\mathcal{D}\) on \(\mathsf{Lpar}\) is efficiently witness samplable which is defined by requiring that there are two efficient (probabilistic) algorithms \(E_1,E_2\) such that \(E_1\) can sample \(\rho \) from \(\mathcal{D}\) along with auxiliary information \(\psi \) (which can be thought of as witness of \(\rho \) in the language \(\mathsf{Lpar}\)), and \(E_2\) can decide w.h.p. if a word x is in \(L_\rho \) given \(\rho \) and \(\psi \), where the probability is defined over choice of \(\rho \) according to \(\mathcal{D}\) and the internal coins of \(E_2\).
Finally, we need a few additional properties of QA-NIZK proofs (Sect. 2) that we now define. We will later show that the single group element QA-NIZK construction for linear-subspaces of [JR14a] already satisfies these properties.
Definition 4
There are various specializations of QA-NIZK of interest:
-
The QA-NIZK (Sect. 2) is said to have composable zero-knowledge [GS08] if the CRS are indistinguishable in the real and simulation worlds, and the simulation is indistinguishable even if the adversary is given the trapdoor. More precisely, for all PPT adversary \({\mathcal{A}}_1, {\mathcal{A}}_2\),
$$\begin{aligned}&\Pr [ \textsc {crs}\leftarrow {\mathsf{crsgen}}(\lambda ,\rho ): {\mathcal{A}}_{1}(\textsc {crs}, \rho ) = 1] \,\approx \, \\&\Pr [ (\textsc {crs}, {\mathsf{trap}}) \leftarrow {\mathsf{crs-sim}}(\lambda , \rho ): \mathcal{A}_{1}(\textsc {crs}, \rho ) = 1 ], \\&\mathbf{and}\\&\Pr [(\textsc {crs}, {\mathsf{trap}}) \leftarrow {\mathsf{crs-sim}}(\lambda , \rho ): \mathcal{A}_{2}^{{\mathsf{prover}}(\textsc {crs}, \cdot , \cdot , \cdot )}(\textsc {crs}, \rho , {\mathsf{trap}}) = 1] \approx \\&\Pr [(\textsc {crs}, {\mathsf{trap}}) \leftarrow {\mathsf{crs-sim}}(\lambda , \rho ): \mathcal{A}_{2}^{{\mathsf{sim^*}}(\textsc {crs}, {\mathsf{trap}}, \cdot , \cdot , \cdot )}(\textsc {crs}, \rho , {\mathsf{trap}}) = 1 ], \end{aligned}$$where \({\mathcal{A}}_2\) is restricted to calling the oracle only on \((x, w, {{ l}})\) with \((x,w) \in R_\rho \).
-
The QA-NIZK is called true-simulation-sound [Har11] if the verifier is sound even when an adaptive adversary has access to simulated proofs on language members. More precisely, for all PPT \({\mathcal{A}}\),
$$ \Pr \left[ \begin{array}{c} (\textsc {crs}, {\mathsf{trap}}) \leftarrow {\mathsf{crs-sim}}(\lambda , \rho ) \\ (x,{{ l}}, \pi ) \leftarrow {\mathcal{A}}^{{\mathsf{sim}}(\textsc {crs}, {\mathsf{trap}}, \cdot , \cdot )}(\textsc {crs}, \rho ) \end{array} : x \not \in L_\rho \, \wedge \, {\mathsf{ver}}(\textsc {crs}, x,{{ l}}, \pi ) =1 \right] \approx 0, $$where the experiment aborts if the oracle is called with some \(y \not \in L_\rho \).
-
The simulator is said to generate unique acceptable proofs if for all x, all labels \({{ l}}\), and all proofs \(\pi ^*\),
$$ \Pr \left[ \begin{array}{c} (\textsc {crs}, {\mathsf{trap}}) \leftarrow {\mathsf{crs-sim}}(\lambda , \rho ) \\ \pi \leftarrow {\mathsf{sim}}(\textsc {crs}, {\mathsf{trap}}, x, {{ l}}) \end{array} : (\pi ^* \ne \pi ) \wedge {\mathsf{ver}}(\textsc {crs}, x, {{ l}}, \pi ^*) =1 \right] \approx 0. $$
General Construction. We now show that given:
-
1.
An \(\epsilon \)-smooth and \(\epsilon \)-universal\(_2\) (labeled) projective hash proof system for the collection \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\), and
-
2.
A composable zero-knowledge, true-simulation-sound QA-NIZK Q= (pargen, crsgen, prover, ver, crs-sim, sim) for the augmented parameterized language \({L^{*}_{\rho , s}}\) with probability distribution \(\mathcal{D}'\), such that the simulator generates unique acceptable proofs, and
-
3.
Efficient algorithms \((E_1,E_2)\) s.t. \(\mathcal{D}\) is efficiently witness-samplable using \((E_1,E_2)\), and
-
4.
An efficient algorithm \(E_3\) to sample uniformly from \(\Pi \),
one can construct a DSS-QA-NIZK for \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\) with probability distribution \(\mathcal{D}\). We first give the construction, and then prove the required properties. The QA-NIZK Q need not take any labels as input. The various components of the dual-system non-interactive proof system \({\Sigma }\) are as follows.
-
Real World consisting of:
-
–
The algorithm \({\mathsf{K}}_0\) takes a unary string \(1^m\) as input and generates parameters \(\lambda \) using \({\mathsf{pargen}}\) of Q on \(1^m\). The CRS generation algorithm \({\mathsf{K}}_1\) uses \({\mathsf{crsgen}}\) of Q and produces the CRS as follows: it takes \(\lambda \) and the language parameter \(\rho \), and first samples k uniformly from \(K_\lambda \) (recalling that the hash function families are ensembles, one for each \(\lambda \)). It then outputs the CRS to be the pair \(({\mathsf{crsgen}}(\lambda , \langle \rho , \alpha (k) \rangle ), \alpha (k))\).
-
–
The prover \({\mathsf{P}}\) takes a CRS \((\sigma , s)\), input x, witness w, and label \({{ l}}\) and outputs the proof to be \((T,\,W)\) where T is computed using the public evaluation algorithm \(\hat{H}\) as \(\hat{H}(s,\langle x, {{ l}}\rangle , w)\) and \(W = {\mathsf{prover}}(\sigma , \langle x, T, {{ l}}\rangle , w)\).
-
–
The verifier \({\mathsf{V}}\) on input CRS \(=(\sigma ', s)\), x, \({{ l}}\), and proof (T, W), returns the value \({\mathsf{ver}}(\sigma '\), \(\langle x, T, {{ l}}\rangle \), W) (using \({\mathsf{ver}}\) of Q).
-
–
-
Partial-Simulation World consisting of:
-
–
The semi-functional CRS simulator \({\mathsf{sfK}}_1\) takes \(\lambda \) as input and samples \((\rho , \psi )\) using \(E_1\), and also samples k uniformly from \(K_\lambda \). It then uses \({\mathsf{crs-sim}}\) of Q, and key projection algorithm \(\alpha \) to generate the CRS \(\sigma \) as follows: Let \((\sigma ', {\mathsf{trap}})\) \(=\) \({\mathsf{crs-sim}}(\lambda , \langle \rho , \alpha (k) \rangle )\). The CRS \(\sigma \) is then the pair \((\sigma ', \alpha (k))\). \({\mathsf{sfK}}_1\) also outputs \(k, {\mathsf{trap}}\) as proof simulator trapdoors \(\tau \), and \(\rho , \psi , k\) as private verifier trapdoors \(\eta \).
-
–
The semi-functional simulator \({\mathsf{sfSim}}\) uses trapdoors \(k, {\mathsf{trap}}\) to produce a (partially-simulated) proof for a word x, a label \({{ l}}\) and a binary bit \(\beta \) using \({\mathsf{sim}}\) of Q as follows: if \(\beta =1\), output
$$ T = H_k(x, {{ l}}), \, W = {\mathsf{sim}}(\sigma , {\mathsf{trap}}, \langle x, T, {{ l}}\rangle ), $$else sample \(\pi '\) at random from \(\Pi \) (using \(E_3\)) and output
$$ T = \pi ' \;,\; W = {\mathsf{sim}}(\sigma , {\mathsf{trap}}, \langle x, T , {{ l}}\rangle ). $$This proof is partially simulated as it uses the bit \(\beta \).
-
–
The private verifier \({\mathsf{pV}}\) uses trapdoors \((\rho , \psi , k)\) to check a word x, label \({{ l}}\) and a proof T, W as follows: it outputs 1 iff (a) \(E_2\) using \(\rho \) and \(\psi \) confirms that x is in \(L_\rho \), and (b) \(H_k(x, {{ l}})\) = T, and (c) verifier of Q accepts, i.e. \({\mathsf{ver}}(\sigma , \langle x, T, {{ l}}\rangle , W) =1\).
-
–
-
One-time Full Simulation World consisting of:
-
–
The one-time full-simulation CRS generator \({\mathsf{otfK}}_1\) takes as input \(\lambda \) and language parameter \(\rho \), and using \({\mathsf{crs-sim}}\) of Q outputs \(\sigma \) as follows: first it samples k uniformly from \(K_\lambda \). Let \((\sigma ' , {\mathsf{trap}}) = {\mathsf{crs-sim}}(\lambda , \langle \rho , \alpha (k) \rangle )\). Then \(\sigma = (\sigma ', \alpha (k))\). \({\mathsf{otfK}}_1\) also outputs \( k, {\mathsf{trap}}\) as proof simulator trapdoors \(\tau \) and \(\tau _1\), and outputs k as private verifier trapdoor \(\eta \).
-
–
The one-time full simulator \({\mathsf{otfSim}}\) takes as input the trapdoors \(k, {\mathsf{trap}}\) and a word x and a label \({{ l}}\) to produce a proof as follows:
$$ T = H_k(x,{{ l}}), \;\; W = {\mathsf{sim}}(\sigma , {\mathsf{trap}}, \langle x, T, {{ l}}\rangle ). $$ -
–
The semi-functional verifier \({\mathsf{sfV}}\) uses trapdoors k to verify a word x, a label \({{ l}}\) and a proof T, W as follows: output 1 iff (a) \(H_k(x, {{ l}})\) = T, and (b) \({\mathsf{ver}}(\sigma , \langle x, T, {{ l}}\rangle , W) =1\).
-
–
Theorem 1
For a parameterized class of languages \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\) with probability distribution \(\mathcal{D}\), if the above four conditions hold for projective hash family H, QA-NIZK Q, and efficient algorithms \(E_1,E_2, E_3\), then the above dual-system non-interactive proof system \({\Sigma }\) is a DSS-QA-NIZK for \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\) with probability distribution \(\mathcal{D}\).
Remark. In [JR14b] we instantiate the general construction for linear subspaces of vector spaces of hard bilinear groups. As a corollary, it follows that under the SXDH assumption the Diffie-Hellman (DH) language has a DSS-QA-NIZK with only two group elements.
Due to space limitations, we will focus on only the proof of one-time zero-knowledge (otzk) property, as that is the most non-trivial proof. Indeed, this property is a significant generalization of the usual dual-system technique employed in IBE constructions because although in otzk only one proof needs to be fully simulated (i.e. without its membership bit being available), all the private verifier calls in the partial-simulation world need to be simulated in the otzk world without the quasi-adaptive trapdoors (i.e. trapdoor obtained by witness-sampling the language parameters). Recall, in the IBE construction the ciphertext is the counterpart of our verifier, and the IBE private keys are the QA-NIZK proofs. Thus, in IBE only a single ciphertext needs to be simulated when the different private keys are being “fixed” one-by-one by otzk simulation.
The detailed proof of all other properties is given in [JR14b]. The main idea of the proof of these properties is already sketched earlier in this section.
Lemma 2
In the context of Theorem 1, let the maximum probability that the simulator of Q does not generate unique acceptable proofs be \(\delta \). Let H be an \(\epsilon \)-smooth and \(\epsilon \)-universal\(_2\) (labeled) projective hash proof system for the collection \(\{L_\rho \}_{\rho \in \mathsf{Lpar}}\). Let M be the number of calls to the second oracle (verifier) by \(\mathcal{A}_3\) and \(\mathcal{A}_4\) combined in the two experiments of the one-time full-ZK property of DSS-QA-NIZK \({\Sigma }\). Then the maximum statistical distance (over all PPT Adversaries \(\mathcal{A}_3\) and \(\mathcal{A}_4\)) between the views of the adversaries (\({\mathcal{A}_3},{\mathcal{A}_4}\)) in these two experiments, denoted \({{dist}}^{{{otzk}}}({\Sigma })\), is at most \((\epsilon + \delta )*(1 + M)\).
Proof
We will show that the one-time full-ZK property holds statistically. We will define a sequence of experiments and show that the view of the PPT adversary is statistically indistinguishable in every two consecutive experiments. The first experiment \(\mathbf H _{0}\) is identical to the partial-simulation world. First, note that \(\rho \) is identically generated using \(\mathcal{D}\) in both worlds. Next, note that the CRS \(\sigma \) and trapdoors \(\tau \) generated by \({\mathsf{sfK}}_1\) is identically distributed to the CRS \(\sigma \) and both the trapdoors \(\tau \) and \(\tau _1\) generated by \({\mathsf{otfK}}_1\).
The next experiment \(\mathbf H _{1}\) is identical to \(\mathbf H _{0}\) except that on \({\mathcal{A}}_3\) supplied input \((x^*,{{ l}}^*, \beta ^*)\) the proof \(\pi ^*\) generated by \({\mathsf{sfSim}}\) is replaced by proof generated by \({\mathsf{otfSim}}\). If \(\beta ^*\) provided by \({\mathcal{A}}_3\) is not the valid membership bit for \(x^*\) then both experiments abort. So, assume that \(\beta ^*\) is the correct membership bit. In case \(\beta ^*=1\), both \({\mathsf{sfSim}}\) and \({\mathsf{otfSim}}\) behave identically. When \(\beta ^*=0\), the random \(T^*\) produced by \({\mathsf{sfSim}}\) is identically distributed to the \(T^*\) generated by \(H_k(x^*,{{ l}}^*)\) since H is assumed to be smooth.
The next experiment \(\mathbf H _{2}\) is identical to \(\mathbf H _{1}\) except that the second oracle is replaced by \({\mathsf{sfV}}\) (from being \({\mathsf{pV}}\)). In order to show that the view of the adversary is indistinguishable in experiments \(\mathbf H _{2}\) and \(\mathbf H _{1}\), we define several hybrid experiments \(\mathbf H _{1,i}\) (for \(0 \le i \le N\), where N is the total number of calls to the second-oracle by \({\mathcal{A}}_3\) and \({\mathcal{A}}_4\) combined). Experiment \(\mathbf H _{1,0}\) is identical to \(\mathbf H _{1}\), and the intermediate experiments are defined inductively, by modifying the response of one additional second-oracle call starting with the last (N-th) second-oracle call, and ending with the changed response of the first second-oracle call. The last hybrid experiment \(\mathbf H _{1,N}\) will then be same as \(\mathbf H _{2}\). The second-oracle call response in experiment \(\mathbf H _{1,i+1}\) differs only in the \((N-i)\)-th second-oracle call response in \(\mathbf H _{1,i}\). In the latter experiment, this call is still served as in \(\mathbf H _{1}\) (i.e. using \({\mathsf{pV}}\)). In the former experiment \(\mathbf H _{1,i+1}\), the \((N-i)\)-th call is responded to as defined in \(\mathbf H _{2}\) above (i.e. using \({\mathsf{sfV}}\)).
To show that the view of the adversary is statistically indistinguishable in \(\mathbf H _{1,i}\) and \(\mathbf H _{1,i+1}\), first note that the view of the adversary (\({\mathcal{A}}_3\) and \(A_4\) combined) till it’s \((N-i)\)-th call in both experiments is identical. Moreover, as we next show, the dependence on k of this partial view (i.e. till the \((N-i)\)-th call) is limited to \(\alpha (k)\) and at most one evaluation of \(H_k\) (by \({\mathsf{otfSim}}\)) on an input that is not in \(L_\rho \). To start with, the CRS generated by \({\mathsf{sfK}}_1\) depends only on \(\alpha (k)\). Next, the first oracle \({\mathsf{sfSim}}\) produces T using \(H_k\) on its input only if the membership bit \(\beta \) is 1 and correct, and since H is projective this hash value is then completely determined by \(\alpha (k)\). Finally, all calls to the second oracle till the \((N-i)\)-th call are still served using \({\mathsf{pV}}\), and again using the projective property of H, it is clear that the conjunct (b) in \({\mathsf{pV}}\) can be computed using only \(\alpha (k)\), because for non \(L_\rho \) members, the conjunct (a) is already false, and hence (b) is redundant.
Now, the difference in the \((N-i)\)-th call is that the conjunct (a) of \({\mathsf{pV}}\) is missing in \({\mathsf{sfV}}\). Let \(x, {{ l}}, T, W\) be the input supplied by the PPT Adversary to this call. If \(H_k(x, {{ l}})\) is not equal to the supplied T, then both \({\mathsf{pV}}\) and \({\mathsf{sfV}}\) return 0. So, suppose \(H_k(x, {{ l}})\) is equal to T, and yet x is not in \(L_\rho \), i.e. conjunct (a) of \({\mathsf{pV}}\) is false. First, if this input \(x, {{ l}}, T, W\) is same as \((x^*, {{ l}}^*, T^*, W^*)\) associated with the one-time call to \({\mathsf{otfSim}}\), then the experiment aborts. Thus, we can assume that this is a different input. If \((x, {{ l}}) \) is same as \( (x^*, {{ l}}^*)\), then \((T, W) \ne (T^*,W^*)\). Now, by construction (i.e. by definition of \({\mathsf{otfSim}}\)) \(T^* = H_k(x^*, {{ l}}^*)\), and hence either \(T \ne H_k(x, {{ l}})\) which is not possible by hypothesis, or \((x, {{ l}}, T) = (x^*, {{ l}}^*, T^*)\) and \(W \ne W^*\). But, \(W^*\) is proof generated by the simulator of Q, and since the simulator of Q generates unique acceptable proofs (by assumption), the verifier ver of Q rejects \((x, {{ l}}, T, W)\), and thus both \({\mathsf{pV}}\) and \({\mathsf{sfV}}\) return 0.
On the other hand, if \((x, {{ l}}) \ne (x^*, {{ l}}^*)\) then by the \(\epsilon \)-universal\(_2\) property of H, the probability of T being same as \(H_k(x, {{ l}})\) is at most \(\epsilon \). Thus, both \({\mathsf{pV}}\) and \({\mathsf{sfV}}\) return 0. That completes the induction step, and thus the view of the adversary in experiments \(\mathbf H _{1}\) and \(\mathbf H _{2}\) is statistically indistinguishable.
The next experiment \(\mathbf H _{3}\) is identical to \(\mathbf H _{2}\) except that the CRS is generated using \({\mathsf{otfK}}_1\). The only difference is that the (verifier) trapdoor does not include \(\rho , \psi \). But, since the second oracle is served by \({\mathsf{sfV}}\) and it does not need \(\rho , \psi \), the experiment \(\mathbf H _{3}\) is well-defined and statistically indistinguishable from \(\mathbf H _{2}\), Further, \(\mathbf H _{3}\) is identical to the one-time simulation world, and that completes the proof.
The statistical distance between the views of the adversaries (\({\mathcal{A}}_3,{\mathcal{A}}_4\)) in \(\mathbf H _{0}\) and \(\mathbf H _{3}\) is at most \((\epsilon + \delta )*(1 + M)\). \(\square \)
5 Keyed-Homomorphic CCA Encryption
Keyed-Homomorphic Encryption is a primitive, first developed in [EHO+13], which allows homomorphic operations with a restricted evaluation key, while preserving different flavors of semantic security depending on whether access to the evaluation key is provided or not. For an adversary not having access to the evaluation key, the homomorphic operation should not be available and this is ensured by requiring CCA security. However, if an adversary comes into possession of the evaluation key, CCA security can no longer be preserved and thus weaker forms of security, such as CCA1, are required. In [LPJY14], the authors gave improved constructions for multiplicative homomorphism with better security guarantees.
A KH-PKE scheme consists of algorithms (KeyGen, Enc, Dec, Eval), where the first three are familiar from public-key encryption, and KeyGen generates a public key pk, a decryption key \(sk_d\) and an Eval key \(sk_h\). Algorithm Eval takes two ciphertexts and returns a ciphertext or \(\bot \). Detailed definitions can be found in [JR14b]. The scheme is said to be correct if (i) for Enc we have \(Dec(sk_d, Enc(pk, M)) = M\), where \(sk_d\) is the secret decryption key, and (ii) for Eval we have \(Dec(sk_d, Eval(sk_h, C_1, C_2)) = Dec(sk_d, C_1) \odot Dec(sk_d, C_2)\), where \(\odot \) is a binary operation on plaintexts, and if any operand of \(\odot \) is \(\bot \) then the result is \(\bot \). The KH-PKE scheme is defined to be KH-CCA secure by a usual public-key CCA experiment with the following twists: the challenger maintains a set D of ciphertexts dependent on the challenge ciphertext (via Eval); decryption queries are not allowed on ciphertexts in D. Further, an adversary \({\mathcal{A}}\) can adaptively ask for \(sk_h\), which we call the reveal event. After the reveal event, the Eval oracle is not available. Similarly, decryption is not available after \({\mathcal{A}}\) has both requested \(sk_h\) and obtained the challenge ciphertext, in any order. Again, detailed definitions can be found in [JR14b].
Construction. We present a construction of a KH-CCA secure KH-PKE encryption scheme with multiplicative homomorphism which utilizes our general DSS-QA-NIZK construction for the Diffie-Hellman (DH) language. In fact, if we assume that the adversary never invokes RevHK, we can prove security generically assuming any DSS-QA-NIZK (with statistical one-time full-ZK) for the DH language. When the adversary invokes RevHK, the partial-simulation trapdoor is revealed to the Adversary, and hence the one-time full-ZK property of DSS-QA-NIZK may not hold. Thus, we a need a stronger notion of DSS-QA-NIZK that incorporates the reveal event, and includes an additional requirement that the semi-functional verifier remains sound as before. Using this stronger notion, we can prove generic security of the KH-PKE scheme even with RevHK, and we further show that our general construction of Sect. 4 continues to satisfy this stronger property.
We start with the observation that a standard ElGamal encryption scheme \((\mathbf{{g}}^x, m \cdot \mathbf{{f}}^x)\) is multiplicatively homomorphic, but is not CCA secure due to the exact same reason. The main idea of our construction is as follows. The ciphertexts include an ElGamal encryption of the message M, say \(\mathbf{{g}}^r, M\cdot \mathbf{{g}}^{kr}\) for a public key \(\mathbf{{g}}^k\). The public key also consists of a member \(\mathbf{{g}}^a\), and the ciphertext also include \(\mathbf{{g}}^{ar}\) (we refer to this triple in the ciphertext as augmented ElGamal encryption). It is well-known [JR12] that if a one-time simulation-sound NIZK proof of \(\mathbf{{g}}^r\) and \(\mathbf{{g}}^{ar}\) being of the correct form is also included in the ciphertext then it becomes a publicly-verifiable CCA2-secure encryption scheme. In our keyed-homomorphic construction, we include a DSS-QA-NIZK for \(\mathbf{{g}}^r\) and \(\mathbf{{g}}^{ar}\) being of the correct form (i.e. being a DH tuple). Although the DSS-QA-NIZK itself is not homomorphic, we can take advantage of the corresponding Semi-Functional Simulator \({\mathsf{sfSim}}\) and simulate the proof of a multiplicatively generated (augmented) ElGamal encryption when computing a homomorphic evaluation.
So, given a dual-system non-interactive proof \({\Sigma }\), consider the following algorithms for a KH-PKE scheme \(\mathcal{P}\):
-
KeyGen: Generate \(\mathbf{{g}}, a, k\) randomly. Use \({\mathsf{sfK}}_1\) of \({\Sigma }\) to get CRS \(\sigma \) and trapdoors \(\tau \) and \(\eta \), and language parameters \(\rho = (\mathbf{{g}}, \mathbf{{g}}^{a})\). Set \(pk = (\mathbf{{g}}, \mathbf{{g}}^a, \mathbf{{g}}^k, \sigma )\), \(sk_h = \tau \), \(sk_d = k\).
-
Enc: Given plaintext m, generate \(w \leftarrow \mathbb {Z}_q\) and compute (using \({\mathsf{P}}\) of \({\Sigma }\)) \(c := (\mathbf{{g}}^w, \mathbf{{g}}^{aw}, \gamma , {\mathsf{P}}(\sigma , (\mathbf{{g}}^w, \mathbf{{g}}^{aw}), w, {{ l}}= \gamma )), \text{ where } \gamma := m \cdot \mathbf{{g}}^{kw}.\)
-
Dec: Given ciphertext \(c = (\rho , \hat{\rho }, \gamma , \pi )\), first check if \({\mathsf{V}}(\sigma , \pi , (\rho , \hat{\rho }), \gamma )\) of \({\Sigma }\) holds, then compute \(m:= \gamma /\rho ^k\).
-
Eval (Multiplicative): Given ciphertexts \(c_1 = (\rho _1, \hat{\rho }_1, \gamma _1, \pi _1)\) and \(c_2\) = \((\rho _2\), \(\hat{\rho }_2\), \(\gamma _2\), \(\pi _2)\), first check if \({\mathsf{V}}(\sigma , \pi _i, (\rho _i, \hat{\rho }_i), \gamma _i)\) of \({\Sigma }\) holds for all \(i \in \{1,2\}\). Then compute: \(\rho = \rho _1 \rho _2\rho _3\), \(\hat{\rho }= \hat{\rho }_1 \hat{\rho }_2\hat{\rho }_3\), \(\gamma = \gamma _1 \gamma _2\gamma _3\), where \(\langle \rho _3, \hat{\rho }_3, \gamma _3 \rangle \) is a fresh random tuple obtained by picking r at random and setting the tuple to be \(\langle \mathbf{{g}}^r, (\mathbf{{g}}^{a})^r, (\mathbf{{g}}^k)^r \rangle \). Then compute \(\pi := {\mathsf{sfSim}}(\sigma , \tau , (\rho , \hat{\rho }), \beta = 1, {{ l}}= \gamma )\) using \({\mathsf{sfSim}}\) of \({\Sigma }\). Output ciphertext \(c := (\rho , \hat{\rho }, \gamma , \pi )\).
Theorem 2
\(\mathbf {(Security\,of\,Construction).}\) The above algorithms \(\mathcal{P}\)= (KeyGen, Enc, Dec, Eval) constitute a KH-CCA secure Keyed-Homomorphic Public Key Encryption scheme with multiplicative homomorphism, if \({\Sigma }\) is a DSS-QA-NIZK for the parameterized Diffie-Hellman language (with language parameters distributed randomly) and RevHK is not available.
The main idea of the proof of the above theorem is similar to proofs of CCA2-secure public key encryption schemes using alternate decryption. In other words, the ciphertext can be decrypted as \(m:= \gamma /\rho ^k\), or as \(m:= \gamma /(\rho ^{k_0}\hat{\rho }^{k_1})\), where \(k = k_0 + a k_1\). But, this requires that the ciphertext has correct \(\hat{\rho }\) component, i.e. \(\hat{\rho }= \rho ^a\). The ciphertexts include a NIZK for this purpose, but the NIZK needs to be simulation-sound. Additional complication arises because of dependent ciphertexts. To handle this, we first build an intermediate experiment where all dependent ciphertexts are generated using fresh random ElGamal tuples. Indistinguishability of such an intermediate experiment from the KH-CCA experiment is shown inductively, by carefully employing one-time full-ZK and partial-simulation unbounded simulation soundness. The theorem is proved in detail in [JR14b]. The Adversary’s advantage in the KH-CCA security game is at most \((8L+1) \cdot {\textsc {ADV}_\textsc {DDH}} + O(L/q)\), where L is the total number of calls to Eval.
The more general theorem (with RevHK) is stated and proved in [JR14b]. Under the SXDH assumption, the above construction leads to ciphertexts of size only five group elements. Further, using an augmented Diffie Hellman language (augmented with a smooth hash proof of DH tuple) and its DSS-QA-NIZK, we also extend our result to get CCA1-security despite the key being revealed (see [JR14b]). The resulting scheme has KH-PKE ciphertexts of size six group elements.
6 Single-Round UC Password-Based Key Exchange
The essential elements of the Universal Composability framework can be found in [Can01]. In the following, we adopt the definition for password-based key exchange (UC-PAKE) from Canetti et al [CHK+05].
6.1 UC-PAKE Definition
Just as in the normal key-exchange functionality, if both participating parties are not corrupted, then they receive the same uniformly distributed session key and the adversary learns nothing of the key except that it was generated. However, if one of the parties is corrupted, then the adversary determines the session key. This power to the adversary is also given in case it succeeds in guessing the parties’ shared password. Participants also detect when the adversary makes an unsuccessful attempt. If the adversary makes a wrong password guess in a given session, then the session is marked \({\mathsf {interrupted}}\) and the parties are provided random and independent session keys. If however the adversary makes a successful guess, then the session is marked \(\mathsf {compromised}\), and the adversary is allowed to set the session key. If a session remains marked \(\mathsf {fresh}\), meaning that it is neither interrupted nor compromised. uncorrupted parties conclude with both parties receiving the same, uniformly distributed session key. The formal description of the UC-PAKE functionality \({{\mathcal{F}}_{\textsc {pake}}}\) is given in Fig. 2.
The real-world protocol we provide is also shown to be secure when different sessions use the same common reference string (CRS). To achieve this goal, we consider the universal Composability with joint state (JUC) formalism of Canetti and Rabin [CR03]. This formalism provides a “wrapper layer” that deals with “joint state” among different copies of the protocol. In particular, defining a functionality \(\mathcal{F}\) also implicitly defines the multi-session extension of \(\mathcal{F}\) (denoted by \(\hat{\mathcal{F}}\)): \(\hat{\mathcal{F}}\) runs multiple independent copies of \(\mathcal{F}\), where the copies are distinguished via sub-session IDs \({\mathsf{ssid}}\). The JUC theorem [CR03] asserts that for any protocol \(\pi \) that uses multiple independent copies of \(\mathcal{F}\), composing \(\pi \) instead with a single copy of a protocol that realizes \(\hat{\mathcal{F}}\), preserves the security of \(\pi \).
6.2 Main Idea of the UC Protocol Using DSS-QA-NIZK
For the sake of exposition, let’s call one party in the session the server and the other the client. (There is no such distinction in the actual protocol, and in fact each party will run two parallel protocols, one as a client and another as a server, and output the product of the two keys generated). The common reference string (CRS) defines a Diffie-Hellman language, i.e. \(\rho = \mathbf{{g}}_1, \mathbf{{g}}_1^{a}\). The client picks a fresh Diffie-Hellman tuple by picking a witness r and computing \(\langle \mathbf{{x}}_1 = \mathbf{{g}}_1^r, \mathbf{{x}}_2= \mathbf{{g}}_1^{a\cdot r} \rangle \). It also computes a DSS-QA-NIZK proof on this tuple, which is a hash proof T and a QA-NIZK proof W of the augmented Diffie-Hellman tuple. Note, the QA-NIZK proof W is just a single group element [JR14a] (see [JR14b] for details). It next modifies the Diffie-Hellman tuple using the password pwd it possesses. Essentially, it multiplies \(\mathbf{{x}}_2\) by pwd to get a modified group element which we will denote by S - in fact \((\mathbf{{x}}_1, S)\) is an ElGamal encryption of pwd. It next sends this ElGamal encryption \(\mathbf{{x}}_1, S\) and the T component of the proof to the server. It retains W for later use. At this point it can erase the witness r.
As a first step, we intend to utilize an interesting property of the real-world verifier \({\mathsf{V}}\) of the DSS-QA-NIZK: the verifier is just the verifier of the QA-NIZK for the DH language augmented with the hash proof, and the QA-NIZK verifiers for linear subspaces are just a single bi-linear product test. Specifically (see [JR14b]), \({\mathsf{V}}\) on input \(\mathbf{{x}}_1,\mathbf{{x}}_2\) and proof T, W, computes \(\iota = \mathcal{H}(\mathbf{{x}}_1,\mathbf{{x}}_2)\), and outputs true iff
Thus, it outputs true iff the left-hand-size (LHS) equals the right-hand-side (RHS) of the above equation. Note that the client sent \(\mathbf{{x}}_1, S\) (i.e. \(\mathbf{{x}}_2\) linearly modified by pwd) and T to the server. Assuming the server has the same password pwd, it can un-modify the received message and get \(\mathbf{{x}}_2 = S/\mathrm {pwd}\), and hence can compute this LHS (using the CRS). The client retained W, and can compute the RHS (using the CRS).
The intuition is that unless an adversary out-right guesses the password, it cannot produce a different \(\mathbf{{x}}_1', \,S',\, T'\), such that \(\mathbf{{x}}_1',\,S'/{{{pwd}}},\, T'\) used to compute the LHS will match the RHS above. While we make this intuition rigorous later by showing a UC simulator, to complete the description of the protocol, and using this intuition, the client and server actually compute the LHS and RHS respectively of the following equation (for a fresh random \(s \in \mathbb {Z}_q\) picked by the server):
Now note that for the client to be able to compute the RHS, it must have \(\mathbf{{b}}^s\), since s was picked by the server afresh. For this purpose, the protocol requires that the server send \(\mathbf{{b}}^s\) to the client (note this can be done independently and asynchronously of the message coming from the client). It is not difficult to see, from completeness of the prover and verifier of the DSS-QA-NIZK, that both parties compute the same quantity.
As mentioned earlier, each pair of parties actually run two versions of the above protocol, where-in each party plays the part of client in one version, and the part of server in the other version. Each party then outputs the product of the LHS of (1) computation (in the server version) and the RHS of (1) computation (in the client version) as the session-key. We will refer to these two factors in the session-key computation as the server factor and the client factor resp. This is the final UC-PAKE protocol described in Fig. 3 (with the parties identities, session identifiers and \(\mathbf{{b}}^s\) from its server version, used as label). The quantity \(\mathbf{{x}}_1\) is called R in the protocol, as subscripts will be used for other purposes.
Theorem 3
Assuming the existence of SXDH-hard groups, the protocol given in Fig. 3 securely realizes the \({\widehat{\mathcal{F}}_{\textsc {pake}}}\) functionality in the \(\mathcal{F}_ {\textsc {crs}}\) hybrid model, in the presence of adaptive corruption adversaries.
The theorem is proved in [JR14b]. We provide the intuition below.
6.3 Main Idea of the UC Simulator
We first re-define the various verifiers in the DSS-QA-NIZK for the DH language described in [JR14b], to bring them in line with the above description. In particular, the real-world verifier \({\mathsf{V}}\) is defined equivalently to be: the verifier \({\mathsf{V}}\) takes as input \({\textsc {CRS}}_v\), a word \(\langle \mathbf{{x}}_1,\mathbf{{x}}_2 \rangle \), and a proof \(\pi = (T,W)\), computes \(\iota = \mathcal{H}(\mathbf{{x}}_1,\mathbf{{x}}_2, {{ l}})\), picks a fresh random \(s \in \mathbb {Z}_q\), and outputs true iff
This is equivalent as long as \(s \ne 0\).
The partial-simulation world private-verifier \({\mathsf{pV}}\) is now defined as: it checks a word \(\langle \mathbf{{x}}_1,\mathbf{{x}}_2 \rangle \) and a proof T, W as follows: compute \(\iota = \mathcal{H}(\mathbf{{x}}_1,\mathbf{{x}}_2, {{ l}})\); pick s and \(s'\) randomly and independently from \(\mathbb {Z}_q\), and if \(\mathbf{{x}}_2 = \mathbf{{x}}_1 ^{a}\) and \(T = \mathbf{{x}}_1^{d + \iota e}\) then set \(\xi = \mathbf{{1}}_T\) else set \(\xi = e(\mathbf{{g}}_1, \mathbf{{g}}_2)^{s'}\) and output true iff
This is equivalent to the earlier definition of \({\mathsf{pV}}\) with high probability by an information-theoretic argument, if the trapdoors used were generated by the semi-functional CRS generator \({\mathsf{sfK}}_1\).
The UC simulator \(\mathcal{S}\) works as follows: It will generate the CRS for \({\widehat{\mathcal{F}}_{\textsc {pake}}}\) using the semi-functional CRS generator \({\mathsf{sfK}}_1\) for the Diffie-Hellman language. The next main difference is in the simulation of the outgoing message of the real world parties: \(\mathcal{S}\) uses a dummy message \(\mu \) instead of the real password which it does not have access to. Further, it postpones computation of W till the session-key generation time. Finally, another difference is in the processing of the incoming message, where \(\mathcal{S}\) decrypts the incoming message \(R_2', S_2', T_2'\) to compute a \(\text{ pwd }'\), which it uses to call the ideal functionality’s test function. It next generates a \(\text{ sk }\) similar to how it is generated in the real-world (recall the computation of server factor and client factor by LHS and RHS of (1)) except that it uses the Eq. (2) corresponding to the private verifier. It sends \(\text{ sk }\) to the ideal functionality to be output to the party concerned.
Note, \(\mathcal{S}\) simulating the server factor computation can compute the LHS of Eq. (2), except \(\mathcal{S}\) does not have direct access to pwd and hence cannot get \(\mathbf{{x}}_2\) from the modified \(\hat{S}\) that it receives. However, it can do the following: Use the \(\textsc {TestPwd}\) functionality of the ideal functionality \({\widehat{\mathcal{F}}_{\textsc {pake}}}\) with a pwd\('\) computed as \(\hat{S}/\mathbf{{x}}_1^{a}\). If this pwd\('\) does not match the pwd recorded in \({\widehat{\mathcal{F}}_{\textsc {pake}}}\) for this session and party, then \({\widehat{\mathcal{F}}_{\textsc {pake}}}\) anyway outputs a fresh random session key, which will then turn out to be correct simulation (note, this case is same as \(\mathbf{{x}}_2 \,( = S/pwd) \,\ne \mathbf{{x}}_1^{a}\), which would also have resulted in the same computation on the LHS). If the pwd\('\) matched the pwd, the simulator is notified the same, and hence it can now do the following: if \(T = \mathbf{{x}}_1^{d + \iota e}\) then set \(\xi = \mathbf{{1}}_T\) else set \(\xi = e(\mathbf{{g}}_1, \mathbf{{g}}_2)^{s'}\). Next, it calls \({\widehat{\mathcal{F}}_{\textsc {pake}}}\)’s \(\textsc {NewKey}\) with session key \(e(\mathbf{{x}}_1, (\mathbf{{v}}_1\mathbf{{v}}_2^\iota ) )^s \cdot e(\mathbf{{x}}_1^{a}, \mathbf{{c}})^s \cdot e(T, \mathbf{{g}}_2)^s \cdot \xi \) (multiplied by a RHS computation of (2) in simulation of the client factor, which we will discuss later).
The UC Simulator \(\mathcal{S}\) must also simulate \(\mathbf{{g}}_1^{r}, \mathrm {pwd} \cdot (\mathbf{{g}}_1^{a})^r\) and the T component of the DSS-QA-NIZK, as that is the message sent out to the adversary by the real party (“client” part of the protocol). However, \(\mathcal{S}\) does not have access to pwd. It can just generate a fake tuple \(\mathbf{{g}}_1^{r}, \mu \cdot (\mathbf{{g}}_1^{a})^r \cdot \mathbf{{g}}_1^{r'}\) (for some constant or randomly chosen group element \(\mu \), and some random and independent \(r' \in \mathbb {Z}_q\)). Now, the semi-functional (proof) simulator \({\mathsf{sfSim}}\) of the DSS-QA-NIZK of [JR14b] has an interesting property that when the tuple \(\langle \mathbf{{x}}_1, \mathbf{{x}}_2\rangle \) does not belong to the language (language membership-bit zero), the T component of the simulated proof can just be generated randomly.
The simulator also needs W to compute the client factor, and we had postponed it till the session-key computation phase. As mentioned above, if the password pwd\('\) “decrypted” from the incoming message is not correct then the key is anyway set to be random, and hence a proper W is not even required. However, if the pwd\('\) is correct, the simulator is notified of same, and hence it can compute W component of the proof by passing \(\mathbf{{x}}_2 = \mu \cdot (\mathbf{{g}}_1^{a})^r \cdot \mathbf{{g}}_1^{r'}/\mathrm {pwd}'\) along with \(\mathbf{{x}}_1 \,(= \mathbf{{g}}_1^{r})\) to \({\mathsf{sfSim}}\).
Of course, fixing the above fake tuples employs one-time full-simulation property of the DSS-QA-NIZK (and the DDH assumption).
6.4 Main Idea of the Proof of UC Realization
The proof that the simulator \(\mathcal{S}\) described above simulates the Adversary in the real-world protocol, follows essentially from the properties of the DSS-QA-NIZK, although not generically since the real-world protocol and the simulator use the verifiers \({\mathsf{V}}\) and \({\mathsf{pV}}\) (resp.) in a split fashion. However, as described above the proof is very similar and we give a broad outline here. The proof will describe various experiments between a challenger \(\mathcal C\) and the adversary, which we will just assume to be the environment \(\mathcal Z\) (as the adversary \({\mathcal{A}}\) can be assumed to be just dummy and following \(\mathcal Z\)’s commands). In the first experiment the challenger \(\mathcal C\) will just be the combination of the code of the simulator \(\mathcal{S}\) above and \({\widehat{\mathcal{F}}_{\textsc {pake}}}\). In particular, after the environment issues a \(\textsc {NewSession}\) request with a password pwd, the challenger gets that password. So, while in the first experiment, the challenger (copying \(\mathcal{S}\)) does not use pwd directly, from the next experiment on-wards, it can use pwd. Thus, the main goal of the ensuing experiments is to modify the fake tuples \(\mathbf{{g}}_1^{r}, \mu \cdot (\mathbf{{g}}_1^{a})^r \cdot \mathbf{{g}}_1^{r'}\) by real tuples (as in real-world) \(\mathbf{{g}}_1^{r}, \mathrm {pwd} \cdot (\mathbf{{g}}_1^{a})^r\), since the challenger has access to pwd. This is accomplished by a hybrid argument, modifying one instance at a time using DDH assumption in group \(\mathbb {G}_1\) and using one-time full-ZK property (and using the \({\mathsf{otfSim}}\) proof simulator for that instance). A variant of the one-time full-ZK semi-functional verifier \({\mathsf{sfV}}\) (just as the variants for \({\mathsf{pV}}\) and \({\mathsf{V}}\) described above) is easily obtained. Note that in each experiment, whenever the simulator invokes partial proof simulation it can provide the correct membership bit (with high probability) as in each experiment it knows exactly which tuples are real and which are fake.
Once all the instances are corrected, i.e. R, S generated as \(\mathbf{{g}}_1^{r}, \mathrm {pwd} \cdot (\mathbf{{g}}_1^{a})^r\), the challenger can switch to the real-world because the tuples \(R, S/\mathrm {pwd}\) are now Diffie-Hellman tuples. This implies that the session keys are generated using the \({\mathsf{V}}\) variant described above, which is exactly as in the real-world.
6.5 Adaptive Corruption
The UC protocol described above is also UC-secure against adaptive corruption of parties by the Adversary in the erasure model. In the real-world when the adversary corrupts a party (with a \(\textsc {Corrupt}\) command), it gets the internal state of the party. Clearly, if the party has already been invoked with a \(\textsc {NewSession}\) command then the password pwd is leaked at the minimum, and hence the ideal functionality \({{\mathcal{F}}_{\textsc {pake}}}\) leaks the password to the Adversary in the ideal world. In the protocol described above, the Adversary also gets W and s, as this is the only state maintained by each party between sending \(R,S, T, \hat{\rho }\), and the final issuance of session-key. Simulation of s is easy for the simulator \(\mathcal{S}\) since \(\mathcal{S}\) generates s exactly as in the real world. For generating W, which \(\mathcal{S}\) had postponed to computing till it received an incoming message from the adversary, it can now use the pwd which it gets from \({\widehat{\mathcal{F}}_{\textsc {pake}}}\) by issuing a \(\textsc {Corrupt}\) call to \({\widehat{\mathcal{F}}_{\textsc {pake}}}\). More precisely, it issues the \(\textsc {Corrupt}\) call, and gets pwd, and then calls the semi-functional simulator with \(\mathbf{{x}}_2 = \mu \cdot (\mathbf{{g}}_1^{a})^r \cdot \mathbf{{g}}_1^{r'}/\mathrm {pwd}\) along with \(\mathbf{{x}}_1 \,(= \mathbf{{g}}_1^{r})\) to get W. Note that this computation of W is identical to the postponed computation of W in the computation of client factor of \(\text{ sk }_1\) (which is really used in the output to the environment when pwd\('\) = pwd).
Notes
- 1.
In case the proof simulator is being invoked on a non-language word, it is not immediately clear what this witness can be, unless we also define a language and a distribution for a super-language which includes the language under consideration as a subset.
- 2.
We remark here that the One-time Full Simulation World also uses a semi-functional simulator as can be seen in Fig. 1. It has the same black-box properties as in the Partial-Simulation World, but could potentially have a different internal construction. In this paper it turns out that the same construction suffices for both the worlds, so for the sake of simplicity we forgo making this explicit in the definition.
References
Abdalla, M., Benhamouda, F., Blazy, O., Chevalier, C., Pointcheval, D.: SPHF-friendly non-interactive commitments. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 214–234. Springer, Heidelberg (2013)
Abdalla, M., Benhamouda, F., Pointcheval, D.: Disjunctions for hash proof systems: new constructions and applications. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 69–100. Springer, Heidelberg (2015)
Abdalla, M., Chevalier, C., Pointcheval, D.: Smooth projective hashing for conditionally extractable commitments. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 671–689. Springer, Heidelberg (2009)
Benhamouda, F., Blazy, O., Chevalier, C., Pointcheval, D., Vergnaud, D.: New techniques for SPHFs and efficient one-round PAKE protocols. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 449–475. Springer, Heidelberg (2013)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press, October 2001
Camenisch, J., Chandran, N., Shoup, V.: A public key encryption scheme secure against key dependent chosen plaintext and adaptive chosen ciphertext attacks. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 351–368. Springer, Heidelberg (2009)
Canetti, R., Halevi, S., Katz, J., Lindell, Y., MacKenzie, P.: Universally composable password-based key exchange. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 404–421. Springer, Heidelberg (2005)
Canetti, R., Rabin, T.: Universal composition with joint state. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 265–281. Springer, Heidelberg (2003)
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002)
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: Proceedings of 23rd ACM STOC, pp. 542–552 (1991)
Emura, K., Hanaoka, G., Ohtake, G., Matsuda, T., Yamada, S.: Chosen ciphertext secure keyed-homomorphic public-key encryption. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 32–50. Springer, Heidelberg (2013)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. springer, Heidelberg (2008)
Haralambiev, K.:Efficient cryptographic primitives for non-interactive zero-knowledge proofs and applications. Ph.D. dissertation (2011)
Jutla, C., Roy, A.: Relatively-sound NIZKs and password-based key-exchange. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 485–503. Springer, Heidelberg (2012)
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013)
Jutla, C.S., Roy, A.: Switching lemma for bilinear tests and constant-size NIZK proofs for linear subspaces. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 295–312. Springer, Heidelberg (2014)
Jutla, C.S., Roy, A.: Dual-system simulation-soundness with applications to UC-PAKE and more. Cryptology ePrint Archive, Report 2014/805. https://eprint.iacr.org/2014/805
Katz, J., Vaikuntanathan, V.: Round-optimal password-based authenticated key exchange. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 293–310. Springer, Heidelberg (2011)
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015)
Libert, B., Peters, T., Joye, M., Yung, M.: Non-malleability from malleability: simulation-sound quasi-adaptive NIZK proofs and CCA2-secure encryption from homomorphic signatures. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 514–532. Springer, Heidelberg (2014)
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: 40th FOCS, pp. 543–553. IEEE Computer Society Press, October 1999
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologc Research
About this paper
Cite this paper
Jutla, C.S., Roy, A. (2015). Dual-System Simulation-Soundness with Applications to UC-PAKE and More. In: Iwata, T., Cheon, J. (eds) Advances in Cryptology -- ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science(), vol 9452. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48797-6_26
Download citation
DOI: https://doi.org/10.1007/978-3-662-48797-6_26
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48796-9
Online ISBN: 978-3-662-48797-6
eBook Packages: Computer ScienceComputer Science (R0)







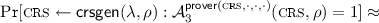
 , where
, where 

