Abstract
A sequence of recent works have constructed constant-size quasi-adaptive (QA) NIZK arguments of membership in linear subspaces of \(\hat{\mathbb {G}}^m\), where \(\hat{\mathbb {G}}\) is a group equipped with a bilinear map \(e:\hat{\mathbb {G}} \times \check{\mathbb {H}} \rightarrow \mathbb {T}\). Although applicable to any bilinear group, these techniques are less useful in the asymmetric case. For example, Jutla and Roy (Crypto 2014) show how to do QA aggregation of Groth-Sahai proofs, but the types of equations which can be aggregated are more restricted in the asymmetric setting. Furthermore, there are natural statements which cannot be expressed as membership in linear subspaces, for example the satisfiability of quadratic equations.
In this paper we develop specific techniques for asymmetric groups. We introduce a new computational assumption, under which we can recover all the aggregation results of Groth-Sahai proofs known in the symmetric setting. We adapt the arguments of membership in linear spaces of \(\hat{\mathbb {G}}^m\) to linear subspaces of \(\hat{\mathbb {G}}^{m} \times \check{\mathbb {H}}^{n}\). In particular, we give a constant-size argument that two sets of Groth-Sahai commitments, defined over different groups \(\hat{\mathbb {G}},\check{\mathbb {H}}\), open to the same scalars in \(\mathbb {Z}_q\), a useful tool to prove satisfiability of quadratic equations in \(\mathbb {Z}_q\). We then use one of the arguments for subspaces in \(\hat{\mathbb {G}}^{m} \times \check{\mathbb {H}}^{n}\) and develop new techniques to give constant-size QA-NIZK proofs that a commitment opens to a bit-string. To the best of our knowledge, these are the first constant-size proofs for quadratic equations in \(\mathbb {Z}_q\) under standard and falsifiable assumptions. As a result, we obtain improved threshold Groth-Sahai proofs for pairing product equations, ring signatures, proofs of membership in a list, and various types of signature schemes.
A. González—Funded by CONICYT, CONICYT-PCHA/Doctorado Nacional/2013-21130937.
C. Ràfols—Part of this work was done while visiting Centro de Modelamiento Matemático, U. Chile. Gratefully acknowledges the support of CONICYT via Basal in Applied Mathematics.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Ideally, a NIZK proof system should be both expressive and efficient, meaning that it should allow to prove statements which are general enough to be useful in practice using a small amount of resources. Furthermore, it should be constructed under mild security assumptions. As it is usually the case for most cryptographic primitives, there is a trade off between these three design goals. For instance, there exist constant-size proofs for any language in NP (e.g. [12]) but based on very strong and controversial assumptions, namely knowledge-of-exponent type of assumptions (which are non-falsifiable, according to Naor’s classification [25]) or the random oracle model.
The Groth-Sahai proof system (GS proofs) [16] is an outstanding example of how these three goals (expressivity, efficiency, and mild assumptions) can be combined successfully. It provides a proof system for satisfiability of quadratic equations over bilinear groups. This language suffices to capture almost all of the statements which appear in practice when designing public-key cryptographic schemes over bilinear groups. Although GS proofs are quite efficient, proving satisfiability of m equations in n variables requires sending some commitments of size \(\varTheta (n)\) and some proofs of size \(\varTheta (m)\) and they easily get expensive unless the statement is very simple. For this reason, several recent works have focused on further improving proof efficiency (e.g. [7, 8, 26])
Among those, a recent line of work [19–22] has succeeded in constructing constant-size arguments for very specific statements, namely, for membership in subspaces of \({\hat{\mathbb {G}}}^{m}\), where \({\hat{\mathbb {G}}}\) is some group equipped with a bilinear map where the discrete logarithm is hard. The soundness of the schemes is based on standard, falsifiable assumptions and the proof size is independent of both m and the witness size. These improvements are in a quasi-adaptive model (QA-NIZK, [19]). This means that the common reference string of these proof systems is specialized to the linear space where one wants to prove membership.
Interestingly, Jutla and Roy [20] also showed that their techniques to construct constant-size NIZK in linear spaces can be used to aggregate the GS proofs of m equations in n variables, that is, the total proof size can be reduced to \(\varTheta (n)\). Aggregation is also quasi-adaptive, which means that the common reference string depends on the set of equations one wants to aggregate. Further, it is only possible if the equations meet some restrictions. The first one is that only linear equations can be aggregated. The second one is that, in asymmetric bilinear groups, the equations must be one-sided linear, i.e. linear equations which have variables in only one of the \(\mathbb {Z}_q\) modules \({\hat{\mathbb {G}}},{\check{\mathbb {H}}}\), or \(\mathbb {Z}_q\).Footnote 1
Thus, it is worth to investigate if we can develop new techniques to aggregate other types of equations, for example, quadratic equations in \(\mathbb {Z}_q\) and also recover all the aggregation results of [20] (in particular, for two-sided linear equations) in asymmetric bilinear groups. The latter (Type III bilinear groups, according to the classification of [11]) are the most attractive from the perspective of a performance and security trade off, specially since the recent attacks on discrete logarithms in finite fields by Joux [18] and subsequent improvements. Considerable research effort (e.g. [1, 10]) has been put into translating pairing-based cryptosystems from a setting with more structure in which design is simpler (e.g. composite-order or symmetric bilinear groups) to a more efficient setting (e.g. prime order or asymmetric bilinear groups). In this line, we aim not only at obtaining new results in the asymmetric setting but also to translate known results and develop new tools specifically designed for it which might be of independent interest.
1.1 Our Results
In Sect. 3, we give constructions of constant-size QA-NIZK arguments of membership in linear spaces of \({\hat{\mathbb {G}}}^{m} \times {\check{\mathbb {H}}}^{n}\). Denote the elements of \({\hat{\mathbb {G}}}\) (respectively of \({\check{\mathbb {H}}}\)) with a hat (resp. with an inverted hat) , as \(\hat{x} \in {\hat{\mathbb {G}}}\) (respectively, as \(\check{y} \in {\check{\mathbb {H}}}\)). Given \({\hat{\mathbf {{M}}}} \in {\hat{\mathbb {G}}}^{m \times t}\) and \(\check{\mathbf {{N}}} \in {\check{\mathbb {H}}}^{n \times t}\), we construct QA-NIZK arguments of membership in the language
which is the subspace of \({\hat{\mathbb {G}}}^{m} \times {\check{\mathbb {H}}}^n\) spanned by \(\begin{pmatrix} {\hat{\mathbf {{M}}}} \\ \check{\mathbf {{N}}}\end{pmatrix}\). This construction is based on the recent constructions of [21]. When \(m=n\), we construct QA-NIZK arguments of membership in
which is the linear subspace of \({\hat{\mathbb {G}}}^{m} \times {\check{\mathbb {H}}}^{m}\) of vectors \(({\hat{\mathbf {x}}},\check{\mathbf {y}})\) such that the sum of their discrete logarithms is in the image of \(\mathbf {{M}}+\mathbf {{N}}\) (the sum of discrete logarithms of \({\hat{\mathbf {{M}}}}\) and \(\check{\mathbf {{N}}}\)).
From the argument for \(\mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {N}}}\), we easily derive another constant-size QA-NIZK argument in the space
where \({\hat{\mathbf {{U}}}}\in {\hat{\mathbb {G}}}^{m \times \tilde{m}}\), \(\check{\mathbf {{V}}} \in {\check{\mathbb {H}}}^{n \times \tilde{n}}\) and \(\mathbf {w} \in \mathbb {Z}_q^{\nu }\). Membership in this space captures the fact that two commitments (or sets of commitments) in \({\hat{\mathbb {G}}},{\check{\mathbb {H}}}\) open to the same vector \(\mathbf {w} \in \mathbb {Z}_q^{\nu }\). This is significant for the efficiency of quadratic GS proofs in asymmetric groups since, because of the way the proofs are constructed, one can only prove satisfiability of equations of degree one in each variable. Therefore, to prove a quadratic statement one needs to add auxiliary variables with commitments in the other group. For instance, to prove that \({\hat{\mathbf {c}}}\) opens to \(b \in \{0,1\}\), one proves that some commitment \(\check{\mathbf {d}}\) opens to \(\overline{b}\) such that \(\{b(\overline{b}-1)=0, b-\overline{b}=0\}\). Our result allows us to aggregate the n proofs of the second statement.
To construct these arguments we introduce a new assumption, the Split Kernel Matrix Diffie-Hellman Assumption (\(\mathsf{SKerMDH}\)). This assumption is derived from the recently introduced Kernel Matrix Diffie-Hellman Assumption (\(\mathsf{KerMDH}\), [24]), which says that it is hard to find a vector in the co-kernel of \(\hat{\mathbf {{A}}}\in {\hat{\mathbb {G}}}^{\ell \times k}\) when \(\mathbf {{A}}\) is such that it is hard to decide membership in \(\mathbf {Im}(\hat{\mathbf {{A}}})\) (i.e. when \(\mathbf {{A}}\) is an instance of a Matrix DH Assumption [8]). Our \(\mathsf{SKerMDH}\) Assumption says that one cannot find a solution to the \(\mathsf{KerMDH}\) problem which is “split” between the groups \({\hat{\mathbb {G}}}\) and \({\check{\mathbb {H}}}\). We think this assumption can be useful in other protocols in asymmetric bilinear groups. A particular case of Kernel MDH Assumption is the Simultaneous Double Pairing Assumption (\(\mathsf{SDP}\), [2]), which is a well established assumption in symmetric bilinear maps, and its “split” variant is the \(\mathsf{SSDP}\) Assumption (see Sect. 2.1) [2].
In Sect. 4 we use the \(\mathsf{SKerMDH}\) Assumption to lift the known aggregation results in symmetric groups to asymmetric ones. More specifically, we show how to extend the results of [20] to aggregate proofs of two-sided linear equations in asymmetric groups. While the original aggregation results of [20] were based on decisional assumptions, our proof shows that they are implied by computational assumptions.
Next, in Sect. 5, we address the problem of aggregating the proof of quadratic equations in \(\mathbb {Z}_q\). For concreteness, we study the problem of proving that a commitment in \({\hat{\mathbb {G}}}\) opens to a bit-string of length n. Such a construction was unknown even in symmetric bilinear groups (yet, it can be easily generalized to this setting, see the full version). More specifically, we prove membership in
where \(({\hat{\mathbf {{U}}}}_1,{\hat{\mathbf {{U}}}}_2)\in {\hat{\mathbb {G}}}^{(n+m)\times n}\times {\hat{\mathbb {G}}}^{(n+m)\times m}\) are matrices which define a perfectly binding and computationally hiding commitment to \(\mathbf {b}\). Specifically, we give instantiations for \(m=1\) (when \(\hat{\mathbf {c}}\) is a single commitment to \(\mathbf {b}\)), and \(m=n\) (when \(\hat{\mathbf {c}}\) is the concatenation of n Groth-Sahai commitments to a bit).
We stress that although our proof is constant-size, we need the commitment to be perfectly binding, thus the size of the commitment is linear in n. The common reference string which we need for this construction is quadratic in the size of the bit-string. Our proof is compatible with proving linear statements about the bit-string, for instance, that \(\sum _{i \in [n]} b_i=t\) by adding a linear number (in n) of elements to the CRS (see the full version). We observe that in the special case where \(t=1\) the common reference string can be linear in n. The costs of our constructions and the cost of GS proofs are summarized in Table 1.
We stress that our results rely solely on falsifiable assumptions. More specifically, in the asymmetric case we need some assumptions which are weaker than the Symmetric External DH Assumption plus the \(\mathsf{SSDP}\) Assumption. Interestingly, our construction in the symmetric setting relies on assumptions which are all weaker than the \(2{\text {-}}\mathsf{Lin}\) Assumption (see the full version).
We think that our techniques for constructing QA-NIZK arguments for bit-strings might be of independent interest. In the asymmetric case, we combine our QA-NIZK argument for \(\mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}},+}\) with decisional assumptions in \({\hat{\mathbb {G}}}\) and \({\check{\mathbb {H}}}\). We do this with the purpose of using QA-NIZK arguments even when \(\mathbf {{M}}+\mathbf {{N}}\) has full rank. In this case, strictly speaking “proving membership in the space” looses all meaning, as every vector in \({\hat{\mathbb {G}}}^m\times {\check{\mathbb {H}}}^m\) is in the space. However, using decisional assumptions, we can argue that the generating matrix of the space is indistinguishable from a lower rank matrix which spans a subspace in which it is meaningful to prove membership.
Finally, in Sect. 6 we discuss some applications of our results. In particular, our results provide shorter signature size of several schemes, more efficient ring signatures, more efficient proofs of membership in a list, and improved threshold GS proofs for pairing product equations.
2 Preliminaries
Let \(\mathsf{Gen}_a\) be some probabilistic polynomial time algorithm which on input \(1^{\lambda }\), where \(\lambda \) is the security parameter, returns the description of an asymmetric bilinear group \((q,{\hat{\mathbb {G}}},{\check{\mathbb {H}}},\mathbb {T},e,\hat{g},\check{h})\), where \({\hat{\mathbb {G}}},{\check{\mathbb {H}}}\) and \(\mathbb {T}\) are groups of prime order q, the elements \(\hat{g}, \check{h}\) are generators of \({\hat{\mathbb {G}}},{\check{\mathbb {H}}}\) respectively, and \(e:{\hat{\mathbb {G}}}\times {\check{\mathbb {H}}}\rightarrow \mathbb {T}\) is an efficiently computable, non-degenerate bilinear map.
We denote by \(\mathfrak {g}\) and \(\mathfrak {h}\) the bit-size of the elements of \({\hat{\mathbb {G}}}\) and \({\check{\mathbb {H}}}\), respectively. Elements \(\hat{x}\in {\hat{\mathbb {G}}}\) (resp. \(\check{y} \in {\check{\mathbb {H}}}\), \(z_\mathbb {T}\in \mathbb {T}\)) are written with a hat (resp, with inverted hat, sub-index \(\mathbb {T}\)) and \(\hat{0},\check{0}\) and \(0_{\mathbb {T}}\) denote the neutral elements. Given \(\hat{x}\in {\hat{\mathbb {G}}},\check{y}\in {\check{\mathbb {H}}}\), \(\hat{x}\check{y}\) refers to the pairing operation, i.e. \(\hat{x}\check{y}=e(\hat{x},\check{y})\). Vectors and matrices are denoted in boldface and any product of vectors/matrices of elements in \({\hat{\mathbb {G}}}\) and \({\check{\mathbb {H}}}\) is defined in the natural way via the pairing operation. That is, given \(\hat{\mathbf {{X}}} \in {\hat{\mathbb {G}}}^{n\times m}\) and \(\check{\mathbf {{Y}}} \in {\check{\mathbb {H}}}^{m \times \ell }\), \(\hat{\mathbf {{X}}} \check{\mathbf {{Y}}} \in \mathbb {T}^{n \times \ell }\). The product \(\check{\mathbf {{X}}}\hat{\mathbf {{Y}}}\in \mathbb {T}^{n\times \ell }\) is defined similarly by switching the arguments of the pairing. Given a matrix \(\mathbf {{T}}=(t_{i,j}) \in \mathbb {Z}_q^{m \times n}\), \(\hat{\mathbf {{T}}}\) (resp. \(\check{\mathbf {{T}}}\)) is the natural embedding of \(\mathbf {{T}}\) in \({\hat{\mathbb {G}}}\) (resp. in \({\check{\mathbb {H}}}\)), that is, the matrix whose (i, j)th entry is \(t_{i,j}\hat{g}\) (resp. \(t_{i,j}\check{h}\)). Conversely, given \({\hat{\mathbf {{T}}}}\) or \(\check{\mathbf {{T}}}\), we use \(\mathbf {{T}}\in \mathbb {Z}_q^{n\times m}\) for the matrix of discrete logarithms of \({\hat{\mathbf {{T}}}}\) (resp. \(\check{\mathbf {{T}}}\)). We denote by \(\mathbf {{I}}_{n\times n}\) the identity matrix in \(\mathbb {Z}_q^{n\times n}\) and \(\mathbf {e}^{n}_i\) the ith element of the canonical basis of \(\mathbb {Z}_q^{n}\) (simply \(\mathbf {e}_i\) if n is clear from the context). We make extensive use of the set \([n+k]\times [n+k]\setminus \{(i,i):i\in [n]\}\) and for brevity we denote it by \(\mathcal {I}_{N,K}\).
2.1 Computational Assumptions
Definition 1
Let \(\ell ,k \in \mathbb {N}\) with \(\ell > k\). We call \(\mathcal {D}_{\ell ,k}\) a matrix distribution if it outputs (in poly time, with overwhelming probability) matrices in \(\mathbb {Z}_q^{\ell \times k}\). We define \(\mathcal {D}_k := \mathcal {D}_{k+1,k}\) and \(\overline{\mathcal {D}_{k}}\) the distribution of the first k rows when \(\mathbf {{A}}\leftarrow \mathcal {D}_{k}\).
Definition 2
(Matrix Diffie-Hellman Assumption [8]). Let \(\mathcal {D}_{\ell ,k}\) be a matrix distribution and \(\varGamma :=(q,{\hat{\mathbb {G}}},{\check{\mathbb {H}}},\mathbb {T},e,\hat{g},\check{h})\leftarrow \mathsf{Gen}_a(1^\lambda )\). We say that the \(\mathcal {D}_{\ell ,k}\)-Matrix Diffie-Hellman (\(\mathcal {D}_{\ell ,k}\)-\(\mathsf{MDDH}_{{\hat{\mathbb {G}}}}\)) Assumption holds relative to \(\mathsf{Gen}_a\) if for all PPT adversaries \(\mathsf{D}\),
where the probability is taken over \(\varGamma \leftarrow \mathsf{Gen}_a(1^\lambda )\), \(\mathbf {{A}} \leftarrow \mathcal {D}_{\ell ,k}, \mathbf {w} \leftarrow \mathbb {Z}_q^k, \hat{\mathbf {u}} \leftarrow {\hat{\mathbb {G}}}^{\ell }\) and the coin tosses of adversary \(\mathsf{D}\).
The \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{MDDH}_{{\check{\mathbb {H}}}}\) problem is defined similarly. In this paper we will refer to the following matrix distributions:
where \(a_i,a_{i,j}\leftarrow \mathbb {Z}_q\), for each \(i,j\in [k]\), \(\mathbf {{B}} \leftarrow \overline{\mathcal {L}}_{k}\), \(\mathbf {{C}} \leftarrow \mathbb {Z}_q^{\ell -k,k}\).
The \(\mathcal {L}_{k}\)-\(\mathsf{MDDH}\) Assumption is the k-linear family of Decisional Assumptions [17, 27]. The \(\mathcal {L}_{1}\)-\(\mathsf{MDDH}_{X}\), \(X \in \{{\hat{\mathbb {G}}},{\check{\mathbb {H}}}\}\), is the Decisional Diffie-Hellman (DDH) Assumption in X, and the assumption that it holds in both groups is the Symmetric External DH Assumption (SXDH). The \(\mathcal {L}_{\ell ,k}\)-\(\mathsf{MDDH}\) Assumption is used in our construction to commit to multiple elements simultaneously. It can be shown tightly equivalent to the \(\mathcal {L}_{k}\)-\(\mathsf{MDDH}\) Assumption. The \(\mathcal {U}_{\ell ,k}\) Assumption is the Uniform Assumption and is weaker than the \(\mathcal {L}_{k}\)-\(\mathsf{MDDH}\). Additionally, we will be using the following family of computational assumptions:
Definition 3
(Kernel Diffie-Hellman Assumption [24]). Let \(\varGamma \leftarrow \mathsf{Gen}_a(1^\lambda )\). The Kernel Diffie-Hellman Assumption in \({\check{\mathbb {H}}}\) (\(\mathcal {D}_{\ell ,k}\)-\(\mathsf{KerMDH}_{{\check{\mathbb {H}}}}\)) says that every PPT Algorithm has negligible advantage in the following game: given \(\check{\mathbf {{A}}}\), where \(\mathbf {{A}}\leftarrow \mathcal {D}_{\ell ,k}\), find \({\hat{\mathbf {x}}} \in {\hat{\mathbb {G}}}^{\ell }\setminus \{ {\hat{\mathbf {0}}} \}\), such that \({\hat{\mathbf {x}}}^{\top }\check{\mathbf {{A}}}=\mathbf {0}_{\mathbb {T}}\).
The Simultaneous Pairing Assumption in \({\check{\mathbb {H}}}\) (\(\mathsf{SP}\) \(_{{\check{\mathbb {H}}}}\)) is the \( \mathcal {U}_1\)-\(\mathsf{KerMDH}_{{\check{\mathbb {H}}}}\) Assumption and the Simultaneous Double Pairing Assumption (\(\mathsf{SDP}_{\check{\mathbb {H}}}\)) is the \(\mathcal {L}_{2,3}\)-\(\mathsf{KerMDH}_{{\check{\mathbb {H}}}}\) Assumption. The Kernel Diffie-Hellman assumption is a generalization and abstraction of these two assumptions to other matrix distributions. The \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{KerMDH}_{{\check{\mathbb {H}}}}\) Assumption is weaker than the \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{MDDH}_{{\check{\mathbb {H}}}}\) Assumption, since a solution allows to decide membership in \(\mathsf {Im}(\check{\mathbf {{A}}})\).
For our construction, we need to introduce a new family of computational assumptions.
Definition 4
(Split Kernel Diffie-Hellman Assumption). Let \(\varGamma \leftarrow \mathsf{Gen}_a(1^\lambda )\). The Split Kernel Diffie-Hellman Assumption in \({\hat{\mathbb {G}}},{\check{\mathbb {H}}}\) (\(\mathcal {D}_{\ell ,k}\)-\(\mathsf{SKerMDH}\)) says that every PPT Algorithm has negligible advantage in the following game: given \(({\hat{\mathbf {{A}}}},\check{\mathbf {{A}}})\), \(\mathbf {{A}} \leftarrow \mathcal {D}_{\ell ,k}\), find a pair of vectors \(({\hat{\mathbf {r}}},\check{\mathbf {s}}) \in {\hat{\mathbb {G}}}^{\ell } \times {\check{\mathbb {H}}}^{\ell }\), \(\mathbf {r} \ne \mathbf {s}\), such that \(\hat{\mathbf {r}}^{\top }\check{\mathbf {{A}}}=\check{\mathbf {s}}^{\top }\hat{\mathbf {A}}\).
As a particular case we consider the Split Simultaneous Double Pairing Assumption in \({\hat{\mathbb {G}}},{\check{\mathbb {H}}}\) (\(\mathsf{SSDP}\)) which is the \(\mathcal {L}_{2}\)-\(\mathsf{SKerMDH}\) Assumption. Intuitively, the Kernel Diffie-Hellman Assumption says one cannot find a non-zero vector in \({\hat{\mathbb {G}}}^{\ell }\) which is in the co-kernel of \(\check{\mathbf {{A}}}\), while the new assumption says one cannot find a pair of vectors in \({\hat{\mathbb {G}}}^{\ell } \times {\check{\mathbb {H}}}^{\ell }\) such that the difference of the vector of their discrete logarithms is in the co-kernel of \(\check{\mathbf {{A}}}\). The name “split” comes from the idea that the output of a successful adversary would break the Kernel Diffie-Hellman Assumption, but this instance is “split” between the groups \({\hat{\mathbb {G}}}\) and \({\check{\mathbb {H}}}\). When \(k=1\), the \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{SKerMDH}\) Assumption does not hold. The assumption is generically as least as hard as the standard,“non-split” assumption in symmetric bilinear groups. This means, in particular, that in Type III bilinear groups, one can use the \(\mathsf{SSDP}\) Assumption with the same security guarantees as the \(\mathsf{SDP}\) Assumption, which is a well established assumption (used for instance in [2, 23]).
Lemma 1
If \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{KerMDH}\) holds in generic symmetric bilinear groups, then \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{SKerMDH}\) holds in generic asymmetric bilinear groups.
Suppose there is a generic algorithm which breaks the \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{SKerMDH}\) Assumption. Intuitively, given two different encodings of \(\mathbf {{A}} \leftarrow \mathcal {D}_{\ell ,k}\), \(({\hat{\mathbf {{A}}}},\check{\mathbf {{A}}})\), this algorithm finds \({\hat{\mathbf {r}}}\) and \(\check{\mathbf {s}}\), \(\mathbf {r} \ne \mathbf {s}\) such that \({\hat{\mathbf {r}}}^{\top }\check{\mathbf {{A}}} =\check{\mathbf {s}}^{\top } {\hat{\mathbf {{A}}}}\). But since the algorithm is generic, it also works when \({\hat{\mathbb {G}}}={\check{\mathbb {H}}}\), and then \({\hat{\mathbf {r}}}-{\hat{\mathbf {s}}}\) is a solution to \(\mathcal {D}_{\ell ,k}\)-\(\mathsf{KerMDH}\). We provide a formal proof in the full version.
2.2 Groth-Sahai NIZK Proofs
The GS proof system allows to prove satisfiability of a set of quadratic equations in a bilinear group. The admissible equation types must be in the following form:
where \(A_1,A_2,A_T\) are \(\mathbb {Z}_q\)-vector spaces equipped with some bilinear map \(f:A_1\times A_2 \rightarrow A_T\), \(\varvec{\alpha }\in A_1^{m_y}\), \(\varvec{\beta }\in A_2^{m_x}\), \(\varvec{\Gamma }=(\gamma _{i,j}) \in \mathbb {Z}_q^{m_x\times m_y}\), \(t \in A_T\). The modules and the map f can be defined in different ways as: (a) in pairing-product equations (PPEs), \(A_1={\hat{\mathbb {G}}}\), \(A_2={\check{\mathbb {H}}}\), \(A_T=\mathbb {T}\), \(f(\hat{x},\check{y})=\hat{x} \check{y} \in \mathbb {T}\), in which case \(t=0_{\mathbb {T}}\), (b1) in multi-scalar multiplication equations in \({\hat{\mathbb {G}}}\) (MMEs), \(A_1={\hat{\mathbb {G}}}\), \(A_2=\mathbb {Z}_q\), \(A_T={\hat{\mathbb {G}}}\), \(f(\hat{x},y)=y \hat{x} \in {\hat{\mathbb {G}}}\), (b2) MMEs in \({\check{\mathbb {H}}}\) (MMEs), \(A_1=\mathbb {Z}_q\), \(A_2={\check{\mathbb {H}}}\), \(A_T={\check{\mathbb {H}}}\), \(f(x,\check{y})=x \check{y} \in {\check{\mathbb {H}}}\), and (c) in quadratic equations in \(\mathbb {Z}_q\) (QEs), \(A_1=A_2=A_T=\mathbb {Z}_q\), \(f(x,y)=xy \in \mathbb {Z}_q\). An equation is linear if \(\mathbf {{\Gamma }}=\mathbf {0}\), it is two-sided linear if both \(\varvec{\alpha }\ne \mathbf {0}\) and \(\varvec{\beta }\ne \mathbf {0}\), and one-sided otherwise.
We briefly recall some facts about GS proofs in the SXDH instantiation used in the rest of the paper. Let \(\varGamma \leftarrow \mathsf{Gen}_a(1^{\lambda })\), \(\mathbf {u}_2,\mathbf {v}_2 \leftarrow \mathcal {L}_1\), \(\mathbf {u}_1:=\mathbf {e}_1+\mu \mathbf {u}_2 \), \(\mathbf {v}_1:=\mathbf {e}_1+\epsilon \mathbf {v}_2\), \(\mu ,\epsilon \leftarrow \mathbb {Z}_q\). The common reference string is \(\mathsf{crs}_{\mathrm {GS}}:=(\varGamma ,{\hat{\mathbf {u}}}_1,{\hat{\mathbf {u}}}_2,\check{\mathbf {v}}_1,\check{\mathbf {v}}_2)\) and is known as the perfectly sound CRS. There is also a perfectly witness-indistinguishable CRS, with the only difference being that \(\mathbf {u}_1:=\mu \mathbf {u}_2\) and \(\mathbf {v}_1:=\epsilon \mathbf {v}_2\) and the simulation trapdoor is \((\mu ,\epsilon )\). These two CRS distributions are computationally indistinguishable. Implicitly, \(\mathsf{crs}_{\mathrm {GS}}\) defines the maps:
The maps \(\iota _X\), \(X \in \{1,2\}\) can be naturally extended to vectors of arbitrary length \({\varvec{\delta }}\in A_X^m\) and we write \(\iota _X(\varvec{\delta })\) for \((\iota _X(\delta _1)|| \ldots ||\iota _X(\delta _m))\).
The perfectly sound CRS defines perfectly binding commitments for any variable in \(A_1\) or \(A_2\). Specifically, the commitment to \(x \in A_1\) is \({\hat{\mathbf {c}}}:=\iota _1(x)+r_1 ({\hat{\mathbf {u}}}_1-{\hat{\mathbf {e}}}_1)+ r_2{\hat{\mathbf {u}}}_2\in {\hat{\mathbb {G}}}^2\), and to \(y \in A_2\) is \(\check{\mathbf {d}}:= \iota _2(y)+ s_1(\check{\mathbf {v}}_1-\check{\mathbf {e}}_1)+s_2\check{\mathbf {v}}_2\), where \(r_1,r_2,s_1,s_2\leftarrow \mathbb {Z}_q\), except if \(A_1=\mathbb {Z}_q\) (resp. \(A_2=\mathbb {Z}_q\)) in which case \(r_1=0\) (resp. \(s_1=0\)).
2.3 Quasi-Adaptive NIZK Arguments
We recall the definition of Quasi Adaptive NIZK (QA-NIZK) Arguments of Jutla et al. [19]. A QA-NIZK proof system enables to prove membership in a language defined by a relation \(\mathcal {R}_\rho \), which in turn is completely determined by some parameter \(\rho \) sampled from a distribution \(\mathcal {D}_\varGamma \). We say that \(\mathcal {D}_\varGamma \) is witness samplable if there exist an efficient algorithm that samples \((\rho ,\omega )\) such that \(\rho \) is distributed according to \(\mathcal {D}_\varGamma \), and membership of \(\rho \) in the parameter language \(\mathcal {L}_\mathsf {par}\) can be efficiently verified with \(\omega \). While the Common Reference String can be set based on \(\rho \), the zero-knowledge simulator is required to be a single probabilistic polynomial time algorithm that works for the whole collection of relations \(\mathcal {R}_\varGamma \).
A tuple of algorithms \((\mathsf{K}_0,\mathsf{K}_1,\mathsf{P},\mathsf{V})\) is called a QA-NIZK proof system for witness-relations \(\mathcal {R}_\varGamma = \{\mathcal {R}_\rho \}_{\rho \in \mathrm {sup}(\mathcal {D}_\varGamma )}\) with parameters sampled from a distribution \(\mathcal {D}_\varGamma \) over associated parameter language \(\mathcal {L}_\mathsf {par}\), if there exists a probabilistic polynomial time simulator \((\mathsf{S}_1, \mathsf{S}_2)\), such that for all non-uniform PPT adversaries \(\mathsf{A}_1\), \(\mathsf{A}_2\), \(\mathsf{A}_3\) we have:
-
Quasi-Adaptive Completeness:
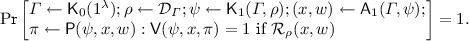
-
Computational Quasi-Adaptive Soundness:
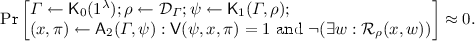
-
Perfect Quasi-Adaptive Zero-Knowledge:
$$\begin{aligned} \Pr [ \varGamma \leftarrow \mathsf{K}_0(1^\lambda ); \rho \leftarrow \mathcal {D}_\varGamma ; \psi \leftarrow \mathsf{K}_1(\varGamma , \rho ): \mathsf{A}_3^{\mathsf{P}(\psi ,\cdot , \cdot )}(\varGamma ,\psi ) = 1] =\;\;\;\\ \Pr [ \varGamma \leftarrow \mathsf{K}_0(1^\lambda ); \rho \leftarrow \mathcal {D}_\varGamma ; (\psi ,\tau ) \leftarrow \mathsf{S}_1(\varGamma , \rho ): \mathsf{A}_3^{\mathsf{S}(\psi ,\tau ,\cdot ,\cdot )}(\varGamma ,\psi )=1] \end{aligned}$$where
-
\(\mathsf{P}(\psi , \cdot , \cdot )\) emulates the actual prover. It takes input (x, w) and outputs a proof \(\pi \) if \((x,w)\in \mathcal {R}_\rho \). Otherwise, it outputs \(\perp \).
-
\(\mathsf{S}(\psi ,\tau , \cdot , \cdot )\) is an oracle that takes input (x, w). It outputs a simulated proof \(\mathsf{S}_2(\psi ,\tau , x)\) if \((x, w) \in \mathcal {R}_\rho \) and \(\perp \) if \((x, w) \notin \mathcal {R}_\rho \).
-
Note that \(\psi \) is the CRS in the above definitions. We assume that \(\psi \) contains an encoding of \(\rho \), which is thus available to \(\mathsf{V}\).
2.4 QA-NIZK Argument for Linear Spaces
In this section we recall the two constructions of QA-NIZK arguments of membership in linear spaces given by Kiltz and Wee [21], for the language:
Algorithm \(\mathsf{K}_0(1^\lambda )\) just outputs \(\varGamma := (q,{\hat{\mathbb {G}}},{\check{\mathbb {H}}},\mathbb {T},e,\hat{g},\check{h}) \leftarrow \mathsf{Gen}_a(1^{\lambda })\), the rest of the algorithms are described in Fig. 1.
The figure describes \(\varPsi _{\mathcal {D}_k}\) when \(\widetilde{\mathcal {D}_{k}}=\mathcal {D}_k\) and \(\tilde{k}=k+1\) and \(\varPsi _{\overline{\mathcal {D}}_k}\) when \(\widetilde{\mathcal {D}_{k}}=\overline{\mathcal {D}}_k\) and \(\tilde{k}=k\). Both are QA-NIZK arguments for \(\mathcal {L}_{{\hat{\mathbf {{M}}}}}\). \(\varPsi _{\mathcal {D}_k}\) is the construction of [21, Sect. 3.1], which is a generalization of Libert et al’s QA-NIZK [22] to any \(\mathcal {D}_k\)-\(\mathsf{KerMDH}_{{\check{\mathbb {H}}}}\) Assumption. \(\varPsi _{\overline{\mathcal {D}}_k}\) is the construction of [21, Sect. 3.2.].
Theorem 1
(Theorem 1 of [21]). If \(\widetilde{\mathcal {D}_{k}}=\mathcal {D}_k\) and \(\tilde{k}=k+1\), Fig. 1 describes a QA-NIZK proof system with perfect completeness, computational adaptive soundness based on the \(\mathcal {D}_{k}\)-\(\mathsf{KerMDH}{}_{{\check{\mathbb {H}}}}\) Assumption, perfect zero-knowledge, and proof size \(k+1\).
Theorem 2
(Theorem 2 of [21]). If \(\widetilde{\mathcal {D}_{k}}=\overline{\mathcal {D}}_k\) and \(\tilde{k}=k\), and \(\mathcal {D}_{\varGamma }\) is a witness samplable distribution, Fig. 1 describes a QA-NIZK proof system with perfect completeness, computational adaptive soundness based on the \(\mathcal {D}_{k}\)-\(\mathsf{KerMDH}{}_{{\check{\mathbb {H}}}}\) Assumption, perfect zero-knowledge, and proof size k.
3 New QA-NIZK Arguments in Asymmetric Groups
In this section we construct three QA-NIZK arguments of membership in different subspaces of \({\hat{\mathbb {G}}}^{m} \times {\check{\mathbb {H}}}^{n}\). Their soundness relies on the Split Kernel Assumption.
3.1 Argument of Membership in Subspace Concatenation
Figure 2 describes a QA-NIZK Argument of Membership in the language
We refer to this as the Concatenation Language, because if we define \(\mathbf {{P}}\) as the concatenation of \({\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}\), that is  , then \(({\hat{\mathbf {x}}},\check{\mathbf {y}}) \in \mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}}\) iff \(\left( {\begin{matrix}{\hat{\mathbf {x}}} \\ \check{\mathbf {y}}\end{matrix}}\right) \) is in the span of \(\mathbf {{P}}\).
, then \(({\hat{\mathbf {x}}},\check{\mathbf {y}}) \in \mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}}\) iff \(\left( {\begin{matrix}{\hat{\mathbf {x}}} \\ \check{\mathbf {y}}\end{matrix}}\right) \) is in the span of \(\mathbf {{P}}\).
Two QA-NIZK Arguments for \(\mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}}\). \(\varPsi _{\mathcal {D}_k,\mathsf{spl}}\) is defined for \(\widetilde{\mathcal {D}_{k}}=\mathcal {D}_k\) and \(\tilde{k}=k+1\), and is a generalization of [21] Sect. 3.1 in two groups. The second construction \(\varPsi _{\overline{\mathcal {D}}_k,\mathsf{spl}}\) corresponds to \(\widetilde{\mathcal {D}_{k}}=\overline{\mathcal {D}_k}\) and \(\tilde{k}=k\), and is a generalization of [21] Sect. 3.2 in two groups. Computational soundness is based on the \(\mathcal {D}_{k}\)-\(\mathsf{SKerMDH}\) Assumption. The CRS size is \((\tilde{k}k+\tilde{k}t+mk)\mathfrak {g}+(\tilde{k}k+\tilde{k}t+nk)\mathfrak {h}\) and the proof size \(\tilde{k}(\mathfrak {g}+\mathfrak {h})\). Verification requires \(2\tilde{k}k+(m+n)k\) pairing computations.
Soundness Intuition. If we ignore for a moment that \({\hat{\mathbb {G}}}, {\check{\mathbb {H}}}\) are different groups, \(\varPsi _{\mathcal {D}_k,\mathsf{spl}}\) (resp. \(\varPsi _{\overline{\mathcal {D}}_k,\mathsf{spl}}\)) is almost identical to \(\varPsi _{\mathcal {D}_k}\) (resp. to \(\varPsi _{\overline{\mathcal {D}}_k}\)) for the language \(\mathcal {L}_{{\hat{\mathbf {{P}}}}}\), and \(\mathbf {{\Delta }}:=(\mathbf {{\Lambda }}||\mathbf {{\Xi }})\), where \(\mathbf {{\Lambda }} \in \mathbb {Z}_q^{\tilde{k} \times m},\mathbf {{\Xi }} \in \mathbb {Z}_q^{\tilde{k} \times n}\). Further, the information that an unbounded adversary can extract from the CRS about \(\mathbf {{\Delta }}\) is:
-
1.
\(\Big \{ \mathbf {{P}}_\varDelta = \mathbf {{\Lambda }} \mathbf {{M}}+ \mathbf {{\Xi }}\mathbf {{N}}, \mathbf {{A}}_{\varDelta } = \mathbf {{\Delta }}^{\top }\mathbf {{A}}=\begin{pmatrix} \mathbf {{\Lambda }}^{\top }\mathbf {{A}} \\ \mathbf {{\Xi }}^{\top }\mathbf {{A}} \end{pmatrix}\Big \}\) from \(\mathsf {crs}_{\varPsi _{\mathcal {D}_k}}\),
-
2.
\(\Big \{ \mathbf {{M}}_\varLambda = \mathbf {{\Lambda }} \mathbf {{M}}+\mathbf {{Z}}, \mathbf {{N}}_\varXi = \mathbf {{\Xi }}\mathbf {{N}}-\mathbf {{Z}}, \begin{pmatrix}\mathbf {{A}}_\varLambda \\ \mathbf {{A}}_\varXi \end{pmatrix} = \begin{pmatrix} \mathbf {{\Lambda }}^{\top }\mathbf {{A}} \\ \mathbf {{\Xi }}^{\top }\mathbf {{A}} \end{pmatrix} \Big \}\) from \(\mathsf {crs}_{\varPsi _{\mathcal {D}_k,\mathsf{spl}}}\).
Given that the matrix \(\mathbf {{Z}}\) is uniformly random, \(\mathsf {crs}_{\varPsi _{\mathcal {D}_k}}\) and \(\mathsf {crs}_{\varPsi _{\mathcal {D}_k,\mathsf{spl}}}\) reveal the same information about \(\mathbf {{\Delta }}\) to an unbounded adversary. Therefore, as the proof of soundness is essentially based on the fact that parts of \(\mathbf {{\Delta }}\) are information theoretically hidden to the adversary, the original proof of [21] can be easily adapted for the new arguments. The proofs can be found in the full version.
Theorem 3
If \(\widetilde{\mathcal {D}_{k}}=\mathcal {D}_k\) and \(\tilde{k}=k+1\), Fig. 2 describes a QA-NIZK proof system with perfect completeness, computational adaptive soundness based on the \(\mathcal {D}_{k}\)-\(\mathsf{SKerMDH}\) Assumption, and perfect zero-knowledge.
Theorem 4
If \(\widetilde{\mathcal {D}_{k}}=\overline{\mathcal {D}}_k\) and \(\tilde{k}=k\), and \(\mathcal {D}_{\varGamma }\) is a witness samplable distribution, Fig. 2 describes a QA-NIZK proof system with perfect completeness, computational adaptive soundness based on the \(\mathcal {D}_{k}\)-\(\mathsf{SKerMDH}\) Assumption, and perfect zero-knowledge.
3.2 Argument of Sum in Subspace
We can adapt the previous construction to the Sum in Subspace Language,
We define two proof systems \(\varPsi _{\mathcal {D}_k,+}\), \(\varPsi _{\overline{\mathcal {D}}_k,+}\) as in Fig. 2, but now with \(\mathbf {{\Lambda }}=\mathbf {{\Xi }}\). Intuitively, soundness follows from the same argument because the information about \(\mathbf {{\Lambda }}\) in the CRS is now \(\mathbf {{\Lambda }}^{\top }\mathbf {{A}},\mathbf {{\Lambda }}(\mathbf {{M}}+\mathbf {{N}})\).
3.3 Argument of Equal Opening in Different Groups
Given the results for Subspace Concatenation of Sect. 3.1, it is direct to construct constant-size NIZK Arguments of membership in:
where \({\hat{\mathbf {{U}}}}\in {\hat{\mathbb {G}}}^{m \times \tilde{m}}\), \(\check{\mathbf {{V}}} \in {\check{\mathbb {H}}}^{n \times \tilde{n}}\) and \(\mathbf {w} \in \mathbb {Z}_q^{\nu }\). The witness is \((\mathbf {w},\mathbf {r},\mathbf {s}) \in \mathbb {Z}_q^{\nu } \times \mathbb {Z}_q^{\tilde{m}-\nu } \times \mathbb {Z}_q^{\tilde{n}-\nu }\). This language is interesting because it can express the fact that \(({\hat{\mathbf {c}}},\check{\mathbf {d}})\) are commitments to the same vector \(\mathbf {w} \in \mathbb {Z}_q^{\nu }\) in different groups.
The construction is an immediate consequence of the observation that \(\mathcal {L}_{\mathsf {com},{\hat{\mathbf {{U}}}},\check{\mathbf {{V}}},\nu }\) can be rewritten as some concatenation language \(\mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}}\). Denote by \({\hat{\mathbf {{U}}}}_1\) the first \(\nu \) columns of \({\hat{\mathbf {{U}}}}\) and \({\hat{\mathbf {{U}}}}_2\) the remaining ones, and \(\check{\mathbf {{V}}}_1\) the first \(\nu \) columns of \(\check{\mathbf {{V}}}\) and \(\check{\mathbf {{V}}}_2\) the remaining ones. If we define:
then it is immediate to verify that \(\mathcal {L}_{\mathsf {com},{\hat{\mathbf {{U}}}},\check{\mathbf {{V}}},\nu }=\mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}}\).
In the rest of the paper, we denote as \(\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}\) the proof system for \(\mathcal {L}_{\mathsf {com},{\hat{\mathbf {{U}}}},\check{\mathbf {{V}}},\nu }\) which corresponds to \(\varPsi _{\overline{\mathcal {D}}_k,\mathsf{spl}}\) for \(\mathcal {L}_{{\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}}\), where \({\hat{\mathbf {{M}}}},\check{\mathbf {{N}}}\) are the matrices defined above. Note that for commitment schemes we can generally assume \({\hat{\mathbf {{U}}}},\check{\mathbf {{V}}}\) to be drawn from some witness samplable distribution.
4 Aggregating Groth-Sahai Proofs in Asymmetric Groups
Jutla and Roy [20] show how to aggregate GS proofs of two-sided linear equations in symmetric bilinear groups. In the original construction of [20] soundness is based on a decisional assumption (a weaker variant of the \(2{\text {-}}\mathsf{Lin}\) Assumption). Its natural generalization in asymmetric groups (where soundness is based on the SXDH Assumption) only enables to aggregate the proofs of one-sided linear equations.
In this section, we revisit their construction. We give an alternative, simpler, proof of soundness under a computational assumption which avoids altogether the “Switching Lemma” of [20]. Further, we extend it to two-sided equations in the asymmetric setting. For one-sided linear equations we can prove soundness under any kernel assumption and for two-sided linear equations, under any split kernel assumption.Footnote 2
Let \(A_1,A_2,A_T\) be \(\mathbb {Z}_q\)-vector spaces compatible with some Groth-Sahai equation as detailed in Sect. 2.2. Let \(\mathcal {D}_{\varGamma }\) be a witness samplable distribution which outputs n pairs of vectors \((\mathbf {\alpha }_\ell , \mathbf {\beta }_\ell ) \in A_1^{m_y} \times A_2^{m_x}\), \(\ell \in [n]\), for some \(m_x,m_y \in \mathbb {N}\). Given some fixed pairs \((\mathbf {\alpha }_\ell , \mathbf {\beta }_\ell )\), we define, for each \(\mathbf {\tilde{t}} \in A_{T}^{n}\), the set of equations \(\mathcal {S}_{\mathbf {\tilde{t}}}\) as:
We note that, as in [20], we only achieve quasi-adaptive aggregation, that is, the common reference string is specific to a particular set of equations. More specifically, it depends on the constants \({\varvec{\alpha }}_{\ell },{\varvec{\beta }}_{\ell }\) (but not on \(\tilde{t}_{\ell }\), which can be chosen by the prover) and it can be used to aggregate the proofs of \(\mathcal {S}_{\mathbf {\tilde{t}}}\), for any \(\mathbf {\tilde{t}}\).
Given the equation types for which we can construct NIZK GS proofs, there always exists (1) \(t_{\ell } \in A_1\), such that \(\tilde{t}_{\ell }=f(t_{\ell },\mathsf {base}_{2})\) or (2) \(\tilde{t}_{\ell } \in A_2,\) such that \(\tilde{t}_{\ell }=f(\mathsf {base}_{1},t_{\ell })\), where \(\mathsf {base}_{i}=1\) if \(A_i=\mathbb {Z}_q\), \(\mathsf {base}_{1}=\hat{g}\) if \(A_1={\hat{\mathbb {G}}}\) and \(\mathsf {base}_{2}=\check{h}\) if \(A_2={\check{\mathbb {H}}}\). This is because \(\tilde{t}_{\ell }=0_{\mathbb {T}}\) for PPEs, and \(A_{T}=A_{i}\), for some \(i \in [2]\), for other types of equations. For simplicity, in the construction we assume that (1) is the case, otherwise change \(\iota _2(a_{\ell ,i}), \iota _1(t_{\ell })\) for \(\iota _1(a_{\ell ,i}), \iota _2(t_{\ell })\) in the construction below.
-
\(\mathsf{K}_0(1^\varLambda )\): Return \(\varGamma := (q,{\hat{\mathbb {G}}},{\check{\mathbb {H}}},\mathbb {T},e,\hat{g},\check{h}) \leftarrow \mathsf{Gen}_a(1^{\varLambda })\).
-
\(\mathcal {D}_\varGamma \): \(\mathcal {D}_\varGamma \) is some distribution over n pairs of vectors \(({\varvec{\alpha }}_{\ell }\), \({\varvec{\beta }}_{\ell }) \in A_1^{m_x} \times A_2^{m_y}\).
-
\(\mathsf{K}_1(\varGamma , \mathcal {S}_{\mathbf {\tilde{t}}})\): Let \(\mathbf {{A}}=(a_{i,j}) \leftarrow \mathcal {D}_{n,k}\). Define
$$\mathsf{crs}:=\left( \mathsf{crs}_{{\mathrm {GS}}}, \left\{ \sum _{\ell \in [n]}\iota _1(a_{\ell ,i} {\varvec{\alpha }}_\ell ), \sum _{\ell \in [n]} \iota _2(a_{\ell ,i} {\varvec{\beta }}_\ell ), \big \{\iota _{2}(a_{\ell ,i}): \ell \in [n]\big \}: i \in [k]\right\} \right) $$ -
\(\mathsf{P}(\varGamma , \mathcal {S}_{\mathbf {\tilde{t}}},\mathbf {x},\mathbf {y})\): Given a solution \(\mathbf {\mathsf{x}}=\mathbf {x}\), \(\mathbf {\mathsf{y}}=\mathbf {y}\) to \(\mathcal {S}_{\mathbf {\tilde{t}}}\), the prover proceeds as follows:
-
Commit to all \(x_j \in A_1\) as \({\hat{\mathbf {c}}}_j\leftarrow \mathsf {Comm}_{{\mathrm {GS}}}(x_j)\), and to all \(\mathsf{y}_j\in A_2\) as \(\check{\mathbf {d}}_j\leftarrow \mathsf {Comm}_{{\mathrm {GS}}}(y_j)\).
-
For each \(i \in [k]\), run the GS prover for the equation \(\sum _{\ell \in [n]} a_{\ell ,i} E_{\ell }(\mathbf {\mathsf{x}},\mathbf {\mathsf{y}})= \sum _{\ell \in [n]} f(t_{\ell }, a_{\ell ,i})\) to obtain the proof, which is a pair \(({\hat{\mathbf {{\Theta }}}}_i,\check{\mathbf {{\Pi }}}_i)\).
Output \((\{{\hat{\mathbf {c}}}_j : j \in [m_x]\}, \{\check{\mathbf {d}}_j: j \in [m_y]\}, \{(\check{\mathbf {{\Pi }}}_{i},{\hat{\mathbf {{\Theta }}}}_{i}) : i \in [k]\})\).
-
-
\(\mathsf{V}(\mathsf{crs},\mathcal {S}_{\mathbf {\tilde{t}}},\{{\hat{\mathbf {c}}}_j\}_{j\in [m_x]}, \{\check{\mathbf {d}}_j\}_{j\in [m_y]}, \{{\hat{\mathbf {{\Theta }}}}_{i},\check{\mathbf {{\Pi }}}_{i}\}_{i \in [k]})\): For each \(i \in [k]\), run the GS verifier for equation
$$\sum _{\ell \in [n]} a_{\ell ,i} E_{\ell }(\mathbf {\mathsf{x}},\mathbf {\mathsf{y}})= \sum _{\ell \in [n]} f(t_{\ell }, a_{\ell ,i}).$$
Theorem 5
The above protocol is a QA-NIZK proof system for two-sided linear equations.
Proof
Completeness. Observe that
Completeness follows from the observation that to efficiently compute the proof, the GS Prover [16] only needs, a part from a satisfying assignment to the equation, the randomness used in the commitments, plus a way to compute the inclusion map of all involved constants, in this case \(\iota _1(a_{\ell ,i} \alpha _{\ell ,j})\), \(\iota _2(a_{\ell ,i} \beta _{\ell ,j})\) and the latter is part of the CRS.
Soundness. We change to a game \(\mathsf {Game}_{1}\) where we know the discrete logarithm of the GS commitment key, as well as the discrete logarithms of \(({\varvec{\alpha }}_{\ell },{\varvec{\beta }}_{\ell })\), \(\ell \in [n]\). This is possible because they are both chosen from a witness samplable distribution.
We now prove that an adversary against the soundness in \(\mathsf {Game}_{1}\) can be used to construct an adversary \(\mathsf{B}\) against the \(\mathcal {D}_{n,k}\)-\(\mathsf{SKerMDH}\) Assumption, where \(\mathcal {D}_{n,k}\) is the matrix distribution used in the CRS generation.
\(\mathsf{B}\) receives a challenge \(({\hat{\mathbf {{A}}}},\check{\mathbf {{A}}})\in {\hat{\mathbb {G}}}^{n\times k}\times {\check{\mathbb {H}}}^{n\times k}\). Given all the discrete logarithms that \(\mathsf{B}\) knows, it can compute a properly distributed CRS even without knowledge of the discrete logarithm of \({\hat{\mathbf {{A}}}}\). The soundness adversary outputs commitments \(\{{\hat{\mathbf {c}}}_j\}_{j\in [m_x]},\{\check{\mathbf {d}}_{j}\}_{j\in [m_y]}\) together with proofs \(\{{\hat{\mathbf {{\Theta }}}}_{i},\check{\mathbf {{\Pi }}}_{i}\}_{i \in [k]}\), which are accepted by the verifier.
Let \(\mathbf {x}\) (resp. \(\hat{\mathbf {x}}\)) be the vector of openings of \(\{{\hat{\mathbf {c}}}_j\}_{j\in [m_x]}\) in \(A_1\) (resp. in the group \({\hat{\mathbb {G}}}\)) and \(\mathbf {y}\) (resp. \(\check{\mathbf {y}}\)) the vector of openings of \(\{\check{\mathbf {d}}_j\}_{j\in [m_y]}\) in \(A_2\) (resp. in the group \({\check{\mathbb {H}}}\)). If \(A_1={\hat{\mathbb {G}}}\) (resp. \(A_2={\check{\mathbb {H}}}\)) then \(\mathbf {x}=\hat{\mathbf {x}}\) (resp. \(\mathbf {y}=\check{\mathbf {y}}\)). The vectors \(\hat{\mathbf {x}}\) and \(\check{\mathbf {y}}\) are efficiently computable by \(\mathsf{B}\) who knows the discrete logarithm of the commitment keys. We claim that the pair \((\hat{{\varvec{\rho }}},\check{{\varvec{\sigma }}}) \in {\hat{\mathbb {G}}}^{n} \times {\check{\mathbb {H}}}^n\), \(\hat{{\varvec{\rho }}}:=({\varvec{\beta }}_1^\top {\hat{\mathbf {x}}} -\hat{t}_{1},\ldots , {\varvec{\beta }}_{n}^\top {\hat{\mathbf {x}}} -\hat{t}_{n}), \check{{\varvec{\sigma }}}:=({\varvec{\alpha }}_1^\top \check{\mathbf {y}},\ldots , {\varvec{\alpha }}_{n}^\top \check{\mathbf {y}})\), solves the \(\mathcal {D}_{n,k}\)-\(\mathsf{SKerMDH}\) challenge.
First, observe that if the adversary is successful in breaking the soundness property, then \({\varvec{\rho }} \ne {\varvec{\sigma }}\). Indeed, if this is the case there is some index \(\ell \in [n]\) such that \(E_{\ell }(\mathbf {x},\mathbf {y}) \ne \tilde{t}_{\ell }\), which means that \(\sum _{j\in [m_y]} f(\alpha _{\ell ,j}, \mathsf{y}_j) \ne \sum _{j\in [m_x]} f(\mathsf{x}_j, \beta _{\ell ,j}) - f(t_{\ell },\mathsf {base}_{2})\). If we take discrete logarithms in each side of the equation, this inequality is exactly equivalent to \({\varvec{\rho }} \ne {\varvec{\sigma }}\).
Further, because GS proofs have perfect soundness, \(\mathbf {x}\) and \(\mathbf {y}\) satisfy the equation \(\sum _{\ell \in [n]} a_{\ell ,i} E_{\ell }(\mathbf {\mathsf{x}},\mathbf {\mathsf{y}})= \sum _{\ell \in [n]} f(t_{\ell }, a_{\ell ,i})\), for all \(i \in [k]\), Thus, for all \(i\in [k]\),
which implies that \(\hat{{\varvec{\rho }}}\check{\mathbf {{A}}}=\check{{\varvec{\sigma }}}{\hat{\mathbf {{A}}}}\).
Zero-Knowledge. The same simulator of GS proofs can be used. Specifically the simulated proof corresponds to k simulated GS proofs.
One-Sided Equations. In the case when \({\varvec{\alpha }}_{\ell }=\mathbf {{0}}\) and \(\tilde{t}_{\ell }=f(t_{\ell },\mathsf {base}_{2})\) for some \(t_{\ell } \in A_1\), for all \(\ell \in [n]\), proofs can be aggregated under a standard Kernel Assumption (and thus, in asymmetric bilinear groups we can choose \(k=1\)). Indeed, in this case, in the soundness proof, the adversary \(\mathsf{B}\) receives \(\check{\mathbf {{A}}}\in {\check{\mathbb {H}}}^{n\times k}\), an instance of the \(\mathcal {D}_{n,k}-\mathsf{KerMDH}_{\check{\mathbb {H}}}\) problem. The adversary \(\mathsf{B}\) outputs \(\hat{{\varvec{\rho }}}:=({\varvec{\beta }}_1^\top {\hat{\mathbf {x}}} -\hat{t}_{1},\ldots , {\varvec{\beta }}_{n}^\top {\hat{\mathbf {x}}} -\hat{t}_{n}) \) as a solution to the challenge. To see why this works, note that, when \({\varvec{\alpha }}_{\ell }=\mathbf {{0}}\) for all \(\ell \in [n]\), equation (3) reads \(\sum _{\ell \in [n]} \check{a}_{\ell ,i} \left( {\varvec{\beta }}_\ell ^\top {\hat{\mathbf {x}}} - {\hat{\mathbf {t}}}_{\ell } \right) = \mathbf {{0}}_\mathbb {T}\) and thus \(\hat{{\varvec{\rho }}}\check{\mathbf {{A}}}=\mathbf {{0}}_\mathbb {T}\). The case when \({\varvec{\beta }}_\ell =\mathbf {{0}}\) and \(\tilde{t}_{\ell }=f(\mathsf {base}_{1},t_{\ell })\) for some \(t_{\ell } \in A_2\), for all \(\ell \in [n]\), is analogous.
5 QA-NIZK Arguments for Bit-Strings
We construct a constant-size QA-NIZK for proving that a perfectly binding commitment opens to a bit-string. That is, we prove membership in the language:
where \({\hat{\mathbf {{U}}}}:=({\hat{\mathbf {{U}}}}_1,{\hat{\mathbf {{U}}}}_2)\in {\hat{\mathbb {G}}}^{(n+m)\times n}\times {\hat{\mathbb {G}}}^{(n+m)\times m}\) defines perfectly binding and computationally hiding commitment keys. The witness for membership is \((\mathbf {b},\mathbf {w})\) and \({\hat{\mathbf {{U}}}} \leftarrow \mathcal {D}_{\varGamma }\), where \(\mathcal {D}_\varGamma \) is some witness samplable distribution.
To prove that a commitment in \({\hat{\mathbb {G}}}\) opens to a vector of bits \(\mathbf {b}\), the usual strategy is to compute another commitment \(\check{\mathbf {d}}\in {\check{\mathbb {H}}}^{\bar{n}}\) to a vector \(\bar{\mathbf {b}}\in \mathbb {Z}_q^n\) and prove (1) \(b_i(\overline{b}_i-1)=0\), for all \(i \in [n]\), and (2) \(b_i-\overline{b}_i=0\), for all \(i \in [n]\). For statement (2), since \({\hat{\mathbf {{U}}}}\) is witness samplable, we can use our most efficient QA-NIZK from Sect. 3.3 for equal opening in different groups. Under the \(\mathsf{SSDP}\) Assumption, which is the \(\mathsf{SKerMDH}\) Assumption of minimal size conjectured to hold in asymmetric groups, the proof is of size \(2(\mathfrak {g}+\mathfrak {h})\). Thus, the challenge is to aggregate n equations of the form \(b_i(\overline{b}_i-1)=0\). We note that this is a particular case of the problem of aggregating proofs of quadratic equations, which was left open in [20].
We finally remark that the proof must include \(\check{\mathbf {d}}\) and thus it may be not of size independent of n. However, it turns out that \(\check{\mathbf {d}}\) needs not be perfectly binding, in fact \(\bar{n}=2\) suffices.
Intuition. A prover wanting to show satisfiability of the equation \(\mathsf{x}(\mathsf{y}-1)=0\) using GS proofs, will commit to a solution \(\mathsf{x}=b\) and \(\mathsf{y}=\overline{b}\) as \(\hat{\mathbf {c}}=b \hat{\mathbf {u}}_1 + r \hat{\mathbf {u}}_2\) and \(\check{\mathbf {d}}=\overline{b} \check{\mathbf {v}}_1 + s \check{\mathbf {v}}_2\), for \(r,s \leftarrow \mathbb {Z}_q\), and then give a pair \((\hat{{\varvec{\theta }}},\check{{\varvec{\pi }}}) \in {\hat{\mathbb {G}}}^{2} \times {\check{\mathbb {H}}}^{2}\) which satisfies the following verification equationFootnote 3:
The reason why this works is that, if we express both sides of the equation in the basis of \(\mathbb {T}^{2\times 2}\) given by \(\{\hat{\mathbf {u}}_1\check{\mathbf {v}}_1^{\top },\hat{\mathbf {u}}_2\check{\mathbf {v}}_1^{\top },\hat{\mathbf {u}}_1\check{\mathbf {v}}_2^{\top },\hat{\mathbf {u}}_2\check{\mathbf {v}}_2^{\top }\}\), the coefficient of \(\hat{\mathbf {u}}_1\check{\mathbf {v}}_1^{\top }\) is \(b(\overline{b}-1)\) on the left side and 0 on the right side (regardless of \((\hat{{\varvec{\theta }}},\check{{\varvec{\pi }}})\)). Our observation is that the verification equation can be abstracted as saying:
Now consider commitments to \((b_1,\ldots ,b_n)\) and \((\overline{b}_1,\ldots ,\overline{b}_n)\) constructed with some commitment key \(\{(\hat{\mathbf {g}}_i,\check{\mathbf {h}}_i): i \in [n+1]\}\subset {\hat{\mathbb {G}}}^{{\overline{n}}}\times {\check{\mathbb {H}}}^{\overline{n}}\), for some \({\overline{n}}\in \mathbb {N}\), to be determined later, and defined as \(\hat{\mathbf {c}}:=\sum _{i \in [n]} b_i \hat{\mathbf {g}}_i + r \hat{\mathbf {g}}_{n+1}\), \(\check{\mathbf {d}}:=\sum _{i \in [n]} \overline{b}_i \check{\mathbf {h}}_i + s \check{\mathbf {h}}_{n+1}\), \(r,s \leftarrow \mathbb {Z}_q\). Suppose for a moment that \(\{ \hat{\mathbf {g}}_{i} \check{\mathbf {h}}_{j}^{\top } : i,j \in [n+1]\}\) is a set of linearly independent vectors. Then,
if and only if \(b_i(\overline{b}_i-1)=0\) for all \(i \in [n]\), because \(b_i(\overline{b}_i-1)\) is the coordinate of \(\hat{\mathbf {g}}_i\check{\mathbf {h}}_i^{\top }\) in the left side of the equation.
Equation 6 suggests to use one of the constant-size QA-NIZK Arguments for linear spaces to get a constant-size proof that \(b_i(\overline{b}_i-1)=0\) for all \(i \in [n]\). Unfortunately, these arguments are only defined for membership in subspaces in \({\hat{\mathbb {G}}}^m\) or \({\check{\mathbb {H}}}^m\) but not in \(\mathbb {T}^m\). Our solution is to include information in the CRS to “bring back” this statement from \(\mathbb {T}\) to \({\hat{\mathbb {G}}}\), i.e. the matrices \(\hat{\mathbf {{C}}}_{i,j}:=\hat{\mathbf {g}}_i\mathbf {h}_j^{\top }\), for each \((i,j)\in \mathcal {I}_{N,1}\). Then, to prove that \(b_i(\overline{b}_i-1)=0\) for all \(i\in [n]\), the prover computes \(\hat{\mathbf {{\Theta }}}_{b(\overline{b}-1)}\) as a linear combination of \(\mathcal {C}:=\{\hat{\mathbf {{C}}}_{i,j}: (i,j)\in \mathcal {I}_{N,1}\}\) (with coefficients which depend on \(\mathbf {b},\mathbf {\overline{b}},r,s\)) such that
and gives a QA-NIZK proof of \({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}\in \mathsf {Span}(\mathcal {C})\).
This reasoning assumes that \(\{\hat{\mathbf {g}}_i \mathbf {h}_j^{\top }\}\) (or equivalently, \(\{\hat{\mathbf {{C}}}_{i,j}\}\)) are linearly independent, which can only happen if \({\overline{n}}\ge n+1\). If that is the case, the proof cannot be constant because \({\hat{\mathbf {{\Theta }}}}_{b(\bar{b}-1)} \in {\hat{\mathbb {G}}}^{{\overline{n}}\times {\overline{n}}}\) and this matrix is part of the proof. Instead, we choose \(\hat{\mathbf {g}}_1,\ldots ,\hat{\mathbf {g}}_{n+1} \in {\hat{\mathbb {G}}}^{2}\) and \(\check{\mathbf {h}}_1,\ldots ,\check{\mathbf {h}}_{n+1} \in {\check{\mathbb {H}}}^{2}\), so that \(\{\hat{\mathbf {{C}}}_{i,j}\} \subseteq {\hat{\mathbb {G}}}^{2 \times 2}\). Intuitively, this should still work because the prover receives these vectors as part of the CRS and he does not know their discrete logarithms, so to him, they behave as linearly independent vectors.
With this change, the statement \({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}\in \mathsf{Span}(\mathcal {C})\) seems no longer meaningful, as \(\mathsf{Span}(\mathcal {C})\) is all of \({\hat{\mathbb {G}}}^{2\times 2}\) with overwhelming probability. But this is not the case, because by means of decisional assumptions in \({\hat{\mathbb {G}}}^2\) and in \({\check{\mathbb {H}}}^2\), we switch to a game where the matrices \(\hat{\mathbf {{C}}}_{i,j}\) span a non-trivial space of \({\hat{\mathbb {G}}}^{2 \times 2}\). Specifically, to a game where \(\hat{\mathbf {{C}}}_{i^*,i^*}\notin \mathsf{Span}(\mathcal {C})\) and \(i^*\leftarrow [n]\) remains hidden to the adversary. Once we are in such a game, perfect soundness is guaranteed for equation \(b_{i^*}(\bar{b}_{i^*}-1)=0\) and a cheating adversary is caught with probability at least 1 / n. We think this technique might be of independent interest.
The last obstacle is that, using decisional assumptions on the set of vectors \(\{\check{\mathbf {h}}_{j}\}_{j\in [n+1]}\) is incompatible with using the discrete logarithms of \(\check{\mathbf {h}}_j\) to compute the matrices \(\hat{\mathbf {{C}}}_{i,j}:=\hat{\mathbf {g}}_i \mathbf {h}_j^{\top }\) given in the CRS. To account for the fact that, in some games, we only know \(\mathbf {g}_i \in \mathbb {Z}_q\) and, in some others, only \(\mathbf {h}_j \in \mathbb {Z}_q\), we replace each matrix \(\hat{\mathbf {{C}}}_{i,j}\) by a pair \((\hat{\mathbf {{C}}}_{i,j},\check{\mathbf {{D}}}_{i,j})\) which is uniformly distributed conditioned on \(\mathbf {{C}}_{i,j}+\mathbf {{D}}_{i,j}=\mathbf {g}_i \mathbf {h}_j^{\top }\). This randomization completely hides the group in which we can compute \(\mathbf {g}_i \mathbf {h}_j^{\top }\). Finally, we use our QA-NIZK Argument for sum in a subspace (Sect. 3.2) to prove membership in this space.
Instantiations. We discuss in detail two particular cases of languages \(\mathcal {\mathcal {L}}_{{\hat{\mathbf {{U}}}},\mathsf{bits}}\). First, in Sect. 5.1 we discuss the case when
-
(a)
\({\hat{\mathbf {c}}}\) is a vector in \({\hat{\mathbb {G}}}^{n+1}\), \({\hat{\mathbf {u}}}_{n+1} \leftarrow \mathcal {L}_{n+1,1}\) and \(\hat{\mathbf {{U}}}_1:=\begin{pmatrix}{\hat{\mathbf {{I}}}}_{n\times n}\\ {\hat{\mathbf {{0}}}}_{1\times n}\end{pmatrix} \in {\hat{\mathbb {G}}}^{(n+1) \times n}, {\hat{\mathbf {{U}}}}_2:={\hat{\mathbf {u}}}_{n+1} \in {\hat{\mathbb {G}}}^{n+1}\), \({\hat{\mathbf {{U}}}}=({\hat{\mathbf {{U}}}}_1|| {\hat{\mathbf {{U}}}}_2)\).
In this case, the vectors \(\hat{\mathbf {g}}_i\) in the intuition are defined as \(\hat{\mathbf {g}}_i=\mathbf {{\Delta }} {\hat{\mathbf {u}}}_i\), where \(\mathbf {{\Delta }}\leftarrow \mathbb {Z}_q^{2\times (n+1)}\), and the commitment to \(\mathbf {b}\) is computed as \({\hat{\mathbf {c}}}:=\sum _{i\in [n]}b_i{\hat{\mathbf {u}}}_i+w{\hat{\mathbf {u}}}_{n+1}\). Then in Sect. 5.3 we discuss how to generalize the construction for a) to
-
(b)
\({\hat{\mathbf {c}}}\) is the concatenation of n GS commitments. That is, given the GS CRS \(\mathsf {crs}_{\mathrm {GS}}=(\varGamma ,{\hat{\mathbf {u}}}_1,{\hat{\mathbf {u}}}_2,\check{\mathbf {v}}_1,\check{\mathbf {v}}_2)\), we define,
$${\hat{\mathbf {{U}}}}_1:= \begin{pmatrix} {\hat{\mathbf {u}}}_1 &{} \ldots &{} {\hat{\mathbf {0}}}\\ \vdots &{} \ddots &{} \vdots \\ {\hat{\mathbf {0}}} &{} \ldots &{} {\hat{\mathbf {u}}}_1 \end{pmatrix} \in {\hat{\mathbb {G}}}^{2n \times n}, {\hat{\mathbf {{U}}}}_2:= \begin{pmatrix} {\hat{\mathbf {u}}}_2 &{} \ldots &{} {\hat{\mathbf {0}}}\\ \vdots &{} \ddots &{} \vdots \\ {\hat{\mathbf {0}}} &{} \ldots &{} {\hat{\mathbf {u}}}_2 \end{pmatrix} \in {\hat{\mathbb {G}}}^{2n \times n}.$$
Although the proof size is constant, in both of our instantiations the commitment size is \(\varTheta (n)\). Specifically, \((n+1)\mathfrak {g}\) for case a) and \(2n\mathfrak {g}\) for case b).
5.1 The Scheme
-
\(\mathsf{K}_0(1^\varLambda )\): Return \(\varGamma := (q,{\hat{\mathbb {G}}},{\check{\mathbb {H}}},\mathbb {T},e,\hat{g},\check{h}) \leftarrow \mathsf{Gen}_a(1^{\varLambda })\).
-
\(\mathcal {D}_\varGamma \): The distribution \(\mathcal {D}_\varGamma \) over \({\hat{\mathbb {G}}}^{(n+1) \times (n+1)}\) is some witness samplable distribution which defines the relation \(\mathcal {R}_\varGamma = \{\mathcal {R}_{{\hat{\mathbf {{U}}}}}\} \subseteq {\hat{\mathbb {G}}}^{n+1}\times (\{0,1\}^{n}\times \mathbb {Z}_q)\), where \({\hat{\mathbf {{U}}}}\leftarrow \mathcal {D}_\varGamma \), such that \(({\hat{\mathbf {c}}},\langle \mathbf {b}, w\rangle )\in \mathcal {R}_{{\hat{\mathbf {{U}}}}}\) iff \({\hat{\mathbf {c}}}={\hat{\mathbf {{U}}}}\left( {\begin{array}{c}\mathbf {b}\\ w\end{array}}\right) \). The relation \(\mathcal {R}_{par}\) consists of pairs \(({\hat{\mathbf {{U}}}},\mathbf {{U}})\) where \({\hat{\mathbf {{U}}}} \leftarrow \mathcal {D}_{\varGamma }\).
-
\(\mathsf{K}_1(\varGamma , {\hat{\mathbf {{U}}}})\): Let \(\mathbf {h}_{n+1}\leftarrow \mathbb {Z}_q^2\) and for all \(i \in [n]\), \(\mathbf {h}_{i}:=\epsilon _{i}\mathbf {h}_{n+1}\), where \(\epsilon _{i} \leftarrow \mathbb {Z}_q\). Define \(\check{\mathbf {{H}}}:= (\check{\mathbf {h}}_1|| \ldots ||\check{\mathbf {h}}_{n+1})\). Choose \(\mathbf {{\Delta }} \leftarrow \mathbb {Z}_q^{2 \times (n+1)}\), define \(\hat{\mathbf {{G}}}:= \mathbf {{\Delta }}{\hat{\mathbf {{U}}}}\) and \(\hat{\mathbf {g}}_{i}:=\mathbf {{\Delta }} \hat{\mathbf {u}}_i \in {\hat{\mathbb {G}}}^2\), for all \(i \in [n+1]\). Let \(\mathbf {a} \leftarrow \mathcal {L}_{1}\) and define \(\check{\mathbf {a}}_{\varDelta }:=\mathbf {{\Delta }}^\top \check{\mathbf {a}} \in {\check{\mathbb {H}}}^{n+1}\). For any pair \((i,j) \in \mathcal {I}_{N,1}\), let \(\mathbf {{T}}_{i,j}\leftarrow \mathbb {Z}_q^{2\times 2}\) and set:
$${\hat{\mathbf {{C}}}}_{i,j}:=\hat{\mathbf {g}}_i \mathbf {h}_j^{\top } - {\hat{\mathbf {{T}}}}_{i,j} \in {\hat{\mathbb {G}}}^{2 \times 2}, \qquad \qquad \check{\mathbf {{D}}}_{i,j}:=\check{\mathbf {{T}}}_{i,j} \in {\check{\mathbb {H}}}^{2 \times 2}.$$Note that \({\hat{\mathbf {{C}}}}_{i,j}\) can be efficiently computed as \(\mathbf {h}_j \in \mathbb {Z}_q^{2}\) is the vector of discrete logarithms of \(\check{\mathbf {h}}_j\).
Let \({\varPsi _{\overline{\mathcal {D}}_k,+}}\) be the proof system for Sum in Subspace (Sect. 3.2) and \({\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) be an instance of our proof system for Equal Opening (Sect. 3.3).
Let \(\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,+}}\leftarrow \mathsf{K}_1(\varGamma , \{{\hat{\mathbf {{C}}}}_{i,j},\check{\mathbf {{D}}}_{i,j}\}_{(i,j)\in \mathcal {I}_{N,1}})\) andFootnote 4 \(\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\leftarrow \mathsf{K}_1(\varGamma , \hat{\mathbf {{G}}},\check{\mathbf {{H}}},n)\). The common reference string is given by:
$$\begin{aligned} \mathsf {crs}_P:= & {} \left( \hat{\mathbf {{U}}}, \hat{\mathbf {{G}}}, \check{\mathbf {{H}}}, \{{\hat{\mathbf {{C}}}}_{i,j},\check{\mathbf {{D}}}_{i,j} \}_{(i,j) \in \mathcal {I}_{N,1}},\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,+}},\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\right) \!, \\ \mathsf {crs}_V:= & {} \left( \check{\mathbf {a}}, \check{\mathbf {a}}_\varDelta , \mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,+}},\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\right) \!. \end{aligned}$$ -
\(\mathsf{P}(\mathsf {crs}_P, {\hat{\mathbf {c}}}, \langle \mathbf {b}, w_g \rangle )\): Pick \(w_h \leftarrow \mathbb {Z}_q\), \(\mathbf {{R}} \leftarrow \mathbb {Z}_q^{2\times 2}\) and then:
-
1.
Define
$${\hat{\mathbf {c}}}_{\varDelta } := \hat{\mathbf {{G}}}\begin{pmatrix} \mathbf {b} \\ w_g \end{pmatrix}\!, \qquad \check{\mathbf {d}} := \check{\mathbf {{H}}}\begin{pmatrix} \mathbf {b} \\ w_h \end{pmatrix}\!.$$ -
2.
Compute \(({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}, \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)})\, :=\)
$$\begin{aligned}&\sum _{i \in [n]}\left( b_i w_h ({\hat{\mathbf {{C}}}}_{i,n+1},\check{\mathbf {{D}}}_{i,n+1})+ w_g(b_i-1) ({\hat{\mathbf {{C}}}}_{n+1,i}, \check{\mathbf {{D}}}_{n+1,i})\right) \nonumber \\&+ \sum _{i \in [n]} \sum _{\begin{array}{c} j \in [n]\\ j\ne i \end{array}} b_i (b_j-1) ({\hat{\mathbf {{C}}}}_{i,j}, \check{\mathbf {{D}}}_{i,j})\nonumber \\&+ w_gw_h ({\hat{\mathbf {{C}}}}_{n+1,n+1}, \check{\mathbf {{D}}}_{n+1,n+1}) + ({\hat{\mathbf {{R}}}},-\check{\mathbf {{R}}}). \end{aligned}$$(8) -
3.
Compute a proof \((\hat{\varvec{\rho }}_{b(\overline{b}-1)},\check{\varvec{\sigma }}_{b(\overline{b}-1)})\) that \(\mathbf {{\Theta }}_{b(\overline{b}-1)}+\check{\mathbf {{\Pi }}}_{b(\overline{b}-1)}\) belongs to the space spanned by \(\{\mathbf {{C}}_{i,j}+\mathbf {{D}}_{i,j}\}_{(i,j)\in \mathcal {I}_{N,1}}\), and a proof \((\hat{{\varvec{\rho }}}_{b-\overline{b}}, \check{{\varvec{\sigma }}}_{b-\overline{b}})\) that \(({\hat{\mathbf {c}}}_\varDelta ,\check{\mathbf {d}})\) open to the same value, using \(\mathbf {b},w_g\), and \(w_h\).
-
1.
-
\(\mathsf{V}(\mathsf {crs}_V, {\hat{\mathbf {c}}}, \langle {\hat{\mathbf {c}}}_{\varDelta }, \check{\mathbf {d}}, ({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}, \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)}), \{(\hat{\varvec{\rho }}_{X}, \check{\varvec{\sigma }}_{X})\}_{X \in \{b(\overline{b}-1), b-\overline{b}\}} \rangle )\):
-
1.
Check if \({\hat{\mathbf {c}}}^\top \check{\mathbf {a}}_\varDelta = {\hat{\mathbf {c}}}_\varDelta ^\top \check{\mathbf {a}}\).
-
2.
Check if
$$\begin{aligned} {\hat{\mathbf {c}}}_{\varDelta } \left( \check{\mathbf {d}}- \sum _{j \in [n]} \check{\mathbf {h}}_{j} \right) ^{\top } = {\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)} \check{\mathbf {{I}}}_{2 \times 2} + {\hat{\mathbf {{I}}}}_{2 \times 2}\check{\mathbf {{\Pi }}}_{b(\overline{b}-1)}. \end{aligned}$$(9) -
3.
Verify that \((\hat{{\varvec{\rho }}}_{b(\overline{b}-1)}, \check{{\varvec{\sigma }}}_{b(\overline{b}-1)}),(\hat{{\varvec{\rho }}}_{b-\overline{b}},\check{{\varvec{\sigma }}}_{b-\overline{b}})\) are valid proofs for \(({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)},\) \(\check{\mathbf {{\Pi }}}_{b(\overline{b}-1)})\) and \(({\hat{\mathbf {c}}}_\varDelta ,\check{\mathbf {d}})\) using \(\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,+}}\) and \(\mathsf{crs}_{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) respectively.
If any of these checks fails, the verifier outputs 0, else it outputs 1.
-
1.
-
\(\mathsf {S}_1(\varGamma ,\hat{\mathbf {{U}}})\): The simulator receives as input a description of an asymmetric bilinear group \(\varGamma \) and a matrix \(\hat{\mathbf {{U}}} \in {\hat{\mathbb {G}}}^{(n+1) \times (n+1)}\) sampled according to distribution \(\mathcal {D}_{\varGamma }\). It generates and outputs the CRS in the same way as \(\mathsf{K}_1\), but additionally it also outputs the simulation trapdoor
$$\tau =\left( \mathbf {{H}}, \mathbf {{\Delta }}, \tau _{\varPsi _{\overline{\mathcal {D}}_k,+}}, \tau _{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\right) \!,$$where \(\tau _{\varPsi _{\overline{\mathcal {D}}_k,+}}\) and \(\tau _{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) are, respectively, \({\varPsi _{\overline{\mathcal {D}}_k,+}}\)’s and \({\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\)’s simulation trapdoors.
-
\(\mathsf {S}_2(\mathsf{crs}_P,\hat{\mathbf {c}},\tau )\): Compute \(\hat{\mathbf {c}}_{\varDelta }:=\mathbf {{\Delta }} \hat{\mathbf {c}}\). Then pick random \(\overline{w}_h \leftarrow \mathbb {Z}_q\), \(\mathbf {{R}} \leftarrow \mathbb {Z}_q^{2 \times 2}\) and define \(\mathbf {d}:= \overline{w}_{h} \mathbf {h}_{n+1}.\) Then set:
$$\begin{aligned} {\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)} \;\; := {\hat{\mathbf {c}}}_\varDelta \left( \mathbf {d}-\sum _{i \in [n]} \mathbf {h}_i\right) ^\top + {\hat{\mathbf {{R}}}}, \quad \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)} \;\; := - \check{\mathbf {{R}}}. \end{aligned}$$Finally, simulate proofs \((\hat{\varvec{\rho }}_{X}, \check{\varvec{\sigma }}_{X})\) for \(X \in \{b(\overline{b}-1), b-\overline{b} \}\) using \(\tau _{\varPsi _{\overline{\mathcal {D}}_k,+}}\) and \(\tau _{\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\).
5.2 Proof of Security
Completeness is proven in the full version. The following theorem guarantees Soundness.
Theorem 6
Let \(\mathsf {Adv}_{\mathcal {PS}}(\mathsf{A})\) be the advantage of an adversary \(\mathsf{A}\) against the soundness of the proof system described above. There exist PPT adversaries \(\mathsf{B}_1,\mathsf{B}_2,\mathsf{B}_3,\mathsf{P}^*_1,\mathsf{P}^*_2\) such that
The proof follows from the indistinguishability of the following games:
-
\(\mathsf {Real}\) This is the real soundness game. The output is 1 if the adversary breaks the soundness, i.e. the adversary submits some
 , for some \(\mathbf {b}\notin \{0,1\}^n\) and \(w \in \mathbb {Z}_q\), and the corresponding proof which is accepted by the verifier.
, for some \(\mathbf {b}\notin \{0,1\}^n\) and \(w \in \mathbb {Z}_q\), and the corresponding proof which is accepted by the verifier. -
\(\mathsf {Game}_0\) This game is identical to \(\mathsf {Real}\) except that algorithm \(\mathsf{K}_1\) does not receive \({\hat{\mathbf {{U}}}}\) as a input but it samples \(({\hat{\mathbf {{U}}}},\mathbf {{U}}) \in \mathcal {R}_{par}\) itself according to \(\mathcal {D}_{\varGamma }\).
-
\(\mathsf {Game}_1\) This game is identical to \(\mathsf {Game_0}\) except that the simulator picks a random \(i^* \in [n]\), and uses \(\mathbf {{U}}\) to check if the output of the adversary \(\mathsf{A}\) is such that \(b_{i^*}\in \{0,1\}\). It aborts if \(b_{i^*}\in \{0,1\}\).
-
\(\mathsf {Game}_{2}\) This game is identical to \(\mathsf {Game}_1\) except that now the vectors \(\hat{\mathbf {g}}_{i}\), \(i \in [n]\) and \(i \ne i^*\), are uniform vectors in the space spanned by \(\hat{\mathbf {g}}_{n+1}\).
-
\(\mathsf {Game}_{3}\) This game is identical to \(\mathsf {Game}_2\) except that now the vector \(\check{\mathbf {h}}_{i^*}\) is a uniform vector in \({\check{\mathbb {H}}}^2\), sampled independently of \(\check{\mathbf {h}}_{n+1}\).
It is obvious that the first two games are indistinguishable. The rest of the argument goes as follows (the remaining proofs are in the full version).
Lemma 2
\(\Pr \left[ \mathsf {Game}_1(\mathsf{A})=1\right] \ge \dfrac{1}{n}\Pr \left[ \mathsf {Game}_0(\mathsf{A})=1\right] .\)
Lemma 3
There exists a \(\mathcal {U}_1\)-\(\mathsf{MDDH}_{\hat{\mathbb {G}}}\) adversary \(\mathsf{B}\) such that \(|\Pr \left[ \mathsf {Game}_{1}(\mathsf{A})=1\right] \) \(-\Pr \left[ \mathsf {Game}_{2}(\mathsf{A})=1\right] |\) \(\le \mathsf {Adv}_{\mathcal {U}_1,{\hat{\mathbb {G}}}}(\mathsf{B}) + 2/q.\)
Proof
The adversary \(\mathsf{B}\) receives \(({\hat{\mathbf {s}}}, {\hat{\mathbf {t}}})\) an instance of the \(\mathcal {U}_1\)-\(\mathsf{MDDH}_{\hat{\mathbb {G}}}\) problem. \(\mathsf{B}\) defines all the parameters honestly except that it embeds the \(\mathcal {U}_1\)-\(\mathsf{MDDH}_{\hat{\mathbb {G}}}\) challenge in the matrix \(\hat{\mathbf {{G}}}\).
Let \({\hat{\mathbf {{E}}}}:=({\hat{\mathbf {s}}}||{\hat{\mathbf {t}}})\). \(\mathsf{B}\) picks \(i^*\leftarrow [n]\), \(\mathbf {{W}}_0\leftarrow \mathbb {Z}_q^{2\times (i^*-1)}\), \(\mathbf {{W}}_1\leftarrow \mathbb {Z}_q^{2\times (n-i^*)}\), \(\hat{\mathbf {g}}_{i^*}\leftarrow {\hat{\mathbb {G}}}^{2}\), and defines \(\hat{\mathbf {{G}}}:= ({\hat{\mathbf {{E}}}}\mathbf {{W}}_0||\hat{\mathbf {g}}_{i^*}||{\hat{\mathbf {{E}}}}\mathbf {{W}}_1|| {\hat{\mathbf {s}}})\). In the real algorithm \(\mathsf {K}_1\), the generator picks the matrix \(\mathbf {{\Delta }} \in \mathbb {Z}_q^{2 \times (n+1)}\). Although \(\mathsf{B}\) does not know \(\mathbf {{\Delta }}\), it can compute \({\hat{\mathbf {{\Delta }}}}\) as \({\hat{\mathbf {{\Delta }}}}= \hat{\mathbf {{G}}}\mathbf {{U}}^{-1}\), given that \(\mathbf {{U}}\) is full rank and was sampled by \(\mathsf{B}\), so it can compute the rest of the elements of the common reference string using the discrete logarithms of \({\hat{\mathbf {{U}}}}\), \(\check{\mathbf {{H}}}\) and \(\check{\mathbf {a}}\).
In case \({\hat{\mathbf {t}}}\) is uniform over \({\hat{\mathbb {G}}}^{2}\), by the Schwartz-Zippel lemma \(\det ({\hat{\mathbf {{E}}}}) = 0\) with probability at most 2 / q. Thus, with probability at least \(1-2/q\), the matrix \({\hat{\mathbf {{E}}}}\) is full-rank and \(\hat{\mathbf {{G}}}\) is uniform over \({\hat{\mathbb {G}}}^{2\times (n+1)}\) as in \(\mathsf{Game}_1\). On the other hand, in case \(\hat{\mathbf {t}}=\gamma {\hat{\mathbf {s}}}\), all of \(\hat{\mathbf {g}}_{i}\), \(i\ne i^*\), are in the space spanned by \(\hat{\mathbf {g}}_{n+1}\) as in \(\mathsf{Game}_2\).
Lemma 4
There exists a \(\mathcal {U}_1\)-\(\mathsf{MDDH}_{\check{\mathbb {H}}}\) adversary \(\mathsf{B}\) such that \(|\Pr \left[ \mathsf {Game}_{2}(\mathsf{A})=1\right] \) \(-\Pr \left[ \mathsf {Game}_{3}(\mathsf{A})=1\right] |\) \(\le \mathsf {Adv}_{\mathcal {U}_1,{\check{\mathbb {H}}}}(\mathsf{B}).\)
Lemma 5
There exists a \(\mathsf{SP}_{{\check{\mathbb {H}}}}\) adversary \(\mathcal {\mathsf{B}}\) and soundness adversaries \(\mathsf{P}^*_1,\mathsf{P}^*_2\) for \({\varPsi _{\overline{\mathcal {D}}_k,+}}\) and \({\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) such that
Proof
\(\Pr [\det ((\mathbf {g}_{i^*}||\mathbf {g}_{n+1}))=0]=\Pr [\det ((\mathbf {h}_{i^*}||\mathbf {h}_{n+1}))=0]\le 2/q\), by the Schwartz-Zippel lemma. Then, with probability at least \(1-4/q\), \(\mathbf {g}_{i^*}\mathbf {h}_{i^*}^\top \) is linearly independent from \(\{\mathbf {g}_{i}\mathbf {h}_j^\top :(i,j)\in [n+1]^2\setminus \{(i^*, i^*)\}\}\) which implies that \(\mathbf {g}_{i^*}\mathbf {h}_{i^*}^\top \notin \mathsf{Span}(\{\mathbf {{C}}_{i,j}+\mathbf {{D}}_{i,j}:(i,j)\in \mathcal {I}_{N,1}\}\})\). Additionally \(\mathsf{Game}_3(\mathsf{A})=1\) implies that \(b_{i^*} \notin \{0,1\}\) while the verifier accepts the proof produced by \(\mathsf{A}\), which is \(({\hat{\mathbf {c}}}_{\varDelta }, \check{\mathbf {d}}, ({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}, \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)}), \{(\hat{\varvec{\rho }}_{X}, \check{\varvec{\sigma }}_{X})\}_{X \in \{b(\overline{b}-1), b-\overline{b}\}} ).\) Since \(\{\check{\mathbf {h}}_{i^*},\check{\mathbf {h}}_{n+1}\}\) is a basis of \({\check{\mathbb {H}}}^2\), we can define \(\overline{w}_h,\overline{b}_{i^*}\) as the unique coefficients in \(\mathbb {Z}_q\) such that \(\check{\mathbf {d}}= \overline{b}_{i^*} \check{\mathbf {h}}_{i^*} + \overline{w}_h \check{\mathbf {h}}_{n+1}\). We distinguish three cases:
-
(1)
If \(\hat{\mathbf {c}}_{\varDelta } \ne \mathbf {{\Delta }} \hat{\mathbf {c}}\), we can construct an adversary \(\mathsf{B}\) against the \(\mathsf{SP}_{{\check{\mathbb {H}}}}\) Assumption that outputs \(\hat{\mathbf {c}}_{\varDelta }-\mathbf {{\Delta }} \hat{\mathbf {c}}\in \ker (\check{\mathbf {{a}}}^\top )\).
-
(2)
If \(\hat{\mathbf {c}}_{\varDelta } = \mathbf {{\Delta }} \hat{\mathbf {c}}\) but \(b_{i^*} \ne \overline{b}_{i^*}\). Given that \((b_{i}\mathbf {g}_{i^*},\bar{b}_{i^*}\mathbf {h}_{i^*})\) is linearly independent from \(\{(\mathbf {g}_{i^*},\mathbf {h}_{i^*}),(\mathbf {g}_{n+1},\mathbf {h}_{n+1})\}\) whenever \(b_{i^*}\ne \bar{b}_{i^*}\), an adversary \(\mathsf{P}^*_2\) against \({\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) outputs the pair \((\hat{{\varvec{\rho }}}_{b-\overline{b}}, \check{{\varvec{\sigma }}}_{b-\overline{b}}) \) which is a fake proof for \(({\hat{\mathbf {c}}}_\varDelta ,\check{\mathbf {d}})\).
-
(3)
If \(\hat{\mathbf {c}}_{\varDelta } = \mathbf {{\Delta }} \hat{\mathbf {c}}\) and \(b_{i^*} = \overline{b}_{i^*}\), then \(b_{i^*}(\overline{b}_{i^*} -1) \ne 0\). If we express \(\mathbf {{\Theta }}_{b(\overline{b}-1)}+\mathbf {{\Pi }}_{b(\overline{b}-1)}\) as a linear combination of \(\mathbf {g}_{i}\mathbf {h}_{j}^{\top }\), the coordinate of \(\mathbf {g}_{i^*}\mathbf {h}_{i^*}^\top \) is \(b_{i^*}(\overline{b}_{i^*}-1)\ne 0\) and thus \(\mathbf {{\Theta }}_{b(\overline{b}-1)}+\mathbf {{\Pi }}_{b(\overline{b}-1)}\notin \mathsf{Span}(\{\mathbf {{C}}_{i,j}+\mathbf {{D}}_{i,j}:(i,j)\in \mathcal {I}_{N,1}\})\). The adversary \(\mathsf{P}^*_1\) against \({\varPsi _{\overline{\mathcal {D}}_k,+}}\) outputs the pair \((\hat{{\varvec{\rho }}}_{b(\overline{b}-1)},\) \(\check{{\varvec{\sigma }}}_{b(\overline{b}-1)})\) which is a fake proof for \(({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}, \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)})\).
This concludes the proof of soundness. Now we prove Zero-Knowledge.
Theorem 7
The proof system is perfect quasi-adaptive zero-knowledge.
Proof
First, note that the vector \(\check{\mathbf {d}}\in {\check{\mathbb {H}}}^2\) output by the prover and the vector output by \(\mathsf {S}_2\) follow exactly the same distribution. This is because the rank of \(\check{\mathbf {{H}}}\) is 1. In particular, although the simulator \(\mathsf {S}_2\) does not know the opening of \({\hat{\mathbf {c}}}\), which is some \(\mathbf {b} \in \{0,1\}^{n}\), there exists \(w_h \in \mathbb {Z}_q\) such that  . Since \(\mathbf {{R}}\) is chosen uniformly at random in \(\mathbb {Z}_q^{2 \times 2}\), the proof \(({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}, \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)})\) is uniformly distributed conditioned on satisfying check 2) of algorithm \(\mathsf{V}\). Therefore, these elements of the simulated proof have the same distribution as in a real proof. This fact combined with the perfect zero-knowledge property of \({\varPsi _{\overline{\mathcal {D}}_k,+}}\) and \({\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) concludes the proof.
. Since \(\mathbf {{R}}\) is chosen uniformly at random in \(\mathbb {Z}_q^{2 \times 2}\), the proof \(({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)}, \check{\mathbf {{\Pi }}}_{b(\overline{b}-1)})\) is uniformly distributed conditioned on satisfying check 2) of algorithm \(\mathsf{V}\). Therefore, these elements of the simulated proof have the same distribution as in a real proof. This fact combined with the perfect zero-knowledge property of \({\varPsi _{\overline{\mathcal {D}}_k,+}}\) and \({\varPsi _{\overline{\mathcal {D}}_k,\mathsf{com}}}\) concludes the proof.
5.3 Extensions
CRS Generation for Individual Commitments. When using individual commitments (distribution b) from Sect. 5), the only change is that \(\mathbf {{\Delta }}\) is sampled uniformly from \(\mathbb {Z}_q^{2 \times 2n}\) (the distribution of \(\check{\mathbf {{H}}}\) is not changed). Thus, the matrix \({\hat{\mathbf {{G}}}}:=\mathbf {{\Delta }} {\hat{\mathbf {{U}}}}\) has 2n columns instead of \(n+1\) and  for some \(\mathbf {w}_g \in \mathbb {Z}_q^{n}\). In the soundness proof, the only change is that in \(\mathsf {Game}_2\), the extra columns are also changed to span a one-dimensional space, i.e. in this game \(\hat{\mathbf {g}}_{i}\), \(i \in [2n-1]\) and \(i \ne i^*\), are uniform vectors in the space spanned by \(\hat{\mathbf {g}}_{2n}\).
for some \(\mathbf {w}_g \in \mathbb {Z}_q^{n}\). In the soundness proof, the only change is that in \(\mathsf {Game}_2\), the extra columns are also changed to span a one-dimensional space, i.e. in this game \(\hat{\mathbf {g}}_{i}\), \(i \in [2n-1]\) and \(i \ne i^*\), are uniform vectors in the space spanned by \(\hat{\mathbf {g}}_{2n}\).
Bit-Strings of Weight 1. In the special case when the bit-string has only one 1 (this case is useful in some applications, see Sect. 6), the size of the CRS can be made linear in n, instead of quadratic. To prove this statement we would combine our proof system for bit-strings of Sect. 5.1 and a proof that \(\sum _{i \in [n]} b_i=1\) as described above. In the definition of \(({\hat{\mathbf {{\Theta }}}}_{b(\overline{b}-1)},\check{\mathbf {{\Pi }}}_{b(\overline{b}-1)})\) in Eq. 8, one sees that for all pairs \((i,j) \in [n] \times [n]\), the coefficient of \(({\hat{\mathbf {C}}}_{i,j},\check{\mathbf {D}}_{i,j})\) is \(b_i(b_j-1)\). If \(i^*\) is the only index such that \(b_{i^*}=1\), then we have:
Therefore, one can replace in the CRS the pairs of matrices \( ({\hat{\mathbf {C}}}_{i,j},\check{\mathbf {D}}_{i,j})\) by \(({\hat{\mathbf {C}}}_{i,\ne },\check{\mathbf {D}}_{i,\ne })\), \(i \in [n]\). The resulting CRS is linear in n.
6 Applications
Many protocols use proofs that a commitment opens to a bit-string as a building block. Since our commitments are still of size \(\varTheta (n)\), our results may not apply to some of these protocols (e.g. range proofs). Yet, there are several applications where bits need to be used independently and our results provide significant improvements. Table 2 summarizes them.
Signatures. Some application examples are the signature schemes of [3–5, 9]. For example, in the revocable attribute-based signature scheme of Escala et. al [9], every signature includes a proof that a set of GS commitments, whose size is the number of attributes, opens to a bit-string. Further, the proof of membership in a list which is discussed below can also be used to reduce the size of Ring Signature scheme of [6], which is the most efficient ring signature in the standard model. To sign a message m, among other things, the signer picks a one-time signature key and certifies the one-time verification key by signing it with a Boneh-Boyen signature under \(vk_\alpha \). Then, the signer commits to \(vk_\alpha \) and shows that \(vk_\alpha \) belongs to the list of Boneh-Boyen verification keys \((vk_1,\ldots ,vk_n)\) of the parties in the ring R.
Threshold GS Proofs for PPEs. There are two approaches to construct threshold GS proofs for PPEs, i.e. proofs of satisfiability of t-out-of-n equations. One is due to [13] and consists of compiling the n equations into a single equation which is satisfied only if t of the original equations are satisfied. For the case of PPEs, this method adds new variables and proves that each of them opens to a bit. Our result reduces the cost of this approach, but we omit any further discussion as it is quite inefficient because the number of additional variables is \(\varTheta (m_{var}+n)\), where \(m_{var}\) is the total number of variables in the original n equations.
The second approach is due to Ràfols [26]. The basic idea behind [26], which extends [14], follows from the observation that for each GS equation type \(\mathsf {tp}\), the CRS space \(\mathcal {K}\) is partitioned into a perfectly sound CRS space \(\mathcal {K}^b_\mathsf {tp}\) and a perfectly witness indistinguishable CRS space \(\mathcal {K}^{h}_\mathsf {tp}\).
In particular, to prove satisfiability of t-out-of-n sets of equations from \(\{\mathcal {S}_i:i\in [n]\}\) of type \(\mathsf {tp}\), it suffices to construct an algorithm \(\mathsf {K}_{\mathsf {corr}}\) which on input \(\mathsf {crs}_{{\mathrm {GS}}}\) and some set of indexes \(A \subset [n]\), \(|A|=t\), generates n GS common reference strings \(\{\mathsf {crs}_i, i \in [n]\}\) and simulation trapdoors \(\tau _{i,sim}\), \(i \in A^c\), in a such a way thatFootnote 5:
-
(a)
it can be publicly verified the set of perfectly sound keys, \(\{\mathsf {crs}_i : \mathsf {crs}_i \in \mathcal {K}_{\mathsf {tp}}^{b}\}\) is of size at least t,
-
(b)
there exists a simulator \(\mathsf {S}_{\mathsf {corr}}\) who outputs \((\mathsf {crs}_i,\tau _{i,sim})\) for all \(i \in [n]\), and the distribution of \(\{\mathsf {crs}_i : i \in [n]\}\) is the same as the one of the keys output by \(\mathsf {K}_{\mathsf {corr}}\) when \(\mathsf {crs}_{{\mathrm {GS}}}\) is the perfectly witness-indistinguishable CRS.
The prover of t-out-of-n satisfiability can run \(\mathsf {K}_{\mathsf {corr}}\) and, for all \(i \in [n]\), compute a real (resp. simulated) proof for \(\mathcal {S}_i\) with respect to \(\mathsf {crs}_i\) when \(i \in A\) (resp. when \(i \in A^c\)).
Ràfols gives two constructions for PPEs, the first one can be found in [26], App. C and the other follows from [26, Sect. 7]Footnote 6. Our algorithm \(\mathsf {K}_\mathsf {corr}\) for PPEsFootnote 7 goes as follows:
-
Define \((b_1,\ldots ,b_n)\) as \(b_i=1\) if \(i \in A\) and \(b_i=0\) if \(i \in A^c\). For all \(i \in [n]\), let \({\hat{\mathbf {z}}}_i:=\mathsf {Comm}(b_i)=b_i {\hat{\mathbf {u}}}_1+ r_i {\hat{\mathbf {u}}}_2\), \(r_i \in \mathbb {Z}_q\), and define \(\tau _{sim,i}=r_i\), for all \(i \in A^c\). Define \(\mathsf {crs}_i:=(\varGamma ,{\hat{\mathbf {z}}}_i,{\hat{\mathbf {u}}}_2,\check{\mathbf {v}}_1,\check{\mathbf {v}}_2)\).
-
Prove that \(\{{\hat{\mathbf {c}}}_i\}\) opens to \(\mathbf {b} \in \{0,1\}^{n}\) and that \(\sum _{i\in [n]} b_i=t\).
The simulator just defines \(\mathbf {b}=\mathbf {0}\). The reason why this works is that when \(b_i=1\), \(({\hat{\mathbf {z}}}_i-{\hat{\mathbf {u}}}_1) \in \mathsf {Span}( {\hat{\mathbf {u}}}_2)\), therefore \(\mathsf {crs}_i \in \mathcal {K}^{b}_{PPE}\) and when \(b_i=0\), \(({\hat{\mathbf {z}}}_i-{\hat{\mathbf {u}}}_1) \notin \mathsf {Span}( {\hat{\mathbf {u}}}_2)\) so \(\mathsf {crs}_i \in \mathcal {K}^{h}_{PPE}\).
More Efficient Proof of Membership in a List. Chandran et al. construct a ring signature of size \(\varTheta (\sqrt{n})\) [6], which is the most efficient ring signature in the standard model. Their construction uses as a subroutine a non-interactive proof of membership in some list \(L=(\hat{l}_1,\ldots ,\hat{l}_n)\) which is of size \(\varTheta (\sqrt{n})\). The trick of Chandran et al. to achieve this asymptotic complexity is to view L as a matrix \({\hat{\mathbf {{L}}}}\in {\hat{\mathbb {G}}}^{m\times m}\), for \(m=\sqrt{n}\), where the i, j th element of \({\hat{\mathbf {{L}}}}\) is \(\hat{l}_{i,j} := \hat{l}_{(i,j)}\) and \((i,j):=(i-1)m+j\). Given a commitment \({\hat{\mathbf {c}}}\) to some element \(\hat{l}_{\alpha }\), where \(\alpha = (i_\alpha ,j_\alpha )\), their construction in asymmetric bilinear groups works as follows :
-
1.
Compute GS commitments in \({\check{\mathbb {H}}}\) to \(b_1\ldots ,b_m\) and \(b'_1,\ldots ,b'_m\), where \(b_i = 1\) if \(i=i_\alpha \) and 0 otherwise, and \(b'_{j}=1\) if \(j=j_\alpha \), and 0 otherwise.
-
2.
Compute a GS proof that \(b_i \in \{0,1\}\) and \(b'_j \in \{0,1\}\) for all \(i,j\in [m]\), and that \(\sum _{i\in [m]}b_i=1\), and \(\sum _{j\in [m]}b'_j=1\).
-
3.
Compute GS commitments to \(\hat{x}_1:=\hat{l}_{(i_\alpha ,1)},\ldots ,\hat{x}_m:=\hat{l}_{(i_\alpha ,m)}\).
-
4.
Compute a GS proof that \(\hat{x}_j = \sum _{i\in [m]}b_i\hat{l}_{(i,j)}\), for all \(j\in [m]\), is satisfied.
-
5.
Compute a GS proof that \(\hat{l}_{\alpha } = \sum _{j\in [m]}b'_j\hat{x}_j\) is satisfied.
With respect to the naive use of GS proofs, Step 2 was improved by Ràfols [26]. Using our proofs for bit-strings of weight 1 from Sect. 5.3, we can further reduce the size of the proof in step 2, see table.
We note that although in step 4 the equations are all two-sided linear equations, proofs can only be aggregated if the list comes from a witness samplable distribution and the CRS is set to depend on that specific list. This is not useful for the application to ring signatures, since the CRS should be independent of the ring R (which defines the list). If aggregation is possible then the size of the proof in step 4 is reduced from \((2\mathfrak {g}+4\mathfrak {h})\sqrt{n}\) to \(4\mathfrak {g}+8\mathfrak {h}\). A complete description of the proof can be found in the full version, where we also show that when the CRS depends on the list and the list is witness samplable, the proof can be further reduced to \(\varTheta (\root 3 \of {n})\).
Notes
- 1.
Jutla and Roy show how to aggregate two-sided linear equations in symmetric bilinear groups. The asymmetric case is not discussed, yet for one-sided linear equations it can be easily derived from their results. This is not the case for two-sided ones, see Sect. 4.
- 2.
- 3.
For readers familiar with the Groth-Sahai notation, Eq. (4) corresponds to \(\mathbf {c} \bullet \left( \mathbf {d}-\iota _2(1)\right) = \mathbf {u}_2 \bullet {\varvec{\pi }} + {\varvec{\theta }} \bullet \mathbf {v}_2\).
- 4.
We identify matrices in \({\hat{\mathbb {G}}}^{2 \times 2}\) (resp. in \({\check{\mathbb {H}}}^{2 \times 2}\)) with vectors in \({\hat{\mathbb {G}}}^{4}\) (resp. in \({\check{\mathbb {H}}}^{4}\)).
- 5.
- 6.
The construction in [26, Sect. 7] is for other equation types but can be used to prove that t-out-of-n of \(\mathsf {crs}_1,\ldots ,\mathsf {crs}_n\) are perfectly binding for PPEs.
- 7.
Properly speaking the construction is for PPEs which are left-simulatable in the terminology of [26].
References
Abe, M., Groth, J., Ohkubo, M., Tango, T.: Converting cryptographic schemes from symmetric to asymmetric bilinear groups. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 241–260. Springer, Heidelberg (2014)
Abe, M., Haralambiev, K., Ohkubo, M.: Signing on elements in bilinear groups for modular protocol design. Cryptology ePrint Archive, Report 2010/133 (2010). http://eprint.iacr.org/2010/133
Blazy, O., Fuchsbauer, G., Pointcheval, D., Vergnaud, D.: Signatures on randomizable ciphertexts. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 403–422. Springer, Heidelberg (2011)
Blazy, O., Pointcheval, D., Vergnaud, D.: Compact round-optimal partially-blind signatures. In: Visconti, I., De Prisco, R. (eds.) SCN 2012. LNCS, vol. 7485, pp. 95–112. Springer, Heidelberg (2012)
Camacho, P.: Fair exchange of short signatures without trusted third party. In: Dawson, E. (ed.) CT-RSA 2013. LNCS, vol. 7779, pp. 34–49. Springer, Heidelberg (2013)
Chandran, N., Groth, J., Sahai, A.: Ring signatures of sub-linear size without random oracles. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 423–434. Springer, Heidelberg (2007)
Escala, A., Groth, J.: Fine-tuning Groth-Sahai proofs. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 630–649. Springer, Heidelberg (2014)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013)
Escala, A., Herranz, J., Morillo, P.: Revocable attribute-based signatures with adaptive security in the standard model. In: Nitaj, A., Pointcheval, D. (eds.) AFRICACRYPT 2011. LNCS, vol. 6737, pp. 224–241. Springer, Heidelberg (2011)
Freeman, D.M.: Converting pairing-based cryptosystems from composite-order groups to prime-order groups. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 44–61. Springer, Heidelberg (2010)
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013)
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006)
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008)
Groth, J., Sahai, A.: Efficient noninteractive proof systems for bilinear groups. SIAM J. Comput. 41(5), 1193–1232 (2012)
Hofheinz, D., Kiltz, E.: Secure hybrid encryption from weakened key encapsulation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 553–571. Springer, Heidelberg (2007)
Joux, A.: A new index calculus algorithm with complexity L(1/4 + o(1)) in small characteristic. In: Lange, T., Lauter, K., Lisoněk, P. (eds.) SAC 2013. LNCS, vol. 8282, pp. 355–380. Springer, Heidelberg (2014)
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013)
Jutla, C.S., Roy, A.: Switching lemma for bilinear tests and constant-size NIZK proofs for linear subspaces. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 295–312. Springer, Heidelberg (2014)
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015)
Libert, B., Peters, T., Joye, M., Yung, M.: Non-malleability from malleability: simulation-sound quasi-adaptive NIZK proofs and CCA2-secure encryption from homomorphic signatures. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 514–532. Springer, Heidelberg (2014)
Libert, B., Peters, T., Yung, M.: Group signatures with almost-for-free revocation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 571–589. Springer, Heidelberg (2012)
Morillo, P., Ràfols, C., Villar, J.L.: Matrix computational assumptions in multilinear groups. Cryptology ePrint Archive, Report 2015/353 (2015). http://eprint.iacr.org/2015/353
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003)
Ràfols, C.: Stretching Groth-Sahai: NIZK proofs of partial satisfiability. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 247–276. Springer, Heidelberg (2015)
Shacham, H.: A cramer-shoup encryption scheme from the linear assumption and from progressively weaker linear variants. Cryptology ePrint Archive, Report 2007/074 (2007). http://eprint.iacr.org/
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologc Research
About this paper
Cite this paper
González, A., Hevia, A., Ràfols, C. (2015). QA-NIZK Arguments in Asymmetric Groups: New Tools and New Constructions. In: Iwata, T., Cheon, J. (eds) Advances in Cryptology -- ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science(), vol 9452. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48797-6_25
Download citation
DOI: https://doi.org/10.1007/978-3-662-48797-6_25
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48796-9
Online ISBN: 978-3-662-48797-6
eBook Packages: Computer ScienceComputer Science (R0)





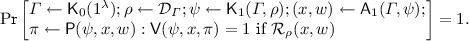
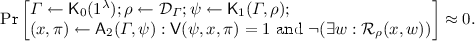


 , for some
, for some