Abstract
We show a framework for constructing identity-based encryption (IBE) schemes that are (almost) tightly secure in the multi-challenge and multi-instance setting. In particular, we formalize a new notion called broadcast encoding, analogously to encoding notions by Attrapadung (Eurocrypt 2014) and Wee (TCC 2014). We then show that it can be converted into such an IBE. By instantiating the framework using several encoding schemes (new or known ones), we obtain the following:
-
We obtain (almost) tightly secure IBE in the multi-challenge, multi-instance setting, both in composite and prime-order groups. The latter resolves the open problem posed by Hofheinz et al. (PKC 2015).
-
We obtain the first (almost) tightly secure IBE with sub-linear size public parameters (master public keys). In particular, we can set the size of the public parameters to constant at the cost of longer ciphertexts and private keys. This gives a partial solution to the open problem posed by Chen and Wee (Crypto 2013).
By applying (a variant of) the Canetti-Halevi-Katz transformation to our schemes, we obtain several CCA-secure PKE schemes with tight security in the multi-challenge, multi-instance setting. One of our schemes achieves very small ciphertext overhead, consisting of less than 12 group elements. This significantly improves the state-of-the-art construction by Libert et al. (in ePrint Archive) which requires 47 group elements. Furthermore, by modifying one of our IBE schemes obtained above, we can make it anonymous. This gives the first anonymous IBE whose security is almost tightly shown in the multi-challenge setting.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
1.1 Backgrounds
In the context of provable security, we reduce the security of a given scheme to the hardness of a computational problem, in order to gain confidence in the security of the scheme. Namely, we assume an adversary \(\mathcal {A}\) who breaks the scheme and then show another adversary \(\mathcal {B}\) who solves the (assumed) hard problem using \(\mathcal {A}\). Such a reduction should be as tight as possible, in the sense that \(\mathcal {B}\)’s success probability is as large as \(\mathcal {A}\). In this paper, we mostly focus on the tight security reduction in identity-based encryption (IBE) [47].
IBE is an advanced form of public key encryption in which one can encrypt a message for a user identity, rather than a public key. The first fully secure (or often called, adaptively secure) construction in the standard model was given in [11]. Later, further developments were made [8, 29, 48, 49]. All the above mentioned papers only deal with the single-challenge, single-instance case. Since it is known that the security in the (much more realistic) multi-challenge and multi-instance setting can be reduced to the security in the single-challenge and single-instance setting [7], these schemes are secure in the former setting in asymptotic sense. However, this reduction incurs \(O(\mu Q_c)\) security loss, where \(Q_c\) is the number of challenge queries made by the adversary and \(\mu \) is the number of instances. Since all the above schemes already loose at least \(O(Q_k)\) security in the reductions, where \(Q_k\) is the number of key extraction queries made by \(\mathcal {A}\), theses schemes loose at least \(O(\mu Q_c Q_k)\) security in total.
Recently and somewhat surprisingly, Chen and Wee [17, 19] showed the first IBE scheme (CW scheme) whose reduction cost is independent of \(Q_k\), resolving an important open question posed in [48]. Subsequently, Blazy et al. [9] were able to obtain anonymous IBE and hierarchical IBE with the same security guarantee. The drawback of these schemes is its large public parameters (master public keys): It is proportional to the security parameter and thus rather large. Note that they only consider the single-challenge and single-instance setting. Very recently, further important development was made by Hofheinz, Koch, and Striecks [31] who extended the proof technique of Chen and Wee in a novel way and proposed the first IBE scheme (HKS scheme) whose reduction cost is independent from all of \(\mu \), \(Q_c\), and \(Q_k\). However, they only give a construction in composite-order groups and explicitly mention that the construction in prime-order groups remains open. We focus on the following two important open problems in this paper:
-
Can we construct a fully, (almost) tightly secure IBE scheme in the multi-challenge and multi-instance setting from a static assumption in the prime-order groups?
-
Can we construct a fully, (almost) tightly secure IBE scheme from a static assumption with constant-size public parameters even in the single-challenge and single-instance setting?
1.2 Our Results
New Tightly-Secure IBE Schemes. In this paper, to tackle the above problems, we revisit the proof technique in [17, 31] and propose a framework for constructing almost tightly secure IBE. The almost tight security means that the reduction cost is independent from \(\mu \), \(Q_c\), and \(Q_k\), and is a small polynomial in the security parameter. In particular, we formalize the notion of broadcast encoding analogously to Attrapadung [4] and Wee [50]. Then we show that it can be converted into fully, (almost) tightly secure IBE scheme, in the multi-challenge and multi-instance setting. We propose such conversions both in prime-order and composite-order groups. Furthermore, we propose two broadcast encoding schemes satisfying our requirement. By instantiating our generic conversion with these schemes, we obtain several new IBE schemes. In particular,
-
We obtain the first IBE scheme in prime-order groups with almost tight security in the multi-challenge and multi-instance setting. The security of our scheme can be shown under the decisional linear (DLIN) assumption. This resolves the first question above.
-
We obtain the first IBE scheme with almost tight security in the multi-challenge and multi-instance setting and with sub-linear public parameter-size (but at the cost of larger private key and ciphertext size). An IBE scheme with almost tight security and sub-linear public parameter size is not known, even in the single-challenge setting. This partially answers the second question above.
Application to Chosen-Ciphertext Secure Public Key Encryption. By applying a variant of Canetti-Halevi-Katz transformation to the new IBE schemes, we obtain several new chosen-ciphertext (CCA) secure public key encryption (PKE) schemes. The conversion is tightness-preserving, namely, if the original IBE is tightly secure in the multi-challenge and multi-instance setting, the resulting PKE scheme is also tightly secure in the same setting. One of our schemes achieves very compact ciphertext size. The ciphertext overhead of the scheme only consists of 10 group elements and 2 elements in \(\mathbb {Z}_p\). This is much shorter than the state-of-the-art construction of PKE scheme with the same security guarantee [34]: their scheme requires 47 group elements.
Extension to Anonymous IBE. Furthermore, by modifying one of the new IBE schemes obtained above, we obtain the first anonymous IBE scheme with (almost) tight security reduction in the multi-challenge settings for the first time. The security proof is done by carefully combining information-theoretic argument due to Chen et al. [16] and a computational argument.
See Table 1 for overview of our schemes.
1.3 Our Techniques
Difficulties. To solve the first question above, a natural starting point would be trying to apply the frameworks for composite-order-to-prime-order-conversion dedicated to identity/attribute-based encryption [2, 3, 16, 18, 35] to the HKS scheme [31]. However, security proofs for CW and HKS schemes significantly deviate from the most standard form of dual system encryption methodology [4, 37, 39, 50], only for which the above mentioned frameworks can be applied. Another approach is to try to convert specific assumptions they use into prime-order. In fact, Chen and Wee [17] were able to accomplish such a conversion for their scheme. However, their technique is non-generic and therefore it is highly unclear whether the same argument is possible for the assumptions that HKS use.
Next, we explain the difficulty of the second question. The reason why all IBE schemes featuring (almost) tight security reduction in previous works [9, 17, 31] require large public parameters is that they use (randomized version of) Naor-Reingold PRF [40] in their construction. Note that the Naor-Reingold PRF requires seed length which is linear in the input size, which in turn implies rather long public parameters in the IBE schemes. A natural approach to improve the efficiency would be, as noted by Chen and Wee [17, 19], to reduce the seed length of the Naor-Reingold PRF. However, this is a long-standing open problem and turns out to be quite difficult.
Our Strategy. In this paper, we introduce new proof techniques for IBE schemes (with almost tight security) that rely only on the subgroup decision assumptions Footnote 1 This allows us to use frameworks for composite-order-to-prime-order conversions in the literature [2, 3, 16, 22, 23, 26, 35, 42] (to name only a few) which converts subgroup decision assumption into a static assumption in prime-order groups, such as the DLIN assumption. Therefore, using these techniques, we are able to convert a variant of HKS scheme into prime-order. This answers the first question above. Note that in the security proof of HKS (and CW), they rely on some specific assumptions in composite-order groups in addition to subgroup decision assumptions. Because of these, it is unclear how to convert HKS scheme into prime-order.
As for the second question, we view Chen and Wee’s scheme as being constructed from, somewhat surprisingly, broadcast encryption mechanism, instead of (Naor-Reingold) PRF, and hence can avoid the above difficulty regarding PRF. More precisely, we show that the task of constructing almost tightly secure IBE scheme is essentially reduced to a construction of broadcast encryption, and based on this idea, we are able to obtain the first IBE scheme with sub-linear size public parameters and almost tight security. In the following, we explain our technique.
Detailed Overview of Our Technique. Let us start from the following variant of the Chen and Wee’s IBE scheme. Let the identity space of the scheme be \( \{ 0,1 \}^\ell \). For \(i\in \{1,2,3\}\), let \(g_i\) be the generator of a subgroup of order \(p_i\) of \(\mathbb {G}\), which is bilinear groups of composite order \(N=p_1 p_2 p_3\). Let also h be a generator of \(\mathbb {G}\). The master public key, a ciphertext, and a private key for an identity \(\mathsf {ID}\) are in the following form:
where \(\mathsf {ID}_i\) is the i-th bit of \(\mathsf {ID}\) and \(\mathsf {M}\) is the message.Footnote 2 Now we are going to show the security. We only consider the single-challenge and single-instance case here for simplicity. In the security proof, at first, the challenge ciphertext is changed to the following form using a subgroup decision assumption:
Then, we consider \(\ell \) hybrid games. In \(\mathsf {Game}_{i}\), all private keys are in the following form:

where \(\mathsf {ID}|_i\) is the length i prefix of the identity \(\mathsf {ID}\) and \(\widehat{\mathsf {R}}_i: \{ 0,1 \}^{i} \rightarrow N\) is a random function. Intuitively, through these hybrid games, the randomizing part of the key (highlighted in the box) are gradually randomized and made dependent on more and more bits of each identity. Finally, in \(\mathsf {Game}_{\ell }\), we can argue that any adversary cannot obtain the information on the message \(\mathsf {M}\), because these randomizing parts prevent it.
A crucial part of the security proof is to establish the indistinguishability between \(\mathsf {Game}_{i^\star -1}\) and \(\mathsf {Game}_{i^\star }\) for all \(i^\star \in [1,\ell ]\). For the target identity \(\mathsf {ID}^\star \) (recall that we are considering the single-challenge and single-instance case for now), we assume that \(b^\star := \mathsf {ID}^\star _{i^\star }\) is known to the reduction algorithm in advance, since it can be guessed with probability 1 / 2. At the core of the proof for this is an indistinguishability of the following distributions:

for all \(\mathsf {ID}\) such that \(\mathsf {ID}_{i^\star } \ne b^\star \), where \(\hat{\alpha } \overset{_\$}{\leftarrow } \mathbb {Z}_N\). Indistinguishability of \(\mathsf {Game}_{i^\star -1}\) and \(\mathsf {Game}_{i^\star }\) is reduced to Eq. (1). The reduction algorithm can create the challenge ciphertext using the first term in Eq. (1). It can also set private key as

where \(\hat{\alpha }=0\) or \(\hat{\alpha } \overset{_\$}{\leftarrow } \mathbb {Z}_N\). It is clear that the game corresponds to \(\mathsf {Game}_{i^\star -1}\) if \(\hat{\alpha }=0\). On the other hand, if \(\hat{\alpha } \overset{_\$}{\leftarrow } \mathbb {Z}_N\), it corresponds to \(\mathsf {Game}_{i^\star }\) with
If \(\hat{\alpha }\) is freshly chosen for every distinct \(\mathsf {ID}|_{i^\star }\), the simulation is perfect. Therefore, our task of the security proof is reduced to establish Eq. (1). To understand better, we decompose the private key in Eq. (1) and restate it again in a slightly stronger form:

Let us consider a bijection map \(f: \{(i,b)\}_{i\in [1,\ell ], b\in \{0,1\}} \rightarrow [1,2\ell ]\) and replace (i, b) with f((i, b)). We can further restate the requirement as:

where \(S^\star = \{ f(i, \mathsf {ID}^\star _i) \}_{i\in [\ell ] }\), \(\tau ^\star = f((i^\star , 1-b^\star ))\), and thus \(\tau ^\star \not \in S^\star .\) We call the terms in the second line above as the challenge terms. (It should not be confused with challenge ciphertext.) At this point, we can now see a similarity to broadcast encryption. We consider the following broadcast encryption which captures the essence of the above requirement. Let the set of user index be \([1,2\ell ]\).
where \(\mathsf {CT}_S\) is a ciphertext for a set \(S\subseteq [2\ell ]\) and \(\mathsf {sk}_\tau \) is a private key for a user index \(\tau \in [2\ell ]\). This is in fact a variant of the broadcast encryption by Gentry and Waters [25]! Indeed, Eq. (2) can be interpreted as a security condition for this broadcast encryption scheme (in the sense of encoding analogous to [4, 50]). It says that given semi-functional ciphertext for a set \(S^\star \), a normal private key for \(\tau ^\star \not \in S^\star \) is indistinguishable from a semi-functional private key for \(\tau ^\star \). At this point, we are able to understand the core technique in Chen and Wee in terms of broadcast encryption scheme.
However, we have not finished yet. In order to make the proof go through, we argue that an adversary cannot distinguish challenge terms in Eq. (2), even if these are given to the adversary unbounded many times with freshly chosen randomness \(\hat{\alpha },r\). Such an indistinguishability can be shown by a standard technique [4, 36, 50] if the challenge term is given to the adversary only once. This can be accomplished by the combination of subgroup decision assumption and the parameter-hiding argument. In parameter-hiding argument, a value which is information-theoretically hidden is used to make normal private key semi-functional [4, 36, 37, 50]. At the first glance, this argument does not seem to be extended to the case where many challenge terms are given to the adversary, since entropy of hidden parameters (in this case, \(w_1,\ldots , w_{2\ell } \mod p_2\)) is limited. However, we have to simulate unbounded number of challenge terms. Chen and Wee [17] resolve this problem by using computational argument instead of information-theoretic argument as above. Namely, they assume a variant of the DDH assumption on \(\mathbb {G}_{p_2}\) Footnote 3 and embed the problem instance into the above challenge terms. Indistinguishability of multiple challenge terms are tightly reduced to the assumption, using the random self-reducibility of the assumption. On the other hand, our technique for boosting to multi-challenge is much simpler. Our key observation is that the challenge term in Eq. (2) can be easily randomized by picking \(a\overset{_\$}{\leftarrow } \mathbb {Z}_N\) and computing
where \(r' = ar\) and \(\hat{\alpha }' = a\hat{\alpha }\). It is easy to see that \(r' \mod p_1\) is uniformly random and independent from anything. We can also see that \(\hat{\alpha }' \mod p_2 = 0\) if \(\hat{\alpha }=0\) and \(\hat{\alpha }' \mod p_2\) is uniformly random if \(\hat{\alpha }\ne 0 \mod p_2\). By this argument, we can see that indistinguishability of the single-challenge-term case implies that for the multi-challenge-term case. Based on all the above discussion, we are able to show the security for the above scheme only using the subgroup decision assumption.
Overview of Our Framework. We refine the idea above and combine it with the technique by HKS to propose our framework for constructing IBE schemes that are (almost) tightly secure in the multi-challenge and multi-instance setting, in both composite and prime-order groups. We first define a broadcast encoding, which is an abstraction of broadcast encryption. The syntax of it is a special case of “pair encoding” in [4] (also similar to “predicate encoding” in [50]). Then, we define perfect master-key hiding (PMH) security and computational-master-key hiding (CMH) security for it. These security notions are also similar to those of [4, 50]. The former is statistical requirement for the encoding, and the latter is computational requirement. We can easily show that the former implies the latter. Then, we also introduce intermediate notion multi-master-key hiding (MMH) security for the encoding. This is more complex notion compared to the PMH and CMH-security, but implied by these, thanks to our boosting technique above. Then, we show that broadcast encoding satisfying the MMH security requirement can be converted into IBE scheme. All these reductions are (almost) tightness-preserving, namely, if the original broadcast encoding is tightly PMH/CMH secure, the resulting IBE scheme is also tightly secure in the multi-challenge and multi-instance setting. Finally, we provide broadcast encoding schemes that satisfy our requirement. One is implicit in Gentry-Waters broadcast encryption scheme [25] and the other is completely new. By instantiating our general framework with the latter construction, we obtain IBE scheme with almost tight security and with sub-linear master public key size.
1.4 Related Works
Related Works on IBE. The first realizations of IBE in the random oracle model were given in [13, 20, 45]. Later, realization in the standard model [10, 14] were given. In the random oracle model, it is possible to obtain efficient and tightly secure IBE scheme [5]. Gentry [24] proposed a tightly secure anonymous IBE scheme under a non-static, parametrized assumption. Chen and Wee proposed the first almost tightly secure IBE scheme under static and simple assumptions [17, 19]. Attrapadung [4] proposed an IBE scheme whose security loss only depends on the number of key queries before the challenge phase. Jutla and Roy [32] constructed very efficient IBE scheme from the SXDH assumption, based on a technique related to NIZK. Blazy, Kiltz, and Pan [9] further generalized the idea and show that a message authentication code with a certain specific algebraic structure implies (H)IBE. They further obtained almost tightly secure anonymous IBE and (non-anonymous) HIBE via the framework. Note that all above mentioned schemes only focus on the single-challenge setting.
Related Works on the Multi-Challenge CCA-Secure PKE. Bellare, Boldyreva, and Micali [7] gave a tight reduction for the Cramer-Shoup encryption [21] in the multi-instance (multi-user) and the single-challenge setting. They posed an important open question of whether it is possible to construct tightly CCA-secure PKE scheme in the multi-instance and the multi-challenge setting. The first PKE scheme satisfying the requirement was proposed by Hofheinz and Jager [30]. Their scheme requires hundreds of group elements in the ciphertexts. Subsequently, Abe et al. [1] reduced the size by improving the efficiency of the underlying one-time signature. Libert et al. [33] greatly reduced the ciphertext and made it constant-size for the first time. The ciphertext overhead of their scheme consist of 68 group elements. Very recently, Libert et al. [34] further reduced it to 47 group elements. Concurrently and independently to us, Hofheinz [27] proposes the first PKE scheme with the same security guarantee and fully compact parameters, which means all parameters are constant-size. While the ciphertext-size (which consists of 60 group elements) is longer than construction in [34], it achieves much shorter public parameters. We note that while the technique is very powerful, it is unclear how to extend it to the IBE setting.
Due to space limitations, many definitions and proofs are omitted from this version. These can be found in the full version of the paper [6].
2 Preliminaries
Notation. Vectors will be treated as either row or column vector matrices. When unspecified, we shall let it be a row vector. We denote by \(\mathbf {e}_i\) the i-th unit (row) vector: its i-th component is one, all others are zero. \(\mathbf {0}\) denotes the zero vector or zero matrix. For an integer \(n\in \mathbb {N}\) and a field \(\mathbb {F}\), \(\mathbb {GL}_{n}(\mathbb {F})\) denotes the set of all invertible matrix in \(\mathbb {F}^{n\times n}\). For a multiplicative group \(\mathbb {G}\), we denote by \(\mathbb {G}^*\) a set of all generators in \(\mathbb {G}\). We also denote by [a, b] a set \(\{a,\ldots , b\}\) for any integer a and b and \([n]=[1,n]\) for any \(n\in \mathbb {N}\). We denote by \(u \overset{_\$}{\leftarrow } U\) the fact that u is picked uniformly at random from a finite set U.
2.1 Identity-Based Encryption
In this section, we define the syntax and security of IBE (in the multi-challenge, multi-instance setting).
Syntax. An IBE scheme with identity space \(\mathcal {ID}\) and message space \(\mathcal {M}\) consists of the following algorithms:
-
\(\mathsf {Par}(1^\kappa )\rightarrow (\mathsf {pp}, \mathsf {sp}) \): The parameter sampling algorithm takes as input a security parameter \(1^\kappa \) and outputs a public parameter \(\mathsf {pp}\) and a secret parameter \(\mathsf {sp}\).
-
\(\mathsf {Gen}(\mathsf {pp},\mathsf {sp})\rightarrow (\mathsf {mpk},\mathsf {msk}) \): The key generation algorithm takes \(\mathsf {pp}\) and \(\mathsf {sp}\) as input and outputs a master public key \(\mathsf {mpk}\) and master secret key \(\mathsf {msk}\).
-
\(\mathsf {Ext}(\mathsf {msk},\mathsf {mpk}, \mathsf {ID})\rightarrow \mathsf {sk}_\mathsf {ID}\): The user private key extraction algorithm takes as input the master secret key \(\mathsf {msk}\), the master public key \(\mathsf {mpk}\), and an identity \(\mathsf {ID}\in \mathcal {ID}\). It outputs a private key \(\mathsf {sk}_\mathsf {ID}\).
-
\(\mathsf {Enc}(\mathsf {mpk}, \mathsf {ID}, \mathsf {M})\rightarrow \mathsf {CT}\): The encryption algorithm takes as input a master public key \(\mathsf {mpk}\), an identity \(\mathsf {ID}\), and a message \(\mathsf {M}\in \mathcal {M}\). It will output a ciphertext \(\mathsf {CT}\).
-
\(\mathsf {Dec}(\mathsf {sk}_\mathsf {ID},\mathsf {CT})\rightarrow \mathsf {M}\): The decryption algorithm takes as input a private key \(\mathsf {sk}_{\mathsf {ID}}\) and a ciphertext \(\mathsf {CT}\). It outputs a message \(\mathsf {M}\) or \(\bot \) which indicates that the ciphertext is not in a valid form.
We refer (standard) notion of correctness of IBE to [6].
In our constructions, we will set identity space \(\mathcal {ID}= \{ 0,1 \}^\ell \) for some \(\ell \in \mathbb {N}\). Note that the restriction on the identity space can be easily removed by applying a collision resistant hash function \(\mathsf {CRH}: \{0,1\}^* \rightarrow \{0,1\}^\ell \) to an identity. Typically, we would set \(\ell = {\varTheta }(\kappa )\) to avoid the birthday attack.
Security Model. We now define \((\mu , Q_c, Q_k )\)-security for an IBE \(\mathsf {\Phi }=(\mathsf {Par}, \mathsf {Gen}, \mathsf {Ext},\mathsf {Enc}, \mathsf {Dec})\). This security notion is defined by the following game between a challenger and an attacker \(\mathcal{A}\).
Setup. The challenger runs \((\mathsf {pp},\mathsf {sp}) \overset{_\$}{\leftarrow } \mathsf {Par}(1^\kappa ) \) and \((\mathsf {mpk}^{(j)},\mathsf {msk}^{(j)}) \overset{_\$}{\leftarrow } \mathsf {Gen}(\mathsf {pp}, \mathsf {sp})\) for \(j\in [\mu ]\). The challenger also picks random coin \(\textsf {coin}\overset{_\$}{\leftarrow } \{ 0,1 \}\) whose value is fixed throughout the game. Then, \((\mathsf {pp}, \{ \mathsf {mpk}^{(j)} \}_{j\in [\mu ]} )\) is given to \(\mathcal{A}\).
In the following, \(\mathcal {A}\) adaptively makes the following two types of queries in an arbitrary order.
-
–Key Extraction Query. The adversary \(\mathcal {A}\) submits \((\texttt {Extraction},j\in [\mu ], \mathsf {ID}\in \mathcal {ID})\) to the challenger. Then, the challenge runs \( \mathsf {sk}^{(j)}_{\mathsf {ID}}\overset{_\$}{\leftarrow } \mathsf {Ext}(\mathsf {msk}^{(j)}, \mathsf {mpk}^{(j)}, \mathsf {ID})\) and returns \(\mathsf {sk}^{(j)}_{\mathsf {ID}}\) to \(\mathcal {A}\).
-
–Challenge Query. The adversary \(\mathcal {A}\) submits \((\texttt {Challenge},j\in [\mu ],\mathsf {ID}\in \mathcal {ID}, \mathsf {M}_0, \mathsf {M}_1 \in \mathcal {M})\) to the challenger. Then, the challenger runs \(\mathsf {CT}\overset{_\$}{\leftarrow } \mathsf {Enc}(\mathsf {mpk}^{(j)},\mathsf {ID}, \mathsf {M}_{\textsf {coin}} )\) and returns \(\mathsf {CT}\) to \(\mathcal {A}\).
Guess. At last, \(\mathcal{A}\) outputs a guess \(\textsf {coin}'\) for \(\textsf {coin}\). The advantage of an attacker \(\mathcal{A}\) in the game is defined as \(\mathsf {Adv}^{\mathsf {IBE}}_{\mathcal {A},\mathsf {\Phi },(\mu , Q_c, Q_k)}(\kappa )=|\Pr [\textsf {coin}' =\textsf {coin}]-\frac{1}{2}|\).
We say that the adversary \(\mathcal {A}\) is valid if and only if \(\mathcal {A}\) never queries \((\texttt {Extraction}, j,\mathsf {ID})\) such that it has already queried \((\texttt {Challenge}, j, \mathsf {ID}, \mathsf {M}_0, \mathsf {M}_1 )\) for the same \((j,\mathsf {ID})\) (and vice versa); \(\mathcal {A}\) has made at most \(Q_c\) challenge queries; and \(\mathcal {A}\) has made at most \(Q_k\) key extraction queries.
Definition 1
We say that IBE \(\mathsf {\Phi }\) is secure if \(\mathsf {Adv}^{\mathsf {IBE}}_{\mathcal {A},\mathsf {\Phi },(\mu , Q_c, Q_k)}(\kappa )\) is negligible for any polynomially bounded \(\mu \), \(Q_c\), \(Q_k\), and any valid PPT adversary \(\mathcal {A}\).
Anonymity. We also consider anonymity for the IBE scheme. To define \((\mu , Q_c, Q_k )\)-anonymity for an IBE scheme, we change the form of challenge queries in the above game as follows.
-
\(-\) Challenge Query. The adversary \(\mathcal {A}\) submits \((\texttt {Challenge},j\in [\mu ],\mathsf {ID}_0, \mathsf {ID}_1 \in \mathcal {ID}, \mathsf {M}_0, \mathsf {M}_1 \in \mathcal {M})\) to the challenger. Then, the challenger runs \(\mathsf {CT}\overset{_\$}{\leftarrow } \mathsf {Enc}(\mathsf {mpk}^{(j)},\mathsf {ID}_{\textsf {coin}}, \mathsf {M}_{\textsf {coin}} )\) and returns \(\mathsf {CT}\) to \(\mathcal {A}\).
We say that the adversary \(\mathcal {A}\) is valid if \(\mathcal {A}\) never queries \((\texttt {Extraction}, j, \mathsf {ID})\) such that it has already queried \((\texttt {Challenge}, j, \mathsf {ID}_0, \mathsf {ID}_1, \mathsf {M}_0, \mathsf {M}_1 )\) for the same j and \(\mathsf {ID}\in \{ \mathsf {ID}_0, \mathsf {ID}_1 \}\) (and vice versa); \(\mathcal {A}\) has made at most \(Q_c\) challenge queries; and \(\mathcal {A}\) has made at most \(Q_k\) key extraction queries. We define the advantage of \(\mathcal {A}\) in this modified game as \(\mathsf {Adv}^{\mathsf {AIBE}}_{\mathcal {A},\mathsf {\Phi },(\mu , Q_c, Q_k)}(\kappa ):= |\Pr [\textsf {coin}'=\textsf {coin}]-\frac{1}{2} |\).
Definition 2
We say that IBE \(\mathsf {\Phi }\) is anonymous if \(\mathsf {Adv}^{\mathsf {AIBE}}_{\mathcal {A},\mathsf {\Phi },(\mu , Q_c, Q_k)}(\kappa )\) is negligible for any polynomially bounded \(\mu \), \(Q_c\), \(Q_k\), and any valid PPT adversary \(\mathcal {A}\).
2.2 Composite-Order Bilinear Groups
We will use bilinear group \((\mathbb {G},\mathbb {G}_T)\) of composite order \(N=p_1p_2p_3 p_4\), where \(p_1\), \(p_2\), \(p_3\), \(p_4\) are four distinct prime numbers, with efficiently computable and non-degenerate bilinear map \(e(\cdot ):\mathbb {G}\times \mathbb {G}\rightarrow \mathbb {G}_T\). For each d|N, \(\mathbb {G}\) has unique subgroup of order d denoted by \(\mathbb {G}_d\). We let \(g_i\) be a generator of \(\mathbb {G}_{p_i}\). For our purpose, we define a (composite order) bilinear group generator \(\mathcal {G}_{\mathsf {comp}}\) that takes as input a security parameter \(1^\kappa \) and outputs \((N,\mathbb {G},\mathbb {G}_T, g_1,g_2, g_3, g_4, e(\cdot ) )\). Any \(h\in \mathbb {G}\) can be expressed as \(h=g_1^{a_1}g_2^{a_2}g_3^{a_3}g_4^{a_4}\), where \(a_i\) is uniquely determined modulo \(p_i\). We call \(g_i^{a_i}\) the \(\mathbb {G}_{p_i}\) component of h. We have that \(e(g^a,h^b)=e(g,h)^{ab}\) for any \(g,h\in \mathbb {G}\), \(a,b\in \mathbb {Z}\) and \(e(g,g)=1_{\mathbb {G}_T}\) for \(g\in \mathbb {G}_{p_i}\) and \(h\in \mathbb {G}_{p_j}\) with \(i\ne j\).
Let \((N,\mathbb {G},\mathbb {G}_T, g_1,g_2, g_3, g_4, e(\cdot ) ) \overset{_\$}{\leftarrow } \mathcal {G}_{\mathsf {comp}}(1^\kappa )\) and \(g\overset{_\$}{\leftarrow } \mathbb {G}^*\). We define advantage function \(\mathsf {Adv}^{\mathsf {P}\mathrm {xx}}_{\mathcal {A}}(\kappa )\) for Problem xx for any adversary \(\mathcal {A}\) as
In each problem, D, \(T_0\), and \(T_1\) are defined as follows. In the following, for \(i,j\in [1,4]\), \(g_{ij}\) is chosen as \(g_{ij} \overset{_\$}{\leftarrow } \mathbb {G}_{p_i p_j}^*\).
Problem 1
\(D=\emptyset \), \(T_0 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1}\), and \(T_1 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1 p_2}\).
Problem 2
\(D=(g_{12}, g_3, g_{24})\), \(T_0 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1p_4}\), and \(T_1 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1 p_2 p_4}\).
Problem 3
\(D=(g_{13}, g_2, g_{34})\), \(T_0 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1p_4}\), and \(T_1 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1 p_3 p_4}\).
Problem 4
\(D=(g_{12}, g_{23})\), \(T_0 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1p_2}\), and \(T_1 \overset{_\$}{\leftarrow } \mathbb {G}^*_{p_1 p_3}\).
Problem 5
\(D=(g_{2}, g_3, g_2^x, g_2^y, g_2^z)\), \(T_0 = e(g_2, g_2)^{xyz}\), and \(T_1 = e(g_2, g_2)^{xyz + \gamma }\), where \(x,y,z \overset{_\$}{\leftarrow } \mathbb {Z}_N\) and \(\gamma \overset{_\$}{\leftarrow } \mathbb {Z}_N^*\).
Problems 1, 2, 3, and 4 are called sub-group decision problems. Problem 5 is called the decisional bilinear Diffie-Hellman problem.
Matrix-in-the-Exponent. Given any vector \(\mathbf {w}=(w_1,\ldots ,w_n) \in \mathbb {Z}_N^n\) and a group element g, we write \(g^{\mathbf {w}}\in \mathbb {G}^n\) to denote \((g^{w_1},\ldots ,g^{w_n}) \in \mathbb {G}^{n}\): we define \(g^\mathbf {A}\) for a matrix \(\mathbf {A}\) in a similar way. \(g^{\mathbf {A}}\cdot g^{\mathbf {B}}\) denotes componentwise product: \(g^{\mathbf {A}}\cdot g^{\mathbf {B}}=g^{\mathbf {A}+\mathbf {B}}\). Note that given \(g^\mathbf {A}\) and a matrix \(\mathbf {B}\) of “exponents”, one can efficiently compute \(g^{\mathbf {B}\mathbf {A}}\) and \(g^{\mathbf {A}\mathbf {B}}=(g^\mathbf {A})^\mathbf {B}\). Furthermore, if there is an efficiently computable map \(e:\mathbb {G}\times \mathbb {G}\rightarrow \mathbb {G}_T\), then given \(g^\mathbf {A}\) and \(g^\mathbf {B}\), one can efficiently compute \(e(g,g)^{\mathbf {A}^\top \mathbf {B}}\) via \((e(g,g)^{\mathbf {A}^\top \mathbf {B}})_{i,j}=\prod _{k}e(g^{A_{k,i}},g^{B_{k,j}})\) where \(A_{i,j}\) and \(B_{i,j}\) denote the (i, j)-th coefficient of \(\mathbf {A}\) and \(\mathbf {B}\) respectively. We will use \(e(g^{\mathbf {A}},g^\mathbf {B})=e(g,g)^{\mathbf {A}^\top \mathbf {B}}\) to denote this operation.
3 Broadcast Encoding: Definitions and Reductions
In this section, we define the syntax and the security notions for broadcast encoding. The syntax of our definition corresponds to a special case of “pair encoding” defined in [4] and is also similar to “predicate encoding” in [50]. As for the security requirement for the encoding, ours are slightly different from both. We define several flavours of the security requirement: perfect master-key hiding security (PMH), computational-master-key hiding (CMH) security, and the multi-master-key hiding (MMH) security. The last one is useful, since we can obtain IBE scheme from broadcast encoding scheme satisfying the security notion, as we will explain in Sect. 4. However, MMH security is defined by relatively complex game and may not be easy to show. Later in this section, we will see that MMH security can be tightly reduced to much simpler CMH and PMH security.
3.1 Broadcast Encoding: Syntax
The broadcast encoding \(\mathsf {\Pi }\) consists of the following four deterministic algorithms.
-
\(\mathsf {Param}(n, N)\rightarrow d_1 :\) It takes as input an integer n and N and outputs \(d_1\in \mathbb {N}\) which specifies the number of common variables in \(\mathsf {CEnc}\) and \(\mathsf {KEnc}\). For the default notation, \(\mathbf {w}=(w_1,\ldots , w_{d_1}) \) denotes the list of common variables.
-
\(\mathsf {KEnc}(\tau , N)\rightarrow (\mathbf {k}, d'_2 ):\) It takes as input \(\tau \in [n]\), \(N\in \mathbb {N}\), and outputs a vector of polynomials \(\mathbf {k}=(k_1, \ldots , k_{d_2})\) with coefficients in \(\mathbb {Z}_N\), and \(d'_2 \in \mathbb {N}\) that specifies the number of its own variables. We assume that \(d_2\) and \(d'_2\) only depend on n and do not depend on \(\tau \) without loss of generality. We require that each polynomials \(\mathbf {k}\) is a linear combination of monomials \(\alpha \), \(r_j\), \(w_k r_j\) where \(\alpha ,r_1,\ldots , r_{d'_2}, w_1,\ldots , w_{d_1}\) are variables. More precisely, it outputs \(\{b_{\iota } \}_{\iota \in [d_2]}\), \(\{ b_{\iota ,j} \}_{(\iota ,j)\in [d_2] \times [d'_2]}\), and \(\{ b_{\iota ,j,k} \}_{(\iota ,j,k)\in [d_2] \times [d'_2] \times [d_1]}\) in \(\mathbb {Z}_N\) such that
$$\begin{aligned}&k_{\iota }\Bigl (\alpha , r_1,\ldots , r_{d'_2},w_1,\ldots , w_{d_1} \Bigr ) \nonumber \\&\qquad \qquad \qquad = b_\iota \alpha + \Bigl (\sum _{j\in [d'_2]} b_{\iota ,j}r_j \Bigr ) + \Bigl (\sum _{(j,k)\in [d'_2]\times [d_1]} b_{\iota ,j,k}w_k r_j \Bigr ) \end{aligned}$$(4)for \(\iota \in [d_2]\).
-
\(\mathsf {CEnc}(S,N)\rightarrow (\mathbf {c}, d'_3):\) It takes as input \(S\subseteq [n]\), \(N\in \mathbb {N}\), and outputs a vector of polynomials \(\mathbf {c}=(c_1, \ldots , c_{d_3})\) with coefficients in \(\mathbb {Z}_N\), and \(d'_3\in \mathbb {N}\) that specifies the number of its own variables. We require that polynomials \(\mathbf {c}\) in variables \(s_0, s_1,\ldots , s_{d'_3}, w_1,\ldots , w_{d_1}\) have the following form:
There exist (efficiently computable) set of coefficients \(\{ a_{\iota ,j} \}_{(\iota ,j)\in [d_3] \times [0,d'_3]}\) and \(\{ a_{\iota ,j,k} \}_{(\iota ,j,k)\in [d_3] \times [0,d'_3] \times [d_1]}\) in \(\mathbb {Z}_N\) such that
$$\begin{aligned}&c_\iota \Bigl (s_0, s_1,\ldots , s_{d'_3},w_1,\ldots , w_{d_1} \Bigr ) \nonumber \\&\qquad \qquad \qquad = \Bigl (\sum _{j\in [0, d'_3]} a_{\iota ,j}s_j \Bigr ) + \Bigl (\sum _{(j,k)\in [0, d'_3]\times [d_1]} a_{\iota ,j,k}w_k s_j \Bigr ) \end{aligned}$$(5)for \(\iota \in [d_3]\). We also require that \(c_1 =s_0\).
-
\(\mathsf {Pair}(\tau , S,N)\rightarrow \mathbf {E}:\) It takes as input \(\tau \in [n]\), \(S\subseteq [n]\), and \(N\in \mathbb {N}\) and outputs a matrix \(\mathbf {E}= (E_{i,j})_{i\in [d_2], j\in [d_3]} \in \mathbb {Z}_N^{d_2 \times d_3 }\).
Correctness. The correctness requirement is as follows.
-
We require that for any n, N, \(d_1 \leftarrow \mathsf {Param}(n,N)\), \(\mathbf {k}\leftarrow \mathsf {KEnc}(\tau ,N)\), \(\mathbf {c}\leftarrow \mathsf {CEnc}(S,N)\), and \(\mathbf {E}\leftarrow \mathsf {Pair}(\tau , S, N)\), we have that
$$\begin{aligned} \mathbf {k}\mathbf {E}\mathbf {c}^\top = \alpha s_0 \qquad \text{ whenever } \qquad \tau \in S. \end{aligned}$$The equation holds symbolically, or equivalently, as polynomials in variables \(\alpha , r_1,\ldots , r_{d'_2},s_0, s_1,\cdots , s_{d'_3}, w_1,\ldots , w_{d_1}\).
-
For p that divides N, if we let \(\mathsf {KEnc}(\tau , N) \rightarrow (\mathbf {k}, d'_2)\) and \(\mathsf {KEnc}(\tau , p) \rightarrow (\mathbf {k}', d''_2)\), then it holds that \(d'_2 = d''_2\) and \(\mathbf {k}\mod p = \mathbf {k}'\). The requirement for \(\mathsf {CEnc}\) is similar.
Note that since \(\mathbf {k}\mathbf {E}\mathbf {c}^\top = \sum _{(i,j)\in [d_2]\times [d_3]} E_{i,j} k_i c_j\), the first requirement amounts to check if there is a linear combination of \(k_ic_j\) terms summed up to \(\alpha s_0\). In the descriptions of proposed broadcast encoding schemes, which will appear later in this paper, we will not explicitly write down \(\mathbf {E}\). Instead, we will check this condition.
3.2 Broadcast Encoding: Security
Here, we define two flavours of security notions for broadcast encoding: perfect security and computational security. As we will see, the former implies the latter. In what follows, we denote \(\mathbf {w}= (w_1,\ldots , w_{d_1})\), \(\mathbf {r}=(r_1,\ldots , r_{d'_2})\), and \(\mathbf {s}=(s_0, s_1,\ldots , s_{d'_3})\).
(Perfect Security). The pair encoding scheme \(\mathsf {\Pi }= (\mathsf {Param}, \mathsf {KEnc}, \mathsf {CEnc}, \mathsf {Pair})\) is Q-perfectly master-key hiding (Q-PMH) if the following holds. For any \(n \in \mathbb {N}\), prime \(p\in \mathbb {N}\), \(\tau \in [n]\), and \(S_1,\ldots , S_Q \subset [n]\) such that \(\tau \not \in S_j\) for all \(j\in [Q]\), let \(\mathsf {Param}(n,p) \rightarrow d_1\), \((\mathbf {k}_{\tau }, d'_2 ) \leftarrow \mathsf {KEnc}(\tau , p)\), and \((\mathbf {c}_{S_j}, d'_{3,j}) \leftarrow \mathsf {CEnc}(S_j,p)\) for \(j\in [Q]\), then the following two distributions are identical:
where \(\mathbf {w}\overset{_\$}{\leftarrow } \mathbb {Z}_p^{d_1}\), \(\alpha \overset{_\$}{\leftarrow } \mathbb {Z}_p\), \(\mathbf {r}\overset{_\$}{\leftarrow } (\mathbb {Z}_p^*)^{d'_2}\), \(\mathbf {s}_j \overset{_\$}{\leftarrow } \mathbb {Z}_p^{d'_3 + 1}\) for \(j\in [Q]\).
(Computational Security on \(\mathbb {G}_{p_2}\) ). We define Q-computational-master-key hiding (Q-CMHFootnote 4 ) security on \(\mathbb {G}_{p_2}\) for a broadcast encoding \(\mathsf {\Pi }= (\mathsf {Param}, \mathsf {KEnc}, \mathsf {CEnc}, \mathsf {Pair})\) by the following game. At the beginning of the game, an (stateful) adversary \(\mathcal {A}\) is given \((1^\kappa ,n)\) and chooses \(\tau ^\star \in [n]\). Then, parameters are chosen as \((N,\mathbb {G},\mathbb {G}_T, g_1, g_2, g_3, g_4, e(\cdot ) ) \overset{_\$}{\leftarrow } \mathcal {G}_{\mathsf {comp}}(1^\kappa )\), \(\mathsf {Param}(n,N) \rightarrow d_1\), and \(\hat{\mathbf {w}} \overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_1}\). The advantage of \(\mathcal {A}\) is defined as
In the above, \(\mathcal {O}_{\tau ^\star , \hat{\mathbf {w}}, b}^{\mathsf {CMH},\mathsf {K}}(\cdot )\) for \(b\in \{ 0,1 \}\) are called only once while \(\mathcal {O}^{\mathsf {CMH}, \mathsf {C}}_{\tau ^\star , \hat{\mathbf {w}}}(\cdot )\) can be called at most Q times. These oracles can be called in any order.
-
\(\mathcal {O}^{\mathsf {CMH}, \mathsf {C}}_{\tau ^\star , \hat{\mathbf {w}} }(\cdot )\) takes \(S\subset [n]\) such that \(\tau ^\star \not \in S\) as input. It then runs \(\mathsf {CEnc}(S,N)\rightarrow (\mathbf {c},d'_3)\), picks \(\hat{\mathbf {s}}=(\hat{s}_0,\hat{s}_1, \ldots , \hat{s}_{d_3'} ) \overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_3' + 1}\), and returns \(g_2^{\mathbf {c}(\hat{\mathbf {s}}, \hat{\mathbf {w}})}\). We note that \(\hat{\mathbf {s}}\) is freshly chosen every time the oracle is called.
-
\(\mathcal {O}_{\tau ^\star , \hat{\mathbf {w}}, b}^{\mathsf {CMH}, \mathsf {K}}(\cdot )\) ignores its input. When it is called, it first runs \(\mathsf {KEnc}(\tau ^\star , N )\rightarrow (\mathbf {k}, d'_2)\) and picks \(\hat{\mathbf {r}} = (\hat{r}_1,\ldots , \hat{r}_{d'_2} ) \overset{_\$}{\leftarrow } \mathbb {Z}_N^{d'_2}\) and \(\hat{\alpha } \overset{_\$}{\leftarrow } \mathbb {Z}_N\). Then it returns
$$\begin{aligned} g_2^{\mathbf {k}(b\cdot \hat{\alpha }, \hat{\mathbf {r}}, \hat{\mathbf {w}} )} = {\left\{ \begin{array}{ll} g_2^{\mathbf {k}(0, \hat{\mathbf {r}}, \hat{\mathbf {w}} )} &{} \text {if b=0} \\ g_2^{\mathbf {k}(\hat{\alpha }, \hat{\mathbf {r}}, \hat{\mathbf {w}} )} &{} \text {if b=1}. \end{array}\right. } \end{aligned}$$
We say that the broadcast encoding is Q-CMH secure on \(\mathbb {G}_{p_2}\) if \(\mathsf {Adv}^{\mathsf {CMH}}_{\mathcal {A},\mathsf {\Pi },Q,\mathbb {G}_{p_2}}(\kappa )\) is negligible for all PPT adversary \(\mathcal {A}\).
(Computational Security on \(\mathbb {G}_{p_3}\) ). We define \(\mathsf {Adv}^{\mathsf {CMH}}_{\mathcal {A},\mathsf {\Pi },Q,\mathbb {G}_{p_3}}(\kappa )\) and Q-CMH security on \(\mathbb {G}_{p_3}\) via similar game, by swapping \(g_{2}\) and \(g_3\) in the above.
Comparison with Definition in [4]. By setting \(Q=1\), the Q-PMH and the Q-CMH security defined as above almost correspond to the perfect security and the co-selective security defined in [4] respectively. We need to deal with the case of \(Q\gg 1\) in order to handle the multi-challenge setting. Another difference is that we use groups with the order being a product of four primes, while they deal with a product of three primes.
We have the following lemma which indicates that Q-PMH security unconditionally implies Q-CMH security on both of \(\mathbb {G}_{p_2}\) and \(\mathbb {G}_{p_3}\).
Lemma 1
Assume that a broadcast encoding \(\mathsf {\Pi }\) satisfies Q-PMH security for some \(Q\in \mathbb {N}\). Then it follows that \(\mathsf {Adv}^{\mathsf {CMH}}_{\mathcal {A},\mathsf {\Pi },Q, \mathbb {G}_{p_i}}(\kappa ) \le d'_2/p_i\) for \(i\in \{ 2,3\}\).
3.3 Multi-master-key Hiding Security in Composite Order Groups
Here, we define multi-master-key hiding security for a broadcast encoding, which is more complex security notion compared to the CMH security. A broadcast encoding scheme that satisfies the security notion can be converted into an IBE scheme as we will see in Sect. 4.
Multi-master-key Hiding Security (on \(\mathbb {G}_{p_2}\) ). We define \((Q_c, Q_k)\)-multi-master-key hiding (\((Q_c, Q_k)\)-MMH) security on \(\mathbb {G}_{p_2}\) for a broadcast encoding \(\mathsf {\Pi }= (\mathsf {Param}, \mathsf {KEnc},\mathsf {CEnc},\mathsf {Pair})\). The security is defined by the following game. At the beginning of the game, \(\mathcal {A}\) is given \((1^\kappa ,n)\) and chooses \(\tau ^\star \in [n]\). Then, parameters are chosen as \((N,\mathbb {G}, \mathbb {G}_T, g_1, g_2, g_3, g_4, e(\cdot ) ) \overset{_\$}{\leftarrow } \mathcal {G}_{\mathsf {comp}}(1^\kappa )\), \(g_{24}\overset{_\$}{\leftarrow } \mathbb {G}^*_{p_2p_4}\), \(d_1 \leftarrow \mathsf {Param}(n,N)\), and \(\mathbf {w}\overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_1}\). The advantage of \(\mathcal {A}\) is defined as
In the above, \(\mathcal {O}^{\mathsf {MMH}, \mathsf {C}}_{\tau ^\star , \mathbf {w}}(\cdot )\) and \(\mathcal {O}_{\tau ^\star , \mathbf {w}, b}^{\mathsf {MMH}, \mathsf {K}}(\cdot )\) for \(b\in \{ 0,1 \}\) can be called at most \(Q_c\) times and \(Q_k\) times, respectively. They can be called in any order.
-
\(\mathcal {O}^{\mathsf {MMH}, \mathsf {C}}_{\tau ^\star , \mathbf {w}}(\cdot )\) takes \(S \subset [n]\) such that \(\tau ^\star \not \in S\) as input. It then runs \(\mathsf {CEnc}(S,N)\rightarrow (\mathbf {c},d'_3)\), picks \(\mathbf {s}\overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_3' + 1}\) and \(\hat{\mathbf {s}} \overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_3' + 1}\) and returns \(g_1^{\mathbf {c}(\mathbf {s}, \mathbf {w})} \cdot g_2^{\mathbf {c}(\hat{\mathbf {s}}, \mathbf {w})}\).
-
\(\mathcal {O}_{\tau ^\star , \mathbf {w}, b}^{\mathsf {MMH}, \mathsf {K}}(\cdot )\) ignores its input. When it is called, it first runs \(\mathsf {KEnc}(\tau ^\star , N)\rightarrow (\mathbf {k}, d'_2)\), picks \(\hat{\alpha } \overset{_\$}{\leftarrow } \mathbb {Z}_N\), \(\mathbf {r}\overset{_\$}{\leftarrow } \mathbb {Z}_N^{d'_2}\), \(\varvec{\delta }\overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_2}\). Then it returns
$$\begin{aligned} g_1^{\mathbf {k}(0, \mathbf {r}, \mathbf {w})} \cdot g_2^{\mathbf {k}(b\cdot \hat{\alpha },\mathbf {0}, \mathbf {0})} \cdot g_{4}^{\varvec{\delta }}= {\left\{ \begin{array}{ll} g_1^{\mathbf {k}(0,\mathbf {r},\mathbf {w})} \cdot g_{4}^{\varvec{\delta }} &{} \text {if b=0} \\ g_1^{\mathbf {k}(0, \mathbf {r}, \mathbf {w})} \cdot g_2^{\mathbf {k}(\hat{\alpha },\mathbf {0}, \mathbf {0})} \cdot g_{4}^{\varvec{\delta }} &{} \text {if b=1}. \end{array}\right. } \end{aligned}$$
In the above, \(\mathbf {r}\), \(\hat{\alpha }\), and \(\varvec{\delta }\) as well as \(\mathbf {s}\) and \(\hat{\mathbf {s}}\) are all freshly chosen every time the corresponding oracle is called. We say that the broadcast encoding is \((Q_c,Q_k )\)-MMH secure on \(\mathbb {G}_{p_2}\) if \(\mathsf {Adv}^{\mathsf {MMH}}_{\mathcal {A},\mathsf {\Pi },(Q_c,Q_k),\mathbb {G}_{p_2}}(\kappa )\) is negligible for all PPT adversary \(\mathcal {A}\).
Multi-master-key Hiding Security (on \(\mathbb {G}_{p_3}\) ). We define \((Q_c, Q_k)\)-MMH security on \(\mathbb {G}_{p_3}\) and \(\mathsf {Adv}^{\mathsf {MMH}}_{\mathcal {A},\mathsf {\Pi },(Q_c,Q_k),\mathbb {G}_{p_3}}(\kappa )\) similarly to the above. The difference is the following.
-
The input to \(\mathcal {A}\) is replaced with \((g_1,g_1^{\mathbf {w}}, g_2^{\mathbf {w}}, g_{34}, g_2, g_4)\).
-
\(g_1^{\mathbf {c}(\mathbf {s}, \mathbf {w})} \cdot g_2^{\mathbf {c}(\hat{\mathbf {s}}, \mathbf {w})}\) in the above is replaced with \(g_1^{\mathbf {c}(\mathbf {s}, \mathbf {w})} \cdot g_3^{\mathbf {c}(\hat{\mathbf {s}}, \mathbf {w})}\).
-
\(g_1^{\mathbf {k}(0, \mathbf {r}, \mathbf {w})} \cdot g_2^{\mathbf {k}(b\cdot \hat{\alpha },\mathbf {0}, \mathbf {0})} \cdot g_{4}^{\varvec{\delta }}\) is replaced with \(g_1^{\mathbf {k}(0, \mathbf {r}, \mathbf {w})} \cdot g_3^{\mathbf {k}(b\cdot \hat{\alpha },\mathbf {0}, \mathbf {0})} \cdot g_{4}^{\varvec{\delta }}\).
3.4 Reduction from MMH Security to CMH Security
We can prove the following theorem that indicates that the \((Q_c,Q_k )\)-MMH security for a broadcast encoding on \(\mathbb {G}_{p_2}\) (resp. \(\mathbb {G}_{p_3}\)) can be tightly reduced to its \(Q_c\)-CMH security on \(\mathbb {G}_{p_2}\)(resp. \(\mathbb {G}_{p_3}\)) and the hardness of the Problem 2 (resp. 3).
Theorem 1
For any \(i\in \{2,3\}\), broadcast encoding \(\mathsf {\Pi }\), and adversary \(\mathcal {A}\), there exist adversaries \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that
and \( \max \{ \mathsf {Time}(\mathcal {B}_1), \mathsf {Time}(\mathcal {B}_2) \} \approx \mathsf {Time}(\mathcal {A}) + (Q_k + Q_c) \cdot \mathsf {poly}(\kappa , n)\) where \(\mathsf {poly}(\kappa ,n)\) is independent of \(\mathsf {Time}(\mathcal {A})\). In the above, \(\mathsf {P}_\mathrm{{xx}} = \mathsf {P}_{2}\) if \(i=2\) and \(\mathsf {P}_\mathrm{{xx}} = \mathsf {P}_{3}\) if \(i=3\).
4 Almost Tight IBE from Broadcast Encoding in Composite-Order Groups
In this section, we show a generic conversion from a broadcast encoding scheme to an IBE scheme. An important property of the resulting IBE scheme is that \((\mu ,Q_c,Q_k)\)-security of the scheme can be almost tightly reduced to the \(Q_c\)-CMH security of the underlying broadcast encoding scheme (and Problems 1, 2, 3, 4, and 5). In particular, the reduction only incurs small polynomial security loss, which is independent of \(\mu \) and \(Q_k\). Therefore, if the underlying broadcast encoding scheme is tightly \(Q_c\)-CMH secure, which is the case for all of our constructions, the resulting IBE scheme obtained by the conversion is almost tightly secure. Note that in the following construction, we have \(\mathsf {sp}= \bot \). This mean that the key generation algorithm \(\mathsf {Par}\) does not output any secret parameter. This property will be needed to convert our IBE scheme into CCA secure PKE scheme in Sect. 8.
Construction. Here, we construct an IBE scheme \(\mathsf {\Phi }^\mathsf {comp}\) from a broadcast encoding \(\mathsf {\Pi }= (\mathsf {Param}, \mathsf {KEnc}, \mathsf {CEnc},\mathsf {Pair})\). Let the identity space of the scheme be \(\mathcal {ID}= \{ 0,1 \}^{\ell }\) and the message space be \(\mathcal {M}= \{ 0,1 \}^m\). We also let \(\mathcal {H}\) be a family of pairwise independent hash functions \( \mathsf {H}: \mathbb {G}_T \rightarrow \mathcal {M}\). We assume that \(\sqrt{\frac{2^m}{p_2}}=2^{-{\varOmega }(\kappa )}\) so that the left-over hash lemma can be applied in the security proof.
-
\(\mathsf {Par}(1^\kappa ):\) It first runs \((N,\mathbb {G},\mathbb {G}_T, g_1, g_2, g_3, g_4, e(\cdot ) ) \overset{_\$}{\leftarrow } \mathcal {G}_{\mathsf {comp}}(1^\kappa )\) and \(\mathsf {Param}(2\ell , N) \rightarrow d_1\). Then it picks \(\mathbf {w}\overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_1}\), \(a \overset{_\$}{\leftarrow } \mathbb {Z}_N^*\), \(\mathsf {H}\overset{_\$}{\leftarrow } \mathcal {H}\) and sets \(h := (g_1 g_2 g_3 g_4)^a\). Finally, it outputs \(\mathsf {pp}= (g_1, g_1^{\mathbf {w}}, g_4, h, \mathsf {H})\) and \(\mathsf {sp}=\bot \).
-
\(\mathsf {Gen}(\mathsf {pp}, \mathsf {sp}):\) It picks \(\alpha \overset{_\$}{\leftarrow } \mathbb {Z}_N\) and outputs \(\mathsf {mpk}= (\mathsf {pp}, e(g_1, h)^\alpha )\) and \(\mathsf {msk}= \alpha \).
-
\(\mathsf {Ext}(\mathsf {msk}, \mathsf {mpk}, \mathsf {ID}):\) It first sets \(S = \{2i - \mathsf {ID}_{i} | i\in [\ell ] \}\) where \(\mathsf {ID}_i \in \{ 0,1 \}\) is the i-th bit of \(\mathsf {ID}\in \{ 0,1 \}^\ell \). Then it runs \(\mathsf {KEnc}(j,N)\rightarrow \bigl (\mathbf {k}_{j}, d'_{2} \bigr )\) and picks \(\mathbf {r}_{j} \overset{_\$}{\leftarrow } \mathbb {Z}_N^{d'_{2}}\) and \(\varvec{\delta }_{j}\overset{_\$}{\leftarrow } \mathbb {Z}_N^{d_2}\) for all \(j \in S\). It also picks random \(\{ \alpha _{j} \in \mathbb {Z}_N \}_{j \in S}\) subject to constraint that \(\alpha = \sum _{j\in S}\alpha _{j} \). Then, it computes \(g_1^{ \mathbf {k}_{j}(0,\mathbf {r}_{j},\mathbf {w}) }\), \(\mathsf {Pair}(j, S, N)\rightarrow \mathbf {E}_{j}\), and
$$\begin{aligned} \mathsf {sk}_{j}= h^{\mathbf {k}_j(\alpha _j, \mathbf {0}, \mathbf {0})} \cdot g_1^{\mathbf {k}_{j}(0,\mathbf {r}_{j},\mathbf {w})} \cdot g_4^{\varvec{\delta }_{j}} \end{aligned}$$for all \(j\in S\). Note that \(g_1^{ \mathbf {k}_{j}(0,\mathbf {r}_{j},\mathbf {w}) }\) can be computed from \(g_1^{\mathbf {w}}\) and \(\mathbf {r}_j=(r_{j,1}, \ldots , r_{j,d'_2})\) efficiently because \(\mathbf {k}_j(0,\mathbf {r}_j,\mathbf {w})\) contains only linear combinations of monomials \(r_{j,i}\), \(r_{j,i} w_{j'}\). Finally, it outputs private key \( \mathsf {sk}_{\mathsf {ID}}= \prod _{j\in S} (\mathsf {sk}_{j} )^{\mathbf {E}_j} . \)
-
\(\mathsf {Enc}(\mathsf {mpk}, \mathsf {ID}, \mathsf {M}):\) It first sets \(S = \{2i - \mathsf {ID}_{i} | i\in [\ell ] \}\). Then it runs \(\mathsf {CEnc}(S,N) \rightarrow (\mathbf {c}, d'_3)\), picks \(\mathbf {s}=(s_0,s_1,\ldots , s_{d'_3}) \overset{_\$}{\leftarrow } \mathbb {Z}_N^{d'_3 +1}\), and computes \(g_1^{\mathbf {c}(\mathbf {s},\mathbf {w})}\). Note that \(g_1^{\mathbf {c}(\mathbf {s},\mathbf {w})}\) can be computed from \(g_1^{\mathbf {w}}\) and \(\mathbf {s}\) efficiently because \(\mathbf {c}(\mathbf {s},\mathbf {w})\) contains only linear combinations of monomials \(s_i\), \(s_i w_j\). Finally, it outputs
$$\begin{aligned} \mathsf {CT}= \left( ~ C_1 = g_1^{\mathbf {c}(\mathbf {s},\mathbf {w})},\quad C_2 = \mathsf {H}\bigl (e(g_1, h)^{s_0 \alpha } \bigr ) \oplus \mathsf {M}~ \right) \!. \end{aligned}$$Here, \(\oplus \) denotes bitwise exclusive OR of two bit strings.
-
\(\mathsf {Dec}(\mathsf {sk}_{\mathsf {ID}}, \mathsf {CT}):\) It parses \(\mathsf {CT}\rightarrow (C_1, C_2)\) and computes \(e(\mathsf {sk}_\mathsf {ID}^\top , C_1^\top )= e(g_1,h)^{s_0 \alpha }\). Then, it recovers the message by \(\mathsf {M}= C_2 \oplus \mathsf {H}(e(g_1,h)^{s_0 \alpha } )\).
Correctness. We show the correctness of the scheme. It suffices to show the following.
The third equation above follows from the correctness of the broadcast encoding.
Security. The following theorem indicates that the security of the IBE is (almost) tightly reduced to the MMH security of the underlying broadcast encoding on \(\mathbb {G}_{p_2}\) and \(\mathbb {G}_{p_3}\) and Problems 1, 4, and 5. Combining the theorem with Theorem 1, the security of the scheme can be almost tightly reduced to the \(Q_c\)-CMH security of the underlying encoding (and Problems 1, 2, 3, 4, and 5). The reduction only incurs \(O(\ell )\) security loss.
Theorem 2
For any adversary \(\mathcal {A}\), there exist adversaries \(\mathcal {B}_i\) for \(i\in [1,5]\) such that
and \(\max \{ \mathsf {Time}(\mathcal {B}_i) | i\in [1,5] \} \approx \mathsf {Time}(\mathcal {A}) + (\mu + Q_c + Q_k)\cdot \mathsf {poly}(\kappa , \ell )\) where \(\mathsf {poly}(\kappa , \ell )\) is independent of \(\mathsf {Time}(\mathcal {A})\).
5 Framework for Constructions in Prime-Order Groups
In Sects. 3 and 4, we show our framework to construct almost tightly secure IBE in composite-order groups. Since we carefully constructed the framework so that we only use the subgroup decision assumptions and the DBDH assumption in the security proof, we can apply recent composite-order-to-prime-order conversion techniques in the literature [2, 3, 16, 18] to the framework. We choose to use [3], but other choices might be possible. In this section, we show our framework for constructing almost tightly secure IBE in prime-order groups. Our framework is almost parallel to that in composite-order groups. Namely, we define CMH security and MMH security in prime-order groups. Then, we show reduction between them. Finally, we show a generic construction of IBE scheme from broadcast encoding and show that the scheme is (almost) tightly secure if the underlying encoding is tightly CMH secure.
In the following, we will use asymmetric bilinear group \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\) of prime order p with efficiently computable and non-degenerate bilinear map \(e(\cdot ):\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\). For our purpose, we define a prime-order bilinear group generator \(\mathcal {G}_{\mathsf {prime}}\) that takes as input a security parameter \(1^\kappa \) and outputs \((p,\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, g,h, e(\cdot ) )\) where g and h are random generator of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), respectively. Let \(\pi _1 : \mathbb {Z}_{p}^{4\times 4} \rightarrow \mathbb {Z}_{p}^{4\times 2}\), \(\pi _2: \mathbb {Z}_{p}^{4\times 4} \rightarrow \mathbb {Z}_{p}^{4\times 1}\), and \(\pi _3: \mathbb {Z}_{p}^{4\times 4} \rightarrow \mathbb {Z}_{p}^{4\times 1}\) be the projection maps that map a \(4 \times 4\) matrix to the leftmost 2 columns, the third column, and the fourth column, respectively.
Intuition. In prime-order groups, we work with \(4\times 4\) matrix. The first two dimensions serve as “normal space” (corresponding to \(\mathbb {G}_{p_1}\)), while the third and the fourth dimension serve as double “semi-functional spaces” (corresponding to \(\mathbb {G}_{p_2}\) and \(\mathbb {G}_{p_3}\)). There is no corresponding dimension to \(\mathbb {G}_{p_4}\). While the use of \(4\times 4\) matrices is similar to Chen and Wee [17, 19]Footnote 5, conceptually, our techniques are quite different from theirs. They use the first two dimensions as a normal space and the last two dimensions as single semi-functional space. In contrast, we introduce additional semi-functional space to be able to prove the multi-challenge security rather than single-challenge security. Furthermore, due to our new proof technique, these semi-functional spaces are smaller compared to those of [17, 19].
5.1 Preparation
Here, we introduce definitions and notations needed to describe our result. Let p be a prime number and \(\mathbf {k}\) and \(\mathbf {c}\) be vectors output by \(\mathsf {KEnc}()\) and \(\mathsf {CEnc}()\) on some input respectively. Here, we assign each variable \(w_i\) in the vector a matrix \(\mathbf {W}_i \in \mathbb {Z}_p^{4\times 4}\) for \(i\in [d_1]\) (rather than assigning a scalar value), variable \(\alpha \) a column vector \(\varvec{\alpha }\in \mathbb {Z}_p^{4\times 1}\), variable \(r_i\) a vector \(\mathbf {x}_i \in \mathbb {Z}_p^{4\times 1}\) for \(i\in [d'_2]\), and variable \(s_i\) a vector \(\mathbf {y}_i \in \mathbb {Z}_p^{4\times 1}\) for \(i\in [0,d'_3]\). The evaluation of polynomials \(\mathbf {k}_{\mathbf {Z}}\) and \(\mathbf {c}_\mathbf {B}\), which are indexed by an invertible matrix \(\mathbf {B}\in \mathbb {Z}_p^{4 \times 4}\) and \(\mathbf {Z}\in \mathbb {Z}_p^{4 \times 4}\), are defined as follows. In the following, we denote
where \(\mathbf {D}\in \mathbb {Z}_p^{4\times 4}\) is a full-rank diagonal matrix with the entries (3, 3) and (4, 4) being 1.
Let \(\mathbf {k}=(k_1, \ldots , k_{d_2})\) be a vector of polynomials in variables \(\alpha ,r_1,\ldots , r_{d'_2}, w_1,\ldots , w_{d_1}\) with coefficients in \(\mathbb {Z}_p\) defined as Eq. (4). We define \(\mathbf {k}_{\mathbf {Z}}(\varvec{\alpha }, \mathbf {X}, \mathbb {W}) \in \mathbb {Z}_p^{4 \times d_2}\) as \(\mathbf {k}_{\mathbf {Z}}(\varvec{\alpha }, \mathbf {X}, \mathbb {W})= \{ k_{\mathbf {Z},\iota }(\varvec{\alpha }, \mathbf {X}, \mathbb {W}) \}_{\iota \in [d_2]}=\)
Let \(\mathbf {c}=(c_1, \ldots , c_{d_3})\) be a vector of polynomials in variables \(s_0, s_1,\ldots , s_{d'_3}, w_1,\ldots , w_{d_1}\) with coefficients in \(\mathbb {Z}_p\) defined as Eq. (5). We define \(\mathbf {c}_{\mathbf {B}}(\mathbf {Y},\mathbb {W}) \in \mathbb {Z}_p^{4\times d_3}\) as
\(\mathbf {c}_{\mathbf {B}}(\mathbf {Y},\mathbb {W}) =\{ c_{\mathbf {B},\iota }(\mathbf {Y},\mathbb {W}) \}_{\iota \in [d_3] } = \)
Restriction on the Encoding. In our framework for prime-order constructions, we define and require regularity of encoding similarly to [3], which is needed to prove the security of our IBE obtained from the broadcast encoding. We omit the definition and defer to the full version for the details [6].
Correctness of Encoding. Let \(\tau \in [n]\) and \(S\subseteq [n]\) be an index and a set such that \(\tau \in S\). Let also \(\mathsf {KEnc}(\tau ,p)\rightarrow \bigl (\mathbf {k}, d'_{2} \bigr )\), \(\mathsf {CEnc}(S,p) \rightarrow (\mathbf {c}, d'_3)\), and \(\mathsf {Pair}(\tau , S, p) \rightarrow \mathbf {E}=(E_{\eta ,\iota })_{(\eta ,\iota )\in [d_2]\times [d_3]} \in \mathbb {Z}_p^{d_2 \times d_3 }\). Then, by the correctness of the broadcast encoding, we have \(\sum _{(\eta ,\iota )\in [d_2]\times [d_3]} E_{\eta ,\iota } k_{\eta } c_{\iota }=\alpha s_0\) (the equation holds symbolically). From this, we have the following. (Note that the claim is shown similarly to Claim 15 in [3].)
Lemma 2
We have \( \sum _{(\eta ,\iota )\in [d_2]\times [d_3]} E_{\eta ,\iota }\cdot k_{\mathbf {Z},\eta }(\varvec{\alpha }, \mathbf {X}, \mathbb {W})^\top c_{\mathbf {B},\iota }(\mathbf {Y},\mathbb {W}) = \varvec{\alpha }^\top \mathbf {B}\mathbf {y}_0. \)
CMH and MMH Security. In the full version [6], we define the Q-CMH security for broadcast encoding on prime-order groups, analogously to the corresponding notion on composite-order groups. We also define the \((Q_c,Q_k)\)-MMH security for broadcast encoding on prime-order groups. The former is (unconditionally) implied by the Q-PMH security. Furthermore, we can show that the latter is tightly reduced to the former, similarly to the case in composite-order groups.
5.2 Almost Tightly Secure IBE from Broadcast Encoding in Prime Order Groups
Here, we construct an IBE scheme \(\mathsf {\Phi }^\mathsf {prime}\) from broadcast encoding scheme \(\mathsf {\Pi }= (\mathsf {Param}, \mathsf {KEnc}, \mathsf {CEnc}, \mathsf {Pair})\). Let the identity space of \(\mathsf {\Phi }^\mathsf {prime}\) be \(\mathcal {ID}= \{ 0,1 \}^{\ell }\) and the message space \(\mathcal {M}\) be \(\mathcal {M}= \mathbb {G}_T\). We will not use pairwise independent hash function differently from our construction in composite-order groups. We note that similarly to our construction in composite-order groups, we have \(\mathsf {sp}= \bot \) in the following.
-
\(\mathsf {Par}(1^\kappa , \ell ):\) It first runs \((p,\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, g,h, e(\cdot ) ) \overset{_\$}{\leftarrow } \mathcal {G}_{\mathsf {prime}}(1^\kappa )\) and \(\mathsf {Param}(2\ell , p) \rightarrow d_1\). Then it picks \(\mathbf {B}\overset{_\$}{\leftarrow } \mathbb {GL}_{4}(\mathbb {Z}_p)\), \(\mathbb {W}=(\mathbf {W}_1,\ldots , \mathbf {W}_{d_1})\overset{_\$}{\leftarrow } (\mathbb {Z}_p^{4 \times 4})^{d_1}\) and a random full-rank diagonal matrix \(\mathbf {D}\in \mathbb {Z}_p^{ 4 \times 4 }\) with the entries (3, 3) and (4, 4) being 1. Finally, it sets \(\mathbf {Z}= \mathbf {B}^{-\top }\mathbf {D}\) and outputs
$$\begin{aligned} \mathsf {pp}=\left( \begin{matrix} g,&{} g^{\pi _1(\mathbf {B})},&{} g^{\pi _1(\mathbf {W}_1 \mathbf {B})}, &{}\ldots ,&{}g^{\pi _1(\mathbf {W}_{d_1} \mathbf {B})} \\ h, &{} h^{\pi _1(\mathbf {Z})},&{} h^{\pi _1(\mathbf {W}^\top _1 \mathbf {Z})},&{} \ldots ,&{} h^{\pi _1(\mathbf {W}^\top _{d_1} \mathbf {Z})} \end{matrix} \right) \quad \text{ and } \quad \mathsf {sp}= \bot . \end{aligned}$$
In the following, we will omit subscript \(\mathbf {B}\) and \(\mathbf {Z}\) from \(\mathbf {c}_{\mathbf {B}}(\mathbf {S},\mathbb {W}) \) and \(\mathbf {k}_{\mathbf {Z}}(\varvec{\alpha }, \mathbf {R}, \mathbb {W})\) and just denote \(\mathbf {c}(\mathbf {S},\mathbb {W}) \) and \(\mathbf {k}(\varvec{\alpha }, \mathbf {R}, \mathbb {W})\) for ease of notation. \(\mathbf {B}\) and \(\mathbf {Z}\) are fixed in the following and clear from the context.
-
\(\mathsf {Gen}(\mathsf {pp}):\) It picks \(\varvec{\alpha }\overset{_\$}{\leftarrow } \mathbb {Z}_{p}^{4\times 1}\) and outputs \(\mathsf {mpk}= (\mathsf {pp},e(g,h)^{\varvec{\alpha }^\top \pi _1(\mathbf {B})} )\) and \(\mathsf {msk}= \varvec{\alpha }\).
-
\(\mathsf {Ext}(\mathsf {msk}, \mathsf {mpk}, \mathsf {ID}):\) It first sets \(S = \{2i - \mathsf {ID}_{i} | i\in [\ell ] \}\) where \(\mathsf {ID}_i \in \{ 0,1 \}\) is the i-th bit of \(\mathsf {ID}\in \{ 0,1 \}^\ell \). Then it runs \(\mathsf {KEnc}(j,p)\rightarrow \bigl (\mathbf {k}_{j}, d'_{2} \bigr )\), picks \(\mathbf {r}_{j,1}, \ldots , \mathbf {r}_{j,d'_2} \overset{_\$}{\leftarrow } \mathbb {Z}_p^{2\times 1}\), and sets
 for all \(j\in S\). It also picks random \(\{ \varvec{\alpha }_{j} \in \mathbb {Z}_p^{4\times 1} \}_{j \in S}\) subject to constraint that \(\varvec{\alpha }= \sum _{j\in S}\varvec{\alpha }_{j} \). Then, it computes \(\mathsf {Pair}(j, S, p)\rightarrow \mathbf {E}_{j}=(E_{j,\eta ,\iota })_{(\eta ,\iota )\in [d_2]\times [d_3]}\) and $$\begin{aligned} \mathsf {sk}_{j}= h^{\mathbf {k}_{j}(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W})} = \{ \mathsf {sk}_{j,\eta } = h^{k_{j,\eta }(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W})} \}_{\eta \in [d_2]} \end{aligned}$$
for all \(j\in S\). It also picks random \(\{ \varvec{\alpha }_{j} \in \mathbb {Z}_p^{4\times 1} \}_{j \in S}\) subject to constraint that \(\varvec{\alpha }= \sum _{j\in S}\varvec{\alpha }_{j} \). Then, it computes \(\mathsf {Pair}(j, S, p)\rightarrow \mathbf {E}_{j}=(E_{j,\eta ,\iota })_{(\eta ,\iota )\in [d_2]\times [d_3]}\) and $$\begin{aligned} \mathsf {sk}_{j}= h^{\mathbf {k}_{j}(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W})} = \{ \mathsf {sk}_{j,\eta } = h^{k_{j,\eta }(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W})} \}_{\eta \in [d_2]} \end{aligned}$$for all \(j\in S\). Note that \(h^{\mathbf {k}_{j}(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W})}\) can be computed from \(\varvec{\alpha }_j\), \(h^{\pi _1(\mathbf {Z})}\), and \(\{ g^{\pi _1(\mathbf {W}_i^\top \mathbf {Z})} \}_{i\in [d_1]}\) efficiently because \(\mathbf {k}_{j}(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W}) = \{ k_{j,\iota }(\varvec{\alpha }_{j},\mathbf {R}_{j},\mathbb {W}) \}_{\iota \in [d_2]}\) contains only linear combination of \(\varvec{\alpha }_j\),
 , and
, and 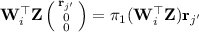 . Finally, it outputs private key \( \mathsf {sk}_{\mathsf {ID}}=\left\{ \prod _{j\in S, \eta \in [d_2]}\right. \left. \mathsf {sk}_{j,\eta }^{E_{j,\eta ,\iota }} \right\} _{\iota \in [d_3]}. \)
. Finally, it outputs private key \( \mathsf {sk}_{\mathsf {ID}}=\left\{ \prod _{j\in S, \eta \in [d_2]}\right. \left. \mathsf {sk}_{j,\eta }^{E_{j,\eta ,\iota }} \right\} _{\iota \in [d_3]}. \)
-
\(\mathsf {Enc}(\mathsf {mpk}, \mathsf {ID}, \mathsf {M}):\) It first sets \(S = \{2i - \mathsf {ID}_{i} | i\in [\ell ] \}\). Then it runs \(\mathsf {CEnc}(S,p) \rightarrow (\mathbf {c}, d'_3)\), picks \(\mathbf {s}_0, \mathbf {s}_1, \ldots , \mathbf {s}_{d'_3} \overset{_\$}{\leftarrow } \mathbb {Z}_p^{2\times 1}\), and sets
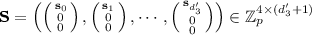 . Then it returns $$\begin{aligned} \mathsf {CT}= \left( ~ C_1 = g^{\mathbf {c}(\mathbf {S},\mathbb {W})}, \quad C_2 = e(g, h)^{ \varvec{\alpha }^\top \pi _1(\mathbf {B}) \mathbf {s}_0 } \cdot \mathsf {M}~ \right) . \end{aligned}$$
. Then it returns $$\begin{aligned} \mathsf {CT}= \left( ~ C_1 = g^{\mathbf {c}(\mathbf {S},\mathbb {W})}, \quad C_2 = e(g, h)^{ \varvec{\alpha }^\top \pi _1(\mathbf {B}) \mathbf {s}_0 } \cdot \mathsf {M}~ \right) . \end{aligned}$$Note that \(g^{\mathbf {c}(\mathbf {S},\mathbb {W})}\) can be computed from \(g^{\pi _1(\mathbf {B})}\) and \(\{ g^{\pi _1(\mathbf {W}_i \mathbf {B})} \}_{i\in [d_1]}\) efficiently because \(\mathbf {c}(\mathbf {S},\mathbb {W})\) contains only linear combinations of
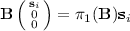 and
and  . \(C_2\) can be computed from \( e(g,h)^{\varvec{\alpha }^\top \pi _1(\mathbf {B})} \).
. \(C_2\) can be computed from \( e(g,h)^{\varvec{\alpha }^\top \pi _1(\mathbf {B})} \). -
\(\mathsf {Dec}(\mathsf {sk}_{\mathsf {ID}}, \mathsf {CT}):\) Let \(\mathsf {CT}\) be \(\mathsf {CT}= (C_1, C_2)\). From \(C_1 = g^{\mathbf {c}(\mathbf {S},\mathbb {W})} = \{ g^{c_{\iota }(\mathbf {S},\mathbb {W})} \}_{\iota \in [d_3]}\), it computes
$$\begin{aligned} \prod _{\iota \in [d_3]} e\left( g^{ c_{\iota }(\mathbf {S}, \mathbb {W})},\prod _{j\in S, \eta \in [d_2]} \mathsf {sk}_{j,\eta }^{E_{\eta ,\iota }} \right) = e(g,h )^{\varvec{\alpha }^\top \pi _1(\mathbf {B})\mathbf {s}_0} \end{aligned}$$(6)and recovers the message by \(C_2/e(g,h )^{\varvec{\alpha }^\top \pi _1(\mathbf {B})\mathbf {s}_0} = \mathsf {M}\).
Correctness. To see correctness of the scheme, it suffices to show Eq. (6).

The second equation above follows from the correctness of the underlying broadcast encoding.
Security. Assume that the broadcast encoding satisfies regularity requirement. Then, we can show that the security of the above IBE is reduced to the hardness of the (standard) decisional linear assumption and the \((Q_c,Q_k)\)-MMH security of the underlying broadcast encoding on prime-order groups. The reduction only incurs \(O(\ell )\) security loss. Since the \(Q_c\)-CMH security tightly implies \((Q_c,Q_k)\)-MMH security, the above IBE scheme is (almost) tightly secure if the underlying broadcast encoding is tightly \(Q_c\)-CMH. The details will appear in the full version [6].
6 Construction of Broadcast Encoding Schemes
In this section, we show two broadcast encoding schemes \(\mathsf {\Pi }_{\mathsf {cc}}\) and \(\mathsf {\Pi }_{\mathsf {slp}}\). For these schemes, we can tightly prove the \(Q_c\)-CMH security for any \(Q_c\). Therefore, by applying the conversion in Sects. 4 and 5, we obtain IBE schemes with almost tight security in the multi-challenge and multi-instance setting both in prime and composite-order groups. An IBE obtained from \(\mathsf {\Pi }_\mathsf {cc}\) achieves constant-size ciphertexts, but at the cost of requiring public parameters with the number of group elements being linear in the security parameter. Our second broadcast encoding scheme \(\mathsf {\Pi }_{\mathsf {slp}}\) partially compensate for this. By appropriately setting parameters, we can realize trade-off between size of ciphertexts and public parameters. For example, from the encoding, we obtain the first almost tightly secure IBE with all communication cost (the size of \(\mathsf {pp}\) and \(\mathsf {CT}\)) being \(O(\sqrt{\kappa })\). Such a scheme is not known even in the single-challenge setting [9, 17]. While the structure of \(\mathsf {\Pi }_{\mathsf {cc}}\) is implicit in [25], \(\mathsf {\Pi }_{\mathsf {slp}}\) is new. The construction of \(\mathsf {\Pi }_{\mathsf {slp}}\) is inspired by recent works on unbounded attribute-based encryption schemes [38, 43, 44]. However, the security proof for the encoding is completely different.
6.1 Broadcast Encoding with Constant-Size Ciphertexts
At first, we show the following broadcast encoding scheme that we call \(\mathsf {\Pi }_{\mathsf {cc}}\). The scheme has the same structure as the broadcast encryption scheme proposed by Gentry and Waters [25]. For \(\mathsf {\Pi }_{\mathsf {cc}}\), we can prove Q-PMH security for any Q. By Lemma 1, we have that Q-CMH security of \(\mathsf {\Pi }_{\mathsf {cc}}\) on \(\mathbb {G}_{p_2}\) and \(\mathbb {G}_{p_3}\) can be tightly proven unconditionally. Similar implication holds in prime-order groups.
-
\(\mathsf {Param}(n,N)\rightarrow d_1:\) It outputs \(d_1 = n\).
-
\(\mathsf {KEnc}(\tau ,N)\rightarrow (\mathbf {k},d'_2):\) It outputs \(\mathbf {k}= (\alpha + r w_{\tau }, rw_1,\ldots , rw_{\tau -1}, r, rw_{\tau +1}, \ldots , rw_n)\) and \(d'_2 = 1\) where \(\mathbf {r}= r\).
-
\(\mathsf {CEnc}(S,N)\rightarrow (\mathbf {c}, d'_3):\) Let \(S\subseteq [n]\). It outputs \(\mathbf {c}= (s,~ \sum _{j\in S}sw_j )\) and \(d'_3=0\) where \(\mathbf {s}= s\).
Correctness. Let \(\tau \in S\). Then, we have
Lemma 3
\(\mathsf {\Pi }_{\mathsf {cc}}\) defined above is Q-PMH secure for any \(Q \in \mathbb {N}\).
Proof
Let \(\tau \not \in \cup _{j\in [Q]} S_j \). It is clear that information on \(w_{\tau }\) is not leaked given \( \{ \mathbf {c}_{S_j}(\mathbf {s}_j,\mathbf {w}) \}_{j\in [Q] }\). Thus, \(\alpha \) is information-theoretically hidden from \( \mathbf {k}_\tau (\alpha , \mathbf {r}, \mathbf {w})\), because \(\alpha \) is masked by \(rw_\tau \) which is uniformly random over \(\mathbb {Z}_p\). Thus, the lemma follows.
6.2 Encoding with Sub-linear Parameters
We propose the following broadcast encoding scheme that we call \(\mathsf {\Pi }_{\mathsf {slp}}\). We can realize trade-off between sizes of parameters by setting \(n_1\). For the encoding scheme, we are not able to show the Q-PMH security. Instead, we show the Q-CMH security.
-
\(\mathsf {Param}(n,N)\rightarrow d_1:\) It outputs \(d_1 = 2 n_1 + 3\). We let \(n_2 = \lceil n/n_1 \rceil \). For ease of the notation, we will denote \(\mathbf {w}= (u_1,\ldots ,u_{n_1}, v, u'_1,\ldots ,u'_{n_1}, v', w)\) in the following.
-
\(\mathsf {KEnc}(\tau ,N)\rightarrow (\mathbf {k},d'_2):\) It computes unique \(\tau _1 \in [n_1]\) and \(\tau _2 \in [n_2]\) such that \(\tau =\tau _1 + (\tau _2 -1 )\cdot n_1 \). Then it sets \(d'_2=1\) and \(\mathbf {r}= r\) and outputs
$$\begin{aligned} \mathbf {k}= \left( ~ \alpha + rw, r, r(v+ \tau _2 u_{\tau _1}), \{ ru_i \}_{i\in [n_1]\backslash \{ \tau _1 \} }, r(v'+ \tau _2 u'_{\tau _1}), \{ ru'_i \}_{i\in [n_1]\backslash \{ \tau _1 \} } \right) \!. \end{aligned}$$ -
\(\mathsf {CEnc}(S,N)\rightarrow (\mathbf {c}, d'_3):\) It first defines \(\tilde{S}_j\) and \(S_j\) for \(j\in [n_2]\) as
$$\begin{aligned} \tilde{S}_j = S \cap [(j-1)n_1 +1, jn_1], \quad S_j = \{ j' - (j-1)n_1 ~ | ~ j'\in \tilde{S}_j \}, \end{aligned}$$sets \(\mathbf {s}= (s_0,t_1,\ldots , t_{n_2}, t'_1,\ldots , t'_{n_2} )\) and \(d'_3= 2n_2 +1\), and outputs
$$\begin{aligned} \mathbf {c}= \Bigl (s_0, ~ \{ ~ s_0w + t_{i} \bigl (v + i \sum _{j \in S_i} u_{j} \bigr ) + t'_{i} \bigl (v' + i \sum _{j \in S_i} u'_{j} \bigr ), \quad t_{i},\quad t'_i ~ \}_{i\in [n_2]} \Bigr ). \end{aligned}$$
Correctness. Let \(\tau \in S\) and \(\tau _1\), \(\tau _2\) be defined as above. Then, we have \(\tau _1 \in S_{\tau _2}\) and
We can tightly prove the Q-CMH security of \(\mathsf {\Pi }_\mathsf {slp}\) on composite-order (resp. prime-order) groups assuming the DLIN assumption on the composite-order (resp. prime-order) group. The details can be found in the full version [6].
6.3 Implications
For \(\mathsf {\Pi }_{\mathrm{xx}}\), we call an IBE scheme obtained by applying the conversion in Sect. 4 to \(\mathsf {\Pi }_{\mathrm{xx}}\) \(\mathsf {\Phi }^\mathsf {comp}_{\mathrm{xx}}\). Similarly, we call a scheme obtained by the conversion in Sect. 5.2 \(\mathsf {\Phi }^\mathsf {prime}_{\mathrm{xx}}\). \(\mathsf {\Phi }^\mathsf {prime}_{{\mathsf {cc}}}\) and \(\mathsf {\Phi }^\mathsf {prime}_{{\mathsf {slp}}}\) are the first IBE schemes that are (almost) tightly secure in the multi-challenge and multi-instance setting, from a static assumption in prime-order groups (the DLIN assumption). \(\mathsf {\Phi }^\mathsf {comp}_{{\mathsf {cc}}}\) and \(\mathsf {\Phi }^\mathsf {prime}_{{\mathsf {cc}}}\) achieve constant-size ciphertext, meaning the number of group elements in ciphertexts is constant. The drawback of the schemes is their long public parameters. In \(\mathsf {\Phi }^\mathsf {comp}_{{\mathsf {slp}}}\) and \(\mathsf {\Phi }^\mathsf {prime}_{{\mathsf {slp}}}\), we can trade-off the size of ciphertexts and public parameters. For example, by setting \(n_1 = \sqrt{n}\), we obtain the first almost tightly secure IBE scheme such that all communication cost (the size of the public parameters, the master public keys, and the ciphertexts) is sub-linear in the security parameter. Such a scheme is not known in the literature, even in the single-challenge and single-instance setting. Also see Table 1 in Sect. 1 for the overview of the obtained schemes.
7 Anonymous IBE with Tight Security Reduction
All our IBE schemes obtained so far is not anonymous. In these schemes, one can efficiently check that a ciphertext is in a specific form using pairing computation, which leads to an attack against anonymity. In this section, we show that \(\mathsf {\Phi }^\mathsf {prime}_\mathsf {cc}\) can be modified to be anonymous, by removing all group elements in \(\mathbb {G}_2\) from the public parameter \(\mathsf {pp}\) and put these in \(\mathsf {sp}\) instead. We call the resulting scheme \(\mathsf {\Phi }_\mathsf {anon}\). This is the first IBE scheme whose anonymity is (almost) tightly proven in the multi-challenge setting. While our technique for making the scheme anonymous is similar to that in [16], the security proof for our scheme requires some new ideas. This is because [16] only deals with the single-challenge setting whereas we prove tight security in the multi-challenge setting. In the security proof, we introduce new combination of information-theoretic argument (as in [16]) and computational argument.
Construction. Let the identity space of the scheme be \(\{ 0,1 \}^\ell \) and the message space be \(\mathbb {G}_T\). We note that we have \(\mathsf {sp}\ne \bot \) in the following, differently from other constructions in this paper.
-
\(\mathsf {Par}(1^\kappa , \ell ):\) It first runs \((p,\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, g,h, e(\cdot ) ) \overset{_\$}{\leftarrow } \mathcal {G}_{\mathsf {prime}}(1^\kappa )\). Then it picks \(\mathbf {B}\overset{_\$}{\leftarrow } \mathbb {GL}_{4}(\mathbb {Z}_p)\), \(\mathbf {W}_1,\ldots , \mathbf {W}_{2\ell } \overset{_\$}{\leftarrow } \mathbb {Z}_p^{4 \times 4}\) and a random full-rank diagonal matrix \(\mathbf {D}\in \mathbb {Z}_p^{ 4 \times 4 }\) with the entries (3, 3) and (4, 4) being 1. Finally, it sets \(\mathbf {Z}= \mathbf {B}^{-\top }\mathbf {D}\) and returns \(\mathsf {pp}=(g, g^{\pi _1(\mathbf {B})}, g^{\pi _1(\mathbf {W}_1 \mathbf {B})}, \ldots ,g^{\pi _1(\mathbf {W}_{2\ell } \mathbf {B})})\) and \(\mathsf {sp}=(h, h^{\pi _1(\mathbf {Z})}, h^{\pi _1(\mathbf {W}^\top _1 \mathbf {Z})},\ldots ,g^{\pi _1(\mathbf {W}^\top _{2\ell } \mathbf {Z})}).\)
-
\(\mathsf {Gen}(\mathsf {pp},\mathsf {sp}):\) It picks \(\varvec{\alpha }\overset{_\$}{\leftarrow } \mathbb {Z}_{p}^{4\times 1}\) and outputs \(\mathsf {mpk}= (\mathsf {pp},e(g,h)^{\varvec{\alpha }^\top \pi _1(\mathbf {B})} )\) and \(\mathsf {msk}= (\varvec{\alpha }, \mathsf {sp})\).
-
\(\mathsf {Ext}(\mathsf {msk}, \mathsf {mpk}, \mathsf {ID}):\) It first sets \(S = \{2i - \mathsf {ID}_{i} | i\in [\ell ] \}\) where \(\mathsf {ID}_i \in \{ 0,1 \}\) is the i-th bit of \(\mathsf {ID}\in \{ 0,1 \}^\ell \). Then it picks random \(\mathbf {r}\overset{_\$}{\leftarrow } \mathbb {Z}_p^{2\times 1}\) and returns \(\mathsf {sk}_{\mathsf {ID}}=(K_1=h^{ \varvec{\alpha }+ \sum _{i\in S} \pi _1(\mathbf {W}_i^\top \mathbf {Z}) \mathbf {r}},~K_2=h^{ -\pi _1(\mathbf {Z}) \mathbf {r}}).\)
-
\(\mathsf {Enc}(\mathsf {mpk}, \mathsf {ID}, \mathsf {M}):\) It first sets \(S = \{2i - \mathsf {ID}_{i} | i\in [\ell ] \}\). Then it picks random \(\mathbf {s}\overset{_\$}{\leftarrow } \mathbb {Z}_p^{2\times 1} \) and returns \(\mathsf {CT}=(C_1=g^{ \pi _1(\mathbf {B}) \mathbf {s}},~ C_2= g^{ \sum _{i\in S} \pi _1(\mathbf {W}_i \mathbf {B}) \mathbf {s}},~ C_3 = e(g,h)^{\varvec{\alpha }^\top \pi _1(\mathbf {B}) \mathbf {s}}\cdot \mathsf {M}).\)
-
\( \mathsf {Dec}(\mathsf {sk}_{\mathsf {ID}}, \mathsf {CT}):\) It parses the ciphertext \(\mathsf {CT}\) as \(\mathsf {CT}\rightarrow (C_1, C_2, C_3)\), and computes \(e(C_1,K_1)e(C_2,K_2)=e(g,h )^{\varvec{\alpha }^\top \pi _1(\mathbf {B})\mathbf {s}}\). Then, it recovers the message by \(C_3/e(g,h )^{\varvec{\alpha }^\top \pi _1(\mathbf {B})\mathbf {s}} = \mathsf {M}\).
Remark. We have to ensure that the key extraction algorithm \(\mathsf {Ext}\) always use the same randomness \(\mathbf {r}\) for the same identity, in order to (tightly) prove the security of the scheme. This can be easily accomplished, for example, using PRF [24]. For the sake of simplicity, we do not incorporate this change into the description of our scheme.
Security. We can prove \((1,Q_c,Q_k)\)-anonymity of \(\mathsf {\Phi }_\mathsf {anon}\) under the DLIN assumption (single instance case). The reduction cost is \(O(\ell )\), which is independent from \(Q_c\) and \(Q_k\). While we think that it is not difficult to extend the result to the multi-instance setting, we do not treat it in this paper.
8 Application to CCA Secure Public Key Encryption
Here, we discuss that our IBE schemes with almost tight security reduction in the multi-instance and multi-challenge setting yield almost tightly CCA secure PKE in the same setting via simple modification of Canetti-Halevi-Katz (CHK) transformation [15]. The difference from the ordinary CHK transformation is that we use (tightly secure) Q-fold one-time signature introduced and constructed in [30]. Another difference is that we need a restriction on the original IBE scheme. That is, we require that the key generation algorithm \(\mathsf {Gen}\) of the IBE scheme does not output any secret parameter. Namely, \(\mathsf {sp}=\bot \). Roughly speaking, this is needed since the syntax of the PKE does not allow key generation algorithm to take any secret parameter. Note that this condition is satisfied by all of our constructions except for that in Sect. 7.
By applying the above conversion to \(\mathsf {\Phi }^{\mathsf {prime}}_{\mathsf {slp}}\) and \(\mathsf {\Phi }^{\mathsf {prime}}_{\mathsf {cc}}\), we obtain new PKE schemes that we call \(\mathsf {\Psi }^{\mathsf {prime}}_{\mathsf {slp}}\) and \(\mathsf {\Psi }^{\mathsf {prime}}_{\mathsf {cc}}\). The former allows flexible trade-off between the size of public parameters and ciphertexts. The latter achieves very short ciphertext-size: The ciphertext overhead of our scheme only consists of 10 group elements and 2 elements in \(\mathbb {Z}_p\). This significantly improves previous results [1, 27, 30, 33, 34] on PKE scheme with the same security guarantee in terms of the ciphertext-size. Note that state-of-the-art construction by [27, 34] require 47 and 59 group elements of ciphertext overhead, respectively. Namely, ciphertext overhead of our scheme is (at least) \(74\,\%\) shorter, compared to theirs. On the other hand, the size of public parameter of the scheme in [27] is much shorter than ours (and those of [33, 34]). The former only requires 17 group elements, but the latter requires many more.
The reason why we can achieve very short ciphertext size is that our strategy to obtain PKE scheme is quite different from other works. Roughly speaking, all of the previous constructions [1, 27, 30, 33, 34] follow the template established by Hofheinz and Jager [30]. They first construct (almost) tightly-secure signature. Then, they use the signature to construct (almost) tightly-secure unbounded simulation sound (quasi-adaptive) NIZK. Finally, they follow the Naor-Yung paradigm [41] and convert the CPA-secure PKE with tight security reduction [12]into CCA-secure one using the NIZK. On the other hand, our construction is much more direct and simpler. Our conversion only requires very small amount of overhead in public parameters and ciphertexts.
Notes
- 1.
In fact, we also require the decisional bilinear Diffie-Hellman (DBDH) assumption on the composite-order groups (Problem 5) in addition to the subgroup decision assumptions. However, the assumption does not use the power of composite-order groups. In other words, it does not imply the factoring assumption. Therefore, it is ready to be converted into prime-order.
- 2.
In the actual scheme, \(\mathsf {sk}_\mathsf {ID}\) is randomized by elements of \(\mathbb {G}_{p_3}\), but we do not care about this point in this overview.
- 3.
Of course, in symmetric bilinear groups, the DDH assumption does not hold. They considered a DDH assumption on \(\mathbb {G}_{p_2}\) where each term is perturbed by a random element in \(\mathbb {G}_{p_3}\), which prevents trivial attack against the assumption.
- 4.
Here, we use CMH to stand for “computational-master-key hiding” (for broadcast encoding), while in [4], CMH refers to “co-selective master-key hiding” (for pair encoding). We hope that this should not be confusing, since our notion of 1-CMH security is in fact almost the same as the notion of co-selective master-key hiding security (for broadcast predicate) anyway.
- 5.
They showed a construction that is secure under the k-LIN assumption for any k, using \(2k\times 2k\) matrices. When \(k=2\), the scheme is secure under the DLIN assumption.
References
Abe, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Tagged one-time signatures: tight security and optimal tag size. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 312–331. Springer, Heidelberg (2013)
Agrawal, S., Chase, M.: A study of Pair Encodings: Predicate Encryption in prime order groups. IACR Cryptology ePrint Archive, Report 2015/390
Attrapadung, N.: Dual System Encryption Framework in Prime-Order Groups. IACR Cryptology ePrint Archive, Report 2015/390
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014)
Attrapadung, N., Furukawa, J., Gomi, T., Hanaoka, G., Imai, H., Zhang, R.: Efficient identity-based encryption with tight security reduction. In: Pointcheval, D., Mu, Y., Chen, K. (eds.) CANS 2006. LNCS, vol. 4301, pp. 19–36. Springer, Heidelberg (2006)
Attrapadung, N., Hanaoka, G., Yamada, S.: A framework for identity-based encryption with almost tight security. IACR Cryptology ePrint Archive 2015:566 (2015)
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000)
Bellare, M., Ristenpart, T.: Simulation without the artificial abort: simplified proof and improved concrete security for waters’ IBE scheme. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 407–424. Springer, Heidelberg (2009)
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) Identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014)
Boneh, D., Boyen, X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004)
Boneh, D., Boyen, X.: Secure identity based encryption without random oracles. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 443–459. Springer, Heidelberg (2004)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001)
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 255–271. Springer, Heidelberg (2003)
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 207–222. Springer, Heidelberg (2004)
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015)
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE from standard assumptions. IACR Cryptology ePrint Archive, Report 2013/803
Chen, J., Wee, H.: Dual system groups and its applications - compact HIBE and more. IACR Cryptology ePrint Archive, Report 2014/265
Chen, J., Wee, H.: Fully, (Almost) Tightly Secure IBE and Dual System Groups. CRYPTO,pp. 435–460 (2013). A merge of two papers [19, 20]
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001)
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for diffie-hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013)
Freeman, D.M.: Converting pairing-based cryptosystems from composite-order groups to prime-order groups. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 44–61. Springer, Heidelberg (2010)
Gentry, C.: Practical identity-based encryption without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 445–464. Springer, Heidelberg (2006)
Gentry, C., Waters, B.: Adaptive security in broadcast encryption systems (with short ciphertexts). In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 171–188. Springer, Heidelberg (2009)
Herold, G., Hesse, J., Hofheinz, D., Ràfols, C., Rupp, A.: Polynomial spaces: a new framework for composite-to-prime-order transformations. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 261–279. Springer, Heidelberg (2014)
Hofheinz, D.: Algebraic partitioning: fully compact and (almost) tightly secure cryptography. IACR Cryptology ePrint Archive, Report 2015/499
Hofheinz, D., Kiltz, E.: Secure hybrid encryption from weakened key encapsulation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 553–571. Springer, Heidelberg (2007)
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 21–38. Springer, Heidelberg (2008)
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012)
Hofheinz, D., Koch, J., Striecks, C.: Identity-based encryption with (almost) tight security in the multi-instance, multi-ciphertext setting. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 799–822. Springer, Heidelberg (2015)
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013)
Libert, B., Joye, M., Yung, M., Peters, T.: Concise multi-challenge CCA-secure encryption and signatures with almost tight security. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 1–21. Springer, Heidelberg (2014)
Libert, B., Joye, M., Yung, M., Peters, T.: Compactly Hiding Linear Spans: Tightly Secure Constant-Size Simulation-Sound QA-NIZK Proofs and Applications. IACR Cryptology ePrint Archive, Report 2015/242
Lewko, A.: Tools for simulating features of composite order bilinear groups in the prime order setting. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 318–335. Springer, Heidelberg (2012)
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010)
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure hibe with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010)
Lewko, A., Waters, B.: Unbounded HIBE and attribute-based encryption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 547–567. Springer, Heidelberg (2011)
Lewko, A., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012)
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: STOC, pp. 427–437 (1990)
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010)
Okamoto, T., Takashima, K.: Fully secure unbounded inner-product and attribute-based encryption. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 349–366. Springer, Heidelberg (2012)
Rouselakis, Y., Waters, B.: Practical constructions and new proof methods for large universe attribute-based encryption. In: ACM-CCS, pp. 463–474 (2013)
Sakai, R., Ohgishi, K., Kasahara, M.: Cryptosystems based on pairing over elliptic curve. In: The 2001 Symposium on Cryptography and Information Security (2001). (in Japanese)
Shacham, H.: A Cramer-Shoup encryption scheme from the linear assumption and from progressively weaker linear variants, IACR Cryptology ePrint Archive, Report 2007/074
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakely, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985)
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005)
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009)
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014)
Acknowledgement
We thank the members of Shin-Akarui-Ango-Benkyo-Kai for valuable comments. We also thank anonymous reviewers for their constructive comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologc Research
About this paper
Cite this paper
Attrapadung, N., Hanaoka, G., Yamada, S. (2015). A Framework for Identity-Based Encryption with Almost Tight Security. In: Iwata, T., Cheon, J. (eds) Advances in Cryptology -- ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science(), vol 9452. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48797-6_22
Download citation
DOI: https://doi.org/10.1007/978-3-662-48797-6_22
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48796-9
Online ISBN: 978-3-662-48797-6
eBook Packages: Computer ScienceComputer Science (R0)




 for all
for all  , and
, and 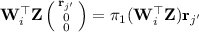 . Finally, it outputs private key
. Finally, it outputs private key 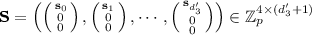 . Then it returns
. Then it returns 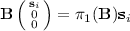 and
and  .
.