Abstract
Motivated by the recent progress in improving efficiency of secure computation, we study cut-and-choose oblivious transfer—a basic building block of state-of-the-art constant round two-party secure computation protocols that was introduced by Lindell and Pinkas (TCC 2011). In particular, we study the question of realizing cut-and-choose oblivious transfer and its variants in the OT-hybrid model. Towards this, we provide new definitions of cut-and-choose oblivious transfer (and its variants) that suffice for its application in cut-and-choose techniques for garbled circuit based two-party protocols. Furthermore, our definitions conceptually simplify previous definitions including those proposed by Lindell (Crypto 2013), Huang et al., (Crypto 2014), and Lindell and Riva (Crypto 2014). Our main result is an efficient realization (under our new definitions) of cut-and-choose OT and its variants with small concrete communication overhead in an OT-hybrid model. Among other things this implies that we can base cut-and-choose OT and its variants under a variety of assumptions, including those that are believed to be resilient to quantum attacks. By contrast, previous constructions of cut-and-choose OT and its variants relied on DDH and could not take advantage of OT extension. Also, our new definitions lead us to more efficient constructions for multistage cut-and-choose OT—a variant proposed by Huang et al. (Crypto 2014) that is useful in the multiple execution setting.
V. Kolesnikov—Supported by the Office of Naval Research under contract N00014-14-C-0113.
R. Kumaresan—Supported by Qatar Computing Research Institute and DARPA Grant number FA8750-11-2-0225. Work done in part while at the Technion.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Secure two-party computation is rapidly moving from theory to practice. While the basic approach for semi-honest security, garbled circuits [33], is extensively studied and is largely settled, security against malicious players has recently seen significant improvements. The main technique for securing garbled circuit protocols against malicious adversaries is cut-and-choose, formalized and proven secure by Lindell and Pinkas [23]. A line of work [11, 22–24, 26, 31] has focused on reducing the concrete overhead of the cut-and-choose approach: it is possible to guarantee probability of cheating \(\le 2^{-\sigma }\) using exactly \(\sigma \) garbled circuits.
The above works have been motivated by the impression that the major overhead of secure two-party computation arises from the generation, transmission, and evaluation of garbled circuits (especially for functions having large circuit size). Indeed, the work of Frederiksen and Nielsen [7] showed that the cost of the circuit communication and computation for oblivious two-party AES is approximately \(80\,\%\) of the total cost; likewise, Kreuter et al. [19] showed that the circuit generation and evaluation for large circuits takes \(99.999\,\%\) of the execution time.
Recent works of [10, 21] consider the multiple-execution setting, where two parties compute the same function on possibly different inputs either in parallel or sequentially. These works show that to evaluate the same function t times, it is possible to reduce the number of garbled circuits to \(O(\sigma /\log t)\). In concrete terms, this corresponds to a drastic reduction in the number of garbled circuits. For instance when \(t = 3500\) and for \(\sigma = 40\), the work of [10, 21] shows a cut-and-choose technique that reduces the number of garbled circuits to less than 8 per execution. Thus it is reasonable to say that the overhead due to generation, transmission, and evaluation of garbled circuits has been significantly reduced.
However, state-of-the-art two-party secure computation protocols, both in the single-execution setting [22] and in the multiple-execution setting [10], suffer from major overheads due to use of public key operations for two reasons:
-
– Use of DDH-based zero-knowledge protocols to enforce circuit-generator’s input consistency.
-
– Use of DDH-based cut-and-choose oblivious transfer protocols [5, 10, 21, 22, 24] to avoid “selective failure” attacks.
Of greater concern is the fact that these state-of-the-art protocols are unlikely to perform well in settings where the inputs of even one of the parties are large (because they use public key operations proportional to the total size of inputs of both parties). It is worthwhile to note that although techniques, most notably amortization via oblivious transfer (OT) extension [12, 14, 29], exist to reduce the number of public key operations required at least for one of the parties, the state-of-the-art two-party secure computation protocols simply are not able to take advantage of these amortization techniques.
If one restricts their attention to constant-round protocols with good concrete efficiency there are very few alternatives [23, 26] that require reduced number of public key operations. For instance the protocols of [23, 26] use public key operations only for the (seed) OTs (which can be amortized using OT extension). Furthermore, at least in the single execution setting, the techniques of [23, 26] can be easily merged with state-of-the-art cut-and-choose techniques to reduce the number of public key operations. However, this results in a considerable overhead in the communication complexity (by factor \(\sigma \)) for proving input consistency of the circuit generator. More importantly the techniques of [23, 26] do not adapt well to the state-of-the-art cut-and-choose techniques for the multiple executions setting, and require strong assumptions such as a programmable random oracle. Specifically, the “XOR-tree encoding schemes” technique employed in [23, 26] to avoid the selective failure attack no longer appears to work with standard garbling techniques. On the other hand, a natural generalization of cut-and-choose OT, namely multistage cut-and-choose OT proposed in [10, 21] can handle the selective failure attack in the multiple executions setting (cf. Sect. 1.2).
Unfortunately the only known constructions of cut-and-choose OT as well as its variants rely on DDH and consequently use public key operations proportional to the size of the cut-and-choose OT instance. This is further amplified by the fact that known cut-and-choose OT protocols require regular exponentiations which are more expensive relative to even fixed-base exponentiations. (Note that on the other hand the DDH-based zero-knowledge protocols to ensure input consistency used in [22, 24] require only fixed-base exponentiations.)
Our Contributions. In this paper, we study cut-and-choose OT and its variants as independently interesting primitives. Motivated by the discussion above, our main goal will be to reduce the number of public key operations required to realize a cut-and-choose OT instance, while minimizing the concrete communication complexity. Towards this, we propose a new formulation of cut-and-choose OT and its variants that (1) is sufficient for its application to design secure two-party computation protocols, (2) allows a realization in an OT-hybrid model (as opposed to specific public key cryptosystems, and also provides alternative realizations which are resistant to quantum attacks), and (3) can be realized with low communication complexity in both concrete terms (roughly factor 4 overhead) as well as asymptotic terms. Furthermore, our formulation provides new insights into the design of multistage cut-and-choose OT protocols resulting in new constructions of the same that offer factor t (where t is the number of executions) improvement over prior work [10]. Note that the benefits of amortization in the multiple execution setting kick in for large t (e.g., 10X improvement when \(t = 10^6\)). Hence our protocols can offer significant gains in efficiency. Conceptually, our work can be considered as
-
– Pinning down the exact formulation of cut-and-choose OT and its variants that suffices for its applications.
-
– Basing cut-and-choose OT on a wide variety of assumptions (including LWE, RSA, DDH).
-
– Showing how to efficiently “extend” cut-and-choose OT (a la OT extension).
-
– An approach for porting “XOR-tree encoding schemes” to work in the multiple execution setting while preserving their efficiency.
Our new formulation of cut-and-choose OT has the following aspects:
-
– Treats cut-and-choose OT (and its variants) as a reactive functionality. This allows us to construct efficient protocols for multistage cut-and-choose OT.
-
– Requires ideal process simulation for corrupt receiver but only privacy against corrupt sender. This will allow us to realize cut-and-choose OT (and its variants) with low concrete communication complexity.
1.1 Cut-and-Choose Oblivious Transfer and Its Variants
We provide an overview of cut-and-choose OT and its variants. In the following, let \(\lambda \) (resp. \(\sigma \)) denote the computational (resp. statistical) security parameter.
Cut-and-Choose Oblivious Transfer. Cut-and-choose oblivious transfer (CCOT) [24], denoted \(\mathcal {F}_{\mathrm {ccot}}\) (see Fig. 1) is an extension of standard OT. The sender inputs n pairs of strings, and the receiver inputs n selection bits to select one string out of each pair of sender strings. However, the receiver also inputs a set J of size n / 2 that consists of indices where it wants both the sender’s inputs to be revealed. Note that for indices not contained in J, only those sender inputs that correspond to the receiver’s selection bits are revealed.
Remark 1
Using a PRG it is possible to obtain OT on long strings given ideal access to OT on short strings of length \(\lambda \) [12]. This length extension technique is applicable to cut-and-choose and its variants. Furthermore, for applications to secure computation, sender input strings (i.e., garbled circuit keys) are of length \(\lambda \). Therefore, we assume wlog that sender input strings are all of length \(\lambda \).
The cut-and-choose OT functionality \(\mathcal {F}_{\mathrm {ccot}}\) from [24].
Batch Single-Choice CCOT. In applications to secure computation, one needs single-choice CCOT, where the receiver is restricted to inputting the same selection bit in all the n / 2 instances where it receives exactly one out of two sender strings. Furthermore, it is crucial that the subset J input by the receiver is the same across each instance of single-choice CCOT. This variant, called batch single-choice CCOT can be efficiently realized under DDH [24].
Modified Batch Single-Choice CCOT. Lindell [22] presented a variant of batch single-choice CCOT, denoted \(\mathcal {F}^\star _{\mathrm {ccot}}\), to address settings where the receiver’s input set J may be of arbitrary size (i.e., not necessarily n / 2). In addition to obtaining one of the sender’s inputs, the receiver also obtains a “check value” for each index not in J. This variant can be realized under DDH [22].
Multistage CCOT. To handle the multiple (parallel) execution setting, a new variant of \(\mathcal {F}^\star _{\mathrm {ccot}}\) called batch single-choice multi-stage cut-and-choose oblivious transfer was proposed in [10]. For sake of simplicity, we refer to this primitive as multistage cut-and-choose oblivious transfer and denote it by \(\mathcal {F}^\star _{\mathrm {mcot}}\). At a high level, this variant differs from \(\mathcal {F}^\star _{\mathrm {ccot}}\) in that the receiver can now input multiple sets \(E_1,\ldots , E_t\) (where J is now implicitly defined as \([n]\setminus \cup _{k\in [t]} E_k\)), and make independent selections for each \(E_1,\ldots , E_t\). In fact the above definition reflects the cut-and-choose technique employed in [10, 21] for the multiple execution setting. The technique proceeds by first choosing a subset of the n garbled circuits to be checked, and then partitioning the remaining garbled circuits into t evaluation “buckets”. An information-theoretic reduction of \(\mathcal {F}^\star _{\mathrm {mcot}}\) to t instances of \(\mathcal {F}^\star _{\mathrm {ccot}}\) with total communication cost \(O(nt^2\lambda )\) was shown in [10].
For lack of space, we present only the multistage cut-and-choose OT functionality in Fig. 2. Note that \(\mathcal {F}^\star _{\mathrm {mcot}}\) generalizes modified batch single-choice CCOT of [22] (simply by setting \(t = 1\)) as well as batch single-choice CCOT of [24] (by setting \(t=1\) and forcing \(|J| = n/2\) and setting all \(\phi _j^k\) values to \(0^\sigma \)).
1.2 Selective Failure Attacks
In garbled circuit protocols, OT is used to enable the circuit generator (referred to as the sender) \(S\) to transfer input keys for the garbled circuit corresponding to the circuit evaluator (referred to as the receiver) \(R\)’s inputs. However, when \(S\) is malicious, this can lead to a “selective failure” attack. To explain this problem in more detail, consider the following naïve scheme. For simplicity assume that \(R\) has only one input bit b. Let the keys corresponding to R’s input be \((x_{j,0}, x_{j,1})\) in the j-th garbled circuit. In the following, let \({\textsf {com}}\) be a commitment scheme.
-
– \(S\) sends \(({\textsf {com}}(x_{1,0}), {\textsf {com}}(x_{1,1})), \ldots , ({\textsf {com}}(x_{n,0}), {\textsf {com}}(x_{n,1}))\) to \(R\).
-
– \(S\) and \(R\) participate in a single instance of \(\mathcal {F}_{\mathrm {OT}}\) where \(S\)’s input \(((d_{1,0},\ldots ,d_{n,0}), (d_{1,1},\ldots ,d_{n,1}))\) where \(d_{j,c}\) is the decommitment corresponding to \({\textsf {com}}(x_{j,c})\), and \(R\)’s input is b. \(R\) obtains \((d_{1,b},\ldots ,d_{n,b})\) from \(\mathcal {F}_{\mathrm {OT}}\).
-
– Then \(R\) sends check indices \(J \subseteq [n]\) to \(S\).
-
– \(S\) sends \(\{d_{j,0},d_{j,1}\}_{j\in J}\) to \(R\).
The selective failure attack operates in the following way: \(S\) supplies \((d_{1,0},\ldots ,d_{n,0}),(d_{1,1}',\ldots ,d_{n,1}')\) where \(d_{i,0}\) is a valid decommitment for \({\textsf {com}}(x_{i,0})\) while \(d_{i,1}'\) is not a valid decommitment for \({\textsf {com}}(x_{i,1})\). Then when \(R\) sends check indices, \(S\) responds with \(\{d_{j,0},d_{j,1}\}_{j\in J}\) where \(d_{j,0}\) and \(d_{j,1}\) are valid decommitments for \({\textsf {com}}(x_{j,0})\) and \({\textsf {com}}(x_{j,1})\) respectively. Suppose \(R\)’s input equals 0. In this case, \(R\) does not detect any inconsistency, and continues the protocol, and obtains output. Suppose \(R\)’s input equals 1. Now \(R\) will not obtain \(x_{j,1}\) for all \(j\in [n]\) since it receives invalid decommitments. If \(R\) aborts then \(S\) knows that \(R\)’s input bit equals 1. In any case, R cannot obtain the final output. I.e., the ideal process and the real process can be distinguished when \(R\)’s input equals 1, and the protocol is insecure since S can force an abort depending on R’s input.
Approaches Based on “XOR-Tree Encoding Schemes”. The first solution to the selective failure attack was proposed in [6, 15, 23] where the idea was to randomly encode \(R\)’s input and then augment the circuit with a supplemental subcircuit (e.g., “XOR-tree”) that performs the decoding to compute \(R\)’s actual input. Note that the “selective failure”-type attack can still be applied by \(S\) but the use of encoding ensures that the event that \(R\) aborts due to the attack is almost statistically independent of its actual input. The basic XOR-tree encoding scheme incurs a multiplicative overhead of \(\sigma \) in the number of OTs and increases the circuit size by \(\sigma \) XOR gates. The “random combinations” XOR-tree encoding [23, 25, 30] incurs a total overhead of \(m' = \max (4m,8\sigma )\) in the number of OTs where m is the length of \(R\)’s inputs, and an additional \(0.3\,mm'\) XOR gates. (Note that use of the free-XOR technique [18] can lead to nullifying the cost of the additional XOR gates.) [13] uses \(\sigma \)-wise independent generators to provide a rate-1 encoding of inputs which can be decoded using an \(\mathbf {NC}^0\) circuit.
Approaches Based on CCOT. CCOT forces \(S\) to “commit” to all keys corresponding to \(R\)’s input and reveals a subset of these keys corresponding to \(R\)’s input but without the knowledge of which subset of keys were revealed. This allows us to intertwine the OT and the circuit checks and avoids the need to augment the original circuit with a supplemental decoding subcircuit. I.e., selective failure attacks are “caught” along with check for incorrectly constructed circuits, and this results in a simpler security analysis.
Approaches for the Multiple Execution Setting. While either approach seems sufficient to solve the selective failure attack, the CCOT based approach offers a qualitative advantage in the multiple parallel execution setting. First let us provide an overview of the cut-and-choose technique in the multiple execution setting [10, 21]. S sends n garbled circuits, and R picks a check set \(J\subseteq [n]\). The garbled circuits corresponding to check sets will eventually be opened by S. The garbled circuits which are not check circuits are randomly partitioned into t evaluation “buckets” denoted by \(E_1, \ldots , E_t\). We now explain the difficulty in adapting XOR-tree encoding schemes to this cut-and-choose technique.
Observe that when using standard garbling schemes [23, 33] in a 2-party garbled circuits protocol, the OT step needs to be carried out before the garbled circuits are sent. This is necessary for the simulator to generate correctly faked garbled circuits (using R’s inputs extracted from the OT) in the simulation for corrupt R. For simplicity assume that R has exactly one input bit (which may vary across different executions). Now when using XOR-tree encoding schemes we need to enforce that in each execution, R inputs the same choice in all the OTs. Batching the OTs together for each execution can be implemented if S knows which circuits are going to be evaluation circuits for each execution, but R cannot reveal which circuits are evaluation circuits because this allows a corrupt S to transmit well-formed check circuits and ill-formed evaluation circuits. Thus it is unclear how to apply the XOR-tree encoding schemes and ensure that corrupt R chooses the same inputs for the evaluation circuits within an execution.
A generalization of CCOT called multistage CCOT (Fig. 2) is well-suited to the multiple parallel execution setting. Indeed, multistage CCOT \(\mathcal {F}^\star _{\mathrm {mcot}}\) takes as inputs (1) from S: all input keys corresponding to R’s inputs in each of the n garbled circuits, and (2) from R: the sets \(E_1,\ldots , E_t\) along with independent choice bits for each of the t executions. Thus \(\mathcal {F}^\star _{\mathrm {mcot}}\) avoids the selective failure attack in the same way as CCOT does it in the single execution setting. Further, it ensures that R is forced to choose the same inputs within each execution.
Remark 2
Surprisingly, CCOT has a significant advantage over XOR-tree encoding schemes only in the parallel execution setting. In the sequential execution setting, it is unclear how to use CCOT since R’s inputs for each of its executions are not available at the beginning of the protocol. It appears necessary to do the OT for each execution after all the garbled circuits are sent. Then one may use adaptively secure garbling schemes [2, 3] (e.g., in the programmable random oracle model) to enable the simulator to generate correctly faked garbled circuits in the simulation for corrupt R. Assuming that the garbling is adaptively secure, XOR-tree encoding schemes suffice to circumvent the selective failure attack in the multiple sequential setting. This also applies to the multiple parallel setting.
1.3 Overview of Definitions and Constructions
As mentioned in the Introduction, all known constructions of CCOT rely on DDH and thus make heavy use of public key operations. A natural approach to remedy the above situation is try and construct CCOT in a OT-hybrid model and then use OT extension techniques [12, 29].
Basing CCOT on OT. A first idea is to use general OT-based 2PC (e.g., [14]) to realize CCOT but it is not clear if this would result in a CCOT protocol with good concrete efficiency. Note that the circuit implementing CCOT has very small depth, and that S’s inputs are of length \(O(n\lambda )\) while R’s is of length O(n) (where the big-Oh hides small constants). Protocols of [23, 26] do not perform well since there’s a multiplicative overhead of (at least) \(\lambda \sigma \) over the instance size (i.e., \(O(n\lambda )\)) simply because of garbling (factor \(\lambda \)) and cut-and-choose (factor \(\sigma \)). Protocols of [10, 22, 24] already rely on CCOT and the instance size of CCOT required inside these 2PC protocols are larger than the CCOT instance we wish to realize. Since the circuit has very small constant depth it is possible to employ non-constant round solutions [29] but this still incurs a factor \(\lambda \) overhead due to use of authenticated OTs. Employing information-theoretic garbled circuit variants [15, 17] in the protocols of [23, 26] still incur a factor \(\sigma \) overhead due to cut-and-choose. In summary, none of the above are satisfactory for implementing CCOT as they incur at least concrete factor \(\mathrm {min}(\lambda ,\sigma )\) multiplicative overhead.
To explain the intuition behind our definitions and constructions, we start with the seemingly close relationship between CCOT and 2-out-of-3 OT. At first glance, it seems that it must be easy to construct CCOT from 2-out-of-3 OT. For example, for each index, we can let S input the pair of real input keys along with a “dummy check value” as its 3 inputs to 2-out-of-3 OT, and then let R pick two out of the three values (i.e., both keys if it’s a check circuit, or the dummy check value along with the key that corresponds to R’s real input). There are multiple issues with making this idea work in the presence of malicious adversaries. Perhaps the most important issue is that this idea still wouldn’t help us achieve our goal of showing a reduction from CCOT to 1-out-of-2 OT. More precisely, we do not know how to construct efficient protocols for 2-out-of-3 OT from 1-out-of-2 OT. Consider the following toy example for the same.
Inputs: \(S\) holds \((x_0,x_1,x_2)\) and \(R\) holds \(b_1\in \{0,2\},b_2 \in \{1,2\}\).
Toy Protocol:
-
– \(S\) sends \((x_0, x_2)\) to \(\mathcal {F}_{\mathrm {OT}}\) and \(R\) sends \(b_1\) to \(\mathcal {F}_{\mathrm {OT}}\).
-
– \(S\) sends \((x_1, x_2)\) to \(\mathcal {F}_{\mathrm {OT}}\) and \(R\) sends \(b_2\) to \(\mathcal {F}_{\mathrm {OT}}\).
Outputs: \(S\) outputs nothing. \(R\) outputs \(x_{b_1},x_{b_2}\).
The problem with the protocol above is that simulation extraction will fail with probability 1/2 since a malicious \(S\) may input different values for \(x_2\) in each of the two queries to \(\mathcal {F}_{\mathrm {OT}}\). Note that even enforcing \(S\) to send \(h = \tilde{H}(x_2)\) to \(R\) where \(\tilde{H}\) is a collision-resistant hash function (or an extractable commitment) does not help the simulator. On the other hand this hash value does enable \(R\) to detect an inconsistency if (1) \(S\) supplied two different values for \(x_2\) in each of the two queries to \(\mathcal {F}_{\mathrm {OT}}\) and (2) \(R\) picked the \(x_2\) value which is not consistent with h. However, if \(R\) aborts on detection of inconsistency this leaks information.
Our main observation is that the attacks on the toy protocol are very similar to the selective failure attacks discussed in Sect. 1.2. Motivated by this one may attempt to use “XOR-tree encoding schemes” to avoid the selective failure attacks, and attempt to construct CCOT directly from 1-out-of-2 OT. However, note that the encoding schemes alone do not suffice to prevent selective failure attacks; they need to be used along with a supplemental decoding circuit. Here our main observation is that known encoding schemes (possibly with the exception of [32]) used to prevent selective failure attacks [13, 23] can be decoded using (a circuit that performs) only XOR operations. Thus, one may use the free-XOR technique [18] to get rid of the need for a supplemental decoding circuit, and instead perform XOR operations directly on strings. Indeed the above idea can be successfully applied to prevent selective failure attacks that could be mounted on the toy protocol, and can also be extended to yield a protocol for CCOT. Although the resulting CCOT protocol is simulatable against a malicious receiver, unfortunately we do not know how to simulate a corrupt sender (specifically, extract sender’s input).
Relaxing CCOT. Our main observation is that for application to 2PC, full simulation against a corrupt sender is not required. It is only privacy that is required. This is because S’s inputs to the 2PC are extracted typically via ZK (or the mechanism used for input consistency checks), and the inputs to the CCOT are just random garbled keys which are unrelated to its real input. Note that in 2PC protocols that use CCOT [10, 22, 24] the following three steps happen after the CCOT protocol is completed: (1) S sends all the garbled circuits, and (2) then R reveals the identity of the evaluation circuits, and (3) then S reveals its keys corresponding to its input for the evaluation circuits. Consider the second step mentioned above, namely that R reveals the identity of the evaluation circuits. This is a relatively subtle step since a malicious R may claim (a) that a check circuit is an evaluation circuit, or (b) that an evaluation circuit is a check circuit. Both these conditions need to be handled carefully since in case (a) corrupt R, upon receiving S’s input keys in step (3) will be able to evaluate the garbled circuits on several inputs of its choice. Case (b) is problematic while simulating a corrupt R as the simulator does not know which circuits to generate correctly and which ones to fake. Therefore, 2PC protocols that use CCOT require R to “prove” the identity of the check/evaluation circuits. In [10, 22], this is done via “check values” and “checkset values”. We use similar ideas in our protocols: if \(j\in [n]\) is such that \(j \not \in J\), then R receives some dummy check value \(\phi _j\), and if \(j \in J\) then R receives “checkset values” \(x_{j,0}, x_{j,1}\) which correspond to S’s inputs. Thus, R can prove the identity of check/evaluation circuits simply by sending the “check values” \(\{\phi _j\}_{j \not \in J}\) and “checkset values” \(\{ x_{j,0}, x_{j,1} \}_{j \in J}\). Observe that this step does not reveal any information about R’s input bits \(\{b_j\}_{j\not \in J}\) to S. To do this, we would need to include a “reveal” step.
Motivated by the discussions above, we formulate a new definition for CCOT and its variants. Our definitions pose CCOT and its variants as reactive functionalities, and in particular include a “reveal phase” where R’s evaluation set \([n]\setminus J\) is simply revealed to S by the functionality. More precisely, in the reveal phase we allow R to decide whether it wants to abort or reveal J. Note that for the case of \(\mathcal {F}^\star _{\mathrm {mcot}}\), the evaluation sets \(E_1,\ldots ,E_t\) is revealed to S by the functionality. This in particular allows us to eliminate the “check values” in the definitions of \(\mathcal {F}^\star _{\mathrm {ccot}}\) [22] and \(\mathcal {F}^\star _{\mathrm {mcot}}\) [10], and allows us to present protocols for (the reactive variant of) \(\mathcal {F}^\star _{\mathrm {mcot}}\) that is more efficient than prior constructions [10]. We formulate CCOT as a reactive functionality because step (1) where S sends all the garbled circuits happens immediately after the CCOT step and before step (2) where R reveals the identity of the evaluation circuits. It is easy to see that this relaxed formulation suffices for applications to secure computation.
Discussion. Such relaxed definitions, in particular requiring only privacy against corrupt sender, is not at all uncommon for OT and its variants (cf. [1, 28]) or PIR (cf. [4, 20]). Similarly, [8] propose “keyword OT” protocols in a client-server setting, and require one to simulate the server’s (which acts as the sender) view alone, without considering its joint distribution with the honest client’s output. For another example, consider [11] who use a CDH-based OT protocol that achieves privacy (but is not known to be simulatable) against a malicious sender, and yet this suffices for their purposes to construct efficient 2PC protocols.
2 Definitions
We formulate CCOT and its variants as reactive functionalities and provide relaxed definitions formally. Recall that the main differences from prior formulations is that we require (1) only privacy against corrupt sender, and (2) R to provide the check set J and evaluation sets \(E_1,\ldots , E_t\) to \(S\) at the end of the protocol. We emphasize that privacy against corrupt sender must hold even after \(J, E_1,\ldots ,E_t\) is revealed. Due to space constraints we describe our new formulation only for the case of multistage CCOT denoted \(\mathcal {F}_{\mathrm {mcot}}^+\) in Fig. 3. (The extensions to all other variants is straightforward.)
We will be using the following definitions (loosely based on analogous definitions for keyword OT [8]) for CCOT as well as its variants. Therefore for convenience we will define these as security notions for an arbitrary functionality F, and then in our theorem statements we will refer to F as being CCOT or one of its variants.
Definition 1
(Correctness). If both parties are honest, then, after running the protocol on inputs (X, Y), the receiver outputs Z such that \(Z = F(X,Y)\).
Definition 2
(Receiver’s privacy: indistinguishability). Let \(\sigma \) be a statistical security parameter. Then, for any ppt \(S'\) executing the sender’s part and for any inputs \(X,Y,Y'\), the statistical distance between the views that \(S'\) sees on input X, in the case that the receiver inputs Y and the case that it inputs \(Y'\) is bound by \(2^{-\sigma +O(1)}\).
Definition 3
(Sender’s privacy: comparison with the ideal model). For every ppt machine \(R'\) substituting the receiver in the real protocol, there exists a ppt machine \(R''\) that plays the receiver’s role in the ideal implementation, such that on any inputs (X, Y), the view of \(R'\) is computationally indistinguishable from the output of \(R''\). (In the semi-honest model \(R' = R\).)
Definition 4
A protocol \(\pi \) securely realizes functionality F with sender-simulatability and receiver-privacy if it satisfies Definitions 1, 2, and 3.
XOR-Tree Encoding Schemes. Selective failure attacks essentially correspond to letting a corrupt sender learn a disjunctive predicate of the receiver’s input. We define an XOR-tree encoding scheme consisting of a tuple \((\mathsf {En},\mathsf {De},\mathsf {En}',\mathsf {De}')\) of randomized algorithms (implicitly parameterized with statistical security parameter \(\sigma \), and possibly public randomness \(\omega _0\)) as satisfying:
-
1. Algorithm \(\mathsf {En}\) takes input \(\{ (x_0^i, x_1^i) \}_{i \in [m]}\) and produces pairs of random \(\lambda \)-bit strings \(\{ u_0^\ell , u_1^\ell \}_{\ell \in [m']}\) s.t. for each \(\ell ,\ell ' \in [m']\), it holds that \(u_0^{\ell '} {\oplus }u_1^{\ell '} = u_0^\ell {\oplus }u_1^\ell \).
-
2. Algorithm \(\mathsf {En}'\) takes input \(\mathbf {b} = (b_1,\ldots ,b_m) \in \{0,1\}^m\) and outputs \(\{ b_\ell '\}_{\ell \in [m']}\).
-
3. For every \(\mathbf {b} = (b_1,\ldots ,b_m) \in \{0,1\}^m\) and every \(\{ (x_0^i, x_1^i) \}_{ i \in [m] }\) it holds that
$$\begin{aligned} \mathrm {Pr}\left[ \begin{array}{l} \{b_\ell '\}_{\ell \in [m']} \leftarrow \mathsf {En}'(\mathbf {b});\\ \{(u_0^\ell , u_1^\ell )\}_{\ell \in [m']} \leftarrow \mathsf {En}(\{(x_0^i,x_1^i)\}_{i \in [m] }) \end{array} :\mathsf {De}( \{ u_{b_\ell '}^\ell \}_{\ell \in [m']}) = \{ x_{b_i}^i \}_{i \in [m] } \right] = 1.\end{aligned}$$We sometimes abuse notation and allow \(\mathsf {De}\) to take sets of pairs of strings as input in which case we require that for every \(\{ (x_0^i, x_1^i) \}_{ i \in [m] }\) it holds that
$$\begin{aligned} \mathrm {Pr}\left[ \begin{array}{l} \{(u_0^\ell , u_1^\ell )\}_{\ell \in [m']} \leftarrow \mathsf {En}(\{(x_0^i,x_1^i)\}_{i \in [m]}) : \\ \qquad \qquad \qquad \mathsf {De}( \{ (u_0^\ell , u_{1}^\ell ) \}_{\ell \in [m']}) = \{ ( x_{0}^i, x_1^i ) \}_{i \in [m] } \end{array} \right] = 1. \end{aligned}$$ -
4. For every \(\mathbf {b}\), it holds that \(\mathrm {Pr}[\mathsf {De}'(\mathsf {En}'(\mathbf {b})) = \mathbf {b}] = 1\).
-
5. Algorithms \(\mathsf {De},\mathsf {De}'\) can be implemented by using (a tree of) XOR gates only.
-
6. For every disjunctive predicate \(P(\cdot )\), the following holds: (1) If P involves at most \(\sigma -1\) literals, then \(\Pr [P (\mathsf {En}'(\mathbf {b})) = 1]\) is completely independent of \(\mathbf {b}\). (2) Otherwise, \(\Pr [P (\mathsf {En}'(\mathbf {b})) = 1] \ge 1- 2^{-\sigma +1}\).
-
7. For every \(\{(x_0^i, x_1^i)\}_{i \in [m] }\) and for every (possibly unbounded) adversary \(\mathcal {A}'\) and for every \(\{b_\ell '\}_{\ell \in [m']} \in \{0,1\}^{m'}\), there exists a ppt algorithm \(\mathcal {S}'\) such that the following holds:
$$\begin{aligned} \begin{array}{l} \mathrm {Pr}[ \{ (u_0^\ell , u_1^\ell ) \}_{\ell \in [m']} \leftarrow \mathsf {En}(\{(x_0^i,x_1^i)\}_{i \in [m] }) : \mathcal {A}'( \{ b_\ell '\}_{\ell \in [m']}, \{ u_{b_\ell '}^\ell \}_{\ell \in [m']} ) = 1 ] = \\ \quad \mathrm {Pr}\left[ \begin{array}{l} (b_1,\ldots ,b_m)\leftarrow \mathsf {De}'(\{b_\ell '\}_{\ell \in [m'] } );\\ \{ \tilde{u}^\ell \}_{\ell \in [m']} \leftarrow \mathcal {S}'( \{ b_\ell '\}_{\ell \in [m']} , \{x^i_{b_i} \}_{i \in [m] } )\end{array} : \mathcal {A}'(\{ b_\ell '\}_{\ell \in [m']}, \{ \tilde{u}^\ell \}_{\ell \in [m']}) = 1 \right] \end{array}\!. \end{aligned}$$(This in particular, implies that \(\mathcal {A}\) obtains no information about \(\{x_{1-b_i}^i\}_{i \in [m]}\).)
Algorithms \((\mathsf {En},\mathsf {De},\mathsf {En}',\mathsf {De}')\) for the basic XOR-tree encoding scheme [23] are simple and implicit in our basic CCOT construction (cf. Fig. 4). For the random combinations XOR-tree encoding [23] algorithm \(\mathsf {En}'\) is simply a random linear mapping (i.e., public randomness \(\omega _0\) defines this random linear mapping, see e.g., [23, 30] for more details). Finally, for the \(\sigma \)-wise independent generators XOR-tree encoding the algorithm \(\mathsf {En}'\) depends on the generator (i.e., public randomness \(\omega _0\) defines this generator) which can be implemented only using XOR gates [27]. Note that in all of the above, \(\mathsf {En}'\) essentially creates a \((\sigma -1)\)-independent encoding of its input, and thus Property 6 holds (see also Lemma 1). In all our constructions, \(\mathsf {En}\) simply maps its inputs to a pairs of random strings such that the XOR of the two strings within a pair is always some fixed \(\varDelta \). Algorithms \(\mathsf {De},\mathsf {De}'\) are deterministic and function to simply reverse the respective encoding algorithms \(\mathsf {En},\mathsf {En}'\). Note that \(\mathsf {De},\mathsf {De}'\) (acting respectively on outputs of \(\mathsf {En},\mathsf {En}'\)) are naturally defined by the supplemental decoding circuit that decodes the XOR-tree encoding, and thus can be implemented using XOR gates only. We point out that algorithm \(\mathsf {De}'\) is used only in the simulation to extract R’s input from its XOR-tree encoded form. Finally, Property 7 is justified by the fact that XOR-tree encoding schemes that are useful in standard two-party secure computation protocols, the receiver R obtains only one of two keys corresponding to the encoding (via OTs), and these keys reveal the output keys of the supplemental decoding circuit (that correspond exactly to the output of the decoding) and nothing else.
3 Constructions

See the protocol in Fig. 4 for the CCOT protocol that uses the basic XOR-tree encoding scheme of [23] in order to implement CCOT when \(n = 1\). The case when \(n \ge 1\) is handled by parallel repetition. While we prove that the resulting CCOT protocol is simulatable against a malicious receiver, unfortunately we do not know how to extract corrupt sender’s input. To see this, note that a corrupt sender may supply values for some \(\ell ,\ell ' \in [\sigma ]\) values \(u_0^\ell ,u_1^\ell , u_0^{\ell '}, u_1^{\ell '}\) such that \(u_0^\ell {\oplus }u_1^\ell \ne u_0^{\ell '}{\oplus }u_1^{\ell '}\). Needless to say, such a deviation is caught by R when \(J \ne \emptyset \). However, this deviation goes undetected when R’s input \(J = \emptyset \). Note that the simulator for a corrupt sender needs to extract S’s input without knowing R’s input; however when S provides inconsistent inputs to \(\mathcal {F}_{\mathrm {OT}}\), it is unclear how to extract S’s inputs. We prove that the protocol in Fig. 4 securely realizes \(\mathcal {F}_{\mathrm {ccot}}\) with sender-simulatability and receiver-privacy. We start by observing that correctness follows from inspection of the protocol.
Simulating Corrupt Receiver. Assume that H is modeled as a (non-programmable) random oracle. Acting as \(\mathcal {F}_{\mathrm {OT}}\) the simulator does the following:
-
– Chooses random \(\varDelta ',\{u_0^\ell , u_2^\ell \}_{\ell \in [\sigma ]}\) and sets for all \(\ell \in [\sigma ]\), value \(u_1^\ell = u_0^\ell {\oplus }\varDelta '\).
-
– For each \(\ell \in [\sigma ]\), acting as \(\mathcal {F}_{\mathrm {OT}}\) obtain values \(\{c_0^\ell , c_1^\ell \}\) and return answers from \(\{u_0^\ell , u_1^\ell , u_2^\ell \}\) exactly as in the protocol.
-
– If there exists \(\ell \in [\sigma ]\) such that \(c_0^\ell = c_1^\ell = 0\), then set \(J = \{1\}\) and send J to the trusted party and receive back \((x_0,x_1)\). Now set \(\varDelta _0' = x_0 {\oplus }{\bigoplus }_\ell u_0^\ell \) and \(\varDelta _1' = x_1 {\oplus }\varDelta ' {\oplus }{\bigoplus }_\ell u_0^\ell \). Pick random \(\varDelta _\phi '\) and random \(h' \leftarrow \{0,1\}^\lambda \). Finally, send \(\varDelta _0',\varDelta _1',\varDelta _\phi ',h'\) to R.
-
– Else if for all \(\ell \in [\sigma ]\), it holds that \(c_0^\ell \ne c_1^\ell \), then for each \(\ell \in [\sigma ]\) compute \(b_\ell '\) such that \(c_{b_\ell '}^\ell = 0\). Extract \(b' = {\bigoplus }_\ell b_\ell '\). Set \(J = \emptyset \), send \((J,b=b')\) to the trusted party and receive back \(x_b\). If \(b = 0\), set \(\varDelta _0' = x_0 {\oplus }{\bigoplus }_\ell u_0^\ell \). Else if \(b= 1\), set \(\varDelta _1' = x_1 {\oplus }\varDelta ' {\oplus }{\bigoplus }_\ell u_0^\ell \). Pick random \(\varDelta _{1-b}', \varDelta _\phi ' \leftarrow \{0,1\}^\lambda \), and set \(h' = H(\varDelta _\phi {\oplus }{\bigoplus }_\ell u_2^\ell )\). Finally, send \(\varDelta _0',\varDelta _1',\varDelta _\phi ',h'\) to R.
-
– Else set \(J = \emptyset \) and choose random \(b' \leftarrow \{0,1\}\) and send \((J, b = b')\) to the trusted party. Receive back \(x_b\). If \(b = 0\), set \(\varDelta _0' = x_0 {\oplus }{\bigoplus }_\ell u_0^\ell \). Else if \(b= 1\), set \(\varDelta _1' = x_1 {\oplus }\varDelta ' {\oplus }{\bigoplus }_\ell u_0^\ell \). Pick random \(\varDelta _{1-b}', \varDelta _\phi '\leftarrow \{0,1\}^\lambda \), and set \(h' = H(\varDelta _\phi {\oplus }{\bigoplus }_\ell u_2^\ell )\). Finally, send \(\varDelta _0',\varDelta _1',\varDelta _\phi ',h'\) to R.
-
– In the reveal phase, if R sends \((J',\varPsi ',\varPhi ')\) such that \(J' \ne J\) or the values \(\varPsi ',\varPhi '\) are not consistent with the values above, then abort the reveal phase. Else, send “reveal” to the trusted party.
It is easy to see that the above simulation is indistinguishable from the real execution. Indeed if there exists any \(\ell \) such that \(c_0^\ell = c_1^\ell = 0\), then in this case corrupt R learns \(\varDelta \) but does not obtain \(u_2^\ell \). Therefore, in this case it misses at least one additive share of \(\phi \) and since \(h = H(\phi )\) does not reveal information (unless H is queried on \(\phi \)), \(\phi \) is statistically hidden from corrupt R. Thus, this case corresponds to \(J \ne \emptyset \) since R could potentially know both \(x_0\) and \(x_1\) (since it knows \(\varDelta \) and potentially at least one of \(u_0^\ell , u_1^\ell \) for each \(\ell \in [\sigma ]\)) but not \(\phi \). On the other hand, if for all \(\ell \in [\sigma ]\) it holds that \(c_0^\ell \ne c_1^\ell \) then it is easy to see that the extracted input \(b'\) equals R’s input \(b_1\) and that the rest of the simulation is indistinguishable from the real execution. Finally the remaining case (i.e., there exists \(\ell \in [\sigma ]\) such that \(c_0^\ell = c_1^\ell = 1\) and there does not exist \(\ell ' \in [\sigma ]\) such that \(c_0^{\ell '} = c_1^{\ell '} = 0\)) is when R obtains only \(\phi \) and neither \(x_0\) nor \(x_1\). This case is rather straightforward to handle; the simulator supplies \(J = \emptyset \) (since R knows \(\phi \)) and a random choice bit \(b'\). This works because there exists some \(\ell \in [\sigma ]\) such that R neither obtains \(u_0^\ell \) nor \(u_1^\ell \). As a result both \(x_0\) and \(x_1\) are information-theoretically hidden from it.
Privacy Against Corrupt Sender. Note that except in the reveal phase, information flows only from S to R. If S is honest, then reveals made by R do not leak any information. (Recall J is revealed to S in the real as well as the ideal execution.) We have to show that even a corrupt S does not learn any information about \(b_1\). Clearly when \(J\ne \emptyset \), R’s actions are independent of its input \(b_1\) and thus does not leak any information. On the other hand when \(J = \emptyset \), observe that R does not reveal \(\tilde{x}_{b_1}\), and thus S only learns whether \(\varPsi = \varPhi = \emptyset \) or not. This translates to learning information about R’s input \(b_1\) only if for some (possibly many) \(\ell \in [\sigma ]\), S provided \((u_0^\ell , u_2^\ell )\) in one instance of \(\mathcal {F}_{\mathrm {OT}}\) and \((u_1^\ell , \hat{u}_2^\ell )\) in the other instance with \(u_2^\ell \ne \hat{u}_2^\ell \). This is because such a strategy would allow S to learn whether R input \(c_0^\ell = 1\) (in which case R does not abort) or \(c_1^\ell = 1\) (in which case R does abort), and consequently leak information about \(b_\ell '\) (i.e., depending on which of \(c_0^\ell , c_1^\ell \) was 0 when \(J = \emptyset \)). More generally, such a strategy allows S to learn any disjunctive predicate of R’s selections \(\{c_0^\ell , c_1^\ell \}_\ell \). To prove that such a strategy does not help S we use the following easy lemma.
Lemma 1
([13]). Let \(\mathsf {En}' : \{0,1\}^m \rightarrow \{0,1\}^{m'}\) be such that for any \(\mathbf {b} \in \{0,1\}^m\), it holds that \(\mathsf {En}'(\mathbf {b})\) is a \(\kappa \)-wise independent encoding of \(\mathbf {b}\). Then for every disjunctive predicate \(P(\cdot )\) the following holds: (1) If P involves at most \(\kappa \) literals, then \(\mathrm {Pr}[P(\mathsf {En}'(\mathbf {b})) = 1]\) is completely independent of \(\mathbf {b}\). (2) Otherwise, \(\mathrm {Pr}[P(\mathsf {En}'(\mathbf {b})) = 1 ]\ge 1-2^{-\kappa }\).
To apply the lemma in our context, note that \(\mathsf {En}'\) here corresponds to the “XOR-tree encoding”, i.e.,. encoding of \(b_1\) into \(\{b_\ell '\}_\ell \). Clearly, \(\mathsf {En}'\) is a \(\kappa = (\sigma -1)\)-wise independent encoding of \(b_1\). Thus we have that if S supplied inconsistent values (i.e., \(u_2^\ell , \hat{u}_2^\ell \)) in at most \((\sigma -1)\) instances, then the S does not learn any information about \(b_1\) in the reveal phase. Further, even if S supplied inconsistent values in all instances, then with all but negligible probability (exponentially negligible in \(\sigma \)) R will abort in the reveal phase (irrespective of R’s true input \(b_1\)). This concludes the proof of privacy against corrupt sender.

Next, we consider the case of single-choice CCOT, where S holds \((x_{1,0},x_{1,1}),\ldots ,(x_{n,0},x_{n,1})\) and R holds \(J \in [n]\) and a single choice bit \(b_1\). At the end of the protocol, R receives \(\{ (x_{j,0}, x_{j,1} )\}_{j \in J}\) and \(\{ x_{j,b_1} \}_{j \not \in J}\). That is, this is exactly the same as CCOT except we enforce that R inputs the same choice across all n pairs of strings held by S. Our protocol in Fig. 5 enforces this using a symmetric-key encryption scheme denoted \((\mathsf {Enc},\mathsf {Dec})\).
We prove that the protocol in Fig. 5 securely realizes single-choice CCOT with sender-simulatability and receiver-privacy. We start by observing that correctness follows from inspection of the protocol.
Simulating Corrupt Receiver. The simulation is quite similar to the simulation of CCOT construction presented in Fig. 4. Obviously the main difference now is that R may attempt to use different \(b_\ell '\) values for \(j, j' \in [n]\) (where \(b_\ell '\) is defined as the value R inputs to \(\mathcal {F}_{\mathrm {OT}}\) in Step 3). However the key observation is that it receives only one key \(K_{\ell , b_\ell '}\) in \(\{K_{\ell ,0}, K_{\ell ,1}\}\). Therefore, even if it attempts to deviate and and obtain \(e_{j',b_\ell ''}^\ell \) for \(b_\ell '' \ne b_\ell '\), it still cannot decrypt since it does not possess the secret key \(K_{\ell ,b_\ell ''}\). Semantic security of the encryption allows us to argue that if such a deviation happens then the value of \(\phi _{j'}\) is hidden from S. Therefore in this case, the simulator can simply add \(j' \) to J, and the simulation can be completed. It is instructive to note that when such a deviation happens, R will be neither be able to provide \(\{x_{j',0}, x_{j',1}\}\) nor the value \(\phi _{j'}\), and thus will get rejected by S during the reveal phase.
We proceed to the formal simulation. Assume that H is modeled as a (non-programmable) random oracle. Acting as \(\mathcal {F}_{\mathrm {OT}}\) the simulator does the following:
-
– Chooses random \(\{\varDelta _j'\}_{j\in [n]},\{ K_{\ell ,0}, K_{\ell ,1} \}_{\ell \in [\sigma ]}, \{u_{j,0}^\ell , u_{j,2}^\ell \}_{j \in [n], \ell \in [\sigma ]}\) and sets for all \(j \in [n], \ell \in [\sigma ]\), value \(u_{j,1}^\ell = u_{j,0}^\ell {\oplus }\varDelta _j'\).
-
– For each \(\ell \in [\sigma ]\), acting as \(\mathcal {F}_{\mathrm {OT}}\) obtain values \(b_\ell '\), return key \(K_{\ell ,b_\ell '}\), and set \(e_{j,b_\ell '}^\ell = \mathsf {Enc}(K_{\ell ,b_\ell '},u_{j,2}^\ell )\), \(e^\ell _{j, 1-b_\ell '} = \mathsf {Enc}(K_{\ell ,1-b_\ell '},\mathbf {0})\). Compute \(b' = {\bigoplus }_\ell b_\ell '\).
-
– For each \(j \in [n], \ell \in [\sigma ]\), acting as \(\mathcal {F}_{\mathrm {OT}}\) obtain values \(\{c_{j,0}^\ell , c_{j,1}^\ell \}\) and return answers using values \(u_{j,0}^\ell , u_{j,1}^\ell , e_{j,b_\ell '}^\ell , e^\ell _{j, 1-b_\ell '}\) (computed as above) exactly as in the protocol.
-
– Initialize \(J = \emptyset \). For each \(j \in [n]\): If there exists \(\ell \in [\sigma ]\) such that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), then add j to J.
-
– Initialize \(\mathsf {flag}= 0\). For each \(j \not \in J\): If there exists \(\ell \in [\sigma ]\) such that either \(c_{j,b_\ell '}^\ell = 0 \) or \(c_{j,1-b_\ell '}^\ell = 1\) do not hold, then add j to J and set \(\mathsf {flag}= 1\).
-
– Send \((J, b')\) to the trusted-party and receive \(\{x_{j,0}, x_{j,1}\}_{j \in J}\) and \(\{x_{j,b'}\}_{j \not \in J}\).
-
– For each \(j \in J\), do: (1) set \(\varDelta _{j,0}' = x_{j,0} {\oplus }{\bigoplus }_\ell u_{j,0}^\ell \) and \(\varDelta _{j,1}' = x_{j,1} {\oplus }\varDelta ' {\oplus }{\bigoplus }_\ell u_{j,0}^\ell \), and (2) pick random \(\varDelta _{j,\phi }'\) and random \(h_j' \leftarrow \{0,1\}^\lambda \).
-
– For each \(j \not \in J\), do: (1) if \(b' = 0\), set \(\varDelta _{j,0}' = x_{j,0} {\oplus }{\bigoplus }_\ell u_0^\ell \), (2) else if \(b' = 1\), set \(\varDelta _{j,1}' = x_{j,1} {\oplus }\varDelta _j' {\oplus }{\bigoplus }_\ell u_0^\ell \), and (3) pick random \(\varDelta _{j,1-b'}', \varDelta _{j,\phi }' \leftarrow \{0,1\}^\lambda \), and set \(h_j' = H(\varDelta _{j,\phi }' {\oplus }{\bigoplus }_\ell u_{j,2}^\ell )\).
-
– Send \(\{\varDelta _{j,0}',\varDelta _{j,1}',\varDelta _{j,\phi }',h_j'\}_{j \in [n]}\) to R.
-
– In the reveal phase, if \(\mathsf {flag}= 1\) or if R sends \((J',\varPsi ',\varPhi ')\) such that \(J' \ne J\) or the values \(\varPsi ', \varPhi '\) are not consistent with the values above, then abort the reveal phase. Else, send “reveal” to the trusted party.
We show that the simulation is indistinguishable from the real execution. First, note that if for some \(j \in [n], \ell \in [\sigma ]\), it holds that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), then R receives both \(u_{j,0}^\ell \) and \(u_{j,1}^\ell \), and therefore knows \(\varDelta _j\). In this case, it is safe to presume that R will end up knowing both \(x_{j,0}\) as well as \(x_{j,1}\) (since for any \(\ell '\), if it receives even one of \(u_{j,0}^{\ell '}, u_{j,1}^{\ell '}\) it will know the other as well since it knows \(\varDelta _j\)). Therefore, \(\mathcal {S}\) includes j in J and obtains both \(x_{j,0}, x_{j,1}\) from the trusted party. Now \(\mathcal {S}\) can carry out the simulation whether or not R obtained both \(x_{j,0}\) and \(x_{j,1}\).
Next, suppose that for some \(j \in [n]\) such that for no \(\ell \in [\sigma ]\), it holds that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), and yet there exists some \(\ell \in [\sigma ]\) such that either \(c_{j,b_\ell '}^\ell = 0\) or \(c_{j,1-b_\ell '}^\ell = 1\) does not hold. In this case, it is easy to see that R will not be able to produce both \(x_{j,0}, x_{j,1}\) (since it is missing one of \(u_{j,0}^\ell , u_{j,1}^\ell \)) in the real execution. Further, it can be shown that except with negligible probability R cannot produce \(\phi _j\) either. This is because (1) R does not obtain \(e_{j, b_\ell '}^\ell \), and (2) R has no information about the plaintext encrypted as \(e_{j,1-b_\ell '}^\ell \), and (3) \(h_j = H(\phi _j)\) does not reveal any information about \(\phi _j\) except with statistically negligible probability (i.e., unless H is queried on \(\phi _j\)). Point (2) above trivially holds in the simulation because \(e_{j,1-b_\ell '}^\ell \) encrypts \(\mathbf {0}\) instead of \(u_{j,2}^\ell \). On the other hand, in the real execution, observe that R does not possess the key \(K_{\ell , 1-b_\ell '}\). It follows from a straightforward reduction to the semantic security of the encryption scheme that the real execution is indistinguishable from the simulation. In particular, in this case R will not be able to produce \((J',\varPsi ',\varPhi ')\) that will be accepted by S in the real execution, and is equivalent to \(\mathcal {S}\) sending abort in the ideal execution.
Finally, suppose that for every \(j \in [n]\), either (1) for all \(\ell \in [\sigma ]\) it holds that \(c_{j,0}^\ell = c_{j,1}^\ell = 1\), or (2) for all \(\ell \in [\sigma ]\) it holds that \(c_{j,b_\ell '}^\ell = 0\) and \(c_{j,1-b_\ell '}^\ell = 1\). This indeed corresponds to honest behavior on the part of R. Specifically, in case (1), we have \(j \in J\), and in case (2), we have \(j \not \in J\). This is exactly how the simulator constructs J. It remains to be shown that in this case, any reveal \((J',\varPsi ',\varPhi ')\) such that \(J' \ne J\) or \(\varPsi ',\varPhi '\) is not consistent with the simulation will be rejected by S in the real execution. This follows from: (a) Any \(j \in J\) cannot be claimed by R to not be in the checkset. This is because in this case, R does not have any information about \(\phi _j\) (other than \(H(\phi _j)\) which leaks no information unless H is queried on \(\phi _j\)). (b) Any \(j \not \in J\) cannot be claimed by R to be in the checkset. This is because in this case, R obtains exactly one of \(\{ u_{j,0}^\ell , u_{j,1}^\ell \}\) for every \(\ell \in [\sigma ]\) and thus is able to reconstruct at most one of \(\{ x_{j,0}, x_{j,1} \}\). This concludes the proof of security against corrupt receiver.
Privacy Against Corrupt Sender. The proof of privacy against corrupt sender is very similar to the corresponding proof for (the basic) CCOT. Specifically, note that except in the reveal phase, information flows only from S to R. Next note that if S is honest, then the reveals made by R in the reveal phase do not leak any information about R’s input \(b_1\). (Recall J is revealed to S in the real as well as the ideal execution.) It remains to be shown that even a corrupt S does not learn any information about \(b_1\). Clearly for \(j \in J\), R’s actions are independent of its input \(b_1\) and thus does not leak any information. On the other hand for \(j \not \in J\), observe that R does not reveal \(\tilde{x}_{j,b_1}\) (i.e., in the reveal phase), and thus the only information learnt by S is whether \(\varPsi = \varPhi = \emptyset \) or not. This translates to learning information about R’s input \(b_1\) only if for some (possibly many) \(j \in [n] , \ell \in [\sigma ]\), S provided \((u_{j,0}^\ell , u_{j,2}^\ell )\) in one instance of \(\mathcal {F}_{\mathrm {OT}}\) and \((u_{j,1}^\ell , \hat{u}_{j,2}^\ell )\) in the other instance with \(u_{j,2}^\ell \ne \hat{u}_{j,2}^\ell \). This is because such a strategy would allow S to learn whether R input \(c_{j,0}^\ell = 1\) (in which case R does not abort) or \(c_{j,1}^\ell = 1\) (in which case R does abort), and consequently leak information about \(b_{\ell }'\) (i.e., depending on which of \(c_{j,0}^\ell , c_{j,1}^\ell \) was 0 when \(j \not \in J\)). More generally, such a strategy allows S to learn any disjunctive predicate of R’s selections \(\{c_{j,0}^\ell , c_{j,1}^\ell \}_\ell \).
To prove that such a strategy does not help S we once again make use of Lemma 1. As before, to apply the lemma in our context, note that \(\mathsf {En}'\) here corresponds to the “XOR-tree encoding”, i.e.,. encoding of \(b_1\) into \(\{b_\ell '\}_\ell \). Clearly, \(\mathsf {En}'\) is a \(\kappa = (\sigma -1)\)-wise independent encoding of \(b_1\). Thus we have that if S supplied inconsistent values (i.e., \(u_2^\ell , \hat{u}_2^\ell \)) in at most \((\sigma -1)\) instances, then S does not learn any information about \(b_1\) in the reveal phase. Further, even if S supplied inconsistent values in all instances, then with all but negligible probability (exponentially negligible in \(\sigma \)) R will abort in the reveal phase (irrespective of R’s true input \(b_1\)). This concludes the proof of privacy against corrupt sender.

This functionality, which has actually been used directly in 2PC constructions of [24] is our next stepping stone. (The description can be obtained by modifying \(\mathcal {F}^\star _{\mathrm {mcot}}\) Fig. 2 by setting \(t=1\), setting \(|J| = n/2\) and setting all \(\phi _j^k\) values to \(0^\sigma \).) The construction of this primitive follows easily merely by repeating the single-choice CCOT protocol batch-wise in parallel. That is, in the m-th (parallel) execution, S and R participate in a single-choice CCOT where S holds \((x_{1,0}^{(i)},x_{1,1}^{(i)}),\ldots ,(x_{n,0}^{(i)},x_{n,1}^{(i)})\) while R holds \(J \subseteq [n]\) and \(b_i\). Obviously the main difficulty is in enforcing that R supplies the same check set J in each execution. However, this is easily enforceable in the following way. Recall that in the reveal phase of each execution of single-choice CCOT (which are now executed in parallel), R will have to reveal \((E_i,\varPsi _i, \varPhi _i)\). In addition to checking whether these values are consistent with its inputs and check value, S additionally checks if \(E_i = E_{i'}\) for every \(i,i' \in [m]\).
Using more efficient “XOR-tree” encoding schemes. Observe that the construction for batch single-choice CCOT described above incurs a multiplicative overhead of (exactly) \(\sigma \) simply because the underlying single-choice CCOT protocol makes use of the basic XOR-tree encoding scheme. Fortunately, the batch setting makes it possible to apply more sophisticated encodings whose overhead is much lower. More concretely, using encoding schemes based on random combinations approach [23], the overhead can be as low as an additional \(\le 6 \cdot \max (4m,8\sigma )\) while using encoding schemes based on \(\sigma \)-wise independent generators [13] one can obtain rate-1/6 communication complexity (and likely to be practical when \(m \gg \sigma \)). We show constructions of batch single-choice CCOT using abstract encoding schemes.
We describe a protocol for \(\mathcal {F}^{\mathrm {bat,sin}}_{\mathrm {ccot}}\) in the \(\mathcal {F}_{\mathrm {OT}}\)-hybrid model that makes use of an arbitrary XOR-tree encoding scheme in Fig. 6. The protocol itself is a straightforward extension combining ideas from protocols in Figs. 4 and 5 while abstracting away the underlying encoding scheme. We now prove that the protocol \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) described in Fig. 6 realizes batch single-choice CCOT with sender-simulatability and receiver-privacy. We start by observing that correctness follows from correctness properties of the XOR-tree encoding schemes (specifically, Property 3).
Simulating Corrupt Receiver. The simulation is quite similar to the simulation of single-choice CCOT construction presented in Fig. 5. Obviously the main difference now is that we need to deal with encodings over R’s entire input. We proceed to the formal simulation. Assume that H is modeled as a (non-programmable) random oracle. \(\mathcal {S}\) first receives public randomness \(\omega _0\) for the XOR-tree encoding scheme \((\mathsf {En},\mathsf {De},\mathsf {En}',\mathsf {De}')\). Acting as \(\mathcal {F}_{\mathrm {OT}}\) the simulator does the following:
-
– Samples for each \(j \in [n]\), uniform \(\{ ( \hat{x}_{j,0}^{(i)}, \hat{x}_{j,1}^{(i)} ) \}_{i \in [m]}\), uniformly random \(\omega _j\) and computes \(\{ ( u_{j,0}^\ell , u_{j,1}^\ell ) \}_{\ell \in [m']} \leftarrow \mathsf {En}_{\omega _0}(\{ (\hat{x}_{j,0}^{(i)}, \hat{x}_{j,1}^{(i)} ) \}_{i\in [m]}; \omega _j)\).
-
– Chooses random \(\{ ( K_{\ell ,0}, K_{\ell ,1} ) \}_{\ell \in [m']}, \{ u_{j,2}^\ell \}_{j \in [n] , \ell \in [m']}\).
-
– For each \(\ell \in [m']\), acting as \(\mathcal {F}_{\mathrm {OT}}\) obtain values \(b_\ell '\), return key \(K_{\ell ,b_\ell '}\), and set \(e_{j,b_\ell '}^\ell = \mathsf {Enc}(K_{\ell ,b_\ell '},u_{j,2}^\ell )\), \(e^\ell _{j, 1-b_\ell '} = \mathsf {Enc}(K_{\ell ,1-b_\ell '},\mathbf {0})\). Compute \((b_1,\ldots ,b_m) = \mathsf {De}'( \{b_\ell ' \}_{\ell \in [m']})\).
-
– For each \(j \in [n], \ell \in [m']\), acting as \(\mathcal {F}_{\mathrm {OT}}\) obtain values \(\{c_{j,0}^\ell , c_{j,1}^\ell \}\) and return answers using values \(u_{j,0}^\ell , u_{j,1}^\ell , e_{j,b_\ell '}^\ell , e^\ell _{j, 1-b_\ell '}\) (computed as above) exactly as in the protocol.
-
– Initialize \(J = \emptyset \). For each \(j \in [n]\): If there exists \(\ell \in [m']\) such that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), then add j to J.
-
– Initialize \(\mathsf {flag}= 0\). For each \(j \not \in J\): If there exists \(\ell \in [m']\) such that either \(c_{j,b_\ell '}^\ell = 0 \) or \(c_{j,1-b_\ell '}^\ell = 1\) do not hold, then add j to J and set \(\mathsf {flag}= 1\).
-
– Send \((J, \{b_i\}_{i\in [m]})\) to the trusted party and receive back \(\{ ( x_{j,0}^{(i)}, x_{j,1}^{(i)} ) \}_{i \in [m], j \in J}\) and \(\{x_{j,b_i}^{(i)}\}_{ i \in [m], j \not \in J}\).
-
– For each \(j \in J\), do: (1) for each \(i \in [m]\), set
 and
and  , and (2) pick random \(\varDelta _{j,\phi }'\) and random \(h_j' \leftarrow \{0,1\}^\lambda \).
, and (2) pick random \(\varDelta _{j,\phi }'\) and random \(h_j' \leftarrow \{0,1\}^\lambda \). -
– For each \(j \not \in J\), do: (1) for each \(i \in [m]\): set
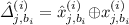 and pick random
and pick random  , and (2) pick random \( \varDelta _{j,\phi }' \leftarrow \{0,1\}^\lambda \), and set \(h_j' = H(\varDelta _{j,\phi }' {\oplus }{\bigoplus }_\ell u_{j,2}^\ell )\).
, and (2) pick random \( \varDelta _{j,\phi }' \leftarrow \{0,1\}^\lambda \), and set \(h_j' = H(\varDelta _{j,\phi }' {\oplus }{\bigoplus }_\ell u_{j,2}^\ell )\). -
– For each \(j \in [n]\): send
 to R.
to R. -
– In the reveal phase, if \(\mathsf {flag}= 1\) or if R sends \((J',\varPsi ',\varPhi ')\) such that \(J' \ne J\) or the values \(\varPsi ', \varPhi '\) are not consistent with the values above, then abort the reveal phase. Else, send “reveal” to the trusted party.
We show that the simulation is indistinguishable from the real execution. First, note that if for some \(j \in [n], \ell \in [m']\), it holds that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), then R receives both \(u_{j,0}^\ell \) and \(u_{j,1}^\ell \), but does not obtain \(u_{j,2}^\ell \). In this case, it is safe to presume that R will end up knowing both \(x_{j,0}^{(i)}\) as well as \(x_{j,1}^{(i)}\) but R definitely misses an additive share of (and consequently has no information about) \(\phi _j\). Therefore, \(\mathcal {S}\) includes j in J and obtains both \(x_{j,0}^{(i)}, x_{j,1}^{(i)}\) from the trusted party. This allows \(\mathcal {S}\) to carry out a correct simulation irrespective of whether or not R obtained both \(x_{j,0}^{(i)}\) and \(x_{j,1}^{(i)}\).
Next, suppose that for some \(j \in [n]\) such that for no \(\ell \in [m']\) it holds that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), and yet there exists some \(\ell \in [m']\) such that either \(c_{j,b_\ell '}^\ell = 0\) or \(c_{j,1-b_\ell '}^\ell = 1\) does not hold. In this case, we claim that R will not be able to produce both \(x_{j,0}^{(i)}, x_{j,1}^{(i)}\) in the real execution. This follows from the properties of the XOR-tree encoding schemes and the fact that R misses one of \(u_{j,0}^\ell , u_{j,1}^\ell \). Further, it can be shown that except with negligible probability R cannot produce \(\phi _j\) either. This is because (1) R does not obtain \(e_{j, b_\ell '}^\ell \), and (2) R has no information about the plaintext encrypted as \(e_{j,1-b_\ell '}^\ell \), and (3) \(h_j = H(\phi _j)\) does not reveal any information about \(\phi _j\) with statistically negligible probability (i.e., unless H is queried on \(\phi _j\)). Point (2) mentioned above trivially holds in the simulation because \(e_{j,1-b_\ell '}^\ell \) encrypts \(\mathbf {0}\) instead of \(u_{j,2}^\ell \). On the other hand, in the real execution, observe that R does not possess the key \(K_{\ell , 1-b_\ell '}\). It then follows from a straightforward reduction to the semantic security of the encryption scheme that the real execution is indistinguishable from the simulation. In particular, in this case R will not be able to produce \((J',\varPsi ',\varPhi ')\) that will be accepted by S in the real execution, and is equivalent to \(\mathcal {S}\) sending abort in the ideal execution.
Finally, suppose that for every \(j \in [n]\), either (1) for all \(\ell \in [m']\) it holds that \(c_{j,0}^\ell = c_{j,1}^\ell = 0\), or (2) for all \(\ell \in [m']\) it holds that \(c_{j,b_\ell '}^\ell = 0\) and \(c_{j,1-b_\ell '}^\ell = 1\). This indeed corresponds to honest behavior on the part of R. Specifically, in case (1), we have \(j \in J\), and in case (2), we have \(j \not \in J\). This is exactly how the simulator constructs J. It remains to be shown that in this case, any reveal \((J',\varPsi ',\varPhi ')\) such that \(J' \ne J\) or \(\varPsi ',\varPhi '\) is not consistent with the simulation will be rejected by S in the real execution. This follows from: (a) Any \(j \in J\) cannot be claimed by R to not be in the checkset. This is because in this case, R does not have any information about \(\phi _j\) (other than \(H(\phi _j)\) which leaks no information unless H is queried on \(\phi _j\)). (b) Any \(j \not \in J\) cannot be claimed by R to be in the checkset. This is because in this case, R obtains exactly one of \(\{ u_{j,0}^\ell , u_{j,1}^\ell \}\) for every \(\ell \in [m']\) and thus by Property 7 of XOR-tree encoding schemes, is able to reconstruct at most one of \(\{ x_{j,0}^{(i)}, x_{j,1}^{(i)} \}\).
Privacy Against Corrupt Sender. The proof of privacy against corrupt sender is very similar to the corresponding proof for (the basic) CCOT. Specifically, note that except in the reveal phase, information flows only from S to R. Next note that if S is honest, then the reveals made by R in the reveal phase do not leak any information about R’s input \(b_1,\ldots ,b_m\). (Recall J is revealed to S in the real as well as the ideal execution.) It remains to be shown that even a corrupt S does not learn any information about \(b_1,\ldots ,b_m\). Clearly for \(j \in J\), R’s actions are independent of its inputs \(b_1,\ldots ,b_m\) and thus does not leak any information. On the other hand for \(j \not \in J\), observe that R does not reveal any information about \(\{ \tilde{x}_{j,b_i}^{(i)} \}_{i \in [m]}\) (i.e., in the reveal phase), and thus the only information learnt by S is whether \(\varPsi = \varPhi = \emptyset \) or not. This translates to learning information about R’s inputs \(b_1,\ldots ,b_m\) only if for some (possibly many) \(j \in [n] , \ell \in [\sigma ]\), S provided \((u_{j,0}^\ell , u_{j,2}^\ell )\) in one instance of \(\mathcal {F}_{\mathrm {OT}}\) and \((u_{j,1}^\ell , \hat{u}_{j,2}^\ell )\) in the other instance with \(u_{j,2}^\ell \ne \hat{u}_{j,2}^\ell \). This is because such a strategy would allow S to learn whether R input \(c_{j,0}^\ell = 1\) (in which case R does not abort) or \(c_{j,1}^\ell = 1\) (in which case R does abort), and consequently leak information about \(b_{\ell }'\) (i.e., depending on which of \(c_{j,0}^\ell , c_{j,1}^\ell \) was 0 when \(j \not \in J\)). More generally, such a strategy allows S to learn any disjunctive predicate of R’s selections \(\{c_{j,0}^\ell , c_{j,1}^\ell \}_\ell \).
To prove that such a strategy does not help S we make use of Property 6 of XOR-tree encoding schemes. Thus we have that if S supplied inconsistent values (i.e., \(u_2^\ell , \hat{u}_2^\ell \)) in at most \((\sigma -1)\) instances, then S does not learn any information about \(b_1,\ldots ,b_m\) in the reveal phase. Further, even if S supplied inconsistent values in all instances, then with all but negligible probability (exponentially negligible in \(\sigma \)) R will abort in the reveal phase (irrespective of R’s true input \(b_1,\ldots ,b_m\)). This concludes the proof of privacy against corrupt sender.
It is easy to see that our construction of batch single-choice CCOT described above is also a realization of modified batch single-choice CCOT.

Note that now R has several evaluation sets \(E_1, \ldots , E_t\) (corresponding to t executions). To realize \(\mathcal {F}_{\mathrm {mcot}}^+\), we will rely on the protocol \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) designed for realizing \(\mathcal {F}^{\mathrm {bat,sin}}_{\mathrm {ccot}}\) presented previously. Indeed as in the protocol designed in [10] we will run \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) t times to obtain a protocol for \(\mathcal {F}_{\mathrm {mcot}}^+\). Our protocol for \(\mathcal {F}_{\mathrm {mcot}}^+\) is described in Fig. 7. Unlike protocols for other variants of CCOT, here we improve over prior work by using the reactive functionality relaxation (as opposed to receiver-privacy relaxation) to obtain a simpler protocol secure against corrupt receiver. Prior work [10] required an overhead of \(t^2\) while our protocol requires only a factor t overhead. We prove that the protocol in Fig. 7 securely realizes multistage CCOT with sender-simulatability and receiver-privacy. We start by observing that correctness follows from correctness of each instance of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\).
Simulating Corrupt Receiver. Using the simulator of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\), the simulator \(\mathcal {S}\) first extracts for all \(k\in [t]\), the check sets \([n]\setminus E_k'\) and the selection bits \(b_{k,1},\ldots ,b_{k,m}\). Note that a malicious R may supply sets \(E_1',\ldots , E_t'\) that may overlap. The simulation extraction for \(\mathcal {F}^\star _{\mathrm {mcot}}\) first initializes each of \(E_1,\ldots ,E_t\) to \(\emptyset \), \(\mathsf {flag}\) to 0 (\(\mathsf {flag}=1\) indicates whether \(\mathcal {S}\) will choose to abort in the reveal phase), and proceeds as follows
-
For every \(j \in [n]\) such that there exists unique \(\alpha \in [t]\) such that \(j \in E_\alpha '\), then add j to \(E_\alpha \).
-
For every \(j \in [n]\) such that there exists \(\alpha ,\beta \in [t]\) such that \(j \in E_\alpha ' \cap E_\beta '\), then add j to J and set \(\mathsf {flag}= 1\).
It is easy to see that \(E_1,\ldots , E_t\) are disjoint sets. The simulator then sends \(E_1,\ldots ,E_t\) (as obtained above), and the values \(\{b_{k,i}\}_{k\in [t], i\in [m]}\) (as obtained from the t invocations of the simulator of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\)) to the ideal functionality \(\mathcal {F}_{\mathrm {mcot}}^+\). Then upon receiving R’s output from \(\mathcal {F}_{\mathrm {mcot}}^+\), \(\mathcal {S}\) additively secret shares each values in R’s output to obtain t additive shares of each value, and then feeds the k-th share of each value to the k-th copy of the invoked simulator for \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\). Then the simulator uses the k-th copy of the invoked simulator for \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) to complete the simulation of each of the t parallel instances of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\). Then in the reveal phase, the simulator sends abort to \(\mathcal {F}_{\mathrm {mcot}}^+\) if \(\mathsf {flag}= 1\). On the other hand if \(\mathsf {flag}= 0\), then the simulator receives \((E_1'',\ldots ,E_t'', \varPsi , \varPhi )\) from R. If \(E_1'',\ldots ,E_t''\) are pairwise nonintersecting, and further for every \(k\in [t]\) it holds that \(E_k = E_k''\), then \(\mathcal {S}\) sends reveal to \(\mathcal {F}_{\mathrm {mcot}}^+\), else sends abort. This completes the description of the simulation. To see why the above simulation works, first note that each of the t copies of the invoked simulator for \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) (each of which independently guarantee correct simulation of a single instance of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\)) are run on random \((t-1)\)-wise independent values. Since \(\mathcal {S}\) generates these \((t-1)\)-wise independent values correctly using the output received from \(\mathcal {F}_{\mathrm {mcot}}^+\), it follows that the t copies of the invoked simulator for \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) taken together also guarantee correct simulation of the protocol realizing \(\mathcal {F}_{\mathrm {mcot}}^+\). In particular, at the end of the output phase, the view of the adversary in real protocol is indistinguishable from that in the simulation. It then remains to be shown that (except with statistically negligible probability) a corrupt R will not be able to reveal \((E_1'',\ldots ,E_t'',\varPsi ,\varPhi )\) that is accepted by the sender in the real protocol and yet \((E_1'',\ldots ,E_t'') \ne (E_1,\ldots , E_t)\), where \(E_1,\ldots ,E_t\) are the sets constructed by \(\mathcal {S}\) as described above. This follows from observing that for every \(j \in [n]\):
-
– If \(j \in E_\alpha '\) for some unique \(\alpha \in [t]\), then R does not have any information about \(\phi _j^\beta \) for any \(\beta \ne \alpha \). Thus, it can successfully reveal \((E_1'',\ldots , E_t'')\) with \(j \in E_\beta ''\) for \(\beta \ne \alpha \) only with probability negligible in \(\sigma \). More precisely in this case R will not be able to provide \(\varPhi _\beta \) consistent with \((E_1'',\ldots ,E_t'')\). That is if \(j \in E_\alpha '\) for some unique \(\alpha \in [t]\), then for every reveal \((E_1'',\ldots ,E_t'')\) that is accepted by the sender it must hold that \(j \in E_\alpha ''\). Stated differently, if for every \(j \in [n]\), there exists unique \(\alpha \in [t]\) such that \(j \in E_\alpha '\), then R can successfully reveal \((E_1'',\ldots ,E_t'')\) only for \((E_1'',\ldots , E_t'') = (E_1',\ldots , E_t')\). Recall that in this case, the simulator \(\mathcal {S}\) set \(\mathsf {flag}= 0\) and thus will reveal \((E_1,\ldots ,E_t) = (E_1',\ldots ,E_t')\) in the reveal phase. Therefore, in this case it holds that the real protocol is indistinguishable from the ideal simulation.
-
– If \(j \in E_\alpha ' \cap E_\beta '\) for \(\alpha \ne \beta \), then one of \(x_{j,0}^{(i,\beta )},x_{j,1}^{(i,\beta )}\) (alternatively one of \(x_{j,0}^{(i,\alpha )},x_{j,1}^{(i,\alpha )}\)) is information-theoretically hidden from R. Thus, it can successfully reveal \((E_1'',\ldots , E_t'')\) with \(j \in E_\beta ''\) (resp. \(j\in E_\alpha ''\)) only if it guesses the missing value, i.e., with probability negligible in \(\lambda \). More precisely in this case R will not be able to provide \(\varPsi _\beta \) (resp. \(\varPsi _\alpha \)) consistent with \((E_1'',\ldots ,E_t'')\). In other words, if \(j \in E_\alpha ' \cap E_\beta '\) for \(\alpha \ne \beta \), then for every reveal \((E_1'',\ldots ,E_t'')\) that is accepted by the sender it must hold that \(j \not \in \cup _k E_k''\). Indeed, it can be observed that any reveal by R will be rejected by S. In particular, R cannot reveal \(j \not \in \cup _k E_k''\) either, since in this case it will be required to produce both \(x_{j,0}^{(i,k)}, x_{j,1}^{(i,k)}\) for every \(k \in [t]\). As pointed out earlier, R cannot do this except with negligible probability for \(k \in \{\alpha ,\beta \}\). Recall that in this case, the simulator \(\mathcal {S}\) set \(\mathsf {flag}= 1\) and thus will abort in the reveal phase. Therefore, in this case it holds that the real protocol is indistinguishable from the ideal simulation.
Privacy Against Corrupt Sender. First observe that in the output phase of each instance of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) information flows only from the sender to the receiver during the output phase. Thus privacy at the end of the output phase trivially holds, and in particular S has no information about the sets \(E_1,\ldots , E_t\). It remains to be shown that the information revealed by R to S in the reveal phase does not leak any information about R’s input bits \(\mathbf {b}_1,\ldots ,\mathbf {b}_t\). For simplicity, first consider the case when S is honest. In this case, observe that in a given instance of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\), say the k-th instance, R’s reveal message depends on input \(\mathbf {b}_k\) and is independent of \(\{\mathbf {b}_\alpha \}_{\alpha \ne k}\). Privacy then follows from the privacy guaranteed by (each instance of) \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\). On the other hand, when S is corrupt, R’s reveal message in the k-th instance of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) depends on its input \(\mathbf {b}_k\) and whether S’s cheating attempt (if any) was detected in any instance. Privacy follows from the fact that each instance of \(\pi _{\mathrm {ccot}}^{\mathrm {bat,sin}}\) preserves privacy of R’s inputs.
Additional Optimizations. Instead of sending the values \(\varPsi = \{ \tilde{x}_{j,0}, \tilde{x}_{j,1} \}_{j \in J}\) and \(\varPhi = \{ \tilde{\phi }_j \}_{j \not \in J} \), R could send \(( J , H'( \varPsi ), H'' ( \varPhi ) )\) to S, where \(H', H''\) are modeled as collision-resistant hash functions (alternatively, random oracles). Note that these optimizations are applicable in a straightforward way in other constructions we present. We omit detailing them to keep the exposition more clear.
In applications to secure computation, full receiver simulation in CCOT is also not required. We require only privacy, i.e., we do not need to consider the joint distribution of receiver’s view and sender’s inputs. This is because sender’s inputs are just random keys for the garbled circuits, and in the simulation of the 2PC protocol, it is the simulator that will generate these keys. On the other hand, extracting receiver inputs is very crucial in order to enable the simulator to generate correctly faked garbled circuits. However our definitions will require full receiver simulation (including extraction). Fortunately, achieving full receiver simulation comes only with a small multiplicative overhead.
Summary of Efficiency. All our protocols are presented in the \(\mathcal {F}_{\mathrm {OT}}\)-hybrid model and thus can take advantage of OT extension techniques. Further, using standard leveraging techniques (such as ones used in [9]), OT extension of [14], the XOR-tree encoding scheme of [13], and the constructions in Figs. 4, 5, 6, and 7, one can obtain a rate-1/6 construction for \(\mathcal {F}^{\mathrm {bat,sin}}_{\mathrm {ccot}}\) (in the non-programmable RO model) with sender-simulatability and receiver-privacy as in Definition 4. In concrete terms, it is easy to verify that the additional overhead of realizing \(\mathcal {F}^{\mathrm {bat,sin}}_{\mathrm {ccot}}\) is \(\le 6 \cdot \max (4m,8\sigma )\). The efficiency of our CCOT protocol in the single execution setting is comparable to that of XOR-tree encodings of [23], but is clearly better than DDH-based CCOT [22, 24] since we take advantage of OT extension (under the assumption that correlation-robust hash functions exist [12, 14, 29]). Finally, we can realize \(\mathcal {F}_{\mathrm {mcot}}^+\) (in the non-programmable random oracle model) with sender-simulatability and receiver-privacy as in Definition 4 while bearing an overhead at most t over the cost of realizing \(\mathcal {F}^{\mathrm {bat,sin}}_{\mathrm {ccot}}\) where t denotes the number of executions.
References
Aiello, W., Ishai, Y., Reingold, O.: Priced oblivious transfer: how to sell digital goods. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 119–135. Springer, Heidelberg (2001)
Applebaum, B., Ishai, Y., Kushilevitz, E., Waters, B.: Encoding functions with constant online rate or how to compress garbled circuits keys. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 166–184. Springer, Heidelberg (2013)
Bellare, M., Hoang, V.T., Rogaway, P.: Adaptively secure garbling with applications to one-time programs and secure outsourcing. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 134–153. Springer, Heidelberg (2012)
Cachin, C., Micali, S., Stadler, M.A.: Computationally private information retrieval with polylogarithmic communication. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 402–414. Springer, Heidelberg (1999)
David, B.M., Nishimaki, R., Ranellucci, S., Tapp, A.: Generalizing efficient multiparty computation. In: Lehmann, A., Wolf, S. (eds.) Information Theoretic Security. LNCS, vol. 9063, pp. 15–32. Springer, Heidelberg (2015)
Feige, U., Kilian, J., Naor, M.: A minimal model for secure computation (extended abstract). In: STOC, pp. 554–563 (1994)
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B.: Faster maliciously secure two-party computation using the GPU. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 358–379. Springer, Heidelberg (2014)
Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 303–324. Springer, Heidelberg (2005)
Garay, J.A., Ishai, Y., Kumaresan, R., Wee, H.: On the complexity of UC commitments. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 677–694. Springer, Heidelberg (2014)
Huang, Y., Katz, J., Kolesnikov, V., Kumaresan, R., Malozemoff, A.J.: Amortizing garbled circuits. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 458–475. Springer, Heidelberg (2014)
Huang, Y., Katz, J., Evans, D.: Efficient secure two-party computation using symmetric cut-and-choose. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 18–35. Springer, Heidelberg (2013)
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003)
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Prabhakaran, M., Sahai, A.: Efficient non-interactive secure computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 406–425. Springer, Heidelberg (2011)
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008)
Kilian, J.: Founding cryptography on OT. In: STOC, pp. 20–31 (1988)
Kolesnikov, V., Kumaresan, R.: Improved OT extension for transferring short secrets. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 54–70. Springer, Heidelberg (2013)
Kolesnikov, V.: Gate evaluation secret sharing and secure one-round two-party computation. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 136–155. Springer, Heidelberg (2005)
Kolesnikov, V., Schneider, T.: Improved garbled circuit: free XOR gates and applications. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 486–498. Springer, Heidelberg (2008)
Kreuter, B., Shelat, A., Shen, C.: Billion-gate secure computation with malicious adversaries. In: USENIX (2012)
Kushilevitz, E., Ostrovsky, R.: Replication is NOT needed: SINGLE database, computationally-private information retrieval. In: FOCS, pp. 364–373 (1997)
Lindell, Y., Riva, B.: Cut-and-Choose Yao-Based secure computation in the online/offline and batch settings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 476–494. Springer, Heidelberg (2014)
Lindell, Y.: Fast cut-and-choose based protocols for malicious and covert adversaries. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 1–17. Springer, Heidelberg (2013)
Lindell, Y., Pinkas, B.: An efficient protocol for secure two-party computation in the presence of malicious adversaries. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 52–78. Springer, Heidelberg (2007)
Lindell, Y., Pinkas, B.: Secure two-party computation via cut-and-choose oblivious transfer. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 329–346. Springer, Heidelberg (2011)
Lindell, Y., Pinkas, B., Smart, N.P.: Implementing two-party computation efficiently with security against malicious adversaries. In: Ostrovsky, R., De Prisco, R., Visconti, I. (eds.) SCN 2008. LNCS, vol. 5229, pp. 2–20. Springer, Heidelberg (2008)
Mohassel, P., Riva, B.: Garbled circuits checking garbled circuits: more efficient and secure two-party computation. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 36–53. Springer, Heidelberg (2013)
Mossel, E., Shpilka, A., Trevisan, L.: On e-biased generators in NC0. In: FOCS, pp. 136–145 (2003)
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: SODA, pp. 448–457 (2001)
Nielsen, J.B., Nordholt, P.S., Orlandi, C., Burra, S.S.: A new approach to practical active-secure two-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 681–700. Springer, Heidelberg (2012)
Pinkas, B., Schneider, T., Smart, N.P., Williams, S.C.: Secure two-party computation is practical. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 250–267. Springer, Heidelberg (2009)
Shelat, A., Shen, C.: Two-output secure computation with malicious adversaries. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 386–405. Springer, Heidelberg (2011)
Shelat, A., Shen, C.: Fast two-party secure computation with minimal assumptions. In: CCS, pp. 523–534 (2013)
Yao, A.: How to generate and exchange secrets. In: FOCS, pp. 162–167 (1986)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologc Research
About this paper
Cite this paper
Kolesnikov, V., Kumaresan, R. (2015). On Cut-and-Choose Oblivious Transfer and Its Variants. In: Iwata, T., Cheon, J. (eds) Advances in Cryptology -- ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science(), vol 9452. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48797-6_17
Download citation
DOI: https://doi.org/10.1007/978-3-662-48797-6_17
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48796-9
Online ISBN: 978-3-662-48797-6
eBook Packages: Computer ScienceComputer Science (R0)











 and
and  , and (2) pick random
, and (2) pick random 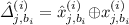 and pick random
and pick random  , and (2) pick random
, and (2) pick random  to R.
to R.