Blind Source Separation from Single Measurements Using Singular Spectrum Analysis

Abstract

Singular Spectrum Analysis (SSA) is a powerful data decomposition/recompose technique that can be used to reduce the noise in time series. Compared to existing solutions aiming at similar purposes, such as frequency-based filtering, it benefits from easier-to-exploit intuitions, applicability in contexts where low sampling rates make standard frequency analyses challenging, and the (theoretical) possibility to separate a signal source from a noisy source even if both run at the same frequency. In this paper, we first describe how to apply SSA in the context of side-channel analysis, and then validate its interest in three different scenarios. Namely, we consider unprotected software, masked software, and unprotected hardware block cipher implementations. Our experiments confirm significant noise reductions in all three cases, leading to success rates improved accordingly. They also put forward the stronger impact of SSA in more challenging scenarios, e.g. masked implementations (because the impact of noise increases exponentially with the number of shares in this case), or noisy hardware implementations (because of the established connection between the amount of noise and the attacks’ success rate in this case). Since noise is a fundamental ingredient for most countermeasures against side-channel attacks, we conclude SSA can be an important element in the toolbox of evaluation laboratories, in order to efficiently preprocess their measurements in a black box manner.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Successful side-channel attacks against embedded cryptographic implementations generally require a multidisciplinary combination of informal steps. First, good measurements of, e.g., the power consumption or electromagnetic radiation of the target devices must be obtained. Second, these measurements are usually sent to a preprocessing phase, in order to facilitate their cryptographic treatment. Third, some modeling is required to extract information from the leakages. Eventually, the information extracted is exploited and turned into, e.g., a key recovery. A look at the literature suggests a wide variety of tools for the last two (modeling and exploitation) steps. They typically include a plethora of (profiled and non-profiled) distinguishers, including but not limited to [4, 9, 17, 39], exploited via simple divide-and-conquer approaches [24], or more elaborate strategies, e.g., collision-based [27] or algebraic [37]. By contrast, the measurement and preprocessing steps are in general less discussed, despite their importance from an engineering point-of-view. Indeed, while quite formal solutions now exist to guarantee that the modeling and exploitation of side-channel leakages are close to optimal [14], the evaluation of measurement setups and preprocessing methods is left with a comparative approach. Namely, we can tell whether one is better than another, but not guarantee that it is good. This situation creates strong incentive to study state-of-the-art methods in this respect, which this paper aims to do in the (limited but relevant) context of preprocessing methods.

State-of-the-Art. An informal classification of some popular preprocessing tools is given in Table 1, based on whether these tools aim at decreasing the noise, increasing the signal, include some feature selection or compress the output.

Table 1. Informal classification of some existing preprocessing methods.

For example, averaging only aims at reducing the noise, and does some implicit feature selection by assuming that the useful part of the measurements is in their means (which is only relevant in the context of unprotected implementations, and would be useless in the context of masked implementations for which the information lies in higher-order moments of the leakage distribution [8]). Detecting Points-of-Interest (POIs) can be viewed as a kind of feature selection that compresses the measurements. Dimensionality reductions such as Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA), introduced to side-channel attacks in [1, 40], and recently revisited in [2, 7, 10, 11], project samples into subspaces that optimize the side-channel signal and Signal-to-Noise Ratio (SNR), respectively. Other “compressive” linear transforms (using other optimization criteria) include [15, 30]. Eventually, filtering typically aims at selecting the frequency band in which side-channel attacks perform best.

Concretely, this latter solution (filtering) is especially interesting since it can be applied to single measurements (contrary to averaging), which makes it relevant to countermeasures such as masking or shuffling [20], and it does not compress the leakage traces, hence nothing prevents to combine it with dimensionality reduction afterwards. As a result, a variety of works have investigated the opportunities offered by filtering methods, or even tried to perform side-channel analysis directly in the frequency domain, including but not limited to [12, 16, 22, 25, 26, 43, 44]. Very summarized, the common outcome of these works is that (i) filtering works best in contexts where the adversary/evaluator has some intuitions regarding the interesting frequency bands and (ii) frequency analysis generally benefits from acquisition devices with higher sampling rates.

Our Contribution. Starting from this state-of-the-art, our main contribution is to introduce Singular Spectrum Analysis (SSA) [19, 45] to the field of side-channel analysis, as an efficient alternative to filtering. SSA is an emerging method in the field of time series analysis, that aims at decomposing the original series into the sum of a small number of independent and interpretable components, which has proved to be relevant to a wide range of applications (in physics and economics, typically), e.g. by allowing significant noise reductions. In this respect, we first note that despite some connection with frequency analysis (see, e.g. [3]), SSA is based on totally a different mathematical background, and is in fact closer to dimensionality reductions such as PCA and LDA. Indeed, it is based on a decomposition in independent components. Intuitively, it can therefore be viewed as a (heuristic) tool enabling blind source separation, such as Independent Component Analysis (ICA) [21], yet with the significant difference that it works based on single observations (whereas ICA requires at least N independent observations to recover the original series made of N sources). Concretely though, and when used for noise reduction purposes as we will consider next, SSA shares the goals of filtering, with two significant advantages. First, it allows easier intuitions in the selection of the components to be integrated in the signal reconstruction, because these components can be “rated” according to their eigenvalues, just as in PCA and LDA. Second, the signal decomposition and reconstruction can be successful even in situations where the sampling rate is low. So it provides actual solutions for the two previously mentioned limitations of the filtering preprocessing. Besides, it can theoretically succeed in contexts where filtering is unapplicable, e.g. when two independent sources (corresponding to some signal and noise) are observed at exactly the same frequency.

In order to confirm the relevance of this new tool, we apply it in three different scenarios: first an unprotected implementation of the AES in a microcontroller, second a masked implementation of the AES in the same microcontroller, third an unprotected FPGA implementation of PRESENT. In all three cases, we show that SSA allows very significant improvements of the traces SNR, which translates into concrete gains in the success rates of attacks exploiting this preprocessing. Our experiments further exhibit the increased interest of SSA in the context of masking (since the impact of noise on the success rate increases exponentially in the number of shares used when masking), and more noisy implementations such as our hardware one (for which the SNR is small enough for its impact on the attacks success rate to follow theoretical predictions such as [13]). Since noise is a fundamental ingredient in the analysis of most countermeasures against side-channel attacks, and in particular for masking [42] and shuffling [46], we conclude SSA can be an important tool in the analysis of the concrete security level of implementations protected by these means.

2 Background

Notations. In the rest of the paper, capital letters are used for random variables and small caps for their realizations. Vectors and matrices are denoted with bold notations, functions with sans serif fonts and sets with calligraphic ones.

2.1 Attacks

Preprocessing leakage traces aims to improve the efficiency of side-channel attacks, allowing for a reduction in their acquisition and computation time. In order to evaluate the efficiency of SSA in this context, raw and preprocessed power traces are compared using state-of-the-art attacks that are briefly summarized next. For this purpose, a cryptographic device performing the key addition $\oplus$ between an input x and the secret key k followed by a b-bit S-box $\mathsf {S}$, i.e., $z=\mathsf {S}(x\oplus k)$, is considered. The leakage trace generated by the target device when performing this S-box computation with the attacker-supplied input $\{x_i\}_{i=1}^n$, where n is the number of queries performed by the adversary, is denoted as $\varvec{l}_{x,k}^i$. Whenever accessing the $t^{\text {th}}$ time sample of this trace, the notation $l_{x,k}^{i,t}$ will be used. Subscripts/superscripts will be omitted when not necessary.

Template Attack (TA). Introduced by Chari et al. [9] at CHES 2002 as a powerful attack against cryptographic implementations, TA essentially extracts secret information based on probabilistic leakage models (next denoted as $\hat{\text {Pr}}_{\text {model}}$). For this purpose, the authors of [9] assume that leakages can be interpreted as the realizations of a random variable which generates samples according to a Gaussian distribution. In the context of this work, where the target intermediate value is a key addition, it holds that $\hat{\text {Pr}}_{\text {model}}[\varvec{l}_{x,k}|x,k]\approx \hat{\text {Pr}}_{\text {model}}[\varvec{l}_{x,k}|x\oplus k]\sim \mathcal {N}(\hat{\varvec{\mu }}^{}_{x,k},\hat{\varvec{\Sigma }}^2_{x,k})$, with $\hat{\varvec{\mu }}_{x,k}$ and $\hat{\varvec{\Sigma }}^2_{x,k}$ the mean vector and covariance matrices corresponding to the target intermediate value $x\oplus k$. In case of univariate attacks (that are typically successful against unprotected implementations), the Gaussian templates are further simplified to the corresponding means and covariances, and can be exploited to compute key probabilities as follows:

$$\begin{aligned} \hat{\mathsf {Pr}}_{\text {model}}[k^*|x_i,l_{x,k}^{i,t}] = \frac{\mathcal {N}(l_{x,k}^{i,t}|\hat{\mu }^{}_{x,k},\hat{\sigma }^2_{x,k})}{\sum _{k^*\in \mathcal {K}}\mathcal {N}(l_{x,k}^{i,t}|\hat{\mu }^{}_{x,k^*},\hat{\sigma }^2_{x,k^*})}, \end{aligned}$$

where $k^*$ is a key candidate. By contrast, cryptographic software implementations protected with a $1^{\text {st}}$-order masking scheme, where the masked intermediate value and the corresponding output mask are processed sequentially at $t_1$ and $t_2$, are vulnerable to bivariate attacks. In such a scenario, adversaries can launch a TA exploiting the two leaking samples by means of Gaussian mixtures:

$$\begin{aligned} \hat{\mathsf {Pr}}_{\text {model}}[k^*|x_i,l_{x,k}^{i,t_1},l_{x,k}^{i,t_2}] = \frac{\sum _{q^*\in \mathcal {Q}}\mathcal {N}(l_{x,k}^{i,t_1},l_{x,k}^{i,t_2}|\hat{\varvec{\mu }}^{}_{x,k,q^*},\hat{\varvec{\Sigma }}^2_{x,k,q^*})}{\sum _{k^*\in \mathcal {K}}\sum _{q^*\in \mathcal {Q}}\mathcal {N}(l_{x,k}^{i,t_1},l_{x,k}^{i,t_2}|\hat{\varvec{\mu }}^{}_{x,k^*,q^*},\hat{\varvec{\Sigma }}^2_{x,k^*,q^*})}, \end{aligned}$$

where $q^*$ is the guessed output mask. In order to recover the key, TA then estimates probabilities for each candidate $k^*$, e.g., in the unprotected case:

$$\begin{aligned} p_{k^*}=\prod _{i=1}^n ~ \hat{\mathsf {Pr}}_{\text {model}}[k^*|x_i,l_{x,k}^{i,t}]. \end{aligned}$$

Correlation Power Analysis (CPA). In order to distinguish the correct key guess among the others, CPA [4] classifies univariate leakages $l_{x,k}^{i,t}$ using Pearson’s correlation coefficient and an a-priori chosen leakage model $m_{k^*}^i=\mathsf {M}(\mathsf {S}(x_i\oplus k^*))$:

$$\begin{aligned} \hat{\rho }^t_{k^*}=\frac{\hat{\mathsf {E}}_i[l_{x,k}^{i,t}\cdot m_{k^*}^i] - \hat{\mathsf {E}}_i[l_{x,k}^{i,t} ] \cdot \hat{\mathsf {E}}_i[m_{k^*}^i]}{\sqrt{\hat{\mathsf {Var}}_i(l_{x,k}^{i,t}) \cdot \hat{\mathsf {Var}}_i(m_{k^*}^i)}}, \end{aligned}$$

where $\hat{\mathsf {E}}$ and $\hat{\mathsf {Var}}$ denote the sample versions of the mean and variance, respectively. Usually in practice, $\mathsf {M}(\cdot )$ corresponds to the Hamming weight ($\mathsf {HW}$) or distance ($\mathsf {HD}$) model when targeting software or hardware implementations, respectively. Finally, the best key candidate $\tilde{k}$ is taken such that:

$$\begin{aligned} \tilde{k}=\mathrm{{\mathop {{arg\,max}}_{ {k^*}}}}~\hat{\rho }^t_{k^*}. \end{aligned}$$

Moments-Correlating DPA (MC-DPA). In [28], Moradi and Standaert proposed a so-called Moments-Correlating Collision DPA (MCC-DPA) as a tweak of Correlation-Enhanced Power Analysis Collision Attack (CEPACA) [27], where the correlation of “moments with moments” is replaced by the correlation of “moments with samples”, hence preserving the metric feature of Pearson’s correlation coefficient. In order to perform a MCC-DPA attack, the $d^\text {th}$-order (raw, central, standardized) moments are estimated “on-the-fly” from a vector of leakage traces $\mathbf {l}^\mathsf {t}_{x_0,k_0}=\{l_{x_0,k_0}^{i,t_1}\}_{i=1}^n$ corresponding to the target S-box computation at time $t_1$, i.e., $z_0=\mathsf {S}(x_0\oplus k_0)$. The leakage traces $\mathbf {l}^\mathsf {t}_{x_1,k_1}=\{l_{x_1,k_1}^{i,t_2}\}_{i=1}^n$ for the second S-box at time $t_2$, i.e., $z_1=\mathsf {S}(x_1\oplus k_1)$, are aligned with the $2^b$ moments $\hat{\mathbf {M}}^d_{x_0,k_0}$ and then correlated by permuting $\mathbf {l}^\mathsf {t}_{x_1,k_1}$ according to $\varDelta =k_0\oplus k_1$ . Lastly, the best value of $\varDelta$ is chosen such that (e.g., for the $d^{\text {th}}$-order raw moments):

$$\begin{aligned} \tilde{\varDelta }=\mathrm{{\mathop {{arg\,max}}_{ {\Delta }}}}~\hat{\rho }(\hat{\mathbf {M}}^d_{x_0,k_0},(\mathbf {l}^\mathsf {t}_{x_1,k_1\oplus {\Delta }})^d). \end{aligned}$$

The profiled extension of CEPACA, i.e., Moments-Correlating Profiled DPA (MCP-DPA), correlates the statistical moments corresponding to one single S-box. First, a profiling vector of leakage traces $\mathbf {l}^\mathsf {p}_{x,k}=\{l_{x,k}^{i,t_1}\}_{i=1}^{n_p}$ for the target intermediate value $z=\mathsf {S}(x\oplus k)$ is used to estimate the $2^b$ moments $\hat{\mathbf {M}}^d_{x,k}$ and then, a second vector of test traces $\mathbf {l}^\mathsf {t}_{x,k}=\{l_{x,k}^{i,t_1}\}_{i=1}^{n_t}$ is correlated with $\hat{\mathbf {M}}^d_{x,k}$ permuted according to the key guess $k^*$. The best key candidate is selected according to (again for the raw moments):

$$\begin{aligned} \tilde{k}=\mathrm{{\mathop {{arg\,max}}_{ {k^*}}}}~\hat{\rho }(\hat{\mathbf {M}}^d_{x,k^*},(\mathbf {l}^\mathsf {t}_{x,k})^d). \end{aligned}$$

In this work MCP-DPA is extended to the bivariate setting in order to evaluate the software implementation of a $1^\text {st}$-order masking scheme. Experiments performed in this case will only consider MCP-DPA with $2^{\text {nd}}$-order moments, i.e., $d_1=d_2=1$, hence the use of central mixed statistical moments:

$$\begin{aligned} \mathbf {CM}_{x,k^*}^{d_1,d_2}=\mathsf {E}\Big (\big (\mathbf {l}_{x,k^*}^{\mathsf {p},t_1}-~\mathsf {E}(\mathbf {l}_{x,k^*}^{\mathsf {p},t_1})\big )^{d_1}\cdot \big (\mathbf {l}_{x,k^*}^{\mathsf {p},t_2}-~\mathsf {E}(\mathbf {l}_{x,k^*}^{\mathsf {p},t_2})\big )^{d_2}\Big ). \end{aligned}$$

Analogously to its univariate counterpart, the best key candidate $\tilde{k}$ can then be chosen according to the following equation:

$$\begin{aligned} \tilde{k}={\text {*}}{arg\,max}_{k^*} ~\hat{\rho }\Big (\mathbf {CM}_{x,k^*}^{d_1,d_2},\big (\mathbf {l}_{x,k}^{\mathsf {t},t_1}-~\mathsf {E}(\mathbf {l}_{x,k}^{\mathsf {t},t_1})\big )^{d_1}\cdot \big (\mathbf {l}_{x,k}^{\mathsf {t},t_2}-~\mathsf {E}(\mathbf {l}_{x,k}^{\mathsf {t},t_2})\big )^{d_2}\Big ). \end{aligned}$$

2.2 Evaluation Metrics

Security evaluations of cryptographic devices usually pursue two objectives [41]. Firstly, it is of interest to measure how much information is leaking from the target implementation, independently of the attacker, and secondly how easy this information can be exploited by an adversary. In the context of this work, both questions deserve attention since the aim of any preprocessing step is to maximize the information leakages in order to make attacks easier. We will therefore use the two types of metrics briefly introduced next.

Information Theoretic Metrics. Information theoretic (IT) metrics are intended to measure how much information is leaking from the device under test. The Signal-to-Noise Ratio (SNR) introduced by Mangard at CT-RSA 2004 [23] is a simple and intuitive solution for this purpose:

$$\begin{aligned} \text {SNR}=\frac{\hat{\mathsf {Var}}_{x,k}\big (\hat{\mathsf {E}}_{i}[\varvec{l}^i_{x,k}]\big )}{\hat{\mathsf {E}}_{x,k}\big [\hat{\mathsf {Var}}_{i}(\varvec{l}^i_{x,k})\big ]}, \end{aligned}$$

where $\hat{\mathsf {Var}}$ and $\hat{\mathsf {E}}$ respectively denote the sample variance and mean that are estimated from a set of test traces. In comparison with other IT metrics, such as the mutual information (MI) introduced in [41] that allows capturing any leakage PDF, the SNR is limited to $1^{\text {st}}$-order moments. However, when considering univariate Gaussian random variables, it has been shown that Pearson’s correlation coefficient can be connected with the SNR [23] and the MI [24]:

Since our goal in the following is to quantify noise reduction by SSA, which applies independently on each trace (i.e. from single measurements), we are indeed in a context where the SNR brings all the necessary intuition, and we will limit our information theoretic analysis to this metric. (As will be detailed, this just requires taking advantage of mask knowledge in the protected case).

Security Metrics. We will evaluate the efficiency of our experimental attacks with the $1^{\text {st}}$ -order success rate defined in [41], i.e., the probability that the correct secret key is the most likely key candidate provided by an attack. In practice, the success rate is widely used in the security evaluation of many cryptographic implementations because of its ease of use and understandability.

3 Singular Spectrum Analysis

SSA is a non-parametric technique used in time series analysis that was first presented in the eighteenth century [33], but only gained interest with the more recent publications by Broomhead and King [5, 6] in the late twentieth century. So far, SSA has been successfully applied in many different areas, e.g., engineering and medicine, becoming a standard tool in some of them, e.g., meteorology and geophysics. In the following, its two main steps (i.e., decomposition and reconstruction) are introduced based on our previous notations. We additionally provide a couple of insights on how to take advantage of SSA in practice.

3.1 Decomposition

The first step of SSA is the decomposition of the original time series into a set of elementary matrices required during the reconstruction phase. This process is based on the embedding and singular value decomposition that we describe next.

Embedding. Given an N-time series $\varvec{l}=(l^1,l^2,\dots ,l^N)$ and the window length W such that $2<W\le N/2$, we define $D=N-W+1$ delayed vectors:

$$\begin{aligned} \mathbf {l}_i = (l^i,l^{i+1},\dots ,l^{i+W-1})^\top \text { for }1\le i\le D, \end{aligned}$$

and the trajectory matrix:

$$\begin{aligned} \mathbf {L} = (\mathbf {l}_1,\mathbf {l}_2,\dots ,\mathbf {l}_D) = \begin{pmatrix} l^1 &{} l^2 &{} \cdots &{} l^{D} \\ l^2 &{} l^3 &{} \cdots &{} l^{D+1} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ l^W &{} l^{W+1} &{} \cdots &{} l^{N} \end{pmatrix}\!\!, \end{aligned}$$

which is a Hankel matrix, i.e., a matrix with constant skew diagonals. The window length W plays a key role in the performance and accuracy of SSA, hence the importance of choosing its optimal value. Too large or too small values can lead to decompositions where the components are mixed-up between them, making the reconstruction step difficult. In the context of noise reduction, conditions are relaxed allowing practitioners to consider other aspects, e.g., performance, while keeping the accuracy of the tool high. In this work, we will use the following rule-of-thumb:

$$\begin{aligned} W=\lfloor \log {(N)}^c\rfloor \text { with }c\in ~[1.5,3], \end{aligned}$$

(1)

which has been shown near optimal for signal vs. noise separation [35].

Singular Value Decomposition. Given the trajectory matrix $\mathbf {L}$ from the previous step, its singular value decomposition (SVD) [18] is computed. First, the eigenvalues of $\mathbf {LL}^\top$ in decreasing order of magnitude $\lambda _1\ge \lambda _2\ge \dots \ge \lambda _d$, i.e., the so called singular spectrum which gives name to SSA, and the corresponding eigenvectors $\mathbf {u}_1,\mathbf {u}_2,\dots ,\mathbf {u}_d$ (with $d=W$ if none of the eigenvalues is zero) are obtained. The SVD decomposition of the trajectory matrix can be written as:

$$\begin{aligned} \mathbf {L}=\mathbf {L}_1+\mathbf {L}_2+\dots +\mathbf {L}_d, \end{aligned}$$

(2)

where the $W\times D$ elementary matrix $\mathbf {L}_i=\sqrt{\lambda _i}\mathbf {u}_i\mathbf {v}_i^\top$ and $\mathbf {v}_i=\mathbf {L}^\top \mathbf {u}_i/\sqrt{\lambda _i}$, for $1\le i\le d$. Computing (2) is the most time-consuming step in SSA, however only the leading components are required during the reconstruction phase. In order to alleviate this complexity burden the partial SVD (PSVD), which only calculates a subset of the $\mathbf {L}_i$ matrices in (2), is considered in the remaining sections.

3.2 Reconstruction

After having obtained the SVD decomposition of the original time series in the previous phase, the reconstruction step aims for the extraction of its underlying components. It is based on the diagonal averaging and grouping described next.

Diagonal Averaging. If $\mathbf {X}$ is a $W\times D$ matrix with elements $x_{i,j}$ for $1\le i\le W$ and $1\le j\le D$, it can be immediately turned into the series $\mathbf {\tilde{x}}=\{\tilde{x}^t\}_{t=1}^N$ if and only if $\mathbf {X}$ is a Hankel matrix. In that case, each entry $\tilde{x}^t$ is equal to all elements $x_{i,j}$ along the anti-diagonal $i+j=t+1$ of $\mathbf {X}$. However, if $\mathbf {X}$ does not have constant skew diagonals, an additional step is required. Namely, the averaging of the anti-diagonals $i+j=k+1$ will transform $\mathbf {X}$ into the series $\mathbf {\tilde{x}}=\{\tilde{x}^t\}_{t=1}^N$ in a process which is also known as Hankelization [38]:

$$\begin{aligned} \tilde{x}^t= \left\{ \begin{array}{l l} \displaystyle \frac{1}{t}\sum _{m=1}^t x_{m,t-m+1}&{} \quad {\text {for}}~1\,\le \,t\,<\,W^*,\\ \displaystyle \frac{1}{W^*}\sum _{m=1}^{W^*} x_{m,t-m+1}&{} \quad {\text {for}}~W^*\,\le \,t\,\le \,D^*,\\ \displaystyle \frac{1}{N-t+1}\sum _{m=t-D^*+1}^{N-D^*} x_{m,t-m+1}&{} \quad {\text {for}}~D^*\,<t\,\le \,N, \end{array} \right. \end{aligned}$$

where $W^*=\mathsf {min}(W,D)$ and $D^*=\mathsf {max}(W,D)$. Because matrices $\mathbf {L}_i$ in (2) are not Hankel matrices, by applying this procedure each matrix $\mathbf {L}_i$ in (2) is transformed into the $i^{\text {th}}$ (so-called) principal component $\mathbf {g}_i$ of length N.

Grouping. Under the assumption of weak separability [19], the original N-time series $\varvec{l}$ can then be reconstructed by:

$$\begin{aligned} \varvec{l} = \mathbf {g}_1 + \mathbf {g}_2 + \dots +\mathbf {g}_d. \end{aligned}$$

At this stage, the set of indices $I=\{1,\dots ,d\}$ is partitioned into m disjoint subsets $I_1,\dots ,I_m$. Since in the context of this work, SSA aims for signal vs. noise decomposition, we are typically looking for a partitioning such that $m=2$ and $I=\{I_{\text {signal}},I_{\text {noise}}\}$. The analysis of the eigenvalues $\lambda _i$ in the SVD step is the most common method for splitting I according to some criteria that depend on the application area. In our case, indices whose respective eigenvalues are small, usually producing a slowly decreasing sequence, are included in the group of noisy components. The remaining components can be exhaustively tested in order to find the combination bringing a better reconstruction of the noise-free signal. In the following, we will determine the best grouping based on the SNR. Summarizing, this section presented the main steps involved in SSA, that can be recalled with the following equation:

$$\begin{aligned} \overbrace{\varvec{l}\longrightarrow \mathbf {L}}^{\text {Embedding}}=\overbrace{\mathbf {L}_1+\mathbf {L}_2+\dots +\mathbf {L}_d}^{\text {SVD}}=\overbrace{\mathbf {g}_1 + \mathbf {g}_2 + \dots +\mathbf {g}_d}^{\text {Averaging}}=\overbrace{\sum _{i\in I_{\text {signal}}}\mathbf {g}_i + \sum _{i\in I_{\text {noise}}}\mathbf {g}_i}^{\text {Grouping}}. \end{aligned}$$

Next, three different case studies will be presented, where raw and preprocessed traces are compared in terms of the corresponding attacks’ performance. Additionally, decisions taken for the application of SSA such as the window length W and the grouping of components will be discussed in more details.

4 Practical Experiments

4.1 Measurement Setup

In order to evaluate the efficiency of SSA in the context of side-channel attacks, two different (software and hardware) platforms have been considered. A LeCroy HRO66Zi WaveRunner 12-bit oscilloscope with maximum 2GS/s sampling rate and a passive probe have been used to measure the voltage drop over a $1\,\mathrm {\Omega }$ resistor in the VDD path of both targets. We tested various sampling rates (between 500 MS/s to 2 GS/s) and consistently found similar experimental results.

Our first target device is an 8-bit Atmel ATMega644p microcontroller clocked at 20 MHz. We considered both an unprotected and a Boolean masked implementation on this platform. The $1^{\text {st}}$-order masking scheme implemented comes from [34]. Two (input and output) mask bytes m and q are considered for each plaintext byte. First, a masked S-box table such that $\mathsf {S'}(x\oplus k\oplus m) = \mathsf {S}(x\oplus k)\oplus q$ is precomputed in memory for every possible state byte $x\oplus k$. Afterwards, the AddRoundkey and MaskedSubBytes operations are performed. Note that in order to avoid possible $1^{\text {st}}$-order leakages, the device has been provided with the masked plaintext byte $x\oplus m$. We evaluated this scheme based on $128\ 000$ profiling traces and $2\ 000$ attack traces. In order to limit our storage requirements, only the last rounds of the precomputation and the subsequent operations have been recorded, together with the randomly chosen bytes used for masking.

Our second target device is the crypto FPGA embedded in a SAKURA-G board, namely a Xilinx Spartan-6 LX75 FPGA, driven at a frequency of 3 MHz. We evaluated an implementation of the PRESENT-80 block cipher based on the Profile 1 in [32] on this platform. It corresponds to a serialized architecture without any countermeasure against side-channel attacks. Because of the higher noise, our evaluations of this second (more noisy) case were based on non-profiled attacks only. We used a total of $100\ 000$ power traces acquired by using randomly generated plaintexts and keeping the secret key value constant for this purpose.

4.2 Unprotected and Masked AES in an Atmel Microcontroller

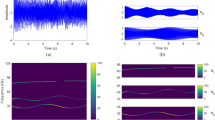
Because of place constraints, our focus in this section will be on the practical evaluation of SSA against the $1^\mathbf{st }$-order Boolean masking scheme implemented on our Atmel chip. The application to the unprotected implementation essentially follows similar steps (and its results will be mentioned at the end of this section, for comparison purposes). Both profiled and non-profiled attacks are considered in this context. In particular, the SNR of our software implementation was (as expected) reasonably high, which allowed us to obtain accurate templates using the previously mentioned sets of $128\ 000$ profiling traces and $2\ 000$ attack traces. For illustration, an exemplary power trace is shown in Fig. 1(a).

Fig. 1.

$1^{\text {st}}$-order masked implementation: power traces & singular spectrum.

In order to keep the efficiency of SSA high, the window length W has been taken accordingly to Eq. (1) by setting $c=1.5$. Preprocessing the raw traces with $W= \lfloor \log (5\ 500)^{1.5}\rfloor =25$ produces the singular spectrum shown in Fig. 1(b). When applied to the problem of signal vs. noise decomposition, such a singular spectrum generally allows for easy detection of interesting components by mere visual inspection. In this particular case, the first component dominates among the others, which usually indicates that it corresponds to low-frequency noise. For the other leading components, and following the heuristic approach used in the context of PCA and LDA, we tested a couple of re-constructions and concluded that most of the useful signal was lying in the second component. As can be seen in Fig. 1(c), the resulting preprocessed trace is very clean.

In order to reach a first intuition regarding the efficiency of SSA, and since it is the criteria used to choose the best grouping, the SNR of the preprocessed traces has been computed. Note that this is possible because the analysis is being conducted in a profiling setting, and thus the knowledge of the masks allows for the computation of the SNR as if the target was an unprotected implementation. Figure 2 shows a comparison of the SNR before and after preprocessing the traces with SSA. As it can be seen, gains are close to a factor of 2.5.

Fig. 2.

$1^{\text {st}}$-order masked implementation, SNR.

In general, higher SNRs should translate into more successful attacks. This has been practically verified by running bivariate attacks using raw and preprocessed traces. The results of a bivariate MCP-DPA and TA exploiting Gaussian mixtures over the number of attack traces, and the corresponding success rate curves, are depicted in Figs. 3 and 4, respectively. As mentioned earlier, the method applies similarly to unprotected devices (since the SSA transform is applied independently on every trace). For comparison purposes, we therefore add the success rate curves of an attack against the same masked implementation, but with all the masks set to zero (which is then equivalent to an unprotected implementation), in Appendix A, Fig. 9. Interestingly, one could expect that the factor 2.5 for the SNR gain translates into a gain in the measurement complexity of the attacks of 2.5 for the unprotected implementation, and $2.5^2$ for the masked one. Yet, and despite significant, these gains are not that large. But this is easily explained by the too high SNRs of our case study. That is, and as carefully discussed in [13], these theoretical expectations are only verified for low enough SNRs (typicaly below 1/10). So based on these first experiments, we can already conclude that SSA is applicable to masking, without any particular intuition regarding the target implementation. And we move to the next section to investigate the relevant case of a more noisy hardware implementation.

Fig. 3.

$1^{\text {st}}$-order masked implementation, attack results.

Fig. 4.

$1^{\text {st}}$-order masked implementation, success rate curves.

4.3 Unprotected PRESENT in a Xilinx FPGA

In this second case study, we performed a very similar evaluation, with the minor difference that our attacks were all performed in a non-profiled attack setting. As previously mentioned, this choice was motivated by the more noisy leakage traces (so the more challenging profiling). Besides, it turned out that a Hamming distance leakage model anyway provided us with satisfying results.

We again start by illustrating a power trace of this implementation, covering 9 clock cycles which correspond to the computation of 9 S-boxes, in Fig. 5(a). The window length for SSA has been taken using $c=1.5$ as in the previous case and thus, $W= \lfloor \log (6\ 000)^{1.5}\rfloor =25$. The singular spectrum in Fig. 5(b) is also interpreted as in the previous section. Hence, only the second component is used for signal reconstruction, leading to quite clean traces in Fig. 5(c).

Fig. 5.

Unprotected PRESENT implem., power traces & singular spectrum.

Fig. 6.

Unprotected PRESENT implem., SNR.

Next, Fig. 6 depicts the SNR gains in this hardware context, which are now close to a factor of 4. Since this time the SNR values are indeed in the range of 1/10, it implies that we should observe gains of similar proportions in the attacks. This is indeed exhibited by the results of CPA using the Hamming distance between two consecutive S-box outputs, and MCC-DPA, that are shown in Fig. 7. The connection between the SNR gains and the attacks’ measurement complexity is further confirmed by the success rate curves in Fig. 8 where a reduction by a factor close to 4 in the number of attack traces is achieved. So despite being in a non-profiled attack scenario, the reduction of the noise now quite accurately follows what is expected for standard DPA attacks.

Fig. 7.

Unprotected PRESENT implem., attack results.

Fig. 8.

Unprotected PRESENT implem., success rate curves.

5 Conclusions

This work has introduced SSA in the context of side-channel attacks. Our different case studies have shown that, even when the amplitude of the signal is small and the noise level high, SNR gains up to a factor 4 are achieved by applying a signal vs. noise decomposition of individual power traces. Furthermore, it has also been verified that these SNR gains translate into successful attacks with reduced measurement complexity. Unlike some advanced signal processing techniques working in the frequency domain, the described technique is very easy to use. Practitioners just have to set a window length (which can take advantage of a standard rule-of-thumb), and then select their components by mere visual inspection of the singular spectrum (in view of the limited amount of components that usually represent the signal, this step can even take advantage of exhaustive testing). In view of these promising results, a natural open problem is to apply SSA to a masked hardware implementation (i.e. with low SNR). Indeed, in this case, an SNR gain factor g should translate into a success rate gain factor $g^d$, where d is the number of shares in the masking scheme. Such a result could be obtained by extending our FPGA experiments towards a $1^{\text {st}}$-order secure masked PRESENT implementation, e.g. based on the glitch-resistant masking scheme proposed in [29]. Besides, and more technically, the experiments in this paper were exploiting oscilloscopes with good sampling frequencies (which corresponds to the usual adversarial power). Yet, it would be interesting to study SSA in the context of limited sampling frequencies, in order to determine how cheap side-channel measurement setups can be (for different device technologies).

A Univariate Attacks

Fig. 9.

Unprotected implementation, success rate curves.