Integral Cryptanalysis on Full MISTY1

Abstract

MISTY1 is a block cipher designed by Matsui in 1997. It was well evaluated and standardized by projects, such as CRYPTREC, ISO/IEC, and NESSIE. In this paper, we propose a key recovery attack on the full MISTY1, i.e., we show that 8-round MISTY1 with 5 FL layers does not have 128-bit security. Many attacks against MISTY1 have been proposed, but there is no attack against the full MISTY1. Therefore, our attack is the first cryptanalysis against the full MISTY1. We construct a new integral characteristic by using the propagation characteristic of the division property, which was proposed in 2015. We first improve the division property by optimizing a public S-box and then construct a 6-round integral characteristic on MISTY1. Finally, we recover the secret key of the full MISTY1 with $2^{63.58}$ chosen plaintexts and $2^{121}$ time complexity. Moreover, if we can use $2^{63.994}$ chosen plaintexts, the time complexity for our attack is reduced to $2^{107.9}$. Note that our cryptanalysis is a theoretical attack. Therefore, the practical use of MISTY1 will not be affected by our attack.

1 Introduction

MISTY [17] is a block cipher designed by Matsui in 1997 and is based on the theory of provable security [19, 20] against differential attack [3] and linear attack [15]. MISTY has a recursive structure, and the component function has a unique structure, the so-called MISTY structure [16]. There are two types of MISTY, MISTY1 and MISTY2. MISTY1 adopts the Feistel structure whose F-function is designed by the recursive MISTY structure. MISTY2 does not adopt the Feistel structure and uses only the MISTY structure. Both ciphers achieve provable security against differential and linear attacks. MISTY1 is designed for practical use, and MISTY2 is designed for experimental use.

Table 1. Summary of single secret-key attacks against MISTY1

MISTY1 is a 64-bit block cipher with 128-bit security, and it has a Feistel structure with FL layers, where the FO function is used in the F-function of the Feistel structure. The FO function is constructed by using the 3-round MISTY structure, where the FI function is used as the F-function of the MISTY structure. Moreover, the FI function is constructed by using the 3-round MISTY structure, where a 9-bit S-box $S_9$ and 7-bit S-box $S_7$ are used in the F-function. MISTY1 is the candidate recommended ciphers list of CRYPTREC [6], and it is standardized by ISO/IEC 18033-3 [11]. Moreover, it is a NESSIE-recommended cipher [18] and is described in RFC 2994 [21]. There are many existing attacks against MISTY1, and we summarize these attacks in Table 1. A higher-order differential attack is the most powerful attack against MISTY1, and this type of cryptanalysis was recently improved in [2]. However, there is no attack against the full MISTY1, i.e., 8-round MISTY1 with 5 FL layers.

Fig. 1.

Specification of MISTY1

Integral Attack. The integral attack [13] was first proposed by Daemen et al. to evaluate the security of Square [7] and was then formalized by Knudsen and Wagner. There are two major techniques to construct an integral characteristic; one uses the propagation characteristic of integral properties [13], and the other estimates the algebraic degree [12, 14]. We often call the seconds technique a “higher-order differential attack.” A new technique to construct integral characteristics was proposed in 2015 [24], and it introduced a new property, the so-called “division property,” by generalizing the integral property [13]. It showed the propagation characteristic of the division property for any secret function restricted by an algebraic degree. As a result, several improved results were reported on the structural evaluation of the Feistel network and SPN.

Our Contribution. In [24], the focus is only on the secret S-box restricted by an algebraic degree. However, many realistic block ciphers use more efficient structures, e.g., a public S-box and a key addition. In this paper, we show that the division property becomes more useful if an S-box is a public function. Then, we apply our technique to the cryptanalysis on MISTY1. We first evaluate the propagation characteristic of the division property for public S-boxes $S_7$ and $S_9$ and show that $S_7$ has a vulnerable property. We next evaluate the propagation characteristic of the division property for the FI function and then evaluate that for the FO function. Moreover, we evaluate that for the FL layer. Finally, we create an algorithm to search for integral characteristics on MISTY1 by assembling these propagation characteristics. As a result, we can construct a new 6-round integral characteristic, where the left 7-bit value of the output is balanced. We recover the round key by using the partial-sum technique [9]. As a result, the secret key of the full MISTY1 can be recovered with $2^{63.58}$ chosen plaintexts and $2^{121}$ time complexity. Moreover, if we can use $2^{63.994}$ chosen plaintexts, the time complexity is reduced to $2^{107.9}$. Unfortunately, we have to use almost all chosen plaintexts, and recovering the secret key by using fewer chosen plaintexts is left as an open problem.

2 MISTY1

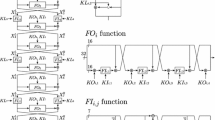
MISTY1 is a Feistel cipher whose F-function has the MISTY structure, and the recommended parameter is 8 rounds with 5 FL layers. Figure 1 shows the structure of MISTY1. Let $X_i^L$ (resp. $X_i^R$) be the left half (resp. the right half) of an i-round input. Moreover, $X_i^L[j]$ (resp. $X_i^R[j]$) denotes the jth bit of $X_i^L$ (resp. $X_i^R$) from the left. MISTY1 is a 64-bit block cipher, and the key-bit length is 128 bits. The component function $FO_i$ consists of $FI_{i,1}$, $FI_{i,2}$, and $FI_{i,3}$, and the four 16-bit round keys $KO_{i,1}$, $KO_{i,2}$, $KO_{i,3}$, and $KO_{i,4}$ are used. The function $FI_{i,j}$ consists of $S_9$ and $S_7$, and a 16-bit round key $KI_{i,j}$ is used. Here, $S_9$ and $S_7$ are defined in Appendix A. The component function $FL_i$ uses two 16-bit round keys, $KL_{i,1}$ and $KL_{i,2}$. These round keys are calculated from the secret key $(K_1, K_2, \ldots , K_8)$ as

Symbol	$KO_{i,1}$	$KO_{i,2}$	$KO_{i,3}$	$KO_{i,4}$	$KI_{i,1}$	$KI_{i,2}$	$KI_{i,3}$	$KL_{i,1}$	$KL_{i,2}$
Key	$K_i$	$K_{i+2}$	$K_{i+7}$	$K_{i+4}$	$K'_{i+5}$	$K'_{i+1}$	$K'_{i+3}$	$K_{\frac{i+1}{2}}$ (odd i)	$K'_{\frac{i+1}{2}+6}$ (odd i)
								$K'_{\frac{i}{2}+2}$ (even i)	$K_{\frac{i}{2}+4}$ (even i)

Here, $K'_i$ is the output of $FI_{i,j}$ where the input is $K_i$ and the key is $K_{i+1}$.

3 Integral Characteristic by Division Property

3.1 Notations

We make the distinction between the addition of $\mathbb {F}_2^n$ and addition of $\mathbb {Z}$, and we use $\oplus$ and $+$ as the addition of $\mathbb {F}_2^n$ and addition of $\mathbb {Z}$, respectively. For any $a \in \mathbb {F}_2^n$, the ith element is expressed in a[i], and the Hamming weight w(a) is calculated as $w(a) = \sum _{i=1}^{n} a[i]$. Moreover, $a[i,\ldots ,j]$ denotes a bit string whose elements are values described into square brackets. Let $1^n \in \mathbb {F}_2^n$ be a value whose all elements are 1. Moreover, let $0^n \in \mathbb {F}_2^n$ be a value whose all elements are 0.

For any $\varvec{a} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$, the vectorial Hamming weight of $\varvec{a}$ is defined as $W(\varvec{a})=(w(a_1), w(a_2), \ldots , w(a_m)) \in \mathbb {Z}^m$. Moreover, for any $\varvec{k} \in \mathbb {Z}^m$ and $\varvec{k}' \in \mathbb {Z}^m$, we define $\varvec{k} \succeq \varvec{k}'$ if $k_i \ge k'_i$ for all i. Otherwise, $\vec k \nsucceq \vec k''$.

Boolean Function. A Boolean function is a function from $\mathbb {F}_2^n$ to $\mathbb {F}_2$. Let $\mathrm {deg}(f)$ be the algebraic degree of a Boolean function f. Algebraic Normal Form (ANF) is often used as representations of the Boolean function. Let f be any Boolean function from $\mathbb {F}_2^n$ to $\mathbb {F}_2$, and it can be represented as

$$\begin{aligned} f( x ) = \bigoplus _{u \in \mathbb {F}_2^n} a_u^f \left( \prod _{i=1}^{n} x[i]^{u[i]} \right) , \end{aligned}$$

where $a_u^f \in \mathbb {F}_2$ is a constant value depending on f and u. If $\mathrm {deg}(f)$ is at most d, all $a_u^f$ satisfying $d<w(u)$ are 0. An n-bit S-box can be regarded as the collection of n Boolean functions. If algebraic degrees of n Boolean functions are at most d, we say the algebraic degree of the S-box is at most d.

3.2 Integral Attack

An integral attack is one of the most powerful cryptanalyses against block ciphers. Attackers prepare N chosen plaintexts and get the corresponding ciphertexts. If the XOR of all corresponding ciphertexts becomes 0, we say that the block cipher has an integral characteristic with N chosen plaintexts. In an integral attack, attackers first create an integral characteristic against a reduced-round block cipher. Then, they guess the round keys that are used in the last several rounds and calculate the XOR of the ciphertexts of the reduced-round block cipher. Finally, they evaluate whether or not the XOR becomes 0. If the XOR does not become 0, they can discard the guessed round keys from the candidates of the correct key.

3.3 Division Property

A division property, which was proposed in [24], is used to search for integral characteristics. We first prepare a set of plaintexts and evaluate the division property of the set. Then, we propagate the division property and evaluate the division property of the set of texts encrypted over one round. By repeating the propagation, we show the division property of the set of texts encrypted over some rounds. Finally, we can easily determine the existence of the integral characteristic from the propagated division property.

Bit Product Function. We first define two bit product functions $\pi _u$ and $\pi _{\varvec{u}}$, which are used to evaluate the division property of a multiset. Let $\pi _u : \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ be a function for any $u \in \mathbb {F}_2^n$. Let $x \in \mathbb {F}_2^n$ be the input, and $\pi _u(x)$ is the AND of x[i] satisfying $u[i]=1$, i.e., it is defined as

$$\begin{aligned} \pi _u(x) := \prod _{i=1}^{n} x[i]^{u[i]}. \end{aligned}$$

Let $\pi _{\varvec{u}} : (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m}) \rightarrow \mathbb {F}_2$ be a function for any ${\varvec{u}} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$. Let $\varvec{x} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$ be the input, and $\pi _{\varvec{u}}({\varvec{x}})$ is defined as

$$\begin{aligned} \pi _{\varvec{u}}({\varvec{x}}) := \prod _{i=1}^{m} \pi _{u_i}(x_i). \end{aligned}$$

Definition of Division Property. The division property is given against a multiset, and it is calculated by using the bit product function. Let $\mathbb {X}$ be an input multiset whose elements take a value of $(\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$. In the division property, we first evaluate a value of $\bigoplus _{\varvec{x} \in \mathbb {X}} \pi _{\varvec{u}}(\varvec{x})$ for all $\varvec{u} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$. Then, we divide the set of $\varvec{u}$ into a subset whose evaluated value becomes 0 and a subset whose evaluated value becomes unknown¹. In [24], the focus was on using the Hamming weight of elements of $\varvec{u}$ to divide the set.

Definition 1

(Division Property). Let $\mathbb {X}$ be a multiset whose elements take a value of $(\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$, and $\varvec{k}$ is an m-dimensional vector whose ith element takes a value between 0 and $n_i$. When the multiset $\mathbb {X}$ has the division property $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{{n}_1, {n}_2, \ldots , {n}_{m}}$, it fulfils the following conditions: The parity of $\pi _{\varvec{u}}(\varvec{x})$ over all $\varvec{x} \in \mathbb {X}$ is always even when

$$\begin{aligned} \varvec{u} \in \left\{ (u_1,\ldots ,u_m) \in (\mathbb {F}_2^{n_1} \times \cdots \times \mathbb {F}_2^{n_m}) \mid W(\varvec{u}) \nsucceq \varvec{k}^{(1)}, \ldots , W({\varvec{u}}) \nsucceq \varvec{k}^{(q)} \right\} . \end{aligned}$$

Moreover, the parity becomes unknown when $\varvec{u}$ is used such that there exists an i $(1 \le i \le q)$ satisfying $W(\varvec{u}) \succeq \varvec{k}^{(i)}$.

Assume that the multiset $\mathbb {X}$ has the division property $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{{n}_1, {n}_2, \ldots , {n}_{m}}$. If there exist $\varvec{k}^{(i)}$ such that $k^{(i)}_j$ is greater than 1, $\bigoplus _{x \in \mathbb {X}} x_j$ becomes 0. See [24] to better understand the concept in detail. Moreover, [22] shows an example, and it helps us understand the division property.

Propagation Rules of Division Property. Some propagation rules for the division property are proven in [24]. We summarize them as follows.

• Rule 1 (Substitution). Let F be a function that consists of m S-boxes, where the bit length and the algebraic degree of the ith S-box is $n_i$ bits and $d_i$, respectively. The input and the output take a value of $(\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})$, and $\mathbb {X}$ and $\mathbb {Y}$ denote the input multiset and the output multiset, respectively. Assuming that the multiset $\mathbb {X}$ has the division property $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{{n}_1, {n}_2, \ldots , {n}_{m}}$, the division property of the multiset $\mathbb {Y}$ is $\mathcal{D}_{\varvec{k}'^{(1)}, \varvec{k}'^{(2)}, \ldots , \varvec{k}'^{(q)}}^{{n}_1, {n}_2, \ldots , {n}_{m}}$ as

  $$\begin{aligned} k'^{(j)}_i = \left\lceil \frac{ k^{(j)}_i }{d_i} \right\rceil ~~ \mathrm{for}~1 \le i \le m,~1 \le j \le q. \end{aligned}$$

• Rule 2 (Copy). Let F be a copy function, where the input x takes a value of $\mathbb {F}_2^{n}$ and the output is calculated as $(y_1,y_2)=(x,x)$. Let $\mathbb {X}$ and $\mathbb {Y}$ be the input multiset and output multiset, respectively. Assuming that the multiset $\mathbb {X}$ has the division property $\mathcal{D}_k^n$, the division property of the multiset $\mathbb {Y}$ is $\mathcal{D}_{\varvec{k}'^{(1)}, \varvec{k}'^{(2)}, \ldots , \varvec{k}'^{(k+1)}}^{n, n}$ as

  $$\begin{aligned} k'^{(i+1)} = (k-i, i) ~~ \mathrm{for}~0 \le i \le k. \end{aligned}$$

• Rule 3 (Compression by XOR). Let F be a function compressed by an XOR, where the input $(x_1,x_2)$ takes a value of $(\mathbb {F}_2^{n} \times \mathbb {F}_2^{n})$ and the output is calculated as $y=x_1\oplus x_2$. Let $\mathbb {X}$ and $\mathbb {Y}$ be the input multiset and output multiset, respectively. Assuming that the multiset $\mathbb {X}$ has the division property $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{n, n}$, the division property of the multiset $\mathbb {Y}$ is $\mathcal{D}_{k'}^{n}$ as

  $$\begin{aligned} k' = \min \{ k^{(1)}_1 + k^{(1)}_2, k^{(2)}_1 + k^{(2)}_2, \ldots , k^{(q)}_1 + k^{(q)}_2 \}. \end{aligned}$$

  Here, if the minimum value of $k'$ is larger than n, the propagation characteristic of the division property is aborted. Namely, a value of $\oplus _{y \in \mathbb {Y}} \pi _v(y)$ is 0 for all $v \in \mathbb {F}_2^n$.

• Rule 4 (Split). Let F be a split function, where the input x takes a value of $\mathbb {F}_2^{n}$ and the output is calculated as $x=y_1 \Vert y_2$, where $(y_1,y_2)$ takes a value of $(\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n-n_1})$. Let $\mathbb {X}$ and $\mathbb {Y}$ be the input multiset and output multiset, respectively. Assuming that the multiset $\mathbb {X}$ has the division property $\mathcal{D}_{k}^{n}$, the division property of the multiset $\mathbb {Y}$ is $\mathcal{D}_{\varvec{k}'^{(1)}, \varvec{k}'^{(2)}, \ldots , \varvec{k}'^{(q)}}^{n_1,n-n_1}$ as

  $$\begin{aligned} \varvec{k}'^{(i+1)} = (k-i, i) ~~ \mathrm{for}~0 \le i \le k. \end{aligned}$$

  Here, $(k-i)$ is less than or equal to $n_1$, and i is less than or equal to $n-n_1$.

• Rule 5 (Concatenation). Let F be a concatenation function, where the input $(x_1,x_2)$ takes a value of $(\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2})$ and the output is calculated as $y=x_1 \Vert x_2$. Let $\mathbb {X}$ and $\mathbb {Y}$ be the input multiset and output multiset, respectively. Assuming that the multiset $\mathbb {X}$ has the division property $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{n_1,n_2}$, the division property of the multiset $\mathbb {Y}$ is $\mathcal{D}_{k'}^{n_1+n_2}$ as

  $$\begin{aligned} k' = \min \{ k^{(1)}_1 + k^{(1)}_2, k^{(2)}_1 + k^{(2)}_2, \ldots , k^{(q)}_1 + k^{(q)}_2 \}. \end{aligned}$$

4 Division Property for Public Function

In an assumption of [24], attackers cannot know the specification of an S-box and only know the algebraic degree of the S-box. However, many specific block ciphers usually use a public S-box and an addition of secret sub keys, where an XOR is especially used for the addition. In this paper, we show that the propagation characteristic of the division property can be improved if an S-box is a public function. The difference between [24] and us is shown in Fig. 2.

Fig. 2.

The difference between [24] and us. The left figure is an assumption used in [24]. The right one is a new assumption used in this paper.

We consider the propagation characteristic of the division property against the function shown in the right figure in Fig. 2. The key XORing first be applied, but it does not affect the division property because it is a linear function. Therefore, when we evaluate the propagation characteristic of the division property, we can remove the key XORing. Next, a public S-box is applied, and we can determine the ANF of the S-box. Assuming that an S-box is a function from n bits to m bits, the ANF is represented as

$$\begin{aligned} y[1]&= f_1(x[1], x[2], \ldots , x[n]), \\ y[2]&= f_2(x[1], x[2], \ldots , x[n]), \\&\vdots \\ y[m]&= f_m(x[1], x[2], \ldots , x[n]), \end{aligned}$$

where $x[i]\,(1 \le i \le n)$ is an input, $y[j]\,(1 \le j \le m)$ is an output, and $f_j\,(1 \le j \le m)$ is a Boolean function. The division property evaluates the input multiset and output one by using the bit product function $\pi _{u}$, and we then divide the set of u into a subset whose evaluated value becomes 0 and a subset whose evaluated value becomes unknown. Namely, we evaluate the equation

$$\begin{aligned} F_u(x[1], x[2], \ldots , x[n]) = \prod _{i=1}^{m} f_i(x[1], x[2], \ldots , x[n])^{u[i]} \end{aligned}$$

and divide the set of u. In [24], a fundamental property of the product of some functions is used, i.e., the algebraic degree of $F_u$ is at most $w(u) \times d$ if the algebraic degree of functions $f_i$ is at most d. However, since we now know the ANF of functions $f_1, f_2, \ldots , f_m$, we can calculate the accurate algebraic degree of $F_u$ for all $u \in \mathbb {F}_2^n$. In this case, if the algebraic degree of $F_u$ is less than $w(u) \times d$ for all u for which w(u) is constant, we can improve the propagation characteristic.

4.1 Application to MISTY S-boxes

Evaluation of ${{\varvec{S}}}_\mathbf{7}$ . The $S_7$ of MISTY is a 7-bit S-box with degree 3. We show the ANF of $S_7$ in Appendix A. We evaluate the property of $(\pi _v \circ S_7)$ to get the propagation characteristic of the division property. The algebraic degree of $(\pi _v \circ S_7)$ increases in accordance with the Hamming weight of v, and it is summarized as follows.

w(v)	0	1	2	3	4	5	6	7
degree	0	3	5	5	6	6	6	7

If we replace the $S_7$ with a modified S-box, which is randomly chosen from all 7-bit S-boxes with degree 3, the algebraic degree of $(\pi _v \circ S)$ is at least 6 with $w(v) \ge 2$. However, for the $S_7$, the increment of the algebraic degree is bounded by 5 with $w(v) = 2$ or $w(v) = 3$ holds². Thus, the propagation characteristic is represented as the following.

$\mathcal{D}_k^7$ for input set $\mathbb {X}$	$\mathcal{D}_0^7$	$\mathcal{D}_1^7$	$\mathcal{D}_2^7$	$\mathcal{D}_3^7$	$\mathcal{D}_4^7$	$\mathcal{D}_5^7$	$\mathcal{D}_6^7$	$\mathcal{D}_7^7$
$\mathcal{D}_k^7$ for output set $\mathbb {Y}$	$\mathcal{D}_0^7$	$\mathcal{D}_1^7$	$\mathcal{D}_1^7$	$\mathcal{D}_1^7$	$\mathcal{D}_2^7$	$\mathcal{D}_2^7$	$\mathcal{D}_4^7$	$\mathcal{D}_7^7$

Notice that the division property $\mathcal{D}_4^7$ is propagated from the division property $\mathcal{D}_6^7$. Assuming that the modified S-box is applied, the division property $\mathcal{D}_2^7$ is propagated from the division property $\mathcal{D}_6^7$ [24]. Therefore, the deterioration of the division property for the $S_7$ is smaller than that for any 7-bit S-box.

Evaluation of ${{\varvec{S}}}_\mathbf{9}$ . The $S_9$ of MISTY is a 9-bit S-box with degree 2. We show the ANF of $S_7$ in Appendix A. We evaluate the property of $(\pi _v \circ S_9)$ to get the propagation characteristic of the division property. The algebraic degree of $(\pi _v \circ S_9)$ increases in accordance with the Hamming weight of v, and it is summarized as follows.

w(v)	0	1	2	3	4	5	6	7	8	9
degree	0	2	4	6	8	8	8	8	8	9

Thus, the propagation characteristic is represented as

$\mathcal{D}_k^9$ for input set $\mathbb {X}$	$\mathcal{D}_0^9$	$\mathcal{D}_1^9$	$\mathcal{D}_2^9$	$\mathcal{D}_3^9$	$\mathcal{D}_4^9$	$\mathcal{D}_5^9$	$\mathcal{D}_6^9$	$\mathcal{D}_7^9$	$\mathcal{D}_8^9$	$\mathcal{D}_9^9$
$\mathcal{D}_k^9$ for output set $\mathbb {Y}$	$\mathcal{D}_0^9$	$\mathcal{D}_1^9$	$\mathcal{D}_1^9$	$\mathcal{D}_2^9$	$\mathcal{D}_2^9$	$\mathcal{D}_3^9$	$\mathcal{D}_3^9$	$\mathcal{D}_4^9$	$\mathcal{D}_4^9$	$\mathcal{D}_9^9$

Unlike the propagation characteristic of the division property for $S_7$, that for $S_9$ is the same as that for any 9-bit S-box with degree 2.

5 New Integral Characteristic

This section shows how to create integral characteristics on MISTY1 by using the propagation characteristic of the division property. We first evaluate the propagation characteristic for the component functions of MISTY1, i.e., the FI function, the FO function, and the FL layer. Finally, by assembling these characteristics, we create an algorithm to search for integral characteristics on MISTY1.

5.1 Division Property for FI Function

We evaluate the propagation characteristic of the division property for the FI function by using those for MISTY S-boxes shown in Sect. 4.1. Since there are a zero-extended XOR and a truncated XOR in the FI function, we use a new representation, in which the internal state is expressed in two 7-bit values and one 2-bit value. Figure 3 shows the structure of the FI function with our representation, where we remove the XOR of sub keys because it does not affect the division property.

Fig. 3.

Structure of FI function

Let $\mathbb {X}_1$ be the input multiset of the FI function. We define every multiset $\mathbb {X}_2, \mathbb {X}_3, \ldots , \mathbb {X}_{11}$ in Fig. 3. Here, elements of the multiset $\mathbb {X}_1$, $\mathbb {X}_5$, $\mathbb {X}_6$, and $\mathbb {X}_{11}$ take a value of $(\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)$. Elements of the multiset $\mathbb {X}_2$, $\mathbb {X}_3$, $\mathbb {X}_{8}$, and $\mathbb {X}_{9}$ take a value of $(\mathbb {F}_2^9 \times \mathbb {F}_2^7)$. Elements of the multiset $\mathbb {X}_4$, $\mathbb {X}_7$, and $\mathbb {X}_{10}$ take a value of $(\mathbb {F}_2^2 \times \mathbb {F}_2^7 \times \mathbb {F}_2^7)$. Since elements of $\mathbb {X}_1$ and $\mathbb {X}_{11}$ take a value of $(\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)$, the propagation for the FI function is calculated on $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{7,2,7}$. Here, the propagation is calculated with the following steps.

• From $\mathbb {X}_1$ to $\mathbb {X}_2$ : A 9-bit value is created by concatenating the first 7-bit value with the second 2-bit value. The propagation characteristic can be evaluated by using Rule 5.

• From $\mathbb {X}_2$ to $\mathbb {X}_3$ : The 9-bit S-box $S_9$ is applied to the first 9-bit value. The propagation characteristic can be evaluated by using Rule 1.

• From $\mathbb {X}_3$ to $\mathbb {X}_4$ : The 9-bit output value is split into a 2-bit value and a 7-bit value. The propagation characteristic can be evaluated by using Rule 4.

• From $\mathbb {X}_4$ to $\mathbb {X}_5$ : The second 7-bit value is XORed with the last 7-bit value, and then, the order is rotated. The propagation characteristic can be evaluated by using Rule 2 and Rule 3.

• From $\mathbb {X}_5$ to $\mathbb {X}_6$ : The 7-bit S-box $S_7$ is applied to the first 7-bit value. The propagation characteristic can be evaluated by using Rule 1.

• From $\mathbb {X}_6$ to $\mathbb {X}_7$ : The first 7-bit value is XORed with the last 7-bit value, and then, the order is rotated. The propagation characteristic can be evaluated by using Rule 2 and Rule 3.

• From $\mathbb {X}_7$ to $\mathbb {X}_8$ : A 9-bit value is created by concatenating the first 2-bit value with the second 7-bit value. The propagation characteristic can be evaluated by using Rule 5.

• From $\mathbb {X}_8$ to $\mathbb {X}_{11}$ : The propagation characteristic is the same as that from $\mathbb {X}_2$ to $\mathbb {X}_5$.

Algorithm 1 creates the propagation characteristic table for the FI function. It calls $\mathtt{SizeReduce}$, where redundant elements are eliminated, i.e., it eliminates $\varvec{k}^{(i)}$ if there exists j satisfying $\varvec{k}^{(i)} \succeq \varvec{k}^{(j)}$. Algorithm 1 only creates the propagation characteristic table for which the input property is represented by $\mathcal{D}_{\varvec{k}}^{7,2,7}$. If any input multiset is evaluated, we need to know the propagation characteristic of $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{7,2,7}$. However, we do not evaluate such propagation in advance because it can easily be evaluated by the table for which the input property is represented by $\mathcal{D}_{\varvec{k}}^{7,2,7}$. We create all propagation characteristic tables by implementing Algorithm 1 and experimentally confirm that Algorithm 1 creates the correct tables.

5.2 Division Property for FO Function

We next evaluate the propagation characteristic of the division property for the FO function by using the propagation characteristic table of the FI function. Figure 4 shows the structure of the FO function, where we remove the XOR of sub keys because it does not affect the division property. The input and output of the FO function take the value of $(\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7 \times \mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)$. Therefore, the propagation for the FO function is calculated on $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{7,2,7,7,2,7}$.

Fig. 4.

Structure of FO function

Similar to that for the FI function, we create the propagation characteristic table for the FO function (see Algorithm 2). We create only a table for which the input property is represented by $\mathcal{D}_{\varvec{k}}^{7,2,7,7,2,7}$ and the output property is represented by $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{7,2,7,7,2,7}$.

5.3 Division Property for FL Layer

MISTY1 has the FL layer, which consists of two FL functions and is applied once every two rounds. In the FL function, the right half of the input is XORed with the AND between the left half and a sub key $KL_{i,1}$. Then, the left half of the input is XORed with the OR between the right half and a sub key $KL_{i,2}$.

Since the input and the output of the FL function take the value of $\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7 \times \mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7$, the propagation for the FL function is calculated on $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{7,2,7,7,2,7}$. FlEval in Algorithm 3 calculates the propagation characteristic table for the FL function, where $\mathtt{SizeReduce}$ eliminates $\varvec{k}^{(i)}$ if there exists j satisfying $\varvec{k}^{(i)} \succeq \varvec{k}^{(j)}$. Moreover, the FL layer consists of two FL functions. Therefore, we have to consider the propagation characteristic of the division property $\mathcal{D}_{\varvec{k}}^{7,2,7,7,2,7,7,2,7,7,2,7}$, where each FL function is applied to the left half and the right one. FlLayerEval in Algorithm 3 calculates the propagation characteristic of the division property for the FL layer.

5.4 Path Search for Integral Characteristic on MISTY1

We created the propagation characteristic table for the FI and FO functions in Sects. 5.1 and 5.2, respectively. Moreover, we showed the propagation characteristic for the FL layer in Sect. 5.3. By assembling these propagation characteristics, we create an algorithm to search for integral characteristics on MISTY1. Since the input and the output are represented as eight 7-bit values and four 2-bit values, the propagation is calculated on $\mathcal{D}_{\varvec{k}^{(1)}, \varvec{k}^{(2)}, \ldots , \varvec{k}^{(q)}}^{7,2,7,7,2,7,7,2,7,7,2,7}$.

The FL layer is first applied to plaintexts, and it deteriorates the propagation of the division property. Therefore, we first remove only the first FL layer and search for integral characteristics on MISTY1 without the first FL layer. The method for passing through the first FL layer is shown in the next paragraph. Algorithm 4 shows the search algorithm for integral characteristics on MISTY1 without the first FL layer.

Fig. 5.

New 6-round integral characteristic

As a result, we can construct 6-round integral characteristics without the first and last FL layers. Each characteristic uses $2^{63}$ chosen plaintexts, where any one bit of the first seven bits is constant and the others take all values. Figure 5 shows the 6-round integral characteristic, where the bit strings labeled B, i.e., the first 7 bits and last 32 bits, are balanced. Notice that the 6-round characteristic becomes a 7-round characteristic if the FL layer that is inserted after the 6th round is removed. Compared with the previous 4-round characteristic [10, 25], our characteristic is improved by two rounds.

Fig. 6.

$KL_{1,2}=1$

Fig. 7.

$KL_{1,1}=0, KL_{1,2}=0$

Fig. 8.

$KL_{1,1}=1, KL_{1,2}=0$

As shown in Sect. 4, the $S_7$ of MISTY1 has the vulnerable property that $\mathcal{D}_4^7$ is provided from $\mathcal{D}_6^7$. Interestingly, assuming that $S_7$ does not have this property (change lines 27–31 in S7Eval), our algorithm cannot construct the 6-round characteristic.

We already know that MISTY1 has the 14th order differential characteristic, which is shown in [23], and the principle was also discussed in [1, 5]. We also evaluate the principle of the characteristic by using the propagation characteristic of the division property. As a result, we confirm that the characteristic always exists if each algebraic degree $S_9$ and $S_7$ is 2 and 3, respectively. This result implies that the existence of the 14th order differential characteristic is only derived from the algebraic degree of S-boxes. Namely, even if different S-boxes are chosen in $S_7$ and $S_9$, the 14th order differential characteristic exists unless the algebraic degree increases.

Passage of First FL Layer. Our new characteristic removes the first FL layer. Therefore, we have to create a set of chosen plaintexts to construct integral characteristics by using guessed round keys $KL_{1,1}$ and $KL_{1,2}$. Here, we have to carefully choose the set of chosen plaintexts to avoid the use of the full code book (see Figs. 6, 7, and 8). In every figure, $A_i$ denotes for which we prepare an input set that i bits are active. As an example, we consider an integral characteristic for which the first one bit is constant and the remaining 63 bits are active. Since all bits of the right half are active, we focus only on the left half. We first guess that $KL_{1,2}[1]=1$, and we then prepare the set of plaintexts like in Fig. 6. We next guess that $(KL_{1,1}[1], KL_{1,2}[1]) = (0,0)$, and we then prepare the set of plaintexts like in Fig. 7. Moreover, we guess that $(KL_{1,1}[1], KL_{1,2}[1]) = (1,0)$, and we then prepare the set of plaintexts like in Fig. 8. Their chosen plaintexts construct 6-round integral characteristics if the guessed key bits are correct. Notice that we do not use $2^{62}$ chosen plaintexts as $(1A_{15}~1A_{15}~A_{16}~A_{16})$. Thus, our integral characteristics use $2^{64}-2^{62} \approx 2^{63.58}$ chosen plaintexts.

6 Key Recovery Using New Integral Characteristic

This section shows the key recovery step of our cryptanalysis, which uses the 6-round integral characteristic shown in Sect. 5. In the characteristic, the left 7-bit value of $X_7^L$ is balanced. To evaluate this balanced seven bits, we have to calculate two FL layers and one FO function by using the guessed round keys. Figure 9 shows the structure of our key recovery step.

Fig. 9.

Key recovery step

6.1 Sub Key Recovery Using Partial-Sum Technique

We guess $KL_{1,1}[i] (= K_1[i])$ and $KL_{1,2}[i] (= K'_7[i])$ and then prepare a set of chosen plaintexts to construct an integral characteristic. In the characteristic, seven bits $X_7^L[1,\ldots ,7]$ are balanced. Therefore, we evaluate whether or not $X_7^L[j]$ is balanced for $j \in \{1,2,\ldots ,7\}$ by using a partial-sum technique [9].

Table 2. Procedure of key recovery step

In the first step, we store the frequency of 34 bits $(C^L, C^R[j, 16+j])$ into a voting table for $j \in \{1,2,\ldots ,7\}$. Then, we partially guess round keys, discard the size of the voting table, and calculate the XOR of $X_7^L[j]$. Table 2 summarizes the procedure of the key recovery step, where every value is defined in Fig. 9. Since the time complexity is the sum of all steps, the time complexity is about $2^{101.5}$. When we repeat the procedure for seven balanced bits, the time complexity becomes $7 \times 2^{101.5}=2^{104.3}$.

The key recovery step has to guess the 124-bit key

$$\begin{aligned}&K_1, K_2, K_5[1,\ldots ,7], K_7, K_8,\\&K'_1[1,\ldots ,7], K'_2[1,\ldots ,7], K'_3[1,\ldots ,7], K'_5, K'_7. \end{aligned}$$

Here, $K_7'$ and $K'_1[1,\ldots ,7]$ are uniquely determined by guessing $K_7, K_8$ and $K_1, K_2$, respectively. Thus, the guessed key bit size is reduced to

$$\begin{aligned}&K_1, K_2, K_5[1,\ldots ,7], K_7, K_8,\\&K'_2[1,\ldots ,7], K'_3[1,\ldots ,7], K'_5, \end{aligned}$$

and it becomes 101 bits. Moreover, since we already guessed 2 bits, i.e., $K_1[i]$ and $K'_7[i]$, to construct integral characteristics, the guessed key bit size is reduced to 99 bits. For wrong keys, the probability that $X_7^L[1,\ldots ,7]$ is balanced is $2^{-7}$. Therefore, the number of the candidates of round keys is reduced to $2^{92}$. Finally, we guess the 27 bits:

$$\begin{aligned} K_5[8,\ldots ,16], K'_2[8,\ldots ,16], K'_3[8,\ldots ,16]. \end{aligned}$$

Notice that $K_3$, $K_4$, and $K_6$ are uniquely determined from $(K_2, K'_2)$, $(K_3, K'_3)$, and $(K_5, K'_5)$, respectively. Therefore, the total time complexity is $2^{92+27}=2^{119}$. We guess the correct key from $2^{119}$ candidates by using two plaintext-ciphertext pairs, and the time complexity is $2^{119}+2^{119-64} \approx 2^{119}$. We have to execute the above procedure against $(K_1[i], K'_7[i])=(0,0),(0,1),(1,0),(1,1)$, and the time complexity becomes $4 \times 2^{119} = 2^{121}$.

6.2 Trade-Off Between Time and Data Complexity

In Sect. 6.1, we use only one set of chosen plaintexts, where $(2^{64}-2^{62})$ chosen plaintexts are required. Since the probability that wrong keys are not discarded is $2^{-7}$, a brute-force search is required with a time complexity of $2^{128-7}=2^{119}$, and it is larger than the time complexity of the partial-sum technique. Therefore, if we have a higher number of characteristics, the total time complexity can be reduced.

To prepare several characteristics, we choose some constant bits from seven bits ($i \in \{1,2,\ldots ,7\}$). If we use a characteristic with $i=1$, we use chosen plaintexts for which plaintext $P^L$ takes the following values

$$\begin{aligned} (00A_{14}~~00A_{14}), (00A_{14}~~01A_{14}), (01A_{14}~~00A_{14}), (01A_{14}~~01A_{14}), \\ (00A_{14}~~10A_{14}), (00A_{14}~~11A_{14}), (01A_{14}~~10A_{14}), (01A_{14}~~11A_{14}), \\ (10A_{14}~~00A_{14}), (10A_{14}~~01A_{14}), (11A_{14}~~00A_{14}), (11A_{14}~~01A_{14}), \end{aligned}$$

where $A_{14}$ denotes that all values appear the same number independent of other bits, e.g., $(00A_{14}~~00A_{14})$ uses $2^{60}$ chosen plaintexts because $P^R$ also takes all values. Moreover, if we use a characteristic with $i=2$, we use chosen plaintexts for which $P^L$ takes the following values

$$\begin{aligned} (00A_{14}~~00A_{14}), (00A_{14}~~10A_{14}), (10A_{14}~~00A_{14}), (10A_{14}~~10A_{14}), \\ (00A_{14}~~01A_{14}), (00A_{14}~~11A_{14}), (10A_{14}~~01A_{14}), (10A_{14}~~11A_{14}), \\ (01A_{14}~~00A_{14}), (01A_{14}~~10A_{14}), (11A_{14}~~00A_{14}), (11A_{14}~~10A_{14}). \end{aligned}$$

When both characteristics are used, they do not require choosing plaintexts for which $P^L$ takes $(11A_{14}~~11A_{14})$. Therefore, $(2^{64}-2^{60})$ chosen plaintexts are required, and the probability that wrong keys are not discarded becomes $2^{-14}$. Similarly, when three characteristics, which require $(2^{64}-2^{58})$ chosen plaintexts, are used, the probability that wrong keys are not discarded becomes $2^{-21}$.

Table 3. Trade-off between time and data complexity

Table 3 summarizes the trade-off between time and data complexity, and it shows that the use of four characteristics is optimized from the perspective of time complexity. Namely, when $(2^{64}-2^{56}) \approx 2^{63.994}$ chosen plaintexts are required, the time complexity to recovery the secret key is $2^{107.3}$.

7 Conclusions

In this paper, we showed a cryptanalysis of the full MISTY1. MISTY1 was well evaluated and standardized by several projects, such as CRYPTREC, ISO/IEC, and NESSIE. We constructed a new integral characteristic by using the propagation characteristic of the division property. Here, we improved the division property by optimizing a public S-box. As a result, a new 6-round integral characteristic is constructed, and we can recover the secret key of the full MISTY1 with $2^{63.58}$ chosen plaintexts and $2^{121}$ time complexity. If we can use $2^{63.994}$ chosen plaintexts, our attack can recover the secret key with a time complexity of $2^{107.9}$.

A MISTY S-boxes

The ANF of $S_7$ is represented as

$$\begin{aligned} y[0]&= x[0] \oplus x[1]x[3] \oplus x[0]x[3]x[4] \oplus x[1]x[5] \oplus x[0]x[2]x[5] \oplus x[4]x[5] \\&\quad \oplus x[0]x[1]x[6] \oplus x[2]x[6] \oplus x[0]x[5]x[6] \oplus x[3]x[5]x[6] \oplus 1, \\ y[1]&= x[0]x[2] \oplus x[0]x[4] \oplus x[3]x[4] \oplus x[1]x[5] \oplus x[2]x[4]x[5] \oplus x[6] \oplus x[0]x[6] \\&\quad \oplus x[3]x[6] \oplus x[2]x[3]x[6] \oplus x[1]x[4]x[6] \oplus x[0]x[5]x[6] \oplus 1, \\ y[2]&= x[1]x[2] \oplus x[0]x[2]x[3] \oplus x[4] \oplus x[1]x[4] \oplus x[0]x[1]x[4] \oplus x[0]x[5] \oplus x[0]x[4]x[5] \\&\quad \oplus x[3]x[4]x[5] \oplus x[1]x[6] \oplus x[3]x[6] \oplus x[0]x[3]x[6] \oplus x[4]x[6] \oplus x[2]x[4]x[6], \\ y[3]&= x[0] \oplus x[1] \oplus x[0]x[1]x[2] \oplus x[0]x[3] \oplus x[2]x[4] \oplus x[1]x[4]x[5] \oplus x[2]x[6] \\&\quad \oplus x[1]x[3]x[6] \oplus x[0]x[4]x[6] \oplus x[5]x[6] \oplus 1, \\ y[4]&= x[2]x[3] \oplus x[0]x[4] \oplus x[1]x[3]x[4] \oplus x[5] \oplus x[2]x[5] \oplus x[1]x[2]x[5] \oplus x[0]x[3]x[5] \\&\quad \oplus x[1]x[6] \oplus x[1]x[5]x[6] \oplus x[4]x[5]x[6] \oplus 1, \\ y[5]&= x[0] \oplus x[1] \oplus x[2] \oplus x[0]x[1]x[2] \oplus x[0]x[3] \oplus x[1]x[2]x[3] \oplus x[1]x[4] \\&\quad \oplus x[0]x[2]x[4] \oplus x[0]x[5] \oplus x[0]x[1]x[5] \oplus x[3]x[5] \oplus x[0]x[6] \oplus x[2]x[5]x[6], \\ y[6]&= x[0]x[1] \oplus x[3] \oplus x[0]x[3] \oplus x[2]x[3]x[4] \oplus x[0]x[5] \oplus x[2]x[5] \oplus x[3]x[5] \\&\quad \oplus x[1]x[3]x[5] \oplus x[1]x[6] \oplus x[1]x[2]x[6] \oplus x[0]x[3]x[6] \oplus x[4]x[6] \oplus x[2]x[5]x[6]. \end{aligned}$$

Moreover, the ANF of $S_9$ is represented as

$$\begin{aligned} y[0]&= x[0]x[4] \oplus x[0]x[5] \oplus x[1]x[5] \oplus x[1]x[6] \oplus x[2]x[6] \oplus x[2]x[7] \oplus x[3]x[7] \oplus x[3]x[8] \\&\quad \oplus x[4]x[8] \oplus 1, \\ y[1]&= x[0]x[2] \oplus x[3] \oplus x[1]x[3] \oplus x[2]x[3] \oplus x[3]x[4] \oplus x[4]x[5] \oplus x[0]x[6] \oplus x[2]x[6] \\&\quad \oplus x[7] \oplus x[0]x[8] \oplus x[3]x[8] \oplus x[5]x[8] \oplus 1,\\ y[2]&= x[0]x[1] \oplus x[1]x[3] \oplus x[4] \oplus x[0]x[4] \oplus x[2]x[4] \oplus x[3]x[4] \oplus x[4]x[5] \oplus x[0]x[6] \\&\quad \oplus x[5]x[6] \oplus x[1]x[7] \oplus x[3]x[7] \oplus x[8], \\ y[3]&= x[0] \oplus x[1]x[2] \oplus x[2]x[4] \oplus x[5] \oplus x[1]x[5] \oplus x[3]x[5] \oplus x[4]x[5] \oplus x[5]x[6]\\&\quad \oplus x[1]x[7] \oplus x[6]x[7] \oplus x[2]x[8] \oplus x[4]x[8], \\ y[4]&= x[1] \oplus x[0]x[3] \oplus x[2]x[3] \oplus x[0]x[5] \oplus x[3]x[5] \oplus x[6] \oplus x[2]x[6] \oplus x[4]x[6] \\&\quad \oplus x[5]x[6] \oplus x[6]x[7] \oplus x[2]x[8] \oplus x[7]x[8], \\ y[5]&= x[2] \oplus x[0]x[3] \oplus x[1]x[4] \oplus x[3]x[4] \oplus x[1]x[6] \oplus x[4]x[6] \oplus x[7] \oplus x[3]x[7] \\&\quad \oplus x[5]x[7] \oplus x[6]x[7] \oplus x[0]x[8] \oplus x[7]x[8], \\ y[6]&= x[0]x[1] \oplus x[3] \oplus x[1]x[4] \oplus x[2]x[5] \oplus x[4]x[5] \oplus x[2]x[7] \oplus x[5]x[7] \oplus x[8] \\&\quad \oplus x[0]x[8] \oplus x[4]x[8] \oplus x[6]x[8] \oplus x[7]x[8] \oplus 1, \\ y[7]&= x[1] \oplus x[0]x[1] \oplus x[1]x[2] \oplus x[2]x[3] \oplus x[0]x[4] \oplus x[5] \oplus x[1]x[6] \oplus x[3]x[6] \\&\quad \oplus x[0]x[7] \oplus x[4]x[7] \oplus x[6]x[7] \oplus x[1]x[8] \oplus 1, \\ y[8]&= x[0] \oplus x[0]x[1] \oplus x[1]x[2] \oplus x[4] \oplus x[0]x[5] \oplus x[2]x[5] \oplus x[3]x[6] \oplus x[5]x[6] \\&\quad \oplus x[0]x[7] \oplus x[0]x[8] \oplus x[3]x[8] \oplus x[6]x[8] \oplus 1. \end{aligned}$$