Zusammenfassung
Die Differentialgeometrie (siehe z. B. [20]) beschäftigt sich mit Objekten, die nicht mehr geradlinig sind, wie zum Beispiel krumme Linien und Flächen. Die Krümmung, die die Abweichung von der Geraden oder der Ebene misst, ist der zentrale Begriff. Während die Krümmung einer Kurve an jeder Stelle durch eine einzige Zahl gegeben wird, ist bei einer Fläche (oder einem höherdimensionalen Gebilde) eine symmetrische Matrix erforderlich, deren Eigenwerte die „Hauptkrümmungen“ der Fläche sind; die Eigenvektoren heißen Hauptkrümmungsrichtungen. Wir werden einen kleinen Teil dieser Geometrie entfalten, und zwar nur im Hinblick auf das nachfolgende Kapitel, in dem die einfachsten krummen Flächen, die von Kugelgestalt, eine besondere Rolle spielen. Diese werden wir unter allen krummen Flächen durch die Eigenschaft kennzeichnen, dass alle tangentialen Richtungen Hauptkrümmungsrichtungen sind. Wir untersuchen sodann eine Klasse krummliniger Koordinatensysteme im Raum, die von den winkeltreuen Abbildungen des folgenden Kapitels erhalten werden, nämlich solche, bei denen sich alle Koordinatenflächen senkrecht schneiden. Die Tangenten der Schnittlinien sind dann Hauptkrümmungslinien für beide Koordinatenflächen, die sich dort schneiden.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Eratosthenes von Kyrene, 276 – 194 v.Chr., vermutete die Kugelgestalt der Erde und bestimmte sogar den Erdumfang, siehe Übung 37.
- 2.
Carl Gustav Jacob Jacobi, 1804 (Potsdam) – 1851 (Berlin).
- 3.
Die Variable in (5.1) ist h, während u und \(\varphi (u)\) als Konstanten zu betrachten sind.
- 4.
Man erhält \(\nu \) folgendermaßen: Für jedes \(u \in \mathbb {R}^{n-1}_o\) ist die Abbildung \(x \mapsto \det (\varphi _1(u),\ldots ,\varphi _{n-1}(u), x)\) eine Linearform auf dem \(\mathbb {R}^n\) (ein Zeilenvektor), differenzierbar von u abhängig. Der zugehörige Spaltenvektor ist \(\nu (u)\), also \(\det (\varphi _1(u),\ldots , \varphi _{n-1}(u),x) = \langle \nu (u), x\rangle \). Im Fall \(n = 3\) ist dies das Kreuzprodukt: \(\nu = \varphi _1 \times \varphi _2\). Offensichtlich ist \(\langle \nu ,\varphi _i\rangle = \det (\varphi _1,\ldots ,\varphi _i,\ldots ,\varphi _{n-1},\varphi _i) = 0\), also ist \(\nu (u) \in N_u\).
- 5.
Johann Carl Friedrich Gauß, 1777 (Braunschweig) – 1855 (Göttingen), schrieb 1828 im Zusammenhang mit der von ihm geleiteten Vermessung des Königreichs Hannover die Arbeit „Disquisitiones generales circa superficies curvas“, „allgemeine Abhandlung über krumme Flächen“ (https://archive.org/details/disquisitionesg00gausgoog). Dort führt er diese Abbildung und die damit zusammenhängende Gaußsche Krümmung ein. Für eine mathematische Würdigung dieser grundlegenden Arbeit siehe M. Spivak: A Comprehensive Introduction to Differential Geometry, Vol. 2, Publish or Perish Inc., 1970, 1999.
- 6.
Wir haben aus Bequemlichkeit die Argumente weggelassen: Die Funktionen \(\varphi ',\nu ',g, h\) sind an der Stelle u zu nehmen und \(\tilde{\varphi }',\tilde{\nu }',\alpha ',\tilde{g},\tilde{h}\) an der Stelle \(\tilde{u}\) mit \(\alpha (\tilde{u}) = u\).
- 7.
Unter den Kreisen, die eine ebene Kurve \(\varphi \) im Punkt \(x=\varphi (u)\) berühren (d. h. durch x gehen und dort die gleiche Tangente haben wie die Kurve) gibt es solche, die nahe x rechts und solche, die nahe x links von der Kurve liegen. Der Kreis, der diese beiden Scharen trennt, ist der Krümmungskreis (vgl. Hilbert, Cohn-Vossen [2]).
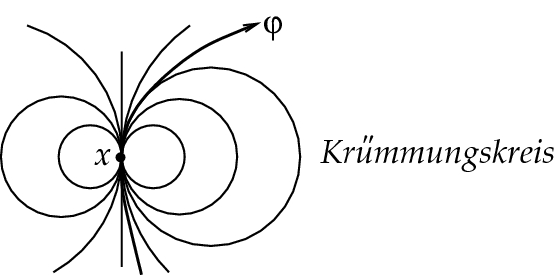
- 8.
Julius Weingarten, 1836 (Berlin) – 1910 (Freiburg/Br.).
- 9.
Leopold Kronecker, 1823 (Liegnitz) – 1891 (Berlin).
- 10.
Georg Friedrich Bernhard Riemann, 1826 (Breselenz bei Dannenberg a.d. Elbe) – 1866 (Selasca bei Verbania, Lago Maggiore).
- 11.
- 12.
Albert Einstein, 1879 (Ulm) – 1955 (Princeton).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2020 Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature
About this chapter
Cite this chapter
Eschenburg, JH. (2020). Krümmung: Differentialgeometrie. In: Geometrie – Anschauung und Begriffe. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-28225-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-658-28225-7_5
Published:
Publisher Name: Springer Spektrum, Wiesbaden
Print ISBN: 978-3-658-28224-0
Online ISBN: 978-3-658-28225-7
eBook Packages: Life Science and Basic Disciplines (German Language)


