Skip to main content
SpringerLink
Log in

H∞ — Optimal Control, LQG Polynomial Systems Techniques and Numerical Solution Procedures

  • Conference paper
Modelling, Robustness and Sensitivity Reduction in Control Systems

Part of the book series: NATO ASI Series ((NATO ASI F,volume 34))

  • 167 Accesses

Abstract

The introductory material first relates the general background of the robustness problem. This is followed by more specific material giving the context for the LQG and polynomial systems approach to the problem of H∞ optimal control design.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Abbreviations

ℝ:

set of real numbers

ℝn :

n-tuple of real numbers

ℝnxm :

nxm — tuple of real numbers

ℙ(.):

set of polynomials with real coefficients

ℝ(.):

set of ratios a(.)/b(.) where a,b ε ℙ(.)

Toep(A):

Toeplitz matrix formed from A ε ℙ (.)

Toep(A) Δ:

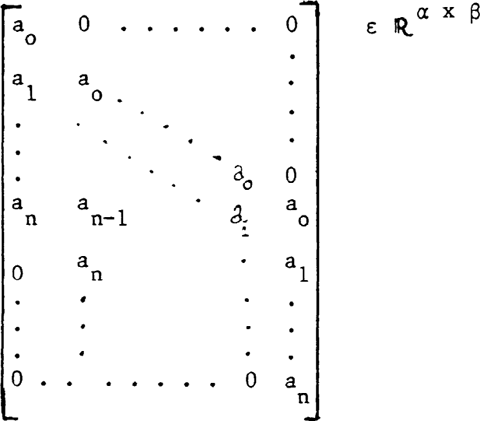
where A = a0 + a1z-1 +...+ anz-n ε ℙ(z-1) and dimensions α, β depend on the order of the polynomial multiplication being represented.

References

  1. Horowitz, I., ‘Synthesis of Feedback Systems’, Academic Press, New York, 1963.

    Google Scholar 

  2. Safonov M.G., and Athans, M., ‘Gain and phase margin for multiloop LQG regulators’, IEEE Trans, on Automatic Control, Vol. AC-22, No. 2, pp. 173–179, 1977.

    Article  MathSciNet  Google Scholar 

  3. Doyle, J.G., ‘Guaranteed margins for LQG regulators’, IEEE Trans. Automatic Control, Vol. AC-23, No. 4, pp. 756–757, 1978.

    Article  Google Scholar 

  4. Doyle J.C., and Stein, G., ‘Robustness with observers’, IEEE Trans. Automatic Control, Vol. AC-24, No. 4, pp. 607–611, August 1979.

    Article  MathSciNet  Google Scholar 

  5. Moore, J.B. and Blight, J.D., ‘Performance and robustness trade-offs in LQG regulator design’, IEEE CDC Conference, San Diego, USA, pp. 1191–1200, 1981.

    Google Scholar 

  6. Grimble, M.J., ‘Robustness of combined state and state-estimate feedback control schemes’, IEEE Trans. Automatic Control, Vol. AC-29, No. 7, pp. 667–669, July 1984.

    Article  MathSciNet  Google Scholar 

  7. Safonov, M.G., Laub, A.J., and Hartmann, G.L., ‘Feedback properties of multivariable systems: The role and use of the return difference matrix’, IEEE Trans. Automatic Control, Vol. AC-26, pp. 47–65, 1981.

    Article  MathSciNet  Google Scholar 

  8. Grimble, M.J., ‘Robust LQG design of discrete systems using a dual criterion’, IEEE CDC Conference, San Antonio, Texas, 1983.

    Google Scholar 

  9. Zaraes, G., 1981, ‘Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms, and approximate inverses’, IEEE Trans. Automatic Control Vol. AC-26, No. 2, pp. 301–320, 1981.

    Google Scholar 

  10. Freudenberg J.S. and Looze, D.P., ‘An analysis of H-optimization design methods’, Research Report, Co-ordinated Science Laboratory University of Illinois, 1983.

    Google Scholar 

  11. Zames, G., and Francis, B.A., ‘A new approach to classical frequency methods: Feedback and minimax sensitivity’, IEEE CDC Conference, San Diego, California, 1981.

    Google Scholar 

  12. Kwakernaak, H., ‘Optimal robustness of linear feedback systems’, Research Report, Mem. Nr.395, Dept. of Appl. Maths, Twente University of Tech. Enschede, The Netherlands, July, 1982.

    Google Scholar 

  13. Kwakernaak, H., ‘Robustness optimization of linear feedback systems’, 22nd IEEE CDC Conference, San Antonio, Texas, Dec. 1983.

    Google Scholar 

  14. Kwakernaak, H., ‘Minimax frequency domain optimization of multivariable linear feedback systems’, IFAC World Congress, Budapest, Hungary, 1984.

    Google Scholar 

  15. Kwakernaak, H., ‘Minimax frequency domain performance and robustness optimization of linear feedback systems’, IEEE Trans. Automatic Control, AC-30, No. 10, pp. 994–1004, 1985.

    Article  MathSciNet  Google Scholar 

  16. Grimble, M.J., ‘Controller for LQG self-tuning applications with coloured measurement noise and dynamic costing’, Proc. IEE Pt. D, Vol. 133, No. 1, Jan. 1986.

    Google Scholar 

  17. Grimble, M.J., ‘Optimal H -robustness and the relationship to LQG design problems’, Int. J. of Control, Vol. 43, No. 2, pp. 351–372, January 1986.

    Article  MATH  Google Scholar 

  18. Saeki, M., ‘Polynomial approach to H∞ — optimal control problem for a discrete time system’. Report ICU/103/1986, Industrial Control Unit, University of Strathclyde, Glasgow, Scotland, UK, (Submitted for Publication).

    Google Scholar 

  19. Saeki, M., and Kornegoor, E., ‘Numerical algorithm for solving a polynomial equation in an H -optimization problems’ Report ICU/121 /1986, Industrial Control Unit, University of Strathclyde, Glasgow, Scotland, UK.

    Google Scholar 

  20. Grimble, M.J., ‘LQG design of discrete systems using a dual criterion’, IEE Proc. Vol. 132, No. 2, pp. 612–68, 1985.

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Information Sciences and Electronics, University of Tsukuba, Niiharigun, Ibaraki, 305, Japan

    M. Saeki

  2. Industrial Control Unit, University of Strathclyde, Glasgow, G1 1XW, Scotland, UK

    M. J. Grimble & M. A. Johnson

  3. Department of Applied Mathematics, Twente University of Technology, 7500 AE, Enschede, The Netherlands

    E. Kornegoor

Authors
  1. M. Saeki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. J. Grimble
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. Kornegoor
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. A. Johnson
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Mathematics Institute, University of Groningen, 9700 AV, Groningen, The Netherlands

    Ruth F. Curtain

Rights and permissions

Reprints and permissions

Copyright information

© 1987 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Saeki, M., Grimble, M.J., Kornegoor, E., Johnson, M.A. (1987). H∞ — Optimal Control, LQG Polynomial Systems Techniques and Numerical Solution Procedures. In: Curtain, R.F. (eds) Modelling, Robustness and Sensitivity Reduction in Control Systems. NATO ASI Series, vol 34. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-87516-8_21

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-87516-8_21

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-87518-2

  • Online ISBN: 978-3-642-87516-8

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation