Abstract
This chapter provides an overview of solid mechanics with applications in biomechanics. It begins wih a coverage of tensors, including the tensor transformation law and tensor invariants, before proceeding to the basic mechanical concepts of stress and strain. Stress and strain are then related via material constitutive laws, the most basic being that of linear elasticity. The concepts of hydrostatic stresses and strains are also introduced, along with the notion of von Mises stress as a representative scalar stress indicator. Other material laws relevant to biological tissues are presented, including linear viscoelasticity and hyperelasticity, as well as anisotropic hyperelastic material laws. Detailed examples of models solved in COMSOL include a strap tension testing device for a respirator mask, as well simulations of simple shear experiments in myocardial tissue. The chapter ends with a set of theoretical and computational COMSOL problems, with fully-worked answers provided in the solution section of the text.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The descriptions here and in the following sections pertain to 3D space by default, however these descriptions are readily generalizable to lower dimensions. For example in 2D, vectors have two components, second-order tensors have four components, and third-order tensors have eight components .
- 2.
This notation was introduced by Albert Einstein (1879–1955) in his 1916 paper on the General Theory of Relativity [5].
- 3.
Augustin-Louis Cauchy (1789–1857) , prolific French mathematician who contributed numerous works in mathematical analysis and the theory of elasticity.
- 4.
Co-named after George Green (1793–1841), British mathematical physicist. We can also define the left Cauchy–Green deformation tensor as \(\mathbf {B} = \mathbf {F}\mathbf {F}^{\mathrm {T}}\).
- 5.
Robert Hooke , 1635–1703, English scientist, mathematician and architect who made numerous contributions to the fields of physics, biology, astronomy and mechanics.
- 6.
Named after the French mathematician Gabriel Léon Jean Baptiste Lamé (1795–1870), who made important contributions to the mathematical theory of elasticity.
- 7.
Thomas Young (1773–1829) , English scientist who made contributions to many fields, including solid mechanics.
- 8.
Siméon Denis Poisson (1781–1840) , French mathematician and physicist.
- 9.
Named after Richard Edler von Mises (1883–1953), German scientist and mathematician who made important contributions to the fields of solid mechanics, fluid mechanics, statistics and probability theory.
- 10.
- 11.
Named after American rheologists Melvin Mooney (1893–1968) and Ronald Samuel Rivlin (1915–2005) .
- 12.
It should also be noted that in some descriptions, the invariants of Eq. 8.41 refer to the standard first and second invariants of the Cauchy–Green deformation tensor.
- 13.
So named because this modified deformation preserves local volume. Defining
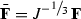 , where \(J = \det \mathbf {F}\), then \(\det \bar{\mathbf {F}} =1\), and
, where \(J = \det \mathbf {F}\), then \(\det \bar{\mathbf {F}} =1\), and  .
. - 14.
Many of these expressions will appear orange-coloured in COMSOL when first entered, indicating that some terms have not yet been defined. This is because we have not yet added the hyperelastic material description, which we will do in the next step.
- 15.
Many of COMSOL’s solid mechanics in-built variables include the term ‘el’, which is short for elastic. COMSOL separates deformations into elastic and inelastic components, with inelastic components arising from non-elastic effects such as thermal expansion and plasticity. For the models presented in this chapter, there are no inelastic effects, hence COMSOL terms such as the elastic isochoric right Cauchy Green tensor are equivalent to the standard definitions presented.
References
Atkin RJ, Fox N (2005) An introduction to the theory of elasticity, Dover edn. Dover, Mineola
Chadwick P (1999) Continuum mechanics: concise theory and problems, Dover edn. Dover, Mineola
Dokos S, Smaill BH, Young AA, LeGrice IJ (2002) Shear properties of passive ventricular myocardium. Am J Physiol Heart Circ Physiol 283:H2650–H2659
Eglit ME, Golublatnikov AN, Kamenjarzh JA, Karlikov VP, Kulikovsky AG, Petrov AG, Shikina IS, Sveshnikova EI (1996) In: Eglit ME, Hodges DH (eds) Continuum mechanics via problems and exercises. World scientific series on nonlinear science. Series A, vol 19. World Scientific, Singapore
Einstein A (1916) The foundation of the general theory of relativity (Tranlated by Engel A). In: Kox AJ, Klein MJ, Schulmann R (eds) The collected papers of Albert Einstein. The Berlin years: Writings, 1914–1917, vol 6, Princeton University press, Princeton, pp 146–200 (1997)
Fung YC (1984) Biomechanics: circulation, 2nd edn. Springer, New York
Fung YC (1994) A first course in continuum mechanics, 3rd edn. Prentice-Hall, Upper Saddle River
Fung YC, Tong P (2001) Classical and computational solid mechanics. World Scientific, Singapore
Holzapfel GA (2000) Nonlinear solid mechanics: a continuum approach for engineering. Wiley, Chichester
Holzapfel G, Gasser T, Ogden R (2000) A new constitutive framework for arterial wall mechanics and a comparative study for material models. J Elast 61:1–48
Schmid H, Wang YK, Ashton J, Ehret AE, Krittian SBS, Nash MP, Hunter PJ (2009) Myocardial material parameter estimation: a comparison of invariant based orthotropic constitutive equations. Comput Meth Biomech Biomed Eng 12:283–295
Spencer AJM (1980) Continuum mechanics. Longman, Burnt Mill
Author information
Authors and Affiliations
Corresponding author
Problems
Problems
8.1
(a) Show that the triple scalar product \((\mathbf {a}\times \mathbf {b})\cdot \mathbf {c}\) is given by
where \(\varepsilon _{ijk}\) is the permutation symbol (a third-order tensor) defined by
(b) Verify that \(\sigma _{ij}^{\mathrm {H}}\varepsilon _{ij}^{\mathrm {D}} = \sigma _{ij}^{\mathrm {D}}\varepsilon _{ij}^{\mathrm {H}} = 0\).
8.2
Determine the Cauchy and Green strain tensors for the following deformations:
(a) Simple shear:

(b) Uniform inflation:

(c) Rotation:

8.3
Consider the left ventricle to be approximated by a spherical shell with inner and outer radii A and B. A uniform pressure is applied to the endocardial (i.e. inner) surface such that the ventricle passively expands to new inner and outer radii of a and b respectively.
(a) Assuming that the myocardium is incompressible, find b as a function of a, A, and B.
(b) Determine the resulting Cauchy strain tensor in the ventricular wall.
8.4
A \(100\times 100\times 1\) mm square piece of rabbit skin tissue is subjected to a tensile test in the laboratory as shown schematically below:

Assume that the constitutive law of the skin tissue obeys a Mooney–Rivlin relationship with material parameters \(C_1\) and \(C_2\) equal to 20 kPa, density \(\rho \) = 1100 kg m\(^{-3}\) and bulk modulus \(K = 1\times 10^6\,\mathrm {kPa}\) . Assume that the leftmost edge of the tissue is clamped (fixed) in place, and that the rightmost edge is subjected to a prescribed displacement only in the x-direction. All other edges are free.
(a) Use COMSOL’s stationary solver to simulate this tensile test and plot the applied force magnitude F (in mN) against skin displacement from 0 to 50 mm.
(b) Plot the spatial distribution of strain energy in the deformed skin sample at its maximum displacement of 50 mm.
8.5
The left ventricle of the heart can be approximated by a circular half-ellipsoidal shell, with endocardial semi-axes of \(a_{\mathrm {endo}}\) and \(b_{\mathrm {endo}}\), and epicardial semi-axes of \(a_{\mathrm {epi}}\) and \(b_{\mathrm {epi}}\), as shown in the figure below:

Assuming the myocardium follows a two-parameter Mooney–Rivlin strain energy formulation , use COMSOL to simulate passive inflation of the venticle using a 2D axisymmetric implementation , and determine endocardial volume in ml as a function of filling pressures from 0 to 50 mmHg. Use the model parameters in the table below, and employ a stationary solver for each pressure. Assume the upper boundary (base) of the ventricle is held fixed, and take the external pressure on the epicardial surface to be zero .
Parameter | Value | Description |
|---|---|---|
\(a_{\mathrm {endo}}\) | 2 cm | Endocardial radius |
\(a_{\mathrm {epi}}\) | 3 cm | Epicardial radius |
\(b_{\mathrm {endo}}\) | 6 cm | Endocardial long semi-axis |
\(b_{\mathrm {epi}}\) | 7 cm | Epicardial long semi-axis |
\(\rho \) | 1200 kg m\(^{-3}\) | Myocardial density |
K | \(1\times 10^6\) kPa | Bulk modulus |
\(C_1\) | 3 kPa | Mooney–Rivlin material parameter |
\(C_2\) | 5 kPa | Mooney–Rivlin material parameter |
Rights and permissions
Copyright information
© 2017 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Dokos, S. (2017). Solid Mechanics. In: Modelling Organs, Tissues, Cells and Devices. Lecture Notes in Bioengineering. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-54801-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-642-54801-7_8
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-54800-0
Online ISBN: 978-3-642-54801-7
eBook Packages: EngineeringEngineering (R0)


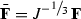 , where
, where  .
.