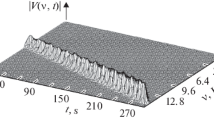
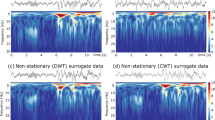
Abstract
We present a new approach to image analysis in temporal sequence of images (data cube). Our method is based on high-order statistical moments (skewness and kurtosis) giving interesting information about a dynamic event in the temporal sequence. The moments enable precise determination of the ”turning points” in the temporal sequence of images. The moment’s curves are analyzed by continuous complex Morlet wavelet that leads to the description of quasi-periodic processes in the investigated event as a time sequence of local spectra. These local spectra are compared with Fourier spectrum. We experimentally illustrate the performance on the real data from astronomical observations.
Chapter PDF
Similar content being viewed by others
References
Dudewicz, E.J., Mishra, S.N.: Modern Mathematical Statistics. Wiley and Sons, New York (1988)
Flusser, J., Suk, T., Zitová, B.: Moments and Moment Invariants in Pattern Recognition. Wiley, Chichester (2009)
Coles, P., Jones, B.: A lognormal model for the cosmological mass distribution. Monthly Notices of the Royal Astronomical Society 248, 1–13 (1991)
Burkhart, B., Falceta-Gonçalves, D., Kowal, G., Lazarian, A.: Density Studies of MHD Interstellar Turbulence: Statistical Moments, Correlations and Bispectrum. Astronomical Journal 693, 250–266 (2009)
Takada, M., Jain, B.: The kurtosis of the cosmic shear field. Monthly Notices of the Royal Astronomical Society 337, 875–894 (2002)
Pain, J.C., Gilleron, F., Bauche, J., Bauche-Arnoult, C.: Effect of third- and fourth-order moments on the modeling of unresolved transition arrays. High Energy Density Physics 5, 294–301 (2009)
Grossi, M., Branchini, E., Dolag, K., Matarrese, S., Moscardini, L.: The mass density field in simulated non-Gaussian scenarios. Monthly Notices of the Royal Astronomical Society 390, 438–446 (2008)
Nita, G.M., Gary, D.E.: The generalized spectral kurtosis estimator. Monthly Notices of the Royal Astronomical Society 406, L60–L64 (2010)
Nita, G.M., Gary, D.E.: Statistics of the Spectral Kurtosis Estimator. Publications of the Astronomical Society 122, 595–607 (2010)
Alipour, N., Safari, H., Innes, D.E.: An Automatic Detection Method for Extreme-ultraviolet Dimmings Associated with Small-scale Eruption. Astronomical Journal 746, 12 (2012)
Marr, D., Hildreth, E.: Theory of edge detection. Proceedings of the Royal Society of London. Series B, Biological Sciences 207(1167), 187–217 (1980)
Li, H.: Complex Morlet wavelet amplitude and phase map based bearing fault diagnosis. In: Proceedings of the 8th World Congress on Intelligent Control and Automation, pp. 6923–6926. IEEE (July 2010)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Šimberová, S., Suk, T. (2013). Analysis of Dynamic Processes by Statistical Moments of High Orders. In: Ruiz-Shulcloper, J., Sanniti di Baja, G. (eds) Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications. CIARP 2013. Lecture Notes in Computer Science, vol 8258. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41822-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-642-41822-8_5
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-41821-1
Online ISBN: 978-3-642-41822-8
eBook Packages: Computer ScienceComputer Science (R0)