Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

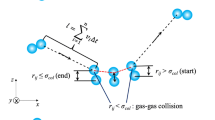
In the present work, the behavior of solid particles of micro- and nanosize in a gas flow is modeled. The motion of solid particles is considered in a coordinate system which moves along with the gas flow. We describe this as a Brownian motion, resulting from the influence of gas on the particles due to thermal fluctuations in the gas pressure. In absence of a temperature gradient (∇T) the time-averaged value of the Brownian fluctuations is zero. Otherwise, it is nonzero because of asymmetric action of the gas flow on the nanoparticles, resulting in a thermophoretic force [1, 2] which shifts the mean position of a particle. The modeling of the thermophoretic force is related to the problem of making traps for particles and their agglomerates without any electro-magnetic or chemical actions on these particles. Here we treat only the simplest case of ∇T = 0.

The following assumptions are made:

  • The influence of the gas on the micro- nanoparticles is negligible;

  • The influence of the micro- nanoparticles on each other is negligibly small as compared to the influence of gas on the particles;

  • Micro-nanoparticles can move in the gas flow in different directions. At each time step a particle moves by certain distance, not necessarily to the next position.

These assumptions are quite natural if, e.g., the concentration of solid particles is sufficiently small, and if external forces are absent. This situation is typical in many important applications dealing with dilute particle flows. Based on these assumptions, first we build up a discrete one-dimensional model, and then we obtain a continuous model as a initial-value boundary problem for certain integro-differential equation. A probabilistic interpretation of the model is given and its solvability is studied. Finally, a generalization to the two-dimensional case is performed.

2 A Discrete One-Dimensional Model

We have build a discrete one-dimensional model based on the following assumptions:

  1. (A)

    At each time moment t = 0, Δ t, 2Δ t, 3Δ t, … each of the micro–nanoparticles can have one of the coordinates 0, ±Δ x, ±2Δ x, ±3Δ x ….

  2. (B)

    If any of the particles in the 1D volume has coordinate i  Δ x (i = 0, ±1, ±2, …) at time moment \(n\,\varDelta t\;(n \in \left \{0 \cup \mathbb{N}\right \})\), then in the next time moment \((n + 1)\varDelta t\;(n \in \left \{0 \cup \mathbb{N}\right \})\) it can have any one of the coordinates j  Δ x (j = 0, ±1, ±2, …) with probability

    $$\displaystyle{ p_{n;i,j}\quad (n \in \left \{0 \cup \mathbb{N}\right \};\,i,j = 0,\pm \varDelta x,\pm 2\varDelta x,\pm 3\varDelta x\ldots ) }$$
    (1)
  3. (C)

    The transition probabilities correspond to the Markov process.

  4. (D)

    The particle-gas system is considered as almost homogeneous and it is assumed that the properties of the system do not depend on the direction of particle motion.

In the limit case, where the number of particles U(m, n) at any coordinate mΔx and time nΔt tends to infinity, we have the following balance equation

$$\displaystyle\begin{array}{rcl} U(m_{1},n + 1) - U(m_{1},n)& \approx & \sum \limits _{{ m_{2}=0,\pm 1,\pm 2,\ldots \atop m_{2}\neq m_{1}} }U(m_{2},n)\,p_{n;m_{2},m_{1}} \\ & -& U(m_{1},n)\sum \limits _{{ m_{2}=0,\pm 1,\pm 2,\ldots \atop m_{2}\neq m_{1}} }p_{n;m_{1},m_{2}}\;.{}\end{array}$$
(2)

This relation is useful to derive an integro-differential equation in the continuum limit considered further on.

3 Continuum Model

Considering the limit, where the number of particles U(m, n) is large, we introduce the particle mass density

$$\displaystyle{ \rho (x,t) = \frac{M} {\varDelta x} U(m,n)\;. }$$
(3)

Here M is the mass of a particle, which is assumed to be constant. In the continuum limit Δ x → 0, Δ t → 0 we have

$$\displaystyle{ \frac{\partial \rho (x,t)} {\partial t} =\lim \limits _{\varDelta x\rightarrow 0}\lim \limits _{\varDelta t\rightarrow 0}\frac{M} {\varDelta x} \,\frac{U(m,n + 1) - U(m,n)} {\varDelta t} \;. }$$
(4)

Dividing both sides of (2) by Δ t, we obtain after certain limit procedures a continuous model as a initial-value boundary problem for the integro-differential equation

$$\displaystyle{ \frac{\partial \rho (x,t)} {\partial t} =\int \limits _{ -l}^{+l}K(t;y,x)\,\rho (y,t)dy -\rho (x,t)\int \limits _{ -l}^{+l}K(t;x,y)dy\;, }$$
(5)

where

$$\displaystyle{ K(t;x,y) =\lim \limits _{{ \varDelta x\rightarrow 0 \atop m_{i}\rightarrow \pm \infty } }\lim \limits _{{ \varDelta t\rightarrow 0 \atop n\rightarrow \pm \infty } }\frac{p(n\varDelta t;m_{1}\varDelta x,m_{2}\varDelta x)} {\varDelta x\,\varDelta t} }$$
(6)

(here i = 1, 2) is the kernel of the integro–differential equation. The used here limit procedures are such that the coordinates \(x\,=\,\lim \limits _{{ \varDelta x\,\rightarrow \,0 \atop m_{1}\,\rightarrow \,\pm \infty } }m_{1}\varDelta x\), \(y\,=\,\lim \limits _{{ \varDelta x\,\rightarrow \,0 \atop m_{2}\,\rightarrow \,\pm \infty } }m_{2}\varDelta x\) and the time \(t\,=\,\lim \limits _{{ \varDelta t\,\rightarrow \,0 \atop n\,\rightarrow \,\pm \infty } }n\varDelta t\) tend to finite values.

Equation (5) has to be solved with appropriate initial and boundary conditions, e.g.,

$$\displaystyle\begin{array}{rcl} & & \rho (x,t)\mid _{t=0} =\rho _{0}(x)\;,\quad x \in [-l,+l]{}\end{array}$$
(7)
$$\displaystyle\begin{array}{rcl} & & \left (\alpha _{1}\rho (x,t) +\beta _{1}\rho {^\prime}(x,t)\right )\mid _{x=-l} =\rho _{1}(t)\;,\quad t \in [0,T]{}\end{array}$$
(8)
$$\displaystyle\begin{array}{rcl} & & \left (\alpha _{2}\rho (x,t) +\beta _{2}\rho {^\prime}(x,t)\right )\mid x = l =\rho _{2}(t)\;,\quad t \in [0,T]\;,{}\end{array}$$
(9)

where ρ 0(x) is the initial distribution which obeys the boundary conditions.

The kernel of the integro–differential equation K(t; z 1, z 2) is equal to the probability density for moving a particle from \(z_{1} \in [-l,+l]\) to \(z_{2} \in [-l,+l]\) (z 1 ≠ z 2) at t ∈ [0, T]. More precisely, \(K(t;z_{1},z_{2})dz_{2}dt\) is the probability that a jump from a given point z 1 to z ∈ [z 2, z 2 + dz] occurs within a time interval dt. Due to the assumed isotropy and homogeneity of the model, we have \(K(t;z_{1},z_{2}) \equiv K(t;\mid z_{1} - z_{2}\mid )\).

The density ρ(x, t) of micro-nanoparticles in gas flow can be interpreted as the density of mathematical expectation of particle mass. If we consider a random walk of a single particle, then ρ(x, t) is the probability density for finding this particle at coordinate x at time t.

4 Solvability of the Model

We have investigated the solvability of the model and have found a sufficient condition in the form of an inequality

$$\displaystyle{ 12\,{(\varDelta x)}^{2}\int \limits _{ 0}^{l}K(t;z){z}^{2}dz \gg \int \limits _{ 0}^{l}K(t;z){z}^{4}dz\;,\qquad \forall x \in [-l,+l],\;t \in (0,T]\quad }$$
(10)

for the existence and uniqueness of the solution, where Δ x is the average jump interval. It implies a sufficiently fast convergence of a Taylor series expansion around y = x in our integro–differential equation (5).

5 The Fokker–Planck Equation

If the stability condition (10) is satisfied, then the Fokker–Planck equation [3]

$$\displaystyle{ \frac{\partial \rho (x,t)} {\partial t} = {a}^{2}(t)\,\frac{{\partial }^{2}\rho (x,t)} {\partial {x}^{2}} }$$
(11)

is obtained by truncating the Taylor series, where

$$\displaystyle{ {a}^{2}(t) =\int \limits _{ 0}^{l}K(t;z)\,{z}^{2}dz > 0 }$$
(12)

is the sensitivity or the diffusion coefficient. It can depend on time t in general.

6 The Two-Dimensional Case

Our model can be easily extended to the two-dimensional case, where we have

$$\displaystyle\begin{array}{rcl} \frac{\partial \rho (x_{1},x_{2},t)} {\partial t} & =& \int \limits _{-l_{1}}^{+l_{1} }dy_{1}\int \limits _{-l_{2}}^{+l_{2} }K(t;y_{1},y_{2};x_{1},x_{2})\,\rho (y_{1},y_{2},t)dy_{2} \\ & -& \rho (x_{1},x_{2},t)\int \limits _{-l_{1}}^{+l_{1} }dy_{1}\int \limits _{-l_{2}}^{+l_{2} }K(t;x_{1},x_{2};y_{1},y_{2})dy_{2}\;.{}\end{array}$$
(13)

Here ρ(x 1, x 2, t) is the two-dimensional particle mass density (or probability density for finding a single randomly walking particle at certain position). The kernel \(K(t;x_{1},x_{2};y_{1},y_{2})\) is the probability density for moving a particle from certain point (x 1, x 2) in the two-dimensional domain to vicinity of another point (y 1, y 2).

7 Conclusions

A mathematical model is developed, describing the motion of micro-nanoparticles in a gas flow by means of an integro–differential equation. Solvability of this model has been studied, showing that it has a unique solution under certain conditions. The Fokker–Planck equation can be obtained from the integro–differential equation at this condition.