Abstract
The ninth-century treatise Scolica enchiriadis (SE) offers two notions of “interval,” namely ratio (proportion) and step distance. The latter notion entails a “generic” distance (cf. “fifth”); however, suggestive diagrams clarify that a “specific” distance is assumed as well (cf. “perfect fifth”). SE raises the question, how to pair step distances such as perfect octave (diapason), perfect fifth (diapente), and perfect fourth (diatessaron), with ratios such as 2:1, 3:2, and 4:3, respectively. In answer, SE departs from the Boethian tradition whereby the distinction between say, duple (2:1) and diapason, is merely terminological. Moreover, SE points out that multiplication of ratios corresponds to addition of step distances, in a manner to which a modern-day mathematician would apply the term homomorphism. Even though the “daseian” tone system proposed in SE (and the “sister” treatise Musica enchiriadis) was discarded already in the middle ages, the SE insights into “proto-tonal” theory, the background system of tones prior to the selection of a central tone or “final,” are still relevant.
This chapter is reprinted by permission from Music Theory Spectrum 35(1), pp. 103–110, with minor adaptations. Copyright © 2013 Society for Music Theory.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Erickson (1995), p. 79. All excerpts from Musica enchiriadis (ME) and Scolica enchiriadis (SE) cited henceforth are in Erickson’s translation. Unless otherwise noted, all excerpts from Boethius’s De institutione musica (IM) are in Bower’s translation (Boethius 1989). All excerpts from Ptolemy’s Harmonics are in Solomon’s (2000) translation. Special thanks to Oliver Wiener for granting permission to use his Dasia font.
- 2.
In the course of the mathematical discussion the author presents a diagram that represents the musically most important proportions in terms of the integers 6, 8, 9, 12, 16, 18, and 24. For an interesting interpretation of this diagram see Carey and Clampitt (1996).
- 3.
This is in fact “another argument” which, the master believes, “adds credence” to the two answers that he gives to the disciple’s question Q. I shall consider the answers presently.
- 4.
Erickson (1995, footnote on p. 75) notes here that “from this exchange it is clear that the discussion concerns the Greater Perfect System rather than the daseian system described earlier in the treatise, since the latter does not ‘always’ (semper) produce the diapason at the eighth step.” An alternative explanation is that the enchiriadis theorists are simply unable to reconcile the contradiction, inherent in their tone system, between octave periodicity and fifth periodicity. Concerning the enchiriadis tone system, see Fig. 1.1 and its discussion. See also footnote 12.
- 5.
A summary of the proto-tonal insights closes this chapter. The insights are largely independent of the enchiriadis tone system (see Fig. 1.1 and its discussion), where of course the existence of four modal qualities is assumed a priori (the enchiriadis system, in other words, is not a proto-tonal theory in the sense defined). For example, the “C-major scale” of Fig. 1.5 specifically avoids the augmented octave that the system occasionally dictates. Moreover, the modality of the scale does not seem to be of any particular concern; rather, the relation “fifth plus fourth equals fourth plus fifth,” is the focus of attention. See also footnotes 12 and 14.
- 6.
This is so even though Boethius’s intervallic terminology, inherited from the Greeks, is double-sided (for example, diapason/duple). For example, in the statement from IM just quoted “duple” is tacitly exchanged with “diapason” (“because the recognition of the duple is easier, Nicomachus considers the diapason to be the optimum consonance”). Indeed, in I.7 Boethius poses a question that seems remarkably similar to Q: “Which ratios should be fitted to which musical consonances”? However, unlike SE, the answer that he provides is tautological: “… All musical consonances consist of a duple, triple, quadruple, sesquialter, or sesquitertian ratio. Moreover, that which is sesquitertian in number will be called ‘diatessaron’ in sounds; that which is sesquialter in number is called ‘diapente’ in pitches; that which is duple in ratios, ‘diapason’ among consonances….” Despite an occasional lapse, the rigor with which SE pursues the distinction between symphonies (as type-1 intervals) and proportions (as type-2 intervals) is, to the best of my knowledge, unprecedented.
- 7.
Note that the master inadvertently refers to the proportions 3:2 and 3:1 as “symphonies.”
- 8.
Erickson (1995, footnote on p. 80) follows Bower (Boethius 1989, footnote on p. 73) in translating sensus as “critical faculty,” since “this word… cannot refer to the senses, regarded as untrustworthy by the Pythagoreans .” Note, however, that it is “the ear” that perceives the diapente to be “next in rank” after the diapason.
- 9.
Ptolemy ’s Harmonics, the basis for Book V of Boethius ’s IM, sets a notable precedent in this regard. Prior to pairing them with ratios, Ptolemy (pp. 22–23) partitions the intervals into (1) “homophones” (the octave and its compounds), “which make an impact on our hearing in the conjunction of one sound”; (2) “consonances” (fourths and fifths), which “are nearest the homophones”; and (3) “emmelic,” “those nearest the consonances, for example, the whole tones and the rest of the intervals of that sort” (I.7, “How the Ratios of the Consonances Could Be More Properly Defined”). For Boethius’s rendering of this passage (which he conflates with Ptolemy’s I.4), see IM, V.11. Recall that in I.7, Boethius, unlike Ptolemy, for all practical purposes equates consonances with ratios.
- 10.
Compare the following statement in ME (p. 15) concerning the diapason: “In this symphony the pitches can be said to be not so much ‘sounding well together’ (consonae) as ‘equal-sounding’ (aequisonae), for in this symphony a pitch is revealed anew.” See also Boethius , IM, V.12 (paraphrasing Ptolemy ).
- 11.
- 12.
Note that despite the fifth-periodicity of the tone system, in the enchiriadis treatises the agent of equivalence is the perfect octave and no other type-1 interval (the notes of an octave are “equal-sounding,” whereas those of a fifth “are different in highness and lowness”). It seems fair to say that, in the final analysis, the enchiriadis theorists are unable to reconcile the conflict between octave and fifth periodicity. This failure may have contributed to the system’s relatively early demise.
- 13.
“Line of fifths” is Temperley ’s (2000) term.
- 14.
The present reader has chosen, of course, not to take the existence of only four types of note at face value. Indeed, as discussed in connection with Fig. 1.1a, I believe the enchiriadis system allows for an infinite number of note types in principle, though for practical reasons only ten can be used. The protus, deuterus, tritus, and tetrardus types, I believe, serve a purely modal purpose.
- 15.
- 16.
As several authors have pointed out, at this point the author of SE “bends” the conventions of the daseian notational system such that the symbols relinquish to some extent their “absolute” meaning in favor of a “relative” one. For a particularly insightful account, see Cohen (2002, pp. 328−329).
- 17.
In another representation of the same type E is altered to E
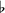 relative to the D-A-D pentachord. Also relative to both the C-G-C and D-A-D pentachords, SE illustrates the alteration of F to F
relative to the D-A-D pentachord. Also relative to both the C-G-C and D-A-D pentachords, SE illustrates the alteration of F to F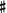 . Though the term “semitonal grid” may seem anachronistic, it seems to be the only interpretation of the graphics proposed to date. Phillips
, for example (1990, p. 105; 2000, p. 323) states that “there are … many diagrams in Scolica enchiriadis in which series of little blocks represent semitones,” noting that the idea of a “semitone-per-block” (Halbton pro Block) representation may be traced back to Boethius
’s “wing” diagram of the modes (IM, IV.16). Erickson
(1995, p. 39, footnote) explains that in the block diagrams “… horizontal lines [are] being used to indicate semitone boundaries.” As shall be clarified shortly, equal temperament is not necessarily implied.
. Though the term “semitonal grid” may seem anachronistic, it seems to be the only interpretation of the graphics proposed to date. Phillips
, for example (1990, p. 105; 2000, p. 323) states that “there are … many diagrams in Scolica enchiriadis in which series of little blocks represent semitones,” noting that the idea of a “semitone-per-block” (Halbton pro Block) representation may be traced back to Boethius
’s “wing” diagram of the modes (IM, IV.16). Erickson
(1995, p. 39, footnote) explains that in the block diagrams “… horizontal lines [are] being used to indicate semitone boundaries.” As shall be clarified shortly, equal temperament is not necessarily implied. - 18.
The next set of diagrams, illustrating the alteration of F to F
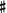 relative to the D-A-D pentachord, also forms a triple.
relative to the D-A-D pentachord, also forms a triple. - 19.
That is, the semitone follows the second tone rather than the third.
- 20.
In addition to being graphically viable, this interpretation receives at least partial terminological support, for the daseian signs are identified with the first four ordinal numbers (protus is Greek for “first,” deuterus is “second,” etc.).
- 21.
Since we are interested primarily in intervals, (0, 0) as origin is an arbitrary (though convenient) choice. For present purposes, any two sets of eight and five consecutive integers will do.
- 22.
See Agmon (1990), where “cognitive interval” is given a similar integer-pair interpretation. Needless to say, the author of SE never explicitly identifies type-1 intervals with integer pairs (at least in so far as “explicit” refers to verbally, as opposed to graphically, encoded information).
- 23.
The verbs intendo and remitto (literally, “to increase” and “to decrease”), used by Boethius in IM III.3, are translated by Bower as “to add” (or “ascend”) and “to subtract” (or “descend”). However, multiplication and division are in fact the operations performed in this passage.
- 24.
Once again, Ptolemy (Harmonics, I.5) may have paved the way. In the context of “… the Pythagoreans’ Positions Concerning the Hypotheses of the Consonances” he states (p. 18) that “… it happens that the diapason is composed from the two, successive first consonances, the diapente and the diatessaron, while the duple ratio is composed of the two, successive first superparticular ratios, the sesquialter (3:2) and the sesquitertian (4:3).” However, only in SE is it explicitly clear, both verbally and graphically, that addition of step sizes, as distinct from multiplication of ratios, is the sense in which the diapason is “composed” of the diapente and the diatessaron. The idea that the octave (as the ratio 2:1) is composed of the fourth and fifth (as the ratios 4:3 and 3:2) is stated by the early Pythagorean Philolaus as follows (Barker 1989, p. 37): “The magnitude of harmonia is syllaba and di’oxeian.”
- 25.
Boethius (IM, II.20) presents a similar diagram. It appears after citing in II.19 the early Pythagoreans Eubulides and Hippasus as saying that “… increments of multiplicity correspond to diminution of superparticularity in a fixed order. Accordingly, there cannot be a duple unless a half occurs nor a triple unless a third part occurs” (emphasis added).
- 26.
See Fig. 44 in Erickson (1995). Even though strict equal temperament (ET) may seem incompatible with a ninth-century musical system, it might be worth noting that it shares with Pythagorean intonation (PI) the homomorphism property (in ET intervals (u, v) are mapped, though not one-to-one, into frequency ratios 2 to-the-power-of u/12). Indeed, in addition to the perfect octave ET shares with PI the tuning of the crucially important perfect fifth, at least insofar as the difference between the irrational 2 to-the-power-of 7/12 (approximately 1.4983) and the rational 1.5 is, for all practical purposes, negligible. Proving the homomorphism property of both PI and ET as mappings from “type-1” into “type-2” interval space is a relatively straightforward mathematical exercise. In the case of PI it is important to note that for every type-1 interval (u, v) there exist unique integers k and l such that (u, v) = k(7, 4) + l(12, 7).
References
Agmon, E. (1990). Music theory as cognitive science: Some conceptual and methodological issues. Music Perception, 7(3), 285–308.
Babb, W. (Trans.). (1978). Hucbald, Guido, and John on music: Three medieval treatises. New Haven: Yale University Press.
Barker, A. (Ed.). (1989). Greek musical writings II: Harmonic and acoustic theory. Cambridge: Cambridge University Press.
Boethius, A. M. S. (1989). Fundamentals of music (C. Bower, Trans.). New Haven: Yale University Press.
Carey, N., & Clampitt, D. (1996). Regions: A theory of tonal spaces in early medieval treatises. Journal of Music Theory, 40(1), 113–141.
Clough, J., & Myerson, G. (1985). Variety and multiplicity in diatonic systems. Journal of Music Theory, 29(2), 249–270.
Cohen, D. (2002). Notes, scales, and modes in the earlier middle ages. In T. Christensen (Ed.), The Cambridge history of Western music theory (pp. 307–363). Cambridge: Cambridge University Press.
Erickson, R. (Trans.). (1995). Musica enchiriadis and Scolica enchiriadis. New Haven: Yale University Press.
Jacobsthal, G. (1897). Die chromatische Alteration im liturgischen Gesang der abendländischen Kirche. Berlin: Springer. 1970. Reprint, Hildesheim: Olms.
Phillips, N. (1990). Classical and late Latin sources for ninth-century treatises on music. In A. Barbera (Ed.), Music theory and its sources: Antiquity and the Middle Ages (pp. 100–135). Notre Dame: University of Notre Dame Press.
Phillips, N. (2000). Notationen und Notationslehren von Boethius bis zum 12. Jahrhundert. In T. Ertelt & F. Zaminer (Eds.), Geschichte der Musiktheorie 4 (pp. 293–623). Darmstadt: Wissenschaftliche Buchgesellschaft.
Schmid, H. (Ed.). (1981). Musica et scolica enchiriadis una cum aliquibus tractatulis adiunctis. Munich: Bayerische Akademie der Wissenschaften. Electronic ed. in Thesaurus Musicarum Latinarum, G. Di Bacco (Director). http://www.chmtl.indiana.edu. Accessed 10 Jan 2012.
Solomon, J. (2000). Ptolemy Harmonics: Translation and commentary. Leiden: Brill.
Temperley, D. (2000). The line of fifths. Music Analysis, 19(3), 289–319.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Agmon, E. (2013). Proto-tonal Theory: Tapping into Ninth-Century Insights. In: The Languages of Western Tonality. Computational Music Science. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-39587-1_1
Download citation
DOI: https://doi.org/10.1007/978-3-642-39587-1_1
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-39586-4
Online ISBN: 978-3-642-39587-1
eBook Packages: Computer ScienceComputer Science (R0)


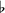 relative to the D-A-D pentachord. Also relative to both the C-G-C and D-A-D pentachords, SE illustrates the alteration of F to F
relative to the D-A-D pentachord. Also relative to both the C-G-C and D-A-D pentachords, SE illustrates the alteration of F to F . Though the term “semitonal grid” may seem anachronistic, it seems to be the only interpretation of the graphics proposed to date. Phillips
, for example (
. Though the term “semitonal grid” may seem anachronistic, it seems to be the only interpretation of the graphics proposed to date. Phillips
, for example (