Abstract
Given a point A in the real Grassmannian, it is well-known that one can construct a soliton solution u A (x,y,t) to the KP equation. The contour plot of such a solution provides a tropical approximation to the solution when the variables x, y, and t are considered on a large scale and the time t is fixed. In this paper we give an overview of our work on the combinatorics of such contour plots. Using the positroid stratification and the Deodhar decomposition of the Grassmannian (and in particular the combinatorics of Go-diagrams), we completely describe the asymptotics of these contour plots when y or t go to ±∞. Other highlights include: a surprising connection with total positivity and cluster algebras; results on the inverse problem; and the characterization of regular soliton solutions—that is, a soliton solution u A (x,y,t) is regular for all times t if and only if A comes from the totally non-negative part of the Grassmannian.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The convention of [25] was to place the boundary vertices in clockwise order.
- 2.
This forbidden pattern is in the shape of a backwards L, and hence is denoted
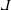 and pronounced “Le.”
and pronounced “Le.” - 3.
Actually Postnikov’s convention was to set π :(i)=j above, so the decorated permutation we are associating is the inverse one to his.
- 4.
Our numbering differs from that in [22] in that the rows of our matrices in SL n are numbered from the bottom.
- 5.
Since
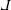 -diagrams are a special case of Go-diagrams, one might also refer to them as Lego diagrams.
-diagrams are a special case of Go-diagrams, one might also refer to them as Lego diagrams. - 6.
Recall from Definition 2.11 that our convention is to label boundary vertices of a plabic graph 1,2,…,n in counterclockwise order. If one chooses the opposite convention, then one must replace the word counterclockwise in Definition 9.7 by clockwise.
References
M. J. Ablowitz, P. A. Clarkson, Solitons, nonlinear evolution equations and inverse scattering, Cambridge University Press, Cambridge, 1991.
G. Biondini, S. Chakravarty, Soliton solutions of the Kadomtsev-Petviashvili II equation, J. Math. Phys. 47 (2006), 033514 (26 pp).
G. Biondini, Y. Kodama, On a family of solutions of the Kadomtsev-Petviashvili equation which also satisfy the Toda lattice hierarchy, J. Phys. A, Math. Gen. 36 (2003), 10519–10536.
A. Bjorner, F. Brenti, Combinatorics of Coxeter groups, Graduate Texts in Mathematics 231, Springer, New York, 2005.
S. Chakravarty, Y. Kodama, Classification of the line-solitons of KPII, J. Phys. A, Math. Theor. 41, (2008) 275209 (33 pp).
S. Chakravarty, Y. Kodama, A generating function for the N-soliton solutions of the Kadomtsev-Petviashvili II equation, Contemp. Math. 471 (2008), 47–67.
S. Chakravarty, Y. Kodama, Soliton solutions of the KP equation and applications to shallow water waves, Stud. Appl. Math. 123 (2009), 83–151.
V. Deodhar, On some geometric aspects of Bruhat orderings. I. A finer decomposition of Bruhat cells, Invent. Math. 79, no. 3 (1985), 499–511.
L. A. Dickey, Soliton equations and Hamiltonian systems, Advanced Series in Mathematical Physics 12, World Scientific, Singapore, 1991.
S. Fomin, A. Zelevinsky, Cluster algebras I: foundations, J. Am. Math. Soc. 15 (2002), 497–529.
N. Freeman, J. Nimmo, Soliton-solutions of the Korteweg-deVries and Kadomtsev-Petviashvili equations: the Wronskian technique, Phys. Lett. A 95 (1983), 1–3.
R. Hirota, The direct method in soliton theory, Cambridge University Press, Cambridge, 2004.
B. B. Kadomtsev, V. I. Petviashvili, On the stability of solitary waves in weakly dispersive media, Sov. Phys. Dokl. 15 (1970), 539–541.
D. Kazhdan, G. Lusztig, Representations of Coxeter groups and Hecke algebras, Invent. Math. 53, no. 2 (1979), 165–184.
D. Kazhdan, G. Lusztig, Schubert varieties and Poincaré duality, Geometry of the Laplace operator (Proc. sympos. pure math., Univ. Hawaii, Honolulu, Hawaii, 1979), 185–203, Proc. Sympos. Pure Math. XXXVI, Am. Math. Soc., Providence, 1980.
Y. Kodama, Young diagrams and N-soliton solutions of the KP equation, J. Phys. A, Math. Gen. 37 (2004), 11169–11190.
Y. Kodama, KP solitons in shallow water, J. Phys. A, Math. Theor. 43 (2010), 434004 (54 pp).
Y. Kodama, L. Williams, KP solitons, total positivity, and cluster algebras, Proc. Natl. Acad. Sci. USA 108, no. 22 (2011), 8984–8989.
Y. Kodama, L. Williams, KP solitons and total positivity for the Grassmannian, arXiv:1106.0023.
Y. Kodama, L. Williams, A Deodhar decomposition of the Grassmannian and the regularity of KP solitons, Adv. Math. 244 (2013), 979–1032.
G. Lusztig, Total positivity in partial flag manifolds, Represent. Theory 2 (1998), 70–78.
R. Marsh, K. Rietsch, Parametrizations of flag varieties, Represent. Theory 8 (2004).
T. Miwa, M. Jimbo, E. Date, Solitons: differential equations, symmetries and infinite-dimensional algebras, Cambridge University Press, Cambridge, 2000.
S. Novikov, S. V. Manakov, L. P. Pitaevskii, V. E. Zakharov, Theory of solitons: the inverse scattering method, Contemporary Soviet Mathematics, Consultants Bureau, New York, 1984.
A. Postnikov, Total positivity, Grassmannians, and networks, http://front.math.ucdavis.edu/math.CO/0609764.
M. Sato, Soliton equations as dynamical systems on an infinite dimensional Grassmannian manifold, RIMS Kokyuroku 439 (1981), 30–46.
J. Satsuma, A Wronskian representation of N-soliton solutions of nonlinear evolution equations, J. Phys. Soc. Jpn. 46 (1979), 356–360.
J. Scott, Grassmannians and cluster algebras, Proc. Lond. Math. Soc. (3) 92 (2006), 345–380.
J. Stembridge, On the fully commutative elements of Coxeter groups, J. Algebr. Comb. 5 (1996), 353–385.
Acknowledgements
The first author (YK) was partially supported by NSF grants DMS-0806219 and DMS-1108813. The second author (LW) was partially supported by an NSF CAREER award and an Alfred Sloan Fellowship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Kodama, Y., Williams, L. (2013). Combinatorics of KP Solitons from the Real Grassmannian. In: Buan, A., Reiten, I., Solberg, Ø. (eds) Algebras, Quivers and Representations. Abel Symposia, vol 8. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-39485-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-642-39485-0_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-39484-3
Online ISBN: 978-3-642-39485-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


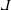 and pronounced “Le.”
and pronounced “Le.”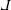 -diagrams are a special case of Go-diagrams, one might also refer to them as Lego diagrams.
-diagrams are a special case of Go-diagrams, one might also refer to them as Lego diagrams.