Abstract
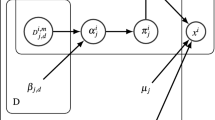
In this paper, a Bayesian framework for non-parametric density estimation with spatial smoothness constraints is presented for image segmentation. Unlike common parametric methods such as mixtures of Gaussians, the proposed method does not make strict assumptions about the shape of the density functions and thus, can handle complex structures. The multiclass kernel density estimation is considered as an unsupervised learning problem. A Dirichlet compound multinomial (DCM) prior is used to model the class label prior probabilities and a Markov random field (MRF) is exploited to impose the spatial smoothness and control the confidence on the Dirichlet hyper-parameters, as well. The proposed model results in a closed form solution using an expectation-maximization (EM) algorithm for maximum a posteriori (MAP) estimation. This provides a huge advantage over other models which utilize more complex and time consuming methods such as Markov chain Monte Carlo (MCMC) or variational approximation methods. Several experiments on natural images are performed to present the performance of the proposed model compared to other parametric approaches.
Chapter PDF
Similar content being viewed by others
Keywords
References
Ding, L., Yilmaz, A., Yan, R.: Interactive Image Segmentation Using Dirichlet Process Multiple-View Learning. IEEE Transactions on Image Processing 21(4), 2119–2129 (2012)
Nikou, C., Likas, A.C., Galatsanos, N.P.: A Bayesian Framework for Image Segmentation With Spatially Varying Mixtures. IEEE Transactions on Image Processing 19(9), 2278–2289 (2010)
Andreetto, M., Zelnik-Manor, L., Perona, P.: Non-Parametric Probabilistic Image Segmentation. In: IEEE 11th International Conference on Computer Vision, ICCV 2007, October 14-21, pp. 1–8 (2007)
Zhang, Y., Brady, M., Smith, S.: Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging 20(1), 45–57 (2001)
Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, New York (2006)
Martin, D., Fowlkes, C., Tal, D., Malik, J.: A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, vol. 2, pp. 416–423 (2001)
The Berkeley Segmentation Dataset and Benchmark, http://www.eecs.berkeley.edu/Research/Projects/CS/vision/bsds
Bowyer, K., Kranenburg, C., Dougherty, S.: Edge detector Evaluation Using Empirical ROC Curves. Computer Vision and Image Understanding 84(1), 77–103 (2001)
Carson, C., Belongie, S., Greenspan, H., Malik, J.: Blobworld: image segmentation using expectation-maximization and its application to image querying. IEEE Transactions on Pattern Analysis and Machine Intelligence 24(8), 1026–1038 (2002)
Zelnik-Manor, L., Perona, P.: Self-Tuning Spectral Clustering. In: Advances in Neural Information Processing Systems (NIPS), pp. 1601–1608 (2005)
Frigyik, B.A., Kapila, A., Gupta, M.R.: Introduction to the Dirichlet Distribution and Related Processes. UWEE Technical report (2010)
Li, S.Z.: Markov Random Field Modeling in Image Analysis. Springer, Tokyo (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Amid, E. (2013). Bayesian Non-parametric Image Segmentation with Markov Random Field Prior. In: Kämäräinen, JK., Koskela, M. (eds) Image Analysis. SCIA 2013. Lecture Notes in Computer Science, vol 7944. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-38886-6_8
Download citation
DOI: https://doi.org/10.1007/978-3-642-38886-6_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-38885-9
Online ISBN: 978-3-642-38886-6
eBook Packages: Computer ScienceComputer Science (R0)