Abstract
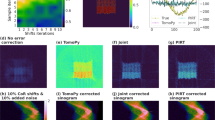
As tomographic imaging is being performed at increasingly smaller scales, the stability of the scanning hardware is of great importance to the quality of the reconstructed image. Instabilities lead to perturbations in the geometrical parameters used in the acquisition of the projections. In particular for electron tomography and high-resolution X-ray tomography, small instabilities in the imaging setup can lead to severe artifacts. We present a novel alignment algorithm for recovering the true geometrical parameters after the object has been scanned, based on measured data. Our algorithm employs an optimization algorithm that combines alignment with reconstruction. We demonstrate that problem-specific design choices made in the implementation are vital to the success of the method. The algorithm is tested in a set of simulation experiments. Our experimental results indicate that the method is capable of aligning tomography datasets with considerably higher accuracy compared to standard cross-correlation methods.
Chapter PDF
Similar content being viewed by others
References
Slaney, M., Kak, A.: Principles of computerized tomographic imaging. Society for Industrial and Applied Mathematics (1988)
Jing, Z., Sachs, F.: Alignment of tomographic projections using an incomplete set of fiducial markers. Ultramicroscopy 35(1), 37–43 (1991)
Szeliski, R.: Image alignment and stitching: A tutorial. Foundations and Trends® in Computer Graphics and Vision 2(1), 1–104 (2006)
Viola, P., Wells III, W.: Alignment by maximization of mutual information. International Journal of Computer Vision 24(2), 137–154 (1997)
Zitova, B., Flusser, J.: Image registration methods: a survey. Image and Vision Computing 21(11), 977–1000 (2003)
Frank, J.: Electron tomography: Three-dimensional imaging with the transmission electron microscope. Plenum Pub. Corp. (1992)
Brandt, S., Heikkonen, J., Engelhardt, P.: Automatic alignment of transmission electron microscope tilt series without fiducial markers. Journal of Structural Biology 136(3), 201–213 (2001)
Fitchard, E., Aldridge, J., Reckwerdt, P., Mackie, T.: Registration of synthetic tomographic projection data sets using cross-correlation. Physics in Medicine and Biology 43(6), 1645 (1999)
Houben, L., Bar Sadan, M.: Refinement procedure for the image alignment in high-resolution electron tomography. Ultramicroscopy (2011)
Parkinson, D., Knoechel, C., Yang, C., Larabell, C., Le Gros, M.: Automatic alignment and reconstruction of images for soft X-ray tomography. Journal of Structural Biology (2011)
Yang, C., Ng, E., Penczek, P.: Unified 3-D structure and projection orientation refinement using quasi-Newton algorithm. Journal of Structural Biology 149(1), 53–64 (2005)
Katsevich, A., Silver, M., Zamyatin, A.: Local tomography and the motion estimation problem. SIAM Journal on Imaging Sciences 4(1), 200–219 (2011)
Kingston, A., Sakellariou, A., Varslot, T., Myers, G., Sheppard, A.: Reliable automatic alignment of tomographic projection data by passive auto-focus. Medical Physics 38(9), 4934 (2011)
Nocedal, J., Wright, S.: Numerical optimization, 2nd edn. Springer (2006)
Hyman, J., Larrouturou, B.: The numerical differentiation of discrete functions using polynomial interpolation methods. Applied Mathematics and Computation 10, 487–506 (1982)
Chartrand, R.: Numerical differentiation of noisy, nonsmooth data. Los Alamos National Laboratory 13 (2005)
Joseph, P.: An improved algorithm for reprojecting rays through pixel images. IEEE Transactions on Medical Imaging 1(3), 192–196 (1982)
Fong, D., Saunders, M.: LSMR: An iterative algorithm for sparse least-squares problems. Arxiv preprint arXiv:1006.0758 (2010)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bleichrodt, F., Batenburg, K.J. (2013). Automatic Optimization of Alignment Parameters for Tomography Datasets. In: Kämäräinen, JK., Koskela, M. (eds) Image Analysis. SCIA 2013. Lecture Notes in Computer Science, vol 7944. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-38886-6_46
Download citation
DOI: https://doi.org/10.1007/978-3-642-38886-6_46
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-38885-9
Online ISBN: 978-3-642-38886-6
eBook Packages: Computer ScienceComputer Science (R0)