Abstract
In this chapter, we show how the task of pricing and hedging financial derivatives can be reduced to that of solving related backward stochastic differential equations, called stochastic pricing equations in this book, equivalent to the deterministic pricing equations that arise in Markovian setups. The deterministic pricing equations, starting with the celebrated Black–Scholes equation, are better known to practitioners. However, these deterministic partial-differential equations, also including integral terms in models with jumps, are more “model dependent” than the stochastic pricing equations. Moreover, the deterministic pricing equations are less general since they are only available in Markovian setups. In addition, the mathematics of pricing and hedging financial derivatives is simpler in terms of the stochastic pricing equations. Indeed, rigorous demonstrations based on the deterministic pricing equations involve technical notions of viscosity or Sobolev solutions (at least as soon as the problem is nonlinear, e.g. when early exercise clauses and related obstacles in the deterministic equations come into the picture).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
As soon as early exercise clauses and related obstacles in the deterministic equations come into the picture.
- 2.
This classical assumption is, of course, seriously challenged and, in fact, unrealistic since the crisis; see Remark 4.1.1.
- 3.
Typically nonnegative, but not necessarily so, as seen with the Swiss currency during the 2011 Euro sovereign debt crisis.
- 4.
Default-free and without call protection and so, in particular, ϑ≡0.
- 5.
With priority of a put over a call here, though this is immaterial in terms of pricing and hedging.
- 6.
Equation (4.11) being here assumed to yield a well-defined semimartingale.
- 7.
For an appropriately chosen call time θ ∗; see Proposition 4.1.15 below for a precise statement.
- 8.
Starting from 0 by definition; see Sect. 3.1.5.
- 9.
Not necessarily continuous.
- 10.
Special semimartingale with additional integrability properties; see Sect. 12.1.2.2.
- 11.
See Definition 12.2.4 for formal statements.
- 12.
At least in principle, leaving alone the computational issues; these will be dealt with in Chap. 9.
- 13.
Or
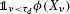 , upon exercise at a stopping time ν, for American or game claims.
, upon exercise at a stopping time ν, for American or game claims. - 14.
See Example 12.4.6 for a precise statement.
- 15.
Otherwise a more general but less constructive representation for M t can be given in terms of Malliavin calculus.
- 16.
See Sect. 2.2.
- 17.
See Sect. 6.9.3 for an example of the dividend-adjustment which is otherwise required in the equations.
- 18.
In which β now refers to the discount factor associated with an arbitrary numéraire B.
- 19.
Otherwise a more general but less constructive representation for m t can be given in terms of Malliavin calculus.
- 20.
Or
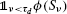 upon exercise at a stopping time ν, in the cases of American or game claims.
upon exercise at a stopping time ν, in the cases of American or game claims. - 21.
See Sect. 14.1 for the case of discrete coupons.
- 22.
Since the 2011 Euro sovereign debt crisis, defaultability is also a feature of many Euro government bonds.
- 23.
Otherwise a more general but less constructive representation for \(\widetilde{M}_{t}\) can be given in terms of Malliavin calculus.
- 24.
Boolean-valued processes.
- 25.
Model calibration will be the topic of Chap. 9.
References
Assefa, S., Bielecki, T., Crépey, S., & Jeanblanc, M. (2011). CVA computation for counterparty risk assessment in credit portfolios. In T. Bielecki, D. Brigo, & F. Patras (Eds.), Credit risk frontiers (pp. 397–436). New York: Wiley.
Bachelier, L. (1900). Théorie de la spéculation. Annales Scientifiques de L’École Normale Supérieure, 17, 21–86.
Bielecki, T., Brigo, D., & Crépey, S. (2013). Counterparty risk modeling—collateralization, funding and hedging. Taylor & Francis (in preparation).
Bielecki, T. R., Cousin, A., Crépey, S., & Herbertsson, A. (2012). Dynamic hedging of portfolio credit risk in a Markov copula model. Journal of Optimization Theory and Applications (doi:10.1007/s10957-013-0318-4, forthcoming).
Bielecki, T., & Crépey, S. (2011). Dynamic hedging of counterparty exposure. In T. Zariphopoulou, M. Rutkowski, & Y. Kabanov (Eds.), The Musiela Festschrift. Berlin: Springer (forthcoming).
Bielecki, T. R., Crépey, S., & Jeanblanc, M. (2010). Up and down credit risk. Quantitative Finance, 10(10), 1137–1151.
Bielecki, T. R., Crépey, S., Jeanblanc, M., & Rutkowski, M. (2007). Valuation of basket credit derivatives in the credit migrations environment. In J. Birge & V. Linetsky (Eds.), Handbook of financial engineering. Amsterdam: Elsevier.
Bielecki, T. R., Crépey, S., Jeanblanc, M., & Rutkowski, M. (2008). Defaultable options in a Markovian intensity model of credit risk. Mathematical Finance, 18, 493–518 (updated version on www.defaultrisk.com).
Bielecki, T. R., Crépey, S., Jeanblanc, M., & Rutkowski, M. (2009). Valuation and hedging of defaultable game options in a hazard process model. Journal of Applied Mathematics and Stochastic Analysis. Article ID 695798 (long preprint version on www.defaultrisk.com).
Bielecki, T. R., Crépey, S., Jeanblanc, M., & Rutkowski, M. (2010). Arbitrage pricing of defaultable game options with applications to convertible bonds. Quantitative Finance, 8(8), 795–810.
Bielecki, T. R., Crépey, S., Jeanblanc, M., & Rutkowski, M. (2011). Convertible bonds in a defaultable diffusion model. In A. Kohatsu-Higa, N. Privault, & S. Sheu (Eds.), Stochastic analysis with financial applications (pp. 255–298). Basel: Birkhäuser.
Bielecki, T. R., Jeanblanc, M., & Rutkowski, M. (2009). CSFI lecture notes series: Vol. 2. Credit risk modeling. Osaka University: Osaka University Press.
Bielecki, T. R., & Rutkowski, M. (2002). Credit risk: modeling, valuation and hedging. Berlin: Springer.
Bielecki, T. R., Vidozzi, A., & Vidozzi, L. (2008). A Markov copulae approach to pricing and hedging of credit index derivatives and ratings triggered step-up bonds. The Journal of Credit Risk, 4(1), 47–76.
Bismut, J. (1973). Conjugate convex functions in optimal stochastic control. Journal of Mathematical Analysis and Applications, 44, 384–404.
Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81, 635–654.
Brigo, D., & Mercurio, F. (2006). Interest rate models—theory and practice. With smile, inflation and credit (2nd ed.). Berlin: Springer.
Carmona, R., & Crépey, S. (2010). Importance sampling and interacting particle systems for the estimation of Markovian credit portfolios loss distribution. International Journal of Theoretical and Applied Finance, 13(4), 577–602.
Cesari, G., Aquilina, J., Charpillon, N., Filipovic, Z., Lee, G., & Manda, I. (2010). Modelling, pricing, and hedging counterparty credit exposure. Berlin: Springer.
Cherny, A., & Shiryaev, A. (2002). Vector stochastic integrals and the fundamental theorems of asset pricing. Proceedings of the Steklov Institute of Mathematics, 237, 6–49.
Coculescu, D., & Nikeghbali, A. (2012). Hazard processes and martingale hazard processes. Mathematical Finance, 22(3), 519–537.
Cont, R., & Minca, A. (2011). Recovering portfolio default intensities implied by CDO quotes. Mathematical Finance, online first 22 June 2011.
Crépey, S. (2013). Bilateral counterparty risk under funding constraints—Part I: Pricing. Mathematical Finance (online December 2012, doi:10.1111/mafi.12004).
Crépey, S. (2013). Bilateral counterparty risk under funding constraints—Part II: CVA. Mathematical Finance (online December 2012, doi:10.1111/mafi.12005).
Crépey, S., Jeanblanc, M., & Zargari, B. (2010). Counterparty risk on a CDS in a Markov chain copula model with joint defaults. In M. Kijima, C. Hara, Y. Muromachi, & K. Tanaka (Eds.), Recent advances in financial engineering 2009 (pp. 91–126). Singapore: World Scientific.
Delbaen, F., & Schachermayer, W. (1997). The fundamental theorem of asset pricing for unbounded stochastic processes. Mathematische Annalen, 312, 215–250.
Delbaen, F., & Schachermayer, W. (2005). The mathematics of arbitrage. Berlin: Springer.
Dellacherie, C., & Meyer, P.-A. (1982). Probabilities and potential. Amsterdam: North-Holland.
De Spiegeleer, J., Schoutens, W., & Jabre, P. (2011). The handbook of convertible bonds: pricing, strategies and risk management. Chichester: Wiley.
El Karoui, N., Kapoudjian, E., Pardoux, C., Peng, S., & Quenez, M.-C. (1997). Reflected solutions of backward SDEs, and related obstacle problems for PDEs. Annals of Probability, 25, 702–737.
El Karoui, N., Peng, S., & Quenez, M.-C. (1997). Backward stochastic differential equations in finance. Mathematical Finance, 7, 1–71.
El Karoui, N., & Quenez, M.-C. (1997). Nonlinear pricing theory and backward stochastic differential equations. In W. Runggaldier (Ed.), Lecture notes in mathematics: Vol. 1656. Financial mathematics, Bressanone, 1996 (pp. 191–246). Berlin: Springer.
Föllmer, H., & Sondermann, D. (1986). Hedging of non-redundant contingent claims. In A. Mas-Colell & W. Hildenbrand (Eds.), Contributions to mathematical economics (pp. 205–223). Amsterdam: North-Holland.
Frey, R., & Backhaus, J. (2008). Pricing and hedging of portfolio credit derivatives with interacting default intensities. International Journal of Theoretical and Applied Finance, 11(6), 611–634.
Hamadène, S. (2006). Mixed zero-sum differential game and American game options. SIAM Journal on Control and Optimization, 45(2), 496–518.
Harrison, J. M., & Pliska, S. R. (1981). Martingales and stochastic integrals in the theory of continuous trading. Stochastic Processes and Their Applications, 11(3), 215–260.
Herbertsson, A., & Rootzén, H. (2008). Pricing kth-to-default swaps under default contagion: the matrix-analytic approach. Journal of Computational Finance, 12(1), 49–78.
Jarrow, R. A., & Turnbull, S. (1995). Pricing derivatives on financial securities subject to credit risk. Journal of Finance, 50(1), 53–85.
Kallsen, J., & Kühn, C. (2005). Convertible bonds: financial derivatives of game type. In A. Kyprianou, W. Schoutens, & P. Wilmott (Eds.), Exotic option pricing and advanced Lévy models (pp. 277–288). Chichester: Wiley.
Karatzas, I. (1988). On the pricing of American options. Applied Mathematics & Optimization, 17, 37–60.
Kifer, Y. (2000). Game options. Finance and Stochastics, 4, 443–463.
Kusuoka, S. (1999). A remark on default risk models. Advances in Mathematical Economics, 1, 69–82.
Lando, D. (1994). Three essays on contingent claims pricing. PhD Thesis, Cornell University.
Laurent, J.-P., Cousin, A., & Fermanian, J.-D. (2011). Hedging default risks of CDOs in Markovian contagion models. Quantitative Finance, 11(12), 1773–1791.
Lepeltier, J.-P., & Maingueneau, M. (1984). Le jeu de Dynkin en théorie générale sans l’hypothèse de Mokobodski. Stochastics, 13, 25–44.
Lipton, A. (2001). Mathematical methods for foreign exchange—a financial engineer’s approach. Singapore: World Scientific.
Ma, J., & Cvitanić, J. (2001). Reflected forward–backward SDEs and obstacle problems with boundary conditions. Journal of Applied Mathematics and Stochastic Analysis, 14(2), 113–138.
Nikeghbali, A., & Yor, M. (2005). A definition and some characteristic properties of pseudo-stopping times. Annals of Probability, 33, 1804–1824.
Pallavicini, A., Perini, D., & Brigo, D. (2011). Funding valuation adjustment: a consistent framework including CVA, DVA, collateral, netting rules and re-hypothecation (working paper).
Pardoux, E., & Peng, S. (1990). Adapted solution of a backward stochastic differential equation. Systems & Control Letters, 14, 55–61.
Protter, P. E. (2001). A partial introduction to financial asset pricing theory. Stochastic Processes and Their Applications, 91(2), 169–203.
Protter, P. E. (2004). Stochastic integration and differential equations (2nd ed.). Berlin: Springer.
Schoutens, W. (2012). In The handbook of hybrid securities: strategies, pricing and risk management. Wiley (e-book).
Schweizer, M. (1991). Option hedging for semimartingales. Stochastic Processes and Their Applications, 37, 339–363.
Schweizer, M. (2001). A guided tour through quadratic hedging approaches. In E. Jouini, J. Cvitanic, & M. Musiela (Eds.), Option pricing, interest rates and risk management (pp. 538–574). Cambridge: Cambridge University Press.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Crépey, S. (2013). Martingale Modeling. In: Financial Modeling. Springer Finance(). Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-37113-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-642-37113-4_4
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-37112-7
Online ISBN: 978-3-642-37113-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


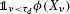 , upon exercise at a stopping time ν, for American or game claims.
, upon exercise at a stopping time ν, for American or game claims.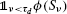 upon exercise at a stopping time ν, in the cases of American or game claims.
upon exercise at a stopping time ν, in the cases of American or game claims.