Abstract
From Chap. 16 we know that self-adjoint operators are represented as arrows, from the state space \(\underline{\varSigma}\) to the quantity value object \(\underline {\mathbb {R}}^{\leftrightarrow}\). The natural question to ask is whether such a representation can be extended to all normal operators. To this end one needs to, first of all, define the topos analogue of the complex numbers. Of course there exists the trivial object \(\underline {\mathbb {C}}\) but this, as we will see, can not be identified with the complex number object since (a) it does not reduce to \(\underline {\mathbb {R}}^{\leftrightarrow}\), and (b) the presheaf maps in \(\underline {\mathbb {C}}\) are the identity maps which do not respect the ordering induced by the daseinisation of normal operators, yet to be defined.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The presheaf \(\underline {\mathbb {R}}\) is defined on each \(V\in \mathcal{V}(\mathcal{H})\) as \(\underline {\mathbb {R}}_{V}:=\mathbb {R}\) and given the maps i:V′⊆V then the respective presheaf morphisms are simply the identity maps. See Definition 20.9.
- 2.
Recall that a local is essentially a frame (see Definition 17.1) but a morphisms between two locales is a morphisms between the frames which goes in the opposite direction.
- 3.
Note that in this internal approach one is working with co-presheaves instead of presheaves.
- 4.
A set P is directed if for any x,y∈P there exists a z∈P such that x,y⊑z.
- 5.
Here ⨆↑ indicates the supremum of a directed set and the relation x≪y indicates that x approximates y. In particular x≪y if, for any directed set S with a supremum, then y⊑⨆↑ S⇒∃s∈S:x⊑s.
- 6.
Here l([α,β] n ) represents the length of the largest side of the rectangle and thus is defined as l([α,β] n )=Max{|a n −c n |,|b n −d n |} where α=a+ib and β=c+id.
- 7.
We recall that, given a poset 〈P,≤〉 a subset G is said to be Scott-open if (i) x∈G∧x≤y⇒y∈G; (ii) for any directed set S with supremum then ⨆↑ S∈G⇒∃s∈S|s∈G. In other words all supremums in G have a non-empty intersection with G.
- 8.
Given this topology then it is clear that, as topological spaces \(\mathbb {C}\simeq max\mathbf{I}\mathbb {C}\) where \(\mathbb {C}\) is equipped with the (general) open rectangles topology and \(max\mathbf{I}\mathbb {C}\) has the topology inherited by \(\mathbf{I}\mathbb {C}\). The homeomorphisms can be see by the fact that
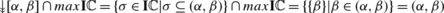 .
.
References
S. MacLane, I. Moerdijk, Sheaves in Geometry and Logic: A First Introduction to Topos Theory (Springer, London, 1968)
C. Heunen, N.P. Landsman, B. Spitters, A topos for algebraic quantum theory. Commun. Math. Phys. 291, 63 (2009). arXiv:0709.4364 [quant-ph]
W. Brenna, C. Flori, Complex numbers and normal operators in topos quantum theory. arXiv:1206.0809 [quant-ph]
G. Helmberg, Introduction to Spectral Theory in Hilbert Space (Dover Publications, New York, 2008)
R. Whitley, The spectral theorem for a normal operator. Am. Math. Mon. 75, 856–861 (1968)
H.F. de Groote, On a canonical lattice structure on the effect algebra of a von Neumann algebra (2007). arXiv:math-ph/0410018
B. Banaschewski, C.J. Mulvey, The spectral theory of commutative C ∗-algebras: the constructive spectrum. Quaest. Math. 23, 4 (2009)
B. Banaschewski, C.J. Mulvey, A globalisation of the Gelfand duality theorem. Ann. Pure Appl. Log., vol. 137 (2006)
C. Rousseau, Topos theory and complex analysis, in Applications of Sheaves. Lecture Notes in Mathematics, vol. 753 (1979)
A. Doering, B. Dewitt, Self-adjoint operators as functions I (2012). arXiv:1208.4724v1 [math-ph]
A. Doering, R.S. Barbosa, Unsharp values, domains and topoi (2011). arXiv:1107.1083v1 [quant-ph]
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Flori, C. (2013). Normal Operators. In: A First Course in Topos Quantum Theory. Lecture Notes in Physics, vol 868. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-35713-8_18
Download citation
DOI: https://doi.org/10.1007/978-3-642-35713-8_18
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-35712-1
Online ISBN: 978-3-642-35713-8
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


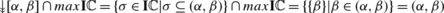 .
.