Zusammenfassung
Mit dem allgemeinen Raum- oder Translationsgitter mit a0 ≠ b0 ≠ c0; α ≠ β ≠ γ lassen sich alle Kristalle beschreiben. Allerdings liegen in dem größten Teil der Kristalle spezielle Translationsgitter vor (gleiche Gitter-Translationen in verschiedenen Richtungen, Winkel zwischen den Gitter-Translationen von 60°, 90°, 120°, 54° 44′ usw.). Alle zwei- und dreidimensionalen Translationsgitter werden in diesem Kapitel vorgestellt.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
- 2.
Vgl. Fußnote 1 in Kap. 6.
- 3.
X g = 2, 4, 6. In Abb. 7.14 sind jedoch nur die Verhältnisse für X g = 2 dargestellt. Die Aussage des Satzes ist nicht allgemein, da \({{m}}+\overline{1}\) nur 2 erzeugt.
- 4.
Das Zeichen
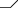 dokumentiert Spiegelebenen parallel zur Papierebene im Niveau 0 und
1/2. Nur wenn die Spiegelebenen auf einem anderen Niveau
liegen, z. B. in 1/4 und 3/4, ist dies durch
1/4 angegeben. Regel: Liegen m, 2, \(\overline{1}\) auf 0, so auch
auf 1/2; auf 1/4 dann auch auf 3/4
usw.
dokumentiert Spiegelebenen parallel zur Papierebene im Niveau 0 und
1/2. Nur wenn die Spiegelebenen auf einem anderen Niveau
liegen, z. B. in 1/4 und 3/4, ist dies durch
1/4 angegeben. Regel: Liegen m, 2, \(\overline{1}\) auf 0, so auch
auf 1/2; auf 1/4 dann auch auf 3/4
usw. - 5.
2∕m bedeutet, dass eine 2 senkrecht zu einer m angeordnet ist. Durch das Hinzufügen des Translationstyps P wird die Parallelschar von 2 und m erzeugt.
- 6.
Außer der hier verwendeten Achsenwahl mit b∕∕2, ⊥m (2. Aufstellung) gibt es die sog. 1. Aufstellung mit c∕∕2, ⊥m. Letztere würde besser in das hier gezeigte System passen, da sie sich auf eine Elementarzelle bezieht, die durch Stapelung von kongruenten allgemeinen Netzebenen mit a 0 ≠ b 0, γ ≠ 90° im Abstand c 0 entsteht (vgl. Tab. 7.1).
- 7.
Die Symmetrieangaben in den Projektionen der Symmetriegerüste der Raumgruppen in Abb. 7.10d–7.13d sind unvollständig, da noch Gleitspiegelebenen und Schraubenachsen auftreten (vgl. Abschn. 10.1 „Gleitspiegelung und Schraubung“). Diese Symmetrieelemente sind hier praktisch bedeutungslos und deshalb fortgelassen.
- 8.
Die Ausdrucksweise bei der Bezeichnung der Gitter ist nicht ganz korrekt. Wenn man z. B. von einem C-Gitter spricht, meint man ein Gitter mit einer C-flächenzentrierten Elementarzelle.
- 9.
Die Elementarzelle des rhomboedrischen P-Gitters hat die Form eines Rhomboeders, das 6 Rhomben als Begrenzungsflächen besitzt. Spezialfälle des rhomboedrischen P-Gitters sind a) für 90° das kubische P-Gitter, b) für 60° das kubische F-Gitter und c) für 109°28′ das kubische I-Gitter.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Borchardt-Ott, W., Sowa, H. (2013). Die 14 Translations-(Bravais-)gitter. In: Kristallographie. Springer-Lehrbuch. Springer Spektrum, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-34811-2_7
Download citation
DOI: https://doi.org/10.1007/978-3-642-34811-2_7
Published:
Publisher Name: Springer Spektrum, Berlin, Heidelberg
Print ISBN: 978-3-642-34810-5
Online ISBN: 978-3-642-34811-2
eBook Packages: Life Science and Basic Disciplines (German Language)


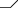 dokumentiert Spiegelebenen parallel zur Papierebene im Niveau 0 und
1/2. Nur wenn die Spiegelebenen auf einem anderen Niveau
liegen, z. B. in 1/4 und 3/4, ist dies durch
1/4 angegeben. Regel: Liegen m, 2,
dokumentiert Spiegelebenen parallel zur Papierebene im Niveau 0 und
1/2. Nur wenn die Spiegelebenen auf einem anderen Niveau
liegen, z. B. in 1/4 und 3/4, ist dies durch
1/4 angegeben. Regel: Liegen m, 2,