Abstract
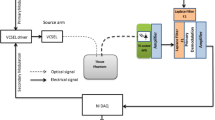
Light transport has been analyzed extensively, in both the primal domain and the frequency domain; the latter provides intuition of effects introduced by free space propagation and by optical elements, and allows for optimal designs of computational cameras for tailored, efficient information capture. Here, we relax the common assumption that the speed of light is infinite and analyze free space propagation in the frequency domain considering spatial, temporal, and angular light variation. Using this analysis, we derive analytic expressions for cross-dimensional information transfer and show how this can be exploited for designing a new, time-resolved bare sensor imaging system.
Chapter PDF
Similar content being viewed by others
References
Edgerton, H.E.: Electronic Flash, Strobe. MIT (1987)
Hamamatsu: Hamamatsu Streak Camera (2012), http://learn.hamamatsu.com/tutorials/java/streakcamera/
Durand, F., Holzschuch, N., Soler, C., Chan, E., Sillion, F.X.: A Frequency Analysis of Light Transport. ACM Trans. Graph (SIGGRAPH) 24, 1115–1126 (2005)
Edward, R., Dowski, J., Cathey, W.T.: Extended depth of field through wave-front coding. Applied Optics 34, 1859–1866 (1995)
Levin, A., Hasinoff, S.W., Green, P., Durand, F., Freeman, W.T.: 4d frequency analysis of computational cameras for depth of field extension. ACM Trans. Graph. (Siggraph) 28, 97:1–97:14 (2009)
Veeraraghavan, A., Raskar, R., Agrawal, A., Mohan, A., Tumblin, J.: Dappled photography: Mask enhanced cameras for heterodyned light fields and coded aperture refocusing. ACM Trans. Graph (SIGGRAPH) 26, 69 (2007)
Ng, R.: Fourier slice photography. ACM Trans. Graph (SIGGRAPH) 24, 735–744 (2005)
Levin, A., Durand, F.: Linear view synthesis using a dimensionality gap light field prior. In: Proc. CVPR, pp. 1–8 (2010)
Raskar, R., Davis, J.: 5D Time-Light Transport Matrix: What Can We Reason about Scene Properties? MIT Technical Report (2008)
Zomet, A., Nayar, S.K.: Lensless imaging with a controllable aperture. In: Proc. CVPR, pp. 339–346 (2006)
Koppal, S.J., Gkioulekas, I., Zickler, T., Barrows, G.L.: Wide-angle micro sensors for vision on a tight budget. In: Proc. CVPR, pp. 361–368 (2011)
Andersen, G.: Large optical photon sieve. Opt. Lett. 30, 2976–2978 (2005)
Gill, P.R., Lee, C., Lee, D.G., Wang, A., Molnar, A.: A microscale camera using direct fourier-domain scene capture. Opt. Lett. 36, 2949–2951 (2011)
Saleh, B.: Introduction to Subsurface Imaging. Cambridge University Press (2011)
Velten, A., Willwacher, T., Gupta, O., Veeraraghavan, A., Bawendi, M., Raskar, R.: Recovering three-dimensional shape around a corner using ultra-fast time-of-flight imaging. Nature Communications 3, 745–758 (2012)
Naik, N., Zhao, S., Velten, A., Raskar, R., Bala, K.: Single view reflectance capture using multiplexed scattering and time-of-flight imaging. ACM Trans. Graph (SIGGRAPH Asia) 30, 171 (2011)
Pandharkar, R., Velten, A., Bardagjy, A., Lawson, E., Bawendi, M., Raskar, R.: Estimating motion and size of moving non-line-of-sight objects in cluttered environments. In: Proc. CVPR, pp. 265–272 (2011)
Wu, D., O’Toole, M., Velten, A., Agrawal, A., Raskar, R.: Decomposing global light transport using time of flight imaging. In: Proc. CVPR, pp. 1–8 (2012)
Isaksen, A., McMillan, L., Gortler, S.J.: Dynamically reparameterized light fields. ACM Trans. Graph (SIGGRAPH), 297–306 (2000)
Chai, J.X., Tong, X., Chan, S.C., Shum, H.Y.: Plenoptic sampling. ACM Trans. Graph (SIGGRAPH), 307–318 (2000)
Kajiya, J.T.: The Rendering Equation. ACM Trans. Graph (SIGGRAPH) 20, 143–150 (1986)
Smith, A., Skorupski, J., Davis, J.: Transient Rendering. Technical Report UCSC-SOE-08-26, School of Engineering, University of California, Santa Cruz (2008)
Kak, A.C., Slaney, M.: Principles of Computerized Tomographic Imaging. Society for Industrial Mathematics (2001)
Herman, G.T.: Image reconstruction from projections. Real-Time Imaging 1, 3–18 (1995)
Chandrasekaran, V., Wakin, M., Baron, D., Baraniuk, R.: Surflets: A sparse representation for multidimensional functions containing smooth discontinuities. In: Proceedings of International Symposium on Information Theory, ISIT 2004, p. 563. IEEE (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wu, D. et al. (2012). Frequency Analysis of Transient Light Transport with Applications in Bare Sensor Imaging. In: Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C. (eds) Computer Vision – ECCV 2012. ECCV 2012. Lecture Notes in Computer Science, vol 7572. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-33718-5_39
Download citation
DOI: https://doi.org/10.1007/978-3-642-33718-5_39
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-33717-8
Online ISBN: 978-3-642-33718-5
eBook Packages: Computer ScienceComputer Science (R0)