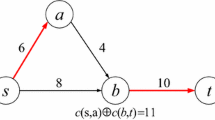
Abstract
Input data for communication network design/optimization problems involving multi-hour or uncertain traffic can consist of a large set of traffic matrices. These matrices are explicitly considered in problem formulations for link dimensioning. However, many of these matrices are usually dominated by others so only a relatively small subset of matrices would be sufficient to obtain proper link capacity reservations, supporting all original traffic matrices. Thus, elimination of the dominated matrices leads to substantially smaller optimization problems, making them treatable by contemporary solvers. In the paper we discuss the issues behind detecting domination of one traffic matrix over another. We consider two basic cases of domination: (i) total domination when the same traffic routing must be used for both matrices, and (ii) ordinary domination when traffic dependent routing can be used. The paper is based on our original results and generalizes the domination results known for fully connected networks.
Chapter PDF
Similar content being viewed by others
Keywords
References
Ben-Ameur, W., Kerivin, H.: Routing of uncertain traffic demands. Optimization and Engineering 3, 283–313 (2005)
Ben-Ameur, W., Pióro, M.: On traffic domination and total traffic domination in communication networks with arbitrary graphs. Technical report, Institute of Telecommunications, Warsaw University of Technology
Jungnickel, D.: Graphs, Networks and Algorithms. Springer, Heidelberg (1999)
Lasdon, L.: Optimization Theory for Large Systems. McMillan Publishing Co., Inc. (1970)
Okamura, H., Seymour, P.D.: Multicommodity flows in planar graphs. Journal of Combinatorial Theory 31(1), 75–81 (1981)
Oriolo, G.: Domination between traffic matrices. Mathematics of Operations Research 33(1), 91–96 (2008)
Pavon-Marino, P., Garcia-Manrubia, B., Aparicio-Pardo, R.: Multi-hour network planning based on domination between sets of traffic matrices. To be Published in Computer Networks
Pavon-Marino, P., Pióro, M.: On total traffic domination in non-complete graphs. submitted to OR Letters
Pióro, M., Medhi, D.: Routing, Flow, and Capacity Design in Communication and Computer Networks. Morgan-Kaufmann (2004)
Shepherd, B., Zhang, L.: A cycle augmentation algorithm for minimum cost multicommodity flows on a ring. Discrete Applied Mathematics 110(2-3), 301–315 (2001)
Terblanche, S.E.: Contributions towards survivable Network Design with Uncertain Traffic Requirements. PhD thesis, North-West University, South Africa (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 IFIP International Federation for Information Processing
About this chapter
Cite this chapter
Ben-Ameur, W., Pavon-Marino, P., Pióro, M. (2011). On Traffic Domination in Communication Networks. In: Hummel, K.A., Hlavacs, H., Gansterer, W. (eds) Performance Evaluation of Computer and Communication Systems. Milestones and Future Challenges. PERFORM 2010. Lecture Notes in Computer Science, vol 6821. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-25575-5_16
Download citation
DOI: https://doi.org/10.1007/978-3-642-25575-5_16
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-25574-8
Online ISBN: 978-3-642-25575-5
eBook Packages: Computer ScienceComputer Science (R0)