Abstract
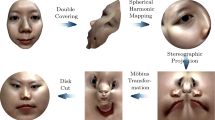
We introduce a new method to compute conformal parameterizations using a recent definition of discrete conformity, and establish a discrete version of the Riemann mapping theorem. Our algorithm can parameterize triangular, quadrangular and digital meshes. It can be adapted to preserve metric properties. To demonstrate the efficiency of our method, many examples are shown in the experiment section.
Chapter PDF
Similar content being viewed by others
References
Ahlfors, L.V.: Complex analysis, 3rd edn. McGraw-Hill Book Co., New York (1978); an introduction to the theory of analytic functions of one complex variable, International Series in Pure and Applied Mathematics
Bobenko, A.I., Mercat, C., Schmies, M.: Conformal Structures and Period Matrices of Polyhedral Surfaces. In: Computational Approach to Riemann Surfaces. Springer, Heidelberg (2011)
Bobenko, A.I., Schröder, P., Sullivan, J.M., Ziegler, G.M. (eds.): Discrete differential geometry, Oberwolfach Seminars, vol. 38. Birkhäuser, Basel (2008), http://dx.doi.org/10.1007/978-3-7643-8621-4 (papers from the seminar held in Oberwolfach, May 30-June 5, 2004)
Desbrun, M., Meyer, M., Alliez, P.: Intrinsic parameterizations of surface meshes. Computer Graphics Forum 21, 209–218 (2002)
Floater, M.S.: Mean value coordinates. Computer Aided Geometric Design 20(1), 19–27 (2003)
Fourey, S., Malgouyres, R.: Normals estimation for digital surfaces based on convolutions. Computers & Graphics 33(1), 2–10 (2009)
Gu, X.D., Yau, S.T.: Computational conformal geometry, Advanced Lectures in Mathematics (ALM), vol. 3. International Press, Somerville (2008); with 1 CD-ROM (Windows, Macintosh and Linux)
Kharevych, L., Springborn, B., Schröder, P.: Discrete conformal mappings via circle patterns. ACM Transactions on Graphics (TOG) 25(2), 438 (2006)
Lévy, B., Petitjean, S., Ray, N., Maillot, J.: Least squares conformal maps for automatic texture atlas generation. ACM Transactions on Graphics 21(3), 362–371 (2002)
Mercat, C.: Discrete Riemann surfaces and the Ising model. Communications in Mathematical Physics 218(1), 177–216 (2001)
Mercat, C.: Discrete complex structure on surfel surfaces. In: Coeurjolly, D., Sivignon, I., Tougne, L., Dupont, F. (eds.) DGCI 2008. LNCS, vol. 4992, pp. 153–164. Springer, Heidelberg (2008)
Nocedal, J., Wright, S.J.: Numerical optimization. Springer, Heidelberg (1999)
Pinkall, U., Polthier, K.: Computing discrete minimal surfaces and their conjugates. Experimental Mathematics 2(1), 15–36 (1993)
Sheffer, A., de Sturler, E.: Parameterization of faceted surfaces for meshing using angle-based flattening. Engineering with Computers 17(3), 326–337 (2001)
Tutte, W.: Convex representations of graphs. Proceedings of the London Mathematical Society 3(1), 304 (1960)
Wegert, E.: Nonlinear Riemann-Hilbert problems—history and perspectives. In: Computational Methods and Function Theory 1997 (Nicosia), Ser. Approx. Decompos., vol. 11, pp. 583–615. World Sci. Publ., River Edge (1999)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Cartade, C., Malgouyres, R., Mercat, C., Samir, C. (2011). Smooth 2D Coordinate Systems on Discrete Surfaces. In: Debled-Rennesson, I., Domenjoud, E., Kerautret, B., Even, P. (eds) Discrete Geometry for Computer Imagery. DGCI 2011. Lecture Notes in Computer Science, vol 6607. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-19867-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-642-19867-0_5
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-19866-3
Online ISBN: 978-3-642-19867-0
eBook Packages: Computer ScienceComputer Science (R0)