Skip to main content
SpringerLink
Log in

Global Exponential Stability of Equilibrium Point of Hopfield Neural Network with Delay

  • Conference paper
Advances in Neural Networks - ISNN 2010 (ISNN 2010)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 6063))

Included in the following conference series:

  • 1797 Accesses

Abstract

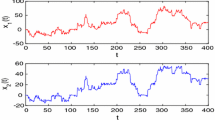
In this paper, the global exponential stability of the Hopfield neural network with delay is studied. By using of the methods of constant variation and variable substitution, a new sufficient global exponential stable criterion for the equilibrium point of the network is derived. The result is different to the known references and is realizable easily.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Shao, J.-L., Huang, T.-Z.: Global exponential stability analysis of a class of dynamical neural networks. Journal of electronic science technology of China 7(2), 171–174 (2009)

    MathSciNet  Google Scholar 

  2. Yan, Y.-L., Liao, W.-T.: Globally exponential stability of equilibrium for new Hopfield neural networks. Acta electronic sinica 36(8), 1543–1546 (2008)

    MathSciNet  Google Scholar 

  3. Yang, F.-J., Zhang, C.-L., Wu, Q.-D.: Global exponential stability of Hopfield neural networks with delays. Pure and applied mathematics 24(1), 179–185 (2008)

    MATH  MathSciNet  Google Scholar 

  4. Chen, W.-Y.: Globally exponential asymptotic stability of Hopfield neural network with time-varying delays. Acta scientiarum naturalium university Nankaiensis 38(5), 81–86 (2005)

    Google Scholar 

  5. Zhang, L.-J.: Global exponential stability of Hopfield neural networks with time-varying delay and the estimation of decay rate. Journal of northwest normal university (natural science) 43(2), 1–4 (2007)

    MATH  MathSciNet  Google Scholar 

  6. Chen, W.-Y.: On the globally asymptotic stability for a class of Hopfield neural networks with Delay. Journal of biomathematics 19(2), 175–179 (2004)

    MathSciNet  Google Scholar 

  7. Xu, J., Zhong, S.-M., Zhang, C.-F.: Stability of Hopfield type neural network with distributed time delay. Journal of UEST of China 33(2), 200–203 (2004)

    MATH  MathSciNet  Google Scholar 

  8. Qian, Y., Feng, X.-M., Jiang, H.-J.: On Global Stability Criterion of High—order Hopfield Neural Networks with Distributed Delays. Journal of Xinjiang university (Natural science edition) 26(2), 53–59 (2009)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Aeronautical Automation, Civil Aviation University of China, TianJin, 300300, China

    Xiaolin Liu

  2. College of Astronautics, Northwestern Polytechnical University, XiAn, 710072, China

    Kun Yuan

Authors
  1. Xiaolin Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kun Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science and Engineering, Shanghai Jiao Tong University, 800 Dongchuan Road, 200240, Shanghai, China

    Liqing Zhang

  2. Department of Computer Science and Engineering, Shanghai Jiao Tong University, 800, Dongchuan Road, 200240, Shanghai, China

    Bao-Liang Lu

  3. Department of Computer Science and Engineering, The Hong Kong University of Science and Technology, Clear Water bay, Kowloon, Hong Kong, China

    James Kwok

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Liu, X., Yuan, K. (2010). Global Exponential Stability of Equilibrium Point of Hopfield Neural Network with Delay. In: Zhang, L., Lu, BL., Kwok, J. (eds) Advances in Neural Networks - ISNN 2010. ISNN 2010. Lecture Notes in Computer Science, vol 6063. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-13278-0_70

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-13278-0_70

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-13277-3

  • Online ISBN: 978-3-642-13278-0

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation