Abstract
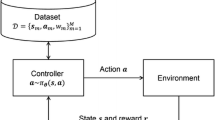
Direct policy search is a promising reinforcement learning framework in particular for controlling in continuous, high-dimensional systems such as anthropomorphic robots. Policy search often requires a large number of samples for obtaining a stable policy update estimator due to its high flexibility. However, this is prohibitive when the sampling cost is expensive. In this paper, we extend an EM-based policy search method so that previously collected samples can be efficiently reused. The usefulness of the proposed method, called Reward-weighted Regression with sample Reuse (R3), is demonstrated through a robot learning experiment.
Chapter PDF
Similar content being viewed by others
Keywords
- Reinforcement Learning
- Importance Sampling
- Importance Weight
- Reward Function
- Neural Information Processing System
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Bagnell, J.A., Kakade, S., Ng, A.Y., Schneider, J.: Policy search by dynamic programming. In: Neural Information Processing Systems, vol. 16 (2003)
Dayan, P., Hinton, G.E.: Using expectation-maximization for reinforcement learning. Neural Computation 9(2), 271–278 (1997)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society B 39, 1–38 (1977)
Hachiya, H., Akiyama, T., Sugiyama, M., Peters, J.: Adaptive importance sampling with automatic model selection in value function approximation. In: Proceedings of the Twenty-Third National Conference on Artificial Intelligence (2008)
Kakade, S.: A natural policy gradient. In: Neural Information Processing Systems, vol. 14, pp. 1531–1538 (2002)
Kober, J., Peters, J.: Policy search for motor primitives in robotics. In: Neural Information Processing Systems, vol. 21 (2008)
Peshkin, C.R., Shelton, L.: Learning from scarce experience. In: Proceedings of International Conference on Machine Learning, pp. 498–505 (2002)
Peters, J., Schaal, S.: Reinforcement learning by reward-weighted regression for operational space control. In: Proceedings of the International Conference on Machine Learning (2007)
Peters, J., Vijayakumar, S., Shaal, S.: Natural actor-critic. In: Proceedings of the 16th European Conference on Machine Learning, pp. 280–291 (2005)
Precup, D., Sutton, R.S., Singh, S.: Eligibility traces for off-policy policy evaluation. In: Proceedings of International Conference on Machine Learning, pp. 759–766 (2000)
Rao, C.R.: Linear Statistical Inference and Its Applications. Wiley, Chichester (1973)
Schaal, S.: The SL Simulation and Real-Time Control Software Package. University of Southern California (2007)
Shelton, C.R.: Policy improvement for POMDPs using normalized importance sampling. In: Proceedings of Uncertainty in Artificial Intelligence, pp. 496–503 (2001)
Shimodaira, H.: Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference 90(2), 227–244 (2000)
Sugiyama, M., Krauledat, M., Müller, K.-R.: Covariate shift adaptation by importance weighted cross validation. Journal of Machine Learning Research 8, 985–1005 (2007)
Sutton, R.S., Barto, A.G.: Reinforcement Learning: An Introduction. MIT Press, Cambridge (1998)
Sutton, R.S., Mcallester, M., Singh, S., Mansour, Y.: Policy gradient methods for reinforcement learning with function approximation. In: Advances in Neural Information Processing Systems, vol. 12, pp. 1057–1063. MIT Press, Cambridge (2000)
Williams, R.J.: Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning 8, 229–256 (1992)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hachiya, H., Peters, J., Sugiyama, M. (2009). Efficient Sample Reuse in EM-Based Policy Search. In: Buntine, W., Grobelnik, M., Mladenić, D., Shawe-Taylor, J. (eds) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2009. Lecture Notes in Computer Science(), vol 5781. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04180-8_48
Download citation
DOI: https://doi.org/10.1007/978-3-642-04180-8_48
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-04179-2
Online ISBN: 978-3-642-04180-8
eBook Packages: Computer ScienceComputer Science (R0)