Abstract
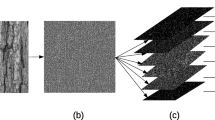
Taxonomical classification of plants is a very complex and time-consuming task. This is mostly due to the great biodiversity of species and the fact of most measures extracted from plants are traditionally performed manually. This paper presents a novel approach to plant identification based on leaf texture. Initially, the texture is modelled as a surface, so complexity analysis using Multi-scale fractal dimension can be performed over the generated surface, resulting in a feature vector which represents texture complexity in terms of the spatial scale. Yielded results show the potential of the approach, which overcomes traditional texture analysis methods, such as Co-occurrence matrices, Gabor filters and Fourier descriptors.
Chapter PDF
Similar content being viewed by others
References
Judd, W., Campbell, C., Kellog, E., Stevens, P.: Plant Systematics: A Phylogenetic Approach. Sinauer Associates, Massachusetts (1999)
Kurmann, M.H., Hemsley, A.R.: The Evolution of Plant Architecture. Royal Botanic Gardens, Kew (1999)
Hickey, L.R.: Classification of archictecture of dicotyledonous leaves. Amer. J. Bot. 60(1), 17–33 (1973)
Haralick, R.M.: Statistical and structural approaches to texture. Proc. IEEE 67(5), 786–804 (1979)
Murino, V., Ottonello, C., Pagnan, S.: Noisy texture classification: A higher-order statistics approach. Pattern Recognition 31(4), 383–393 (1998)
Shen, L., Bai, L.: A review on gabor wavelets for face recognition. Pattern Anal. Appl. 9(2-3), 273–292 (2006)
Bianconi, F., Fernández, A.: Evaluation of the effects of gabor filter parameters on texture classification. Pattern Recognition 40(12), 3325–3335 (2007)
Jain, A.K., Farrokhnia, F.: Unsupervised texture segmentation using Gabor filters. Pattern Recognition 24(12), 1167–1186 (1991)
Daugman, J., Downing, C.: Gabor wavelets for statistical pattern recognition. In: Arbib, M.A. (ed.) The Handbook of Brain Theory and Neural Networks, pp. 414–419. MIT Press, Cambridge (1995)
Manjunath, B.S., Ma, W.-Y.: Texture features for browsing and retrieval of image data. IEEE Trans. Pattern Anal. Mach. Intell 18(8), 837–842 (1996)
Azencott, R., Wang, J.-P., Younes, L.: Texture classification using windowed fourier filters. IEEE Trans. Pattern Anal. Mach. Intell 19(2), 148–153 (1997)
Bajcsy, R.K.: Computer identification of visual surfaces. Computer Graphics Image Processing 2, 118–130 (1973)
Sengür, A., Türkoglu, I., Ince, M.C.: Wavelet packet neural networks for texture classification. Expert Syst. Appl. 32(2), 527–533 (2007)
Unser, M.: Texture classification and segmentation using wavelet frames. IEEE Trans. Image Processing 4(11), 1549–1560 (1995)
Huang, P.W., Dai, S.K., Lin, P.L.: Texture image retrieval and image segmentation using composite sub-band gradient vectors. J. Visual Communication and Image Representation 17(5), 947–957 (2006)
Kaplan, L.M.: Extended fractal analysis for texture classification and segmentation. IEEE Transactions on Image Processing 8(11), 1572–1585 (1999)
Schroeder, M.: Fractals, Chaos, Power Laws: Minutes From an Infinite Paradise. W.H. Freeman, New York (1996)
Tricot, C.: Curves and Fractal Dimension. Springer, Heidelberg (1995)
Backes, A.R., Bruno, O.M.: A new approach to estimate fractal dimension of texture images. In: Elmoataz, A., Lezoray, O., Nouboud, F., Mammass, D. (eds.) ICISP 2008 2008. LNCS, vol. 5099, pp. 136–143. Springer, Heidelberg (2008)
Chen, Y.Q., Bi, G.: On texture classification using fractal dimension. IJPRAI 13(6), 929–943 (1999)
de O. Plotze, R., Falvo, M., Pádua, J.G., Bernacci, L.C., Vieira, M.L.C., Oliveira, G.C.X., Bruno, O.M.: Leaf shape analysis using the multiscale minkowski fractal dimension, a new morphometric method: a study with passiflora (passifloraceae). Canadian Journal of Botany 83(3), 287–301 (2005)
Li, J., Sun, C., Du, Q.: A new box-counting method for estimation of image fractal dimension. In: International Conference on Image Processing, pp. 3029–3032 (2006)
da F. Costa, L., Cesar Jr., R.M.: Shape Analysis and Classification: Theory and Practice. CRC Press, Boca Raton (2000)
Carlin, M.: Measuring the complexity of non-fractal shapes by a fractal method. PRL: Pattern Recognition Letters 21(11), 1013–1017 (2000)
Bruno, O.M., de O. Plotze, R., Falvo, M., de Castro, M.: Fractal dimension applied to plant identification. Information Sciences 178, 2722–2733 (2008)
Emerson, C.W., Lam, N.N., Quattrochi, D.A.: Multi-scale fractal analysis of image texture and patterns. Photogrammetric Engineering and Remote Sensing 65(1), 51–62 (1999)
Gonzalez, R.C., Woods, R.E.: Digital Image Processing, 2nd edn. Prentic-Hall, New Jersey (2002)
Everitt, B.S., Dunn, G.: Applied Multivariate Analysis, 2nd edn. Arnold (2001)
Fukunaga, K.: Introduction to Statistical Pattern Recognition, 2nd edn. Academic Press, London (1990)
Smith, G.D.: Numerical Solution of Partial Differential Equations: Finite Difference Methods, 3rd edn., Oxford (1986)
Idrissa, M., Acheroy, M.: Texture classification using gabor filters. Pattern Recognition Letters 23(9), 1095–1102 (2002)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Backes, A.R., Bruno, O.M. (2009). Plant Leaf Identification Using Multi-scale Fractal Dimension. In: Foggia, P., Sansone, C., Vento, M. (eds) Image Analysis and Processing – ICIAP 2009. ICIAP 2009. Lecture Notes in Computer Science, vol 5716. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04146-4_17
Download citation
DOI: https://doi.org/10.1007/978-3-642-04146-4_17
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-04145-7
Online ISBN: 978-3-642-04146-4
eBook Packages: Computer ScienceComputer Science (R0)