Abstract
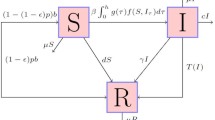
Epidemic thresholds were deduced and simulated from SIR models of Susceptible – Infected – Recovered individuals, through local stability analysis of the disease free and endemic equilibrium, with an algorithmic method. One and two types of infected individuals were modeled, considering the influence of sub clinical, undiagnosed or unrecognized infected cases in disease transmission.
Chapter PDF
Similar content being viewed by others
References
Brown, C., El Kahoui, M., Novotni, D., Weber, A.: Algorithmic methods for investigating equilibria in epidemic modelling. Journ. Symb. Comp. 41, 1157–1163 (2006)
Anderson, R.M., May, R.M.: Infectious diseases of humans: dynamics and control. Oxford University Press, New York (1992)
Diekmann, O., Heesterbeek, J.A.P.: Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. John Wiley and Sons, New York (2000)
Chowell, G., Hengartner, N.W., Castillo-Chavez, C., Fenimore, P.W., Hyman, J.M.: The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. Journal of Theoretical Biology 229(1), 119–126 (2004)
Hsua, S.-B., Hsiehb, Y.-H.: On the Role of Asymptomatic Infection in Transmission Dynamics of Infectious Diseases. Bulletin of Mathematical Biology 70, 134–155 (2008)
Ball, F., Becker, N.: Control of transmission with two types of infection. Mathematical Biosciences 200, 170–187 (2006)
Águas, R., Gonçalves, G., Gabriela, M., Gomes, M.: Pertussis: increasing disease as a consequence of reducing Transmisión. Lancet Infect. Dis. 6, 112–117 (2006)
Bailey, N.T.J.: The mathematical theory of epidemics, p. 194. Charles Griffin and company limited, London (1957)
Panamerican Health Organization. Health conditions and trends. Health in the Americas, edn. Washington, DC, pp. 58–207 (2007)
Ospina, J., Hincapie, D.: Mackendrick: A Maple Package Oriented to Symbolic Computational Epidemiology. In: Alexandrov, V.N., van Albada, G.D., Sloot, P.M.A., Dongarra, J. (eds.) ICCS 2006. LNCS, vol. 3991, pp. 920–923. Springer, Heidelberg (2006)
Glass, K., Grenfell, B.T.: Waning immunity and subclinical measles infections in England. Vaccine 22, 4110–4116 (2004)
Glass, K., Grenfell, B.T.: Antibody Dynamics in Childhood Diseases: Waning and Boosting of Immunity and the Impact of Vaccination. J. theor. Biol. 221, 21–131 (2003)
Van Boven, M., Melker, H., Schellekens, J., Kretzschmar, M.: Waning immunity and sub-clinical infection in an epidemic model: implications for pertussis in The Netherlands. Mathematical Biosciences 164, 161–182 (2000)
Eames, K., Keeling, M.: Contact tracing and disease control. Proc. R. Soc. Lond. B 270, 2565–2571 (2003)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hincapié P., D., Ospina G., J., Uyi Afuwape, A., Gómez A., R.D. (2008). Epidemic Thresholds in SIR and SIIR Models Applying an Algorithmic Method. In: Zeng, D., Chen, H., Rolka, H., Lober, B. (eds) Biosurveillance and Biosecurity . BioSecure 2008. Lecture Notes in Computer Science(), vol 5354. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-89746-0_12
Download citation
DOI: https://doi.org/10.1007/978-3-540-89746-0_12
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-89745-3
Online ISBN: 978-3-540-89746-0
eBook Packages: Computer ScienceComputer Science (R0)