Abstract
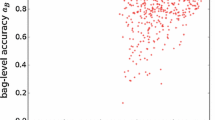
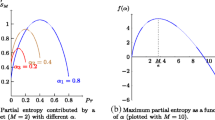
In traditional multi-instance (MI) learning, a single positive instance in a bag produces a positive class label. Hence, the learner knows how the bag’s class label depends on the labels of the instances in the bag and can explicitly use this information to solve the learning task. In this paper we investigate a generalized view of the MI problem where this simple assumption no longer holds. We assume that an “interaction” between instances in a bag determines the class label. Our two-level learning method for this type of problem transforms an MI bag into a single meta-instance that can be learned by a standard propositional method. The meta-instance indicates which regions in the instance space are covered by instances of the bag. Results on both artificial and real-world data show that this two-level classification approach is well suited for generalized MI problems.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Dietterich, T.G., Lathrop, R.H., Lozano-Perez, T.: Solving the Multiple Instance Problem with Axis-Parallel Rectangles. Artificial Intelligence 89, 31–71 (1997)
Gärtner, T., Flach, P.A., Kowalczyk, A., Smola, A.J.: Multi-Instance Kernels. In: Proc. 19th Int. Conf. on Machine Learning, pp. 179–186. Morgan Kaufmann, San Francisco (2002)
Ramon, J., De Raedt, L.: Multi Instance Neural Networks. In: Proc. ICML Workshop on Attribute-Value and Relational Learning (2000)
Maron, O., Lozano-Pérez, T.: A Framework for Multiple-Instance Learning. In: Advances in Neural Information Processing Systems, vol. 10, MIT Press, Cambridge (1998)
Zucker, J.D., Chevaleyre, Y.: Solving multiple-instance and multiple-part learning problems with decision trees and decision rules. Application to the mutagenesis problem. In: Internal Report, University of Paris 6 (2000)
De Raedt, L.: Attribute-Value Learning Versus Inductive Logic Programming: The Missing Links. In: Page, D.L. (ed.) ILP 1998. LNCS, vol. 1446, pp. 1–8. Springer, Heidelberg (1998)
Kohavi, R., John, G.H.: Wrappers for Feature Subset Selection. Artificial Intelligence 97, 273–324 (1997)
Friedman, J., Hastie, T., Tibshirani, R.: Additive logistic regression: A statistical view of boosting. Annals of Statistics 28, 307–337 (2000)
Quinlan, R.: C4.5: Programs for Machine Learning. Morgan Kaufmann, San Francisco (1993)
Frank, E., Witten, I.: Making Better Use of Global Discretization. In: Proc. 16th Int. Conf. on Machine Learning, pp. 115–123. Morgan Kaufmann, San Francisco (1999)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Weidmann, N., Frank, E., Pfahringer, B. (2003). A Two-Level Learning Method for Generalized Multi-instance Problems. In: Lavrač, N., Gamberger, D., Blockeel, H., Todorovski, L. (eds) Machine Learning: ECML 2003. ECML 2003. Lecture Notes in Computer Science(), vol 2837. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-39857-8_42
Download citation
DOI: https://doi.org/10.1007/978-3-540-39857-8_42
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-20121-2
Online ISBN: 978-3-540-39857-8
eBook Packages: Springer Book Archive