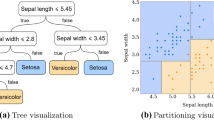
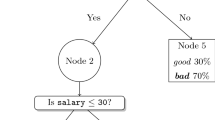
Abstract
Tree induction methods and linear models are popular techniques for supervised learning tasks, both for the prediction of nominal classes and continuous numeric values. For predicting numeric quantities, there has been work on combining these two schemes into ‘model trees’, i.e. trees that contain linear regression functions at the leaves. In this paper, we present an algorithm that adapts this idea for classification problems, using logistic regression instead of linear regression. We use a stagewise fitting process to construct the logistic regression models that can select relevant attributes in the data in a natural way, and show how this approach can be used to build the logistic regression models at the leaves by incrementally refining those constructed at higher levels in the tree. We compare the performance of our algorithm against that of decision trees and logistic regression on 32 benchmark UCI datasets, and show that it achieves a higher classification accuracy on average than the other two methods.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Blake, C.L., Merz, C.J.: UCI repository of machine learning databases (1998), http://www.ics.uci.edu/~mlearn/MLRepository.html
Breiman, L., Friedman, H., Olshen, J.A., Stone, C.J.: Classification and Regression Trees. Wadsworth, Belmont (1984)
Chaudhuri, P., Lo, W.-D., Loh, W.-Y., Yang, C.-C.: Generalized regression trees. Statistica Sinica 5, 641–666 (1995)
Frank, E., Wang, Y., Inglis, S., Holmes, G., Witten, I.H.: Using model trees for classification. Machine Learning 32(1), 63–76 (1998)
Freund, Y., Schapire, R.E.: Experiments with a new boosting algorithm. In: Proc. Int. Conf. on Machine Learning, pp. 148–156. Morgan Kaufmann, San Francisco (1996)
Friedman, J., Hastie, T., Tibshirani, R.: Additive logistic regression: a statistical view of boosting. The Annals of Statistic 38(2), 337–374 (2000)
Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer, Heidelberg (2001)
Lim, T.-S.: Polytomous Logistic Regression Trees. PhD thesis, Department of Statistics, University of Wisconsin (2000)
Nadeau, C., Bengio, Y.: Inference for the generalization error. In: Advances in Neural Information Processing Systems 12, pp. 307–313. MIT Press, Cambridge (1999)
Perlich, C., Provost, F.: Tree induction vs logistic regression. In: Beyond Classification and Regression (NIPS 2002 Workshop) (2002)
Quinlan, J.R.: Learning with Continuous Classes. In: 5th Australian Joint Conference on Artificial Intelligence, pp. 343–348 (1992)
Quinlan, R.: C4.5: Programs for Machine Learning. Morgan Kaufmann, San Francisco (1993)
Wang, Y., Witten, I.: Inducing model trees for continuous classes. In: Proc of Poster Papers, European Conf. on Machine Learning (1997)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Landwehr, N., Hall, M., Frank, E. (2003). Logistic Model Trees. In: Lavrač, N., Gamberger, D., Blockeel, H., Todorovski, L. (eds) Machine Learning: ECML 2003. ECML 2003. Lecture Notes in Computer Science(), vol 2837. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-39857-8_23
Download citation
DOI: https://doi.org/10.1007/978-3-540-39857-8_23
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-20121-2
Online ISBN: 978-3-540-39857-8
eBook Packages: Springer Book Archive