Abstract
The methodologies of computer algebra are about making algebra (in the broad sense) algorithmic, and efficient as well. There are ingenious algorithms, even in the obvious settings, and also mechanisms where problems are translated into other (generally smaller) settings, solved there, and translated back. Much of the efficiency of modern systems comes from these translations. One of the major challenges is sparsity, and the complexity of algorithms in the sparse setting is often unknown, as many problems are NP-hard, or much worse.
In view of this, it is argued that the traditional complexity-theoretic method of measuring progress has its limits, and computer algebra should look to the work of the SAT community, with its large families of benchmarks and serious contests, for lessons.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Abbott, J.A.: Factorisation of polynomials over algebraic number fields. Ph.D. thesis, University of Bath (1988)
Abbott, J.A.: Bounds on factors in \({{\bf Z}}[x]\). J. Symb. Comp. 50, 532–563 (2013)
Amzallag, E., Pogudin, G., Sun, M., Vo, N.T.: Complexity of triangular representations of algebraic sets. https://arxiv.org/abs/1609.09824v6 (2018)
Arnold, E.A.: Modular algorithms for computing Gröbner bases. J. Symb. Comp. 35, 403–419 (2003)
Bareiss, E.H.: Sylvester’s identity and multistep integer-preserving Gaussian elimination. Math. Comp. 22, 565–578 (1968)
Berlekamp, E.R.: Factoring polynomials over finite fields. Bell. Syst. Tech. J. 46, 1853–1859 (1967)
Berlekamp, E.R.: Factoring polynomials over large finite fields. Math. Comp. 24, 713–735 (1970)
Brain, M.N., Davenport, J.H., Griggio, A.: Benchmarking solvers, SAT-style. In: SC\(^2\) 2017 Satisfiability Checking and Symbolic Computation CEUR Workshop 1974, no. RP3, pp. 1–15 (2017)
Brown, W.S.: On Euclid’s algorithm and the computation of polynomial greatest common divisors. In: Proceedings of SYMSAC 1971, pp. 195–211 (1971)
Brown, W.S.: On Euclid’s algorithm and the computation of polynomial greatest common divisors. J. ACM 18, 478–504 (1971)
Buchberger, B.: Ein Algorithmus zum Auffinden des Basiselemente des Restklassenringes nach einem nulldimensionalen Polynomideal. Ph.D. thesis, Math. Inst. University of Innsbruck (1965)
Chen, C., Moreno Maza, M.: Quantifier elimination by cylindrical algebraic decomposition based on regular chains. J. Symb. Comp. 75, 74–93 (2016)
Chistov, A.L.: Double-exponential lower bound for the degree of any system of generators of a polynomial prime ideal. St. Petersb. Math. J. 20, 983–1001 (2009)
Collins, G.E.: Subresultants and reduced polynomial remainder sequences. J. ACM 14, 128–142 (1967)
Collins, G.E.: Quantifier elimination for real closed fields by cylindrical algebraic decompostion. In: Brakhage, H. (ed.) Automata Theory and Formal Languages 2nd GI Conference Kaiserslautern. LNCS, vol. 33, pp. 134–183. Springer, Heidelberg (1975). https://doi.org/10.1007/3-540-07407-4_17
Coppersmith, D., Davenport, J.H.: Polynomials whose powers are sparse. Acta Arith. 58, 79–87 (1991)
Cox, D.A.: Why Eisenstein proved the Eisenstein criterion and why Schönemann discovered it first. Am. Math. Monthly 118, 3–31 (2011)
Cox, D.A., Little, J., O’Shea, D.: Ideals, Varieties, and Algorithms. Undergraduate Texts in Mathematics. Springer, Heidelberg (2015). https://doi.org/10.1007/978-0-387-35651-8
Davenport, J.H., Carette, J.: The sparsity challenges. In: Watt, S., et al. (eds.) Proceeding of SYNASC 2009, pp. 3–7 (2010)
Dodgson, C.L.: Condensation of determinants, being a new and brief method for computing their algebraic value. Proc. R. Soc. Ser. A 15, 150–155 (1866)
England, M., Davenport, J.H.: The complexity of cylindrical algebraic decomposition with respect to polynomial degree. In: Gerdt, V.P., Koepf, W., Seiler, W.M., Vorozhtsov, E.V. (eds.) CASC 2016. LNCS, vol. 9890, pp. 172–192. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45641-6_12
Kalkbrener, M.: A generalized Euclidean algorithm for computing triangular representations of algebraic varieties. J. Symb. Comp. 15, 143–167 (1993)
Kaltofen, E., Li, B., Yang, Z., Zhi, L.: Exact certification of global optimality of approximate factorizations via rationalizing sums-of-squares with floating point scalars. In: Jeffrey, D.J. (ed.) Proceedings of ISSAC 2008, pp. 155–164 (2008)
Lenstra, A.K., Lenstra Jun, H.W., Lovász, L.: Factoring polynomials with rational coefficients. Math. Ann. 261, 515–534 (1982)
Liouville, J.: Premier Mémoire sur la Détermination des Intégrales dont la Valeur est Algébrique. J. l’École Polytech. 14(22), 124–148 (1833)
Mayr, E.W., Ritscher, S.: Dimension-dependent bounds for Gröbner bases of polynomial ideals. J. Symb. Comp. 49, 78–94 (2013)
Mignotte, M.: An inequality about factors of polynomials. Math. Comp. 28, 1153–1157 (1974)
Musser, D.R.: On the efficiency of a polynomial irreducibility test. J. ACM 25, 271–282 (1978)
Nguy
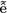 n, P.Q., Stehlé, D.: An LLL algorithm with quadratic complexity. SIAM J. Comput. 39, 874–903 (2009)
n, P.Q., Stehlé, D.: An LLL algorithm with quadratic complexity. SIAM J. Comput. 39, 874–903 (2009)Pemantle, R., Peres, Y., Rivin, I.: Four random permutations conjugated by an adversary generate \(S_n\) with high probability. Random Struct. Algorithms 49, 409–428 (2015)
Plaisted, D.A.: Some polynomial and integer divisibility problems are \(NP\)-hard. SIAM J. Comp. 7, 458–464 (1978)
Roche, D.S.: What can (and can’t) we do with sparse polynomials? In: Proceedings of ISSAC 2018, pp. 25–30 (2018)
Sasaki, T., Sasaki, M.: Analysis of accuracy decreasing in polynomial remainder sequence and floating-point number coefficients. J. Inform. Proc. 12, 394–403 (1989)
Sasaki, T., Yamaguchi, S.: An analysis of cancellation error in multivariate Hensel construction with floating-point arithmetic. In: Gloor, O. (ed.) Proceedings of ISSAC 1998, pp. 1–8 (1998)
Schinzel, A.: On the greatest common divisor of two univariate polynomials, I. In: A Panorama of Number Theory or the View from Baker’s Garden, pp. 337–352. C.U.P. (2003)
Shirayanagi, K.: Floating point Gröbner bases. Math. Comput. Simul. 42, 509–528 (1996)
Swinnerton-Dyer, H.P.F.: Letter to E.H. Berlekamp. Mentioned in [7] (1970)
Tarski, A.: A decision method for elementary algebra and geometry. In: Caviness, B.F., Johnson, J.R. (eds.) Quantifier Elimination and Cylindrical Algebraic Decomposition, pp. 24–84. Springer, Vienna (1998). https://doi.org/10.1007/978-3-7091-9459-1_3
Wang, P.S.: An improved multivariable polynomial factorising algorithm. Math. Comp. 32, 1215–1231 (1978)
Wang, P.S., Guy, M.J.T., Davenport, J.H.: \(p\)-adic reconstruction of rational numbers. SIGSAM Bull. 16(2), 2–3 (1982)
Wu, W.-T.: Basic principles of mechanical theorem proving in elementary geometries. J. Syst. Sci. and Math. Sci. (Beijing) 4, 207–235 (1984)
Zassenhaus, H.: On Hensel factorization I. J. Number Theor. 1, 291–311 (1969)
Zippel, R.E.: Effective Polynomial Computation. Kluwer Academic Publishers, Boston (1993)
Acknowledgements
I am grateful to Russell Bradford, Akshar Nair, Zak Tonks and the AISC 2018 organisers for useful comments and corrections. As always, I am grateful to David Carlisle for  advice.
advice.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Davenport, J. (2018). Methodologies of Symbolic Computation. In: Fleuriot, J., Wang, D., Calmet, J. (eds) Artificial Intelligence and Symbolic Computation. AISC 2018. Lecture Notes in Computer Science(), vol 11110. Springer, Cham. https://doi.org/10.1007/978-3-319-99957-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-99957-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-99956-2
Online ISBN: 978-3-319-99957-9
eBook Packages: Computer ScienceComputer Science (R0)


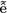 n, P.Q., Stehlé, D.: An LLL algorithm with quadratic complexity. SIAM J. Comput. 39, 874–903 (2009)
n, P.Q., Stehlé, D.: An LLL algorithm with quadratic complexity. SIAM J. Comput. 39, 874–903 (2009)