Keywords

1 Introduction

In recent days, natural or man-made disasters of large scale have occurred more frequently than ever. A large number of people are impacted significantly and a lot of assets are damaged severely. Upon these disasters, rapid and effective responses to these emergency events should be conducted. A set of relief centers should be determined to accommodate evacuees and a variety of multi-commodity should be distributed to these relief centers to provide basic life support there. However, relief centers may have surplus commodities or shortages because of the imperfect multi-commodity distribution at the peacetime. Hence, these surplus commodities should be redistributed to others to make the effective and efficient use of these commodities. Generally, disaster response activities are divided into the four phases that come from the “disaster cycle”: (a) mitigation, (b) preparedness, (c) response, (d) recovery (or rehabilitation) [1]. In this study, our work mainly focuses on the multi-commodity redistribution process, which belongs to the latter part of response phase.

At the beginning of the multi-commodity redistribution process, the quantities for each kind of commodities are estimated and considered uncertain at relief centers. For each kind of commodities, some relief centers may be considered as demand relief centers while others are considered as supply relief centers. In addition to demand and supply uncertainties, another uncertain element is the availability of transportation network [2]. Tasks to redistribute surplus commodities to demand relief centers and to deliver these commodities over the transportation network are very difficult to complete under those uncertainties. Against the backdrop of uncertainties, the aim of this paper is to present this multi-commodity redistribution problem with stochastic elements and understand it using the mathematical programming.

Clark and Culkin [3] summarized three principles that were used to define humanitarianism: humanity, impartiality and neutrality based on some earlier research [4, 5]. In this study, the fairness in the multi-commodity redistribution process is taken into account. In addition to the fairness, we introduce another principle, the timeliness, because these commodities should be delivered as quickly as possible.

The rest of this paper is organized as follows. Section 2 reviews the previous research that are related to stochastic programming models for both commodity distribution and redistribution. Section 3 provides a problem description of concern in this study. A two-stage mixed-integer stochastic programming model is presented in Sect. 4. The solution method is provided in Sect. 5. Then, a numerical analysis and computational results are presented and discussed in Sect. 6. Finally, Sect. 7 concludes this study with contributions and further directions.

2 Literature Review

Humanitarian logistics research has attracted growing attention as the human suffering caused by disaster events continues to increase. We reviewed the prior studies about disaster management that focus on the commodity distribution problem and paid careful attention on how to handle uncertainty in the humanitarian logistics using scenario-based approaches.

Many studies mainly surveyed on the treatment of uncertainty in humanitarian logistics for disaster management [2, 6]. Several studies [1, 7,8,9] emphasized that a suitable model for post-disaster humanitarian logistics should address human suffering, at least through a proxy measure, instead of only focusing on the monetary objective of commercial logistics. Various mathematical programming methods have been proposed for analyzing the humanitarian logistics problems considering fairness and equity.

Stochastic programming models are widely used and have been successfully applied to handle uncertain elements in humanitarian logistics. We reviewed some stochastic programming models with a single commodity. Jia et al. [10] proposed several models with solution approaches to determine facility locations of medical suppliers in response to a large-scale emergency disaster, which addressed the demand uncertainty and medical supply insufficiency.

Humanitarian logistics usually involves multiple kinds of commodities and multiple stages of relief operations. Under these considerations, a number of multi-stage and multi-commodity stochastic programming models has been developed to handle humanitarian logistics problems. Rawls and Turnquist [11] presented a two-stage stochastic mixed-integer programming model that provided a pre-positioning strategy for hurricanes or other disaster threats considering uncertain demand. Noyan et al. [12] developed a two-stage stochastic programming model that incorporated the hybrid allocation policy to achieve high levels of accessibility and equity simultaneously, while demand and network-related uncertainties were considered through a finite set of scenarios. Zhou et al. [13] designed a multi-objective optimization model for a multi-period dynamic emergency resource scheduling problem. The objectives were to minimize unsatisfied demand of affected points with the purpose of satisfying the demand of people in disaster areas, and to minimize the risk of choosing the damaged road to guide the rescue team to select appropriate and efficient roads. Caunhye et al. [14] proposed a two-stage location-routing model with recourse for integrated preparedness and response planning under uncertainty, where the locations of warehouses and their inventory levels were determined in the first stage, and transshipment quantities, delivery quantities, and vehicle routes were determined for every scenario of uncertain realization in the second stage.

These previous studies depict that multi-stage stochastics programming models can handle uncertain elements efficiently in humanitarian logistics. And little research concerning multi-commodity redistribution process has been conducted in the past. Lubashevski et al. [15, 16] implemented the required redistribution of vital resources between the affected and neighboring cities in the disaster area, which did not consider uncertainty. In comparison with the previous models, we study the multi-commodity redistribution process, considering three uncertain elements, which are transportation network, supply and demand. This study proposes a two-stage mixed-integer stochastic programming model for this multi-commodity redistribution problem. In the first stage, the goal is to minimize the total dissatisfaction cost for all relief centers. In the second stage, we try to minimize the total transportation time. The decisions at the second stage are subject to the decisions in the first stage [17,18,19,20].

3 Problem Description

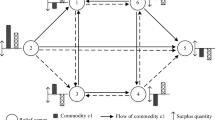
A transportation network which consists of a number of roads and relief centers is considered in this study. A set of commodities has been delivered to these relief centers before the disaster. Upon the disaster, surplus commodity at some relief centers needs to be shipped to other relief centers to satisfy unmet demand. Due to the uncertainty in disastrous situations, we do not know who will need how much of which commodities. It makes the surplus and the demand at relief centers uncertain. In addition, the availability of transportation network may be uncertain because the roads may be damaged or destructed in the disaster area. A vehicle depot is the place to store multiple types of vehicles, which are used to deliver these commodities between relief centers.

To take these uncertainties into account, we propose a two-stage mixed-integer stochastic programming model based on a scenario-based approach. In the first stage, we capture the uncertainties in demand and supply by representing each of them in terms of a number of discrete realizations of stochastic quantities that constitute distinct scenarios. Here, a specific realization of an uncertain element is called a scenario. For each kind of commodities in a demand or supply relief center, we have a set of scenarios \( \varXi \). For a particular scenario \( \xi \in \varXi \), there is a probability of occurrence \( \uppi(\xi ) \), such that \( \uppi\left( \xi \right) > 0 \) and \( \mathop \sum \nolimits_{\xi \in \varXi }\uppi\left( \xi \right) = 1 \). In the second stage, similarly, three transportation network availabilities (scenarios) with different probabilities are considered. According to the previous descriptions, some main assumptions are made.

  1. (1)

    Both the levels of supply and demand for each kind of commodities are uncertain. The supply and demand commodity quantities are consecutive integer numbers (scenarios) with equivalent probabilities in each of relief centers.

  2. (2)

    Roads can be damaged in different degrees, which leads to uncertain availability of the transportation network.

  3. (3)

    Types of vehicles have different capacities and speeds, which are allowed to deliver mixed commodities. Each vehicle cannot be used more than once.

4 Stochastic Programming Model

The notations used in this model are as follows:

Sets

Set of stages, indexed by

\( {\mathcal{R}} \)

Set of relief centers

Set of supply relief centers, indexed by

\( {\mathcal{D}} \)

Set of demand relief centers, indexed by

\( {\mathcal{E}} \)

Set of commodities, indexed by \( e \in {\mathcal{E}} \)

Set of vehicle types, indexed by

\( \varXi \)

Set of scenarios, indexed by \( \xi \in \varXi \)

Deterministic parameters

\( AS_{es}^{min} \)

The minimal quantity of commodity \( e \) should be transported out from relief center \( s \)

\( AS_{es}^{max} \)

The maximal quantity of commodity \( e \) can be transported out from relief center \( s \)

\( AD_{ed}^{min} \)

The minimal quantity of commodity \( e \) should be transported to relief center \( d \)

\( AD_{ed}^{max} \)

The maximal quantity of commodity \( e \) can be transported to relief center \( d \)

\( M \)

A big positive number

\( AN^{l} \)

Available number of vehicle type \( l \)

\( W^{e} ,V^{e} \)

Weight and volume of commodity \( e \)

\( C^{lw} ,C^{lv} \)

Weight and volume capacities of vehicle type \( l \)

\( Z^{s} ,Z^{d} \)

The size of relief center \( s \) and \( d \)

\( D_{sd} \)

Distance between relief centers \( s \) and \( d \)

\( VS^{l} \)

Travel speed of vehicle type \( l \)

\( LU^{l} \)

Loading and unloading time of vehicle type \( l \)

Stochastic parameters

\( r_{sd} (\xi ) \)

Availability of road between relief centers \( s \) and \( d \) in scenario \( \xi \)

\( p_{sd} (\xi ) \)

Probability of occurrence for \( r_{sd} (\xi ) \)

\( oc_{s}^{e} (\xi ) \)

Outgoing quantity of commodity \( e \) at relief center \( s \) in scenario \( \xi \)

\( ic_{d}^{e} (\xi ) \)

Incoming quantity of commodity \( e \) at relief center \( d \) in scenario \( \xi \)

\( p_{d}^{e} (\xi ) \)

Probability of occurrence for \( ic_{d}^{e} (\xi ) \)

\( p_{s}^{e} (\xi ) \)

Probability of occurrence for \( oc_{s}^{e} (\xi ) \)

Decision variables in the first stage

\( ad_{s}^{e} \)

The expected amount of commodity \( e \) delivered in relief center \( s \)

\( ar_{d}^{e} \)

The expected amount of commodity \( e \) received in relief center \( d \)

Decision variables in the second stage

\( w_{sd}^{e} (\xi ) \)

Amount of commodity \( e \) delivered from \( s \) to \( d \) in scenario \( \xi \)

\( n_{sd}^{le} (\xi ) \)

Number of vehicle type \( l \) used to deliver commodity \( e \) from \( s \) to \( d \) in scenario \( \xi \)

\( n_{sd}^{l} (\xi ) \)

Number of vehicle type \( l \) from \( s \) to \( d \) in scenario \( \xi \)

In the proposed model, the objective is to minimize the total dissatisfaction cost (\( \varPsi_{1} \)) plus the expected value of the second stage objective function (total transportation time).

$$ {\text{Min}}\,\varPsi_{1} + E_{\xi } [Q\left( {ar_{d}^{e} ,ad_{s}^{e} ,\xi } \right)] $$
(1)

The completed formulation is given as the following two-stage mixed-integer stochastic programming model. In the first stage (\( {\mathcal{F}}1 \)), for the set of scenarios, we model the stochastic programming as a deterministic optimization problem, by expressing the expected value \( \varPsi_{1} \) as follows:

(2)

Subject to:

(3)
(4)
(5)
(6)
(7)
(8)
$$ AD_{ed}^{min} \le ar_{sd}^{e} \le AD_{ed}^{max} \quad \forall d \in {\mathcal{D}},e \in {\mathcal{E}}. $$
(9)
(10)
(11)

The objective function (2) aims to minimize the total dissatisfaction cost considering the relief center size, unmet demand and oversupply of commodity in the relief center. Constraint (3) guarantees the balance of outgoing and incoming for each kind of commodities for all the relief centers. Constraint sets (4)–(7) guarantee that the dissatisfaction costs of relief center \( s \) and \( d \) are positive numbers. Constraints (8) and (9) define the constraints of variables. Constraints (10) and (11) are auxiliary binary variables. After that, we can solve the second stage problem after we obtain the decision variables from the first stage [19]. So, the second stage problem can be written as:

(12)

Subject to:

(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)

The objective function (12) is to minimize the total transportation time. Constraint (13) ensures that the total incoming shipment from relief center \( s \) should be bigger than or equal to the demand in relief center \( d \). Constraint (14) ensures the total outgoing shipment from relief center \( d \) cannot exceed the quantity of commodity in relief center \( s \). Constraint (15) guarantees the transportation balance between relief centers \( s \) and \( d \). Constraints (16) and (17) restrict that assigned vehicles should be able to deliver the mixed commodities. Constraint (18) ensures that the total number of vehicles cannot exceed the total available quantity. Constraints (19) and (20) are nonnegative constraints of variables.

5 Solution Method

Before we get the optimal solution of the second stage problem, we can calculate the best upper bound \( \varPsi_{2}^{ *} \). The upper bound \( \varPsi_{2}^{ *} \) can be found by generating a feasible solution using the model \( U_{P} \), where a vehicle carry only one kind commodity. The upper bound model \( U_{P} \) is written as:

(21)

Subject to:

$$ (13){-}(15),(20). $$
(22)
(23)
(24)
(25)
(26)

where objective function (21) aims to minimize the total transportation time. Constraints (23) and (24) guarantee that the assigned vehicles are able to deliver commodity \( e \). Constraint (25) restricts the available number of vehicles. Constraint (26) is nonnegative constraint. However, decision variable \( n_{sd}^{l} (\xi ) \) can be reduced by allowing the vehicle to deliver mixed commodities. Then, the second stage problem can be re-written as:

(27)

Subject to:

$$ (18)\;\text{and}\;(19). $$
(28)
$$ \varPsi_{2} < \varPsi_{2}^{ *} . $$
(29)
(30)
(31)
(32)
(33)
(34)

where objective function (27) aims to minimize the total transportation time under the upper bound \( \varPsi_{2}^{ *} \) (29). Constraints (30) and (31) ensure the capability of vehicles cannot exceed the upper bound of solution in model \( U_{P} \). Constraints (32) and (33) restrict that assigned vehicles are able to deliver the mixed commodities. Constraint (34) is nonnegative constraint.

6 Numerical Analysis

To illustrate the effectiveness of the proposed solution approach, a numerical analysis is carried out and related results are reported in this section. 10 relief centers, 4 kinds of commodities (water, food, tents and medicine) and 2 vehicle types (small and big vehicles) are considered. Relief center size is an integer number randomly generated in the interval \( [20, 50] \). The minimal and maximal values that denote the quantities of demand and supply commodity are integer numbers multiplied by 10 and drawn from the intervals \( [0, 5] \) and \( [8, 12] \), respectively. Each kind of commodities has two characteristics which are weight and volume for per unit of commodity. Then, we have the weights \( 1.5, 1.0, 1.5 \;{\text{and}}\; 1.0 \), and the volumes \( 1.0, 2.0, 2.0\;{\text{and}}\; 2.0 \) for each kind of commodities, respectively. Two vehicle types with different weight and volume capacities are considered, which are \( 20 \;{\text{and}}\; 30 \), and \( 26 \;{\text{and}}\; 40 \) for small and big vehicles, respectively. Besides, different loading and unloading time \( 3\;{\text{and}}\; 5 \) are considered for the small and big vehicles respectively. And travel time is related to the vehicle speeds, which are 0.2 and 0.125 for small and big vehicles, respectively. In this instance, three different road availabilities in the transportation network are considered with probabilities 0.5, 0.3 and 0.2, respectively. The distance pairs between relief centers in each of availabilities (\( D_{sd} \cdot r_{sd} \left( \xi \right) \)) are random integer numbers generated from the intervals \( [5, 20] \), \( [20, 30] \) and \( [30, 50] \), respectively. In the first stage, the possible supply commodity quantities are consecutive integer numbers from \( AS_{es}^{min} \) to \( AS_{es}^{max} \) with probability \( 1/(AS_{es}^{max} - AS_{es}^{min} + 1) \), and the demand commodity quantities are also consecutive integer numbers from \( AD_{ed}^{min} \) to \( AD_{ed}^{max} \) with probability \( 1/(AD_{ed}^{max} - AD_{ed}^{min} + 1) \), respectively.

The main results for the first stage problem are provided in Fig. 1, which shows the minimal and maximal quantities of commodities can be delivered, and minimal and maximal quantities of commodities hope to be received. Besides, decision variables of anticipated amount of delivered and received commodity for each relief centers are also provided. Besides, for each kind of commodities, we can observe that the anticipated amount of delivered commodity is closely related to parameters \( AS_{es}^{min} \), \( AS_{es}^{max} \) and \( Z^{s} \). Similarly, the anticipated amount of received commodity is closely related to parameters \( AD_{ed}^{min} \), \( AD_{ed}^{max} \) and \( Z^{d} \).

Fig. 1.
figure 1

Optimal redistribution strategies in the first stage

Full size image

After the decision variables are obtained in the first stage, we can make the optimal set of the second stage decisions. The solution is summarized in Table 1 for the upper bound model \( U_{P} \) and the optimal model \( {\mathcal{F}}_{2} \). Besides, the results also reveal that a higher objective function value \( \varPsi_{2}^{ *} \) is obtained in the upper bound model \( U_{P} \) because of each type of vehicles carrying only one kind commodity during the transportation process. On the other hand, we can obtain a smaller objective function value \( \varPsi_{2} \) and a better solution because we improve the vehicle utilization by allowing vehicles to carry mixed commodities.

Table 1. Solution strategies of upper bound model \( U_{P} \) and second stage model \( {\mathcal{F}}_{2} \)
Full size table

7 Conclusions

This study presents a two-stage mixed-integer stochastic programming model for the multi-commodity redistribution problem. Three uncertain elements including supply, demand and transportation network are introduced into the proposed model. Besides, a numerical analysis is applied to demonstrate the applicability of the solution method for the proposed model. At the end, we can explore the problem of interests from the following aspects in future studies. It is interesting to generate multi-commodity redistribution planning considering multi-period process. Another future consideration is to extend this work to the budget-based uncertain cases. These questions will be considered in further research.