Keywords

1 Introduction

For several years, Japanese farmers’ surroundings have been drastically changed. Particularly, aging problem and globalization of food production are critical problems to give some negative impacts to Japanese agriculture. Therefore, various solution approaches to overcome these disadvantages are nowadays discussed. On the other hand, by using recent Information and Communication Technology (ICT), Japanese agriculture may have a big opportunity to change traditional system and to positively construct a new advanced system.

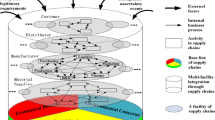
In the standard Japanese agricultural system, agricultural products were sold from farmers to a central wholesale market, to some suppliers, and finally sent to consumers. In this traditional system, it is difficult for consumers to get to know detailed production information of the purchased agricultural products. In addition, it is also difficult for farmers to get their sufficient returns sustainably. In terms of information sharing between farmers and consumers, ICT-based agricultural systems are proposed all over the world (Holzworth et al. [2], Janssen et al. [3], Wright et al. [5]). Furthermore, some agricultural information systems dedicated to Japanese agriculture were also recently developed. Particularly, Kashima et al. [4] proposed Farmer’s Information System (FIS) to improve Japanese traditional agriculture by ICT in terms of sustainable agricultural management. FIS can also adjust their farming schedule in a way that by the time they grow agricultural products, and their products are actually sought upon by consumers.

Thus, useful ICT-based agricultural systems have been proposed, but there are still few studies of quantitative and qualitative analyses of the agricultural supply chain management in terms of optimization. We [1] recently proposed a mathematical programming problem on the FIS-based agricultural system in terms of environmental load. However, our previous proposed model considered only minimizing the total discarding volume. In addition, the preferences between farmers and retailers are also not considered. In terms of sustainable development of Japanese agriculture, it is generally important to consider that both each farmer maximizes the profit and the retailers buy the needed high quality agricultural product to achieve the Win-Win relationship among them. Furthermore, a transportation cost from the farmer to the retailer is also one of the most important factors to maximize their profits. We could not introduce the transportation cost into our previous model, and do the sensitivity analysis directly. In order to achieve these objectives, we need to consider optimal matching between farmers and retailers considering their preferences.

FIS can collect POS data of the agricultural product, and hence, it is also important to formulate a sustainable agricultural supply chain with the optimal matching between farmers and retailers as a mathematical programming problem and to apply the data-driven approach based on FIS. Particularly, we consider that each farmer contracts to the retailer. The contract is that production volume of the agricultural product at the contract farmer is all shipped to the retailer, because farmer need not discard a large quantity of unsold agricultural product. On the other hand, this contract is that the burdens of retailers are increasing, and hence, in terms of risk aversion, the retailers order the cultivated filed to the contracted farmer considering consumers’ demands.

From the above-mentioned, we extend our previous agricultural supply chain model to the risk sharing and optimal matching problem by introducing contracts and preferences of both farmers and retailers, and develop the efficient algorithm to obtain the optimal ordering cultivate field at each contracted farm. By integrating this paper’s mathematical approach into FIS, an advanced agricultural system with both theoretical and practical evaluations can be constructed as an important application of this paper. In addition, in this future advanced agricultural system, both farmers and retailers will make grate efforts to raise preference levels, because to put the optimal matching each other into practice is directly related to achieve their target profits.

2 Mathematical Formulation

In terms of Win-Win relationship shown in Introduction, we focus on achieving each target profit to set all retailers and farmers as much as possible. In the case that the risk is considered as the total cost, the risk sharing is directly related to maximizing the total profit considering the cost at all farmers and retailers. We assume that n retailers purchase one agricultural product from m local farmers in terms of local production for local consumption. In order to do modeling our agricultural supply chain model, we assume the following situations.

  • The production volume of the agricultural product at each farmer is given as a random variable, and the actual production volume is all shipped to the contracted retailers.

  • Consumer’s demand at each retailer is also random variable.

  • Unsold volume at each retailer is discarded. The discarding cost is paid by each retailer.

  • The decision variable is the cultivated field of the agricultural product at each contracted farmer.

Furthermore, the following assumption is introduced to ensure the target profit of each farmer.

  • Each farmer initially sets the contract fee per cultivated field and minimum cultivated field considering the target profit.

  • The objective is to maximize the total profit of all retailers satisfying the target profit of each retailer through the multiperiod.

2.1 Notation of Parameters

(For contract farmers)

m::

Total numbers of farmers.

\( \hat{C}_{i} : \) :

Contract fee per cultivated field of the agricultural product at ith farmer. In this paper, the contract fee is the same to all retailers.

\( S_{ij} : \) :

Contract cultivated areas of the agricultural product from jth retailer to ith farmer (decision variable).

\( S_{i}^{min} : \) :

Minimum cultivated areas of the agricultural product of kth quality at ith farmer which is dependent on the contract fee. This parameter is initially set by each farmer as well as setting parameter \( C_{i} : \) according to target profit.

\( S_{i}^{max} : \) :

Maximum cultivated areas of the agricultural product at ith farmer which is the same as the total field owned by the ith farmer.

\( Q_{i} : \) :

Amount of the agricultural product per cultivated area for ith farmer. In the real-world agricultural system, \( Q_{i} \) is dependent on current weather and climate conditions, and hence, \( Q_{i} \) is assumed to be a random variable with mean value \( \bar{Q}_{i} \) and variance \( \sigma_{i}^{2} \) in this paper

(For retailers of our proposed model)

n::

Total number of retailers.

\( p_{j} \)::

Selling price of unit volume to the agricultural product at jth retailer.

\( s_{j} \)::

Shortage cost to the agricultural product at jth retailer.

\( \beta_{j} \)::

Discarding cost of unit unsold volume at jth retailer.

\( D_{j} \)::

Consumers demand to the agricultural product at jth retailer which is assumed to be a random variable with mean value \( \bar{D}_{j} \) and variable \( \hat{\sigma }_{j}^{2} \).

\( g_{j} \)::

Target profit of jth retailer

(For contract and preference between farmers and retailers)

\( z_{ij} : \) :

0-1 decision variable between ith farmer and jth retailer for the agricultural product. In the case of contract, \( z_{ij} = 1 \). Otherwise, \( z_{ij} = 0 \).

\( C_{ij} \)::

Transportation cost by a truck from ith farmer to jth retailer regardless of production volume. \( C_{ij} \) is initially set as a constant value dependent on distance between ith farmer and jth retailer. To simplify the following discussion, we assume that production volume from ith farmer to jth retailer can be all packed into the only one truck.

A::

Set of possible all matching patterns between farmers and retailers, i.e., \( \left( {i,j} \right) \in A \), \( \left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right) \).

\( A_{p} \)::

Set of preference matching patterns between farmers and retailers. This means that a retailer selects some farmers who want to buy the agricultural product and the farmer also wants to contract. For instance, retailer 3 selects farmers 1, 2, 3 and 4, and farmers 1, 3 and 4 want to contract. In this case, \( \left( {1,3} \right), \left( {3,3} \right), \left( {4,3} \right) \in A_{p} \) and \( \left( {2,3} \right) \notin A_{p} \)

Consequently, we decide the optimal decision of \( S_{ij} \) and \( z_{ij} \) derived from contracts between farmers and retailers under several uncertainties considering transportation cost and their preferences.

2.2 Mathematical Modelling of Our Proposed Model

We formulate an FIS-based agricultural supply chain model. The best cases of our proposed model are to achieve that all matchings between farmers and retailers are included in \( A_{p} \), and to maximize each total profit of all retailers.

To check the first case, we formulate the following mathematical programming problem:

$$ \begin{array}{*{20}l} {Maximize\;\sum\nolimits_{{\left( {i, j} \right) \in A_{p} }} {z_{ij} } } \hfill \\ {subject\,to\;\;R_{j} \left( \varvec{S} \right) \ge g_{j} , \left( {j = 1,2, \ldots ,n} \right)} \hfill \\ {\quad \quad \quad \quad \,\,\,S_{i}^{min} z_{ij} \le S_{ij} \le S_{i}^{max} z_{ij} , \left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right)} \hfill \\ {\quad \quad \quad \quad \,\,\,\sum\nolimits_{j = 1}^{n} {S_{ij} \le S_{i}^{max} , \left( {i = 1,2, \ldots ,m} \right)} } \hfill \\ {\quad \quad \quad \quad \,\,\,S_{ij} \ge 0, z_{ij} \in \left\{ {0,1} \right\}, \left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right)} \hfill \\ \end{array} $$
(1)

where \( R_{j} \left( \varvec{S} \right) \) is the profit function of jth retailer formulated as follows:

$$ \begin{array}{*{20}c} {R_{j} \left( \varvec{S} \right) = p_{j} \left( {\mathop \sum \limits_{i = 1}^{m} Q_{i} S_{ij} - \left[ {\mathop \sum \limits_{i = 1}^{m} Q_{i} S_{ij} - D_{j} } \right]^{ + } } \right) - \mathop \sum \limits_{i = 1}^{m} \hat{C}S_{ij} - \mathop \sum \limits_{i = 1}^{m} C_{ij} z_{ij} } \\ { - s_{j} \left[ {D_{j} - \mathop \sum \limits_{i = 1}^{m} Q_{i} S_{ij} } \right]^{ + } - \beta_{j} \left[ {\mathop \sum \limits_{i = 1}^{m} Q_{i} S_{ij} - D_{j} } \right]^{ + } } \\ \end{array} $$
(2)

where \( \left[ x \right]^{ + } = { \hbox{max} }\left\{ {x,0} \right\} \). In problem (1), the first constraint is for each retailer, and the second and third constraints are for each farmer. This problem is a 0-1 nonlinear and stochastic programming problem, because it includes some max functions \( \left[ x \right]^{ + } \) and random demands and production volume, and hence, it is impossible to solve problem (1) directly.

In the real-world situations to apply our proposed FIS, it is important to deal with our proposed model efficiently as well as to obtain the optimal solution. Actually, numerical datasets of demands and production volume can be collected by FIS. Therefore, we introduce a data-driven approach called a scenario-based approach to our proposed model. We consider the following S scenarios derived from FIS:

$$ \begin{array}{*{20}c} {\varvec{D} \to \varvec{d}_{s} = \left\{ {d_{1s} ,d_{2s} , \ldots ,d_{nS} } \right\},\,\varvec{Q} \to \varvec{q}_{s} = \left\{ {q_{1s} ,q_{2s} , \ldots ,q_{ms} } \right\}} \\ {{ \Pr }\left\{ {\varvec{D} = \varvec{d}_{s} {\bigcap }\varvec{Q} = \varvec{q}_{s} } \right\} = \frac{1}{S}, \left( {s = 1,2, \ldots ,S} \right)} \\ \end{array} $$
(3)

Using these scenario data and considering expected value of \( R_{j} \left( \varvec{S} \right) \), we equivalently transform expected value E \( \left[ {R_{j} \left( \varvec{S} \right)} \right] \) as follows:

$$ \begin{array}{*{20}l} {E\left[ {R_{j} \left( \varvec{S} \right)} \right]} \hfill \\ { = \frac{1}{S}\left( {p_{j} \left( {\sum\nolimits_{i = 1}^{m} {q_{is} S_{ij} - \xi_{ijs} } } \right) - \sum\nolimits_{i = 1}^{m} {\left( {\hat{C}_{i} S_{ij} + C_{ij} z_{ij} } \right)} - s_{j} \eta_{ijs} - \beta_{j} \xi_{ijs} } \right),} \hfill \\ {\xi_{ijs} \ge \sum\nolimits_{i = 1}^{m} {q_{is} S_{ij} - d_{js} , \xi_{ijs} \ge 0,\,\eta_{ijs} \ge d_{js} - \sum\nolimits_{i = 1}^{m} {q_{is} S_{ij} , \eta_{ijs} \ge 0} } } \hfill \\ \end{array} $$
(4)

From transformation (4), problem (1) can be also transformed into a standard 0-1 linear programming problem, and hence, it is not difficult to solve 0-1 linear programming problems even if the number of decision variables is much increasing.

Furthermore, in the optimal solution, if all contracts between farmers and retailers are included in \( A_{p} \), it may be possible to improve the profit of each retailer. Therefore, we consider the following auxiliary problem:

$$ \begin{array}{*{20}l} {Maximize \,\lambda } \hfill \\ {subject\,to \,E\left[ {R_{j} \left( \varvec{S} \right)} \right] - g_{j} \ge \lambda , \left( {j = 1,2, \ldots ,n} \right)} \hfill \\ {\quad \quad \quad \quad \,\,\,\sum\nolimits_{{\left( {i, j} \right) \in A_{p} }} {z_{ij} = z^{*} } } \hfill \\ {\quad \quad \quad \quad \,\,\,S_{i}^{min} z_{ij} \le S_{ij} \le S_{i}^{max} z_{ij} , \left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right)} \hfill \\ {\quad \quad \quad \quad \,\,\,\sum\nolimits_{j = 1}^{n} {S_{ij} \le S_{i}^{max} } , \left( {i = 1,2, \ldots ,m} \right)} \hfill \\ {\quad \quad \quad \quad \,\,\,S_{ij} \ge 0, z_{ij} \in \left\{ {0,1} \right\}, \left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right)} \hfill \\ \end{array} $$
(5)

where \( z^{ * } \) is the optimal value of problem (1). This problem is also transformed into a 0-1 linear programming problem. Consequently, our proposed model with FIS will be useful in terms of real-world application, because all mathematical programming problems can be efficiently solved using optimization solvers.

3 Numerical Example

We provide the following simple dataset with 4 farmers and 3 retailers. To simplify the mathematical programming problem, shortage cost \( s_{j} \) and discarding cost \( \beta_{j} \) at all retailers are the same as \( s_{j} = 10, \beta_{j} = 5 \), respectively. Furthermore, \( A_{p} \) is initially set as {(1,1), (3, 1), (4, 1), (1, 2), (3, 2), (3, 3), (4, 3)} based on questionnaires among all farmers and retailers.

From this optimal cultivated areas \( S_{ij} \) as shown in Table 1, preferences between farmers and retailers defined by \( A_{p} \) are held satisfying the target profits of all retailers.

Table 1. Dataset and optimal solution of farmers and retailers.
Full size table

4 Conclusion

This paper proposed mathematical modelling for agricultural supply chain management under several uncertainty in terms of sustainability and preferences. Using the data-driven approach based on FIS, the proposed problem is transformed into a 0-1 linear programing problem. Therefore, it is possible to solve the large-scale problems using our modelling and solution approach in the real-world agricultural system.