Functional Thinking: The History of a Didactical Principle

Abstract

Establishing the habit of functional thinking in higher maths education was one of the major goals of the Prussian reform movement at the beginning of the 20th century. It had a great impact on the German school system. Using examples taken from contemporary schoolbooks and publications, this paper illustrates that functional thinking did not mean teaching the concept of function as we understand it today. Rather, it focusses on a specific kinematic mental capability that can be described by investigating change, variability, and movement.

The Prussian Meraner Lehrplan (Meran curriculum) first called for education in functional thinking as a requirement of teaching mathematics in high schools in 1905. Henceforth it became a widely accepted motto of the reform movement in Germany and elsewhere (Hamley 1934). What then did Felix Klein and his contemporaries mean by this concept?

Firstly, this paper outlines the objectives of the Meraner Lehrplan. Secondly, it illustrates how functional thinking focussed on a specific habit of thinking with examples from contemporary representative textbooks and mathematical journals for teachers. Furthermore, functional thinking emerged in the Meraner Lehrplan as a guiding category for teaching mathematics in order to concentrate, unify and structure different areas of mathematics taught in schools. It marks an important stage in the development of so-called fundamental ideas (fundamentale Ideen), a didactical category that is now widely used in German-speaking countries. This paper pays particular attention to the practical work of mathematics teachers—contemporaries of Felix Klein—highlighting their efforts in developing subject-related teaching methods. This paper will demonstrate that education in functional thinking was connected with the idea of using mental representations of mathematical concepts (Grundvorstellungen, according to vom Hofe and Blum 2016). The focus lies on the conceptual interpretation that gives it meaning (Greefrath et al. 2016).

1 The Demand for Functional Thinking in the Meraner Lehrplan, 1905

The motto “education in functional thinking” is connected to an extensive reform movement of high school mathematics at the beginning of the 20th century. In the history of mathematical teaching, this reform became known as the Kleinsche or Meraner Reform. Felix Klein is recognized as the leader of this reform movement. He succeeded in combining reform proposals of the late 19th century (see Krüger 2000; Hamley 1934, p. 49 ff.; Schubring 2007) and initiated the establishment of a teaching committee at the annual general assembly of the Society of German Researchers and Physicians (Gesellschaft Deutscher Naturforscher und Ärzte) in 1904. The committee was instructed to reform the curricula for the whole complex of mathematical and scientific education. A prime objective was to close the gap between school and university mathematics education. As one means of doing this, the reformers introduced the function concept as the central theme in school mathematics. In addition, they included elements of analytical geometry and differential and integral calculus in secondary mathematical education. Furthermore, the committee put greater emphasis on applications in school mathematics and the so-called principle of movement (Prinzip der Bewegung), referring to the Neuere Geometrie (for elements of projective geometry as the “new geometry”, see Krüger 2000, Chaps. 3.2 and 5.3).

The reformers’ resolutions were condensed in a curriculum that was presented one year later in the next general assembly in Meran. Therefore, the so-called Meraner Lehrplan was not an official national curriculum but a proposal for mathematics education in high schools from Grade 5 to Grade 13, in the classical humanistisches Gymnasium.¹ Besides Felix Klein, the university mathematician Prof. August Gutzmer and representatives of high schools such as Dr. Friedrich Pietzker and Dr. Heinrich Schotten took a great role in this reform of mathematics education (Gutzmer 1908, p. 88). Both teachers were well known in these times as they were editors of relevant mathematical journals for teachers and board members of the Verein zur Förderung des Unterrichts in Mathematik und Naturwissenschaften (Association for the Promotion of Teaching of Mathematics and Sciences, founded in 1891; shortened to Förderverein) (Fig. 3.1).

Fig. 3.1

Meran reformers: members of the teaching commission (Lorey 1938, pp. 18, 20, 26, 41)

Using the motto “education in functional thinking,” the Meraner Lehrplan not only refers to the subject-related modernisation of teaching mathematics, but also incorporated educational principles that were central in public debates at that time (Hamley 1934, p. 53; Krüger 2000, p. 168 f.; Schimmack 1911, p. 210; Schubring 2007). The efforts for alignment are already conveyed in the introduction of the Meraner Lehrplan:

It is necessary (as it is for all other subjects) to bring the course of teaching more closely in line with the natural process of mental development than has formerly been, to take preliminary mental representations everywhere into account, to establish organic connections between new insights and previous knowledge, and finally to bring the coherence of mathematical knowledge in itself as well as its relation to other educational subjects [Bildungsstoff] to mind gradually. With full recognition of the formal educational value [Bildungswert] of mathematics, it will furthermore be necessary to relinquish all unilateral and practically meaningless specialized knowledge, but rather to develop as far as possible the faculty for contemplating natural phenomena from a mathematical point of view. Two special tasks arise from here: the development of the ability of space perception and education in the habit of functional thinking. (Gutzmer 1908, p. 104; own translation, for original see Appendix 1)

In this preface, a psychological principle is described, as the students’ mental development should be taken into account with regard to teaching mathematics. Special emphasis is placed on the role of previous knowledge and mental representations of mathematical concepts. With regard to functions and differential calculus, this psychological principle will be concretised in Sects. 3.2.1 and 3.3. In German-speaking countries, this idea of mental mathematical representations was developed later into the didactic category of Grundvorstellungen (see vom Hofe and Blum 2016) in the tradition of Stoffdidaktik (subject matter didactics).

The demand for developing “as far as possible the faculty for contemplating natural phenomena from a mathematical point of view” (Gutzmer 1908, p. 104) can be attributed to earlier reform attempts.² This “utilitarian principle” was associated with the plea for better introduction of applications in mathematical education that was recommended by the Förderverein at its inception. Students should thereby learn to contemplate “the mathematical in phenomena from their environment” instead of applying mathematics to artificial contexts (Braunschweiger Beschlüsse 1891; see Lorey 1938, p. 243). Functions and differential and integral calculus had proven themselves to explore motion and change as well as methods of analytical geometry.

The preface to the Meraner Lehrplan emphasised the didactical principle in mathematics teaching of requiring greater coherence of mathematical knowledge per se as well as greater coherence in relation to other educational subjects (Bildungsstoff). The recognized mathematical educationalist Walther Lietzmann later characterised it as a concentration principle (Konzentrationsprinzip), as this demand leads to the concentration of the whole of school mathematics to one “unified basic idea,” the concept of function “in the guise of algebra or arithmetic.”

They saw an essential demand in concentrating all of the subjects of the curriculum to one thought. The various mathematical branches that needed to be covered at school were supposed to be reconciled to one unified basic idea…

The Meraner Lehrplan chose the function concept as a binder. This concept had caught on in the guise of algebra or arithmetic and was not foreign to schools.… But the systematic enforcement of whole school mathematics on the basis of this idea was missing. (Lietzmann 1926, p. 231; own translation, for original see Appendix 2)

When characterising the “concentration principle,” Lietzmann does not speak of functional thinking but of the function concept as a “binder” (Bindemittel) that unifies different branches of school mathematics such as geometry, arithmetic, and algebra. In his main work, Methodik des mathematischen Unterrichts, Lietzmann describes the idea of concentrating and unifying the subject matter of school mathematics as an important didactical achievement of the Meran reform movement. He was a close confidant of Felix Klein and popularised the function concept through numerous textbooks and writings on mathematics teaching. Revised editions of his renowned Methodik have been published in Germany until as late as 1985. This may explain why the idea of concentrating and unifying the subject matter in mathematics education has remained influential until the present day.

From the present point of view, functional thinking as a “unifying principle” or “concentration principle” can be described as a prototype of a fundamental idea (Fundamentale Idee; Krüger 2000, Chap. 9.4). Vohns (2016) describes fundamental ideas as a guiding category of mathematical teaching. Up to the present, no other fundamental idea (such as symmetry, approximation, measure, and algorithm) has caused so many discussions about its importance for educational issues.

The demand for “education in the habit of functional thinking” has been attributed as a “special task” and a consequence of the aforementioned didactic, utilitarian, and psychological principle. “Functional thinking” in the Meraner Lehrplan does not mean a habit of thinking with respect to the function concept in arithmetic teaching only, rather it applies to mathematical education overall. Therefore, formal mental training remained the main objective of higher mathematics education. However, the adjective “functional” indicates a shift: In contrast to the traditional goal of mathematics instruction of “formation of logical thinking” with a focus on classical Euclidean geometry, functional thinking implied material aspects such as the selection and organisation of subject matter. Under the new programmatic principle, “education in the habit of functional thinking,” isolated mathematical topics and methods of problem solving that were based on special techniques were excluded from the curriculum. Some subjects, such as “unilateral and insignificant special knowledge” in the fields of teaching equations and trigonometry (see quote from Gutzmer [1908] in Sect. 1) were considered as expandable by the Meran reformers. The remaining and newly added topics were organised to align with the principle of “education in the habit of functional thinking.” But what did the Meran reformers around Felix Klein mean by this principle?

2 Education in the Habit of Functional Thinking in Arithmetic, Algebra, and Geometry

During his lecture “Die Meraner Vorschläge in der Praxis des mathematischen Unterrichts” at the general meeting of the Förderverein in 1909, Schotten characterised the principle of functional thinking as follows:

Considering functional thinking first, it has not always been understood as it was meant to be. It is about making students aware of the variability of quantities in arithmetic or geometric contexts and of their shared dependence and mutual relationship, and getting them accustomed to observing the “vitality” of quantities and to engaging in contemplating the “variable”. (Schotten 1909, p. 97; own translation, for original see Appendix 3)

Education in functional thinking soon became a motto of the reform movement at that time, as it was referred to as a coherent and universally agreed-upon principle. This consensus was pointed out by the Austrian philosopher and professor of pedagogy Alois Höfler in his book Didaktik des mathematischen Unterrichts:

As one of the two content-related aims of the Meran proposals, “functional thinking,” gained universal and unreserved approval, the general thesis does not need to be proven, but proposals for its didactical effective realisation are required. (Höfler 1909, p. 19; own translation, for original see Appendix 4)

In fact, one can find many didactic and methodical instructions on how to realise functional thinking in mathematical education in the form of exercises or teaching materials. In the following, this comprehension of functional thinking is presented by giving extracts of curricula from that time and representative textbook exercises from the main areas of secondary mathematics education at that time: arithmetic (including algebra) and geometry. Therefore, textbooks that have been specially designed in the “spirit of the Meran reform movement” (Schimmack 1911, Chap. C.4; Hamley 1934, pp. 86–89) are used to exemplify what the reformers around Felix Klein meant by using functional thinking as a means of unifying these areas of school mathematics.

2.1 Functional Dependencies in Arithmetic and Algebra Teaching

Education in the habit of functional thinking began to be prepared in Grade 7 (Quarta). By evaluating and interpreting algebraic expressions such as terms and exploring functional aspects of formulas, students would practice functional thinking. The following exercises are taken from textbooks of teachers who actively supported the Meran reform (Schwab and Lesser 1912, Chap. IA, Behrendsen and Götting 1911, III. Sects. § 5, §10, §18, §22).

Fig. 3.2

Graphs of linear functions: How does the position of the line in the coordinate system change when “Factor 2” or “Summand 1” are varied? (Malsch et al. 1929, p. 89)

Fig. 3.3

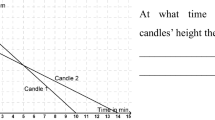
Graphical train schedule of the route Northeim–Münden in winter 1906/7 (Klein and Schimmack 1907, p. 35)

• Which value does the term s = a + b have for a = 6, b = 3, … ?

• Which values do n = a + b · c and m = (a + b) · c have for a = 2, b = 3, c = 4, …?

This approach is comparable with recent teaching methods when introducing algebra at schools. The above mentioned Grundvorstellungen of variables (Einsetzungsaspekt and Veränderlichenaspekt) refer to the first steps towards teaching the variable and the function concept (Malle 1993, p. 46 ff.).

From Grade 9 (Obertertia) up to Grade 11 (Obersekunda), students were to be familiarised with different types of functions (e.g., linear, quadratic, trigonometric, exponential, logarithmic) and different representations such as equations, graphs, and tables. Graphical representations were considered very important, as they were already introduced in Grade 8 (Untertertia). Students should for example explore the effects of parameter variations (Fig. 3.2): How do variations of a parameter in a function equation affect the location and shape of the graph? In this way, functions and their graphical representations became a central issue in high school curricula, which has remained so even to the present day. The effects of parameter variations may now be easily investigated with digital tools (Vollrath and Weigand 2007, p. 153).

In addition, graphical representations were used to solve equations and illustrate empirical functional dependencies or time functions. Distance-time graphs were used to represent motion. Figure 3.3 shows a variety of such distance-time functions in a graphical train schedule. Each graph represents a train ride. Students could learn to read these graphs to determine in which direction the train goes, which trains are faster, and what the relationship between the slope of the graph and the velocity of the train is.

From today’s point of view, it is conspicuous that the Meraner Lehrplan does not demand a formal definition of the function concept as a one-to-one correspondence of the elements of a domain and a co-domain. Instead, the curriculum refers to mutual or functional dependencies and thereby to prior conceptions of functions established during the history of mathematics. Felix Klein reflected on this pedagogical decision later in his famous book Elementarmathematik vom höheren Standpunkt:

We desire merely, that the general concept of function, according to theone or other of Euler’s understandings should permeate as a ferment the entire mathematical teaching in the secondary schools. It should not, of course, be introduced by means of abstract definitions, but should be transmitted to the student as a living possession, by means of elementary examples, such as one finds in large number in Euler. (Klein 1933, p. 221)

These conceptions of functions were considered more adaptable to the main application contexts (predominantly mechanics) as they were connected to the exploration of “variation behaviour” (Änderungsverhalten according to Vollrath und Weigand 2007, p. 140). A coherent view of different types of functions was not developed until Grades 11 and 12 (Prima). Functions were then regarded as “a whole” and mutual dependencies and motion could be explored by methods of calculus (see Sect. 3.3).

Fig. 3.4

Triangle transformations from Treutlein (1911, Appendix)

2.2 The Principle of Movement and Functional Thinking in Geometry

In the geometry part of the Meraner Lehrplan one can also find instructions on how to familiarise students with functional thinking.

This habit of functional thinking should be cultivated also in geometry by perpetually exploring the changes that result from variation of length, position, or form of geometric figures such as quadrilaterals or circles. At the same time, the consideration of the occurring relationships, which can be arranged in rows by various aspects, offers an exquisite technique to the education to logical thinking. This technique is to be made advantage of as well as the consideration of transitional cases and the examination of limits. (Gutzmer 1908, p. 113; own translation, for original see Appendix 5)

By introducing the concept of moving geometric objects (Prinzip der Bewegung), the Meran reformers turned against the traditional Euclidean method of teaching geometry that had dominated mathematical education during the 19th century. The Euclidean method was criticised at that time, as it was considered to be inappropriate for the students’ mental development. It was described as “stiff” and “lifeless” on two accounts. Firstly, it followed a stiff pattern of definition, theorem, and proof. Secondly, the Euclidian method was seen as a stiff mathematical proof technique making use of congruencies. The intent of focussing constantly on functional thinking was to invigorate geometry teaching.

At the beginning, the focus was on mobilising whole figures or parts of figures in order to make underlying measures and location relations emerge: How do changes in size and position of single parts affect the characteristics of a whole figure? Moveable figures should be increasingly represented in the mind when exploring functional dependencies. Considering previous Euclidean methods, activities involving Flächenverwandlungen (transformation of geometric figures where the area remains invariant) were very popular. The following invariants are fundamental for teaching the subject of areas: If base and height of parallelograms and triangles are both of equal length, the areas are also equal. In his book Der geometrische Anschauungsunterricht, Treutlein (1911) emphasises Gestaltveränderungen (changes of geometric shape), for which he provided various exercises that included sequences of illustrations. In addition, a draft of a student’s workbook based on Treutlein’s proposal for geometry teaching was published as an appendix. The following geometric constructions show different triangles that are built by holding the base and varying one point of the triangle along a parallel to the basis. In Fig. 3.4 one can find dashed lines illustrating that the area of a triangle is based on the one for a parallelogram. These sketches make clear that Treutlein used the movement of geometrical forms by showing them merging into each other or originating from each other. By considering geometric figures in a functional way and studying their varying structures, one could explore whether features remain invariant or change systematically.

In the years that followed, many teaching materials that realised the demand for movement by mechanical techniques or animated illustrations were developed. Other teachers came up with mathematical films, flicker books (geometrische Kinohefte; see Fig. 3.5), and mechanical models with joint mechanisms (Krüger 2000, Chap. 7.5, Kitz). Thereby the students reinforce their functional imagination. From a contemporary point of view, access to the subject matter was provided through all of Bruner’s (1974, p. 16 ff.) modes of representation: enactive, iconic, and symbolic. Nowadays, the exploration of moveable figures may be facilitated by digital tools such as dynamic geometry systems.

Fig. 3.5

Geometric flicker book visualising moving figures (Detlefs 1913, p. 39)

The Meraner Lehrplan proposed that transitional cases should be explored, for example, when introducing triangles. Both equilateral and right-angle triangles as a transitional case to the family of triangles are presented in Fig. 3.4. Other examples are variations in shape of quadrilaterals such as squares and rectangles as limit cases to rhombuses and parallelograms. By exploring these Gestaltverwandlungen, the notion of limit should be prepared in a geometrically vivid way. Taking into account these geometric proposals for education in functional thinking, the habit of mind can be characterised as kinematic and flexible.

3 Functional Thinking and Mental Representations in Differential Calculus

The new subject matter about differential and integral calculus was not supposed to act as additional theme on top of the curriculum. Rather, an “organic” structure of school mathematics would be realised by underlining calculus as a culmination of higher mathematical education. Thinking in variations and functional dependencies should be practiced and made more flexible in order to prepare for learning calculus. Education in the habit of functional thinking can therefore be considered as an attempt to establish a propaedeutic of calculus in high schools.

The Förderverein’s vote about this issue ended in a draw. Friedrich Pietzker, who was the association’s chairman, claimed that calculus was only described as an optional subject within the Meraner Lehrplan.

Coherent consideration of the functions that have hitherto occurred with respect to trends in decrease or increase (possibly bringing in the notions of Differenzialquotient and integral), using numerous examples from geometry and physics, especially mechanics. (Gutzmer 1908, p. 111; own translation, for original see Appendix 6)

Pietzker doubts regarding infinitesimal calculus were not without cause.

An integration of infinitesimal calculus into school mathematics will result in teaching students another formal technique without enabling them to have a use for it. Instead of providing them further mental education, an external skill will be achieved that will be soon forgotten by all those who are not concerned with those precise sciences at a later time. (Pietzker 1904, p. 129; own translation, for original see Appendix 7)

Even a century later, procedure-orientated teaching of calculus in German high schools is being criticised (see Blum and Schmidt 2000).

The journal Zeitschrift für den mathematisch-naturwissenschaftlichen Unterricht published a column about the Meran reform movement, showcasing both supporters and opponents of the movement:

As is well known, infinite calculus contains many formulas that need to become second nature to students if mathematics education is to fulfil its purpose. As a result, there is the risk of students’ believing that the substance lies within these formulas and that knowing and applying them suffices to a mathematical qualification (Weinmeister 1907, p. 13; own translation, for original see Appendix 8).

It took another 20 years until differential and integral calculus became a compulsory topic within Richerts’ Richtlinien (1925), the new curriculum for high schools (Gymnasien) in Prussia. The Meran reformers took the chance to broaden their ideas about advanced teacher training. Summer schools (Ferienkurse) at different universities (e.g., Göttingen, Berlin, and Frankfurt a. M.; see Tobies 2000, p. 23 ff.) were offered so that high school teachers could become familiar with functional thinking and teaching infinitesimal calculus. Subject-related teaching methods were developed and set down in textbooks based on the Meraner Lehrplan. Felix Klein found support in Otto Behrendsen and Eduard Götting, two experienced teachers in Göttingen. Both were familiar with secondary mathematics education and were able to realise the reformers’ proposals. Together they developed a course in school mathematics that provided ideas about functional thinking across several grades. This course functioned as a model for the Meran curriculum (Götting 1919).

The familiarisation with functional thinking in geometry and arithmetic teaching was supposed to help close the gap between mathematics education on the university and high school levels and help make the transition from school to university less arduous. This didactical approach is realised in Behrendsen and Götting’s well known textbooks Lehrbuch der Mathematik nach modernen Grundsätzen (1911, 1912).

If students who have followed our course of instruction come to differential calculus, it will be taken for granted and as a natural consequence of the representation of functions that have been dealt with for many years up to this stage. It would be almost unnatural to follow certain dubiousness apostles’ demand for stopping at this point. Nevertheless, differential and integral calculus are based on purely empirical geometric and related real mental representations that are clear of speculations. (Behrendsen and Götting 1912, preface; own translation, for original see Appendix 9)

By taking a closer look at the following textbook extracts, the authors’ conception of teaching differential calculus in a “purely empirical” way can be illustrated. Practical experience had shown that it was difficult for students to understand the notions of limit and Differenzialquotient dy/dx (derivative of a function). The term Differenzial was found to be particularly challenging as it was characterised as an “infinitely small quantity” (ibid.). It took Behrendsen and Götting some time until these complex concepts were considered sufficiently developed from an educational point of view. Their introduction in differential calculus starts with a question that arises from generalising known characteristics of the slope of a linear function: Can the slope of any graph of a function be described by the ratio ∆y/∆x? Figure 3.6 leads to functional considerations how the slope of single small arcs varies:

Fig. 3.6

Exploring slope of secants (Behrendsen and Götting 1912, p. 232)

We simply notice that on the arc PP₁ the slope of smaller sections of this arc changes, in fact increases. When we move point P₁ closer to P up to P₂, meaning we decrease Δx₁, the chord PP₂ coincide with the arc in more detail. But this will be even more the case with PP₃, so that the quotient $\frac{{P_{3} Q_{3} }}{{PQ_{3} }}$ can be considered as the PP₃ arc’s slope quotient with greater approximation as $\frac{{P_{2} Q_{2} }}{{PQ_{2} }}$ and $\frac{{P_{1} Q_{1} }}{{PQ_{1} }}$. (Behrendsen and Götting 1912, p. 232; own translation, for original see Appendix 10)

Hereby they obtain the slope of not only a single small arc but also the slope in a certain point of a function graph. This method visualises the moving secants, with a tangent as a mentally represented limit.

It is easy to realise that accuracy increases when the points P and P₃ come closer to each other, meaning the secant P₃T approximates the characteristics of a tangent. The actual slope in a certain point of the curve is given by the direction of the tangent in the same point.… (ibid., p. 233; own translation, for original see Appendix 11)

It is remarkable that neither the tangent nor the slope of a function (by using tangents) are formally defined until this point. Instead, the authors use the mental geometrical representation of a tangent as a limit case and the idea of approximation instead. Behrendsen and Götting then provided a new function, the Steigungsfunktion (function of slopes). Therefore, they use a graphical method to obtain this function of slopes by sketching the curves’ tangents and their slopes and thereby represent the Steigungsfunktion in a graphical manner (see Fig. 3.7).

Fig. 3.7

Graphisches Differenzieren according to Behrendsen and Götting (1912, p. 235)

After providing a geometric-graphical approach to the approximation of a function’s slope, the Differenzenquozient (increment ratio) was used to find the “true” slope of a tangent by analytical means. Finally, the Differenzialquotient (derivative) was introduced as the limit of increment ratios. Thereby, an additional meaning with regard to its application in mechanics was obtained: velocity (Grundvorstellung of local rate of change) or, more explicitly, the instantaneous velocity or speed of a process (see Greefrath et al. 2016, p. 108).

These textbook extracts document that the concept of a derivative was introduced using a geometric mental representation as a tangent slope (Grundvorstellung of tangent slope; ibid., p. 109). By determining a function’s slope with the help of the limit of the secant’s slopes, Behrendsen and Götting provided an approach to the concept of derivative. This was popular in German high school mathematics for the following decades; however, it was also criticised (see Danckwerts and Vogel 2006, p. 45).

By familiarising students with functional thinking in the context of moving figures and shapes, the concept of limit was used in an informal manner in school mathematics but not established by a formal definition. This qualitative approach uses functional imaginations of limit processes as the basis for concept formation: How does the incremental ratio or slope change when the secant shifts?

The “coherent consideration of functions that have hitherto occurred with respect to trends in decrease or increase” was then established as a possibility for practicing functional thinking (Gutzmer 1908, p. 111). Graphical representations were still used to explore slopes of function graphs with the help of the Differnzialquotient (derivative).

When discussing bandy lines, determinations of maxima and minima, etc., one gets along with simple considerations of geometric sketches. The maximum, for example, is characterized by the fact that the tangent is first increasing and then decreasing afterwards. The graphical representation of the first Differenzialquotienten as a curve itself therefore is a decreasing function merging from positive to negative at the point in question. Regarding this consideration, long calculations can be avoided and functional thinking can be trained in an excellent way. (Behrendsen and Schimmack 1908, p. 21; own translation, for original Appendix 12)

Many school teachers developed concepts and materials for teaching calculus that aligned with functional thinking in the 20 years following the publication of the Meraner Lehrplan. Soon, the demand for more rigor in secondary mathematical education arose in terms of how to combine the need for scientific rigor and the respect for students’ mental capacity. In 1925, differential and integral calculus were finally introduced in the national Prussian curriculum.

By introducing infinitesimal methods, students gain knowledge about the most important tool of mathematics. It is a task of mathematical education on the one hand to steer a middle course between entitled scientific rigor and the regard to practical needs and on the other hand to use the tool of geometric visualizations extensively. (from annotations on methods for mathematics education in the 1925 Prussian directives; quoted from Lietzmann 1926, p. 263; own translation, for original see Appendix 13)

4 Conclusion

Functional thinking in the sense of the Meran reformers meant more than providing knowledge about elementary functions and techniques of calculus. “Education in the habit of functional thinking” has to be considered a certain ability to perceive and analyse the variability of quantities and their functional dependencies. It was regarded as a didactical principle for teaching mathematics in high schools that refers to the modernisation of subject matter and focusses on the concentration and unification of different branches of school mathematics. Therefore, it may be indicated as a precursor of the didactic category of fundamentale Ideen. Moreover, the attempt to build school curricula on psychological principles leads to the use of mental representations of mathematical concepts (Grundvorstellungen) emerging together with the demand for functional imagination. This idea became widely accepted and extended in German-speaking countries at the end of the 20th century. Grundvorstellungen of numerous basic mathematical concepts were elaborated at that time (such as variable, function, number, fraction, probability, derivative, and integral). The development of the subject-related didactic categories of fundamentale Ideen and Grundvorstellungen was stimulated by the challenging task of teaching calculus in high schools.

In addition to Felix Klein’s Göttingen colleagues, Behrendsen, Götting, Lietzmann, and Schimmack, dedicated mathematics teachers such as Oskar Lesser, Georg Wolff, Peter Treutlein, and many more played important roles in modernising school mathematics based on Felix Klein’s reform agenda. Without their creative application of these concepts into school curricula, the Meraner Lehrplan may not have had such an influence on high school mathematics. When highlighting Klein’s unquestionable merits in initiating and organising the Meran reform movement, the efforts of these practitioners in mathematical education should not be understated.

Appendix

• 1 Einmal gilt es (wie in allen anderen Fächern), den Lehrgang mehr als bisher dem natürlichen Gange der geistigen Entwicklung anzupassen, überall an den vorhandenen Vorstellungskreis anzuknüpfen, die neuen Kenntnisse mit dem vorhandenen Wissen in organische Verbindung zu setzen, endlich den Zusammenhang des Wissens in sich und mit dem übrigen Bildungsstoff der Schule von Stufe zu Stufe mehr und mehr zu einem bewußten zu machen. Ferner wird es sich darum handeln, unter voller Anerkennung des formalen Bilduugswertes der Mathematik doch auf alle einseitigen und praktisch bedeutungslosen Spezialkenntnisse zu verzichten, dagegen die Fähigkeit zur mathematischen Betrachtung der uns umgebenden Erscheinungswelt zu möglichster Entwicklung zu bringen. Von hier aus entspringen zwei Sonderaufgaben: die Stärkung des räumlichen Anschauungsvermögens und die Erziehung zur Gewohnheit des funktionalen Denkens.

• 2 Sie erkannten es als eine wesentliche Forderung an, den gesamten Lehrstoff um einen großen Gedanken zu konzentrieren. Das Vielerlei der mathematischen Gebiete, die auf der Schule zu Wort kommen, mußte unter eine einheitliche Grundidee gebracht werden …

  Die Meraner Vorschläge wählten als Bindemittel den Funktionsbegriff. Dieser Begriff, der ebenso im geometrischen wie im arithmetischen Gewande die gesamte Mathematik durchsetzt, war selbstverständlich der Schule vorher nicht fremd. … Was aber fehlte, war die systematische Durchdringung des gesamten Schulstoffs mit diesem Gedanken.

• 3 Was zunächst das funktionale Denken betrifft, so ist es nicht überall so aufgefaßt worden, wie es aufgefaßt werden sollte. Es handelt sich darum, die Variabilität der Größen –, seien es arithmetische oder geometrische –, ihre gemeinsame Abhängigkeit und ihren wechselseitigen Zusammenhang den Schülern zu Bewußtsein zu bringen: und sie daran zu gewöhnen, gerade auf diese ‘Lebendigkeit’ der Größen zu achten und ihr ihr Denken auf die Betrachtung des ‘Veränderlichen’ einzustellen.

• 4 Von den beiden inhaltlichen Zielpunkten der Meraner Vorschläge … hat der zweite, das ‘funktionale Denken’, so allgemeine und rückhaltlose Zustimmung gefunden, daß nicht mehr Beweise für die allgemeine These nötig, sondern nur noch Ratschläge für ihre didaktisch wirksame Durchführung erwünscht sind.

• 5 Diese Gewohnheit des funktionalen Denkens soll auch in der Geometrie durch fortwährende Betrachtung der Änderungen gepflegt werden, die die ganze Sachlage durch Größen- oder Lageänderung im einzelnen erleidet, z. B. bei Gestaltsänderung der Vierecke, Änderung in der gegenseitigen Lage zweier Kreise usw. Zugleich aber bietet die Betrachtung der hierbei auftretenden Beziehungen, die man nach mannigfachen Gesichtspunkten in Reihen ordnen kann, ein vorzügliches Mittel zur Schulung des logischen Denkens, das möglichst auszunützen ist, ebenso die Betrachtung der Übergangsfälle und die Herausarbeitung der Grenzfälle.

• 6 Zusammenhängende Betrachtung der bisher aufgetretenen Funktionen in ihrem Ge-samtverlauf nach Steigen und Fallen (unter eventueller Heranziehung der Begriffe des Differentialquotienten und des Integrals), mit Benutzung zahlreicher Beispiele aus Geometrie und Physik, insbesondere der Mechanik.

• 7 … eine Aufnahme der Systematik der Infinitesimal-Rechnung in den Unterricht [wird] im allgemeinen nur darauf hinauslaufen, den Schülern eine formelle Technik mehr beizu-bringen, ohne dass sie dadurch befähigt werden, nun mit dieser Technik gegebenenfalls viel anzufangen, statt der Erhöhung der geistigen Durchbildung, die man ihnen dadurch ver-schaffen möchte, wird eine gewisse äusserliche Fertigkeit erzielt werden, die bei allen, die nachher keine Veranlassung zur Beschäftigung mit den exakten Wissenschaften haben, bald genug vergessen werden wird.

• 8 Bekanntlich enthält die Unendlichkeitsrechnung sehr viel Formeln, die dem Schüler in Fleisch und Blut übergehen müssen, soll der Unterricht seinen Zweck erfüllen. Da liegt denn die Gefahr nahe, dass der Schüler glaubt, das Wesen des Unterrichts liege in diesen Formeln, und es genüge deren Kenntnis und ihre Anwendung zu seiner mathematischen Ausbildung.

• 9 Wenn der Schüler, der unserem Lehrgange gefolgt ist, an die Differentialrechnung ge-langt, so pflegt ihm dieselbe als etwas so Selbstverständliches und als eine so notwendige Konsequenz der seit Jahren gepflegten Funktionsdarstellungen zu erscheinen, daß es geradezu unnatürlich wäre, wollte man den Warnungsrufen gewisser Bedenklichkeitsapostel wirklich Folgschaft leisten und hier halt machen. Allerdings ist die Differential- und Integralrechnung in einer rein empirischen, von allen Spekulationen freien Weise auf geometrische und ähnliche reale Vorstellungen gestützt gegeben worden.

• 10 Wir bemerken ohne weiteres, daß auf dem Kurvenbogen PP₁ die Steigung einzelner kleinerer Teilbogen desselben wechselt und zwar in unserer Figur zunimmt. Rücken wir den Punkt P₁ naher an P heran bis P₂, d.h. machen wir … Δx₁ kleiner, so fällt schon die Sehne PP₂ genauer mit dem Bogen zusammen als vorher; noch mehr wird dies bei PP₃ der Fall sein, so daß der Quotient $\frac{{P_{3} Q_{3} }}{{PQ_{3} }}$ mit größerer Annäherung als Steigung des Bogens PP₃ angesehen werden kann als $\frac{{P_{2} Q_{2} }}{{PQ_{2} }}$ und $\frac{{P_{1} Q_{1} }}{{PQ_{1} }}$.

• 11 Es ist leicht einzusehen, daß die Genauigkeit zunimmt, wenn die Punkte P und P₃ einander näher kommen, d.h. wenn die Sekante P₃T also immer mehr sich dem Charakter einer Tangente nähert. Die wirkliche Steigung in einem bestimmten Punkte der Kurve wird somit durch die Richtung der Tangente an dieselbe in diesem Punkt gegeben, …

• 12 Bei der Diskussion krummer Linien, Bestimmung von Extremwerten usw. kommt man mit einfachen Überlegungen an geometrischen Skizzen aus. Das Maximum ist beispielsweise dadurch gekennzeichnet, daß die Tangente vorher ansteigt, nachher fällt; die graphische Darstellung des ersten Differentialquotienten selbst als Kurve ist daher an der betreffenden Stelle, eine abnehmende, vom Positiven zum Negativen übergehende Funktion. Bei dieser Behandlungsweise wird alles lange Rechnen vermieden und das funktionale Denken vor-trefflich geschult.

• 13 Durch die Einführung inifinitesimaler Methoden erhalten die Schüler Kenntnis von dem wichtigsten Werkzeug der Mathematik. Hier hat der Unterricht einen Mittelweg zu suchen zwischen berechtigten Anforderungen an wissenschaftliche Strenge und der Rücksicht auf die praktischen Bedürfnisse, und er wird das Hilfsmittel geometrischer Veranschaulichung ausgiebig benutzen müssen.